Как найти число колебаний математического маятника

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,662
  • гуманитарные
    33,654
  • юридические
    17,917
  • школьный раздел
    611,985
  • разное
    16,906

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник

Колебательное движение. Математический маятник

  1. Механические колебания
  2. Математический маятник
  3. Параметры колебаний математического маятника
  4. Задачи
  5. Лабораторная работа №4. Исследование колебаний математического маятника

п.1. Механические колебания

Кроме прямолинейного и криволинейного движения, с которыми мы уже познакомились, существует еще один вид механического движения – колебательный.

Механические колебания — это движения тел, которые в той или иной степени повторяются через определенные промежутки времени.

Примеры колебательных движений:

  • движение маятника в часах;
  • колебание автомобиля на рессорах;
  • покачивание деревьев на ветру;
  • раскачивание качели;
  • сокращения сердца и легких;
  • движение крыльев насекомых и птиц.

п.2. Математический маятник

Математическим маятником называют тело, подвешенное на длинной нерастяжимой нити, размеры которого значительно меньше длины нити.
Нить считается нерастяжимой и невесомой, а тело – материальной точкой на этой нити.

Математический маятник В положении равновесия тело (шарик) находится внизу.
Отклонение от положения равновесия называют смещением тела, обозначают буквой x и измеряют в метрах (в СИ).
Наибольшее смещение маятника от положения равновесия называют амплитудой колебаний, обозначают буквой A.
В проекции на горизонтальную ось OX смещение изменяется в интервале (-Aleq xleq A).
В положении равновесия x=0.
Если маятник после смещения в положение 1, прошел положение равновесия 2, отклонился в положение 3, опять прошел положение 2, и вернулся в положение 1, говорят, что маятник совершил полное колебание.

п.3. Параметры колебаний математического маятника

Период колебаний математического маятника – это время, за которое маятник совершает одно полное колебание. Период колебаний равен: $$ T=2pisqrt{frac Lg} $$ где (L) – длина маятника, (g) – ускорение свободного падения.
На поверхности Земли (gapprox 9,8 м/с^2)

Частота колебаний математического маятника – это количество полных колебаний, которые маятник совершает за единицу времени: $$ f=frac 1T=frac{1}{2pi}sqrt{frac gL} $$

Период и частота колебаний – взаимно обратные величины
Период в СИ измеряют в секундах, частоту – в герцах: 1 Гц=1 c-1
Формула для периода колебаний справедлива для небольших отклонений маятника (на угол порядка 15-20° от положения равновесия).

п.4. Задачи

Задача 1. Маятник совершил 3 полных колебания за 9 с. Найдите период и частоту его колебаний. Чему равна длина нити, на которой подвешен маятник (ответ дайте в см, с округлением до целых)?

Дано:
(N=3)
(t=9 c)
__________________
(T, f, L-?)
Период колебаний: (T=frac tN)
Частота колебаний: (f=frac 1T=frac Nt)
Длина нити: $$ T=2pisqrt{frac Lg}Rightarrow sqrt{frac Lg}=frac{T}{2pi}Rightarrow frac Lg=left(frac{T}{2pi}right)^2Rightarrow L=gleft(frac{T}{2pi}right)^2 $$ Подставляем: begin{gather*} T=frac 93=3 (c)\ f=frac 13 (Гц)\ L=9,8cdotleft(frac{3}{2pi}right)^2approx 2,234 (м)approx 223 (см) end{gather*} Ответ: 3 с; 1/3 Гц; 223 см

Задача 2. Математический маятник колеблется с частотой 20?тиы кГц. Найдите период колебаний и число колебаний в минуту.

Дано:
(f=20 кГц=2cdot 10^4 Гц)
(t=1 мин=60 с)
__________________
(T, N-?)
Период колебаний: (T=frac 1f)
Частота колебаний за время (t: N=ft)
Подставляем: begin{gather*} T=frac{1}{2cdot 10^4}=0,5cdot 10^{-4} (c)=50cdot 10^{-6} (c)=50 (мкс)\ N=2cdot 10^4cdot 60=1,2cdot 10^6 end{gather*} Ответ: 50 мкс; 1,2·106

Задача 3. Расстояние от улья до цветочного поля 600 м. Пчела летит за нектаром со скоростью 8 м/с и машет крылышками с частотой 440 Гц. Возвращаясь в улей с нектаром, пчела летит со скоростью 5 м/с и машет крылышками с частотой 320 Гц. Найдите разность в количестве взмахов крылышками на пути туда и обратно.

Дано:
(s=600 м )
(v_1=8 м/с)
(f_1=440 Гц)
(v_2=5 м/с)
(f_2=320 Гц)
__________________
(triangle N-?)

Время полета из улья за нектаром (t_1=frac{s}{v_1})
Количество взмахов крылышками (N_1=f_1 t_1=f_1frac{s}{v_1})
Аналогично количество взмахов на пути назад (N_2=f_2frac{s}{v_2})
Найдем каждое из (N): begin{gather*} N_1=440cdotfrac{600}{8}=33000\ N_2=320cdotfrac{600}{5}=38400 end{gather*} На пути обратно пчела с грузом делает больше взмахов. Искомая разность: $$ triangle N=N_2-N_1=38400-33000=5400 $$ Ответ: 5400

Задача 4. Определите длину математического маятника с периодом колебаний 1с, если он находится: а) на Луне ((g_л=1,6 м/с^2)); б) на Марсе ((g_м=3,6 м/с^2)). Ответ запишите в см, с точностью до десятых.

Дано:
(T=1 с )
(g_л=1,6 м/с^2 )
(g_м=3,6 м/с^2)
__________________
(L_л, L_м-?)

Длина нити: begin{gather*} T=2pisqrt{frac Lg}Rightarrowsqrt{frac Lg} =frac{T}{2pi}Rightarrowfrac Lg=left( frac{T}{2pi}right)^2Rightarrow L = gleft(frac{T}{2pi}right)^2 end{gather*} На Луне: $$ L_л=1,6cdotleft(frac{1}{2pi}right)^2approx 0,0405 (м)approx 4,1 (см) $$ На Марсе: $$ L_м=3,6cdotleft(frac{1}{2pi}right)^2approx 0,0912 (м)approx 9,1 (см) $$ Ответ: 4,1 см; 9,1 см

п.5. Лабораторная работа №4. Исследование колебаний математического маятника

Цель работы
Исследовать, от каких величин зависит период колебаний математического маятника.

Теоретические сведения
При малых отклонениях (порядка 15-20° от вертикали) период колебаний математического маятника определяется формулой: $$ T=2pisqrt{frac Lg} $$ где (L) – длина маятника, (g) – ускорение свободного падения.
Для работы принять (gapprox 9,80665 м/с^2).
При заданном периоде колебаний для длины маятника получаем: $$ L=gleft(frac{T}{2pi}right)^2 $$

Приборы и материалы
Два лабораторных грузика по 100 г, крепкая нить (1,5-2 м), линейка (30-50 см), штатив, секундомер.

Ход работы
1. Рассчитайте длину нитей, необходимых для создания маятников с периодами колебаний (T_1=1 с; T_2=2 с).
2. Закрепите один грузик на нити и подвесьте его на штативе так, чтобы длина подвеса была равна расчетной длине (L_1).
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний. Повторите опыт 5 раз. Проведите расчеты для определения периода колебаний (T_{1 эксп}) по методике, изложенной в лабораторной работе №2 (см. §4 данного справочника).
4. Теперь подвесьте грузик так, чтобы длина подвеса была равна расчетной длине (L_2). Повторите серию из 5 экспериментов и определите (T_{2 эксп}).
5. При длине подвеса (L_2) подвесьте к первому грузику второй. Повторите серию из 5 экспериментов и определите (T ‘). Сравните (T ‘) и (T_{2 эксп}).
6. Сделайте выводы о проделанной работе.

Результаты измерений и вычислений

Расчет длины нитей begin{gather*} L=gleft(frac{T}{2pi}right)^2\ T_1=1 c, L_1=9,80665cdotleft(frac{1}{2pi}right)^2approx 0,248 (м)=24,8 (см)\ T_2=2 c, L_1=9,80665cdotleft(frac{2}{2pi}right)^2approx 0,9994 (м)=99,4 (см) end{gather*}

Определение (T_{1 эксп})
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1 c)
Время 10 колебаний

№ опыта 1 2 3 4 5 Сумма
(t, c) 9,7 10,2 9,8 9,9 10,3 50
(triangle c) 0,3 0,2 0,2 0,1 0,3 1

begin{gather*} t_{cp}=frac{50}{5}=10\ triangle_{cp}=frac 15=0,2 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,2right}=0,2 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(10,0pm 0,2) c end{gather*} Период колебаний в 10 раз меньше: $$ T_{1 эксп}=frac{1}{10}(t_0pmtriangle t), T_{1 эксп}=(1,00pm 0,02) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_{1 эксп}}cdot 100text{%}=frac{0,02}{1}cdot 100text{%}=2,0text{%} $$

Определение (T_{2 эксп})
Время 10 колебаний

№ опыта 1 2 3 4 5 Сумма
(t, c) 19,7 20,1 19,8 20,2 19,7 99,5
(triangle c) 0,2 0,2 0,1 0,3 0,2 1

begin{gather*} t_{cp}=frac{99,5}{5}=19,9\ triangle_{cp}=frac 15=0,2 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,2right}=0,2 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(19,9pm 0,2) c end{gather*} Период колебаний в 10 раз меньше: $$ T_{2 эксп}=frac{1}{10}(t_0pmtriangle t), T_{2 эксп}=(1,99pm 0,02) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_{2 эксп}}cdot 100text{%}=frac{0,02}{1,99}cdot 100text{%}approx 1,0text{%} $$

Определение (T ‘) (с двумя грузиками)
Время 10 колебаний

№ опыта 1 2 3 4 5 Сумма
(t, c) 20,2 19,7 19,6 20,0 20,3 99,8
(triangle c) 0,24 0,26 0,36 0,04 0,34 1,24

begin{gather*} t_{cp}=frac{99,8}{5}=19,96\ triangle_{cp}=frac{1,24}{5}approx 0,25 end{gather*} Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,25right}=0,25 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(19,96pm 0,25) c end{gather*} Период колебаний в 10 раз меньше: $$ T’=frac{1}{10}(t_0pmtriangle t), T’=(1,996pm 0,025) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T’}cdot 100text{%}=frac{0,025}{1,996}cdot 100text{%}approx 1,3text{%} $$

Полученные на опыте интервалы для (T_{2 эксп}) и (T’) (одинаковая длина нити (L_2) и разные массы грузиков – 100 г и 200 г соответственно): begin{gather*} 1,97leq T_{2 эксп}leq 2,01\ 1,971leq T’leq 2,021 end{gather*} Таким образом, (T_{2 эксп}approx T’), т.е. период колебаний математического маятника не зависит от массы груза.

Выводы
На основании проделанной работы можно сделать следующие выводы.

В работе с помощью расчетной формулы были определены длины нитей подвеса для маятников с периодами колебаний (T_1=1 с; T_2=2 с).
Полученный на опыте период колебаний для подвеса с (L_1=24,8 см) с грузиком 100 г равен $$ T_{1 эксп}=(1,00pm 0,02) c, delta=2,0text{%} $$ Полученный на опыте период колебаний для подвеса с (L_2=99,4 см) с грузиком 100 г равен $$ T_{2 эксп}=(1,99pm 0,02) c, delta=1,0text{%} $$ Полученный на опыте период колебаний для подвеса с (L_2=99,4 см) с грузиком 200 г равен $$ T’=(1,996pm 0,025) c, delta=1,3text{%} $$ Формула (T=2pisqrt{frac Lg}) данными экспериментами подтверждена.
Период колебаний математического маятника зависит от длины подвеса и не зависит от массы грузика на подвесе.

Источник

Формулы математического маятника в физике

Формулы математического маятника

Определение и формулы математического маятника

Определение

Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Формулы математического маятника, рисунок 1

Уравнение движения математического маятника

Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]

где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $varphi (t):$

[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]

где $alpha $ — начальная фаза колебаний; ${varphi }_0$ — амплитуда колебаний; ${omega }_0$ — циклическая частота.

Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса:

[ {omega }_0=sqrt{frac{g}{l}}left(3right).]

Период колебаний математического маятника ($T$) в этом случае равен:

[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]

Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]

где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:

[varphi =frac{x}{l}left(6right).]

Максимальное значение потенциальной энергии математического маятника равно:

[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]

Максимальная величина кинетической энергии:

[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]

где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ — максимальная скорость.

Примеры задач с решением

Пример 1

Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?

Решение. Сделаем рисунок.

Формулы математического маятника, пример 1

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:

[frac{mv^2}{2}=mgh left(1.1right).]

Из уравнения (1.1) найдем искомую высоту:

[h=frac{v^2}{2g}.]

Ответ. $h=frac{v^2}{2g}$

Пример 2

Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}

Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:

[T=2pi sqrt{frac{l}{g}}left(2.1right).]

Выразим из нее ускорение:

[g=frac{4{pi }^2l}{T^2} .]

Проведем вычисления ускорения силы тяжести:

[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]

Ответ. $g=9,87 frac{м}{с^2}$

Читать дальше: формулы пружинного маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

«Мир,
в котором мы живём,

удивительно
склонен к колебаниям….

Колеблются
даже атомы,

из
которых мы состоим».

Данная
тема посвящена решению задач на математический маятник.

Задача
1.
Математический маятник совершил 30 колебаний за минуту. Найдите период и
частоту колебаний, а также длину маятника.

ДАНО:

СИ

РЕШЕНИЕ

Период колебаний можно определить по формуле

Частота колебаний рассчитывается по формуле

Период колебаний математического маятника рассчитывается
также по формуле

Преобразуем эту формулу и выразим из неё длину маятника

Ответ:
период – 2 с, частота – 0,5 Гц, длина маятника – 99 см.

Задача
2.
При уменьшении длины математического маятника на 2 см, период его колебаний
уменьшается в 1,5 раза. Найдите первоначальную длину маятника.

ДАНО:

СИ

РЕШЕНИЕ

Период колебаний математического маятника определяется по
формуле

В соответствии с этим,
составим выражения для начального и конечного периода колебаний

Т.к. период колебаний уменьшился в 1,5 раза, то получаем

Преобразуем полученную
формулу

Ответ:
3,6 см.

Задача
3.
Математический маятник, проходя нижнюю точку имеет скорость 1 м/с, а его
длина равна 20 см. Определите вертикальное отклонение маятника от положения
равновесия в момент времени t = 5 с,
если в начальный момент времени маятник находится на максимальной высоте.

ДАНО:

СИ

РЕШЕНИЕ

Поскольку в начальный момент
времени отклонение максимально, мы можем заключить, что маятник колеблется по
закону косинуса.

Запишем уравнение гармонических
колебаний в общем виде

Исходя из начального
условия, сдвиг фаз равен нулю. Очевидно, что максимальное значение y – это и есть амплитуда колебаний.

Запишем закон сохранения энергии, который выполняется для
математического маятника

Тогда

Циклическая частота
математического маятника рассчитывается по формуле

Т.к амплитуда и циклическая
частота соответственно равны

То уравнение гармонических
колебаний представленного математического маятника примет вид

А по прошествии 5 с

Ответ:
4,5 см.

Задача
4.
Шарик массой 200 г, подвешенный на нити совершает колебания. Шарику сообщили
заряд 300 мкКл и поместили всю систему в электростатическое поле, линии
напряжённости которого направлены вертикально вниз. После этого циклическая
частота колебаний увеличилась вдвое. Найдите напряжённость поля.

ДАНО:

СИ

РЕШЕНИЕ

Циклическая частота
математического маятника определяется по формуле

Сила тяжести

Электростатическая сила
равна произведению заряда и напряжённости электрического поля

В электростатике заряд – это
величина, аналогичная массе в механике. Ускорение свободного падения – это
силовая характеристика гравитационного поля, а напряжённость – это силовая
характеристика электрического поля. Поэтому, необходимо найти, так
называемое, эффективное ускорение свободного падения, в соответствии с тем,
что на маятник действует ещё и электростатическая сила

Запишем теперь выражение для
начальной циклической частоты (то есть, до сообщения шарику заряда)

Для конечной циклической
частоты

Т.к. по условию задачи

Преобразуем данную формулу и
выразим из неё Напряженность поля

 

Ответ:
1960 Н/Кл.

Задача
5.
Материальная точка на нерастяжимой нити длиной 0,3 м совершает колебания,
так что максимальный угол отклонения нити от вертикали составляет 30º.
Найдите положение материальной точки в момент времени t = 5 с
в системе отсчёта, связанной с положением равновесия. В начальный момент
времени точка находится в положении равновесия.

ДАНО:

РЕШЕНИЕ

Запишем уравнение
гармонических колебаний для каждой оси с учетом того, что сдвиг фаз равен
нулю

Очевидно, что амплитуда
равны максимальным отклонениям

Циклическая частота математического
маятника определяется по формуле

Тогда с учётом того, что

Уравнения гармонических
колебаний для каждой оси принимают вид

Тогда координаты точки через
5 с равны

Ответ:
(–4,8 см; 1,3 см).

Источник

Математический маятник

Определения и формулы математического маятника

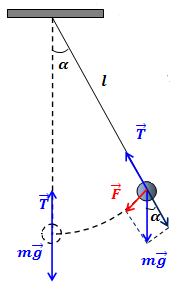
Рис.1. Математический маятник

Математический маятник – это модель системы, совершающей гармонические колебания. Свободные колебания математического маятника при малых углах отклонения описываются уравнением гармонических колебаний.

В положении равновесия сила тяжести и сила упругости нити уравновешивают друг друга, и материальная точка находится в покое. При отклонении материальной точки от положения равновесия на малый угол alpha на тело будет действовать возвращающая сила overline{F}, которая является тангенциальной составляющей силы тяжести:

    [F=mgsin alpha ]

Эта сила сообщает материальной точке тангенциальное ускорение, направленное по касательной к траектории, и материальная точка начинает двигаться к положению равновесия с возрастающей скоростью. По мере приближения к положению равновесия возвращающая сила, а следовательно, и тангенциальное ускорение точки, уменьшаются. В момент прохождения положения равновесия угол отклонения alpha =0, тангенциальное ускорение также равно нулю, а скорость материальной точки максимальна. Далее материальная точка проходит по инерции положение равновесия и, двигаясь в направлении, противоположном силе overline{F}, сбавляет скорость. В крайнем положении материальная точка останавливается, и затем начинает двигаться в обратном направлении.

Период колебаний математического маятника

    [T=2pi sqrt{frac{l}{g}} ]

Период колебаний математического маятника не зависит от массы груза и амплитуды колебаний.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник

Понравилась статья? Поделить с друзьями:
  • Форум как найти общий язык
  • Как в гугле найти гугл магазин
  • Как найти песню которую не знаешь название
  • Как найти урсофальк в суспензии
  • Как найти номер телефона зная улицу