Как найти число композиций

Разбиением числа N, как известно, является представление N в виде суммы положительных целых чисел. Например, для N = 4 получаем набор:

1. 1+1+1+1
2. 1+1+2
3. 1+3
4. 2+2
5. 4

Если речь идет о композиции числа N, то здесь имеет роль порядок слагаемых. Для того же N получаем набор:

1. 1+1+1+1
2. 1+1+2
3. 1+2+1
4. 1+3
5. 2+1+1
6. 2+2
7. 3+1
8. 4

Общее количество композиций для N равно $%2^{N-1}$%. А как быть если слагаемые должны лежать в интервале [1,K]?
Здесь приводится формула $%R(N,K)$%, но она зацикливается. Полагаю, что в ней допущена опечатка.
В общем случае получаем:

• $%R(K,K) = 2^{K-1}$%
• $%R(K+1,K) = 2^K — 1$%
• $%R(K+2,K) = 2^{K+1} — 3$%
• $%R(K+3,K) = 2^{K+2} — 8$%
• $%R(K+4,K) = 2^{K+3} — 20$%
• $%R(K+5,K) = 2^{K+4} — 48 $%
• $%R(K+6,K) = 2^{K+5} — 112$%
• ….

Представленные вычеты {3,8,20,48,112,…} образуют такую последовательность, но когда каждый раз, когда N становится кратным K происходит смещение. Вывести формулу пока не получилось.

Поэтому буду благодарен, если Вы поделитесь корректным вариантом формулы R(N,K) или литературой, где можно об этом почитать.

It’s not hard to find the generating functions, at least. Let $A$ be the set of allowable parts; then the number of compositions of $n$ into exactly $k$ allowable parts is easily seen to be

$$[x^n]left(sum_{ain A}x^aright)^k;.$$

Since

$$frac1{1-sum_{ain A}x^a}=sum_{kge 0}left(sum_{ain A}x^aright)^k;,$$

the number of compositions of $n$ into allowable parts is

$$[x^n]left(frac1{1-sum_{ain A}x^a}right);.$$

If $A=Bbb Z^+setminus{2}$, this is

$$[x^n]left(frac1{1-x-sum_{age 3}x^a}right)=[x^n]left(frac1{1-x-frac{x^3}{1-x}}right)=[x^n]left(frac{1-x}{1-2x+x^2-x^3}right);.$$

Added: This clearly implies that $a_n$, the number of allowable compositions of $n$, satisfies the recurrence

$$a_n=2a_{n-1}-a_{n-2}+a_{n-3};.$$

To derive this combinatorially, suppose that $m_1+ldots+m_k$ is a composition of $n$. If $m_1=1$, this composition is obtained by adding $1$ at the beginning of the allowable composition $m_2+ldots+m_k$ of $n-1$. Conversely, every allowable composition of $n-1$ can be extended to an allowable composition of $n$ by adding $1$ at the beginning. Thus, $n$ has $a_{n-1}$ allowable compositions that begin with $1$.

If $m_1+m_2+ldots+m_k$ is an allowable composition of $n-1$, we can also produce the composition $(m_1+1)+m_2+ldots+m_k$ of $n$, which will be allowable if and only if $m_1ne 1$. We just saw that $n-1$ has $a_{n-2}$ allowable compositions beginning with $1$, so this procedure of adding $1$ to the first term of a composition of $n-1$ produces $a_{n-1}-a_{n-2}$ allowable compositions of $n$ that do not start with $1$.

However, this procedure does not produce any composition of $n$ that begins with $3$, since that would require starting with a non-allowable composition of $n-1$. To get the allowable compositions of $n$ that begin with $3$, we must start with an allowable composition of $n-3$ and add $3$ at the beginning. There are $a_{n-3}$ such compositions, so altogether we have

$$a_n=a_{n-1}+(a_{n-1}-a_{n-2})+a_{n-3}=2a_{n-1}-a_{n-2}+a_{n-3};.$$

В
математике композиция функций
(суперпозиция функций) – это применение
одной функции к результату другой.
Композиция функций F
и G
обычно обозначается G
° F.

Определение:

Пусть 
 и 
 две
функции. Тогда их композицией называется
функция 
,
определённая равенством:

.

Свойства
композиции:

• Композиция ассоциативна:

.

• Если 
   — тождественное
  отображение на 
  ,
  то есть

,

то

.

• Если 
   —
  тождественное отображение на 
  ,
  то есть

,

то

.

Композиция
числа.

В
теории чисел композицией, или разложением,
натурального числа называется его
представление в виде упорядоченной
суммы натуральных слагаемых. Слагаемые,
входящие в композицию, называют частями,
а их количество – длиной композиции.

В
отличие от композиции, разбиение числа
не учитывает порядок следования частей.
Поэтому число разбиений числа никогда
не превосходит числа композиций.

Существует
8 композиций числа 4:

4
= 4

4
= 3 + 1

4
= 2 + 2

4
= 2 + 1 + 1

4
= 1 + 3

4
= 1 + 2 + 1

4
= 1 + 1 + 2

4
= 1 + 1 + 1 + 1

В
общем случае существует 2^n-1
композиций числа n,
из которых в точности

имеют длину k.

17.
Понятие композиции. Теорема о числе
композиций n из k частей при рi>0.

Композиции
и разбиения.
Пусть стоит задача порождения разбиения
положительного числа n в
последовательность неотрицательных
целых чисел {p₁,p₂,…,p_k}, так
чтоp₁+p₂+…+p_k=n причем
на р_i могут
накладываться различные ограничения.

Если
порядок чисел р_i важен,
то (p₁,p₂,…,p_k)
называется композицией n.
Поиск композиций ведется с ограничением р_i>0.

Если k фиксировано,
то такие композиции называются
композициями n из k частей.
При их поиске ограничение р_i>0
может сниматься, т.е. разрешается р_i=0.

Если
порядок р_i не
важен и р_i>0,
то {p₁,p₂,…,p_k}
является мультимножеством и называется
разбиением n.

Поясним
различие между композициями, композициями
из k частей
и разбиениями на следующем примере:

n=3,

композиции:
(3), (1,2), (2,1), (1,1,1),

композиции
из двух частей (р_i>0):
(1,2), (2,1),

композиции
из двух частей (р_i³0):
(0,3), (1,2), (2,1), (3,0),

разбиения:
{3}, {1,2}, {1,1,1}.

Ч
исло
композиций n из k частей с ограничением
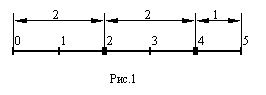
рi>0 равно .Доказательство. Представим
композицию как на рис 1 Каждая композиция
n из k частей (рi>0) соответствует способу
выбора (k-1)-элементного подмножества
точек из n-1 точек. То есть число таких
композиций равно.

18. Понятие композиции. Теорема о числе композиций n из k частей при рi0.

Понятие
композиции см. вопрос. 17

Число
композиций n из k частей,
если p_i³0
равно 
 .

Доказательство.
Каждой композиции n из k частей
при р_i³0
взаимно однозначно соответствует
двоичный набор, такой, что первое
слагаемое равно числу единиц, стоящих
перед первым нулем в наборе, второе —
числу единиц, стоящих перед первым и
вторым нулями, и т.д. Пример такого
представления композиции n=4, k=3
приведен в табл.1.

Длина
набора равна n+k-1,
число нулей равно k-1,
следовательно, число наборов (искомых
композиций) равно числу способов
выбора k-1
мест для нулей из n+k-1
мест (
 )
или тоже самое числу способов выбора n мест
для единиц из n+k-1
мест ( 
 ).

Таблица
1.

Доказательство
данной теоремы можно было также получить
путем установки взаимно однозначного
соответствия между данными композициями
и множеством всех сочетания из k элементов
по n с повторениями.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Сообщения без ответов | Активные темы | Избранное

	Количество способов разложить число в сумму (композиции) 11.12.2006, 18:57
11/12/06 1	Задача следующая: Найти количество возможных вариантов разложения натурального числа в сумму натуральных чисел. Дополнительное условие: два одинаковых ряда с разным порядком слагаемых в них считать различными. Заранее благодарен.

maxal	11.12.2006, 19:07
Модератор 11/01/06 5613

hclubmk	Re: Количество способов разложить число в сумму (композиции) 17.11.2010, 17:58
17/11/10 19	Я извиняюсь за поднятие старой темы, но вопрос касается именно этой задачи. Каково будет решение (число композиций) при условии, что слагаемые могут принадлежать диапазону, предположим от 1 до m (где m<n)? Спасибо.

maxal	Re: Количество способов разложить число в сумму (композиции) 17.11.2010, 18:49
Модератор 11/01/06 5613	Каково будет решение (число композиций) при условии, что слагаемые могут принадлежать диапазону, предположим от 1 до m (где m<n)? Производящая функция равна ( индексирует количество частей в композиции): Коэффициент при равен: Ну и остается заметить, что

hclubmk	Re: Количество способов разложить число в сумму (композиции) 17.11.2010, 21:12
17/11/10 19	maxal Спасибо за ответ. Для меня такие выкладки достаточно сложны. Я прекрасно понимаю, что Вы можете меня послать курить матчасть, но если существует такая возможность, объясните «на пальцах» (на примере), как практически применить Ваши формулы.

maxal	Re: Количество способов разложить число в сумму (композиции) 17.11.2010, 22:19
Модератор 11/01/06 5613	Я прекрасно понимаю, что Вы можете меня послать курить матчасть, но если существует такая возможность, объясните «на пальцах» (на примере), как практически применить Ваши формулы. Ну, например, на PARI/GP указанные формулы можно реализовать так: Код: ? aux(t,m) = sum(i=0,t(m+1), binomial(t-m*i,i) * (-1)^i * 2^(t-(m+1)*i) ) %1 = (t,m)->sum(i=0,t(m+1),binomial(t-m*i,i)*(-1)^i*2^(t-(m+1)*i)) ? ncomp(n,m) = aux(n,m) — aux(n-1,m) %2 = (n,m)->aux(n,m)-aux(n-1,m) ? matrix(10,10,n,m,ncomp(n,m)) %3 = [1 1 1 1 1 1 1 1 1 1] [1 2 2 2 2 2 2 2 2 2] [1 3 4 4 4 4 4 4 4 4] [1 5 7 8 8 8 8 8 8 8] [1 8 13 15 16 16 16 16 16 16] [1 13 24 29 31 32 32 32 32 32] [1 21 44 56 61 63 64 64 64 64] [1 34 81 108 120 125 127 128 128 128] [1 55 149 208 236 248 253 255 256 256] [1 89 274 401 464 492 504 509 511 512] Как видим, полученные значения для сходятся с приведёнными в последовательности A126198. Значит, я нигде не наглюкал.

hclubmk	Re: Количество способов разложить число в сумму (композиции) 18.11.2010, 13:27
17/11/10 19	Жесть. Кроме матчасти — курить семантику PARI/GP. Нет ли возможности всё-же разъяснить назначение операторов, поскольку есть необходимость реализовывать на другом языке программирования (скажем «С»).

maxal	Re: Количество способов разложить число в сумму (композиции) 18.11.2010, 17:11
Модератор 11/01/06 5613	Нет ли возможности всё-же разъяснить назначение операторов, поскольку есть необходимость реализовывать на другом языке программирования (скажем «С»). Может, мне ещё за вас программу написать?! Вам нужно — вы и разбирайтесь. Вся необходимая информация приведена выше.

hclubmk	Re: Количество способов разложить число в сумму (композиции) 18.11.2010, 23:04
17/11/10 19	maxal Я не специалист в таких узких областях, поэтому и попросил разъяснений , а не готовое решение (наверно есть разница?). Впрочем, Вы и так достаточно много внимания уделили моей новоявленной на форуме персоне. В любом случае, спасибо.

scwec	Re: Количество способов разложить число в сумму (композиции) 04.12.2010, 20:55
Заслуженный участник 17/09/10 2088	Хотел бы обратить внимание модераторов и других активных участников на их большую готовность отвечать на совершенно бессмысленные вопросы мало касающиеся математики и неготовность отвечать на принципиальные вопросы. Не хочу делать глубокомысленных выводов, однако их пора, видимо, пришла. Успехов Вам.  !  Предупреждение за оффтопик! — Сб дек 04, 2010 22:33:11 — Приношу глубокие извинения за, может быть, обидные слова. Такие у Вас, выходит, правила. Онако, ведь «За Державу обидно». Ну что же, как есть, так пусть и будет. С уважением Швецов.

tess	Re: Количество способов разложить число в сумму (композиции) 18.07.2011, 10:53
21/06/11 45

maxal	Re: Количество способов разложить число в сумму (композиции) 18.07.2011, 15:07
Модератор 11/01/06 5613	Есть ли решение для числа вариантов, если считать варианты, отличающиеся порядком слагаемых в сумме, за один вариант? Такие «варианты» называются разбиениями — см., например, в википедии.

SaDiSt007	Re: Количество способов разложить число в сумму (композиции) 24.10.2011, 14:20
Заблокирован 24/10/11 ∞ 2	ну да уж…  !  Предупреждение за бессмысленные сообщения и оффтопик!

Модераторы: Модераторы Математики, Супермодераторы

Сообщения без ответов | Активные темы

Автор	Сообщение
VasiliiSocratov	Заголовок сообщения: Композиция числа с учётом нолей Добавлено: 24 мар 2021, 15:06
Начинающий Зарегистрирован: 24 мар 2021, 15:00 Сообщений: 4 Cпасибо сказано: 2 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Здравсвтуйте! Число композиций одного числа вычисляется по формуле 2[math]^{n-1}[/math] Но как определить число композиций числа, учитывая нули, то есть считать композиции тройки — 3+0+0 и 0+3+0 разными композициями? Это необходимо, чтобы заранее определять число слагаемых в крупных полиномах.
Вернуться к началу

StepUp	Заголовок сообщения: Re: Композиция числа с учётом нолей Добавлено: 24 мар 2021, 16:53
	VasiliiSocratov писал(а): как определить число композиций числа, учитывая нули, Этой формулой и пользуйтесь. Все композиции будут разными с учетом нулей, что так: [math]2^4 Rightarrow (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16)[/math] или так: [math]2^4 Rightarrow (01,02,03,04,05,06,07,08,09,10,11,12,13,14,15,16)[/math] Может вы хотели что-то другое спросить? Тогда уточните вопрос.
Вернуться к началу

VasiliiSocratov	Заголовок сообщения: Re: Композиция числа с учётом нолей Добавлено: 24 мар 2021, 19:51
	Число композиций тройки по фурмуле 2^(3-1) равняется четырём, то есть (3=3, 2+1=3, 1+2=3, 1+1+1=3) Но если мы решаем полином по типу (a + b + c)[math]^{3}[/math] то мы видим, что слагаемых 10, а не 4, т.к. 0+0+3 и 0+3+0 являются разными композициями. Если бы у нас было (а+b+c+d), то учитывать нужно было бы уже 4 перестановки (4,0,0,0)(0,4,0,0) и так далее. Количество подобных композиций числа и являются числом слагаем в полиноме. И интересно, есть ли способ без ручного перебора всех вариантов типа (0,0,0,5,0) (1,2,0,2,0) (1,1,3,0,0)…. сразу посчитать их количество?
Вернуться к началу

StepUp	Заголовок сообщения: Re: Композиция числа с учётом нолей Добавлено: 25 мар 2021, 16:31
	VasiliiSocratov писал(а): если мы решаем полином по типу [math](a + b + c)^3[/math], то мы видим, что слагаемых 10. … И интересно, есть ли способ без ручного перебора всех вариантов …. сразу посчитать их количество? Интересная задачка. Поискал общую формулу для суммы [math]n[/math] чисел в квадрате. Действительно, такая формула имеется. С учетом приведения подобных членов, полином будет иметь следующее число одночленов: [math]N=n+frac {ncdot(n-1)} 2[/math]. Проверьте, кажется не ошибся.
Вернуться к началу
	За это сообщение пользователю StepUp «Спасибо» сказали: VasiliiSocratov

StepUp	Заголовок сообщения: Re: Композиция числа с учётом нолей Добавлено: 25 мар 2021, 17:35
	VasiliiSocratov писал(а): интересно, есть ли способ без ручного перебора всех вариантов… сразу посчитать их количество? Нашел формулу для суммы [math]n[/math] чисел в кубе: [math]N=n+ncdot(n-1) + C_{n}^3[/math]. К сожалению, пока общего со случаем, когда степень [math]=2[/math] мало. Поэтому вероятность наличия общей формулы для всех степеней маловероятна. Пояснение к формуле: первое слагаемое — [math]n[/math] — это число кубов; второе слагаемое — [math]ncdot (n-1)[/math] количество одночленов вида [math]x^2 cdot y[/math]; третье слагаемое — [math]C_{n}^3[/math] — количество одночленов вида [math]x cdot y cdot z[/math].
Вернуться к началу

StepUp	Заголовок сообщения: Re: Композиция числа с учётом нолей Добавлено: 25 мар 2021, 18:06
	Нашел подобный вопрос на Киберфоруме https://www.cyberforum.ru/combinatorics/thread2802514.html только о расчете коэффициентов при одночленах. Там дана общая формула для степени n. Но через функцию [math]P_n(n_1,n_2,…,n_k)[/math]. Хотелось бы почитать про эту функцию. Подскажите, пожалуйста, что за функция, как называется, где о ней взять информацию.
Вернуться к началу

StepUp	Заголовок сообщения: Re: Композиция числа с учётом нолей Добавлено: 25 мар 2021, 23:04
	MihailM писал(а): Тут например Большое спасибо.
Вернуться к началу

VasiliiSocratov	Заголовок сообщения: Re: Композиция числа с учётом нолей Добавлено: 29 мар 2021, 13:12
	Я не нашёл общей формулы, но нашёл алгоритм действий, чтобы самому без перебора найти число одночленов полинома. Для примера можно разобрать (a + b + c + d)[math]^{4}[/math]. Нам потребуются композиции четвёрки это: 4=4; 3+1=4; 2+2=4; 2+1+1=4 и 1+1+1+1=4. Эти композиции отвечают за, если можно так выразиться, типы одночленов. Чтобы посчитать количество одночленов одного типа, например 2+1+1 (то есть один член в квадрате, второй и третий в первой степени, а четвёртый в нулевой) нужно посчитать количество перестановок из {2,2,1,0}. [math]frac{ 4! }{ 2!*2!*1!*0! }[/math] Получается 6 членов. Подобным же образом можно расчитать для всех остальных композиций четвёрки: [math]frac{ 4! }{ 3! } + frac{ 4! }{ 2! } + frac{ 4! }{ 2! } + frac{ 4! }{ 2!+2! } + frac{ 4! }{ 4! } = 35[/math]
Вернуться к началу