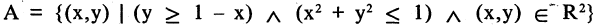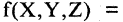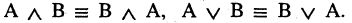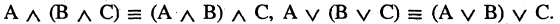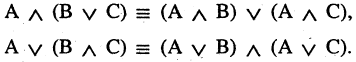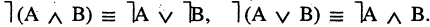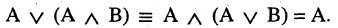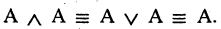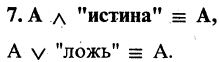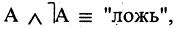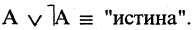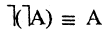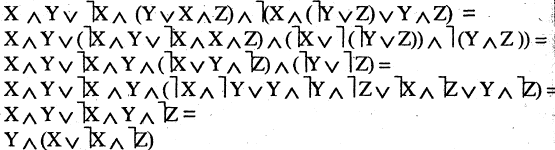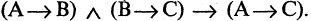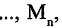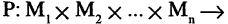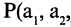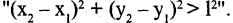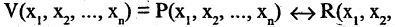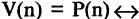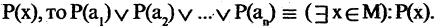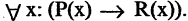На уроке рассмотрен материал для подготовки к огэ по информатике, решение задания 3
3-е задание: «Значение логического выражения»
Уровень сложности — базовый,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
* до 2020 г — это задание № 2 ОГЭ
Содержание:
- Объяснение 3 задания ОГЭ по информатике
- ОГЭ информатика разбор задания 3
- Актуальное
- Тренировочные
- Для подготовки к решению 3 задания ОГЭ по информатике следует вспомнить знаки сравнения. В логических выражениях используются следующие знаки сравнения:
- В логических выражениях участвуют всего два значения выражений: ИСТИНА и ЛОЖЬ.
- Рассмотрим результат выполнения логических выражений для двух высказываний — А и Б:
- Если отрицание НЕ стоит перед скобкой с выражением, то НЕ ставится перед каждой частью выражения в скобках и при этом операция внутри скобок меняется:
|
> |
больше |
|
< |
меньше |
|
= |
равно |
|
≥ |
больше или равно |
|
≤ |
меньше или равно |
| 1 | А ИЛИ Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | если А=истина И Б=ложь | |
| 3 | если А=ложь И Б=истина | |
| 4 | А ИЛИ Б = ЛОЖЬ → | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией ИЛИ легче проверить «на ложь»:
с операцией ИЛИ результатом будет ЛОЖЬ только в одном единственном случае, — когда оба выражения — А и Б — ложны
| 1 | А И Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | А И Б = ЛОЖЬ → | если А=истина И Б=ложь |
| 3 | если А=ложь И Б=истина | |
| 4 | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией И легче проверить «на истинность»:
с операцией И результатом будет ИСТИНА только в одном единственном случае, — когда оба выражения — А и Б — истинны
| Исходные значения | Результат | |
|---|---|---|
| 1 | НЕ А если А=истина |
А = ЛОЖЬ |
| НЕ(5 > 0) | 5 ≤ 0 | |
| 2 | НЕ А если А=ложь |
А = ИСТИНА |
| НЕ(-2 > 0) | -2 ≤ 0 | |
| 3 | НЕ (НЕ А) | = А |
| 1 | НЕ |
| 2 | выражение в скобках |
| 3 | И |
| 4 | ИЛИ |
| 1 | НЕ (А ИЛИ Б) | НЕ А И НЕ Б |
| 2 | НЕ (А И Б) | НЕ А ИЛИ НЕ Б |
ОГЭ информатика разбор задания 3
Подробный видеоразбор по ОГЭ 3 задания:
📹 Видеорешение на RuTube здесь
Актуальное
Значение логического выражения
Разбор задания 3.7. Демонстрационный вариант ОГЭ 2022 г ФИПИ:
Напишите наименьшее число x, для которого истинно высказывание:
(x > 16) И НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x > 16) И (x чётное)
(x > 16) И (x чётное) = ИСТИНА истина истина
Ответ: 18
Разбор задания 3.12:
Напишите наименьшее число x, для которого ложно высказывание:
(x ≤ 15) ИЛИ НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x ≤ 15) ИЛИ (x чётное) = 0 (ложь)
(x ≤ 15) ИЛИ (x чётное) = ЛОЖЬ ложь ложь
Ответ: 17
Тренировочные
Разбор задания 3.1:
Для какого из приведённых значений числа X ложно высказывание:
НЕ (X < 6) ИЛИ (X < 5) ?
1) 7
2) 6
3) 5
4) 4
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 6) (X < 6) - ложь, значит результат: X ≥ 6
(X ≥ 6) ИЛИ (X < 5)
(X ≥ 6) ИЛИ (X < 5) = ЛОЖЬ ложь ложь
1. (X ≥ 6) = ЛОЖЬ => X < 6 2. (X < 5) = ЛОЖЬ => X ≥ 5
5 < 6 и 5 ≥ 5
Ответ: 3
Разбор задания 3.2:
Для какого из приведённых значений числа X истинно высказывание:
(X < 8) И НЕ (X < 7) ?
1) 9
2) 8
3) 7
4) 6
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 7) (X < 7) - ложь, значит результат: X ≥ 7
(X < 8) И (X ≥ 7)
(X < 8) И (X ≥ 7) = ИСТИНА истина истина
1. (X < 8) = ИСТИНА => X < 8 2. (X ≥ 7) = ИСТИНА => X ≥ 7
7 < 8 и 7 ≥ 7
Ответ: 3
Разбор задания 3.3:
Для какого из приведённых имён ЛОЖНО высказывание:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) ?
1) Анна
2) Елена
3) Павел
4) Егор
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) = = (НЕ(Третья буква согласная) ИЛИ НЕ(Последняя буква гласная))
1. НЕ(Третья буква согласная) => Третья буква НЕ согласная 2. НЕ(Последняя буква гласная) => Последняя буква НЕ гласная
(Третья буква не согласная) ИЛИ (Последняя буква не гласная)
(Третья буква не согласная) ИЛИ (Последняя буква не гласная) = ЛОЖЬ
ложь ложь
1. (Третья буква не согласная) = ЛОЖЬ => Третья буква согласная 2. (Последняя буква не гласная) = ЛОЖЬ => Последняя буква гласная
Третья буква "н" согласная и Последняя буква "а" гласная
Ответ: 1
Разбор задания 3.4:
Для какого из приведённых имён ИСТИННО высказывание:
НЕ ((число > 50) ИЛИ НЕ(число четное)) ?
1) 43
2) 50
3) 61
4) 72
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ в малых скобках:
НЕ(число четное) => число нечетное
НЕ ((число > 50) ИЛИ (число нечетное)) = = (НЕ(число > 50) И НЕ(число нечетное))
1. НЕ(число > 50) => число <= 50 2. НЕ(число нечетное) => число четное
(число <= 50) И (число четное)
(число <= 50) И (число нечетное) = ИСТИНА
истина истина
Ответ: 2
Разбор задания 3.5.:
Для какого из приведённых слов ЛОЖНО высказывание:
(последняя буква согласная) ИЛИ НЕ ((первая буква согласная) И (вторая буква гласная)) ?
1) Тигр
2) Выдра
3) Енот
4) Краб
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((первая буква согласная) И (вторая буква гласная)) = = (НЕ(первая буква гласная) ИЛИ НЕ(вторая буква гласная))
1. НЕ(первая буква согласная) => первая буква гласная 2. НЕ(вторая буква гласная) => вторая буква согласная
(первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква согласная) ИЛИ
ложь ложь
(вторая буква согласная) = ЛОЖЬ
ложь
1. (последняя буква согласная) = ЛОЖЬ => последняя буква гласная 2. (первая буква гласная) = ЛОЖЬ => первая буква согласная 3. (вторая буква согласная) = ЛОЖЬ => вторая буква гласная
Ответ: 2
Разбор задания 3.6:
Для какого из приведённых слов верно высказывание:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) ?
1) АИДА
2) СЕРГЕЙ
3) СТЕПАН
4) АРТЕМ
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении находятся большие скобки, с которых необходимо начать решение.
- Внешняя операция, т.е. последняя по приоритету — это операция И. Рассмотрим ее подробней, разделив общее высказывание на две части относительно этой операции:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная))
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) истина истина
((последняя буква согласная) ИЛИ (вторая буква согласная))
истина ИЛИ истина
(первая буква гласная) И (или первая или вторая буква в слове согласная) истина истина
Ответ: 4
Осуществление поиска в готовой базе данных по сформулированному условию
* до 2020 г — это задание № 12 ОГЭ
Разбор задания 3.8:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Рига | скорый | 15:45 | Рижский |
| Ростов | фирменный | 17:36 | Казанский |
| Самара | фирменный | 14:20 | Казанский |
| Самара | скорый | 17:40 | Казанский |
| Самара | скорый | 15:56 | Казанский |
| Самара | скорый | 15:56 | Павелецкий |
| Самара | фирменный | 23:14 | Курский |
| Санкт-Петербург | скорый | 8:00 | Ленинградский |
| Санкт-Петербург | скорый | 4:00 | Ленинградский |
| Саратов | скорый | 14:57 | Павелецкий |
| Саратов | пассажирский | 15:58 | Павелецкий |
| Саратов | скорый | 15:30 | Павелецкий |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») ИЛИ (Вокзал = «Павелецкий»)?
✍ Решение:
- В условии находится логическая операция ИЛИ, которая истинна тогда, кода хоть одно из логических выражений истинно. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
1. Категория поезда = «скорый» и Вокзал = любой 2. Категория поезда = «скорый» и Вокзал = «Павелецкий» 3. Категория поезда = любой и Вокзал = «Павелецкий»
Ответ: 9
Разбор задания 3.9:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») И (Время в пути > 40:00)?
✍ Решение:
- В условии находится логическая операция И, которая истинна только тогда, кода оба (все) выражения истинны. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
Категория поезда = «скорый» и Время в пути > 40:00 одновременно
Ответ: 3
Разбор задания 3.10:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Пункт назначения = «Волгоград») ИЛИ (Категория поезда = «пассажирский») И (Время в пути < 50:00)?
В ответе укажите одно число — искомое количество записей.
✍ Решение:
- В условии находятся две логических операции: И и ИЛИ. Первой всегда выполняется операция И, затем добавляются записи для операции ИЛИ.
- Операция И истинна только тогда, кода оба (все) выражения истинны.
(Категория поезда = «пассажирский») И (Время в пути < 50:00) одновременно
(Пункт назначения = «Волгоград») добавить к предыдущему результату
Ответ: 4
Разбор задания 3.11:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Махачкала | скорый | 39.25 | Павелецкий |
| Махачкала | скорый | 53.53 | Курский |
| Мурманск | скорый | 35.32 | Ленинградский |
| Мурманск | скорый | 32.50 | Ленинградский |
| Мурманск | пассажирский | 37.52 | Ленинградский |
| Мурманск | пассажирский | 37.16 | Ленинградский |
| Назрань | пассажирский | 40.23 | Павелецкий |
| Нальчик | скорый | 34.55 | Казанский |
| Нерюигри | скорый | 125.41 | Казанский |
| Новосибирск | скорый | 47.30 | Ярославский |
| Нижневартовск | скорый | 52.33 | Казанский |
| Нижний Тагил | фирменный | 31.36 | Ярославский |
Сколько записей в данном фрагменте удовлетворяют условию:
НЕ (Вокзал = «Ленинградский») И (Время в пути > 50.00)?
✍ Решение:
- В условии находятся две логических операции: НЕ и И.
- Первой всегда выполняется операция НЕ, затем добавляются записи для операции И.
- Операция НЕ обозначает обратное высказывание:
НЕ(Вокзал = «Ленинградский»)
то же самое, что
(Вокзал ≠ «Ленинградский»)
(Вокзал ≠ «Ленинградский») И (Время в пути > 50.00) одновременно
Ответ: 3
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д2 № 2
i
Для какого из приведённых значений числа X ложно высказывание: НЕ (X < 6) ИЛИ (X < 5)?
1) 7
2) 6
3) 5
4) 4
2
Задания Д2 № 22
i
Для какого из приведённых значений числа X истинно высказывание: НЕ (X < 6) И (X < 7)?
1) 5
2) 6
3) 7
4) 8
3
Задания Д2 № 42
i
Для какого из приведённых значений числа X истинно высказывание: (X < 
1) 9
2) 8
3) 7
4) 6
4
Задания Д2 № 62
i
Для какого из приведённых значений числа X истинно высказывание: НЕ(X > 5) И (X > 4)?
1) 4
2) 5
3) 6
4) 7
5
Задания Д2 № 82
i
Для какого из приведённых значений числа X истинно высказывание: НЕ(X < 5) И (X < 6)?
1) 6
2) 5
3) 4
4) 3
Пройти тестирование по этим заданиям
Задание №3. Определение истинности составного высказывания.
Уровень сложности: базовый; макс. балл за задание: 1; примерное время выполнения: 3 минуты.
Знать: логические значения, операции, выражения.
Уметь: определять истинность составного высказывания.
Пример задания.
Напишите наименьшее число x, для которого истинно высказывание:
(x > 16) И НЕ (x нечётное).
Разбор задания.
Мы имеем составное высказывания из двух простых связанных между собой конъюнкцией (операцией логического умножения). Конъюнкция истинна только в одном случае, когда оба простых высказывания истинны. Следовательно требуемое число должно быть больше 16 и не нечётное (т.е. чётное). Наименьшее такое число — 18.
Ответ: 18.
Пример задания.
Напишите наибольшее число x, для которого ложно высказывание:
НЕ ((x < 54) И (x простое число)) ИЛИ НЕ (x <= 16)
Разбор задания.
Это задание гораздо сложнее предыдущего. Для решения таких логических примеров не мешало бы знать законы алгебры логики для того, чтобы можно было упростить выражение.
Сначала «избавимся» от отрицания:
(x >= 54) ИЛИ (x не простое число) ИЛИ (x > 16)
В данном примере трудно сообразить, для какого наибольшего числа x это высказывание будет ложно. Но можно ко всему выражению применить «отрицание» и найти для какого наибольшего числа x это высказывание будет истинным!
(x < 54) И (x простое число) И (x <= 16)
Глядя на это выражение можно понять, что наибольшее простое число х , которое меньше 54, меньше либо равно 16 — это число 13, что и будет ответом к нашему заданию.
Ответ: 13.
Проводя анализ результатов пробного ОГЭ по информатике в нашем районе и увидев процент решаемости заданий на логику (задание №3), я пришел к такому выводу, что просто необходимо разобрать побольше типичных задач. Предлагаю Вам решить некоторые такие задания.
Задание №1. Напишите наибольшее число x, для которого ложно высказывание:
(x > 72) ИЛИ НЕ (x чётное).
Задание №2. Напишите наибольшее число x, для которого ложно высказывание:
НЕ (x ≤ 26) ИЛИ (x нечётное).
Задание №3. Напишите наименьшее число x, для которого истинно высказывание:
НЕ (x ≤ 25) И (x кратное 5) И (x ≠ 30).
Задание №4. Напишите наибольшее число x, для которого ложно высказывание:
(x ≥ 90) ИЛИ НЕ (x кратное 3) ИЛИ (x ≠ 87).
Задание №5. Напишите наибольшее число x, для которого истинно высказывание:
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) И НЕ (x > 25).
Задание №6. Напишите наименьшее число x, для которого ложно высказывание:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) ИЛИ НЕ (x > 125).
Задание №7. Напишите наибольшее число x, для которого ложно высказывание:
НЕ ((x < 54) И (x простое число)) ИЛИ НЕ (x ≤ 16).
Дальше разберём каждое задание по отдельности, и вы сможете сравнить свои ответы с правильными.
Задание №1. Напишите наибольшее число x, для которого ложно высказывание:
(x > 72) ИЛИ НЕ (x чётное).
Разбор задания №1. Для успешного решения заданий такого типа необходимо знать, что такое конъюнкция, дизъюнкция, отрицание и законы Де Моргана. Также, необходимо для конъюнкции и дизъюнкции уметь строить таблицы истинности.
Итак, перед нами сложное высказывание, состоящее из двух простых:
(x > 72) ИЛИ НЕ (x чётное).
Для удобства я выделил высказывания разным цветом. Необходимо помнить, что связками между простыми высказываниями будут конъюнкция (логическое И), дизъюнкция (логическое ИЛИ), а также и другие логические операции, но их изучают в старших классах и в заданиях ОГЭ они не встречаются.
Когда же это сложное высказывание будет ложным? А ложным оно будет тогда и только тогда, когда оба простых высказывания будут ложными. Следовательно (x > 72) должно давать ложь и НЕ (x чётное) тоже должно давать ложь.
Теперь всё делаем по порядку.
- Все числа x, которые меньше или равны 72, нам подойдут. Из условия знаем, что число должно быть наибольшим. Следовательно, возьмём число 72. Проверяем условие 72 > 72 – нет, это ложь.
- Разберём второе высказывание НЕ (x чётное). Сначала «избавимся» от отрицания. НЕ (x чётное) — это тоже самое, что (x нечётное). При проверке первого высказывания мы выяснили, что число не может быть больше 72. Подставим его во вторую часть высказывания. (72 нечётное) – нет, это ложь, следовательно, нам вполне подходит.
Ответ: 72.
Задание №2. Напишите наибольшее число x, для которого ложно высказывание:
НЕ (x ≤ 26) ИЛИ (x нечётное).
Разбор задания №2. По аналогии с первым заданием выполняем и это. Мы имеем сложное высказывание. Связаны высказывания между собой дизъюнкцией, а дизъюнкция ложна тогда и только тогда, когда ложны все её составляющие!
- Разберём первую часть — НЕ (x ≤ 26). По законам Де Моргана «избавляемся» от отрицания. НЕ (x ≤ 26) = (x > 26). Чтобы эта часть высказывания была ложной нам подойдут все числа, которые меньше, чем 26 и само число 26, т.к. (26 > 26) – это ложь.
- По условию нам нужно наибольшее число x. Подставим во вторую часть высказывания (x нечётное) число 26. (26 нечётное) – нет, это ложь. Нам подходит, следовательно, оно и будет ответом.
Ответ: 26.
Это были задачи попроще. Теперь разберём немного потруднее.
Задание №3. Напишите наименьшее число x, для которого истинно высказывание:
НЕ (x ≤ 25) И (x кратное 5) И (x ≠ 30).
Разбор задания №3. Мы имеем сложное высказывание, но только оно состоит из трёх простых высказываний, связанных между собой конъюнкцией (логической операцией И). Конъюнкция истинна тогда и только тогда, когда все части составного высказывания будут истинны!
- Рассмотрим первую часть НЕ (x ≤ 25). По закону Де Моргана «избавимся» от отрицания. НЕ (x ≤ 25) = (x > 25). Нам подойдёт любое число больше, чем 25, т.е. от 26 до бесконечности. Из условия мы знаем, что нам нужно наименьшее из таких чисел – это 26.
- Рассмотрим вторую часть составного высказывания — (x кратное 5). Число 26 нам не подходит, т.к. оно не кратно пяти. Все числа кратные пяти заканчиваются на пять или на ноль. Нам бы подошло число 30. Оно больше, чем 25 и оно кратно 5.
- Рассмотрим третью часть составного высказывания, она то и даст верный ответ на нашу задачу. Число x не должно равняться 30, следовательно, наш x – это число больше 25, кратное 5, но не равняется 30. Такое ближайшее число – это 35. Оно полностью подходит всем условиям и является ответом к нашему заданию.
Ответ: 35.
Задание №4. Напишите наибольшее число x, для которого ложно высказывание:
(x ≥ 90) ИЛИ НЕ (x кратное 3) ИЛИ (x ≠ 87).
Разбор задания №4. Как и в предыдущем задании, мы имеем сложное, которое состоит из трёх простых, высказывание, только все они связаны дизъюнкцией (логической операцией ИЛИ). А ложно составное высказывание будет ложно только в том случае, когда будут ложны все его части!
- Рассмотрим первую часть (x ≥ 90). Она будет ложной в том случае, когда x будет строго меньше 90, т.е. от 89 до минус бесконечность. Так как от нас требуется найти наибольшее из этих чисел, то пока остановимся на числе 89.
- Далее рассмотрим второе высказывание НЕ (x кратное 3). Если «избавится» от отрицания, то мы имеем выражение (x не кратно 3). Это высказывание будет ложным в тех случаях, когда число на три делится! Ближайшее наибольшее число из диапазона от минус бесконечность до 89 будет число 87. Остановимся пока на нём и перейдем к третьему высказыванию.
- Из высказывания (x ≠ 87) становится ясным, что число 87 нам вполне подходит, т.к. выражение (87 ≠ 87) ложно.
Ответ: 87.
Задание №5. Напишите наибольшее число x, для которого истинно высказывание:
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) И НЕ (x > 25).
Разбор задания №5. Обратите внимание, что всё наше сложное высказывание включает в себя одно сложное высказывание (выделено красными скобками) НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) и одно простое высказывание НЕ (x > 25), это всё связано конъюнкцией (логической операцией И). Всё выражение будет истинным только в том случае, когда обе его части будут истинны!
- В данном примере сразу применим закон Де Моргана. Когда мы отрицаем всё то, что заключено в скобках, то все знаки внутри скобок «переворачиваем».
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) = ((x < 23) И (x нечётное))
Следовательно, наше число x должно быть меньше, чем 23 и нечётное. Подойдёт число 21. Проверим его в следующей части выражения.
- Имеем высказывание НЕ (x > 25). «Избавимся» от отрицания и подставим в него для проверки число 21. Проверяем: (21 ≤ 25) – это истина.
Ответ: 21.
Задание №6. Напишите наименьшее число x, для которого ложно высказывание:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) ИЛИ НЕ (x > 125).
Разбор задания №6. По структуре задание напоминает предыдущее. Оно также включает в себя одно сложное высказывание (выделено красными скобками) НЕ ((x ≥ 100) И НЕ (x кратно 4)) и одно простое высказывание НЕ (x > 125), это всё связано дизъюнкцией (логической операцией ИЛИ). И это всё должно быть ложно.
- «Избавляемся» от отрицания – все знаки внутри скобок «переворачиваем»:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) = ((x < 100) ИЛИ (x кратно 4))
Мы имеем вот такое выражение ((x < 100) ИЛИ (x кратно 4)), осталось понять, когда же оно ложно. А ложно оно будет тогда и только тогда, когда ложны его обе части, т.е. x – это число от 100 до плюс бесконечности и оно не должно делиться нацело на 4. Такое наименьшее число – 101.
- Подставим для проверки это число во вторую часть выражения. НЕ (101 > 125). К сожалению, это выражение истинно, а из условия мы знаем, что всё выражение должно быть ложно. Значит, число x должно быть строго больше 125 и не должно делится на 4. Такое минимальное число — 126.
Ответ: 126.
Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.
Алгебра высказываний
Под высказыванием понимаем всякое утверждение (повествовательное предложение), про которое всегда определенно и объективно можно сказать, является оно истинным или ложным. Например, «5-3 = 2» или «В неделе семь дней» — истинные высказывания, а «5 > 8» или «В русском языке 35 букв» — ложные высказывания. Синонимами слова «высказывания» можно считать: логическое высказывание, булевское выражение, суждение, утверждение и т.п. Фразы: «Ура!», «Который час?» — не являются высказываниями.
Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «ДА» , «И», «+», «true»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «О», «НЕТ», «Л», «-«, «false»). Совокупность возможных значений высказывания образует множество истинности {0,1} и {И,Л}.
Есть два вида высказываний: простые и составные (сложные). Под простым будем понимать высказывание, которое не может быть разбито на более простые высказывания. Про него всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой. Из простых высказываний при помощи логических операций можно строить сложные высказывания, которые всегда только истинны или только ложные. Высказывания обозначаются заглавными латинскими буквами: 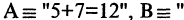
Логические операции
Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.
Отрицание высказывания
Для каждого высказывания А может быть сформировано новое высказывание 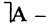
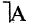
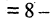
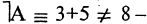
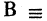
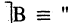
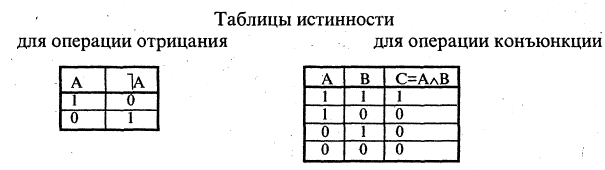
Конъюнкция высказываний
Конъюнкцией высказываний А и В называется высказывание 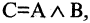

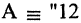
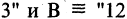

Операцию конъюнкции можно определить и для нескольких высказываний как связку высказываний, объединенных союзом «и». Конъюнкция из п высказываний — новое высказывание, причем высказывание
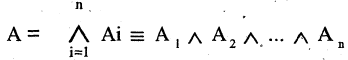
имеет значение «истина», если 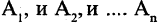
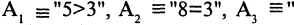
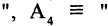
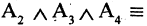
Мурманск севернее Смоленска») — ложное высказывание. В то время как 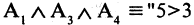
Дизъюнкция высказываний
Дизъюнкцией высказываний А и В называется высказывание 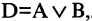

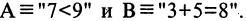
Операцию дизъюнкции можно определить для нескольких высказываний как связку высказываний, объединенных союзом «или»,
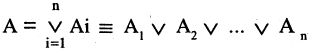
В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Импликация высказываний
Импликацией высказываний А и В называется высказывание 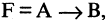
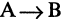
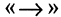


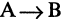

Пусть А и В истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием. Когда же папа не купит сыну велосипед (В — ложно), получив премию (А — истинно), то это, мягко говоря, не логичный поступок, а импликация имеет значение «ложь». Если же папа не получит премию (А — ложно), но купит велосипед (В -истинно), то результат положителен. В том случае, если, не получив премии (А ложно), папа не купит велосипед (В — ложно) -обещание не нарушено, результат можно считать истинным.
Эквивалентность высказываний
Эквивалентностью высказываний А и В называется высказывание 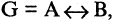
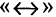






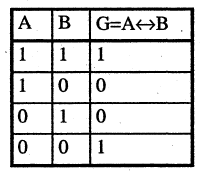
Замечание. Характерной особенностью операций над высказываниями является введение логических союзов с точно определенным смыслом, не допускающим никакой двусмысленности в толковании этих символов. Таким образом, математическая логика применима не для любых высказываний, а только для таких, которые допуск кают четкую оценку в двоичной системе «истина — ложь». Для преодоления такого рода ограничений в рамках нечеткой математики разрабатывается нечеткая логика.
Если в выражении встречаются различные логические операции, то в качестве естественного порядка (выполняемого поочередно слева направо) используется следующая последовательность: 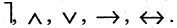
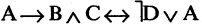
Введя скобки, получим формулу 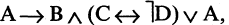
Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:
Использование различных операций позволяет в удобной аналитической форме задавать различные множества.
Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:
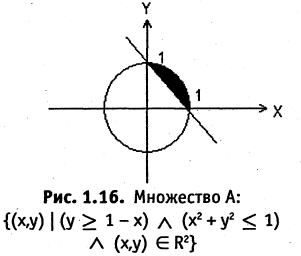
Система операций 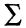
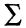
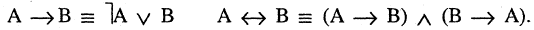
Булевы функции
Всякую формулу логики высказываний можно рассматривать как некоторую функцию: каждая буква (высказывание) может принимать одно из двух значений — «истина» или «ложь», при этом сложное высказывание, заданное этой формулой, также может быть истинным или ложным. Так формула
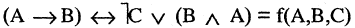
выражает функцию от переменных А, В и С.
Такого рода функции называются булевыми, а их аргументы — булевыми переменными. Аргументы булевых функций могут представлять собой, сокращенные обозначения некоторых конкретных высказываний. Тогда функция обозначает сокращенную запись некоторого сложного высказывания. Например, 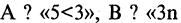
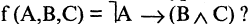
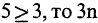
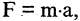
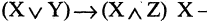
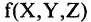
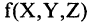
Целый ряд булевых функций обладает тем свойством, что они принимают одни и те же значения при любых значениях истинности аргументов. Такие формулы называются тождественно истинными. Например, при любых X и Y истинны формулы 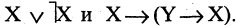
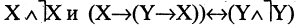
Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.
Основные законы математической логики
1.Коммутативность
2.Ассоциативность
3.Дистрибутивность
4.Законы де Моргана
5.Закон поглощения
6.Закон идемпотентности
8.Закон противоречия
9.Закон исключения третьего
10.Закон двойного отрицания
Пример:
Упростить выражение, используя тождественны преобразования
Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.
Основные методы доказательств
При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.
Формально каждая теорема может быть выражена в форме импликации 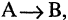
Метод цепочек импликаций
Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из 
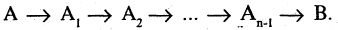
В основе этого метода лежит закон цепного высказывания или закон силлогизма
Метод от противного
Метод от противного. Используя этот метод, вместо доказательства прямого следствия «из А следует В» доказывают, что из «не В» следует «не А». Этот метод основан на законе контрапозиций, имеющем следующий вид:
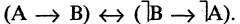
Метод необходимого и достаточного
Метод необходимого и достаточного. Теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В». Доказательство такого вида теоремы распадается на две части:
а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);
б) если имеет место В, то имеет место и А (В достаточно для А).
Доказательство таким методом базируется на законе тавтологии:
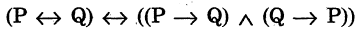
Алгебра предикатов
Предикатом 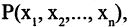
называется функция Р, отображающая их прямое произведение на двоичное множество, т. е. 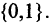
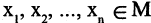
Рассмотрим примеры, 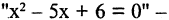
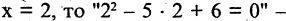
положив 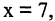
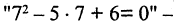
Всякий предикат 
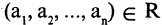
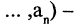

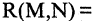
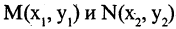
Если в 
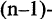
Логические операции над предикатами
Отрицание предиката
Пусть предикат 
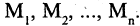


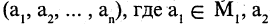
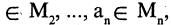
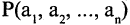
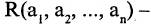
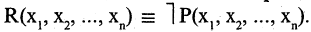
Например, предикат «

Конъюнкция предикатов
Пусть на множествах 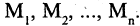

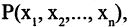

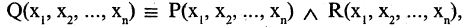
который истинен для одних и тех же кортежей только тогда, когда оба предиката — и 
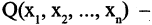
Например, конъюнкция предикатов 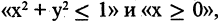
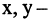
Дизъюнкция предикатов
Дизъюнкция предикатов 


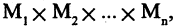


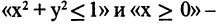
Импликация предикатов
Импликация предикатов 

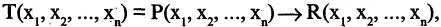
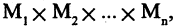


Например, импликация «



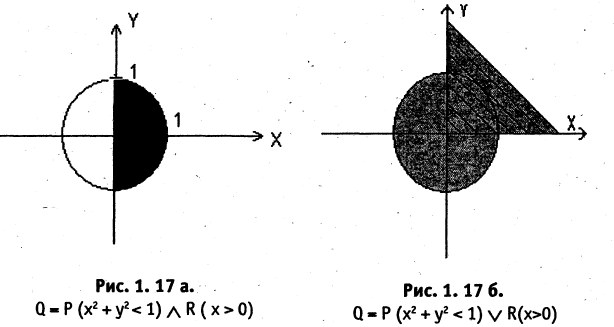
Эквивалентность предикатов
Эквивалентность предикатов 

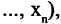



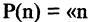
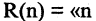

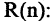


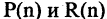
Наряду с логическими операциями важную роль играют операции, называемые кванторами. Квантор всеобщности есть операция, которая предикат 


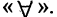



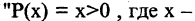



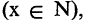

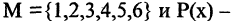

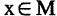
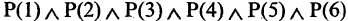
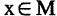
Квантор существования
Квантор существования есть операция, которая предикат 
из М, обладающий свойством 
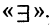







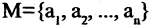
Кванторы обладают свойствами, являющимися аналогами законов де Моргана:
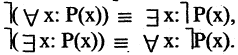
С помощью кванторов можно выражать ряд часто используемых на практике отношений между множествами. Например, высказывание «все объекты 

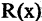
Переход от 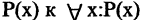



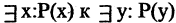
Рассмотрим пример. На множестве чисел задан двухместный предикат 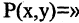


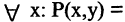

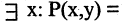

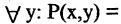

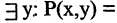

Связывая обе переменные данного предиката, получим высказывания:
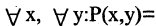
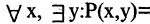
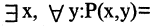
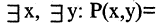
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
В демо-версии присутствует типовое задание 3 без выбора вариантов ответов, так что скорее всего и на реальном ОГЭ это задание будет не тестовым, а нужно будет посчитать и написать в ответе свое число.
Как решать. Если есть НЕ, в первую очередь избавимся от него, поменяв знак сравнения на противоположный. Если это >, меняем на ≤; если <, меняем на ≥. Четное меняется на нечетное, все остальное меняется на противоположное. То же самое, когда истинное переделываем в ложное и наоборот.
Далее, в истинном высказывании И означает, что выполняются ОБА условия одновременно; ИЛИ — выполняется хоть то, хоть другое, хоть оба сразу.
I закон де Моргана: Отрицание дизъюнкции двух простых высказываний равносильно конъюнкции отрицаний этих высказываний.
II закон де Моргана: Отрицание конъюнкции двух простых высказываний равносильно дизъюнкции отрицаний этих высказываний.
Пояснение ГДЗответ ру: Конъюнкция И, дизъюнкция ИЛИ.
Логическое ИЛИ ложно только тогда, когда ложны оба высказывания. Значит, когда переделываем ложное в истинное, меняем не только знаки и четность, но ИЛИ на И, а И на ИЛИ (по законам де Моргана)! Если есть НЕ перед скобкой с несколькими условиями, то при избавлении от отрицания внутри этой скобки так же помимо изменения условий И меняется на ИЛИ и наоборот.
В ложных высказываниях можно сразу применять законы де Моргана, не избавляясь предварительно от НЕ, но мы в ответах будем делать пошагово и избавляться от отрицания для наглядности.
В заключение заметим, что в логических выражениях, представленных в заданиях, могут быть также не числа, а слова. Подобные задания выполняются аналогично заданиям с числами.
Варианты задания 3 ОГЭ по информатике с ФИПИ
Напишите натуральное число x, для которого ложно высказывание:
НЕ (x < 
Решение:
Сначала избавимся от НЕ и запишем выражение в виде
(х >=ИЛИ (х < 7). Оно ложно.
Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания.
То есть нам надо найти натуральное число не больше и не равное 8 (значит <И не меньше 7 (значит >= 7).
Переделаем ложное высказывание в истинное, применяя закон де Моргана:
(х <И (х >= 7) — истинно
7 8
__.____.__
Это 7
Проверяем:
7 >= 8 ? НЕТ, ложно
7 < 7 ? НЕТ, ложно. Оба высказывания ложны, значит мы нашли верный ответ.Ответ: 7
1A3B0C
Напишите натуральное число x, для которого ложно высказывание:
НЕ (x < 6) ИЛИ (x < 5).
Решение:
Сначала избавимся от НЕ и запишем выражение в виде
(х >= 6) ИЛИ (х < 5). Оно ложно.
Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания.
То есть нам надо найти натуральное число не больше и не равное 6 (значит < 6) И не меньше 5 (значит >= 5).
Переделаем ложное высказывание в истинное, применяя закон де Моргана:
(х < 6) И (х >= 5) — истинно
5 6
___.____.___
Это 5Ответ: 5
C2590F
Напишите наибольшее трёхзначное число x, для которого истинно высказывание:
НЕ (Первая цифра нечётная) И (x делится на 3).
Решение:
Избавимся от НЕ.
(Первая цифра чётная) И (x делится на 3) — истинное, значит должны выполняться ОБА условия.
Первая цифра — четная, максимум — 8.
Число делится на 3, если сумма его цифр делится на 3.
Проверяем 899. 8 + 9 +9 = 26 = 8, не делится на 3.
Проверяем 898. 25 = 7, не делится на 3.
Проверяем 897. 8 + 9 + 7 = 24 = 6, делится на 3.Ответ: 897
24647F
Напишите наибольшее трёхзначное число x, для которого истинно высказывание:
НЕ (Первая цифра чётная) И (x делится на 3).
Решение:
Избавимся от НЕ
(Первая цифра нечётная) И (x делится на 3) — истинно
Наибольшая нечетная цифра — 9
Наибольшее трехзначное число, начинающееся с девятки 999 — делится на 3.
Ответ: 999
AB2DCD
Напишите натуральное число x, для которого ложно высказывание:
(x < 4) ИЛИ НЕ (x < 5).
Решение:
Избавимся от НЕ:
(x < 4) ИЛИ (x ≥ 5) — ложно
Тогда по законам де Моргана
(x ≥ 4) И (x < 5) истинно
4 5
_______._____._______
Это 4
Ответ: 4
BA3498
Напишите наибольшее трёхзначное число x, для которого истинно высказывание:
(Первая цифра нечётная) И НЕ (x делится на 3).
Решение:
Избавимся от НЕ:
(Первая цифра нечётная) И (x не делится на 3) — истинно
Наибольшая нечетная цифра 9, наибольшее трехзначное число на девятку — 999, но оно делится на 3. Проверим 998 — не делится нацело на 3, значит второе условие выполняется.
Ответ: 998
668CE8
Напишите натуральное число x, для которого ложно высказывание:
(X < 
Решение:
Избавимся от НЕ:
(X <ИЛИ (X ≥ 9) — ложно
Тогда по законам де Моргана
(X ≥И (X < 9) истинно
8 9
_______._____._______
Это 8
Ответ: 8
820268
Напишите наибольшее трёхзначное число x, для которого истинно высказывание:
НЕ (Первая цифра нечётная) И НЕ (x делится на 3).
Решение:
Избавимся от НЕ:
(Первая цифра чётная) И (x не делится на 3)
Наибольшая четная цифра 8,
наибольшее трехзначное число на восьмерку 899, оно не делится на 3.
Ответ: 899
997D3D
Определите наименьшее трёхзначное число x, для которого истинно логическое выражение:
(x оканчивается на 3) И НЕ (x < 230).
Решение:
Избавимся от НЕ:
(x оканчивается на 3) И (x ≥ 230)
По первому условию последний разряд числа 3.
По второму условию это число больше или равно 230.
Наименьшее число, удовлетворяющее обоим условиям 233
Ответ: 233
0A6843
Определите наименьшее натуральное число x, для которого логическое выражение истинно:
(НЕ (x ≥ 15) И НЕ (x < 8)) И (x нечётное).
Решение:
Избавимся от НЕ:
((x < 15) И (x ≥ 8)) И (x нечётное) истинно,
значит нужно найти наименьшее нечетное натуральное число от 8 (включаядо 15 (не включая 15).
Это 9
Ответ: 9
5F2747
Определите количество натуральных двузначных чисел x, для которых ложно логическое выражение:
НЕ (x чётное) И НЕ (x > 39).
Решение:
Зададим вопрос: «Если среди N некоторых чисел, некоторому условию удовлетворяют M из них, то сколько чисел не удовлетворяют этому условию?». — Конечно, N – M чисел.
Учитывая это, определим сначала количество натуральных двузначных чисел х, для которых заданное выражение истинно.
Запишем его без операций отрицания:
(x нечётное) И (x <= 39)
Далее рассуждения такие. Двузначные натуральные числа, меньшие или равные 39 и являющиеся нечетными:
11, 13, 15, …, 39.
Всего их (39 – 11) : 2 + 1 = 15.
Но это количество чисел, для которых полученное логическое выражение истинно, а в задании требуется количество чисел, для которых оно ложно. В искомое количество входят все остальные двузначные числа. Это количество равно 90 – 15 = 75 (напомним, что общее количество натуральных двузначных чисел равно 90).Ответ: 75.
Можно также поступить по-другому.
Вопрос: «Если для некоторых чисел результат проверки заданного логического выражения является ложным, то для какого выражения эти же числа дадут истинный результат?» — Для противоположного логического выражения.
Пример: для положительных чисел логическое выражение (число <= 0) является ложным — для них истинным является противоположное логическое выражение (число > 0).
Как известно, для определения логического выражения, противоположного выражению с операциями конъюнкции и дизъюнкции (с логическими связками И и ИЛИ), можно применить так называемые «законы де Моргана».
Применим соответствующий закон к заданному в условии выражению
(НЕ (x чётное) И НЕ (x > 39)) — получим логическое выражение для определения количества чисел, требуемого по условию:
(x чётное) ИЛИ (x > 39)
С учетом того, что должны учитываться только двузначные числа, полученному выражению будут соответствовать числа:
10, 12, 14, … 38, 40, 41, 42, 43, …, 99.
Их общее число ((38 – 10) : 2 + 1) + (99 – 40 + 1) = 75.Ответ: 75.
Примечание. В данном случае первый способ решения лучше.
7C8BF1
! Определите наименьшее натуральное число x, для которого логическое выражение ложно:
НЕ ((x < 
Решение:
НЕ ((x <
И (x < 21)) ИЛИ (x нечётное) — ложно
Из (x <И (x < 21) можем оставить только (x < 8), потому что любое число менее 8-ми одновременно меньше 21-го, получится
НЕ (x <ИЛИ (x нечётное) — ложно
Тогда по законам де Моргана
(x <И (x чётное) истинно, то есть нужно найти наименьшее натуральное четное число меньше 8.
Ответ: 2Другой вариант решения
Можно было применить закон де Моргана ко всему начальному выражению.
НЕ ((x <И (x < 21)) ИЛИ (x нечётное) ложно по условию
Избавимся от НЕ. НЕ отрицает все условия из скобки, значит И оно тоже отрицает, меняем его на ИЛИ:
((x ≥ИЛИ (x ≥ 21) ИЛИ (x нечётное) — ложное
По закону де Моргана
((x <И (x < 21)) И (x чётное) истинное
Ответ: 2
5986FB
Определите наименьшее натуральное число x, для которого истинно логическое выражение:
НЕ ((x ≥ 15) ИЛИ (x < 7)).
Решение:
Избавимся от НЕ:
(x < 15) И (x ≥ 7) истинно
7 15
_______._____._______
Это 7
Ответ: 7
75C77D
! Определите количество натуральных чисел x, для которых логическое выражение ложно:
НЕ ((x < 
Решение:
Прежде всего, ясно, что вместо составного высказывания (x <
И (x < 21) можно записать только (x < 8), то есть все заданное выражение примет вид:
НЕ (x <ИЛИ (x нечётное)
Отказ от отрицания: (x >=ИЛИ (x нечётное) не позволит сразу найти искомое значение.
Тогда применим закон де Моргана к краткому варианту (НЕ (x <ИЛИ (x нечётное)) — получим логическое выражение для определения количества чисел, требуемого по условию:
(x <И (x чётное)
Итак, искомое количество равно количеству четных натуральных чисел, меньших 8, то есть трём (это числа 2,4,6).
Можно было также применить закон де Моргана ко всему выражению в условии:
(x <И (x < 21) И (x чётное)
В этом случае искомое количество чисел также равно трём.
Ответ: 3.
1ED874
! Определите наибольшее натуральное число x, для которого логическое выражение ложно:
НЕ ((x < 
Решение:
По законам де Моргана
((x <И (x < 21)) И (x чётное) истинно,
то есть нужно найти наибольшее натуральное четное число меньше 8-ми.
Ответ: 6
568E7E
! Определите количество натуральных двузначных чисел x, для которых истинно логическое выражение:
НЕ (x чётное) И НЕ (x кратно 5).
Решение:
Отказавшись, от операций отрицания, можно получить другое логическое выражение:
(x нечётное) И (x не кратно 5)
Как определить искомое количество? Можно рассуждать так.
Общее количество натуральных двузначных чисел равно 90 (99 – 10 + 1). Из них нечетных — 45. В числе этих 45 не следует учитывать числа, кратные 5. Их 9 (15, 25, …, 95).
Следовательно, количество нечетных натуральных двузначных чисел, не кратных 5, равно 45 – 9 = 36.Ответ: 36.
578573
! Определите количество натуральных двузначных чисел x, для которых истинно логическое выражение:
НЕ (x нечётное) И НЕ (x > 51).
Решение:
Избавимся от НЕ:
(x чётное) И (x <= 51) истинно,
то есть нужно найти количество натуральных двузначных четных чисел < либо = 51, это 12, 14, 16, … 48, 50.
Интервал от 10 до 51, но только четные.
Тогда 51-10=41 и прибавляем еще 1, так как подсчет не учитывает включительно крайнее число. Получаем 42. Делим пополам, так как нужны только четные.
42/2 =21
Ответ: 21
A9E611
Определите количество натуральных чисел x, для которых логическое выражение истинно:
(НЕ (x ≥ 15) И НЕ (x < 8)) И (x нечётное).
Решение:
Отказ от операций отрицания позволяет получить другое логическое выражение:
((x < 15) И (x >= 8)) И (x нечётное)
Числа, удовлетворяющие указанным границам: 8, 9, 10, 11, 12, 13, 14. Из них нечетными являются три числа.Ответ: 3
7AEE27
! Определите наибольшее натуральное число x, для которого логическое выражение истинно:
(НЕ (x ≥ 15) И НЕ (x < 8)) И (x нечётное).
Решение:
Избавимся от НЕ:
((x < 15) И (x ≥ 8)) И (x нечётное) истинно
то есть нужно найти наибольшее натуральное нечетное число от 8 (включительно) до 15 (не включая 15). Это 13
Ответ: 13
C4D725
! Определите количество натуральных чисел x, для которых истинно логическое выражение:
НЕ ((x ≥ 33) ИЛИ (x < 19)) И (x чётное).
Решение:
Здесь в заданном логическом выражении отрицание применено к двум простым высказываниям, соединенных дизъюнкцией (логической связкой ИЛИ). Вспомнив соответствующий закон де Моргана, можем заменить отрицание:
((x < 33) И (x >= 19)) И (x чётное)
то есть это натуральные четные числа от 19-ти (включая 19) и до 33 (не включая 33).
Соответствующие четные числа: 20, 22, 24, 26, 28, 30, 32.
32-19=13 и учитываем крайнее показание не включенного числа 23+1 = 14
14/2=7
Их общее число равно 7.
Ответ: 7.
C63DD8
! Определите количество натуральных двузначных чисел x, для которых истинно логическое выражение:
НЕ (x чётное) И НЕ (x > 67).
Решение:
Избавимся от НЕ:
(x нечётное) И (x <= 67) истинно
то есть, нужно найти количество натуральных двузначных нечетных чисел меньше или равное 67.
Интервал от 10 до 67.
67-10=57 чисел, к результату прибавляем 1, чтобы включить крайнее число, то есть 57+1=58. Так как числа нечетные, это половина от общего количества.
58/2=29
Ответ: 29
40FF5E
Определите наибольшее трёхзначное число x, для которого истинно логическое выражение:
НЕ (x оканчивается на 3) И НЕ (x > 115).
Решение:
Избавимся от НЕ:
(x не оканчивается на 3) И (x ≤ 115)
По первому условию число не оканчивается на 3.
По второму условию число меньше или равно 115.
Наибольшее трёхзначное ≤ 115, не оканчивающееся на 3 — это 115
Ответ: 115
CAA4AD
Напишите наименьшее натуральное число x, для которого истинно высказывание:
((x > 3) И НЕ (x < 4)) ИЛИ (x < 1).
Решение:
Избавимся от НЕ:
((x > 3) И (x ≥ 4)) ИЛИ (x < 1)
Первое условие: 4 и больше.
Второе: меньше 1.
Но так как меньше 1 — это уже не натуральное, то наименьшее натуральное будет в диапазоне от 4 до бесконечности. Наименьшее из них 4.
Ответ: 4
09B748
! Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 2) И ((x < 4) ИЛИ (x > 4)).
Решение:
(x > 2) И ((x < 4) ИЛИ (x > 4)) истинно
Первое условие: значения больше 2-х.
Второй диапазон: все, кроме числа 4.
Между ними И, значит оба условия выполняются одновременно.
2 4
_______._____._______…..
Наименьшее натуральное 3
Ответ: 3Будьте внимательны, смотрите, где стоят круглые скобки, какие именно условия они обобщают.
5C6C4C
Напишите наибольшее натуральное число x, для которого истинно высказывание:
НЕ (x < 5) И (x < 6).
Решение:
Избавимся от НЕ:
(x ≥ 5) И (x < 6) истинно
5 6
_______._____._______
Это 5
Ответ: 5
83F641
Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 7) И НЕ (x < 6).
Решение:
Избавимся от НЕ:
(x < 7) И (x ≥ 6)
6 7
_______._____._______
Это 6
Ответ: 6
742DF5
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x > 3) ИЛИ НЕ (x > 2).
Решение:
По законам де Моргана
(x ≤ 3) И (x > 2)
2 3
_______._____._______
Это 3
Ответ: 3
1259F7
! Напишите наибольшее натуральное число x, для которого ложно высказывание:
НЕ (x < 6) ИЛИ ((x < 5) И (x ≥ 4)).
Решение:
По законам де Моргана
(x < 6) И ((x ≥ 5) ИЛИ (x < 4)) — истинное высказывание
4 5 6
…___.___.___.___
То есть число меньше 6-ти и ≥ 5; либо меньше 6-ти и меньше 4-х.
Наибольшее натуральное, соответствующее условиям, число 5
Ответ: 5
5FC8F4
Напишите количество натуральных двузначных чисел, для которых истинно высказывание:
НЕ (Число < 88) И НЕ (Число нечётное).
Решение:
Избавимся от отрицания:
(Число ≥ 88) И (Число чётное) так же истинно
Подходят четные числа больше или равные 88. По условию они двузначные, значит интервал от 88 до 99.
99-88=11 чисел, при этом учитываем включительно крайнее число, которое не включено при подсчете.
11+1=12
Так как четных чисел в два раза меньше, то
12/2=6
Ответ: 6
A4BCFA
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x ≥ 3) ИЛИ НЕ (x ≥ 2).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x < 3) И (x ≥ 2) истинно
2 3
__.____.______
Наименьшее натуральное из этого интервала — число 2
Ответ: 2
2AD501
Дано четыре числа: 638, 442, 357, 123. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И НЕ (Сумма цифр чётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра нечётная) И (Сумма цифр нечётная) — тоже истинное высказывание
Рассмотрим 357 и 123.
3+5+7=15 и 1+2+3=6.
Подходит 357
Ответ: 357
D1CC0C
Напишите наименьшее трёхзначное число, большее 121, для которого ложно высказывание:
НЕ (Число > 50) ИЛИ (Число чётное).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив один из законов де Моргана:
(число > 50) И (число нечётное) — истинное высказывание.
Наименьшее трёхзначное число, большее 121, удовлетворяющее условию — это 123.Ответ: 123
908105
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 4) И НЕ (x > 5).
Решение:
Избавимся от отрицания:
(x > 4) И (x ≤ 5) — тоже истинно
4 5
__.____.____
Ответ: 5
E9780D
Напишите наибольшее натуральное двузначное число, для которого истинно высказывание:
НЕ (Число нечётное) И (Число кратно 11).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число кратно 11) — тоже истинно
Наибольшее четное, кратное 11-ти — это 88
Ответ: 88
7FBEB2
Напишите наименьшее натуральное число x, для которого ложно высказывание:
НЕ (x > 2) ИЛИ ((x < 4) И (x > 1)).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x > 2) И ((x ≥ 4) ИЛИ (x ≤ 1)) истинно
х не может быть больше 2-х и ≤ 1 одновременно, так что условие (x ≤ 1) можно вычеркнуть. Остается:
(x > 2) И (x ≥ 4) истинно
1 2 4
_.____.______._______…..
Наименьшее 4
Ответ: 4
4F2C17
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число нечётное) И НЕ (Число > 18).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число ≤ 18) — тоже истинно
То есть ищем количество четных натуральных чисел до 18-ти включительно.
18 натуральных чисел, из которых каждое второе четное (половина лишь четных).
18/2=9
Ответ: 9
481611
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 1) И (x > 2) И (x ≠ 3).
Решение:
1 2 3
___.___.___.____…
Наименьшее из натуральных в подходящем диапазоне — число 4.
Ответ: 4
4C6A11
Дано четыре числа: 648, 452, 357, 123. Для какого из приведённых чисел истинно высказывание:
(Первая цифра чётная) И НЕ (Сумма цифр чётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра чётная) И (Сумма цифр нечётная) — тоже истинно
По первому условию 648 или 452.
По второму 6+4+8=18 — не подходит
4+5+2=11 — подходит
Ответ: 452
9E2E1E
Напишите наименьшее натуральное трехзначное число, для которого истинно высказывание:
НЕ (Число нечётное) И (Число кратно 3).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число кратно 3) — тоже истинно
Получается, это число 102, так как оно четное и делится на 3, при этом минимальное трехзначное (больше 100).
Ответ: 102
E5BC1A
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(НЕ (x ≥ 6) И НЕ (x = 5)) ИЛИ (x ≤ 7).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив один из законов де Моргана:
((x ≥ 6) ИЛИ (x = 5)) И (x > 7) истинно
5 6 7
___.___.___._________
Наименьшее натуральное, соответствующее условиям, число 8
Ответ: 8
1EAF20
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x ≤ 2) И НЕ (x ≤ 1).
Решение:
Избавимся от отрицания:
(x ≤ 2) И (x > 1) — тоже истинно
1 2
___.___.___
Ответ: 2
D1C824
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x < 3) И НЕ (x < 2).
Решение:
Избавимся от отрицания:
(x < 3) И (x ≥ 2) — тоже истинно
2 3
___.___.__
Ответ: 2
DCCB2A
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число нечётное) И НЕ (Число > 14).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число ≤ 14) — тоже истинно
Надо узнать количество четных от 1 до 14, где четное каждое второе.
14/2=7 четных чисел.
Ответ: 7
A0DD26
Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 5) И НЕ (x < 4).
Решение:
Избавимся от отрицания:
(x < 5) И (x ≥ 4) — тоже истинно
4 5
___.____.___
Ответ: 4
C93020
Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 
Решение:
Избавимся от отрицания:
(x <И (x ≥ 7) — тоже истинно
7 8
__.___.__
Ответ: 7
97E220
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число > 19) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Число ≤ 19) И (Число нечётное) — тоже истинно
То есть, надо найти количество нечетных натуральных от 1 по 19 включительно. Их 10.
Ответ: 10
9FCC22
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ (x > 5) И (x > 4).
Решение:
Избавимся от отрицания:
(x ≤ 5) И (x > 4) — тоже истинно
4 5
__.___.___
Ответ: 5
603E2F
! Напишите наибольшее двузначное число, меньшее 55, для которого истинно высказывание:
(Число < 75) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Число < 75) И (Число нечётное) — тоже истинно
То есть под условия подходят все нечетные менее 75-ти. Но нам сказано найти наибольшее двузначное, меньшее 55. Из нечетных это число 53
Ответ: 53
67AF2A
Дано четыре числа: 6843, 4562, 3561, 1234. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И (Последняя цифра нечётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра нечётная) И (Последняя цифра нечётная) — тоже истинно
Ответ: 3561
31FE21
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 2) И НЕ (x > 3).
Решение:
Избавимся от отрицания:
(x > 2) И (x ≤ 3) — тоже истинно
2 3
__.___.__
Ответ: 3
8A9928
Дано четыре числа: 6843, 4562, 3561, 1234. Для какого из приведённых чисел истинно высказывание:
(Первая цифра чётная) И НЕ (Последняя цифра нечётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра чётная) И (Последняя цифра чётная) — тоже истинно
Первая и последняя четная.
Ответ: 4562
592550
Напишите наибольшее натуральное число x, для которого истинно высказывание:
НЕ (x < 10) И (x < 11) И (x > 8).
Решение:
Избавимся от отрицания:
(x ≥ 10) И (x < 11) И (x >— тоже истинно
8 10 11
___._____.___.____
Ответ: 10
5E6651
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ (x < 6) И (x < 7).
Решение:
Избавимся от отрицания:
(x ≥ 6) И (x < 7) — тоже истинно
6 7
__.___.___
Ответ: 6
CF5FA5
Напишите наименьшее натуральное трёхзначное число, для которого истинно высказывание:
НЕ (Число нечётное) И (Число кратно 11).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число кратно 11) — тоже истинно
Первое условие — четное.
Второе: делится на 11 без остатка.
Еще и наименьшее трехзначное при этом.
110 : 11 = 10, подходит.
Ответ: 110
F10CCC
! Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x < 3) И ((x < 2) ИЛИ (x > 2)).
Решение:
(x < 3) И ((x < 2) ИЛИ (x > 2)) — тоже истинно
То есть, х меньше 3-х, кроме числа 2.
Наименьшее натуральное число 1
Ответ: 1
291BC6
Дано четыре числа: 35, 4598, 54321, 24. Для какого из приведённых чисел истинно высказывание:
(Число > 100) И НЕ (Число нечётное)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Число > 100) И (Число чётное) — тоже истинно
То есть, четное больше сотни.
Подходит 4598.
Ответ: 4598
DC5FC8
! Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 5) ИЛИ НЕ (x > 3).
Решение:
Избавимся от отрицания:
(x < 5) ИЛИ (x ≤ 3) — тоже истинно
3 5
…___.___.__
Ответ: 4
93C0C4
Напишите наибольшее натуральное число x, для которого ложно высказывание:
НЕ (x < 7) ИЛИ (x < 6).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x < 7) И (x ≥ 6) истинно,
в соответствии с этим высказыванием можем построить числовой луч и отметить нужный интервал:
6 7
__.___.____
Ответ: 6
3E8BCD
Напишите наибольшее натуральное двузначное число, для которого истинно высказывание:
НЕ (Число нечётное) И (Число кратно 3).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число кратно 3) — тоже истинно
Ищем наибольшее натуральное двузначное четное, кратное 3-м.
Ответ: 96
4A4395
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x > 4) И (x < 7) И (x < 6).
Решение:
4 6 7
__._____.___._
Ответ: 5
BED497
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x > 2) ИЛИ НЕ (x > 1).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x ≤ 2) И (x > 1) истинно
1 2
__.____.__
Ответ: 2
C8BAED
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число нечётное) И НЕ (Число > 12).
Решение:
Избавимся от отрицания:
(Число чётное) И (Число ≤ 12) — тоже истинно
То есть, нужны четные с 1 по 12 включительно.
Так как четные числа идут через одно, то берем половину от общего количества чисел.
12/2=6
Ответ: 6
3B55E9
Напишите наибольшее натуральное число x, для которого истинно высказывание:
НЕ (x < 3) И (x < 4).
Решение:
Избавимся от отрицания:
(x ≥ 3) И (x < 4) — тоже истинно
3 4
_.___.___
Ответ: 3
B9AD6A
Дано четыре числа: 638, 442, 357, 123. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И (Сумма цифр чётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра не чётная) И (Сумма цифр чётная) — тоже истинно
Первая нечетная у 357, 123.
3+5+7=15 — нечетное 1+2+3=6 — четное.
Ответ: 123
D47460
Напишите наибольшее трехзначное число, меньшее 124, для которого истинно высказывание:
(Сумма цифр кратна 5) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Сумма цифр кратна 5) И (Число нечётное) — тоже истинно
Подбираем, перебирая нечетные числа меньше 124-х.
113 — нечетное, меньше 124, 1+1+3=5 делится на 5
Ответ: 113
AB9560
Напишите наименьшее двузначное число, большее 54, для которого ложно высказывание:
(Число < 40) ИЛИ НЕ (Число чётное).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(Число ≥ 40) И (Число чётное) истинно
Наименьшее четное ≥ 40 больше 54 — это число 56
Ответ: 56
6D4D61
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x = 2) ИЛИ НЕ (x < 3).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x ≠ 2) И (x < 3) — истинное выражение
2 3
…__.___.___
Ответ: 1
3BC762
Напишите количество натуральных двузначных чисел, для которых истинно высказывание:
НЕ (Число < 83) И (Число нечётное).
Решение:
Избавимся от отрицания:
(Число ≥ 83) И (Число нечётное) — тоже истинно
У нас условие, что это 83 и больше и нечетные числа.
100-83=17 чисел с 83 до 100. И прибавляем 1, дабы включить крайнее неучтенное число. 17+1=18.
Нечетных — половина из них: 18/2=9
Ответ: 9
44FE34
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число > 15) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Число ≤ 15) И (Число нечётное) — тоже истинно
Нечетные до 15 включительно.
(15+1):2=8
Ответ: 8
4A2239
Дано четыре числа: 6843, 4562, 3561, 1234. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И НЕ (Последняя цифра нечётная)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Первая цифра нечётная) И (Последняя цифра чётная) — тоже истинно
Ответ: 1234
013A31
Напишите наибольшее двузначное число большее 50, для которого истинно высказывание:
НЕ (Число > 75) И (Число чётное).
Решение:
Избавимся от отрицания:
(Число ≤ 75) И (Число чётное) — тоже истинно
Ищем наибольшее четное двузначное большее 50, но ≤ 75
Ответ: 74
204E3B
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ ((x > 3) ИЛИ (x < 2)) И (x > 2).
Решение:
НЕ ((x > 3) ИЛИ (x < 2)) И (x > 2)
Избавимся от отрицания:
((x ≤ 3) И (x ≥ 2)) И (x > 2) — тоже истинно
По первым двум условиям получается интервал
2 3
___.___._____
По второму условию x > 2, значит это 3
Ответ: 3
20BF36
Напишите наибольшее натуральное число x, для которого ложно высказывание:
НЕ (x < 6) ИЛИ (x < 5).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x < 6) И (x ≥ 5) — истинное выражение
5 6
__.__.__
Ответ: 5
54C33D
Напишите количество натуральных чисел, для которых истинно высказывание:
НЕ (Число > 13) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Число ≤ 13) И (Число нечётное) — тоже истинно
Нечетные до 13-ти включительно.
Числа можно разбить на пары чет/нечет, нечетных среди них будет половина. 13-ти до пары не хватает 1.
(13+1):2=7
Ответ: 7
97A63B
Напишите наибольшее двузначное число, меньшее 75, для которого истинно высказывание:
(Сумма цифр нечетная) И НЕ (Число чётное).
Решение:
Избавимся от отрицания:
(Сумма цифр нечетная) И (Число нечётное) — тоже истинно
Подберем нечетное число с нечетной суммой цифр, меньшее 75. Оно должно начинаться на четное число, иначе сумма будет четной. Проверяем седьмой десяток: 69 подходит.
Ответ: 69
836839
Дано четыре числа: 54321, 45980, 125, 24. Для какого из приведённых чисел истинно высказывание:
НЕ (Число > 10000) И (Число нечётное)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Число ≤ 10000) И (Число нечётное) — тоже истинно
10000 и меньше и нечетное. Это 125
Ответ: 125
B5AB8F
! Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x > 3) ИЛИ НЕ ((x < 4) И (x > 2)).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x ≤ 3) И ((x < 4) И (x > 2)) — истинное выражение
2 3 4
__.___.__.___
Ответ: 3
B16C83
! Напишите наименьшее натуральное число x, для которого ложно высказывание:
НЕ (x > 2) ИЛИ (x = 4).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x > 2) И (x ≠ 4) — истинное выражение
2 4
__.___.__…
Ответ: 3
1A868B
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x < 4) И (x > 1) И (x ≠ 2).
Решение:
1 2 4
__.___._____._
Наименьшее, да и единственное натуральное число из этого интервала — число 3
Ответ: 3
293C81
Дано четыре числа: 54324, 4597, 46, 25. Для какого из приведённых чисел истинно высказывание:
НЕ (Число < 100) И НЕ (Число чётное)?
В ответе запишите это число.
Решение:
Избавимся от отрицания:
(Число ≥ 100) И (Число нечётное) — тоже истинно
Больше или равно 100 и одновременно нечетное.
Ответ: 4597
8D4389
! Определите количество натуральных трёхзначных чисел x, для которых истинно логическое выражение:
(x оканчивается на 7) И НЕ (x > 119).
Решение:
Избавимся от отрицания:
(x оканчивается на 7) И (x ≤ 119) — тоже истинно
Берем все числа, оканчивающиеся на 7 до 119. И мы знаем, что в каждом десятке только одно число может иметь вариацию числа, где оно оканчивается на 7. И нам надо трехзначное число, то есть берем десятки со 100 до 110. Это один десяток. И получаем 1 неполный десяток, где также можно встретить число 7 в конце, в числе 117. Итого 1+1 =2.
Ответ: 2
83D5CA
Определите наименьшее натуральное двузначное число x, для которого ложно логическое выражение:
НЕ (x нечётное) И НЕ (x > 88).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x нечётное) ИЛИ (x > 88) — истинное выражение
То есть выбор из всех двузначных нечетных, потому что среди них значения меньше, чем после 88.
Ответ: 11
5F31E5
Определите количество натуральных чисел x, для которых истинно логическое выражение:
НЕ ((x ≥ 53) ИЛИ (x < 29)).
Решение:
Избавимся от отрицания:
(x < 53) И (x ≥ 29) тоже истинно
29 53
__._____.____
То есть, если брать только натуральные числа, это интервал от 29 по 52 включительно.
52-29+1=24
Ответ: 24Обратите внимание, что оба условия отрицаются в одних скобках, значит ИЛИ меняем на И.
3FE867
! Определите наибольшее натуральное двузначное число x, для которого ложно логическое выражение:
(x чётное) ИЛИ НЕ (x > 92).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x нечётное) И (x > 92) — истинное выражение
Наибольшее из нечетных больше чем 92 — это 99.
Ответ: 99
674B8F
!! Определите количество натуральных двузначных чисел x, для которых ложно логическое выражение:
НЕ (x чётное) И НЕ (x кратно 13).
Решение:
Здесь удобно определить логическое выражение, противоположное заданному, применив законы де Моргана:
(x чётное) ИЛИ (x кратно 13) — истинное выражение
То есть это все натуральные четные двузначные числа + нечетные двузначные числа, которые делятся нацело на 13.
Двузначных четных 45 штук. (Интервал от 10 до 99; 99-10=89, 89+1 (крайнее число, которое не учтено)=90, 90/2=45)
Делятся на 13 следующие: 13, 26, 39, 52, 65, 78, 91. Но все четные мы уже учли в первом условии, так что берем только нечетные, их 4.
45 + 4 = 49
Ответ: 49
367282
Определите наибольшее натуральное число x, для которого истинно логическое выражение:
НЕ ((x ≥ 23) ИЛИ (x < 18)).
Решение:
Избавимся от отрицания:
(x < 23) И (x ≥ 18) — тоже истинно
18 23
__.___.__
Наибольшее натуральное в этом интервале 22.
Ответ: 22
88B087