
Число измерений фазового пространства. Если число степе-
ней свободы частицы f, то для N независимых частиц число координат n = fN , тогда вместе с проекциями импульсов число измерений фа-
зового пространства системы 2 fN .
2.2. Число микросостояний
Объем микросостояния. Элемент объема фазового пространства для N независимых частиц
dVX = dq1 dq2…dqn dp1 dp2…dpn = d fN q d fN p .
Для одномерного движения частицы N =1, f =1, n = fN =1 единица измерения
[VX ] =[ p][x] = кг м2 с−1 = Дж с =[h],
где h – постоянная Планка. Молекулы, атомы, электроны подчиняются законам квантовой механики – микрочастицы одной природы тождественны друг другу, выполняется соотношение Гейзенберга
для неопределенностей координаты и импульса частицы
δVX ≡ δx δp ≥ h .
Это ограничивает снизу фазовый объем микросостояния с n =1. Сле-
довательно, минимальный объем элементарной ячейки двухмерно-
го фазового пространства, который занимает одно микросостояние, равен постоянной Планка h. Форма элементарной ячейки произвольна и может изменяться с течением времени. В 2fN-мерном
фазовом пространстве минимальный объем микросостояния h fN .
Число микросостояний газа из N частиц, находящихся в эле-
менте объема фазового пространства d fN q d fN p , равно безразмерному объему
|
dX = |
d fN q d fN p |
. |
(2.1) |
||
|
h fN N ! |
|||||
|
Множитель N! учитывает тождественность микрочастиц, их взаимная |
|||||
|
перестановка дает N! физически |
одинаковых |
состояний, которые |
49

Г л а в а 2. СТАТИСТИЧЕСКАЯ ФИЗИКА КЛАССИЧЕСКИХ СИСТЕМ
должны учитываться однократно. Из (2.1) получаем число микросостояний газа в объеме VX фазового пространства
|
∆X N = ∫ dX = |
1 |
∫ d fN q d fN p . |
(2.2) |
|||
|
h |
fN |
N ! |
||||
|
VX |
VX |
|||||
Микросостояния с фиксированной энергией E находятся в 2fN-мерном фазовом пространстве на гиперповерхности H (X ) = E , где H (X ) –
гамильтониан системы. Число состояний внутри гиперповерхности получаем из (2.2)
|
∆X N (E) = ∫ dX = ∫H[E − H (X )] dX , |
(2.3) |
|
|
H ( X )=E |
||
|
где H(E) – функция Хевисайда, или функция включения: |
||
|
1, |
x > 0, |
|
|
H(x) = |
x < 0. |
|
|
0, |
При отсутствии внешнего силового воздействия координаты и импульсы частиц не зависят друг от друга, тогда интегрирования в (2.2) разделяются:
|
∆X N (Vf ,Vp ) = |
1 |
∫ |
d fN q ∫ d fN p = |
VfN |
Vp,N , |
(2.4) |
|||||
|
h |
fN |
N ! |
h |
fN |
N ! |
||||||
|
V f |
Vp |
||||||||||
|
где Vf – объем сосуда, в котором находится газ; |
Vp,N = ∫ d fN p – объ- |
||||||||||
|
Vp |
ем импульсного пространства, доступный для N частиц газа.
Для идеального изолированного классического газа с потенциальной энергией U = const и массами частиц m, не зависящими от направления, полная и кинетическая энергии постоянны и связаны с импуль-
сами законом дисперсии
E −U = 21m (p12 + p22 +…+ pn2 ).
50

2.2. ЧИСЛО МИКРОСОСТОЯНИЙ
В импульсном пространстве получаем уравнение сферы
p12 + p22 +…+ pn2 =1.
2m(E −U )
Микросостояния идеального газа с полной энергией Е и потенциальной энергией U = const находятся в импульсном пространстве
на сфере радиусом p = 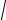
|
V = |
2πn/2 |
pn . |
(2.5) |
|
n |
n Г(n / 2) |
||
|
Для газа из N частиц в объеме Vf |
с полной энергией E ≥U из (2.4) и |
|||||||
|
(2.5) получаем число микросостояний |
||||||||
|
∆X N (E,Vf ) = |
2 |
VfN |
[2πm(E −U )] fN /2 . |
(2.6) |
||||
|
fN Γ( fN / 2) h fN N ! |
||||||||
В общем случае не все микросостояния реализуются с одинаковой вероятностью для конкретного макросостояния системы. Степень их реализации описывает функция распределения по микросостояниям.
Число микросостояний частицы. Обобщенные координаты q
и импульсы p частицы связаны с ее энергией дисперсионным соотношением ε = εкин(p) +u(q) . Микросостояния с фиксированной энер-
гией находятся в 2f-мерном фазовом пространстве на гиперповерхности ε = ε( p, q) . Число состояний внутри гиперповерхности получаем из
(2.2) и (2.3) при N =1
|
∆X1(ε) = |
1 |
∫ |
d f q d f p = |
1 |
∫H[ε−ε( p, q)] d f q d f p , |
(2.7) |
|
|
f |
f |
||||||
|
h |
ε( p,q) |
h |
|||||
|
где H(ε) – функция Хевисайда. Число состояний с энергией ε в еди- |
|||||||
|
ничном объеме сосуда около точки q |
|||||||
|
nq (ε, q) = |
1 |
∫H[ε−ε( p, q)] d f p . |
(2.8) |
||||
|
f |
|||||||
|
h |
51

Г л а в а 2. СТАТИСТИЧЕСКАЯ ФИЗИКА КЛАССИЧЕСКИХ СИСТЕМ
Число состояний в единичном интервале импульсов около значения p в объеме Vf
|
np (ε, p) = |
1 |
∫ H[ε−ε( p, q)] d f q . |
(2.9) |
|
f |
|||
|
h |
V f |
||
Выполняется
∆X1(ε) = ∫nq (ε, q) d f q = ∫np (ε, p) d f p .
Для частицы с законом дисперсии ε = spt +u(q) , где s и t – веще-
ственные числа; p – модуль импульса, при фиксированных энергии и координатах гиперповерхность в импульсном пространстве является
сферой радиусом p ={[ε−u(q)]/ s}1/t . Интеграл по импульсам в (2.7)
|
равен объему шара (2.5) |
||||
|
Vf (ε, q) = |
2πf /2 |
{[ε−u(q)]/ s}f /t |
||
|
f |
Г( f /2) |
|||
Результат интегрируем по координатам области, верхностью u(q) = ε, и из (2.7) получаем
|
∆X1 |
(ε) = |
2πf /2 |
∫ [ε−u(q)] f |
|||
|
f Γ( f / 2) h |
f |
s |
f /t |
|||
|
u(q)≤ε |
Если энергия частицы зависит от импульса ε = ε( p) и не зависит от координат u(q) = u = const , тогда в (2.7) интегрирования по коорди-
натам и импульсам разделяются. Получаем число состояний частицы с энергией ε
|
∆X1(ε,Vf ) = |
Vf |
Vp, f |
(ε) , |
(2.11) |
|
|
h f |
|||||
|
где Vp, f (ε) = ∫H[ε−ε( p)] d f p = ∫ |
d f p – |
объем |
импульсного про- |
||
|
ε( p) |
странства, ограниченный гиперповерхностью ε = ε( p) .
52
Соседние файлы в папке Лекции Квант.мех. СГФ
- #
- #
- #
- #
- #
- #
Содержание
- 1 Микро- и макросостояния
- 2 Статистический вес макросостояния
- 3 Статистическое определение энтропии
- 4 Аддитивность энтропии
- 5 Закон возрастания энтропии
Микро- и макросостояния
Микросостояние — это состояние системы, определяемое одновременным заданием координат и импульсов всех составляющих систему
частиц. Знание микросостояния в некоторый момент времени позволяет однозначно предсказать эволюцию системы во все последующие моменты.
Макросостояние — это состояние системы, характеризуемое небольшим числом макроскопических параметров. Одно макросостояние может быть реализовано большим числом микросостояний за счет перестановки частиц, не меняющей наблюдаемого состояния.
Статистическое описание больших систем существенно опирается на следующие постулаты.
1. Все разрешенные микросостояния равновероятны.
2. Термодинамически равновесным является то макросостояние, которое реализуется наибольшим числом микросостояний, т. е. является
наиболее вероятным состоянием.
Статистический вес макросостояния
Элемент объема фазового пространства равен dT = d^(3N)qd^(3N)p или, более подробно,
dГ = П(i=1..N) d^(3N)q_i d^(3N)p_i,
где (q, р) — совокупность координат и импульсов всех частиц. Например, в случае двух частиц (N = 2)
dГ = d^6 q d^6 p.
Здесь, в частности,
d^6 q = (dx1dy1dz1)(dx2dy2dz2) = d^3 q1 d^3 q2 = dV1 dV2.
Если разбить все фазовое пространство на ячейки объемом Г0, полагая, что на одну ячейку приходится одно микросостояние, то число состояний в объеме dГ окажется равным dG = dГ/Г0. В рамках классической механики нужно положить Го -> 0. Согласно квантовой механике элементарный объем следует выбрать равным Г0 = (2pi h)^(3N), где h — постоянная Планка. Поэтому число микросостояний (число элементарных ячеек) в элементе фазового пространства dГ можно найти по формуле
dG = dГ/(2pi h)^(3N).
Согласно сказанному одной ячейке соответствует одно микросостояние. Различные ячейки отвечают различным микросостояниям, но могут
отвечать одному макросостоянию, если получаются перестановками одинаковых частиц. Пусть суммарный объем ячеек, отвечающих некоторому макросостоянию, есть Г. Тогда число микросостояний, реализующих данное макросостояние, равно G = Г/(2pi h)^(3N). Величина G называется статистическим весом рассматриваемого макросостояния (или термодинамической вероятностью). Она пропорциональна обычной вероятности W реализации данного макросостояния.
Для иллюстрации смысла статистического веса рассмотрим следующую модель. Пусть система содержит 4 частицы, а ее фазовое пространство состоит из двух ячеек (ящиков). В зависимости от распределения частиц по ячейкам возможны 5 различных макросостояний
При подсчете числа микросостояний следует учесть, что расположение частиц в пределах одной ячейки не играет роли. Тогда полное число различных микросостояний оказывается равным C0,4 + C1,4 + C2,4 + C3,4 + C4,4 = 16. Наибольшее число микросостояний отвечает макросостоянию № 3. Это состояние имеет наибольшую вероятность появления, ему отвечает наибольший статистический вес G = 6. Если бы
система состояла из N частиц, то статистический вес макросостояния, в котором в одной ячейке находится n частиц, а в другой — N-n, оказался бы равным G = C(из N по n).
Статистическое определение энтропии
В статистической физике энтропия системы определяется формулой Больцмана:
S = k ln G.
Это определение можно переписать в виде G = exp(S/k). Иначе говоря, чем больше энтропия, тем больше статистический вес состояния.
Аддитивность энтропии
Разобьем систему на две подсистемы. Статистические веса подсистем обозначим соответственно G1 и G2. Если подсистемы слабо взаимодействуют друг с другом, то почти независимо меняются и их микросостояния. Поэтому статистический вес всей системы равен произведению чисел способов, которыми могут быть осуществлены состояния каждой из подсистем: G = G1G2. Но это означает, что
S = k ln G = k ln G1 + k ln G2 = S1 + S2.
Таким образом, энтропия системы равна сумме энтропии ее частей (свойство аддитивности энтропии). В частности, если система состоит из N одинаковых макроскопических тел, то энтропия одного тела равна S1 = S/N, где S — энтропия всей системы. Последнее утверждение можно получить и непосредственно, исходя из выражения для статистического веса G = N! / (N1! N2! … Nm!):
S = k ln G = -kN сумма(i=1..m) N_i/N ln (N_i/N) = -kN сумма(i=1..m) W_i ln W_i = NS_1,
где S1 = -k <ln W_i>. Полученная формула позволяет вычислять энтропию отдельных тел, входящих в систему.
Закон возрастания энтропии
Среди всех направлений эволюции системы предпочтительным является то, при котором вероятность конечного состояния оказывается наибольшей. Это означает, что
1) с наибольшей вероятностью энтропия замкнутой системы растет (не убывает): dS/dt >= 0;
2) в состоянии термодинамического равновесия энтропия максимальна: S = Smax, dS/dt = 0.
Следует иметь в виду, что эти утверждения носят не абсолютный характер: с некоторой вероятностью энтропия замкнутой системы может и
убывать. Более того, если в какой-то момент энтропия достигает максимального значения, то почти наверняка в следующий момент она уменьшится. Таким образом, энтропия системы, находящейся с макроскопической точки зрения в состоянии термодинамического равновесия, совершает небольшие колебания.
Число — микросостояние
Cтраница 1
Число микросостояний, которыми осуществляется данное макросостояние, называется статистическим весом Р или термодинамической вероятностью этого макро-состояния. Статистический вес является функцией состояния.
[1]
Число микросостояний, которые соответствуют данному макросостоянию вещества, называется термодинамической вероятностью его состояния W. Таким образом, величина Ж — это число способов, которыми молекулы, составляющие систему, можно распределить по доступным для них уровням энергии при заданных объеме системы К и ее внутренней энергии U. Число доступных уровней энергии, следовательно, и W, растет с повышением температуры и увеличением объема. Таким образом, величина W есть число различных способов реализации данного состояния вещества.
[2]
Число микросостояний w, которым характеризуется макросостояние системы, называется термодинамической вероятностью этого состояния.
[3]
Число микросостояний в баллончике записывается 1017 цифрами… Значит, чтобы записать интересующее нас число микросостояний, потребовалась бы книга в сто миллиардов раз ( Ю11) более толстая, чем эта.
[4]
Число микросостояний, с помощью которых может быть осуществлено данное макросостояние, называется термодинамической вероятностью. В отличие от математической вероятности, которая, в соответствии с определением ( отношение числа случаев, благоприятствующих данному событию, к общему числу равновозможных случаев), колеблется в пределах от нуля до единицы, термодинамическая вероятность является очень большой величиной. Очевидно, математическая вероятность состояния равна отношению термодинамической вероятности состояния к общему числу возможных микросостояний с одинаковой энергией.
[5]
Число микросостояний, отвечающих данному макросостоянию системы, называется термодинамической вероятностью ( W или Q) состояния.
[6]
Число микросостояний, которые соответствуют данному макросостоянию вещества х называется термодинамической вероятностью его состояния W. Таким образом, величина Ж — это число способов, которыми молекулы, составляющие систему, можно распределить по доступным для них уровням энергии при заданных объеме системы К и ее внутренней энергии U. Число доступных уровней энергии, следовательно, и W, растет с повышением температуры и увеличением объема. Таким образом, величина W есть число различных способов реализации данного состояния вещества.
[7]
Число микросостояний, с помощью которых может быть осуществлено данное макросостояние, называется термодинамической вероятностью. В отличие от математической вероятности, которая в соответствии с ее определением ( отношение числа случаев, благоприятствующих данному событию, к общему числу равновоз-м о ж н ы х случаев) колеблется в пределах от нуля до единицы, термодинамическая вероятность всегда больше единицы и обычно является очень большой величиной. Очевидно, математическая вероятность состояния равна отношению термодинамической вероятности состояния к общему числу возможных микросостояний с одинаковой энергией.
[8]
Число микросостояний, при которых реализуется данное значение энергии, называется ее статистическим весом ДГ.
[9]
Число микросостояний Г, называется также термодинамической вероятностью макроскопического состояния. Это число не является вероятностью в математическом смысле, поскольку она всегда или равна или меньше единицы, число же Г, очень большое. Тем не менее оно получило название вероятности ( термодинамической), поскольку с его помощью по формуле (5.1) находится вероятность соответствующего макросостояния.
[10]
Число микросостояний, отвечающих данному макросостоянию системы, называется термодинамической вероятностью состояния W. Система самопроизвольно оказывается в состоянии, которому соответствует наибольшее число возможностей его реализации.
[11]
Число Wn микросостояний, соответствующих л-му макросостоянию, называют статистическим весом, или, иначе, термодинамической вероятностью п-то макросостояния. Согласно ( 5), термодинамическая вероятность макросостояния пропорциональна его вероятности w, но отнюдь не равна ей.
[12]
Число микросостояний W, которым может быть реализовано данное макросостояние, называется термодинамической вероятностью этого состояния. V функция (3.46) имеет острый максимум, отвечающий равномерному распределению частиц по объему. Подсчет по формуле (3.46) показывает, что для 1 м3 газа при нормальных условиях термодинамическая вероятность равномерного распределения частиц по объему в Ю1 10 раз больше вероятности состояния, при котором все молекулы газа располагаются лишь в одной из половин этого объема. Поэтому замкнутая система, предоставленная самой себе, будет находиться практически всегда в наивероятнейшем состоянии, которому соответствует максимум термодинамической вероятности.
[13]
Число микросостояний Q называется еще статистическим весом макросостояния. Как правило, эта величина принимает очень большие значения. Термодинамическую вероятность обычно не нормируют на единицу.
[14]
Число микросостояний W является функцией последовательности чисел заполнения ftг, которая определяет макросостояние.
[15]
Страницы:
1
2
3
4
Если из N молекул системы, имеющей объем V, в одну половину этого объема попадают в другую N2=N—молекул, то число возможных распределений различимых молекул, отвечающих указанному суммарному распределению между двумя половинами объема (число микросостояний, т. е. термодинамическая вероятность), W определяется формулой [c.104]
Процесс растворения сопровождается значительным возрастанием энтропии системы, так как в результате равномерного распределения частиц одного вещества в другом резко увеличивается число микросостояний системы. Поэтому, несмотря на эндотермичность растворения большинства кристаллов, изменение энергии Г иббса системы при растворении отрицательно и процесс протекает самопроизвольно. [c.219]
Полное число микросостояний, т. е. термодинамическая вероятность данного макросостояния, получится теперь умножением найденного числа распределений по группам на числа распределений внутри групп. [c.195]
Одно и то же макросостояние системы, т. е. состояние, заданное термодинамическими параметрами, может существовать (при условии постоянства средней энергии) при различном распределении энергии между отдельными молекулами, другими словами, осуществляется очень большим числом микросостояний. [c.93]
Разобьем фазовое пространство на ряд ячеек с ребрами йх, йу, йг,, й тю ), й(тьу), й ти ). Объем этих ячеек равен йх-йу-йг- (1 тюх) й mvy) й(ти ). В данную фазовую ячейку попадают молекулы, координаты которых заключены в пределах от х до л + х, от у ло у йу я т. д. Теперь становится возможным все молекулы системы распределить согласно значениям их координат по соответствующим ячейкам фазового пространства, а распределение молекул позволяет найти число микросостояний, отвечающих данному макросостоянию, т. е. термодинамическую вероятность. [c.94]
Вычисление термодинамической вероят. ности. Состояние каждой простой молекулы в газе определяется тремя пространственными координатами (х, у, г) и тремя координатами движения или импульсов mvx, mVy, ти ). Если считать, что эти величины изменяются непрерывно, то любому макросостоянию будет отвечать бесконечно большое число микросостояний. Различие между микросостояниями выявится, если задать узкие интервалы координат и импульсов, а затем сравнивать количества молекул, соответствующие этим интервалам. В статистической термодинамике состояние молекул представляют в воображаемом многомерном пространстве , которое в отличие от геометрического пространства называется фазовым — пространство координат положения и импульсов. Разобьем фазовое пространство на ряд ячеек с ребрами х, у, (12, й (тЮх), й (ши ), (1 (ти ). Объем таких ячеек равен йх с1у йг с1 mVл) й тОу) х X й mVг). В данную фазовую ячейку попадают молекулы, координаты которых заключены в пределах от л до л + х, от у цр у йу, от г до 2 + йг. Все молекулы системы можно распределить согласно значениям их координат по соответствующим ячейкам фазового пространства. Молекулы, находящиеся в разных ячейках, становятся различимыми. Этот постулат, принятый в статистике Больцмана, позволяет найти число микросостояний, определяющих данное макросостояние системы, т. е. найти термодинамическую вероятность. Таким образом, для нахождения термодинамической вероятности надо подсчитать число комбинаций, которыми может быть осуществлено распределение молекул по фазовым ячейкам. Оно равно числу перестановок из наличного числа молекул. Учитывается, что перестановки внутри фазовой ячейки не дают нового микросостояния, поскольку там молекулы неразличимы. Допустим, что имеется всего три молекулы, которые могут размещаться только в двух ячейках фазового пространства. Обозначим ячейки клетками, а молекулы — цифрами. Рассмотрим такое макросостояние, когда в одной ячейке имеется две молекулы, а в другой одна. Очевидно, данное макросостояние реализуется тремя перестановками молекул между ячейками, т. е. тремя микросостояниями [c.100]
Установление статистической природы второго закона термодинамики дало возможность Больцману в конце XIX в. определить статистический смысл энтропии. Рассмотрим предварительно смысл понятия термодинамической вероятности. Одно и то же заданное термодинамическими параметрами макросостояние системы (если средняя энергия остается постоянной) может отвечать различным распределениям энергии между отдельными молекулами (частицами). Термодинамической вероятностью называется число микросостояний, с помощью которых может быть осуществлено данное макросостояние системы. Чтобы найти термодинамическую вероятность состояния, необходимо подсчитать число комбинаций, с помощью которых может быть осуществлено данное пространственное распределение частиц. Эта величина определяется числом перестановок из наличного числа частиц. Следует различать термо- [c.105]
Понятие термодинамической вероятности (т. е. число способов распределения частиц по значениям координат и импульсов, отвечающее данному макросостоянию), очевидно, будет иметь смысл, если мы согласимся, что небольшие изменения переменных (импульсов и координат) не создают новых микросостояний. Иными словами, необходимо принять, что частицы имеют одну и ту же энергию, если их координаты и импульсы лежат в интервале. [c.300]
Чем ближе система, в к-рой протекает И. о., к состоянию равнораспределения, тем больше число вариантов распределения изотопов в системе, т. е, выше число микросостояний, через к-рое м. б. реализована система. Т. обр., при И. о. энтропия системы растет максимум энтропии достигается при равнораспределении. [c.198]
Хотя введение в статистическую механику займет целую главу, основная идея очень проста, и мы поясним ее двумя примерами — распространением газа в вакууме и распределением энергии по энергетическим уровням атомов в небольших идеализированных кристаллах. Основной идеей является то, что большие группы молекул могут существовать в очень многих микросостояниях и будут стремиться к равновесию, потому что равновесие —это термодинамическое состояние с наибольшим числом микросостояний. [c.520]
Когда кран открывается, газ, как известно, начинает поступать во второй сосуд. С микроскопической точки зрения это происходит потому, что в новых условиях для газа существует большее число доступных микросостояний. Если отдельная молекула может переходить в новый объем, то число микросостояний по существу удваивается, поскольку для молекулы в новом положении число новых микросостояний равно числу микросостояний, ранее доступных для всех других молекул в первом объеме. Таким образом, когда газ реализует все доступные в новом полном объеме микросостояния, то многие из микросостояний будут состояниями, обусловленными присутствием газа в новом объеме, который стал доступен при открытом кране. Следовательно, в равновесном состоянии газ будет распределен по всему объему. [c.520]
Число микросостояний W в каком-либо распределении можно рассчитать с помощью соотношения [c.521]
Рис. 17.2. а — — число способов распределения трех квантов энергии между тремя различными осцилляторами с одинаково расположенными колебательными уровнями. Эти числа являются числами микросостояний для каждого распределения, а Wi — полное число микросостояний б — способы распределения пяти квантов энергии между пятью различными осцилляторами с одинаково расположенными колебательными уровнями в — способы распределения семи квантов энергии между семью различными осциЛ ляторами с одинаково расположенными колебательными уровнями. [c.523]
СТО того чтобы выписывать все эти микросостояния, мы просто просуммируем числа различных распределений. Эти числа рассчитаны с помощью уравнения (17.1). В табл. 17.2 средние числа заполнения N1, [c.524]
Для заданного распределения N1, Л/ г,,.. можно выбрать системы многими различными способами. Рассмотрим число способов, при помощи которых системы могут быть распределены по энергетическим уровням. Число способов, которыми Я систем могут быть распределены так, что Ы систем имеют энергию Е, N2 систем — энергию Е2 и т. д., дается уравнением (17,1), в котором N в числителе заменяется на Jf. Будем считать, что существует одно распределение с таким большим числом микросостояний, намного превосходящим число микросостояний любого другого распределения, что термодинамические величины системы могут быть рассчитаны из одного этого распределения. При более подробном анализе, чем тот, который возможно здесь провести, можно показать, что это предположение дает превосходные результаты. В следующем разделе мы увидим, как можно вычислить значения Л ь N2,. … которые дают максимальное число перестановок (микросостояний) подчиняющихся ограничениям, накладываемым уравнениями (17.8) и (17.9). [c.528]
Особенность гетерополимера состоит в относительно малом числе микросостояний, отвечающих данной энергии. Маловероятно, чтобы два разных распределения клубков и спиралей по цепи с теми же значениями Л/ь Л/2 и п имели одинаковую [c.511]
Но распределение частиц типа (2.77) не является единственным. Возможны И другие наборы чисел 1 , удовлетворяющие условиям (2.78) и (2.79). Число микросостояний, соответствующих каждому из таких распределений (или наборов) чисел будет выражаться формулой (2.80) с соответственно новыми значениями N . Общее число всех возможных микросостояний будет равно сумме выражений вида (2.80) по всем возможным распределениям чисел удовлетворяющим условиям (2.78) и (2.79) [c.47]
Можно себе представить также и такое макросостояние, в котором распределение по энергиям отличается от распределения Максвелла — Больцмана. Почему же система всегда самопроизвольно приходит именно к этому распределению В соответствии с кинетической теорией такое распределение и есть то состояние, которое может быть осуществлено при помощи наибольшего числа. микросостояний, то есть с наибольшим числом различных индивидуальных распределений . Число возможностей для осуществления данного состояния есть одновременно и мера его вероятности (пример с игрой в кости). Из этого следует, что распределение Максвелла — Больцмана по энергиям есть наиболее вероятное состояние, которое наступает вследствие обмена энергией между всеми молекулами. [c.120]
Так как энтропия равновесного состояния выше, чем неравновесного, то, следовательно, при равновесном распределении изотопов в системе размешение изотопов возможно большим числом вариантов (т. е. число микросостояний W больше), чем в отсутствие равновесия. Можно показать, что равновесному состоянию при реакциях изотопного обмена отвечает так называемое равнораспределение изотопов, т. е. такое состояние, при котором все фазы и все химические формы имеют одинаковый изотопный состав. [c.125]
Рассмотрим теперь энтропию, связанную с распределением частиц по возможным энергетическим состояниям (термическая энтропия). Как и в пятой главе, рассмотрим систему из N частиц с энергетическими уровнями 6i, которые заняты iii частицами. Подсчитаем число различающихся микросостояний W, т. е. число вариантов распределения N частиц по энергетическим уровням 8,, причем величины [c.96]
Заполнение подуровня электронами проводится, пока не будут исчерпаны все варианты. Значение Л11 для каждого микросостояния находится суммированием значений каждого электрона, а значение Л15 — суммированием значений (для электронов, обозначенных и значения т = +Чз и — /г соответственно). Для проверки распределения подсчитывают общее число микросостояний N для электронной конфигурации I, т. е. имеющей х электронов на подуровне с данным орбитальным квантовым числом I, по формуле [c.618]
Статистическая механика, которую иногда называют механикой больших коллективов , и рассматривает распределение множества частиц в данной системе по различным возможным состояниям. Если система в заданных условиях характеризуется определенным суммарным макросостоянием (температурой, давлением), то ему может отвечать множество разных микросостояний отдельных составляющих ее частиц. Такие микросостояния представляют собой различные способы осуществления данного макросостояния. Следовательно, число микросостояний выражает число способов, которыми может быть реализовано данное макросостояние, и чем их больше, тем больше и вероятность его осуществления. [c.60]
Числа микросостояний возможных для разных распределений трех молекул по трем частям Л, В и С объема [c.405]
Исходным понятием является термодинамическая вероятность состояния системы . В главе И (стр. 104) эта величина уже определялась как число микросостояний, т. е. число разных распределений молекул по их состоянию (координаты, скорости, энергия), соответствующее данному макросостоянию или термодинамическому состоянию. Там же было дано уравнение Больцмана (1П, 34) S=AlnlF, связывающее термодинамическую вероятность с энтропией. [c.327]
Определим термодинамическую вероятность различного распределения молекул по ячейкам, т. е. число микросостояний, отвечающих данному мак эосостоянию. Если все молекулы расположены в одной ячейке, то термодинамическая вероятность равна единице = так как перестановки внутри ячейки не учитываются. Таких ма-кросостоямий может быть три [c.150]
Если каждый компонент (индивидуальное вещество или вид) рассматривать как микросостояние единой макросистемы, то, в соответствии со вторым началом термодинамики, число микросостояний увеличивается. Иными словами, увеличивается особая энтропия поликомао-нентности (ЭПК). Показано, что основные термодинамические особенности многокомпонентных, сложных систем заключаются в неоднородном распределении их химического состава по какому-либо свойству. [c.27]
Очевидно, что то и,ли иное макрососто-яние системы т,ем более вероятно, чем большим числом микросостояний оно может осуществиться. В рассматриваемом с.пучае (две. молек. ы) равномерное распределение газа по сосуду вдвое вероятнее, че.м переход всего газа в часть сосуда А. [c.179]
Как видим, максимальное число микросостояний, совместимое с данным макросостоянием, соответствует равномерному распределению молекул между двумя объемами. В общем слзп1ае можно рассчитать количество микросостояний, соответствующих дешному макросостоянию, по правилам комбинаторной алгебры, в соответствии с которыми число перестановок из ЛГ молекул равно 1 2 3… (ЛГ — 1)ЛГ = ЛП. Однако при распределении N молекул по п ячейкам, ЛГ,1 состояний, соответствующих перестановкам молекул в каждой -й ячейке, не дают новых микрооостояний, поэтому [c.372]
Различные способы распределения трех квантов энергии между атомами а, Ь и с а, б и в — макросостояния соответственно I, II и III с числом микросостояний = 31/111111 = 6, 1Уц = 31/21011 = 3 и и>щ = 31/013Ю = 1 [c.375]
В табл. 2.2 показаны все 6 реализаций распределения 5. Чем больше реализаций имеет распределение, тем выше его вероятность. Назовем 6 перечисленных выше юзможных распределений с различными количествами частиц (молекул) в праюй и леюй частях системы ее макроскопическими состояниями (макросостояния). Число микросостояний, соответствующих данному макросостоянию, принято называть термодинамической вероятностью или статистическим весом макросостояния и обозначать символом IV. [c.22]
В статистике, построенной по методу Больцмана, числа микросостояний, отвечающие данному макросостоянию, обычно называют комплексиями-, они же определяют собой термодинамическую вероятность каждого данного макросостояния. При распределении шести частиц по двум ячейкам наиболее вероятным, по Больцману, оказьгоается последнее, седьмое распределение, когда в каждой ячейке находится поровну частиц. Как мы увидим, трактовка макро- и микросостояний по Бозе — Эйнштейну и Ферми — Дира- [c.133]
Каждое такое распределение называется комплексией. Ком-плексия — это микросостояние системы в данный момент. Термодинамическая вероятность есть в то же время число комплексий, посредством которого данное пространственное распределение может осуществиться. Число комплексий, или число микросостояний, определяется по алгебраическим комбинационным формулам [c.63]

