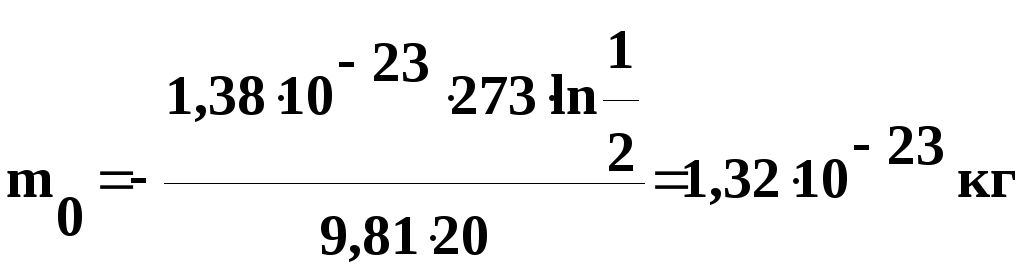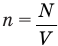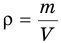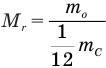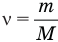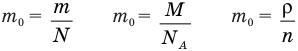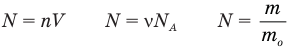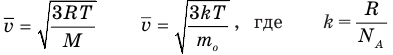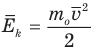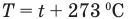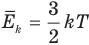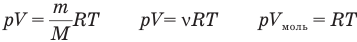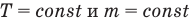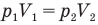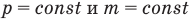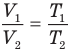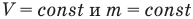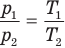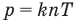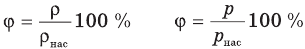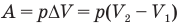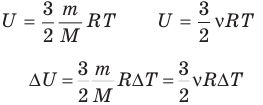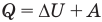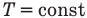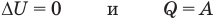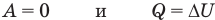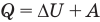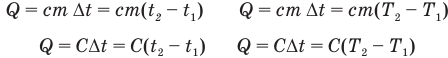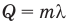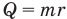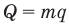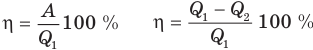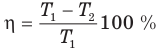• Основное уравнение
кинетической теории газов
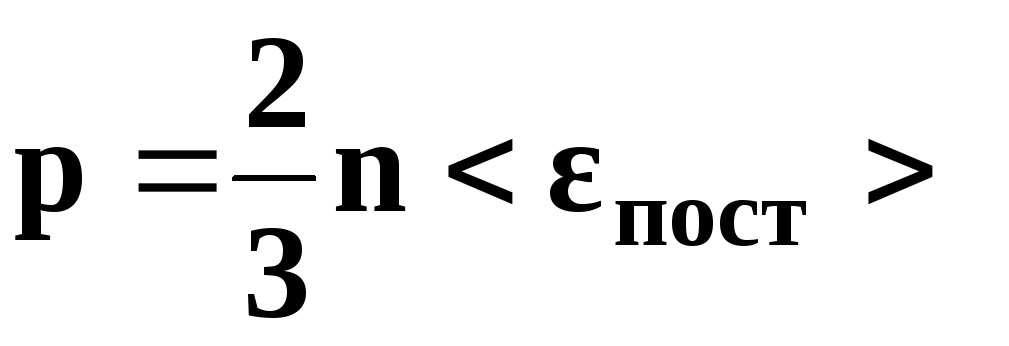
где
р — давление
газа, n
– концентрация
молекул (число молекул в единице объема),
—
средняя кинетическая энергия
поступательного движения одной молекулы,
угловые скобки обозначают осреднение
по
большому
ансамблю частиц, m0
– масса
молекулы,
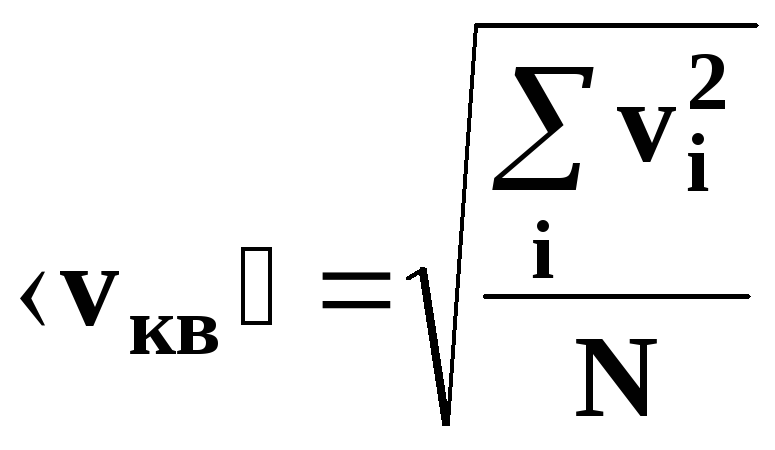
средняя квадратичная скорость движения
молекул.
• Средняя
кинетическая энергия поступательного
движения одной молекулы
,
где
k
=
1,38·10-23
Дж/К –
постоянная Больцмана, Т
– абсолютная температура.
•
Энергия теплового
движения молекул (внутренняя энергия
идеального газа):
,
где
i
– число степеней свободы молекулы, m
– масса газа, М
– молярная
масса данного вещества, R
= 8,31 Дж/(кг·К) –
универсальная газовая постоянная, Т
– абсолютная
температура.
• Числом степеней
свободы называется число независимых
координат полностью определяющих
положение тела в пространстве. Любая
молекула имеет 3 поступательных степени
свободы (iпост=3).
Молекулы,
кроме одноатомных, имеют еще вращательные
степени свободы (у двухатомных молекул
iвр
= 2, у
многоатомных iвр
= 3) и
колебательные степени свободы, которые
при невысоких (комнатных) температурах
не учитываются.
• В соответствии
с законом Больцмана о равномерном
распределении энергии по степеням
свободы, в
среднем на каждую степень свободы
молекулы приходится одинаковая энергия,
равная
.
• Средняя
кинетическая энергия вращательного
движения одной молекулы:
•
Средняя суммарная
кинетическая энергия одной молекулы:
,
где
i
– число степеней свободы молекулы
(i=iпост+
iвр).
• Средняя
квадратичная скорость молекулы:
• Средняя
арифметическая скорость (средняя
скорость теплового движения)молекулы:
,
где m0
– масса одной молекулы, М
– молярная масса вещества, причем
,
NA=
6,023·1023
1/моль –
число Авогадро.
• Барометрическая
формула характеризует изменение давления
газа с высотой в поле сил тяжести:
или
,
где
p
– давление
на высоте h
над уровнем
моря, p0
– давление на высоте h
= 0,
g
– ускорение
свободного падения. Эта формула
приближенная, так как температуру нельзя
считать постоянной для большой разности
высот.
•
Распределение
Больцмана для концентрации частиц в
силовом поле имеет вид:
,
где
n
– концентрация частиц, обладающих
потенциальной энергией Wп
, n0
— концентрация
частиц в точках поля с Wп
= 0.
Примеры
решения задач
Задача
1. Найти
среднюю кинетическую энергию
вращательного движения одной молекулы
кислорода при температуреТ
= 350 К, а также среднюю кинетическую
энергию
вращательного движения всех молекул
кислорода массойm
= 4 г.
Решение.
Согласно закону Больцмана о равном
распределении энергии по степеням
свободы на каждую степень свободы
приходится энергия равная
,
гдеk
– постоянная Больцмана, Т
– абсолютная
температура.
Так
как молекула кислорода двухатомная, у
нее две вращательных степени свободы,
поэтому средняя кинетическая энергия
вращательного движения выразится
формулой:
Подставим
в полученную формулу значения k
= 1,38·10-23
Дж/К, и Т
= 350 К, получим
Кинетическая
энергия всех N
молекул, содержащихся в 4 г кислорода
равна:
Число
всех молекул газа можно вычислить по
формуле:
,
где NA
– число
Авогадро,
—
количество вещества,m
– масса газа, М
– молярная
масса. Учтя приведенные выражения,
получим:
Подставляем
числовые значения: NA
= 6,023·1023
1/моль ; m
= 4 г = 4·10-3
кг ; М
= 32·10-3
кг/моль;
=
4,83·10-21
Дж:
Выведем
размерность полученной величины:
Задача
2. В
воздухе при нормальных условиях взвешены
одинаковые частицы. Известно, что
концентрация частиц уменьшается в два
раза на высоте h
= 20 м. Определить массу частицы.
Решение.
Воспользуемся формулой распределения
Больцмана:
,
где
Wп
= m0gh
– потенциальная
энергия частицы в поле сил тяжести.
Подставив
это выражение в формулу распределения
Больцмана, получим:
Логарифмируем
обе части уравнения по основанию е,
тогда:
,
откуда
Подставив
числовые значения в полученную формулу,
найдем
Выведем
размерность полученной величины:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Формулы молекулярной физики
Формула концентрации молекул
Здесь n — концентрация 

Формула плотности
Здесь 


Формула относительной молекулярной массы
Здесь 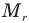

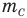
Формула количества вещества (количества молей)
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
Здесь 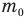
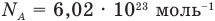



Формулы количества молекул
Здесь A — количество молекул (безразмерное), п — концентрация молекул 

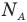
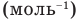

Формулы средней квадратичной скорости молекул
Здесь 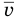
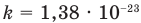

Основное уравнение кинетической теории идеального газа
Здесь р — давление газа (Па), 

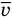

Формула средней кинетической энергии молекул
Здесь 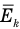
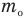
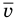
Связь шкал Цельсия и Кельвина
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
Здесь 
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
Здесь р — давление газа (Па), V — объем 
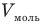
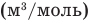
Объединенный газовый закон — уравнение Клапейрона
при
Здесь 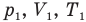

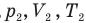

Закон Бойля — Мариотта (изотермический процесс)
при
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 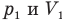

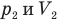

Закон Гей-Люссака (изобарный процесс)
при
Здесь р — давление газа (Па), m — масса газа (кг), 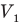
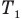

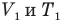

Закон Шарля
при
Здесь V — объем газа 
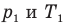
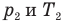
Связь давления идеального газа с концентрацией его молекул и температурой
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа 
Формулы относительной влажности
Здесь 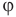
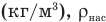
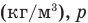
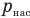
Работа при изобарном изменении объема газа
Здесь А — работа (Дж), р — давление газа (Па), 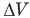
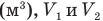

Внутренняя энергия идеального одноатомного газа
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 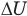
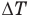
Первый закон термодинамики
Здесь Q — количество теплоты, переданное термодинамической системе (Дж), 
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при
к изохорному: при V = const
к изобарному: при р = const
к адиабатному: при Q = 0
Здесь Т — абсолютная температура (К), 
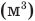
Формулы количества теплоты при нагревании или охлаждении тел
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 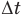
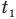
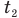
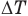
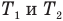
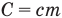
Формула количества теплоты при плавлении или кристаллизации
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 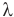
Формула количества теплоты при парообразовании или конденсации
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
Здесь 
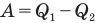
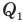
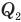
Коэффициент полезного действия идеального теплового двигателя
Здесь 
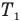
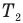
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
В этой статье мы коснемся нескольких краеугольных понятий в химии, без которых совершенно невозможно
решение задач. Старайтесь понять смысл физических величин, чтобы усвоить эту тему.
Я постараюсь приводить как можно больше примеров по ходу этой статьи, в ходе изучения вы увидите множество примеров
по данной теме.

Относительная атомная масса — Ar
Представляет собой массу атома, выраженную в атомных единицах массы. Относительные атомные массы указаны в периодической
таблице Д.И. Менделеева. Так, один атом водорода имеет атомную массу = 1, кислород = 16, кальций = 40.
Относительная молекулярная масса — Mr
Относительная молекулярная масса складывается из суммы относительных атомных масс всех атомов, входящих в состав вещества.
В качестве примера найдем относительные молекулярные массы кислорода, воды, перманганата калия и медного купороса:
Mr (O2) = (2 × Ar(O)) = 2 × 16 = 32
Mr (H2O) = (2 × Ar(H)) + Ar(O) = (2 × 1) + 16 = 18
Mr (KMnO4) = Ar(K) + Ar(Mn) + (4 × Ar(O)) = 39 + 55 + (4 * 16) = 158
Mr (CuSO4*5H2O) = Ar(Cu) + Ar(S) + (4 × Ar(O)) + (5 × ((Ar(H) × 2) +
Ar(O))) = 64 + 32 + (4 × 16) + (5 × ((1 × 2) + 16)) = 160 + 5 * 18 = 250
Моль и число Авогадро
Моль — единица количества вещества (в системе единиц СИ), определяемая как количество вещества, содержащее столько же структурных единиц
этого вещества (молекул, атомов, ионов) сколько содержится в 12 г изотопа 12C, т.е. 6 × 1023.
Число Авогадро (постоянная Авогадро, NA) — число частиц (молекул, атомов, ионов) содержащихся в одном моле любого вещества.

Больше всего мне хотелось бы, чтобы вы поняли физический смысл изученных понятий. Моль — международная единица количества вещества, которая
показывает, сколько атомов, молекул или ионов содержится в определенной массе или конкретном объеме вещества. Один моль любого вещества
содержит 6.02 × 1023 атомов/молекул/ионов — вот самое важное, что сейчас нужно понять.
Иногда в задачах бывает дано число Авогадро, и от вас требуется найти, какое вам дали количество вещества (моль). Количество вещества в химии
обозначается N, ν (по греч. читается «ню»).
Рассчитаем по формуле: ν = N/NA количество вещества 3.01 × 1023 молекул воды и 12.04 × 1023 атомов углерода.
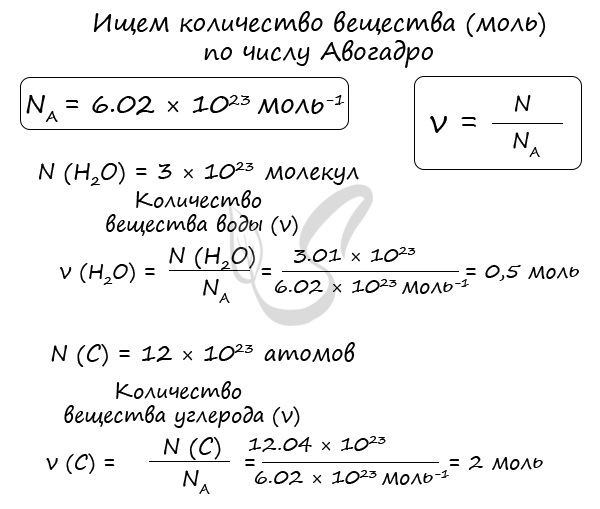
Мы нашли количества вещества (моль) воды и углерода. Сейчас это может показаться очень абстрактным, но, иногда не зная, как найти
количество вещества, используя число Авогадро, решение задачи по химии становится невозможным.
Молярная масса — M
Молярная масса — масса одного моля вещества, выражается в «г/моль» (грамм/моль). Численно совпадает с изученной нами ранее
относительной молекулярной массой.
Рассчитаем молярные массы CaCO3, HCl и N2
M (CaCO3) = Ar(Ca) + Ar(C) + (3 × Ar(O)) = 40 + 12 + (3 × 16) = 100 г/моль
M (HCl) = Ar(H) + Ar(Cl) = 1 + 35.5 = 36.5 г/моль
M (N2) = Ar(N) × 2 = 14 × 2 = 28 г/моль
Полученные знания не должны быть отрывочны, из них следует создать цельную систему. Обратите внимание: только что мы рассчитали
молярные массы — массы одного моля вещества. Вспомните про число Авогадро.
Получается, что, несмотря на одинаковое число молекул в 1 моле (1 моль любого вещества содержит 6.02 × 1023 молекул),
молекулярные массы отличаются. Так, 6.02 × 1023 молекул N2 весят 28 грамм, а такое же количество молекул
HCl — 36.5 грамм.
Это связано с тем, что, хоть количество молекул одинаково — 6.02 × 1023, в их состав входят разные атомы, поэтому и
массы получаются разные.

Часто в задачах бывает дана масса, а от вас требуется рассчитать количество вещества, чтобы перейти к другому веществу в реакции.
Сейчас мы определим количество вещества (моль) 70 грамм N2, 50 грамм CaCO3, 109.5 грамм HCl. Их молярные
массы были найдены нам уже чуть раньше, что ускорит ход решения.

ν (CaCO3) = m(CaCO3) : M(CaCO3) = 50 г. : 100 г/моль = 0.5 моль
ν (HCl) = m(HCl) : M(HCl) = 109.5 г. : 36.5 г/моль = 3 моль
Иногда в задачах может быть дано число молекул, а вам требуется рассчитать массу, которую они занимают. Здесь нужно использовать
количество вещества (моль) как посредника, который поможет решить поставленную задачу.
Предположим нам дали 15.05 × 1023 молекул азота, 3.01 × 1023 молекул CaCO3 и 18.06 × 1023 молекул
HCl. Требуется найти массу, которую составляет указанное число молекул. Мы несколько изменим известную формулу, которая поможет нам связать
моль и число Авогадро.

Теперь вы всесторонне посвящены в тему. Надеюсь, что вы поняли, как связаны молярная масса, число Авогадро и количество вещества.
Практика — лучший учитель. Найдите самостоятельно подобные значения для оставшихся CaCO3 и HCl.
Молярный объем
Молярный объем — объем, занимаемый одним молем вещества. Примерно одинаков для всех газов при стандартной температуре
и давлении составляет 22.4 л/моль. Он обозначается как — VM.
Подключим к нашей системе еще одно понятие. Предлагаю найти количество вещества, количество молекул и массу газа объемом
33.6 литра. Поскольку показательно молярного объема при н.у. — константа (22.4 л/моль), то совершенно неважно, какой газ мы
возьмем: хлор, азот или сероводород.
Запомните, что 1 моль любого газа занимает объем 22.4 литра. Итак, приступим к решению задачи. Поскольку какой-то газ
все же надо выбрать, выберем хлор — Cl2.


Моль (количество вещества) — самое гибкое из всех понятий в химии. Количество вещества позволяет вам перейти и к
числу Авогадро, и к массе, и к объему. Если вы усвоили это, то главная задача данной статьи — выполнена 

Относительная плотность и газы — D
Относительной плотностью газа называют отношение молярных масс (плотностей) двух газов. Она показывает, во сколько раз одно вещество
легче/тяжелее другого. D = M (1 вещества) / M (2 вещества).
В задачах бывает дано неизвестное вещество, однако известна его плотность по водороду, азоту, кислороду или
воздуху. Для того чтобы найти молярную массу вещества, следует умножить значение плотности на молярную массу
газа, по которому дана плотность.
Запомните, что молярная масса воздуха = 29 г/моль. Лучше объяснить, что такое плотность и с чем ее едят на примере.
Нам нужно найти молярную массу неизвестного вещества, плотность которого по воздуху 2.5

Предлагаю самостоятельно решить следующую задачку (ниже вы найдете решение): «Плотность неизвестного вещества по
кислороду 3.5, найдите молярную массу неизвестного вещества»

Относительная плотность и водный раствор — ρ
Пишу об этом из-за исключительной важности в решении
сложных задач, высокого уровня, где особенно часто упоминается плотность. Обозначается греческой буквой ρ.
Плотность является отражением зависимости массы от вещества, равна отношению массы вещества к единице его объема. Единицы
измерения плотности: г/мл, г/см3, кг/м3 и т.д.
Для примера решим задачку. Объем серной кислоты составляет 200 мл, плотность 1.34 г/мл. Найдите массу раствора. Чтобы не
запутаться в единицах измерения поступайте с ними как с самыми обычными числами: сокращайте при делении и умножении — так
вы точно не запутаетесь.

Иногда перед вами может стоять обратная задача, когда известна масса раствора, плотность и вы должны найти объем. Опять-таки,
если вы будете следовать моему правилу и относится к обозначенным условным единицам «как к числам», то не запутаетесь.
В ходе ваших действий «грамм» и «грамм» должны сократиться, а значит, в таком случае мы будем делить массу на плотность. В противном случае
вы бы получили граммы в квадрате 
К примеру, даны масса раствора HCl — 150 грамм и плотность 1.76 г/мл. Нужно найти объем раствора.

Массовая доля — ω
Массовой долей называют отношение массы растворенного вещества к массе раствора. Важно заметить, что в понятие раствора входит
как растворитель, так и само растворенное вещество.
Массовая доля вычисляется по формуле ω (вещества) = m (вещества) / m (раствора). Полученное число будет показывать массовую долю
в долях от единицы, если хотите получить в процентах — его нужно умножить на 100%. Продемонстрирую это на примере.

Решим несколько иную задачу и найдем массу чистой уксусной кислоты в широко известной уксусной эссенции.
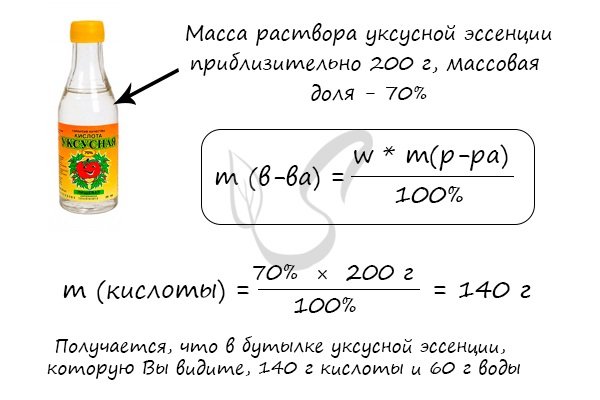
© Беллевич Юрий Сергеевич 2018-2023
Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение
(в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов
без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования,
обратитесь, пожалуйста, к Беллевичу Юрию.
Количество вещества (моль)
ν — количество вещества
N — число молекул
N_A — Число Авогадро
Мольная масса
M — мольная масса
m — масса
ν — количество вещества
Масса молекулы
m0 — масса молекулы
m — масса
N — число молекул
Мольная масса
M — мольная масса
m0 — масса молекулы
N_A — Число Авогадро
Число молекул
N — число молекул
m — масса
N_A — Число Авогадро
M — мольная масса
Основное уравнение молекулярно-кинетической теории
p — давление
n — концентрация
m0 — масса молекулы
v — скорость
Внутренняя энергия молекул
E — энергия
m — масса
v — скорость
Давление идеального газа
p — давление
n — концентрация
E — энергия
Концентрация молекул
n — концентрация
N — число молекул
V — объём
Газ: давление, объем, средняя кинетическая энергия
p — давление
V — объём
N — число молекул
E — средняя кинетическая энергия
Газ: давление, объем, температура
p — давление
V — объём
N — число молекул
k — постоянная больцмана
T — температура
Средняя кинетическая энергия
E — средняя кинетическая энергия
k — постоянная больцмана
T — температура
Газ: давление, концентрация, температура
p — давление
n — концентрация
k — постоянная больцмана
T — температура
Газ: количество вещества, громкость
ν — количество вещества
V — объём
V_M — мольный (молярный) объём
Уравнение среднеквадратичной скорости молекулы
v — скорость
k — постоянная больцмана
T — температура
m0 — масса молекулы
Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона)
p — давление
V — объём
m — масса
R — универсальная газовая постоянная
T — температура
M — мольная масса
Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона)
p — давление
V — объём
T — температура
ν — количество вещества
R — универсальная газовая постоянная
Закон бойля-мариотта (изотермический процесс)
p1, p2 — давление
V1, V2 — объемы
Закон гей-люссака (изобарный процесс)
T1, T2 — температуры
V1, V2 — объемы
Тепловое расширение газа
V — объём
V0 — объем при 0 C
α — коэффициент объемного расширения
T — температура
Закон Шарля (изохорный процесс)
p1, p2 — давление
V1, V2 — объемы
Температурная зависимость давления газа
p — давление
p0 — давление газа при 0 C
T — температура
γ — термический коэффициент давления газа
Молекулярная физика – это раздел физики, который рассматривает свойства вещества с точки зрения его внутренней структуры (взаимодействия и движения молекул). Любое вещество в мире состоит из молекул, которые находятся в постоянном и хаотичном движении, притягиваются и отталкиваются. Они обладают кинетической энергией. Все видимые процессы протекают на уровне взаимодействия этих мельчайших частиц, и то, что мы видим невооруженным глазом — лишь следствие этих тонких глубинных связей.
Основные понятия
Молекулярная физика иногда рассматривается как теоретическое дополнение термодинамики. Возникшая намного раньше, термодинамика (раздел физики) занималась изучением перехода тепла в работу, преследуя чисто практические цели. Она не производила теоретического обоснования, описывая лишь результаты опытов. Этот раздел физики изучает общие свойства макроскопических систем, которые пребывают в состоянии термостатического равновесия. Молекулярная физика уходит немного глубже и изучает свойства веществ, исходя из молекулярно кинетических представлений. Оба раздела физики призваны дополнять друг друга. Стоит отметить, что основные понятия молекулярной физики возникли позже, в XIX веке.
Это направление физики изучает взаимодействие тел на молекулярном уровне, руководствуясь статистическим методом, определяющим закономерности в хаотических движениях минимальных частиц (единиц) – молекул. Молекулярная физика и термодинамика дополняют друг друга, рассматривая процессы с разных точек зрения. При этом термодинамика не касается атомарных процессов, имея дело только с макроскопическими объектами, а молекулярная физика, напротив, рассматривает любой процесс с точки зрения взаимодействия отдельных структурных единиц.
Все понятия и процессы в молекулярной физике имеют собственные обозначения и описываются специальными формулами, которые наглядно представляют взаимодействия тех или иных параметров друг от друга. Процессы и явления пересекаются в своих проявлениях, разные формулы могут содержать одни и те же величины, быть выражены разными способами.
Молекулярно-кинетическая теория в физике – это теория, которая объясняет свойства и строение тел, а также взаимодействие малейших частиц из которых они состоят. Она включает в себя следующие основные положения:
- все тела (объекты) состоят из мельчайших частиц, которые разделены между собой промежутками;
- частицы объектов взаимодействуют между собой;
- молекулы находятся в постоянном, непрерывном и хаотическом движении.
Данное направление в физике позволяет изучить свойства определенного тела, основываясь на взаимодействии молекул из которых оно состоит. Перед тем, как переходить непосредственно к формулам, необходимо определить, в каких состояниях может пребывать вещество. Физика определяет, что все вещества в природе могут находится в трех агрегатных состояниях – газообразном, жидком и твердом. Также еще одним четвертым состоянием называют плазму. Если вещество или объект может пребывать в нескольких агрегатных состояниях, то это обуславливается за счет взаимодействия и теплового движения его молекул при нестабильных или различных условиях. Переходы одного состояния в другое сопровождаются сильными изменениями некоторых физических свойств объекта. Например, теплопроводности или плотности.
Первое агрегатное состояние, в котором может пребывать вещество – газ. В нем сила притяжения между мельчайшими структурными единицами очень мала. Расположены они далеко друг от друга и порядок в их размещении отсутствует. Исходя из этого молекулярная физика смогла объяснить следующие свойства газа – не имеет формы, легко сжимается и занимает весь объем сосуда.
Второе агрегатное состояние, которое изучает физика, это жидкость. Молекулы тесно взаимодействуют и близко расположены. Имеют ближний порядок. Основные свойства жидкости, описанные с помощью молекулярной физики – определенный объем, не могут сохранять форму, текут и практически не способны к сжатию.
Твердые тела характеризуются тем, что в них структурные единицы тесно связаны между собой. Переместится на большое расстояние они не могут. Движение их – это колебания относительно узлов кристаллической решетки (их положение равновесия). Основные свойства – сохраняют форму, объем, сжимаются мало, плавятся под воздействием определенной температуры.
Количество вещества
Количественное значение вещества определяет взаимосвязь между весом (массой) и числом молекул, содержащихся в этой массе. Дело в том, что разные вещества при одинаковом весе имеют не одинаковое число минимальных структурных единиц. Процессы, проходящие на молекулярном уровне, могут быть поняты только при рассмотрении именно числа атомных единиц, участвующих во взаимодействиях. В молекулярной физике единица измерения количества вещества, принятая в системе СИ, — моль.
[warning]Один моль всегда содержит одинаковое число минимальных частиц. Оно называется числом (или постоянной) Авогадро и равняется 6,02×1023.[/warning]
Эта константа используется в случаях, когда для расчетов требуется учитывать микроскопическое строение. Иметь дело с молекулами сложно, так как придется оперировать огромными числами, поэтому в физике часто используется моль – число, определяющее численность частиц в единице массы.
Формула, определяющая количество вещества:
Где:
- m — масса;
- μ — молярная масса;
- N — число структурных единиц;
- Na = 6,02⋅1023 моль−1 — число Авогадро.
Расчет производится в разных случаях, используется во многих формулах и является важным значением в молекулярной физике.
Давление газа
Давление газа в физике — важная величина, имеющая не только теоретическое, но и практическое значение. Рассмотрим формулу, используемую в молекулярной физике, с пояснениями, необходимыми для лучшего понимания.
Для ее составления придется сделать некоторые упрощения. Молекулы представляют собой сложные системы, имеющие многоступенчатое строение. Для простоты рассмотрим газовые частицы в определенном сосуде как упругие однородные шарики, не взаимодействующие друг с другом (идеальный газ). Скорость их движения будем считать одинаковой. Введя такие упрощения, не сильно меняющие истинное положение, можно вывести определение: давление газа — это сила, которую оказывают удары мельчайших структурных единиц на стенки сосудов.
При этом, учитывая трехмерность пространства, наличие двух направлений каждого измерения, можно ограничить численность структурных единиц, воздействующих на стенки, как 1/6 часть.
Таким образом, сведя воедино все эти условия и допущения, можем вывести формулу давления газа в идеальных условиях.
Она выглядит так:
Где:
- P — давление газа;
- n — концентрация мельчайших единиц;
- Ek — их кинетическая энергия.
В физике существует еще один вариант:
Где:
- n — концентрация мельчайших структурных единиц;
- k — постоянная Больцмана (1,38 .10-23);
- T — абсолютная температура.
Формула объема газа в физике
Объем газа — это пространство, которое занимает данное количество газа в определенных условиях. В отличие от твердых объектов с постоянным объемом, практически не зависящим от окружающих условий, газ может менять объем в зависимости от давления или температурного режима.
Формула объема газа в физике – это уравнение Менделеева-Клапейрона:
Где:
- P — давление газа;
- V — его объем;
- n — концентрация молей газа;
- R — универсальная газовая постоянная;
- T — температура газа.
Путем простейших перестановок получаем:
[stop]Согласно закону Авогадро, одинаковые объемы любых газов, помещенные в идентичные условия — давление, температура — будут всегда содержать одинаковое количество минимальных структурных единиц.[/stop]
Кристаллизация
Кристаллизация в молекулярной физике — это фазовый переход вещества из жидкого в твердое состояние, т.е. процесс, обратный плавлению. Кристаллизация происходит с выделением теплоты, которую требуется отводить. Температура совпадает с точкой плавления, весь процесс в физике описывается формулой:
Где:
- Q — количество теплоты;
- λ — теплота плавления;
- m — масса.
В молекулярной физике приведенная формула описывает как кристаллизацию, так и плавление, поскольку они, по сути, являются двумя сторонами одного процесса. Для того чтобы вещество кристаллизовалось, необходимо охладить его до температуры плавления, а затем отвести количество тепла, равное произведению массы на удельную теплоту плавления (λ). Во время кристаллизации температура не меняется.
Существует еще один вариант понимания этого термина, используемого в молекулярной физике — кристаллизация из перенасыщенных растворов. В этом случае причиной перехода становится не только достижение определенной температуры, но и степень насыщения раствора определенным веществом. На определенном этапе количество частиц растворенного вещества становится слишком большим, что вызывает образование мелких монокристалликов. Они присоединяют минимальные структурные единицы из раствора, производя послойный рост. В зависимости от условий роста кристаллы имеют не одинаковую форму.
Число молекул
Молекулярная физика позволяет определить численность частиц, содержащееся в данной массе вещества, при помощи формулы:
Отсюда выходит, что число минимальных частиц равняется:
То есть необходимо прежде всего определить численность молекул, приходящихся на определенную массу. Без того не будет возможности правильно провести подсчет числа минимальных частиц. Затем она умножается на число Авогадро, в результате чего получаем количество структурных единиц. Для соединений подсчет ведется суммированием атомного веса компонентов. Рассмотрим простой пример из молекулярной физики:
Определим численность молекул воды в 3 граммах. Формула воды (H2O) содержит два атома водорода и один кислорода.
Общий атомный вес минимальной частицы воды составит: 1 + 1 + 16 = 18 г/моль.
Количество вещества в 3 граммах воды: 3 : 18 = 1/6.
Число молекул: 1/6 × 6 × 1023 = 1023.
Масса молекулы
В молекулярной физике есть такое положение — один моль содержит равное число минимальных частиц. От этого отталкиваются при решении физических задач. Зная точную массу моля, можно разделить ее на количество минимальных частиц (число Авогадро), получив в результате массу структурной единицы:
Такое вычисление из физики применимо к неорганическим молекулам. Размеры органических частиц намного больше, их величина или вес имеют другие значения.
Молярная масса газа
Молярная масса (ММ) — это масса в килограммах одного моля вещества. Одно из положений молекулярной физики — в одном моле содержится одинаковое количество структурных единиц. Поэтому формула будет иметь такой вид:
Где:
- k — коэффициент пропорциональности;
- Mr — атомная масса вещества.
Данная величина может быть рассчитана по уравнению Менделеева-Клапейрона:
из которой можно вывести:
Таким образом, ММ прямо пропорциональна произведению массы на температуру и универсальную газовую постоянную и обратно пропорциональна произведению давления газа , его объема.
[warning]Следует учесть, что ММ газа как элемента может отличаться от газа как вещества, например, ММ элемента кислорода (О) равна 16 г/моль, а кислорода как вещества (О2) равна 32 г/моль.[/warning]
Положения молекулярной физики:
Физика (молекулярная) за 5 минут:
<span data-mce-type=»bookmark» style=»display: inline-block; width: 0px; overflow: hidden; line-height: 0;» class=»mce_SELRES_start»></span>
Формулы, которые содержат молекулярная физика и термодинамика, позволяют вычислить количественные значения процессов, происходящих с твердыми веществами и газами. Такие расчеты необходимы как в теоретических изысканиях, так и на практике, поскольку они способствуют решению практических задач.