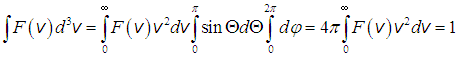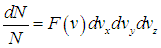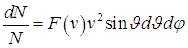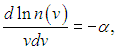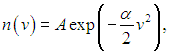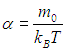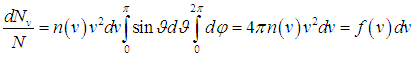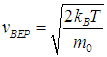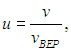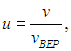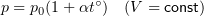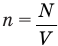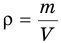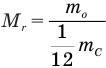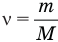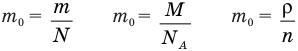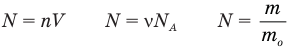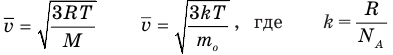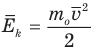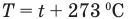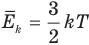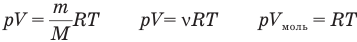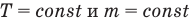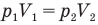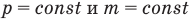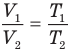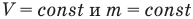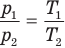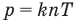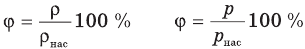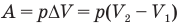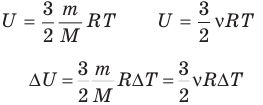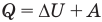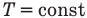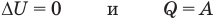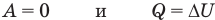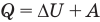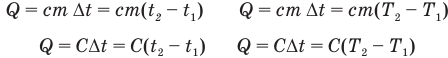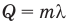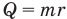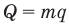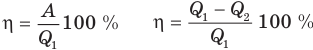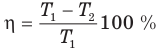6.1. Основное уравнение молекулярно-кинетической теории газов для давления. Распределение Максвелла-Больцмана молекул газа по скоростям.
Рассмотрим
упрощенную модель газа. Вводится 2
упрощения.
1.Все
молекулы движутся с одной и той же
скоростью.
2.Все
молекулы газа движутся только в
направлениях перпендикулярных к стенкам
сосуда.
Рассмотрим
газ, находящийся в сосуде, имеющего
форму параллелепипеда. Необходимо
вычислить давление газа, оказываемое
на стенку.
vΔt
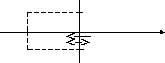
ΔS
2p=Δp1
p
Молекулы,
которые за время Δt
могут столкнуться с участком ΔS,
находятся внутри цилиндра, высота
которого равна vΔt.
Вычислим
число ударов молекул с участком ΔS
за время Δt.
—
число молекул внутри цилиндра
всех
молекул движущихся в направлении стенки
(т.к. стенок всего 6)
Рассмотрим
одно столкновение. Импульс р, а изменение
импульса молекулы при упругом ударе о
стенку составляет 2р. 2p=Δp1
Запишем
импульс, переданный стенке за время Δt.
Тогда
сила, действующая на участок ΔS
Давление
—
давление
—
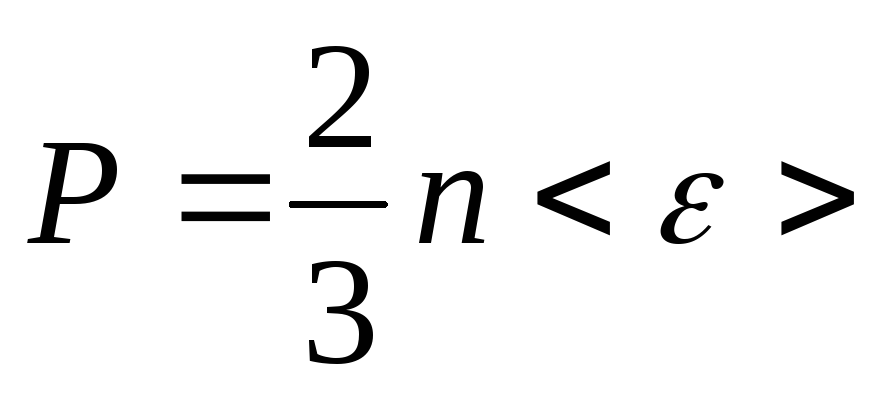
основное уравнение МКТ газов
если
поводить точный расчет (без упрощений)
—
средняя кинетическая энергия одной
молекулы.
Оно
связывает между собой макропараметры
газа (Р — давление) и микропараметры (
)
газа.
m1
– масса
одной молекулы
Распределение Максвелла. Распределение молекул по скоростям.
Скорости
молекул идеального газа неодинаковы и
подчиняются определённым закономерностям,
имеющим статистический характер. Найти
закон распределения молекул по скоростям
– это значит определить число молекул
dn,
скорости которых находятся в заданном
интервале скоростей от v
до v +dv.
Опираясь на формулу Больцмана, найдём,
как распределены молекулы идеального
газа по скоростям. Задачу решим для
идеального газа, находящегося в состоянии
теплового равновесия.
Рассмотрим
вертикальный столб газа с основанием
в 1 м2,
находящийся в однородном поле силы
тяжести. Направим ось z
вверх и вначале найдём распределение
молекул по значениям лишь компоненты
скорости vz.
Пусть n1
– полное число молекул в 1 м3
газа, а функция
f(vz)
определяет долю числа молекул с данным
значением компоненты скорости vz.
Тогда число молекул в 1 м3
газа со значениями этой компоненты
скорости, лежащими в интервале от vz
до vz+dvz
равно
.
Функция
f(vz),
собственно, и определяет распределение
молекул по vz.
Она называется функцией распределения
молекул по компоненте скорости vz.
Согласно
формуле (4), число молекул на высоте z = h
меньше их числа на высоте z = 0.
Причину этого легко указать: все те
молекулы, для которых составляющая
скорости vz
недостаточно велика, не могут достичь
высоты h.
Для того чтобы какая-то молекула могла
достичь этой высоты, она должна, двигаясь
снизу вверх, пересечь плоскость z = 0
со скоростью vz,
удовлетворяющей условию
.(7)
Скорость,
соответствующую здесь знаку равенства,
обозначим vh.
Все молекулы, удовлетворяющие этому
условию, пересекут также с некоторой
скоростью vz ≥ 0
плоскость z = h.
Число молекул, достигающих с некоторой
скоростью vz = 0 > 0
плоскость z = 0,
обозначим n(0).
Мы
считаем, что температура во всём столбе
газа одинакова. Соответственно
распределение молекул по скоростям на
всех высотах также одинаково. Отсюда,
принимая во внимание полную беспорядочность
движения, можно заключить, что число
молекул, пересекающих горизонтальную
плоскость на том или ином уровне,
пропорционально числу молекул на этом
уровне.
Используя
формулу , находим
.
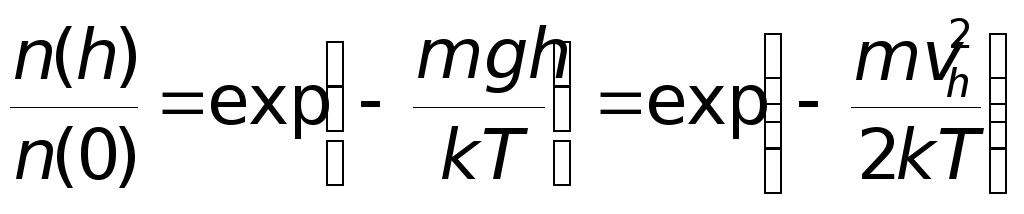
Выразим
теперь число n(h)
(т.е. число молекул, пересекающих плоскость
z = h
со скоростью vz ≥ 0
и плоскость z = 0
со скоростью vz ≥ vh)
через функцию распределения f(vz).
Нас интересует число молекул, прошедших
через плоскость z = 0
снизу вверх за 1 с. Если vz
– скорость молекул в вертикальном
направлении, то число молекул, пересекающих
рассматриваемую плоскость с такой же
скоростью за 1 с, очевидно, равно числу
молекул с этой скоростью в столбе газа
с высотой vz,
т.е. равно
.
Полное число молекул, пересекающих
плоскостьz = 0
со скоростями vz ≥ vh,
определится интегралом от полученного
выражения в пределах от vh
до ∞, т.е.
.
.
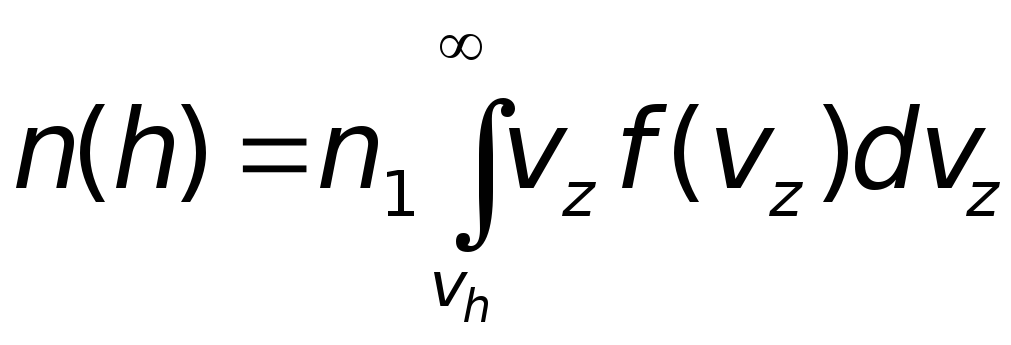
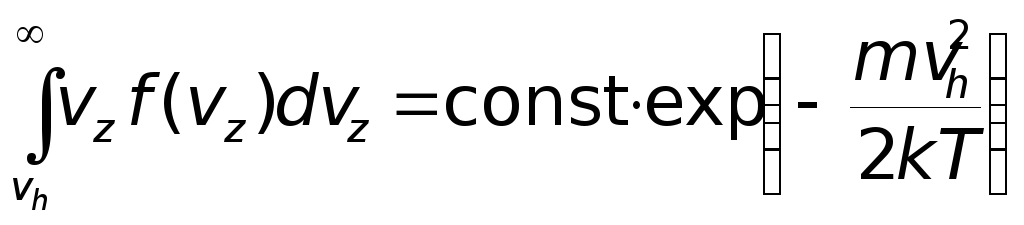
Продифференцировав
это выражение по vh
и выполнив несложные вычисления, находим
(множитель
dvh
в правой и левой частях подчёркивает,
что мы имеем дело с распределениями).
Поскольку h
– произвольная
высота, то мы вернёмся теперь к исходным
обозначениям и заменим vh
на vz.
Из определения функции f(vz)
следует, что
.
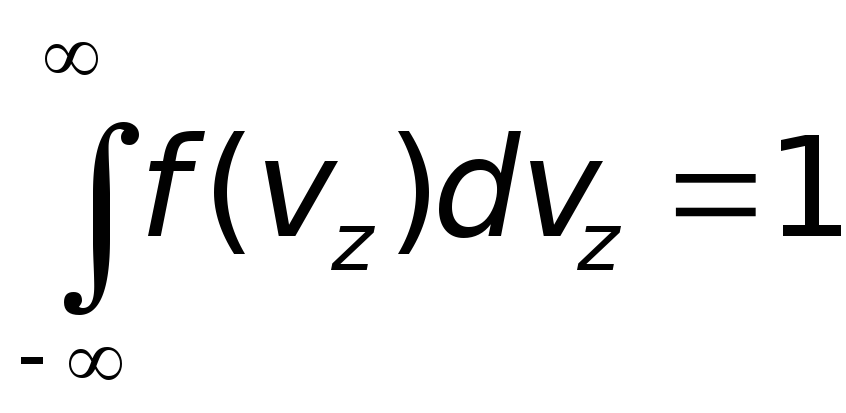
Для
определения постоянной С,
воспользуемся тем, что
.
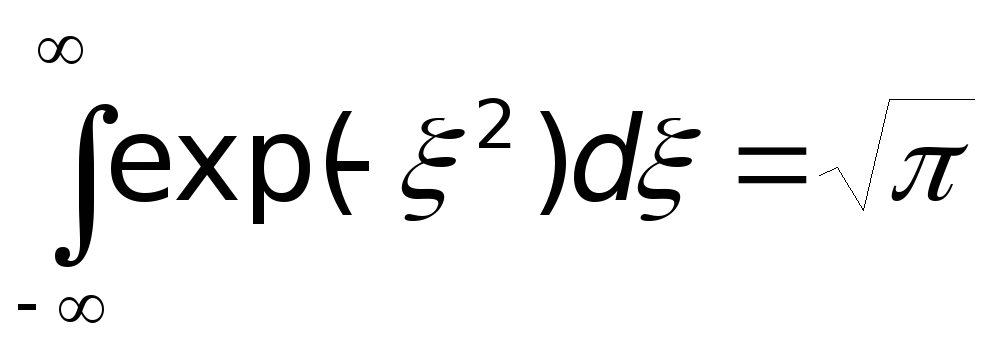
Из
этих соотношений следует, что
и, следовательно
.
Итак,
мы нашли искомую функцию, описывающую
распределение молекул по вертикальной
компоненте скорости.
Мы
нашли распределение молекул по значениям
одной определённой компоненты их
скорости. Вследствие полной беспорядочности
движения точно такие же выражения
справедливы и для других компонент
скорости.
Формулу
можно преобразовать так, чтобы она
давала распределение молекул по
абсолютной величине скорости. Эта задача
была решена Максвеллом, который показал,
что число молекул dn,
скорости которых лежат и интервале
скоростей от v
до v +dv
определяется соотношением:
Соотношение
называется распределением Максвелла
по абсолютным значениям скорости.
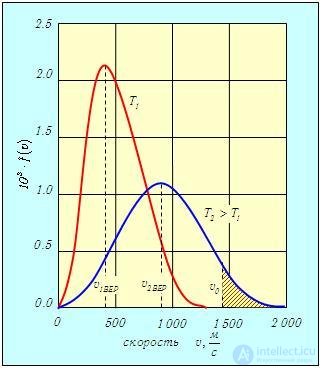
Вид
распределения (приведён на рисунке для
двух температур. При v = 0
f(v) = 0,
при v0
эта функция достигает максимума и очень
быстро стремится к нулю с дальнейшим
возрастанием скорости. Более пологая
кривая отвечает более высокой температуре,
но площади под обеими кривыми одинаковы
и в соответствии с соотношением равны
1. Максимум кривой соответствует скорости
,
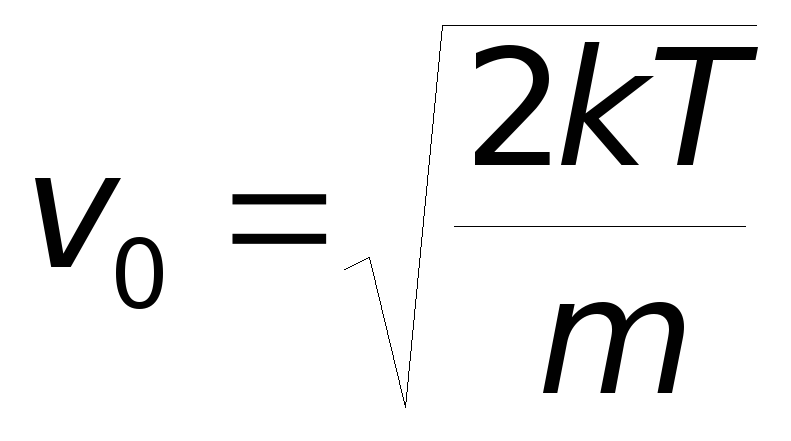
которая называется наиболее вероятной
скоростью движения молекул. Из соотношения
дляv0
следует, что с увеличением температуры
газа его наиболее вероятная скорость
увеличивается. При этом, доля медленных
молекул газа уменьшается, а доля быстрых
молекул растёт.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
25.03.20152.69 Mб2171.doc
Это продолжение увлекательной статьи про .
…
положениях в пространстве скоростей, в общем случае, число частиц будет различным).
Таким образом,
Однако, выше было заявлено и обосновано, что в состоянии термодинамического равновесия распределение молекул по направлениям движения изотропное. На «языке» функции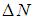 
это означает, что она может зависеть только от модуля вектора скорости и не может зависеть от его направления.
Следовательно, во-первых,
Во- вторых, естественно предположить, что при достаточно малых величинах объема 
, число молекул в нем (число молекул с вектором скорости, принадлежащем этому объему) будет пропорционально его величине, то есть
Можно показать, что при стремлении объема в пространстве скоростей 
к нулю, написанное выше приближенное равенство переходит в точное. Введенная выше функция 
имеет простой смысл: это концентрация частиц в пространстве скоростей
В-третьих, представляется очевидным, что чем больше частиц в системе, тем «при прочих равных» будет больше частиц и в объеме 
и их концентрация 
. Поэтому естественно от концентрации частиц перейти к удельной величине не зависящей от полного числа частиц в системе
Эта функция зависит только от скорости и дает относительное количество (долю) молекул, имеющих скорость в единичном объеме в пространстве скоростей вблизи скорости с модулем 
. Эта функция 
называется функцией распределения молекул для вектора скорости. Если взять несколько порций одного и того же газа, находящихся в идентичных условиях (одинаковы р и Т), то распределение молекул по скоростям в них также будет идентично. Зная вид 
, можно найти количество молекул dN из общего числа молекул N, проекции вектора скорости которых одновременно принадлежат интервалам
Это число равно
,
или, при использовании сферических координат в пространстве скоростей,
Подчеркнем, что это распределение вероятностей для вектора скорости, то есть сразу для трех величин: либо для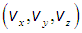 
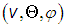
либо для 
, в зависимости от используемой в пространстве скоростей системы координат . Об этом говорит сайт https://intellect.icu .
Концентрация частиц в пространстве скоростей должна подчиняться условию, имеющему простой физический смысл: число молекул со всевозможными векторами скорости, которым соответствуют все возможные объемы 
, на которые можно разбить все пространство скоростей, должно быть равно полному числу частиц в системе. При переходе к пределу, то есть от 
к 
, суммирование превращается в интегрирование по всему пространству скоростей и мы имеем:
|
|
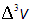
(3.10) |
,откуда следует условие нормировки функции распределения
.
Вычисление, написанного выше, нормировочного интеграла разумеется возможно при использовании любой системы координат в пространстве скоростей. Например, в декартовой системе
.
Однако, «грех» не воспользоваться фактом изотропности распределения молекул по направлениям движения, отражением которого является зависимость функции распределения 
только от модуля вектора скорости. В сферических координатах нормировочный интеграл имеет существенно проще, так как два из трех интегрирований можно провести в общем виде:
Функция распределения для газов была найдена теоретически Максвеллом (1859) и носит его имя. Далее мы установим ее вид.
Распределение Максвелла. Поскольку все направления движения молекул в пространстве равноправны, распределение скоростей должно быть изотропным и функция распределения n(v) не может зависеть от направления скорости. Это означает, что n(v) не может быть произвольной функцией от компонент скорости vх, vy, vz, а должна зависеть лишь от абсолютной величины скорости
В зависимости от выбранной системы координат вероятность 
имеет различный вид.
В декартовой системе
|
|
(3.11) |
В цилиндрической системе
|
|
(3.12) |
В сферической системе
|
|
(3.13) |
Далее предлагается простой, хотя и не вполне строгий вывод вида функции распределения. Рассмотрим процесс столкновения двух частиц, движущихся со скоростями v1 и v2. Пусть в результате соударения скорости молекул изменяются и превращаются в vi и v4. Число таких столкновений в единицу времени в единице объема газа должно быть пропорционально числу молекул со скоростями вблизи v1 и v2, то есть произведению n(v1)·n(v2). Рассмотрим далее процесс соударения, являющийся обратным данному. При этом скорости молекул изменяются от значений v3 и v4 до значений v1 и v2. Число таких соударений в единицу времени в объеме пропорционально количеству молекул со скоростями вблизи v3 и v4, то есть n(v3)·n(v4).
В силу предположения о молекулярном хаосе и предположения о том, что число молекул с данными значениями скорости не изменяется процессами молекулярных столкновений в газе, находящемся в стационарном состоянии, можно считать, что число молекул, у которых скорости изменяются от значений v1 и v2 до значений v3 и v4, равно числу молекул, у которых скорости изменяются от v3 и v4 до v1 и v2. Отсюда следует, что
|
|
(3.14) |
Равенство (3.14) выражает баланс частиц, получающих и теряющих соответствующую скорость, причем в процессе таких упругих соударений энергия молекул сохраняется (m0 — масса молекулы):
|
|
(3.15) |
Равенства (3.10), (3.14) и (3.15) представляют совокупности условий, которым должна удовлетворять искомая функция распределения.
Используя (3.15), выразим v4 через v1, v2, v3:
|
|
(3.16) |
Функциональные уравнения (3.14) и (3.16) легко превратить в простое дифференциальное уравнение. Взяв логарифм от (3.14), имеем
|
|
(3.17) |
Продифференцируем (3.17) по аргументу v1:
|
|
(3.18) |
Аналогично
|
|
(3.19) |
Учитывая выражение (3.16), находим
|
|
(3.20) |
Подставляя (3.20) в правые части соотношений (3.18) и (3.19), приходим к равенству
|
|
(3.21) |
При этом мы должны помнить, что это равенство справедливо при совершенно произвольных значениях v1, v2, которые являются независимыми переменными. Это значит, что равенство (3.21) должно иметь место при совершенно произвольных значениях скоростей, поэтому оно может быть выполнено только тогда, когда правая и левая части (3.21) равны некоторой постоянной (которую мы обозначим через ( –α)):
|
|
(3.22) |
где переменная v может принимать значения v1, v2 или любое иное. Разделяя переменные, записываем (3.22) в виде
|
|
(3.23) |
Интегрируя (3.23), находим
|
|
(3.24) |
где А — постоянная интегрирования. Из физических соображений очевидно, что
Большие скорости молекул маловероятны. Поэтому коэффициент α > 0. Постоянная А определяется из условия нормировки (3.10):
|
|
(3.25) |
Далее будет показано, что параметр α должен быть связан с абсолютной температурой T соотношением
|
|
(3.26) |
С учетом (3.26) из (3.24) получим
|
|
(3.27) |
Формула (3.27) и представляет собой искомое распределение молекул по скоростям.
Учитывая, что n(v) зависит только от модуля скорости, а их направления равновероятны, можно ввести функцию распределения f(v) молекул по абсолютной величине скорости. Для этого надо проинтегрировать выражение (3.13) по углам, что дает
|
|
(3.28) |
Отсюда и из (3.27) следует выражение для функции распределения Максвелла для модуля вектора скорости f(v):
|
|
(3.29) |
Величина f(v)dv есть вероятность найти частицу с модулем скорости, лежащим в интервале от v до v + dv. Условие нормировки распределения f(v) принимает теперь вид
|
|
3.3. Характерные скорости молекул
В этом разделе приводятся некоторые следствия, вытекающие из формул (3.29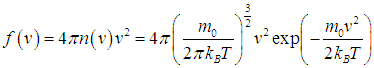
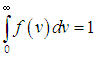
) и (3.30
). В качестве примера на рис. 3.3 изображены две кривые, соответствующие распределениям f(v) молекул кислорода O2 по абсолютным величинам скоростей при температурах Т1 = 300 К и Т2 = 1 300 К.
Рис. 3.3. Распределение молекул кислорода по скоростям при разных температурах T1 = 300 К и T2 = 1 300 К
Наиболее вероятная скорость. При бесконечно малых и неограниченно больших значениях скоростей функция распределения стремится к нулю
то есть такие предельные значения скоростей маловероятны в системе. Следовательно, при каком-то значении скорости функция f(v) достигает своего максимума.
Наиболее вероятная скорость vВЕР — это скорость, отвечающая максимальному значению функции распределения.
Ее можно найти, решая уравнение
откуда следует, что
|
|
(3.31) |
Иными словами, наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул. В этой точке f(v) принимает максимальное значение:
|
|
(3.32) |
Соотношения (3.31), (3.32) могут быть полезны для анализа изменения функции распределения при изменении температуры газа или при изменении рода газа, то есть массы молекул. Отметим, что как следует из (3.26) – (3.29), распределение Максвелла зависит не отдельно от массы молекул и отдельно от температуры газа, а от их отношения 
. Поэтому распределение не только «буквенно» но и численно одно и тоже, например, для молекулярного водорода 
при температуре 
и для гелия 
при температуре 
.
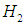
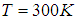
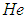
С ростом температуры наиболее вероятная скорость vВЕР (3.31) увеличивается, то есть максимум функции f(v) сдвигается вправо (см. рис. 3.3), Т2 > Т1. При этом f(vВЕР) уменьшается, то есть кривая становится более пологой. Так же деформируется кривая, если температура постоянна, но масса молекул уменьшается. Напомним, что при любых деформациях функции распределения f(v) площадь под кривыми постоянна и равна единице в соответствии с формулой (3.30).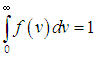
Относительное количество молекул, скорость которых превышает некоторое значение v0, определяется выражением
|
|
(3.33) |
На графике (см. рис. 3.3) этому интегралу соответствует лежащая справа от v0 часть площади (отмечена штриховкой), ограниченная кривой f(v) и осью скоростей. Как видно из рис. 3.3, относительное количество молекул, имеющих скорости, превышающие v0, растет с повышением температуры.
В заключение этого раздела заметим, что во всех формулах для функции распределения и характерных скоростей входит отношение массы молекулы к постоянной Больцмана
Умножая числитель и знаменатель на число Авогадро NA и учитывая, что
— молярная масса газа, a
— универсальная газовая постоянная, мы всюду можем использовать это отношение в наиболее удобной для конкретной задачи форме
Распределение молекул по величинам безразмерной скорости. Если при графическом изображении функции распределения Максвелла (3.29) по оси абсцисс откладывать скорости молекул v, то форма кривой и положение максимума будут зависеть от массы молекул и от температуры газа. Но если по горизонтальной оси откладывать отношение скорости к наиболее вероятной скорости, то есть безразмерную скорость
то для всех температур и любых масс молекул (любых газов) получится одна и та же кривая (рис. 3.4).
Рис. 3.4. Распределение Максвелла по величинам безразмерной скорости
Сделав замену переменной
в (3.29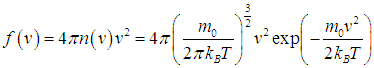) и учитывая, что
получим распределение Максвелла в форме
|
|
(3.34) |
Эта формула и соответствующий ей график (см. рис. 3.4) удобны для решения многих задач.
Пример. Найдем, какая часть общего числа молекул кислорода имеет при температуре 27 °С скорости, отличающиеся от наиболее вероятной не более, чем на 1 %; а также скорости в интервале 562–572 м/с.
Произведем необходимые вычисления. Чтобы ответить на первый вопрос задачи, учтем, что u = 1 при v = vВЕР. Величина интервала du = 0,02. Следовательно,
Вычислим наиболее вероятную скорость:
Найдем отношение v = 562 м/с к vВЕР = 395 м/с
Определим по кривой (см. рис. 3.4) значение функции f(u) при u = 1,42. Получаем f(u) = 0,62. Ширина интервала Dv = 10 м/с (Du = 10/395 = 0,0253). Следовательно, доля молекул в этом интервале
Интересно отметить, что молекула кислорода проходит за секунду путь, равный в среднем 0,4 км. Но не нужно забывать о соударениях молекул. Из-за них молекула по прямой движется очень недолго, и ее путь представляет собой ломаную линию. Поэтому молекула, двигаясь с огромной скоростью по отдельным звеньям ломаной траектории, передвигается от слоя к слою газа со сравнительно небольшой скоростью.
Средняя арифметическая скорость. Знание функции распределения молекул по скоростям f(v) дает возможность найти среднее значение скорости, а также любой величины, являющейся функцией скорости, например квадрата скорости v2 или кинетической энергии молекулы mv2/2.
Средняя арифметическая скорость — это отношение суммы абсолютных величин скоростей всех молекул в системе к числу этих молекул.
Разобьем интервал всех возможных значений скорости от 0 до бесконечности на малые интервалы Dvi. Каждому интервалу соответствует количество молекул
|
|
(3.35) |
Так как интервалы Dvi, малы, то можно приближенно считать скорости молекул данного интервала одинаковыми и равными vi. Сумма значений скоростей молекул интервала
|
|
(3.36) |
Сумма значений скоростей всех молекул
|
|
(3.37) |
Разделив эту сумму на число молекул, получим выражение для средней арифметической скорости
|
|
(3.38) |
Переходя от суммы к интегралу, получаем
|
|
(3.39) |
Вычисляя интеграл, получаем среднюю арифметическую скорость молекул
|
|
(3.40) |
Среднеквадратичная скорость. Чтобы найти среднее значение произвольной функции L(v) скорости, нужно эту функцию умножить на функцию распределения и проинтегрировать по всем возможным значениям
продолжение следует…
Продолжение:
Часть 1 3. Распределение молекул по скоростям и координатам
Часть 2 — . Распределение молекул по скоростям и координатам
Часть 3 — . Распределение молекул по скоростям и координатам
Часть 4 — . Распределение молекул по скоростям и координатам
Молекулярная физика Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества
m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа
p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;
— среднее значение квадрата скорости молекул.
1.3 Средняя квадратичная скорость молекул идеального газа
k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа
1.5 Давление идеального газа
n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта
p — давление;
V — объем газа.
1.7 Закон Шарля
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака
V0 — объем газа при 0 °С.
1.9 Уравнение Менделеева-Клапейрона
1.10 Объединенный закон газового состояния (уравнение Клапейрона)
1.11 Закон Дальтона
pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа
ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV
p — давление газа.
При изменении объема от V1 до V2
2.3 Первый закон термодинамики
ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа
ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
Формулы молекулярной физики
Формула концентрации молекул
Здесь n — концентрация 
, N — количество молекул (безразмерное), V — объем 
.
Формула плотности
Здесь 
— плотность вещества 
, m — масса вещества (кг), V — объем .
Формула относительной молекулярной массы
Здесь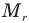 
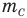
— относительная молекулярная масса (безразмерная), 
— масса одной молекулы (кг), 
— масса атома углерода (кг).
Формула количества вещества (количества молей)
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
Здесь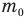 
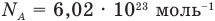
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 
— число Авогадро, — плотность вещества , n — концентрация молекул .
Формулы количества молекул
Здесь A — количество молекул (безразмерное), п — концентрация молекул , V— объем , v — количество вещества (количество молей) (моль), 
— число Авогадро 
, m — масса вещества (кг), 
— масса одной молекулы.
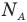
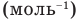
Формулы средней квадратичной скорости молекул
Здесь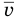 
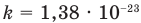
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 
Дж/К — постоянная Больцмана, — масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа
Здесь р — давление газа (Па), — масса одной молекулы (кг), n — концентрация молекул , 
— средняя квадратичная скорость молекул (м/с), 
— средняя кинетическая энергия молекул (Дж).
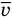
Формула средней кинетической энергии молекул
Здесь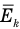 
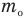
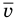
— средняя кинетическая энергия молекул (Дж), 
— масса одной молекулы (кг), 
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
Здесь — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
Здесь р — давление газа (Па), V — объем , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 
— объем моля 
.
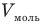
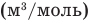
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь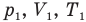 
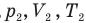
— давление (Па), объем 
и абсолютная температура (К) газа в первом состоянии, 
— давление (Па), объем и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 
Здесь Т — абсолютная температура газа (К), m — масса газа (кг),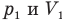 
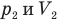
— давление (Па) и объем газа в первом состоянии, 
— давление (Па) и объем газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 
Здесь р — давление газа (Па), m — масса газа (кг),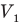 
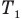
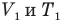
и 
— объем и абсолютная температура (К) газа в первом состоянии, 
— объем и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 
Здесь V — объем газа , m — масса газа (кг), 
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
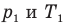
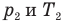
Связь давления идеального газа с концентрацией его молекул и температурой
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа , абсолютная температура Т (К).
Формулы относительной влажности
Здесь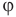 
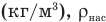
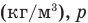
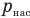
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 
— плотность насыщенного водяного пара при той же температуре 
— давление водяного пара в воздухе при данной температуре (Па), 
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
Здесь А — работа (Дж), р — давление газа (Па),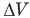 
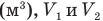
— изменение объема газа 
— соответственно начальный и конечный объемы газа .
Внутренняя энергия идеального одноатомного газа
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль),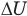 
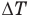
— изменение внутренней энергии (Дж), 
— изменение температуры (К).
Первый закон термодинамики
Здесь Q — количество теплоты, переданное термодинамической системе (Дж), 
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 
к изохорному: при V = const
к изобарному: при р = const
к адиабатному: при Q = 0
Здесь Т — абсолютная температура (К), — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем 
, р — давление (Па).
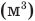
Формулы количества теплоты при нагревании или охлаждении тел
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг),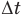 
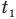
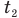
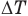
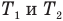
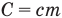
— изменение температуры тела по шкале Цельсия, 
и 
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 
— изменение абсолютной температуры тела (К), 
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
Здесь Q — количество теплоты (Дж), т — масса тела (кг),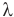 
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
Здесь 
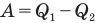
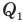
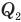
— коэффициент полезного действия (безразмерный или в %), 
— работа, совершенная двигателем (Дж), 
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
Здесь — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 
— абсолютная температура нагревателя (К), 
— абсолютная температура холодильника(К).
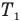
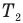
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Как определить количество молекул, которое содержится в газе, если известна средняя квадратичная скорость?
Средняя квадратичная
скорость молекул некоторого газа при температуре T
= 296 K равна
480 м/с. Сколько молекул содержится в 10,0 граммах этого газа?
Решение.
Число молекул, содержащихся
в массе газа m, определим по следующей
формуле.
Для нахождения молярной
массы газа воспользуемся формулой средней квадратичной скорости молекул, откуда
и найдем M.
Подставив значение
молярной массы в исходную формулу, получим N.
Ответ: N = 1,88•1023
.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
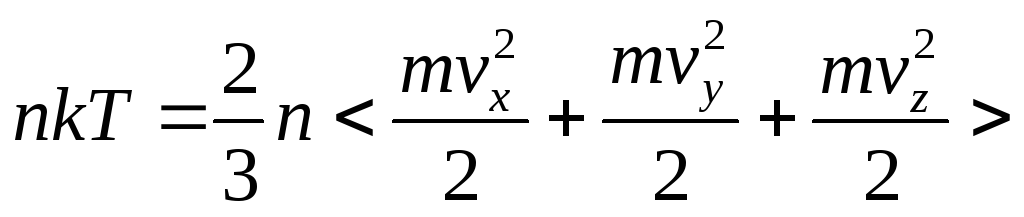
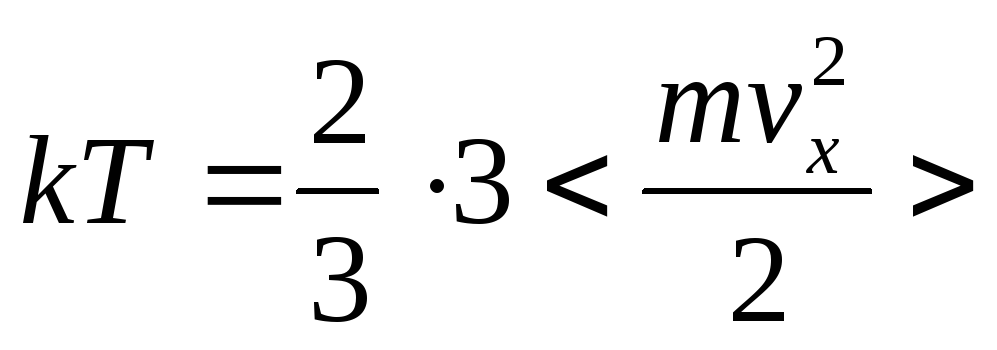
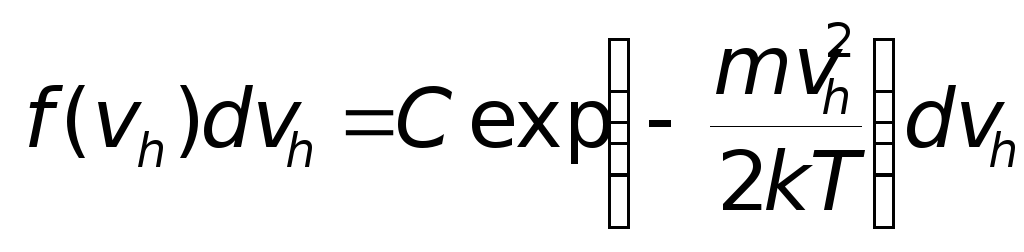
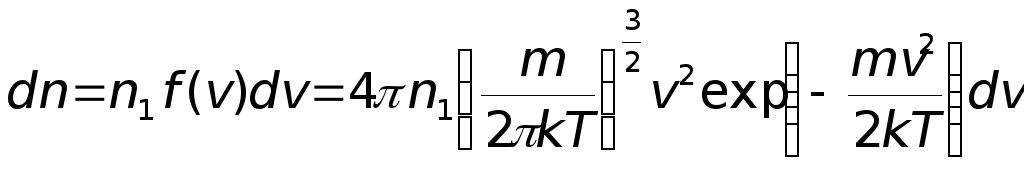
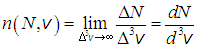