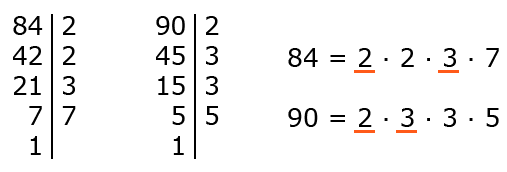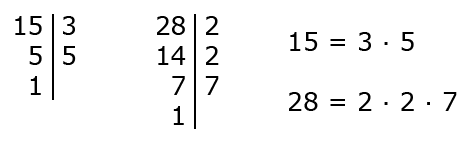Как найти число общих делителей двух чисел - Исправление недочетов и поиск решений вместе с Examum.ru

Понятие наибольшего общего делителя

Для начала разберемся, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.

Делитель натурального числа — это такое целое натуральное число, на которое делится данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.

Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общими делителями будут 4 и 1. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4.

Любое число можно разделить на 1 и на само себя. Значит, у любого набора целых чисел будет как минимум два общих делителя.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).

Например, для 4 и 16 НОД будет 4. Как мы к этому пришли:

Зафиксируем все делители четырех: 4, 2, 1.

А теперь все делители шестнадцати: 16, 8, 4 и 1.

Выбираем общие: это 4, 2, 1. Самое большое общее число: 4. Вот и ответ.

Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.

Найдем наибольший общий делитель нескольких целых чисел: 12, 6, 42, 18. Он будет равен шести. Ответ можно записать так: НОД (12, 6, 42, 18) = 6. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.

Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.

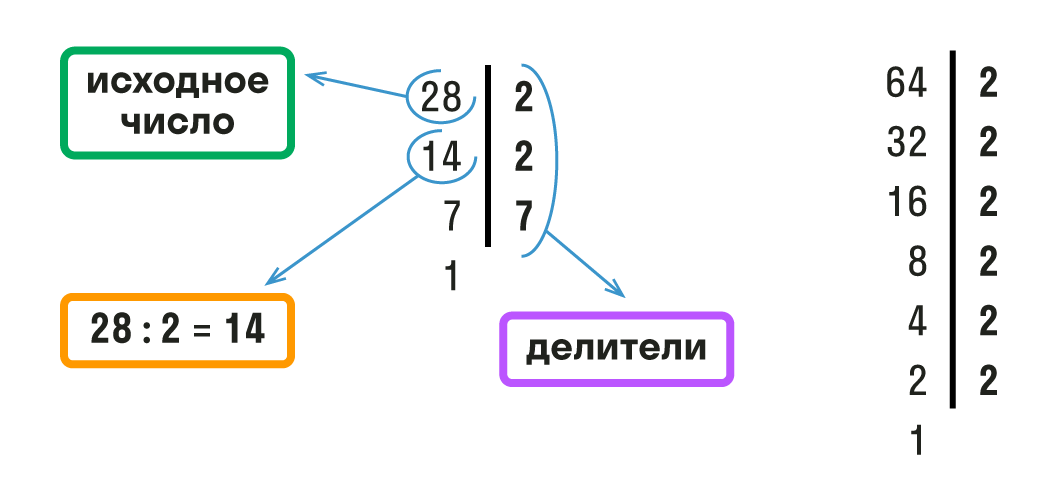
Еще один пример. Рассчитаем НОД для 28 и 64.

Как находим:

Распишем простые множители для каждого числа и подчеркнем одинаковые
Д (28) = 2 * 2 * 7

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

Найдем произведение одинаковых простых множителей и запишем ответ
НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Способы нахождения наибольшего общего делителя

Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.

1. Разложение на множители

Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.

Пример 1. Найти НОД (84, 90).

Как решаем:

Разложим числа 84 и 90 на простые множители:

Подчеркнем все общие множители и перемножим их между собой:
2 * 3 = 6.

Ответ: НОД (84, 90) = 6.

Пример 2. Найти НОД (15, 28).

Как решаем:

Разложим 15 и 28 на простые множители:

Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.

Ответ: НОД (15, 28) = 1.

Пример 3. Найти НОД для 24 и 18.

Как решаем:

Разложим оба числа на простые множители:

Найдем общие множители чисел 24 и 18: 2 и 3. Для удобства общие множители можно подчеркнуть.

Перемножим общие множители:
НОД (24, 18) =2 * 3 = 6

Ответ: НОД (24, 18) = 6

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

2. Алгоритм Евклида

Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.

Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.

Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.

Пример 1. Найти НОД для 24 и 8.

Как рассуждаем:

Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, = 8.

В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:

Большее число поделить на меньшее.

Меньшее число поделить на остаток, который получается после деления.

Первый остаток поделить на второй остаток.

Второй остаток поделить на третий и т. д.

Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.

Пример 2. Найти наибольший общий делитель чисел 140 и 96:

Как решаем:

140 : 96 = 1 (остаток 44)

96 : 44 = 2 (остаток

44 : 8 = 5 (остаток 4)

8 : 4 = 2

Последний делитель равен 4 — это значит: НОД (140, 96) = 4.

Ответ: НОД (140, 96) = 4

Пошаговое деление можно записать столбиком:

Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:

Найти наибольший общий делитель любых двух чисел из данных.

Найти НОД найденного делителя и третьего числа.

Найти НОД последнего найденного делителя и четвёртого числа и т. д.

Свойства наибольшего общего делителя

У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.

Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.

Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.

Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.

Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.

Доказательство

Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.

Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.

В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.

Например, НОД (25, 25) = 25.

Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.

Например, НОД (4, 40) = 4, так как 40 кратно 4.

Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.

Доказательство

Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.

Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.

Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).

Доказательство

Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.

Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.

Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.

Источник

Given two integer numbers, the task is to find count of all common divisors of given numbers?

Examples :

Input : a = 12, b = 24
Output: 6
// all common divisors are 1, 2, 3, 
// 4, 6 and 12

Input : a = 3, b = 17
Output: 1
// all common divisors are 1

Input : a = 20, b = 36
Output: 3
// all common divisors are 1, 2, 4

It is recommended to refer all divisors of a given number as a prerequisite of this article.

Naive Solution
A simple solution is to first find all divisors of first number and store them in an array or hash. Then find common divisors of second number and store them. Finally print common elements of two stored arrays or hash. The key is that the magnitude of powers of prime factors of a divisor should be equal to the minimum power of two prime factors of a and b.

Find the prime factors of a using prime factorization.
Find the count of each prime factor of a and store it in a Hashmap.
Prime factorize b using distinct prime factors of a.
Then the total number of divisors would be equal to the product of (count + 1)
of each factor.
count is the minimum of counts of each prime factors of a and b.
This gives the count of all divisors of a and b.

C++

#include <bits/stdc++.h>

using namespace std;

map<int, int> ma;

void primeFactorize(int a)

{

for(int i = 2; i * i <= a; i += 2)

{

int cnt = 0;

while (a % i == 0)

{

cnt++;

a /= i;

}

ma[i] = cnt;

}

if (a > 1)

{

ma[a] = 1;

}

int commDiv(int a, int b)

{

primeFactorize(a);

int res = 1;

for(auto m = ma.begin();

m != ma.end(); m++)

{

int cnt = 0;

int key = m->first;

int value = m->second;

while (b % key == 0)

{

b /= key;

cnt++;

}

res *= (min(cnt, value) + 1);

}

return res;

}

int main()

{

int a = 12, b = 24;

cout << commDiv(a, b) << endl;

return 0;

}

Java

import java.util.*;

import java.io.*;

class GFG {

static HashMap<Integer, Integer> ma = new HashMap<>();

static void primeFactorize(int a)

{

for (int i = 2; i * i <= a; i += 2) {

int cnt = 0;

while (a % i == 0) {

cnt++;

a /= i;

}

ma.put(i, cnt);

}

if (a > 1)

ma.put(a, 1);

}

static int commDiv(int a, int b)

{

primeFactorize(a);

int res = 1;

for (Map.Entry<Integer, Integer> m : ma.entrySet()) {

int cnt = 0;

int key = m.getKey();

int value = m.getValue();

while (b % key == 0) {

b /= key;

cnt++;

}

res *= (Math.min(cnt, value) + 1);

}

return res;

}

public static void main(String args[])

{

int a = 12, b = 24;

System.out.println(commDiv(a, b));

}

Python3

import math

ma = {}

def primeFactorize(a):

sqt = int(math.sqrt(a))

for i in range(2, sqt, 2):

cnt = 0

while (a % i == 0):

cnt += 1

a /= i

ma[i] = cnt

if (a > 1):

ma[a] = 1

def commDiv(a, b):

primeFactorize(a)

res = 1

for key, value in ma.items():

cnt = 0

while (b % key == 0):

b /= key

cnt += 1

res *= (min(cnt, value) + 1)

return res

a = 12

b = 24

print(commDiv(a, b))

C#

using System;

using System.Collections.Generic;

class GFG{

static Dictionary<int,

int> ma = new Dictionary<int,

int>();

static void primeFactorize(int a)

{

for(int i = 2; i * i <= a; i += 2)

{

int cnt = 0;

while (a % i == 0)

{

cnt++;

a /= i;

}

ma.Add(i, cnt);

}

if (a > 1)

ma.Add(a, 1);

}

static int commDiv(int a, int b)

{

primeFactorize(a);

int res = 1;

foreach(KeyValuePair<int, int> m in ma)

{

int cnt = 0;

int key = m.Key;

int value = m.Value;

while (b % key == 0)

{

b /= key;

cnt++;

}

res *= (Math.Min(cnt, value) + 1);

}

return res;

}

static void Main()

{

int a = 12, b = 24;

Console.WriteLine(commDiv(a, b));

}

Javascript

<script>

let ma = new Map();

function primeFactorize(a)

{

for(let i = 2; i * i <= a; i += 2)

{

let cnt = 0;

while (a % i == 0)

{

cnt++;

a = parseInt(a / i, 10);

}

ma.set(i, cnt);

}

if (a > 1)

{

ma.set(a, 1);

}

function commDiv(a,b)

{

primeFactorize(a);

let res = 1;

ma.forEach((values,keys)=>{

let cnt = 0;

let key = keys;

let value = values;

while (b % key == 0)

{

b = parseInt(b / key, 10);

cnt++;

}

res *= (Math.min(cnt, value) + 1);

})

return res;

}

let a = 12, b = 24;

document.write(commDiv(a, b));

</script>

Output:

Time Complexity: O(√n log n)
Auxiliary Space: O(n)

Efficient Solution –
A better solution is to calculate the greatest common divisor (gcd) of given two numbers, and then count divisors of that gcd.

C++

#include <bits/stdc++.h>

using namespace std;

int gcd(int a, int b)

{

if (a == 0)

return b;

return gcd(b % a, a);

}

int commDiv(int a, int b)

{

int n = gcd(a, b);

int result = 0;

for (int i = 1; i <= sqrt(n); i++) {

if (n % i == 0) {

if (n / i == i)

result += 1;

else

result += 2;

}

return result;

}

int main()

{

int a = 12, b = 24;

cout << commDiv(a, b);

return 0;

}

Java

class Test {

static int gcd(int a, int b)

{

if (a == 0)

return b;

return gcd(b % a, a);

}

static int commDiv(int a, int b)

{

int n = gcd(a, b);

int result = 0;

for (int i = 1; i <= Math.sqrt(n); i++) {

if (n % i == 0) {

if (n / i == i)

result += 1;

else

result += 2;

}

return result;

}

public static void main(String args[])

{

int a = 12, b = 24;

System.out.println(commDiv(a, b));

}

Python3

from math import sqrt

def gcd(a, b):

if a == 0:

return b

return gcd(b % a, a)

def commDiv(a, b):

n = gcd(a, b)

result = 0

for i in range(1,int(sqrt(n))+1):

if n % i == 0:

if n/i == i:

result += 1

else:

result += 2

return result

if __name__ == "__main__":

a = 12

b = 24;

print(commDiv(a, b))

C#

using System;

class GFG {

static int gcd(int a, int b)

{

if (a == 0)

return b;

return gcd(b % a, a);

}

static int commDiv(int a, int b)

{

int n = gcd(a, b);

int result = 0;

for (int i = 1; i <= Math.Sqrt(n); i++) {

if (n % i == 0) {

if (n / i == i)

result += 1;

else

result += 2;

}

return result;

}

public static void Main(String[] args)

{

int a = 12, b = 24;

Console.Write(commDiv(a, b));

}

PHP

<?php

function gcd($a, $b)

{

if ($a == 0)

return $b;

return gcd($b % $a, $a);

}

function commDiv($a, $b)

{

$n = gcd($a, $b);

$result = 0;

for ($i = 1; $i <= sqrt($n);

$i++)

{

if ($n % $i == 0)

{

if ($n / $i == $i)

$result += 1;

else

$result += 2;

}

return $result;

}

$a = 12; $b = 24;

echo(commDiv($a, $b));

?>

Javascript

<script>

function gcd(a, b)

{

if (a == 0)

return b;

return gcd(b % a, a);

}

function commDiv(a, b)

{

let n = gcd(a, b);

let result = 0;

for (let i = 1; i <= Math.sqrt(n); i++) {

if (n % i == 0) {

if (n / i == i)

result += 1;

else

result += 2;

}

return result;

}

let a = 12, b = 24;

document.write(commDiv(a, b));

</script>

Output :

Time complexity: O(n^1/2) where n is the gcd of two numbers.
Auxiliary Space: O(1)

This article is contributed by Aarti_Rathi and Shashank Mishra ( Gullu ). If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Another Approach:

1. Define a function “gcd” that takes two integers “a” and “b” and returns their greatest common divisor (GCD) using the Euclidean algorithm.
2. Define a function “count_common_divisors” that takes two integers “a” and “b” and counts the number of common divisors of “a” and “b” using their GCD.
3. Calculate the GCD of “a” and “b” using the “gcd” function.
4. Initialize a counter “count” to 0.
5. Loop through all possible divisors of the GCD of “a” and “b” from 1 to the square root of the GCD.
6. If the current divisor divides the GCD evenly, increment the counter by 2 (because both “a” and “b” are divisible by the divisor).
7. If the square of the current divisor equals the GCD, decrement the counter by 1 (because we’ve already counted this divisor once).
8. Return the final count of common divisors.
9. In the main function, define two integers “a” and “b” and call the “count_common_divisors” function with these integers.
10. Print the number of common divisors of “a” and “b” using the printf function.

C

#include <stdio.h>

int gcd(int a, int b) {

if(b == 0) {

return a;

}

return gcd(b, a % b);

}

int count_common_divisors(int a, int b) {

int gcd_ab = gcd(a, b);

int count = 0;

for(int i = 1; i * i <= gcd_ab; i++) {

if(gcd_ab % i == 0) {

count += 2;

if(i * i == gcd_ab) {

count--;

}

return count;

}

int main() {

int a = 12;

int b = 18;

int common_divisors = count_common_divisors(a, b);

printf("The number of common divisors of %d and %d is %d.n", a, b, common_divisors);

return 0;

}

C++

#include <bits/stdc++.h>

using namespace std;

int gcd(int a, int b) {

if(b == 0) {

return a;

}

return gcd(b, a % b);

}

int count_common_divisors(int a, int b) {

int gcd_ab = gcd(a, b);

int count = 0;

for(int i = 1; i * i <= gcd_ab; i++) {

if(gcd_ab % i == 0) {

count += 2;

if(i * i == gcd_ab) {

count--;

}

return count;

}

int main() {

int a = 12;

int b = 18;

int common_divisors = count_common_divisors(a, b);

cout<<"The number of common divisors of "<<a<<" and "<<b<<" is "<<common_divisors<<"."<<endl;

return 0;

}

Java

import java.util.*;

public class Main {

public static int gcd(int a, int b) {

if(b == 0) {

return a;

}

return gcd(b, a % b);

}

public static int countCommonDivisors(int a, int b) {

int gcd_ab = gcd(a, b);

int count = 0;

for(int i = 1; i * i <= gcd_ab; i++) {

if(gcd_ab % i == 0) {

count += 2;

if(i * i == gcd_ab) {

count--;

}

return count;

}

public static void main(String[] args) {

int a = 12;

int b = 18;

int commonDivisors = countCommonDivisors(a, b);

System.out.println("The number of common divisors of " + a + " and " + b + " is " + commonDivisors + ".");

}

Python3

import math

def gcd(a, b):

if b == 0:

return a

return gcd(b, a % b)

def count_common_divisors(a, b):

gcd_ab = gcd(a, b)

count = 0

for i in range(1, int(math.sqrt(gcd_ab)) + 1):

if gcd_ab % i == 0:

count += 2

if i * i == gcd_ab:

count -= 1

return count

a = 12

b = 18

common_divisors = count_common_divisors(a, b)

print("The number of common divisors of", a, "and", b, "is", common_divisors, ".")

C#

using System;

public class MainClass

{

public static int GCD(int a, int b)

{

if (b == 0)

{

return a;

}

return GCD(b, a % b);

}

public static int CountCommonDivisors(int a, int b)

{

int gcd_ab = GCD(a, b);

int count = 0;

for (int i = 1; i * i <= gcd_ab; i++)

{

if (gcd_ab % i == 0)

{

count += 2;

if (i * i == gcd_ab)

{

count--;

}

return count;

}

public static void Main()

{

int a = 12;

int b = 18;

int commonDivisors = CountCommonDivisors(a, b);

Console.WriteLine("The number of common divisors of {0} and {1} is {2}.", a, b, commonDivisors);

}

Javascript

function gcd(a, b) {

if(b === 0) {

return a;

}

return gcd(b, a % b);

}

function count_common_divisors(a, b) {

let gcd_ab = gcd(a, b);

let count = 0;

for(let i = 1; i * i <= gcd_ab; i++) {

if(gcd_ab % i === 0) {

count += 2;

if(i * i === gcd_ab) {

count--;

}

return count;

}

let a = 12;

let b = 18;

let common_divisors = count_common_divisors(a, b);

console.log(`The number of common divisors of ${a} and ${b} is ${common_divisors}.`);

Output

The number of common divisors of 12 and 18 is 4.

The time complexity of the gcd() function is O(log(min(a, b))), as it uses Euclid’s algorithm which takes logarithmic time with respect to the smaller of the two numbers.

The time complexity of the count_common_divisors() function is O(sqrt(gcd(a, b))), as it iterates up to the square root of the gcd of the two numbers.

The space complexity of both functions is O(1), as they only use a constant amount of memory regardless of the input size.

Last Updated :
13 Apr, 2023

Like Article

Save Article

Источник

Загрузить PDF

Нахождение наибольшего общего делителя (НОД) для определенного количества чисел может быть легкой задачей, если вы умеете это делать.

1

Найдите делители чисел. Начните с поиска всех делителей первого и второго числа.
2

Сравните делители обоих чисел и найдите самое большое число, которое есть в списке делителей как первого, так и второго числа. Это число равно НОД.

Реклама

1

Разложите каждое число на простые множители. Простое число — это число, большее 1 и которое делится только на 1 и на само себя. Примеры простых чисел: 5, 17, 97, 331.
2

Найдите общие простые множители. Общий простой множитель может быть только один, или их может быть несколько.
3

Если у двух чисел есть только один общий простой множитель, то он равен НОД. Если у двух чисел есть несколько общих простых множителей, то их произведение равно НОД.
4

Изучите пример. Чтобы продемонстрировать этот метод, изучите пример, приведенный на рисунке.

Реклама

Советы

Простое число — это число, которое делится только на 1 и на само себя.
Знаете ли вы, что в третьем веке до н.э. математик Евклид создал алгоритм для вычисления наибольшего общего делителя двух натуральных чисел и двух многочленов?

Об этой статье

Эту страницу просматривали 7441 раз.

Была ли эта статья полезной?

Источник

Наибольшим общим делителем (НОД) двух целых чисел называется наибольший из их общих делителей. К примеру для чисел 12 и 8, наибольшим общим делителем будет 4.

Как найти НОД?

Способов найти НОД несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОД при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:

разложить оба числа на простые множители (подробнее о разложении чисел на простые множители смотрите тут);
выбрать одинаковые множители, входящие в оба разложения;
найти их произведение.

Примеры нахождения наибольшего общего делителя

Рассмотрим приведенный алгоритм на конкретных примерах:

Пример 1: найти НОД 12 и 8

1. Раскладываем 12 и 8 на простые множители:

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 2 и 2

3. Перемножаем эти множители и получаем: 2 · 2 = 4

Ответ: НОД (8; 12) = 2 · 2 = 4.

Пример 2: найти НОД 75 и 150

Этот пример, как и предыдущий с легкостью можно высчитать в уме и вывести ответ 75, но для лучшего понимания работы алгоритма, проделаем все шаги:

1. Раскладываем 75 и 150 на простые множители:

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 3, 5 и 5

3. Перемножаем эти множители и получаем: 3 · 5 · 5 = 75

Ответ: НОД (75; 150) = 3 · 5 · 5 = 75.

Частный случай или взаимно простые числа

Нередко встречаются ситуации, когда оба числа взаимно простые, т.е. общий делитель равен единице. В этом случае, алгоритм будет выглядеть следующим образом:

Пример 3: найти НОД 9 и 5

1. Раскладываем 5 и 9 на простые множители:

Видим, что одинаковых множителей нет, а значит, что это частный случай (взаимно простые числа). Общий делитель — единица.

Источник

Как найти НОД

Нахождение путём разложения на множители
Алгоритм Евклида

Рассмотрим два способа нахождения наибольшего общего делителя.

Нахождение путём разложения на множители

Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.

Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.

Пример 1. Найти НОД (84, 90).

Решение: Раскладываем числа 84 и 90 на простые множители:

Итак, мы подчеркнули все общие простые множители, осталось перемножить их между собой:

2 · 3 = 6.

Таким образом, НОД (84, 90) = 6.

Пример 2. Найти НОД (15, 28).

Решение: Раскладываем 15 и 28 на простые множители:

Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.

НОД (15, 28) = 1.

Алгоритм Евклида

Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.

Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.

Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.

Пример 1. Возьмём два числа 27 и 9. Так как 27 делится на 9 и 9 делится на 9, значит, 9 является общим делителем чисел 27 и 9. Этот делитель является в тоже время и наибольшим, потому что 9 не может делиться ни на какое число, большее 9. Следовательно:

НОД (27, 9) = 9.

В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:

Из двух данных чисел большее число делят на меньшее.
Затем, меньшее число делят на остаток, получившийся от деления большего числа на меньшее.
Далее, первый остаток делят на второй остаток, который получился от деления меньшего числа на первый остаток.
Второй остаток делят на третий, который получился от деления первого остатка на второй и т. д.
Таким образом деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель как раз и будет наибольшим общим делителем.

Пример 2. Найдём наибольший общий делитель чисел 140 и 96:

1) 140 : 96 = 1 (остаток 44)

2) 96 : 44 = 2 (остаток

3) 44 : 8 = 5 (остаток 4)

4) 8 : 4 = 2

Последний делитель равен 4 — это значит:

НОД (140, 96) = 4.

Последовательное деление так же можно записывать столбиком:

Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:

Сперва находим наибольший общий делитель любых двух чисел из нескольких данных.
Затем находим НОД найденного делителя и какого-нибудь третьего данного числа.
Затем находим НОД последнего найденного делителя и четвёртого данного числа и так далее.

Пример 3. Найдём наибольший общий делитель чисел 140, 96 и 48. НОД чисел 140 и 96 мы уже нашли в предыдущем примере (это число 4). Осталось найти наибольший общий делитель числа 4 и третьего данного числа — 48:

48 : 4 = 12

48 делится на 4 без остатка. Таким образом:

НОД (140, 96, 48) = 4.

Источник