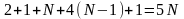Как найти число операций

Ниже представлен код, в котором реализован обычный алгоритм сортировки выбором. Напомню, что сложноть этого алгоритма O(n^2). Я передаю в функцию сортировки массив размером 7 элементов. Если посчитать O(n^2), то получается 7 * 7 = 49 операций. В коде я пытаюсь посчитать тоже самое, создав переменную operations и инкрементируя её в конце каждой итерации цикла, ведь, итерация — это и есть операция (или нет?). В итоге у меня получилось 28, хотя ожидал увидеть 49. Где моя ошибка?

const sort = (collection) => {

let operations = 0;
const length = collection.length - 1;
	
  for (let i = 0; i <= length; i++) {
		let minIndex = i;
    for (let j = i + 1; j <= length; j++) {
      if (collection[j] < collection[minIndex]) {
        minIndex = j;
			}
			operations++;
		}
		if (minIndex !== i) {
			[collection[minIndex], collection[i]] = [collection[i], collection[minIndex]];
		}
		operations++
	}
	console.log('Количество операций: ', + operations);
	return collection;
};
console.log(sort([2, 1, 3, 5, 6, 3, 9]));

1. Подсчет числа простейших операций

В соответствии с методом подсчета
простейших операций алгоритм
представляется в виде программы на
развитом языке программирования
(например, Pascal). Определяется
множество простейших операций высокого
уровня, которые не зависят от языка
программирования. К таким операциям
относятся:

1. присваивание переменной значения,

2. вызов метода (процедуры или функции),

3. выполнение арифметической операции,

4. сравнение двух значений,

5. индексация массива,

6. переход по ссылке на объект,

7. возвращение из метода.

Данный метод основан на неявном
предположении, что время выполнения
простейших операций приблизительно
одинаково. Таким образом, К простейших
операций, выполняемых внутри алгоритма,
пропорционально действительному времени
выполнения данного алгоритма.

Рассмотрим процесс подсчета простейших
операций на примере алгоритма определения
максимального значения в одномерном
массиве X, состоящего из
N элементов. На
рисунке 3.2 приводится код данного
алгоритма на языке Pascal.

begin

currentMax:=
X[0];

for
i:= 1 to
N-1 do

if
currentMax < X[i] then
currentMax:= X[i];

end;

Рисунок
3.2 – Pascal-код алгоритма
определения максимального значения в
массиве

Приведем рассуждения, формулируемые в
процессе анализа:

• на этапе инициализации переменной
  currentMax
  и присваивания ее значения X[0]
  выполняются две простейшие операции
  (индексация массива и присваивание
  значения); таким образом, счетчик
  операций равен 2;

• в начале цикла for
  счетчик i
  получает значение 1, что соответствует
  одной простейшей операции присваивания;

• перед выполнением тела цикла проверяется
  условие i<
  N (операция
  сравнения); такое сравнение выполняется
  N раз, поэтому счетчик
  простейших операций увеличивается еще
  на N единиц;

• тело цикла выполняется для значений
  i,
  равных 1, 2, …, N-1.
  При каждой итерации X[i]
  сравнивается с currentMax
  (две простейших операции – индексирование
  и сравнение), значение X[currentMax],
  возможно, присваивается переменной
  currentMax
  (две операции – сложение и присваивание),
  а счетчик i
  увеличивается на 1 (две операции –
  сложение и присваивание). Следовательно,
  при каждой итерации цикла выполняется
  4 или 6 простейших операций, в зависимости
  от выполнения одного из условий X[i]
  currentMax
  или X[i]>
  currentMax.
  Таким образом, при выполнении тела
  цикла в счетчик операций добавляется
  4(N–1) или 6(N–1);

• при возвращении значения переменной
  currentMax
  однократно выполняется одна простейшая
  операция.

Итак, число простейших операций К(N),
выполняемых алгоритмом, минимально
равно

,

а
максимально

.

Число выполняемых простейших операций
равно минимально (К(N)
= 5N) в том случае, если
X[0]
является максимальным элементом массива,
т. е. переменной currentMax
не присваивается нового значения.
Число выполняемых операций максимально
равно 7N–2 в том случае,
если элементы массива упорядочены по
возрастанию, и переменной currentMax
присваивается значение при каждой
итерации цикла.

1. О-нотация

Для выражения характеристик быстродействия
в вычислительной технике используется
короткая схема – О-нотация (big-Oh
notation). В этой нотации
используется специальная математическая
функция от N, т. е.
количества исходных данных, которому
пропорционально быстродействие
алгоритма. Утверждается, что алгоритм
принадлежит к классу О(f(N)),
где f(N)
– некоторая функция от N.
Приведенное обозначение читается как
«О большое от f(N)»
или, менее строго, «пропорционально
f(N)»

Например, исследования показали, что
алгоритм А принадлежит к классу О(N),
а алгоритм В – к классу О(log(N)).
Поскольку для положительных чисел
log(N) < N,
можно сделать вывод о том, что алгоритм
В всегда эффективнее алгоритма А.

О-нотация подчиняется простым
арифметическим правилам. Во-первых,
умножение математической функции внутри
скобок в О-нотации на константу не
оказывает никакого влияния на О-нотацию.
Например, О(3f(N))
и О(24f(N))
эквивалентно О(f(N)),
поскольку константы 3 или 24 можно без
последствий вынести за скобки как
коэффициент пропорциональности, который
игнорируется.

Во-вторых, О-нотация демонстрирует
асимптотическое поведение, проявляющееся
в том, что для больших значений N
О-нотация определяет тот класс алгоритма,
к которому принадлежит его доминантная
часть. Пусть некоторый алгоритм
принадлежит к классу О(N²
+ N). Если величина N
достаточно велика, то влияние члена
«+N» поглощается членом
«N²». Другими
словами при больших значениях N
алгоритм О(N²
+ N) эквивалентен
алгоритму О(N²).
То же можно сказать и для более высоких
степеней N.

Предположим, что есть алгоритм, который
выполняет три различных задачи. Первая
задача выполняется алгоритмом класса
О(N), вторая –
алгоритмом класса О(N²),
третья – алгоритмом класса О(log(N)).
Каково будет быстродействие алгоритма
в целом. Ответ будет О(N²),
поскольку к этому классу принадлежит
доминантная часть алгоритма.

Таким образом, значения О большого
характеризуют алгоритм для больших
значений N, а для
маленьких значений N
О-нотация не имеет смысла.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Что такое алгоритм?

Алгоритм — это последовательность указаний, которые нужно исполнить, чтобы решить чётко сформулированную задачу. Мы описываем задачи исходя из ввода и вывода, и алгоритм становится способом превращения ввода в вывод. При этом формулировка задачи должна быть точной и недвусмысленной — это помогает избежать неверной интерпретации.

Когда вы закончили проектировать алгоритм, необходимо ответить на два важных вопроса: «Правильно ли он работает?» и «Сколько времени занимает выполнение?». Разумеется, вас не устроит алгоритм, который выдаёт правильный результат лишь в половине случаев или требует $1,000$ лет для поиска ответа.

Псевдокод

Чтобы понять, как работает алгоритм, нам необходимо перечислить шаги, которые он выполняет. Для этого мы будем использовать псевдокод — язык, которым пользуются разработчики для описания алгоритмов. Он игнорирует многие детали, необходимые в языках программирования, но он более точен, чем рецепт из кулинарной книги.

Задача и экземпляр задачи

Задача описывает класс возможных входных данных. Экземпляр задачи — это один конкретный ввод такого класса. Чтобы продемонстрировать понятия задачи и экземпляра задачи, рассмотрим следующий пример. Вы оказались в книжном магазине и собираетесь купить книгу за $4,23$＄, расплатившись купюрой в $5$＄. Вам должны вернуть $77$ центов в качестве сдачи. Теперь кассир принимает решение, как именно это сделать. Согласитесь, неприятно получить горсть из $77$ пенни или $15$ никелей и $2$ пенни. Возникает вопрос: как выдать сдачу, не расстроив клиента? Большинство кассиров стараются уместить сумму сдачи в наименьшее количество монет.

💡 Остановитесь и подумайте:
Каково минимальное количество монет номиналом $(25, 10, 5, 1)$, необходимо для сдачи в $77$ центов?

Пример с $77$ центами представляет собой экземпляр задачи Размен. Предполагается, что есть $d$ номиналов, которые представлены массивом $c = (c_1, c_2, dotsc, c_d)$. Для упрощения будем считать, что номиналы даны в порядке убывания. Например, $c = (25, 10, 5, 1)$ для монет, используемых в США.

Задача "Размен"

Переведите определенное количество денег в данные номиналы, используя как можно меньше монет.

• Входные данные: Целое число $money$ и массив из $d$ номиналов $c = (c_1, c_2, dotsc, c_d)$ в порядке убывания ( $c_1 > c_2 > dotsb > c_d$ ).
• Выходные данные: Список из $d$ целых чисел $i_1, i_2, dotsc , i_d$, в котором $c_1cdot i_1+c_2 cdot i_2+dotsm+ c_d cdot i_d = money$ и $i_1 + i_2 +dotsm +i_d$ как можно меньше.

Кассиры по всему миру решают эту проблему с помощью простого алгоритма:

Change(money, c, d):
    while money > 0:
        coin = ... // монета с самым большим номиналом, который не превышает money
        // дать монету с номиналом coin клиенту
        money = money - coin

Вот быстрая версия Change:

Change(money, c, d):
    for k in range(1, d + 1) 
        i_k = floor(money / c[k]) // наибольшее количество монет номинала c[k]
        // дать i_k монет с номиналом c_k клиенту
        money = money - c[k] * i_k

Корректные и некорректные алгоритмы

Мы называем алгоритм корректным, если на каждый получаемый ввод он делает правильный вывод. Алгоритм считается некорректным, если хотя бы один ввод приводит к неправильному выводу.

💡 Остановитесь и подумайте:
Каково минимальное количество монет номиналами $(25, 20, 10, 5, 1)$, необходимое для сдачи в $40$ центов?

Change — это некорректный алгоритм! Представьте сдачу в 40 центов, выданную в номиналах $c_1 = 25$, $c_2 = 20$, $c_3 = 10$, $c_4 = 5$ и $c_5 = 1$. Change привел бы к неправильному результату: он выдал бы 1 четвертак (25 центов), 1 дайм (10 центов) и 1 никель (5 центов) вместо 2 монет по двадцать центов. Хоть это и может выглядеть надуманно, в 1875 году в США существовала монета в двадцать центов. Насколько мы можем быть уверены, что Change выдаст минимальное количество монет в современных номиналах Соединенных Штатов или любой другой страны?

Чтобы исправить алгоритм Change, нам нужно рассмотреть все возможные комбинации монет с номиналами $c_1, c_2, dotsc , c_d$, которые дают в сумме $money$, и выдать комбинацию с минимальным количеством монет. Мы рассматриваем только комбинации, в которых $i_1 le money/c_1$ и $i_2 le money/c_2$ (в целом, величина $i_k$ не должна превышать $money/c_k$), в ином случае мы вернем большее количество денег, чем $money$. В псевдокоде, приведенном ниже, используется символ $sum$. Он обозначает суммирование: $sum^m_{i=1} a_i = a_1 + a_2 + dotsm + a_m$. Псевдокод также использует концепт «бесконечность» (обозначается $infty$) в качестве начального значения для $smallestNumberOfCoins$. Реализация описанного подхода на реальных языках программирования может различаться, но сейчас подробности для нас не важны.

BruteForceChange(money, c, d):
    smallestNumberOfCoins = ∞
    for each combinations of coins (i_1,...,i_d)
    // от (0,...,0) до (money/c[1],...,money/c[d])
        valueOfCoins = ∑ i_k*c_k // сумма по всем k от 1 до d
        if valueOfCoins = M:
            numberOfCoins = ∑ i_k // суммарное количество монет
            if numberOfCoins < smallestNumberOfCoins:
                smallestNumberOfCoins = numberOfCoins
                change = (i_1, i_2, ... ,i_d)
    return change

Вторая строка повторяется с каждой возможной комбинацией $(i_1, dotsc, i_d)$ из $d$ индексов и останавливается, когда достигает

$$
left(frac{money}{c_1}, dotsc, frac{money}{c_d}right),
$$

Как мы можем узнать, что BruteForceChange не содержит ту же проблему, что и Change, — неверный результат при каком-то вводе? Раз BruteForceChange рассматривает все возможные комбинации номиналов, рано или поздно алгоритм придёт к оптимальному решению и запишет его в массив $change$. В любой комбинации монет, которая даёт в сумме $M$, должно быть как минимум столько же монет, сколько и в оптимальной. Таким образом, BruteForceChange никогда не завершит работу с неоптимальным набором $change$.

На данный момент мы ответили только на один из двух важных вопросов об алгоритмах: «Работает ли он?». Однако мы не ответили на вопрос: «Сколько времени занимает выполнение?».

💡 Остановитесь и подумайте:
Сколько примерно итераций цикла for выполняет BruteForceChange?

• money
• $money^d$
• $d$

Быстрые и медленные алгоритмы

Настоящие компьютеры требуют определенное количество времени на выполнение таких операций, как сложение, вычитание или проверка условий цикла while. Суперкомпьютер может выполнить сложение за $10^{-10}$ секунды, а калькулятор — за $10^{-5}$. Представьте, что у вас есть компьютер, которому требуется $10^{-10}$ секунды на выполнение простой операции (например, сложения), и вы знаете, сколько операций выполняет какой-то конкретный алгоритм. Вы могли бы рассчитать время выполнения алгоритма, просто взяв произведение количества операций и времени, которое занимает одна операция. Однако компьютеры постоянно улучшаются, благодаря чему им требуется меньше времени на операцию. Так, ваше представление о времени выполнения быстро стало бы устаревшим. Вместо того, чтобы рассчитывать время выполнения на каждом компьютере, мы описываем время выполнения через общее количество операций, необходимых алгоритму, — это характеристика самого алгоритма, а не компьютера, который вы используете.

К сожалению, нам не всегда легко определить, сколько операций выполнит алгоритм. Однако если мы можем рассчитать количество базовых операций, выполняемых алгоритмом, то это позволит сравнить его с другим алгоритмом, решающим ту же задачу. Чтобы мучительно не подсчитывать каждое умножение и сложение, можно сравнивать только те участки кода, которые при увеличении размера ввода потребуют больше операций.

Представьте, что алгоритм $A$ выполняет $n^2$ операций при вводе размера $n$, и алгоритм $B$ решает ту же задачу за $3n+2$ операций. Какой алгоритм быстрее: $A$ или $B$? Хотя $A$ и может быть быстрее, чем $B$, при более малом значении $n$ (например, при $n$ между 1 и 3), $B$ будет быстрее при больших значениях $n$ (например, $n >4$). См. рис.. Так как $f(n)=n^2$ — это, в каком-то смысле, более «быстрорастущая» функция относительно $n$, чем $g(n)=n$. При этом константы 3 и 2 в $3n+2$ не влияют на конкуренцию между двумя алгоритмами при больших значениях $n$. Мы называем $A$ квадратичным алгоритмом и $B$ — линейным. $A$ менее эффективен, чем $B$, потому что он выполняет больше операций для решения задачи, когда значение $n$ большое. Так, иногда мы будем допускать неточности при подсчете операций алгоритма: поведение алгоритма при маленьком вводе неважно.

Рассчитаем примерное количество операций, которое потребуется для BruteForceChange при вводе из $M$ центов и номиналов $(c_1, c_2, dotsc, c_d)$. Чтобы рассчитать общее количество операций в цикле for, нам необходимо взять примерное число операций, выполняемое при каждой итерации, и умножить его на общее количество итераций. Так как в нашем случае около

$$
frac{money}{c_1} times frac{money}{c_2} times dotsm times frac{money}{c_d}
$$

Такой тип алгоритмов называется экспоненциальным в противоположность квадратичным, кубическим или другим полиномиальным алгоритмам. Выражение времени выполнения экспоненциального алгоритма использует $n^d$, где $n$ и $d$ — это параметры задачи (например, $n$ и $d$ можно произвольно сделать большими, изменив ввод для алгоритма). Время выполнения полиномиального алгоритма ограничено $n^k$, где $k$ — это константа, не связанная с величиной параметров задачи.

Например, алгоритм с временем выполнения $n^1$ (линейный), $n^2$ (квадратичный), $n^3$ (кубический) или даже $n^{2018}$ будет полиномиальным. Конечно, алгоритм с временем выполнения $n^{2018}$ не очень практичен. Возможно, даже менее практичен, чем некоторые экспоненциальные алгоритмы. Впрочем, разработчики тратят много усилий, чтобы проектировать всё более и более быстрые полиномиальные алгоритмы. Раз значение $d$ может быть большим при вызове алгоритма с большим количеством номиналов (например, $c = (1, 2, 3, 4, 5, dotsc , 100)$), мы видим, что выполнение BruteForceChange может потребовать много времени.

To count the number of operations is also known as to analyze the algorithm complexity. The idea is to have a rough idea how many operations are in the worst case needed to execute the algorithm on an input of size N, which gives you the upper bound of the computational resources required for that algorithm. And since each operation by itself (like multiplication or comparison for example) is a finite operation and takes deterministic time (even though it might be different on different machines), to get an idea of how good or bad an algorithm is, especially compared to other algorithms, all you need to know is the rough number of operations.

Here’s an example with bubble sort. Let’s say you have an array of two numbers. To sort it you need to compare both numbers and potentially exchange them. Since comparing and exchanging are single operations, the exact time for executing them is minimal and not important by itself. Thus, you can say that with N=2, the number of operations is O(N)=1. For three numbers, though, you need three operations in the worst case — compare the first and the second one and potentially exchange them, then compare the second one and the third one and exchange them, then compare the first one with the second one again. When you continue to generalize the bubble sort, you will find out that potentially to sort N numbers, you need to do N operations for the first number, N-1 for the second and so on. In other words, O(N) = N + (N-1) + … + 2 + 1 = N * (N-1) / 2, which for big enough N can be simplified to O(N) = N^2.

Of course, you could just cheat and find out on the web the O(N) number for each of the three sort algorithms, but I would urge you to spend the time and try to come up with that number yourself at first. Even if you get it wrong, comparing your estimate and how you got it with the actual way to estimate their complexity will help you understand better the process of analyzing the complexity of particular piece of software you write in future.

Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.

Оценка сложности

Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.

Допустим, некоторому алгоритму нужно выполнить 4n3 + 7n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в куб, чем умножение его на 4 или же прибавление 7n. Тогда говорят, что временная сложность этого алгоритма равна О(n3), т. е. зависит от размера входных данных кубически.

Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где её применяют для сравнения асимптотического поведения функций. Формально O(f(n)) означает, что время работы алгоритма (или объём занимаемой памяти) растёт в зависимости от объёма входных данных не быстрее, чем некоторая константа, умноженная на f(n).

Примеры

O(n) — линейная сложность

Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.

O(log n) — логарифмическая сложность

Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.

O(n²) — квадратичная сложность

Такую сложность имеет, например, алгоритм сортировки вставками. В канонической реализации он представляет из себя два вложенных цикла: один, чтобы проходить по всему массиву, а второй, чтобы находить место очередному элементу в уже отсортированной части. Таким образом, количество операций будет зависеть от размера массива как n * n, т. е. n2.

Бывают и другие оценки по сложности, но все они основаны на том же принципе.

Также случается, что время работы алгоритма вообще не зависит от размера входных данных. Тогда сложность обозначают как O(1). Например, для определения значения третьего элемента массива не нужно ни запоминать элементы, ни проходить по ним сколько-то раз. Всегда нужно просто дождаться в потоке входных данных третий элемент и это будет результатом, на вычисление которого для любого количества данных нужно одно и то же время.

Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.

Наглядно

Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10⁶ операций в секунду:

Тут можно посмотреть сложность основных алгоритмов сортировки и работы с данными.

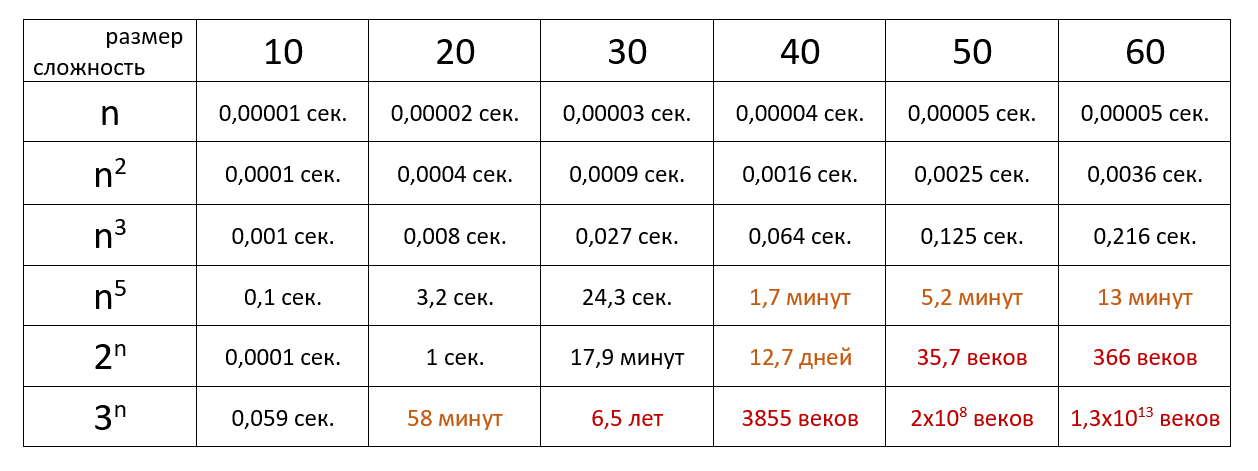
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».