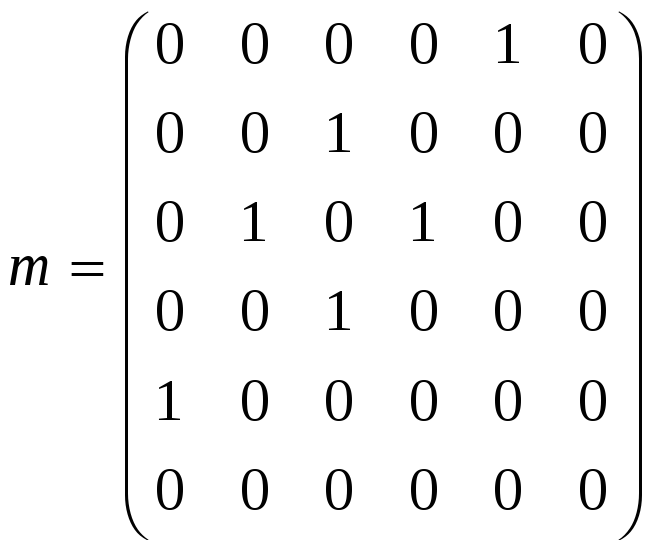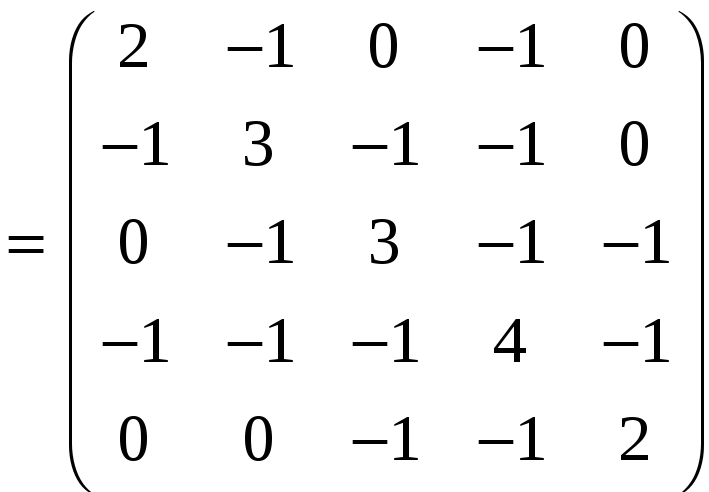Как найти число остовов графа - Исправление недочетов и поиск решений вместе с Examum.ru

Вариант №39.

Задание.
Найти число остовов графа, нарисовать
их и найти остов минимального веса.

Решение:

Теорема (Кирхгоф).
Число остовов в связном графе G
порядка n≥2
равно алгебраическому дополнению
любого элемента матрицы Кирхгофа K(G)
графа G.

Матрицей
Кирхгофа графа G называется матрица:

Алгебраические
дополнения всех элементов матрицы
Кирхгофа равны между собой.

Составим матрицу
Кирхгофа для данного графа:

Отсюда алгебраическое
дополнение, например, элемента

равно 21.

Значит, и число
остовов данного графа равно 21.

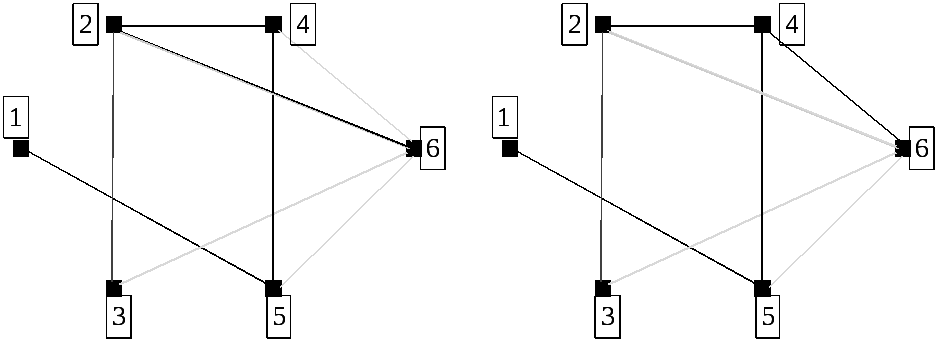
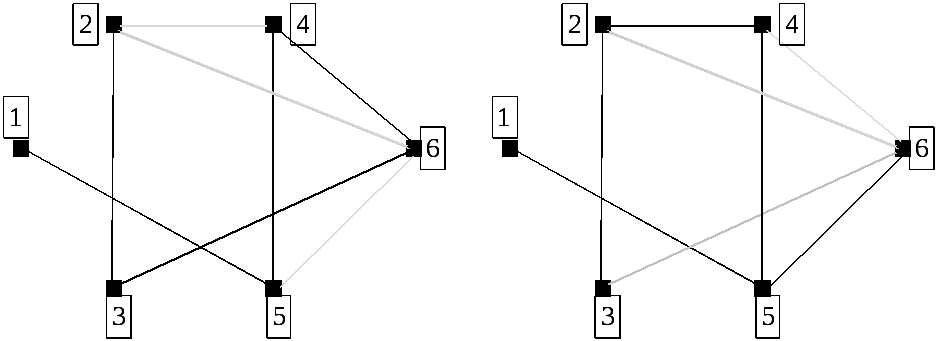
Изобразим их:

Найдем остов
минимального веса с помощью алгоритма
Краскала.

Шаг 1.
Установка начальных значений.

Введем матрицу
длин ребер C:

Шаг 2.
Выберем ребро минимальной длины.

Минимальная длина
ребра равна 390. Это ребро (2,3). Построим
граф G₂,
состоящий из данного ребра и инцидентных
ему вершин 2 и 3. Положим i = 2.

Шаг 3.
Так как n
= 6, то i ≠ n,
поэтому переходим к шагу 4.

Шаг 4.
Строим граф G₃,
добавляя к графу G₂
новое ребро минимальной длины, выбранное
среди всех ребер графа G, каждое из
которых инцидентно одной из вершин 2,
3 и одновременно инцидентно какой-нибудь
вершине графа G, не содержащейся в G₂,
т.е. одной из вершин 1, 4, 5, 6. Таким образом,
нужно выбрать ребро минимальной длины
из ребер (2,4), (2,6), (3,6). Такое ребро имеет
длину 468 и оно одно: (2,4). Вместе с этим
ребром включаем в G₃
вершину 4, не содержащуюся в G₂.
Полагаем i = 3 и переходим к шагу 3.

Шаг 3.
Так как i ≠ n,
поэтому переходим к шагу 4.

Шаг 4.
Строим граф G₄,
добавляя к графу G₃
новое ребро минимальной длины из ребер
(3,6), (2,6), (4,5), (4,6). Такое ребро имеет длину
624 и оно одно: (2,6). Вместе с этим ребром
включаем в G₄
вершину 6, не содержащуюся в G₃.
Полагаем i = 4 и переходим к шагу 3.

Шаг 3.
Так как i ≠ n, поэтому переходим к шагу
4.

Шаг 4.
Строим граф G₅,
добавляя к графу G₄
новое ребро минимальной длины из ребер
(4,5), (6,5). Такое ребро имеет длину 702 и оно
одно: (4,5). Вместе с этим ребром включаем
в G₅
вершину 5, не содержащуюся в G₄.
Полагаем i = 5 и переходим к шагу 3.

Шаг 3.
Так как i ≠ n, поэтому переходим к шагу
4.

Шаг 4.
Строим граф G₆.
Осталась только одна вершина в графе
G,
не включенная в G₆
– это вершина 1. Так как инцидентное ей
ребро только одно, то добавим его в граф
G₆
вместе в вершиной 1. Полагаем i = 6 и
переходим к шагу 3.

Шаг 3.
Так как i = n, то граф G₆
– искомое минимальное остовное дерево.

Суммарная длина
ребер равна 390 + 468 + 624 + 702 + 468 = 2652.

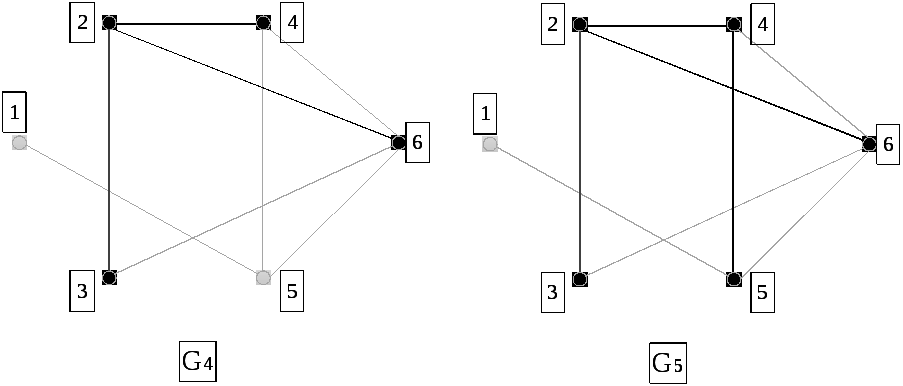
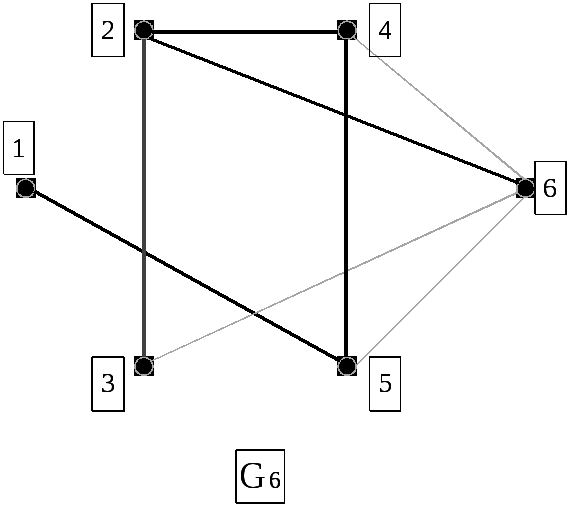
Процесс построения
минимального остовного дерева:

5)
Задание.
Найти нижнюю и верхнюю оценки числа
внутренней устойчивости неориентированного
графа, заданного своей матрицей смежности
m:

Решение:

Для
всех единиц выписываются парные
дизъюнкции:

Приведем
выражение к ДНФ:

Число
внутренней устойчивости равно 2.

Задание.
Построить матрицу смежности, найти её
3-ю степень и число ориентированных
маршрутов длины 3 из вершины 1 в вершину
4.

Решение:

Матрица смежности
A = (a_ij)
– это квадратная матрица порядка n, где
n – число вершин, у которой:

Матрица смежности
данного графа:

Найдем её третью
степень:

Длиной маршрута
называется количество ребер в нем.

Для определения
маршрутов, состоящих из k ребер (дуг),
необходимо возвести в k-ю степень матрицу
смежности вершин A.
Тогда элемент матрицы

даст количество маршрутов длины k
(состоящих из k ребер) из вершины

в вершину
.

Таким образом,
число ориентированных маршрутов длины
3 из вершины 1 в вершину 4 равно элементу

= 4.

Задание.
Построить
матрицу инциденций и найти число остовов.

Матрицей
инцидентности B = (b_ij)
ориентированного графа называется
прямоугольная матрица (n×m), где n – число
вершин, m – число ребер, у которой:

Матрица
инциденций данного графа:

Составим
матрицу Кирхгофа для данного графа:

Отсюда
алгебраическое дополнение, например,
элемента

равно 0.

Значит,
у данного графа остовов нет.

Соседние файлы в папке Diskretka

#
#
#
08.12.201732.77 Кб9DM_MP-2ab_pr_1_2013.xls
#
#
#

Источник

Лемма:

Пусть — обыкновенный — граф, , — матрица инцидентности некоторой его ориентации, — произвольный минор порядка матрицы . Тогда

если не является деревом, то ;
если — дерево, то .

Доказательство:

Заметим, что смена нумерации вершин и нумерации ребер графа приводит к перестановке строк и перестановке столбцов матрицы . Рассматриваемый минор при этом может сменить лишь знак.
Пусть — вершина, соответствующая строке матрицы , не вошедшей в матрицу минора .

Пусть не является деревом. Тогда граф несвязен. Пусть — множество вершин некоторой компоненты связности графа , не содержащей .
1. Если , то — изолированная вершина и в матрице минора имеется нулевая строка, поэтому .
2. Пусть . С помощью подходящей перенумерации вершин и ребер из матрицу приведем к клеточному виду
  ,
  где — матрица инцидентности ориентации компоненты , а вершине отвечает строка, проходящая через . Каждый столбец, проходящий через , содержит точно одну единицу и точно одну (остальные элементы равны нулю). Следовательно, сумма первых строк равна . Так как первые строк входят в матрицу минора , имеем .
Пусть является деревом. Заново перенумеруем вершины и ребра графа с помощью следующей процедуры. В качестве возьмем одну из висячих вершин дерева , отличную от . Через обозначим инцидентное ей висячее ребро. Рассмотрим дерево . Если его порядок , то через обозначим одну из висячих вершин, отличных от , а через — инцидентное ей висячее ребро. Положим . Продолжаем этот процесс до тех пор, пока не получим одноэлементное дерево , единственной вершиной которого обязательно будет вершина . Получим нумерацию вершин и нумерацию ребер . В новой нумерации матрица приведется к виду
,
причем вершине отвечает последняя строка (здесь каждый диагональный элемент равен или , а через обозначены элементы матрицы, значения которых не вписаны в явном виде). Таким образом, матрица минора имеет треугольный вид и .

Определение:

Пусть и — соответственно — матрица и — матрица, где . Положим . Минор порядка матрицы называется соответствующим минором минору порядка матрицы , если множество номеров строк, составляющих матрицу первого минора, равно множеству номеров столбцов, составляющих матрицу второго минора.

Теорема (Формула Бине-Коши^[1]):

Определитель матрицы равен сумме всевозможных попарных произведений миноров порядка матрицы на соответствующие миноры матрицы .

Следствие
При определитель произведения двух квадратных матриц порядка равен произведению определителей этих матриц

Теорема (Кирхгоф, 1847):

Число остовов в связном неодноэлементном обыкновенном графе равно алгебраическому дополнению любого элемента матрицы Кирхгофа .

Доказательство:

Пусть — произвольный связный обыкновенный — граф, и — матрица инцидентности какой-либо ориентации графа . Заметим, что в силу связности графа . По лемме выполняется . Пусть — подматрица матрицы , полученная удалением последней строки. Тогда имеем , где — это — матрица. Очевидно, есть алгебраическое дополнение элемента в матрице Кирхгофа . В силу формулы Бине-Коши равно сумме квадратов всех миноров порядка матрицы . Согласно лемме, доказанной выше, каждый такой минор равен , если остовный подграф графа , ребра которого соответствуют столбцам, вошедшим в матрицу минора , является деревом, и равен в другом случае. Следовательно, равно числу остовов графа . Осталось отметить, что по лемме алгебраические дополнения всех элементов матрицы Кирхгофа равны между собой.

См. также

Связь матрицы Кирхгофа и матрицы инцидентности
Матрица Кирхгофа
Количество помеченных деревьев
Коды Прюфера

Примечания

↑ Формула Бине-Коши

Источники информации

Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ «Регулярная и хаотическая динамика», 2001, 288 стр.

Источник

Дискретная математика: Учебное пособие. Часть 3 — Основы теории графов, страница 13

При формировании каталогов из
множества взаимосвязанных файлов, при организации программных комплексов или
при проектировании вычислительных сетей часто возникает необходимость
спроектировать граф виде дерева без циклов, петель и кратных ребер, но
опирающийся на все множество исходных файлов, программных модулей или
вычислительных станций. Такой граф называют покрывающим деревомили
остовом. Построение остова графа G=<x, r> заключено
в последовательном просмотре ребер графа в произвольном порядке и формировании
фрагмента покрывающего дерева по алгоритму:

шаг 1: выбрать любое ребро
множества r, не являющееся петлей и сформировать фрагмент
покрывающего дерева G_i’=<X_i’,r_i’>,

а концевые
вершины ребра включить в подмножество Х’;

шаг 2: выбрать любое ребро, не
принадлежащее фрагменту и не являющееся петлей:

а) если одна концевая вершина
выбранного ребра принадлежит фрагменту, то вторую концевую вершину включить в
подмножество Х’, а ребро включить в
фрагмент остова G_i’=<X_i’;
r_i’^`>,

б) если ни одна концевая вершина
ребра не принадлежит фрагменту остова, то сформировать фрагмент другого остова
G_j’=<X_j’;
r_j’^`>,

в) если концевые вершины
принадлежат различным остовам, то объединить фрагменты, т. е. G’=G_i’ÈG_j’,
где
X’=X_i’ÈX_j’,
r’=r_i’Èr_j’,

г) если обе концевые
вершины принадлежат фрагменту, то исключить это ребро;

шаг 3: если все вершины графа
вошли во фрагмент остова, т. е. X’=X
то конец, иначе перейти у шагу 2.

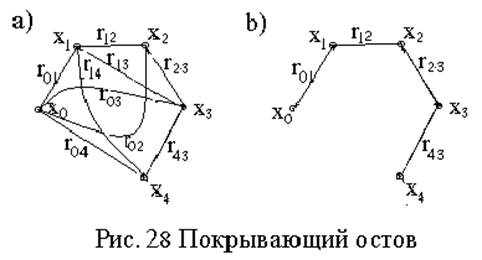
Пример:
На рис. 28а) дан граф, а на рис. 28b)
–его
остов.

Процесс построения покрывающего
дерева приведен в таблице.

шаг	ребра графа	вершины графа
r₀₁	r₀₂	r₀₃	r₀₄	r₁₂	r₁₃	r₁₄	r₂₃	r₃₄	x₀	x₁	x₂	x₃	x₄
1	1	0	0	0	0	0	0	0	0	1	1	0	0	0
2	0	0	0	0	1	0	0	0	0	1	1	1	0	0
3	0	0	0	0	0	0	0	1	0	1	1	1	1	0
4	0	0	0	0	0	0	0	0	1	1	1	1	1	1

Для
пятивершинного графа потребовалось четыре шага итерации. При
этом шесть ребер графа вообще не принимают участия в формировании остова. Иногда
возникает задача не только найти покрывающий остов, но использовать определенный
набор покрывающих ребер. Для этого необходимо прежде всего определить
цикломатическое число l(G), которое позволит знать число ребер,
удаление которых ликвидирует циклы. Далее, используя элементы комбинаторики,
найти число вариантов формирования остова. Для заданного графа l(G)=5,
а число возможных пятивершинных четырехреберных графов, построенных на данном
графе равно 126. Однако, среди них 10 графов сохраняют циклы. Следовательно, возможное
число остовов данного графа равно 116, среди которых можно искать остовы удовлетворяющие
особым требованиям.

3.4.2
Построение остова минимального веса

Решение этой задачи имеет большое
значение в проектировании электрических, кабельных и трубопроводных сетей, в
организации грузоперевозок по транспортной сети, в организации ремонтных работ
на участках дорог и т. п..

Основная идея состоит в следующем:
если есть некоторый фрагмент остова G’=<X’;
r’^`>
и ребро минимального веса l(х_i;х_j), одна из концевых
вершин которого х_i принадлежит фрагменту G’,
то включить в фрагмент вторую вершину ребра х_j и само ребро l(х_i;х_j).
Процедуру продолжать до включения во фрагмент (n-1) ребра графа, где n-число
его вершин. Такой граф будет обладать минимальным суммарным весом всех ребер
остова. Эта идея реализуется двумя алгоритмами:
Дейкстра и Краскала.

По алгоритму
Дейкстра:

шаг 1: определить начальную вершину
остова x₀;

шаг2: выбрать
ребро минимального веса, смежное с начальной вершиной

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Источник

	Нахождение числа остовов графа 10.12.2016, 06:50
30/11/16 13	Попалось мне на зачете такое задание — найти число остовов у данного графа. Вроде бы, все ясно — составить матрицу Кирхгофа, а затем найти алгебраическое дополнение произвольного элемента. Но вот как вычислить это дополнение для матрицы размерности 8х8 — я просто не представляю. Раскладывать по строке — дело долгое и муторное, да и моих серых клеток не хватит для такого. быть может, есть какие-то альтернативные пути решения ?

whitefox

Re: Нахождение числа остовов графа

10.12.2016, 16:41

Заслуженный участник

19/12/10
1546

Есть. Перечисление остовных деревьев. Эффективные алгоритмы можно найти, например, у Д. Кнута в «Искусство программирования» Т. 4, параграф 7.2.1.6 Остовные деревья.

Markiyan Hirnyk	Re: Нахождение числа остовов графа 10.12.2016, 16:48
11/07/16 791

Voenstal	Re: Нахождение числа остовов графа 11.12.2016, 03:31
30/11/16 13	И еще такой вопрос — есть ли разница между остовом и остовным деревом ? Просто много где описываются эти понятия как синонимы.

whitefox

Re: Нахождение числа остовов графа

11.12.2016, 09:55

Заслуженный участник

19/12/10
1546

Voenstal	Re: Нахождение числа остовов графа 11.12.2016, 11:24
30/11/16 13	Имхо, «остов» это слово из студенческого жаргона для обозначение «остовного дерева». Для меня немного странное ИМХО, ибо в задании это — разные понятия, как мне кажется

whitefox

Re: Нахождение числа остовов графа

11.12.2016, 11:39

Заслуженный участник

19/12/10
1546

А мне кажется, что это разные задания:

Подсчитать общее число остовных деревьев.
Построить одно из них (любое).

Но если «остов» не синоним «остовного дерева», то что он может обозначать?

Voenstal	Re: Нахождение числа остовов графа 11.12.2016, 11:48
30/11/16 13	А мне кажется, что это разные задания: Но если «остов» не синоним «остовного дерева», то что он может обозначать? Честно — не знаю. Но судя по всему — оно так и есть. Спасибо за помощь)

Brukvalub

Re: Нахождение числа остовов графа

11.12.2016, 14:18

Заслуженный участник

01/03/06
13626
Москва

Честно — не знаю. Но судя по всему — оно так и есть.

Для меня непререкаемым авторитетом в маркизах графах является монография Дистеля. Так вот, в ней никаких «остовов» у графа не определяется, а определяется «остовное дерево» и кое-где считается число «остовных деревьев».

Модераторы: Модераторы Математики, Супермодераторы

Источник