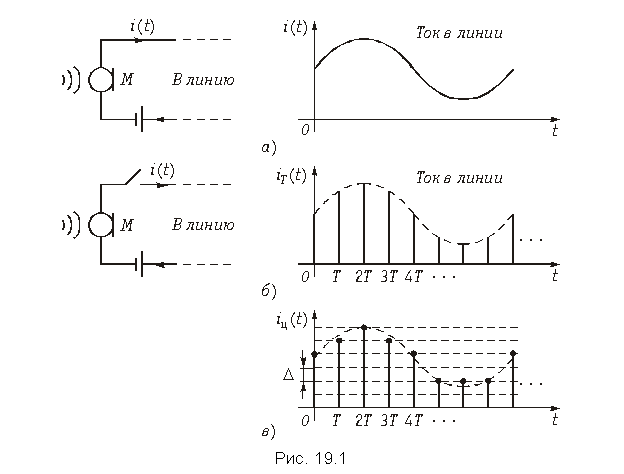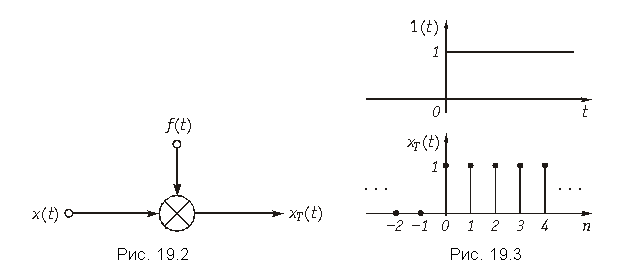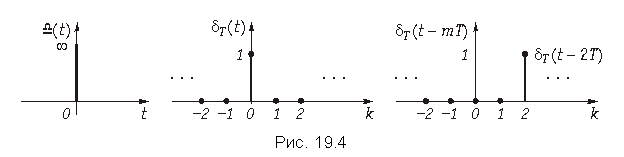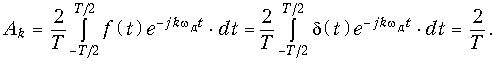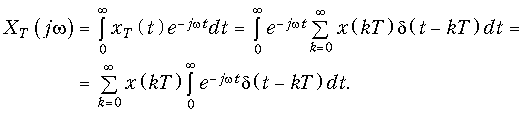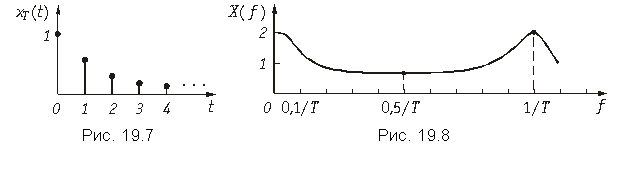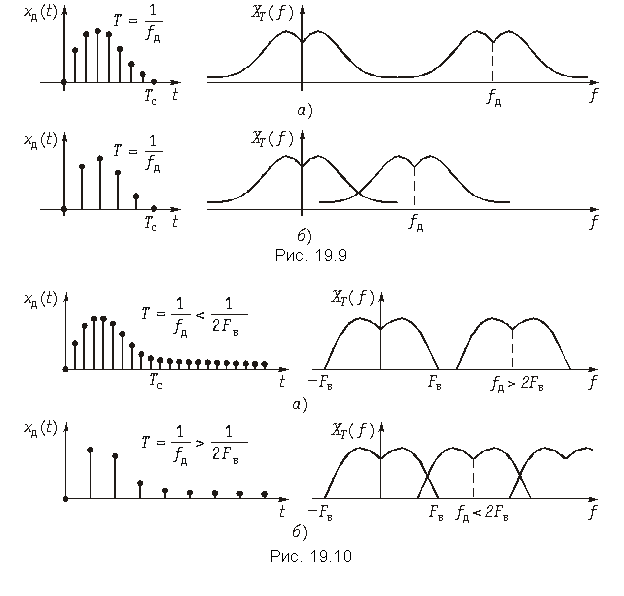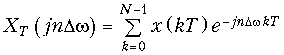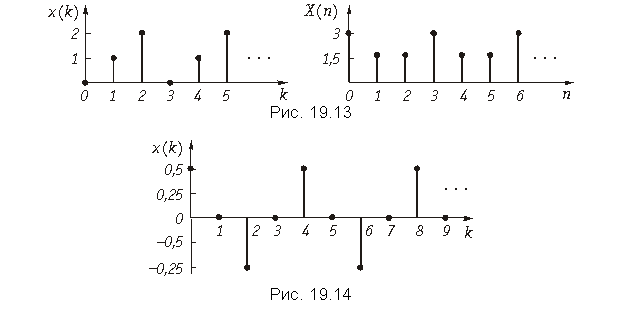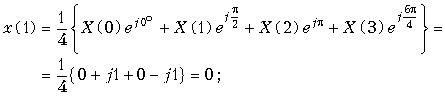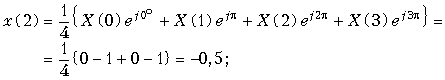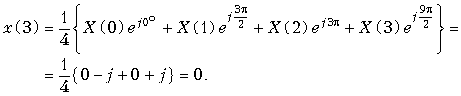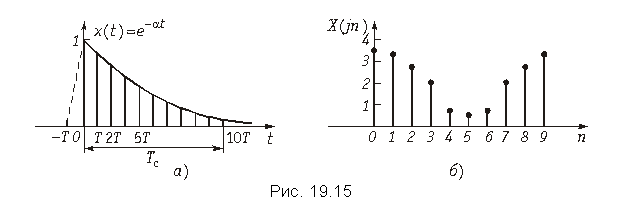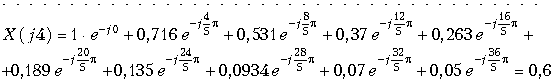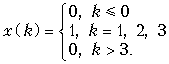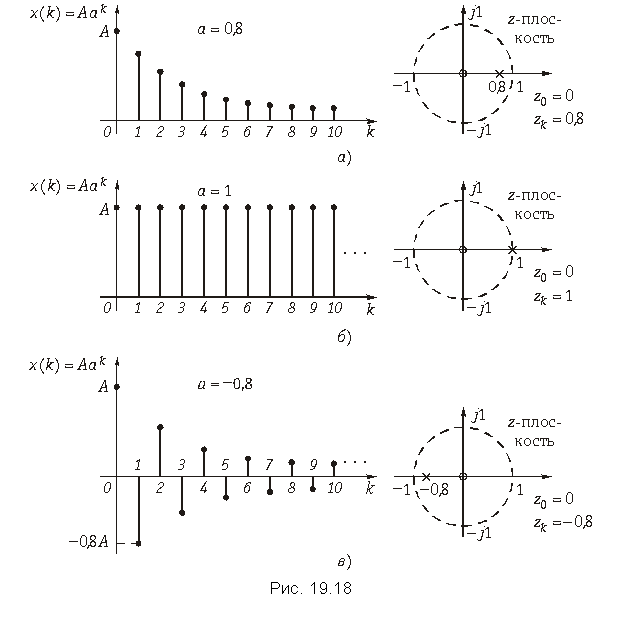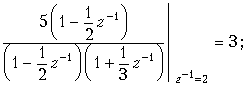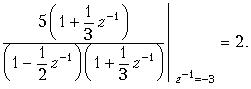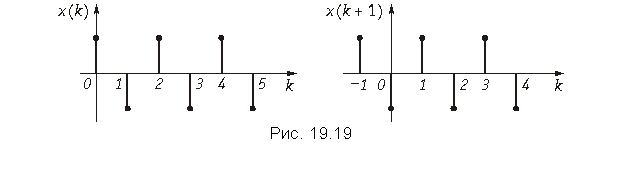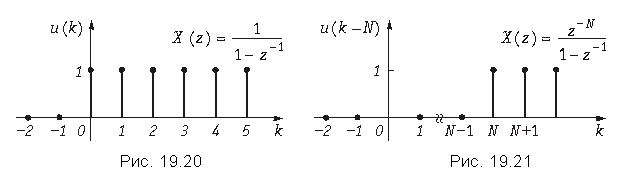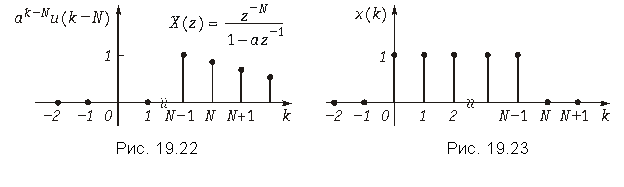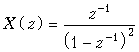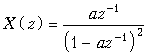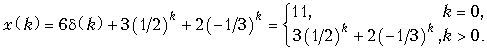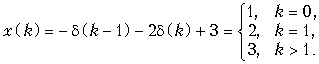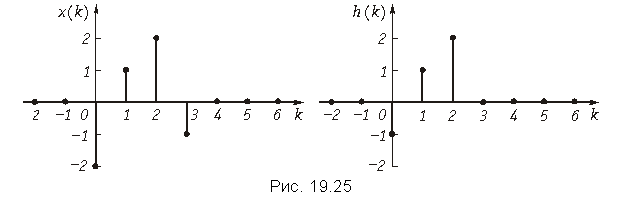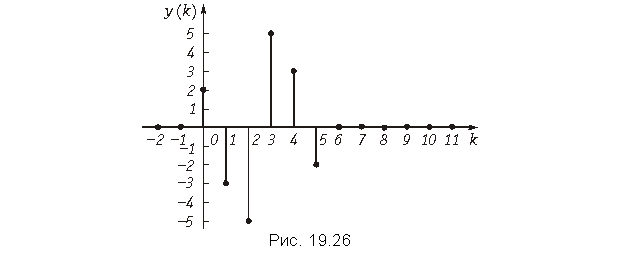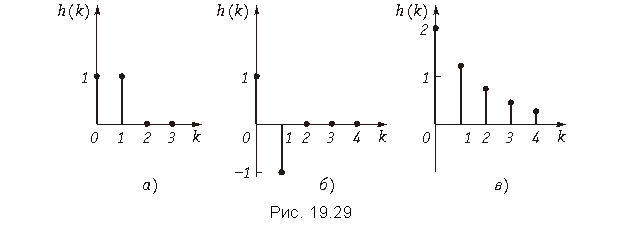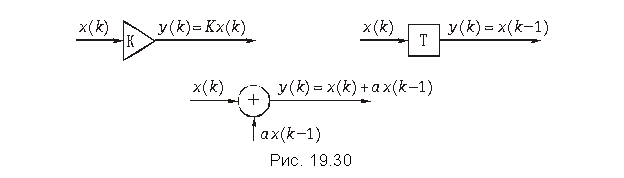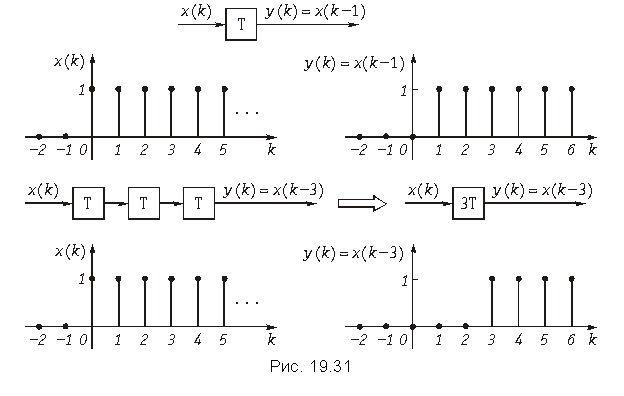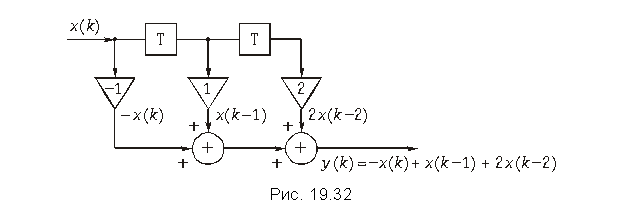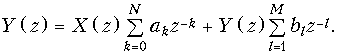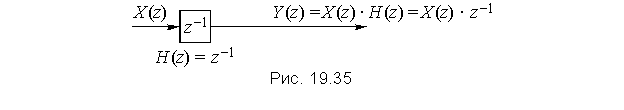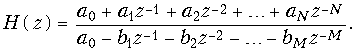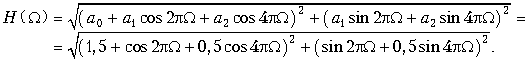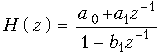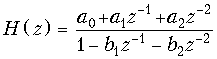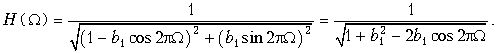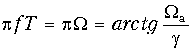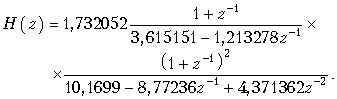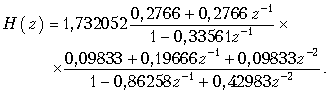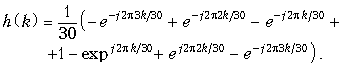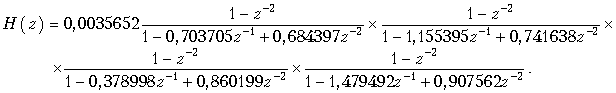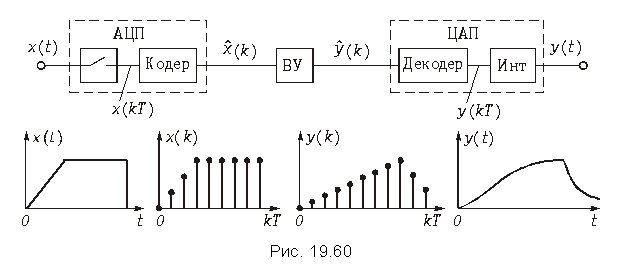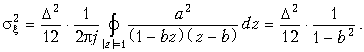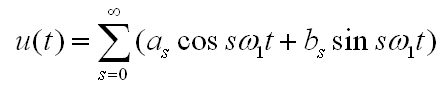19.1. Дискретные сигналы
19.2. Спектр дискретного сигнала
19.3. Z-преобразование и его свойства
19.4. Дискретные цепи
19.5. Типовые звенья дискретных цепей
19.6. Дискретные фильтры и их синтез
19.7. Цифровые фильтры
19.8. Вопросы и задания для самопроверки
19.1. Дискретные сигналы
Дискретизация аналоговых сигналов. Сигнал – это физический процесс (например, изменяющиеся во времени токи и напряжения), содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией.
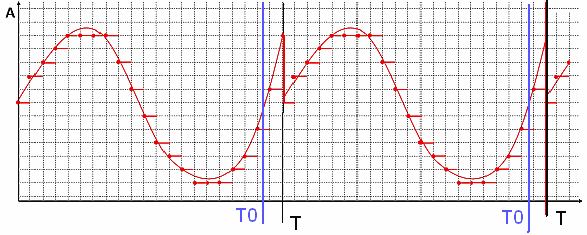
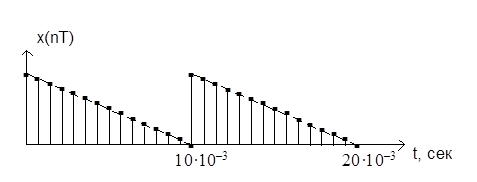
Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией x(t), которая может принимать любые значения в определенном интервале (рис. 19.1, а); дискретные сигналы xТ(t) представляют собой последовательности или отсчеты функции x(t), взятые в определенные дискретные моменты времени kT (рис. 19.1, б); цифровыми являются сигналы, которые в дискретные моменты времени kT принимают конечные дискретные значения – уровни квантования (рис. 19.1, в), которые затем кодируются двоичными числами. (На рис. 19.1, в, D – шаг квантования).
Если в цепь микрофона (рис. 19.1), где ток i(t) является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал. Причем, во всех этих записях k – целое число, принимающее как положительные, так и отрицательные значения.
В отличие от непрерывного сигнала i(t) дискретный сигнал можно обозначить iТ(t). Так, на рис. 19.1 при k < 0 дискретный сигнал iТ(t) º 0. При k = 0 значение iТ(0T) равно значению сигнала i(t) в момент времени t = 0. При k > 0 отсчеты i(kT) повторяют форму сигнала i(t), т. к. их амплитуды равны значениям непрерывного сигнала в моменты времени kT.
Дискретные сигналы можно задавать графиками, как это показано на рис. 19.1, формулами, например, , в виде таблиц дискретных значений или другими способами.
Цифровые сигналы будут рассмотрены в 19.7. Цифровые фильтры.
Математическая модель дискретного сигнала. Аналитически дискретный сигнал хТ(t) удобно представлять с помощью дискретизирующей последовательности d-функций:
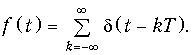
Тогда хТ(t) можно представить в виде
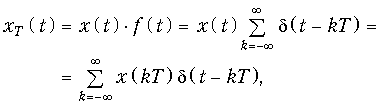
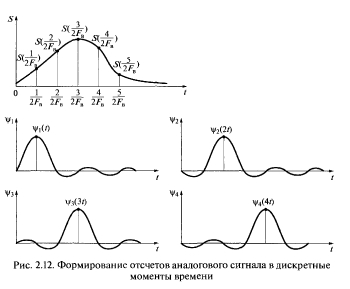
т. е. дискретный сигнал хТ(t) с помощью (19.2) представляется в виде последовательности d-функций с весовыми коэффициентами, равными отсчетам х(kT) аналогового сигнала х(t) в точках kT. На рис. 19.2 изображена схема, иллюстрирующая процедуру формирования дискретного сигнала согласно формулы (19.2).
Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов.
Пример. Единичный ступенчатый аналоговый сигнал 1(t) приведен на рис. 19.3.
Соответствующий ему дискретный сигнал xT(t) называется ступенчатой последовательностью. Он определяется следующим образом:
Такая последовательность приведена на рис. 19.3.
Пример. Импульс Дирака или d-функция в аналоговой области приведена на рис. 19.4.
Дельта-последовательность или дискретная d-функция определяется выражением
Последовательность dT(t), приведенная на рис. 19.4, принимает единственное значение, равное 1, при k = 0. Этот сигнал можно сдвинуть на m интервалов (рис. 19.4):
Интервал времени T, через который отсчитываются значения непрерывного сигнала i(t), называется интервалом дискретизации. Обратная величина 1/T (обозначим ее fд) называется частотой взятия отсчетов или частотой дискретизации.
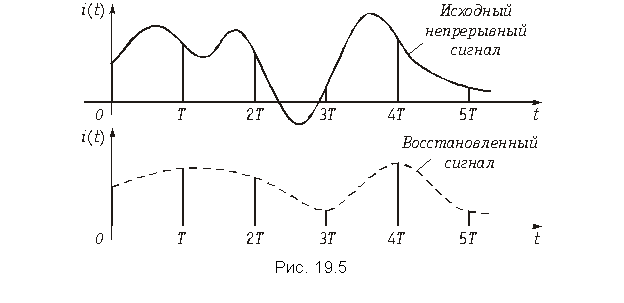
Отсчеты непрерывного сигнала следует брать с такой частотой (или через такой интервал времени), чтобы успевать отследить все, даже самые быстрые, изменения сигнала. Иначе, при восстановлении этого сигнала по дискретным отсчетам часть информации будет потеряна и форма восстановленного сигнала будет отличаться от формы исходного (рис. 19.5). Если обратиться к схеме рис. 19.1, то это означает, что звук на приеме будет восприниматься с искажениями.
Для сигналов с ограниченным спектром, т. е. сигналов, у которых спектр ограничен некоторой верхней частотой wв = 2pFв существует теорема Котельникова, определяющая выбор интервала дискретизации T (или, что то же, частоты дискретизации). Эта теорема впервые была доказана В.А. Котельниковым в 1933 г. в работе «О пропускной способности «эфира» и проволоки в электросвязи» ставшей основополагающей в теории и технике цифровой связи.
Теорема Котельникова. Если функция x(t) имеет спектр, ограниченный верхней частотой Fв, то x(t) полностью определяется последовательностью своих значений (отсчетов) в моменты времени, отстоящие друг от друга на период Т Ô 1/2Fв.
Математически теорема Котельникова записывается следующим образом
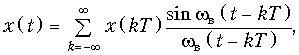
где wв = 2pFв; Т = 1/2Fв; x(kT) – значения (отсчеты) функции x(t) в моменты kT.
Доказательство теоремы Котельникова дается в общей теории связи. Здесь же отметим, что функция вида (t¢ = t – kT) известна нам как функция отсчетов, поэтому теорему Котельникова иногда называют еще теоремой отсчетов.
Физический смысл теоремы Котельникова (19.3) заключается в том, что непрерывная функция x(t) с ограниченным спектром Fв полностью может быть восстановлена, если известны ее отсчеты, взятые через интервал Т Ô 1/2Fв. Эта теорема играет очень большую роль в теории связи, т. к. позволяет передачу аналоговых сигналов заменить передачей дискретных или цифровых сигналов, что позволяет существенно повысить эффективность систем связи.
19.2. Спектр дискретного сигнала
Преобразование Фурье для дискретного сигнала. Определим связь между спектром X(jw) аналогового сигнала x(t) и спектром XТ(jw) дискретного сигнала xТ(t), определенного моделью (19.2). Учитывая, что xТ(t) = x(t)f(t) согласно теоремы свертки (9.30) получим спектральную плотность дискретного сигнала
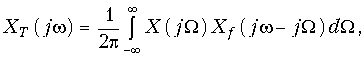
где Xf(jw) – спектральная плотность дискретизирующей последовательности (19.1).
Для нахождения Xf(jw) разложим f(t) в комплексный ряд Фурье (5.6):
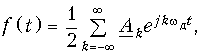
где wд = 2p/Т – частота дискретизации,
Отсюда согласно (9.42) получаем
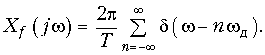
Подставив (19.6) в формулу (19.4) после изменения порядка интегрирования и суммирования и с учетом фильтрующего свойства d-функции окончательно получим
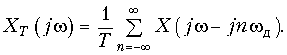
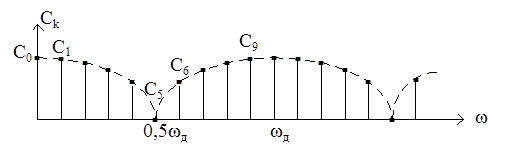
Из (19.7) следует важный вывод: спектр дискретного сигнала xT(t) (рис. 19.6 б) представляет собой сумму бесконечно большого числа «копий» спектра аналогового сигнала (рис. 19.6, а), расположенных на оси частот через одинаковые интервалы.
Следует отметь, что согласно (19.7) и рис. 19.6, б энергия спектра дискретного сигнала оказывается бесконечно велика, что является следствием идеализации реального сигнала моделью (19.2). Если же использовать вместо дискретизирующей последовательности (19.1) последовательность импульсов конечной энергии (например, прямоугольных импульсов), то получим спектр XТ(jw), энергия которого убывает с ростом w («копии» X(jw) с ростом w уменьшаются). В то же время следует еще раз подчеркнуть, что представление дискретного сигнала в форме (19.2) существенно упрощает анализ дискретных сигналов и цепей и широко используется в расчетах.
Спектр дискретного сигнала XТ(jw) можно найти и непосредственно из прямого преобразования Фурье (9.6) для дискретного сигнала (действует в момент t Õ 0).
Отсюда с учетом фильтрующего свойства d-функции получим прямое преобразование Фурье для дискретных сигналов.
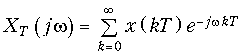
и обратное преобразование Фурье:
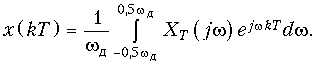
На практике в формулах (19.8), (19.9) часто вместо зависимости XТ(jw) рассматривают зависимости XТ(jf), которые легко можно получить путем замены w = 2pf.
Пример. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета xТ(t) = [a; 0; 0; 0; …].
Воспользуемся формулой (19.8), в которую подставим значения xt(t) заданного сигнала
.
Пример. Рассчитаем спектр экспоненциальной дискретной функции xТ(t) = 0,5k, k 0.
График дискретной функции xТ(t) приведен на рис. 19.7, а ее отсчеты можно записать в виде последовательности x{k} = {1; 0,5; 0,25; 0,125; 0,0625; …}.
Спектр дискретной экспоненты рассчитаем по формуле (19.8)
где для суммирования ряда использована формула
.
Используя формулу Эйлера , получим выражение для расчета спектра амплитуд X(f).
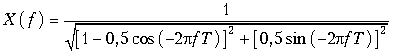
Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать X(f).
График спектра амплитуд X(f) экспоненциальной дискретной функции xT(t) = 0,5k приведен на рисунке 19.8.
Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом fд = 1/Т.
Следует отметить, что если не выполняется условие теоремы Котельникова: fд 2fв, то спектры в (19.7) частично перекрываются. На рис. 19.9, рис. 19.10 показан характер изменения спектра дискретного сигнала XT(f) при изменении частоты дискретизации сигнала xT(t), ограниченного во времени интервалом Tс (рис. 19.9) и неограниченного во времени (рис. 19.10).
Как следует из представленных графиков увеличение периода дискретизации T > 1/2Fв; Fд < 2Fв приводит к наложению смежных спектров в (19.7), что приводит к наложению спектра ХT(f). Эти искажения называются ошибками наложения. Чтобы их устранить необходимо частоту дискретизации увеличить до Fд 2Fв.
Пример. Рассчитаем интервал дискретизации и минимально допустимую частоту дискретизации сигнала, спектральная плотность которого равна нулю при значениях частоты выше 100 кГц.
Из условия задачи следует, что граничная частота спектра Fв равна 100 кГц. Тогда в соответствии с теоремой Котельникова имеем интервал дискретизации
.
Минимально допустимая частота дискретизации fд = 2Fв = 2×100 = 200 кГц.
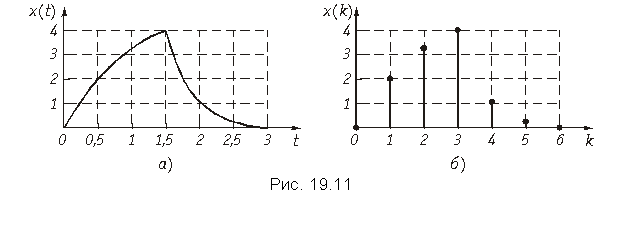
Пример. Определим дискретные отсчеты сигнала длительностью tи = 3 мс, приведенного на рис. 19.11, а, если в качестве граничной частоты спектра Fв принять значение 3/tи, выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.
Хотя сигнал конечной длительности имеет бесконечный спектр частот, однако почти всегда можно определить граничную частоту спектра таким образом, чтобы отсекание частот превышающих Fв, привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.
Граничная частота спектра Fв = 3/tи = 3/(3×103) = 1 кГц.
Интервал дискретизации T = 1/(2Fв) = 1/(2×1×103) = 0,5 мс.
Берем отсчеты сигнала, приведенного на рис. 19.11, а, через интервал времени T = 0,5 мс и получаем последовательность x{k} = {0; 2; 3,2; 4; 1; 0,3; 0}, изображенную графически на рис. 19.11, б.
Отметим, что аналоговый сигнал x(t) можно полностью восстановить по его дискретным отсчетам x(kT) с помощью ФНЧ, частота среза которого wс = 0,5wд = wв. Этот вывод хорошо иллюстрирует рис. 19.10, а из которого видно, что спектр сигнала на выходе ФНЧ совпадает со спектром аналогового сигнала x(t).
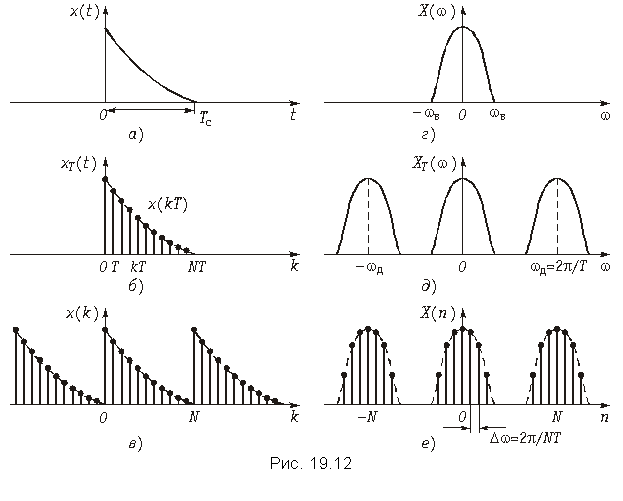
Дискретное преобразования Фурье. Как следует из формулы (19.7) XT(jw) имеет периодическую структуру с wд = 2p/T. Причем, как и спектр аналогового сигнала X(jw) спектр дискретного сигнала XT(jw) является сплошным (см. рис. 19.6, б). Вместе с тем при цифровой обработке сигналов используется не только дискретизация во времени, но и дискретизация в частотной области.
Для сигнала x(t) ограниченного во времени интервалом Tс (рис. 19.12, а) справедлива обратная теорема Котельникова, которая может быть получена из (19.3) путем заменыt ->w; wв->Tс/2; Т-> Dw:
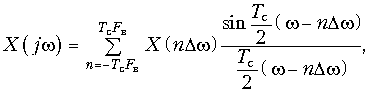
где Dw = 2p/Tс; Tс – длительность сигнала;X(nDw) – отсчеты спектра сигнала в частотной области.
Переходя к дискретному сигналу xT(t) (рис. 19.12, б) отметим, что общее количество отсчетов сигнала будет равно
где T = 2p/wд = p/wв.
Дискретный спектр (рис. 19.12, е) может быть получен путем периодического повторения последовательности {x(kT)} с периодом Tс = NT (рис. 19.12, в). При этом частотный интервал между дискретными отсчетами спектра (рис. 19.12, е) составляет
(19.11)
С учетом вышеизложенного дискретное преобразование Фурье (ДПФ) можно получить, если в преобразовании (19.8) сделать замену w = nDw. Тогда получим
или с учетом (19.11)
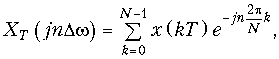
где n = 0; ±1; ±2; ± … N/2.
Для упрощения записи аргумент nDw и kT обычно заменяют индексом n и k соответственно и опускают индекс T, при этом (19.12) примет вид
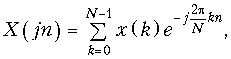
которое определяет прямое ДПФ.
С помощью (19.13) можно определить отсчеты спектра X(jn) по временным отсчетам сигнала x(k).
Обратное ДПФ можно получить из (19.13) воспользовавшись дуальностью прямого и обратного преобразований Фурье:
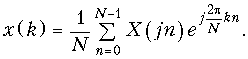
При k < 0 обратное преобразование Фурье определит x(k), расположенную слева от 0 (рис. 19.12, в).
Для ДПФ по аналогии с непрерывными преобразованиями Фурье справедливы основные теоремы и свойства.
В частности, свойство линейности
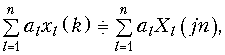
сдвиг дискретного сигнала:
(19.16)
т. е. сдвиг последовательности отсчетов сигнала на m интервалов приводит лишь к изменению фазового спектра дискретного сигнала.
Теорема свертки:
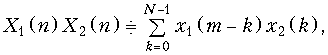
где N = N1 + N2; N1, N2 – число отсчетов х1 и х2 соответственно.
Аналогично можно записать и другие теоремы для ДПФ. Заметим, что ДПФ можно использовать для определения не только спектра дискретных сигналов, но и спектра аналоговых сигналов, для чего его необходимо дискретизировать согласно теоремы Котельникова (19.3).
Пример. Рассчитаем ДПФ дискретного периодического сигнала, заданного тремя отсчетами x{k} = {0; 1; 2}.
Для расчета воспользуемся формулой ДПФ (19.13).
Поскольку
,
,
то ,
.
Графики заданного дискретного периодического сигнала x(k) и рассчитанного дискретного периодического спектра амплитуд X(n) приведены на рис. 19.13.
Пример. Рассчитаем значения дискретного сигнала x(k), ДПФ которого имеет вид X[n] = {0; 1; 0; 1}.
Значения дискретного сигнала x(k) будем рассчитывать по формуле (19.14)
;
График последовательности x{k} = {0,5; 0; –0,5; 0} приведен на рис. 19.14. Сигнал x(k) дискретный и периодический.
Пример. Определить с помощью ДПФ спектр аналогового сигнала, изображенного на рис. 19.15, а.
Ограничим длительность сигнала Tc, где (рис. 9.15, а). Например, при Tc = 3/a,
. Выберем число отсчетов N = 10, определим частоту дискретизации
Согласно (19.13) находим отсчеты спектра сигнала
и т.д.
В таблице приведены результаты расчета спектра,
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
X(jn) |
3.4 |
3.3 |
2.8 |
1.6 |
0.6 |
0.4 |
0.6 |
1.6 |
2.8 |
3.3 |
а на рис. 19.15, б спектр сигнала X(jn). Следует отметить, что с увеличением T (уменьшение числа отсчетов N) погрешность аппроксимации x(t) увеличивается (см. рис. 19.5, а).
Как следует из вышеприведенных примеров и формул (19.13), (19.14), для вычисления ДПФ содержащих N отсчетов необходимо осуществить в общем случае N2 операций с комплексными числами. Если длина обрабатываемых массивов достаточно велика, то вычисление ДПФ даже на современных быстродействующих ЭВМ занимает достаточно много времени. Для сокращения вычислений используют обычно алгоритм быстрого преобразования Фурье (БПФ). Существует много разновидностей БПФ. Здесь мы рассмотрим один алгоритм, основанный на прореживании по времени.
Быстрое преобразование Фурье. Положим, что число отсчетов N = 2q, где q – целое число. Разобьем дискретную последовательность отсчетов {x(k)} не две части:
четную {x(k)}чт = {x(2k)}
и нечетную {x(k)}нч = {x(2k + 1)}, где k = 0, 1, 2, … N/2 – 1.
Представим спектр (19.13) в виде
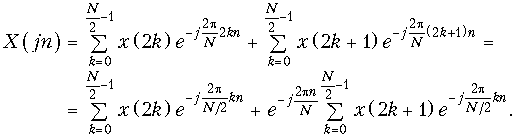
Из (19.18) следует, что
(19.19)
где n = 0, 1, 2, …, ((N/2) – 1).
Из (19.19) следует, что первая половина X(jn) (n = 0, 1, 2, …, (N/2) – 1) выражается через ДПФ двух частных последовательностей: Xчт(jn) и Xнч(jn). Вторую половину (n N/2) X(jn) можно найти, если учесть периодичность его четной и нечетной части с периодом N/2:
и соотношение (при n N/2):
при этом получим
(19.20)
Формула (19.19) и (19.20) лежит в основе БПФ. Как следует из этих формул для вычисления Xчт(jn) и Xнч(jn) требуется (N/2)2 операций и для выполнения операции умножения на exp{×} – N операций:
(19.21)
Для ДПФ (19.13) требуется операций, что существенно выше, чем NБПФ. Например, при N = 103, получаем NДПФ = 106, а NБПФ ~ 250×103, т. е. для БПФ требуется в четыре раза меньше операций, чем при ДПФ.
В общем случае число операций, необходимое в БПФ равно
(19.22)
и выигрыш по сравнению с ДПФ равно
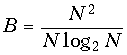
и может достигать сотен и тысяч раз при достаточно больших входных массивах N.
В заключении отметим, что сам процесс вычисления по формулам (19.18), (19.19) производят по итерационному принципу: последовательность отсчетов с четными и нечетными номерами снова разбивают на две части и т. д. Процесс разбиения продолжается до тех пор, пока не получится последовательность, состоящая из одного элемента (исходного ДПФ). Более подробно с алгоритмами БПФ можно ознакомиться в специальной литературе (см. например, Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. М. «Радио и связь. 1990).
19.3. Z-преобразование и его свойства
При анализе и синтезе дискретных и цифровых цепей широко применяют так называемое z-преобразование. Это преобразование играет такую же основополагающую роль по отношению к дискретным сигналам, как преобразование Лапласа по отношению к аналоговым сигналам.
Z-преобразование дискретного сигнала. Заменим в уравнении (19.8) jw на комплексную переменную p:
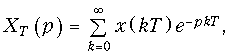
таким образом, мы получим изображение по Лапласу дискретного сигнала. Оригинал, т. е. сам дискретный сигнал можно определить с помощью обратного преобразования Лапласа (7.4):
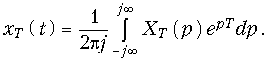
Уравнение (19.25) определяет всю дискретную последовательность . Для определения одного, k-го отсчета формула (19.25) примет вид
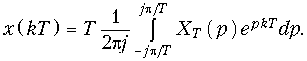
Следует однако отметить, что XT(p) является трансцендентной функцией переменной р вследствие наличия в (19.24) и (19.26) множителя e±pkT.
Для перехода к рациональным функциям осуществим замену переменных:
(19.27)
Тогда формула (19.24) примет вид:
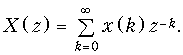
Равенство (19.28) называют прямым односторонним z-преобразованием.
Обратное z-преобразование определяется формулой:
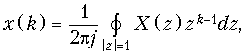
где интегрирование осуществляется по окружности с радиусом |z| = 1.
Доказать справедливость (19.29) можно следующим образом. Пусть X(z) – функция комплексной переменной z, аналитическая в области |z| > r0. Раскроем ряд (19.28):
(19.30)
Домножим левую и правую часть (19.30) на zk–1:
(19.31)
Возьмем контурный интеграл от левой и правой части (19.31) вдоль кривой, лежащей целиком в области аналитичности и охватывающей все полюсы X(z) и учтем равенство Коши:
Тогда все слагаемые, кроме k-го обратятся в нуль:
Отсюда непосредственно следует (19.29), что и требовалось доказать.
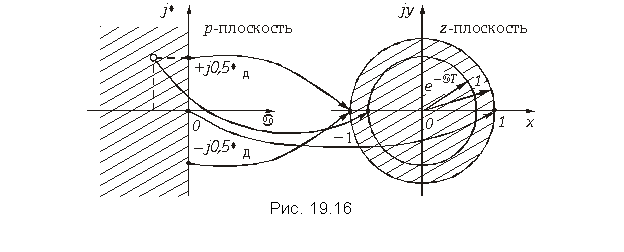
Установим связь между точками на комплексной плоскости p = = a + jw и z-плоскости z = x + jy (рис. 19.16).
Если положить a = 0, то мы будем перемещаться по оси jw в плоскости р. При переходе в z-плоскость точки мнимой оси jw будут располагаться на единичной окружности z = ejwT. Причем, точка j0 на р-плоскости переходит в точку z = +1 на вещественной оси z-плоскости, а точки – в точку z = –1. Это означает, что точки отрезка (
) р-плоскости проектируются в точки на единичной окружности z-плоскости. Так как функция e±jwT периодическая, то последующие отрезки оси jw на p-плоскости такой же длины будут вновь проектироваться на единичную окружность.
Точкам левой р-полуплоскости соответствуют точки внутри единичной окружности z-плоскости, а точкам правой p-полуплоскости – точки вне этой окружности.
Пример. Рассчитаем z-преобразование дискретного сигнала x(k), имеющего вид
Воспользовавшись формулой (19.28), получим
.
Пример. Найдем z-преобразование X(z) дискретного экспоненциального сигнала x(k) = e–akT.
Подставим значение x(k) в формулу (19.28), получим
.
Из теории рядов следует, что при выполнении условия |e–aT×z–1| < 1 сумма ряда X(z) равна 1/(1 – e–aT×z–1) или
.
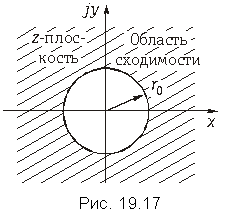
Z-преобразование X(z) дискретного сигнала x(n) определено только для области z, в которой степенной ряд (19.28) сходится. Эта область сходимости включает в себя все значения z, находящиеся вне некоторого круга на комплексной z-плоскости, радиус которого называется радиусом сходимости (рис. 19.17), т. е. при r0 < |z| < ¥ ряд сходится. В области сходимости существует взаимно однозначное соответствие между X(z) и x(k), т. е. каждому x(k) соответствует одно и только одно X(z), определенное для |z| > r0 и наоборот.
Пример. Определим радиус сходимости для z-преобразования сигнала, заданного в предыдущем примере.
Как уже было установлено, z-преобразование сигнала x(k) = e–akT имеет вид
.
Нуль функции X(z) будет в точке z0 = 0, полюс – в точке zk = e–aT. Следовательно, радиус сходимости r0 = e–aT, а функция X(z) сходится при |z| > e–aT.
Окружность, имеющая радиус сходимости r0 = e–aT, приведена на рис. 19.16. Область сходимости находится за пределами этой окружности.
Пример. Найдем z-преобразование сигнала x(k) = Aak, k 0. Этот дискретный сигнал показан на рис. 19.18 для трех различных значений a: а = 0,8; а = 1; а = –0,8.
В соответствии с (19.28) z-преобразование такого дискретного сигнала равно
. (19.32)
Из математики известно, что этот ряд сходится к функции
, (19.33)
если |az–1| < 1 или |z| > a.
Функция X(z) имеет нуль при z = 0, а ее полюс zn = a лежит на окружности радиусом R0 = a, ограничивающей область сходимости.
На рис. 19.18 показано расположение нуля и полюса функции X(z) в z-плоскости при различных а.
Нахождение дискретного сигнала по его z-изображению. Для этого можно воспользоваться обратным z-преобразованием (19.29).
Другой способ заключается в том, чтобы разложить функцию X(z) в степенной ряд по степеням z–1. Тогда коэффициенты при степенях z–1 будут, в соответствии с формулой (19.28), отсчетами дискретного сигнала x(k).
Пример. Найдем дискретный сигнал x(k), которому соответствует z-преобразование X(z) = 1/(1 – 0,5z–1).
Воспользуемся разложением функции (1 – q)–1 в ряд: 1 + q + q2 + q3 + ….
Для заданного z-преобразования q = 0,5z–1, поэтому запишем z-преобразование в виде
.
Сравнивая полученное выражение с общей формулой z-преобразования
, получим последовательность
x{k} = {1; 0,5; 0,25; 0,125; …}.
Общий член этой последовательности x(k) = 0,5k, k 0.
Пример. Найдем отсчеты дискретного сигнала по его z-преобразованию
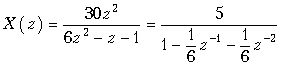
Для разложения функции X(z) в степенной ряд по степеням z–1 выполним деление числа 5 на многочлен . В результате получим частное
. Отсчеты дискретного сигнала равны
и т. д.
Процедура деления здесь не приведена из-за ее громоздкости, хотя выражения полиномов, стоящих в числителе и знаменателе X(z), не слишком сложные.
Более эффективным способом нахождения x(k) по известному X(z) является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.
Пример. Найдем общий член xk дискретного сигнала x(k), которому соответствует z-изображение, заданное в предыдущем примере
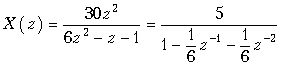
Функция X(z) имеет полюсы в точках z1 = 1/2 и z2 = –1/3, или, что то же, в точках z1–1 = 2 и z2–1 = –3.
Разложим X(z) на сумму простых дробей:
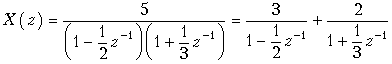
Коэффициенты в числителях каждой дроби вычисляются так же, как при разложении входного сопротивления z(p) реактивных двухполюсников при синтезе их по схеме Фостера:
Подобно тому, как формула (19.33) представляет сумму ряда (19.32), простые дроби в (19.16) являются суммами рядов
и
.
Поскольку z-преобразование – это линейная операция, то последовательность x(k) состоит из суммы двух последовательностей:
.
После выполнения операции возведения в степень k получим отсчеты дискретного сигнала
и т. д.
Свойства z-преобразования. Так же как и для преобразований Лапласа и Фурье, существуют теоремы для z-преобразования. Приведем наиболее важные теоремы одностороннего z-преобразования.
Теорема линейности (суперпозиции). Сумме дискретных сигналов соответствует сумма их z-изображений. Если дискретным сигналам x(k) и y(k) соответствуют z-изображения X(z) и Y(z), то
,
где a и b – некоторые числа.
Доказательство теоремы выполните самостоятельно, используя выражение (19.28) для расчета z-изображения дискретного сигнала.
Теорема опережающего сдвига. Если дискретному сигналу x(k) соответствует одностороннее z-преобразование X(z), то сигналу, сдвинутому на один интервал дискретизации, x(k + 1) соответствует z-преобразование z(X(z) – x(0)).
Математическая запись теоремы имеет вид
,
Чтобы доказать теорему, воспользуемся основным выражением (19.28) для расчета z-преобразования дискретных сигналов x(k) и x(k + 1), а также графиками, приведенными на рис. 19.19.
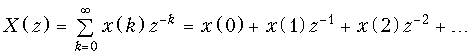
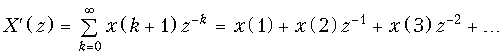
Сравнивая X(z) и X¢(z), получаем X¢(z) = z(X(z) –x(0)), что и требовалось доказать.
Очевидно, что теорема опережающего сдвига выполняет ту же самую роль, что и теорема дифференцирования для преобразований Лапласа.
Теорема задержки. Математическая запись теоремы имеет вид
.
В теореме задержки u(k) – это дискретные отсчеты функции единичного скачка (рис. 19.20)
а u(k – N) – это дискретные отсчет функции u(k), задержанной на N интервалов дискретизации (рис. 19.25).
Доказательство вытекает из основного выражения (19.28) для z-преобразования.
При доказательстве учтено, что единичная ступенчатая функция обращается в нуль при отрицательных значениях ее аргумента, т. е. при n < N. Из теоремы задержки в частности следует, что сдвиг дискретного сигнала на один интервал дискретизации T соответствует умножению z-преобразования на оператор z–1, поэтому часто z–1 называют оператором единичной задержки в z-области.
Теорема умножения на ak. Математическая запись теоремы имеет вид
.
Теорема умножения на n.
.
Теоремы умножения дискретного сигнала x(k) на ak и на k можно также доказать, используя формулу (19.28). Предлагаем проделать это самостоятельно.
Теорема свертки. Свертке дискретных сигналов x(k) и h(k) соответствует произведение их z-преобразований
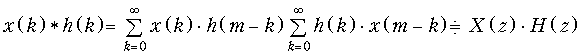
Эту теорему мы приводим здесь без доказательства. При необходимости с ним можно познакомиться в специальной литературе.
Пример. Найдем z-преобразование функции единичного отсчета, задержанной на N интервалов дискретизации.
Найдем z-преобразование дискретного d-импульса d(k) (рис. 19.4), используя выражение (19.28)
.
Используя теорему задержки, найдем z-изображение сигнала d(k – N)
.
На рисунке 19.4 приведен также график задержанной функции единичного отсчета для частного случая N = 2.
Пример. Найдем z-преобразование функции
.
В одном из примеров мы уже находили, что z-преобразование сигнала ak имеет вид (19.33) X(z) = 1/(1 – az–1).
Используя теорему задержки, получаем
.
При a = 1 имеем:
.
Графики дискретных сигналов u(k – N) и ak–Nu(k – N) приведены на рис. 19.21 и 19.22.
Пример. Найдем z-преобразование дискретной последовательности x(k) = = kak, k 0.
Поскольку z-изображение последовательности ak известно (19.15), то, используя теорему умножения на k, получим
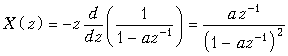
Пример. Найдем z-преобразование дискретной последовательности из N отсчетов единичной амплитуды (рис. 19.23)
Сигнал x(k) можно представить как разность двух сигналов
.
Из теорем линейности и задержки легко получить z-преобразование
,
что совпадает с формулой для частичной суммы геометрической прогрессии
.
Табл. 19.1 – Краткая таблица односторонних z-преобразований
|
Дискретный сигнал x(k), k |
z-преобразование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Вычислим z-преобразование свертки дискретных сигналов x{k} = = {1; 1; 1; 0; 0; 0; …} и y{k} = {0; 0; 1; 1; 0; 0; …}.
Найдем z-преобразование сигнала x(k), используя формулу (19.28)
.
Найдем z-преобразование сигнала y(k)
.
Вычислим z-преобразование свертки сигналов x(k) и y(k), используя теорему свертки
В табл. 19.1 дана сводка z-преобразований наиболее часто встречающихся дискретных последовательностей. Эти табличные сведения также могут быть использованы для расчета z-преобразований сигналов и перехода от z-преобразований к дискретным сигналам.
Пример. Найдем общий член дискретного сигнала x(k), которому соответствует z-изображение
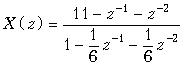
Разложение функции X(z) на простые дроби приводит к выражению
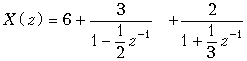
Используя теорему линейности и находя в таблице 19.1 дискретные сигналы, соответствующие каждому из слагаемых в выражении X(z), получаем
По этой формуле легко подсчитать значение x(k)для любого k. Аналогичным образом, разложение
приводит к последовательности
19.4. Дискретные цепи
Дискретная свертка. В предыдущих разделах этой главы бала установлена определенная аналогия между соотношениями, существующими для аналоговых и дискретных сигналов. Подобная аналогия существует и между методами анализа и синтеза аналоговых и дискретных цепей.
Под дискретной цепью понимают любое устройство, которое преобразует одну последовательность x{k} в другую y{k} (рис. 19.24).
Линейной дискретной цепью называют цепь подчиняющуюся принципу суперпозиции.
Связь между входным дискретным сигналом x{k} (воздействием) и выходным сигналом y{k} (отсчетом) определяется дискретной сверткой (сравни с (8.12)):
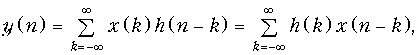
где h(k) – импульсная характеристика дискретной цепи. Она определяется как отклик дискретной цепи на воздействие в виде единичного импульса (d-функция, рис. 19.4).
Иногда свертку (19.35) записывают символически: y(k) = x(k)*h(k) (см. теорему свертки, 19.3. Z-преобразование и его свойства).
Линейная дискретная цепь, будет устойчива, если выполняется условие
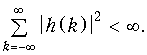
Пример. Рассчитаем значения выходной последовательности y{k} цепи, имеющей дискретную импульсную характеристику h{k} = {–1; 1; 2}, если входная последовательность имеет вид x{k} = {–2; 1; 2: –1}. Графики x(k) и h(k) приведены на рис. 19.25.
Пользуясь формулой (19.35), рассчитаем значения выходной последовательности y(k)
График дискретного сигнала y(k) приведен на рис. 19.26.
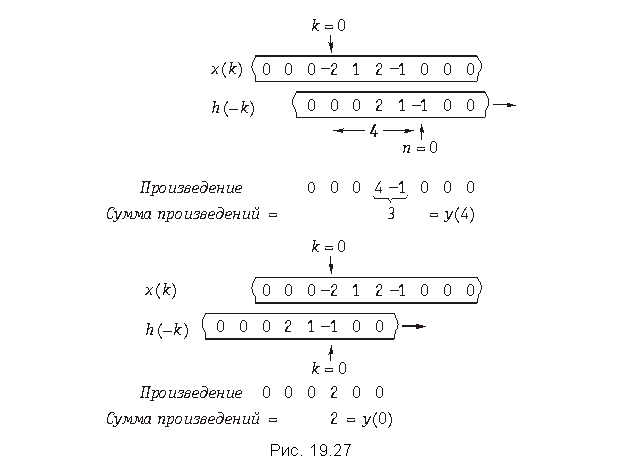
Вычисления по формуле (19.35) можно выполнить также с помощью простого устройства. Запишем последовательности чисел x(k) и h(–k) на отдельных полосках бумаги, как показано на рис. 19.27. На обеих полосках пометим маленькими стрелочками точки k = 0. Обратим внимание на то, что h(–k) является обратной последовательностью относительно h(k), так что она строится в обратном направлении от k = 0. Будем сдвигать нижнюю полоску относительно верхней в направлении стрелки. Вычисление суммы произведений стоящих друг против друга чисел при каждом сдвиге дает последовательность y(k).
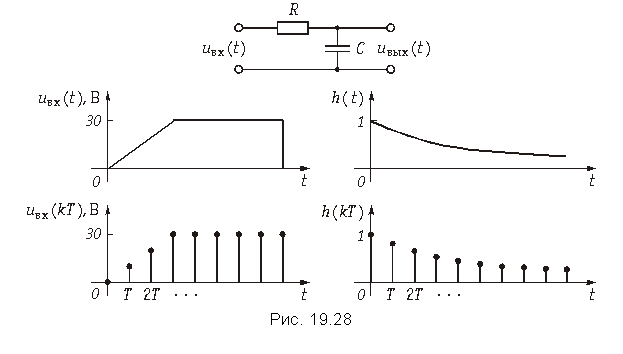
Проведя дискретизацию импульсной характеристики аналоговой цепи можно описать ее дискретной математической моделью. Если, например, для RC-цепи, изображенной на рис. 19.28 взять дискретные значения импульсной характеристики:
то получим дискретную математическую модель RC цепи, выходную реакцию которой можно найти с помощью (19.35). При этом, естественно входной сигнал также должен быть дискретизирован (рис. 19.28). Точно также можно получить дискретные модели других аналоговых цепей. Таким образом формула дискретной свертки (19.35) является достаточно универсальной, пригодной для описания как аналоговых, так и дискретных цепей.
Пример. На вход цепи поступает сигнал в виде дискретной d-функции. Рассчитаем выходные последовательности y(k) цепей, имеющих дискретные импульсные характеристики
а) h{k} = {1; 1; 0; 0; …};
б) h{k} = {1; –1; 0; 0; …};
в) h[k] = 2e–k/2.
Графики импульсных характеристик а), б), в) приведены на рис. 19.28.
Рассчитываем значения y(n),используя формулу (19.17)
y(n) =, в которой x(k) = d{k}.
Для цепи, имеющей дискретную импульсную характеристику
а) h{k} = {1; 1; 0; 0; …}, получаем
Все остальные значения y(n) будут также нулевыми.
Для цепи с импульсной характеристикой
б) h{k} = {1; –1; 0; 0; …} получаем
Остальные значения y(n) равны нулю.
Для цепи с импульсной характеристикой
в) h{k} = 2e–k/2 = {2; 1,22; 0, 74; 0,45; 0,27; …} получаем
Все остальные отсчеты выходной последовательности y{k} повторяют соответствующие отсчеты дискретной импульсной характеристики h(k), также как и в двух предыдущих случаях а) и б). Этот вывод очевиден, т. к. импульсная характеристика – это реакция цепи на d-импульс.
Графики y(k) будут такими же, как графики h(k) на рис. 19.29, что является очевидным, т. к. h(k) по определению есть реакция цепи на d-функцию.
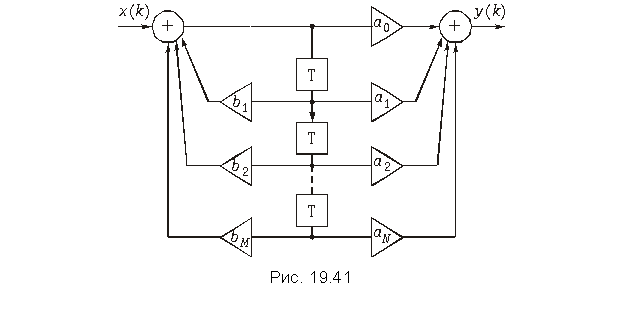
Элементы дискретных цепей. Как следует из уравнения (19.35) при вычислении реакции дискретной цепи на заданное воздействие выполняется всего три операции: умножение, задержка и сложение.
На рис. 19.30 эти действия представлены в виде элементов структурной схемы. Операцию умножения дискретного сигнала x(k) на число К можно представить в виде усилителя с коэффициентом усиления К. На его выходе получаем сигнал y(k) = K×x(k). Сложение чисел естественно отобразить на схеме в виде сумматора. Получение отсчета x(k – 1) = x(kT – T) из x(k) = x(kT) можно связать с задержкой последнего на время Т, т. е. на один «такт». Действие элемента задержки поясняется на рис. 19.30.
Таким образом, алгоритм вычислений дискретного сигнала y(k), описываемый выражением (19.35), можно представить в виде структурной схемы.
Пример. Составим структурную схему цепи, дискретная импульсная характеристика которой дана в предыдущей задаче, т. е. h{k} = {–1; 1; 2} (рис. 19.25).
В соответствии с алгоритмом (19.35) и с учетом заданных значений характеристики h(k) структурная схема цепи приведена на рис. 19.32. По этой схеме несложно определить выражение для выходной последовательности y(k) =–x(k) + x(k – 1) + 2x(k – 2).
Как следует из рис. 19.30 и рис. 19.31 общим свойством элементов дискретных цепей является их однонаправленное действие, показанное на рисунках стрелками. С точки зрения топологии, элементы дискретных цепей представляют собой двухполюсные (элемент задержки, умножитель) или многополюсные элементы (сумматор).
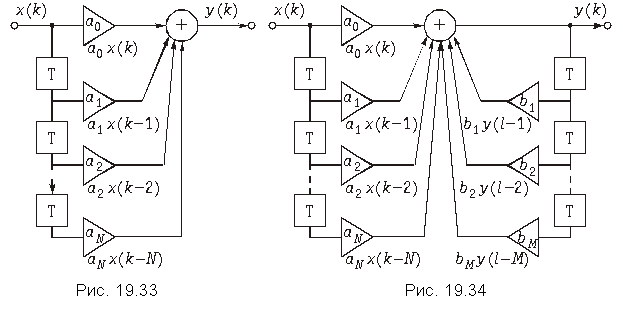
Общее уравнение дискретных цепей. Из уравнения (19.35), рассмотренных примеров и рис. 19.32 отклик дискретной цепи y(k) на воздействие х(k) можно записать в виде следующего уравнения
(19.37)
где a0, a1, a2, …, aN – некоторые числа (веса) представляющие собой по сути отсчеты импульсной характеристики цепи.
Уравнению (19.37) соответствует дискретная цепь, изображенная на рис. 19.33. В литературе эту цепь называют иногда трансверсальным фильтром.
Как следует из (19.37) для получения k-го отсчета выходного сигнала подвергаются обработке (k – N) отсчетов входного сигнала с соответствующими весовыми коэффициентами.
Следует однако отметить, что уравнением (19.37) не исчерпываются все возможные алгоритмы работы дискретных цепей. В частности, этот алгоритм может включать обработку не только отсчетов входного, но и отсчетов выходного сигнала, сдвинутого на определенное число тактов. Поэтому наиболее общее уравнение дискретной цепи имеет следующий вид
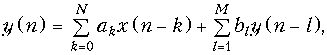
где bl – весовые коэффициенты.
На рис. 19.34 изображена схема дискретной цепи, соответствующей алгоритму (19.38).
Принципиальным отличием схемы, изображенной на рис. 19.34 от схемы на рис. 19.33 является наличие цепи обратной связи, поэтому схемы, описываемые уравнением (19.38), получили название рекурсивных, а цепи, описываемые (19.37), – нерекурсивных.
Для нахождения реакции дискретной цепи необходимо решить разностные уравнения (19.37) и (19.38). Если решение (19.37) обычно не представляет особого труда, то для решения (19.38) необходимо использовать специальные методы. По аналогии с решением дифференциальных уравнений, описывающих аналоговую цепь, решение разностных уравнений можно осуществить как классическим, так и операторным методом. Обычно для решения разностных уравнений в теории дискретных цепей используется операторный метод, причем вместо преобразования Лапласа используют z-преобразование.
Передаточные функции. При анализе и синтезе дискретных систем важнейшую роль играют передаточные или системные функции цепей.
Применим к уравнению (19.38) прямое z-преобразование и учтя основные свойства z-преобразования (см. 19.3. Z-преобразование и его свойства), получим
Отсюда следует
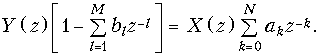
Определим передаточную функцию дискретной цепи как отношение z-преобразований выходного ко входному дискретному сигналу:
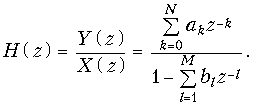
Из (19.40) следует, что коэффициенты ak числителя определяют нерекурсивную часть дискретной цепи, а коэффициенты bl знаменателя – рекурсивную часть.
Для нерекурсивной цепи (M = 0) передаточная функция определится как
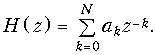
Передаточную функцию (19.41) можно определить как z-преобразование от импульсной характеристики цепи:
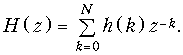
Сравнение (19.41) и (19.42) показывает, что роль коэффициентов ak играют отсчеты импульсной характеристики h(k). Нетрудно также видеть, что импульсная характеристика нерекурсивной цепи согласно (19.37) является конечной, а рекурсивной согласно (19.38) бесконечной, поэтому иногда нерекурсивные дискретные цепи называют цепями с конечной импульсной характеристикой (КИХ), а рекурсивные – с бесконечной импульсной характеристикой (БИХ).
Пример. Положим, что передаточная функция дискретной цепи имеет вид
При a = 1; b = 0 получаем идеальный интегратор с импульсной характеристикой h{k} = {1, 1, …, 1, …}. По нерекурсивной схеме такую импульсную характеристику реализовать нельзя.
Анализ (19.40) показывает, что передаточная функция рекурсивной цепи имеет структуру, аналогичную типичной передаточной функции цепи с ОС (см. гл. 14). H(z) является дробно-рациональной функцией относительно z–1:
Из (19.40) и (19.41) также следует, что H(z) из (19.40) имеет полюса (нули полинома знаменателя), которые могут располагаться в любой точке z-плоскости, а H(z) из (19.41) только полюс кратности N в начале координат.
Пример. Найдем передаточную функцию элемента задержки. Сигнал на его выходе описывается уравнением
Применив к нему z-преобразование, получим
Отсюда получаем
поэтому на структурных операторных схемах дискретных цепей элемент задержки обычно обозначают z–1 (рис. 19.35).
Пример. Найдем импульсную характеристику и передаточную функцию дискретной цепи (рис. 19.36), выходная последовательность которой задана выражением y(k) = 4x(k) – 1,5x(k – 1).
Отсчеты дискретной импульсной характеристики h(k) – это отсчеты y(k), рассчитанные при условии, что на вход цепи подается дискретная d-функция, т. е. x{k} = d{k} = {1; 0; 0; …}.
,
,
при k > 1.
Таким образом, отсчеты дискретной импульсной характеристики h{k} = {4; –1,5} соответствуют коэффициентам усиления усилителей в схеме (рис. 19.36).
Для нахождения передаточной функции H(z) воспользуемся формулой (19.42):
.
Другой способ нахождения передаточной функции H(z) заключается в том, чтобы определить z-изображение выходной последовательности, а затем найти H(z) как отношение Y(z) и X(z):
или
.
Очевидно, что H(z) = 4 – 1,5z–1. На рис. 19.37 приведено z-изображение этой дискретной цепи.
Пример. Найдем передаточную функцию дискретной цепи, входная и выходная последовательности которой имеют вид
x{k} = {1; 0; 1; 2}, y{k} = {0; 1; 2; 1}.
Z-изображения последовательностей
;
.
Следовательно, передаточная функция
.
Зная передаточную функцию дискретной цепи H(z) с помощью формулы
(19.43)
можно найти z-изображение выходного сигнала Y(z) по z-изображению входного Х(z).
Для нахождения отсчетов выходного сигнала y(k) по его z-изображению Y(z) можно точно также как и для аналоговых цепей использовать теорему разложения, которая применительно к дискретным цепям для правильной дробно-рациональной функции Y(z) = P(z)/Q(z) (где P(z), Q(z) – полиномы) имеет вид
(19.44)
где Al – коэффициенты разложения Y(z):
zl – простые полюса Y(z).
Коэффициент Al может быть найден
– вычет функции Y(z) в полюсе z = zl.
Следует отметить, что отсчеты y(k) для нерекурсивной цепи могут быть найдены как коэффициенты при отрицательных степенях z в уравнении для Y(z).
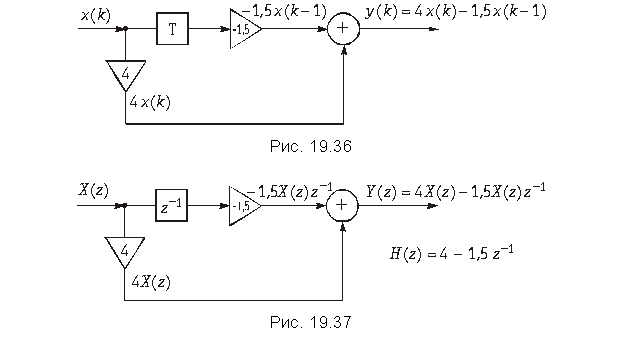
Пример. Найдем отсчеты выходного сигнала y(k) дискретной цепи, z-изображение которой приведено на рис. 19.38, а входной сигнал x{k} = {–2; 1; 2; –1}.
Найдем z-изображение входного сигнала x(k):
Передаточная функция цепи (рис. 19.38) . Она находится непосредственно по схеме либо как z-изображение дискретной импульсной характеристики h{k} = {–1; 1; 2}.
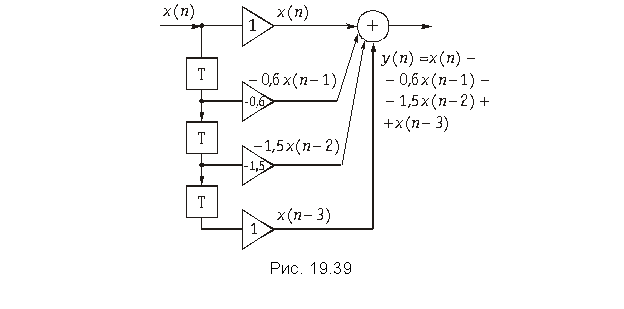
Коэффициенты при z в отрицательных степенях в этом выражении являются отсчетами выходного сигнала y(k) (рис. 19.26):
y{k} = {2; –3; –5; 5; 3; –2}.
Пример. Найдем отсчеты выходного сигнала нерекурсивной дискретной цепи, имеющей дискретную импульсную реакцию h{k} = {1; –0,6; –1,5; 1}, при воздействии на нее дискретного сигнала x{k} = {1; 0; 1; 0}.
Отсчеты дискретной импульсной характеристики – это коэффициенты усиления a0 = 1; a1 = –0,6; a2 = –1,5; a3 = 1. Структурная схема нерекурсивной дискретной цепи с заданной импульсной реакцией приведена на рис. 19.39.
Выходной дискретный сигнал y(k) найдем, используя выражение (19.37)
Отсчеты сигнала y(k) найдем, подставляя значения x(k) в полученное разностное уравнение.
;
;
.
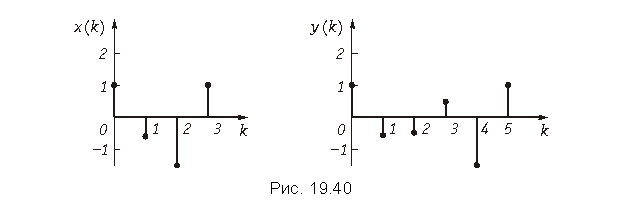
Аналогичным образом рассчитываем y(4) = –1,5; y(5) = 1; y(6) = 0. Все остальные отсчеты также равны нулю.
Таким образом, выходная последовательность y{k} = {1; –0,6; –0,5; 0,4; –1,5; 1}. Графики x(k) и y(k) приведены на рис. 19.40.
Из рис. 19.34 следует, что для реализации алгоритмов рекурсивной обработки сигнала дискретная цепь должна иметь большое количество ячеек памяти, что существенно усложняет схему. Для упрощения дискретной цепи используют, так называемую каноническую схему. Каноническая схема может быть получена из (19.40), если представить Y(z) в виде:
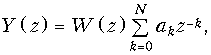
где W(z) – z-преобразование промежуточной последовательности
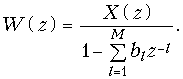
Тогда согласно (19.45) алгоритм дискретной обработки сигнала заключается в том, что вначале реализуется рекурсивное преобразование (19.46), а затем нерекурсивное (рис. 19.41).
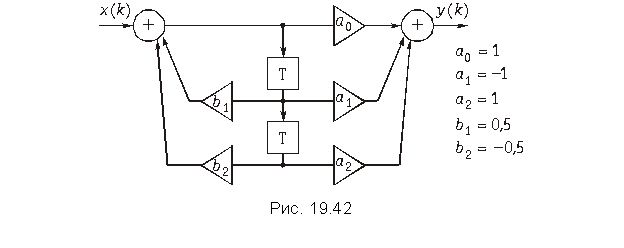
Пример. Найдем реакцию дискретной цепи на воздействие x{k} = {1; –1; 1; –1}, если передаточная функция цепи имеет вид .
Составим структурную каноническую схему дискретной цепи с заданной передаточной функцией (рис. 19.42). Коэффициенты усиления известны: a0 = 1; a1 = –1; a2 = 1; b1 = 0,5; b2 = –0,5.
Найдем выходной сигнал y(k) цепи, используя уравнение (19.37) или непосредственно по схеме:
Рассчитаем отсчеты y(k):
;
;
Аналогичным образом рассчитываем y(3) = –1,125, y(4) = 1,3125 и т. д.
Устойчивость рекурсивных цепей. Дискретная цепь считается неустойчивой, если ограниченное по амплитуде входное воздействие вызывает на ее выходе бесконечно нарастающий отклик. Наоборот, дискретная цепь устойчива, когда отклик на ограниченное воздействие также ограничен.
Известно, что у устойчивой аналоговой цепи полюсы передаточной функции располагаются в левой полуплоскости переменной p. При переходе от аналоговой цепи к дискретной и замене преобразования Лапласа z-преобразованием точки левой полуплоскости p-плоскости переходят в точки, лежащие внутри единичной окружности z-плоскости (рис. 19.16). Таким образом, полюсы передаточной функции устойчивой дискретной цепи располагаются внутри единичной окружности z-плоскости.
Нерекурсивные цепи всегда устойчивы.
Пример. Определим устойчивость цепей, имеющих передаточные функции:
а) ,
б) ,
в) ,
г) .
Полюс передаточной функции
найдем, приравняв знаменатель H1(z) к нулю, 1 – 0,3z–1 = 0.
Получаем полюс = 0,3, который находится внутри единичной окружности z-плоскости. Это означает, что цепь устойчива.
Передаточная функция
имеет полюс в точке = 2; такая цепь неустойчива.
Полюсы передаточной функции
являются комплексно-сопряженными и
. Поскольку эти полюсы лежат внутри единичной окружности (их модули
), то данная дискретная цепь устойчива.
Примером неустойчивой цепи служит цепь с передаточной функцией
,
у которой и
и
.
Частотные характеристики. Для перехода от передаточной функции H(z) к частотной характеристике H(jf) необходимо произвести замену
.
Обычно вводят в рассмотрение нормированную частоту W = fT = = f/fд. С учетом этого формула (19.40) примет вид:
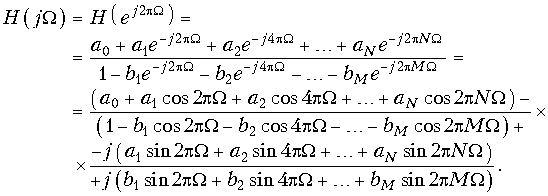
Из (19.47) легко получить амплитудно-частотную и фазо-частотную характеристики дискретной цепи. В частности, амплитудно-частотная характеристика будет представлена выражением
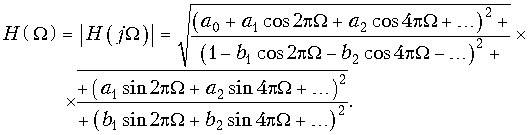
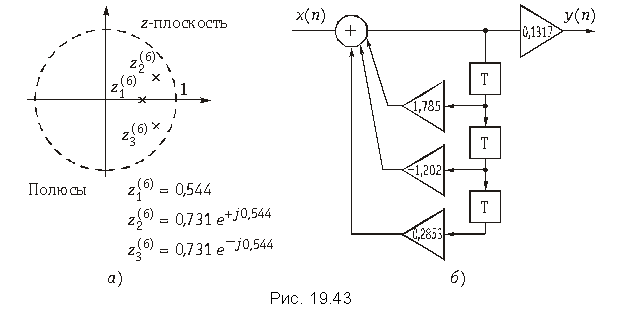
Пример. Дискретная цепь 3-го порядка описывается передаточной функцией
с полюсами и
. Расположение полюсов в плоскости z показано на рис. 19.43, а. Здесь же приведена структурная схема дискретной цепи (рис. 19.43, б). Определить АЧХ цепи.
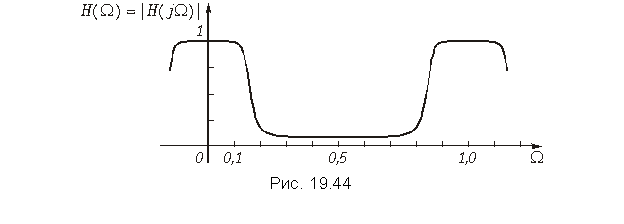
Подставим в (19.49)

На рис. 19.44 изображен график АЧХ H(W) цепи. Из рисунка видно, что АЧХ с передаточной функцией (19.49) соответствует ФНЧ Баттерворта. Как и следовало ожидать, амплитудно-частотная характеристика дискретной цепи является периодической функцией (так как H(jW) есть преобразование Фурье от дискретной импульсной реакции). Ее период равен fд = 1/T или W = fд×T = 1. Поэтому она используется в диапазоне частот от 0 до 0,5fд (или до W = 0,5). Цепь устойчива.
Пример. Найдем частотную характеристику дискретной цепи с импульсной характеристикой h{k} = {1,5; 1; 0,5}.
Запишем передаточную функцию H(z) цифрового фильтра, воспользовав-
шись формулой . Получим
переда-
точную функцию нерекурсивной цепи.
Найдем АЧХ этой цепи, подставляя в формулу (19.48) значения коэффициентов усиления a0 = 1,5; a1 = 1; a2 = 0,5,
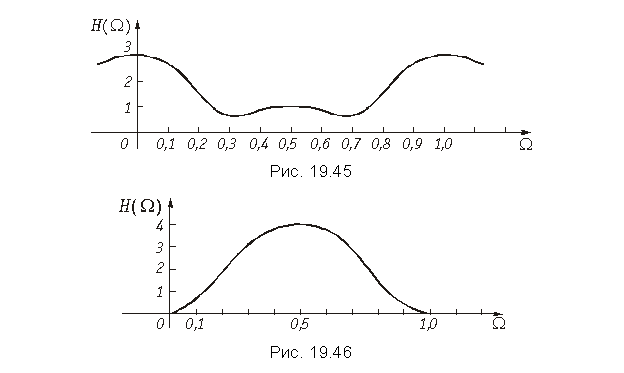
График АЧХ изображен на рис. 19.45.
Пример. Изменим коэффициенты усиления в предыдущем примере. Выберем a0 = a2 = 1, a1 = –2. Вновь найдем выражение H(W) и построим график его амплитудно-частотной характеристики.
Заменим в формуле для H(W), полученной в предыдущем примере, значения коэффициентов a0, a1 и a2. Получим
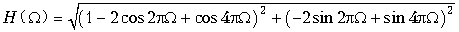
График АЧХ изображен на рис. 19.46. Из графика видно, что нерекурсивная цепь с такими значениями коэффициентов усиления – это режекторный фильтр.
19.5. Типовые звенья дискретных цепей
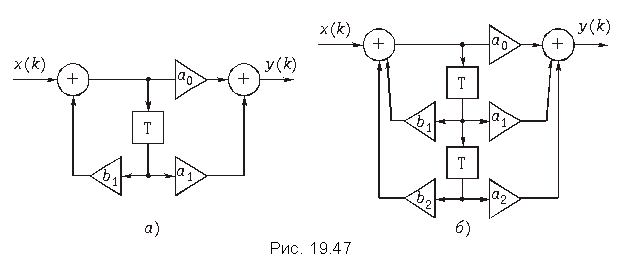
Звенья 1-го и 2-го порядков. В литературе типовыми звеньями дискретных цепей считаются звенья 1-го и 2-го порядков. Они получаются из общей структуры рис. 19.41, если оставить в ней только один либо два элемента задержки.
На рис. 19.47, а показано звено 1-го порядка с передаточной функцией
и АЧХ
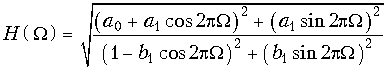
Типовое звено 2-го порядка изображено на рис. 19.47, б. Его передаточная функция
и АЧХ
Пример. Построим график АЧХ звена первого порядка, у которого a0 = 1, a1 = 0.
Передаточная функция такого звена первого порядка
Амплитудно-частотная характеристика
Поскольку полюс zn передаточной функции H(z) равен b1, то для того, чтобы цепь была устойчивой необходимо выбирать значения b1 такими, чтобы выполнялось условие |b1| < 1.
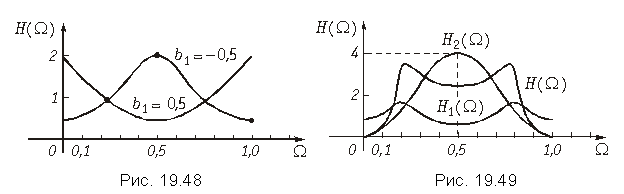
На рис. 19.48 приведены графики АЧХ, построенные для значений b1 = 0,5 и b1 = –0,5.
АЧХ рассматриваемого фильтра зависит от знака коэффициента b1. При b1 > 0 получаем режекторный фильтр, при b1 < 0 – полосовой.
Пример. Найдем передаточную функцию и построим график АЧХ звена 2-го порядка (рис. 19.47, б) при a0 = a2 = 1, a1 = 2, b1 = 0,2 и b2 = –0,4.
Передаточная функция такого звена
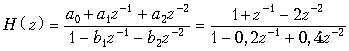
Как указывалось ранее, рекурсивную цепь с прямыми и обратными связями можно представить как каскадное соединение рекурсивного фильтра с передаточной функцией H1(z) и нерекурсивного фильтра с передаточной функцией H2(z). В нашем случае, для звена второго порядка,
График АЧХ для H2(z) уже был построен и приведен на рис. 19.46. АЧХ H1(W) рекурсивного фильтра рассчитывается по формуле
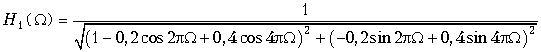
Графики H1(W), H2(W) и H(W) = H1(W)×H2(W) изображены на рис. 19.49.
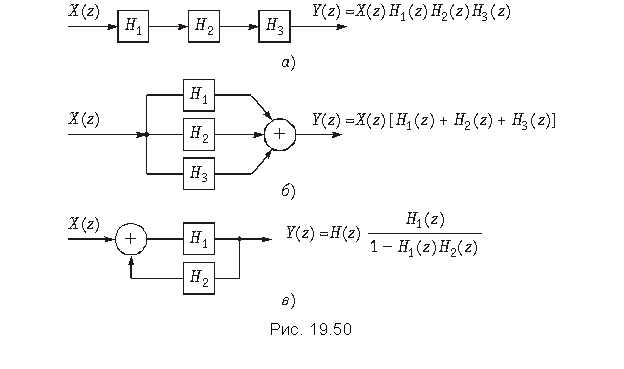
Соединение типовых звеньев. Типовые звенья могут соединяться каскадно (рис. 19.50, а); при этом их передаточные функции перемножаются:
,
где H1, H2, H3 – передаточные функции звеньев.
При параллельном соединении звеньев (рис. 19.50, б) общая передаточная функция определяется как
.
Соединение, показанное на рис. 19.50, в, называют включением цепи H2 в обратную связь цепи H1, причем
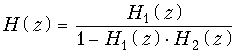
Следует иметь в виду, что все соединения, изображенные на рис. 19.50, справедливы не только для типовых звеньев, но и для любых других структур.
Пример. Найдем передаточные функции при различных способах соединения рекурсивной и нерекурсивной цепей, имеющих и
.
При каскадном соединении этих цепей
;
при параллельном соединении
;
при включении цепи H2 в обратную связь цепи H1
.
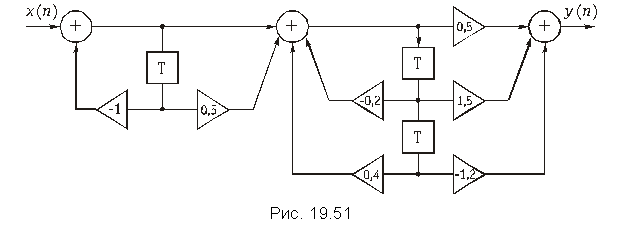
Пример. Найдем передаточную функцию дискретной цепи, изображенной на рис. 19.51.
Цепь, приведенная на рис. 19.51, представляет собой каскадное соединение типовых звеньев 1-го и 2-го порядков. Передаточная функция соединения имеет вид
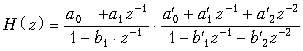
Подставляя в выражение для H(z) заданные значения коэффициентов усиления a0 = 1, a1 = 0,5, b1 = –1 и = 0,5,
= 1,5,
= –1,2,
= –0,2,
= 0,4, получаем
.
19.6. Дискретные фильтры и их синтез
Постановка задачи и этапы синтеза. Дискретная цепь может осуществлять любые операции: фильтрацию сигнала, корректирование характеристик и т. п., т. е. выполнять функции любой аналоговой цепи.
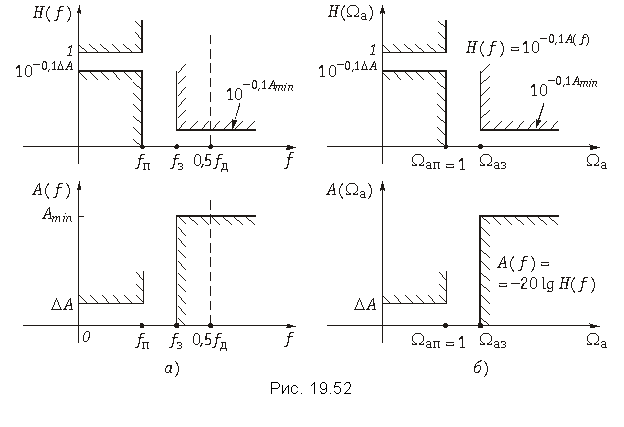
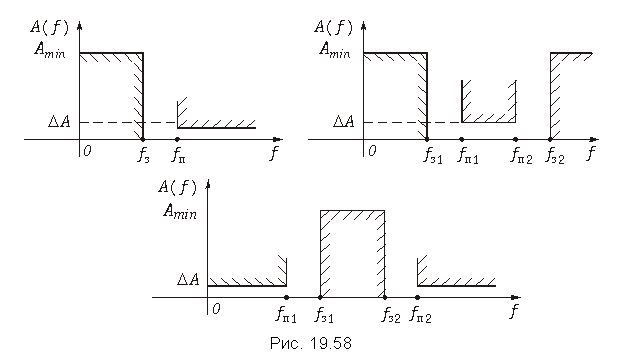
В частности, при синтезе дискретных частотных фильтров нужно найти такие коэффициенты передаточной функции (19.40), или (19.41), частотная характеристика которой удовлетворяла бы нормам ослабления фильтра в полосах пропускания и непропускания (рис. 19.52, а). Определение коэффициентов – это задача аппроксимации. Известен целый ряд методов ее решения. Наиболее распространенным является следующий метод. Сначала рассчитывают аналоговый НЧ-прототип и получают его передаточную функцию H(p), затем путем замены комплексной переменной p = Ф{z} переходят от H(p) к передаточной функции дискретной цепи H(z).
Использование стандартного преобразования z = epT или p = не приведет к дробно-рациональной функции. Поэтому для ФНЧ применяют билинейное преобразование
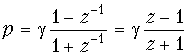
(g – некоторый постоянный множитель), которое является первым приближением стандартного преобразования при разложении его в ряд Тейлора:
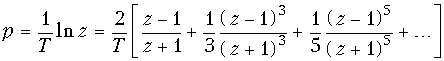
Из разложения (19.51) следует, что необходимо выбирать . Однако, далее мы покажем, что удобнее брать другие значения коэффициента g.
Билинейное преобразование (19.50) переводит все точки из левой полуплоскости переменной p в точки на единичной окружности плоскости z. Так что, если была устойчива аналоговая цепь, будет устойчивой и дискретная. Подтвердим эти утверждения на примере.
Пример. Найдем положения точек на z-плоскости, соответствующих следующим значениям переменной p: p1 = –2; p2 = –2 + j2; p3 = j2.
Из формулы (19.50) найдем выражение для расчета z:
.
Подставляя в эту формулу значение полюса p = p1 = –2, лежащего в левой полуплоскости плоскости p, получаем
.
Поскольку g – число вещественное и положительное, то числитель (g – 2) меньше знаменателя (g + 2), и значит z < 1, т. е. точка z лежит внутри единичной окружности, что говорит об устойчивости цепи.
При p = p2 = –2 + j2 получаем
.
Найдем модуль z
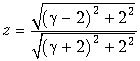
Он меньше единицы, поскольку модуль числителя меньше модуля знаменателя, т. е. точка z также лежит внутри единичной окружности.
При p = p3 = j2 получаем
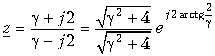
Модуль z равен 1, т. е. точка p = j2, лежащая на мнимой оси плоскости p, переходит в точку на единичной окружности плоскости z при использовании билинейного преобразования.
Переход к аналоговому прототипу применяется обычно для дискретных фильтров, имеющих бесконечную импульсную характеристику h(k), принимающую ненулевые значения на бесконечном множестве значений k = 0, 1, … .
Дискретные цепи с конечной импульсной характеристикой, принимающей ненулевые значения лишь при k = 0, 1, …, N – 1, не имеют аналогов среди пассивных электрических фильтров, поэтому для их расчета применяются другие методы.
Нерекурсивные фильтры с передаточной функцией (19.42) всегда имеют конечные импульсные характеристики. Рекурсивные фильтры с передаточной функцией (19.40) могут иметь как конечные, так и бесконечные импульсные характеристики.
Пример. Найдем дискретные импульсные характеристики фильтров, имеющих передаточные функции
,
,
.
Дискретная импульсная характеристика h(k) связана с передаточной функцией обратным z-преобразованием (см. формулу (19.29)):
,
т. е. . Нерекурсивной цепи с передаточной функцией H1(z) соответствует h{k} = {2; 0,5; –3}, т. е. это фильтр с конечной импульсной характеристикой.
Импульсная характеристика цепи с передаточной функцией H2(z) рассчитывается по формуле h(k) = 0,5k, т. е. это рекурсивный фильтр с бесконечной импульсной характеристикой.
Отсчеты импульсной характеристики рекурсивной цепи с передаточной функцией H3(z) будут конечными и равными 1 только для k = 0, 1, 2, 3, 4, а для k 5 h(k) = 0. Значит этот рекурсивный фильтр имеет конечную импульсную характеристику.
Требования к аналоговому фильтру-прототипу. Следует иметь в виду, что частотная характеристика аналогового фильтра определена на всей положительной полуоси частот, в то время как у дискретного фильтра она имеет тот же смысл только до частоты 0,5fд, затем она периодически повторяется (рис. 19.44). Ясно, что шкала частот дискретного фильтра оказывается деформированной относительно шкалы частот аналогового фильтра. Соответствие этих шкал легко установить из билинейного преобразования (19.50). Перепишем его в виде:
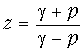
Обозначим, во избежание путаницы, нормированную частоту для аналогового фильтра-прототипа Wа, обычную (т. е. ненормированную) частоту для дискретного фильтра будем, как и ранее, обозначать буквой f, а нормированную – буквой W. Теперь заменим в (19.53) комплексную переменную p на jWа, а комплексную переменную z на и установим соответствие между частотами f (или W) и Wа:
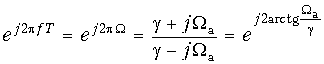
Отсюда легко получить, что
или
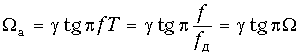
При изменении частоты f от 0 до 0,5fд, или нормированной частоты W от 0 до 0,5, нормированная частота Wа в шкале аналогового прототипа будет пробегать значения от 0 до бесконечности (рис. 19.52).
Во многих справочниках по расчету фильтров граничная частота полосы пропускания принимается равной Wап = 1. Чтобы частота fп (или Wп) дискретного фильтра пересчитывалась в Wап = 1 (рис. 19.52, б), из (19.54) ясно, что коэффициент g нужно взять равным:
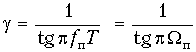
Пример. Рассчитаем дискретный ФНЧ с параметрами: fд = 8 кГц; fп = = 1 кГц; fз = 3 кГц; DA = 1,4 дБ; Amin = 40 дБ.
По формуле (19.55) находим и по формуле (19.54) определяем нормированную граничную частоту полосы непропускания Wаз аналогового НЧ-прототипа:
Wаз = .
Тем самым, произведен пересчет требований, предъявленных к дискретному фильтру (рис. 19.52, а) в требования к аналоговому НЧ-прототипу (рис. 19.52, б).
Расчет аналогового НЧ-прототипа. Исходными данными для расчета являются требования к НЧ-пототипу (рис. 19.52, б). По ним, пользуясь любым справочником, рассчитывают передаточную функцию фильтра-прототипа.
Пример. Для Wаз = 5,82, Amin = 40 дБ и DA = 1,4 дБ, (параметры ФНЧ, взятые из примера), пользуясь справочником Христиана Э., Эйзенмана Е. «Таблицы и графики по расчету фильтров» М.: Связь, 1975, находим, что
. (19.56)
Реализация рекурсивного фильтра. Для перехода от аналогового фильтра к дискретному воспользуемся заменой переменных (19.50)
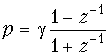
В результате получаем H(z) в виде дробно-рациональной функции, которая может быть реализована.
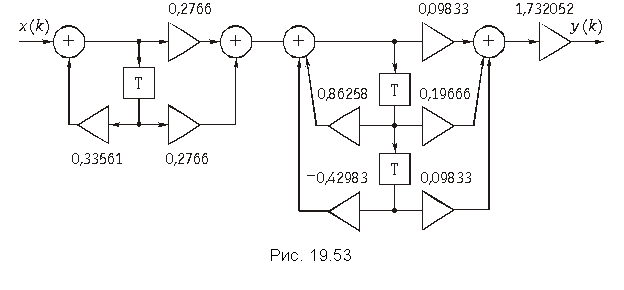
Пример. От передаточной функции (19.56) аналогового фильтра-прототипа перейдем к передаточной функции H(z) дискретного фильтра.
Подставим в выражение (19.56) значение
.
Получим
Дискретный фильтр можно реализовать в виде каскадного соединения типовых звеньев 1-го и 2-го порядка. Для этого функцию H(z) перепишем в виде:
Схема фильтра, имеющего такую передаточную функцию, приведена на рис. 19.53. Амплитудно-частотная характеристика , рассчитанная на основании формул для АЧХ типовых звеньев, показана на рис. 19.54 (кривая 1).
Аналогичным образом производится расчет фильтров со всплесками ослабления (нулями передачи).
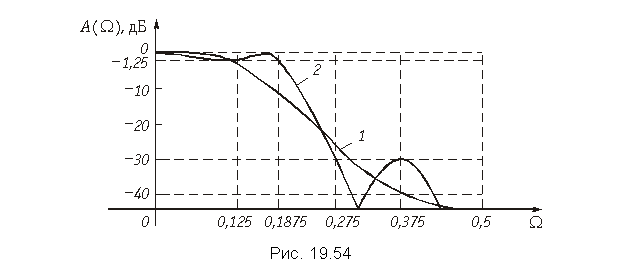
Пример. Найдем передаточную функцию дискретного фильтра НЧ с АЧХ, равноволновой в полосе пропускания и со всплеском ослабления в полосе задерживания. Параметры фильтра: fд = 32 кГц; fп = 6 кГц; fз = 8,8 кГц; DA = = 1,5 дБ; Amin = 30 дБ.
Определяем: и
Wз . Далее находим
и
Wаз .
По справочнику рассчитываем
и с помощью подстановки
переходим к H(z)
Амплитудно-частотная характеристика такого фильтра показана на рис. 19.54 (кривая 2).
Синтез фильтров с конечной импульсной характеристикой. Если известна передаточная функция H(z) дискретного фильтра, то для реализации фильтра с конечной импульсной характеристикой h(k), равной нулю везде кроме , поступают следующим образом. Амплитудно-частотную характеристику H(W) фильтра дискретизируют, разбивая частотный интервал W = 0 ¸ 1 на N равных интервалов. В результате получают последовательность отсчетов АЧХ на N частотах
, т. е.
,
. Поскольку
, то, подставляя эту последовательность в формулу обратного дискретного преобразования Фурье (19.14), получаем выражение для дискретной импульсной характеристики h(k) фильтра
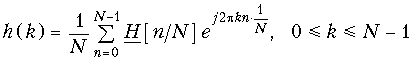
Как известно, конечную импульсную характеристику имеют нерекурсивные фильтры. Это значит, что полученные отсчеты дискретной импульсной характеристики h(k) являются коэффициентами усиления a0, a2, …, aN–1 в схеме нерекурсивного фильтра, приведенной на рис. 19.33.
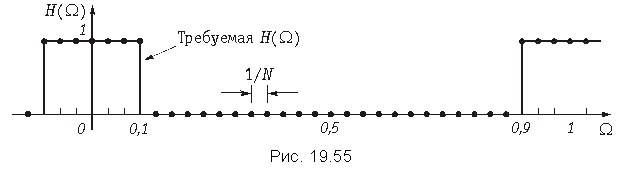
Пример. Найдем импульсную характеристику h(k) фильтра нижних частот, имеющего граничную частоту полосы пропускания W = 0,1, и АЧХ, приведенную на рис. 19.55. Импульсную характеристику будем рассчитывать для значения N = 30.
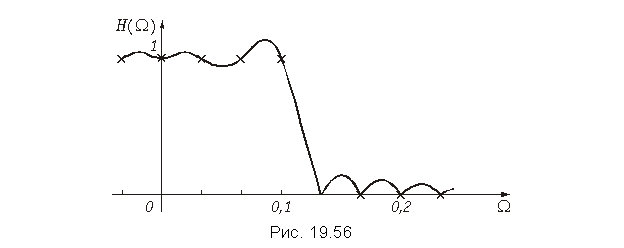
В формуле (19.57) для расчета h(k) используются комплексные значения передаточной функции. Если выбрать значения H[n/N], показанные на рис. 19.55 (H[n/N] = 1 в полосе пропускания и H[n/N] = 0 в полосе непропускания) и фазу передаточной функции argH[n/N], равную нулю, то передаточная функция будет иметь заданные значения в точках W = n/N, но очень сильно отличаться от требуемой формы на частотах W между этими точками.
Гораздо лучшие результаты получаются, если выбрать argH[n/N] = . Выбор такой фазы эквивалентен тому, что H[n/N]
вместо 1 в полосе пропускания. Такой передаточной функции соответствует АЧХ, изображенная на рис. 19.56. Подстановка значений H[n/N] в формулу (19.34) позволяет получить выражение для расчета h(k):
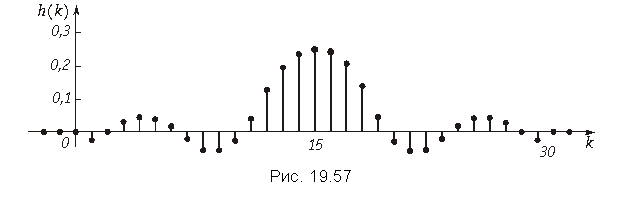
График конечной импульсной характеристики h(k) изображен на рис. 19.57.
Для реализации фильтра с такой импульсной характеристикой по схеме рис. 19.33 потребуется 30 усилителей и 29 элементов задержки, т. е. схема довольно громоздкая. Схема с обратными связями, реализующая АЧХ, изображенную на рис. 19.55, будет иметь гораздо меньше элементов. Однако достоинством нерекурсивных фильтров с конечной импульсной характеристикой является то, что они всегда устойчивы и, кроме того, обеспечивают линейные фазовые характеристики.
Синтез дискретных фильтров верхних частот, полосовых и режекторных. Требования к любому типу фильтра преобразуются в требования к аналоговому ФНЧ-прототипу. Затем рассчитывается аналоговый прототип, как это показано выше, и с помощью замены переменных переходят от H(p) к H(z).
Конечно, формулы замены переменных уже не такие, как для ФНЧ. Они приведены для разных типов фильтров в табл. 19.2. Требования к дискретным фильтрам графически изображены на рис. 19.59.
Пример. Определить передаточную функцию дискретного полосового фильтра с параметрами: fд = 140 Гц; fп1 = 15,5 Гц; fп2 = 30 Гц; fз1 = 7,75 Гц; fз2 = 60 Гц; DA = 0,5 дБ; Amin = 40 дБ.
Определяем:
Wп1 = 15,5/140 = 0,110714; Wп2 = 30/140 = 0,214286;
Wз1 = 7,75/140 = 0,055357; Wз2 = 60/140 = 0,428571;
= 2,964087;
;
W¢аз ;
W²аз ;
Wаз .
По данным Wаз = 3,38, DА = 0,5 дБ и Amin = 40 дБ из справочника находим
Передаточную функцию H(z) найдем, используя подстановку
и разлагая каждый из двух полиномов четвертой степени (в знаменателе H(z)) на множители (полиномы второй степени):
Таблица 19.2 – Формулы замены переменных для различных
19.7. Цифровые фильтры
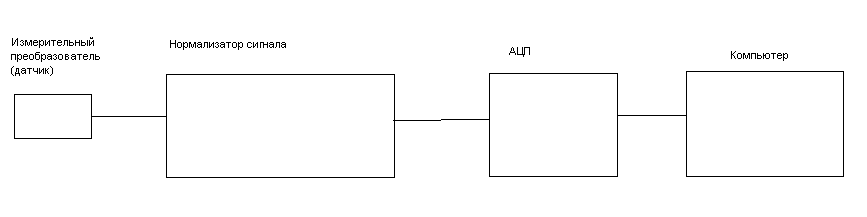
Функциональная схема цифрового фильтра. В отличие от дискретных фильтров в цифровом фильтре (ЦФ) осуществляется обработка цифровых сигналов (рис. 19.1, в). На рис. 19.60 изображена функциональная схема цифровой обработки аналоговых сигналов. Аналоговый сигнал x(t) подается на аналого-цифровой преобразователь (АЦП), где осуществляется дискретизация, квантование непрерывного сигнала и его кодирование. В результате на выходе АЦП формируется цифровой сигнал, представляющий собой последовательность двоичных чисел с фиксированным количеством разрядов.
Например, если отсчет имеет величину 30 В, то запись числа в двоичном 8-разрядном коде будет такой: 00011110. Закодированные в двоичном коде отсчеты на выходе кодера АЦП на рисунке обозначены . Далее двоичная последовательность поступает на вычислительное устройство (ВУ), которое представляет собой универсальную или специализированную микро ЭВМ, микропроцессорное или любое другое вычислительное устройство. Главное состоит в том, что в памяти ВУ должна быть записана программа вычисления, например, выражение (19.35), и отсчеты импульсной реакции, заданной цепи. Следовательно, в результате работы программы ВУ будет выдавать закодированные в двоичном коде отсчеты
. Далее двоичная выходная последовательность поступает на вход цифро-аналогового преобразователя (ЦАП), содержащий декодер и интерполятор. В ЦАП осуществляется декодирование сигнала, в результате формируется дискретный выходной сигнал y(kT) и после интерполяции на выходе ЦАП получаем выходной аналоговый сигнал y(t).
Как видим, ВУ может сыграть роль реальной цепи. И хотя самой физической цепи в наличии может и не быть, а задана она будет лишь в виде отсчетов импульсной реакции и программы вычислений, мы будет наблюдать на выходе описанной системы такое же выходное напряжение y(t), как и на выходе реальной цепи.
Следует отметить, что при цифровой обработке ЦАП может и отсутствовать, если выходной сигнал надо получить в цифровой форме.
Аналогово-цифровое преобразование сигналов. Как следует из рис. 19.60 АЦП осуществляет дискретизацию аналогового сигнала, его квантование по уровню с шагом D (рис. 19.1, в) и кодирование. Обычно процесс квантования осуществляется одновременно с его кодированием, в результате на выходе АЦП получаем сигнал, представленный в некотором цифровом коде.
Одним из основных параметров кода является его основание, соответствующее выбранной системе счисления. Близко к оптимальным реализуются двоичные или бинарные коды, которые нашли наибольшее распространение в связи.
Известно большое количество различных устройств преобразования непрерывного сообщения в бинарный код. Все их можно разбить на три основные группы: преобразователи последовательного счета, поразрядного кодирования и преобразователи считывания. Наибольшее применение в связи нашли преобразователи первых двух типов.
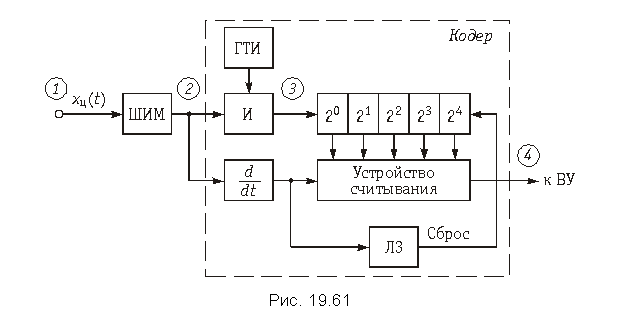
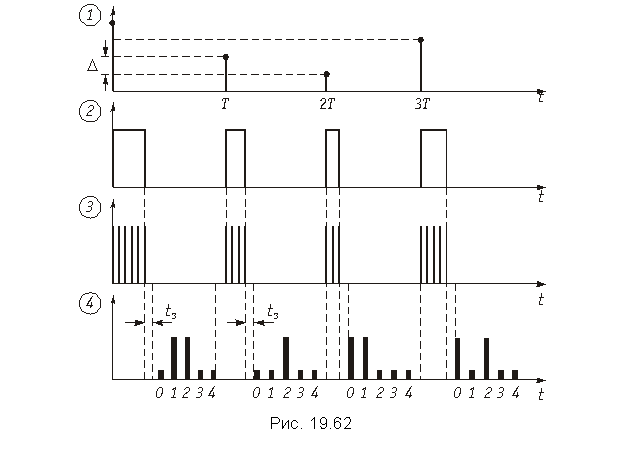
Принцип действия преобразователя последовательного счета с временным преобразованием иллюстрируется схемой изображенной на рис. 19.61 и временными диаграммами на рис. 19.62.
Кодирование в данной схеме осуществляется следующим образом. Аналоговый сигнал после дискретизации и квантования xц(t) поступает на вход широтно-импульсного модулятора (ШИМ), на выходе которого формируются прямоугольные импульсы ширина которых пропорциональна отсчету сигнала xц(t) в моменты kT (рис. 19.62). Далее этот ШИМ-сигнал подается на схему «И», на второй вход которой поступают импульсы с генератора тактовой частоты (ГТИ). На выходе схемы «И» формируются импульсы, число которых в «пачке» пропорционально ширине импульса. Эти импульсы поступают в двоичный счетчик, где число их фиксируется в двоичной системе счисления. Задним фронтом ШИМ-импульса запускается устройство считывания результата, с выхода которого кодовая комбинация поступает в ВУ. Считывание может осуществляться последовательно или параллельно (последовательный или параллельный код).
На рис. 19.62 приведен вид кодовой группы на выходе при последовательном считывании. Для возвращения двоичного счетчика в исходное состояние на него через линию задержки ЛЗ с tз = tсчит подается сигнал сброса, формируемый задним фронтом ШИМ-импульса. С приходом следующего измерительного импульса работа кодера повторяется.
Аналогичным образом можно кодировать и амплитудно-модулированную импульсную последовательность (кодер последовательного счета с частотным преобразованием). Для этого АИМ-сигнал подается на ЧМ-генератор (мультивибратор), и осуществляется счет импульсов этого генератора за фиксированные промежутки времени по рассмотренной выше схеме.
В преобразователях поразрядного кодирования производится последовательное сравнение выходного сигнала с набором эталонных напряжений, каждое из которых соответствует определенному разряду кода. В качестве эталонных напряжений используется геометрическая прогрессия вида
где N – число разрядов в бинарном коде. Причем E > umax, где umax – максимально возможное значение кодирующего сигнала.
При поразрядном кодировании вначале формируется старший разряд кода путем сравнения u(t) с (например, если
, то формируется символ «1», в противном случае – «0»). Одновременно на выходе схемы сравнения образуется напряжение
при
или u(t) при
. Затем указанная процедура повторяется с полученным напряжением для эталонного напряжения
и т. д. В результате N сравнений получается символ самого младшего разряда.
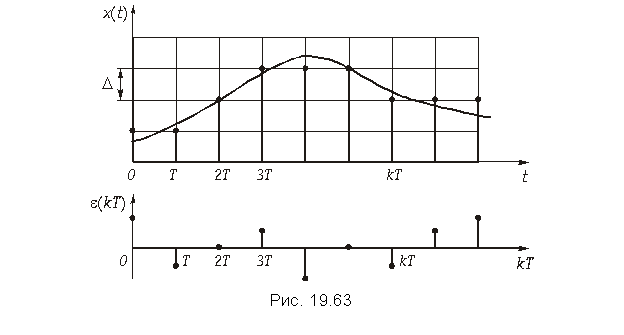
Шумы квантования. При квантовании сигнала минимальный шаг квантования D (расстояние между смежными разрешенными уровнями) соответствует единице младшего двоичного разряда. Причем, поскольку при квантовании происходит округление значений сигнала до ближайшего дискретного уровня, то появляются ошибки округления . Если x(t) известен неточно, то e – является случайной величиной и при малом D распределено по равномерному закону. Последовательность значений ошибки e, возникающей при квантовании дискретного сигнала x(kT) образует дискретный случайный процесс e(kT) называемый шумом квантования (рис. 19.63).
Дисперсия шума квантования определяется для равномерного закона распределения p(e) формулой
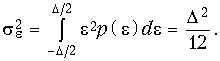
Если шаг квантования D мал, то соседние значения e(kT) можно считать некоррелированными.
Шум квантования является одним из главных источников погрешности цифровой обработки сигнала. Шум на выходе цифрового фильтра x(kT) при условии некоррелированности отсчетов e(kT) можно определить согласно (19.35)
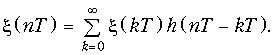
Откуда с учетом (19.59) получим для дисперсии шума на выходе цифрового фильтра:
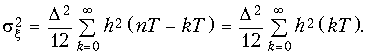
Поскольку для ЦФ обычно выполняется условие (19.36),то дисперсия шума квантования на выходе всегда конечна.
Ошибки округления. При обработке цифрового сигнала в ВУ возникают дополнительные ошибки округления (усечения). Действительно, если при использовании в ВУ чисел с фиксированной запятой сложение чисел не приводит к увеличению разрядов, то при умножении число разрядов возрастает и возникает необходи
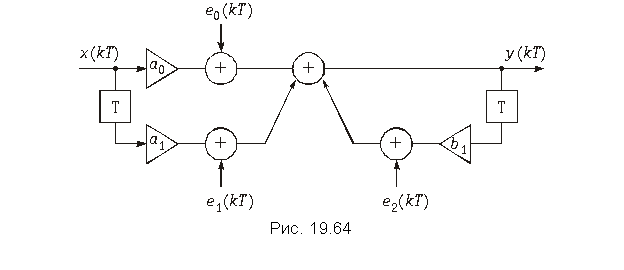
мость округления результата, что естественно приводит к ошибкам называемым ошибками округления. По своему характеру эти ошибки аналогичны шуму квантования. Для их учета обычно в схему ЦФ дополнительно вводят источники шума ei(kT), число которых равно числу умножителей. На рис. 19.64 изображена схема рекурсивного ЦФ звена 1-го порядка с учетом источников шума округления.
Источники шума e(kT) имеют одинаковую дисперсию s2 = , где D определяется числом используемых разрядов. Если принять, что источники e0(kT), e1(kT) и e2(kT) независимы, то дисперсия суммарного шума округления будет равна
Для другой схемы реализации ЦФ результирующая вычисляется в зависимости от того, куда будет подключен источник шума e(kT) и в общем случае может быть найден по формуле (19.60) или с учетом равенства Парсеваля
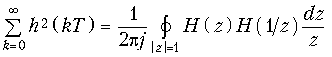
из уравнения
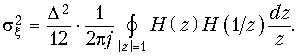
Пример. Определить дисперсию шума на выходе ЦФ 1-го порядка с передаточной функцией
Для нахождения воспользуемся формулой (19.62):
Кроме ошибок квантования и округления при синтезе ЦФ возникают ошибки, вызванные неточными значениями параметров фильтра. Эти ошибки особенно опасны в рекурсивных фильтрах высокого порядка, т. к. могут привести к потере устойчивости ЦФ, поэтому обычно используют звенья 1-го и 2-го порядков (см. § 19.5). Кроме рассмотренных выше при синтезе ЦФ возникают еще ряд дополнительных явлений, приводящих к погрешности цифровой фильтрации. К ним, например, относятся так называемые предельные циклы низкого уровня, представляющие собой периодические колебания, возникающие на выходе ЦФ при низком входном сигнале и обусловленные округлением результатов вычисления. Все эти явления и ошибки подробно исследуются в специальной литературе.
Цифро-аналоговое преобразование. Преобразование цифровых сигналов в аналоговый осуществляется с помощью различных цифро-аналоговых преобразователей (ЦАП). В основе простейшего ЦАП лежит принцип двоично-взвешенного суммирования напряжений или токов. На рис. 19.65 изображены схемы простейших ЦАП на базе резистивных цепей.
В ЦАП с двоично-весовыми резисторами (рис. 19.65, а) требуется меньшее число резисторов, однако при этом необходим целый ряд номиналов прецизионных сопротивлений. Аналоговое выходное напряжение Uан ЦАП определяется как функция двухуровневых входных напряжений:
На цифровых входах UА, UВ, UС … напряжение может принимать лишь два фиксированных значения, например, либо 0, либо 1.
Для ЦАП, в котором используются резисторы R и , требуется больше резисторов (рис. 19.65, б), но только с двумя номиналами. Аналоговое напряжение на выходе такого ЦАП определяется по формуле
где n – число разрядов ЦАП; m – коэффициент, зависящий от числа разрядов ЦАП.
Для обеспечения высокой точности работы резистивные цепи ЦАП должны работать на высокоомную нагрузку. Чтобы согласовать резистивные цепи с низкоомной нагрузкой, используют буферные усилители на основе операционных усилителей, показанные на рис. 19.65, а, б.
Интерполяторы. На выходе ЦАП сигнал обычно имеет форму последовательности импульсов модулированных по амплитуде (АИМ-сигнал). Для восстановления (демодуляции) из АИМ-последовательности аналогового сигнала достаточно использовать ФНЧ с частотой среза wс = 2p/Т, где Т – частота дискретизации АИМ-сигнала. Существуют и более сложные интерполирующие устройства, которые описаны в специальной литературе.
В заключении следует отметить, что в связи с бурным развитием вычислительной, микропроцессорной техники цифровые методы обработки сигналов получают все большее распространение. Они имеют более широкие возможности реализации сложных и эффективных алгоритмов обработки сигналов, которые в большинстве своем недоступны для реализации аналоговыми цепями.
19.8. Вопросы и задания для самопроверки
1. Почему нельзя произвольно выбирать интервал дискретизации?
2. Найдите спектр дискретного сигнала, состоящего из одного отсчета x{k} = {2}.
3. Каким должно быть соотношение между интервалом дискретизации спектра по частоте DF и периодом повторения Тс сигнала?
4. Найдите частоту дискретизации и интервал дискретизации сигнала, имеющего спектр, ограниченный частотой Fв = 10 кГц.
5. Найти дискретную свертку сигналов x1{k} = {1; 1} и x2{k} = {0,5; 0,5; 0,5}. Ответ: x1{k} *x2{k} = {0,5; 1; 1; 0,5}.
6. Вычислить реакцию дискретной цепи с импульсной характеристикой h(k) на входной дискретный сигнал x(k):
а) h{k} = {2; 1; 0,5}, x{k} = {0,5; 0,5}
б) h{k} = {2; 2; 2}, x{k} = {1; 1; 1}.
Ответ: а) y{k} = {1; 1,5; 0,75; 0,25} б) y{k} = {2; 4; 6; 4; 2}. 7. Найти z-преобразование дискретных сигналов а) = {3; 2; 1} б)
в) .
Ответ: а) б)
в)
.
8. Найти z-преобразование дискретного сигнала x3(k), равного сумме сигналов x1{k} = {1; 0; 1; –1} и x2{k} = {2; 1; 0; 1}
Ответ: .
9. Найти дискретные сигналы x(k), имеющие z-преобразования а) б)
. Ответ: а) x{k} = {1; 2; 0; 4} б) x{k}
.
10. Найти ДПФ дискретного сигнала x{k} = {0,5; 0,25; 0,0625}. Построить спектр амплитуд и спектр фаз дискретного сигнала. Ответ: X{n} = {1,875; 0,838; 0,625; 0,838} argX{n} = {0; –0,464; 0,0464}.
11. Найти отсчеты дискретных сигналов x(k), имеющих спектры а) X{n} = {4; 0; 0; 0} б) X{n} = {0; 4; 0; 0}. Ответ: а) x{k} = {1; 1; 1; 1}
б) = {1; 1; 1; 1},
.
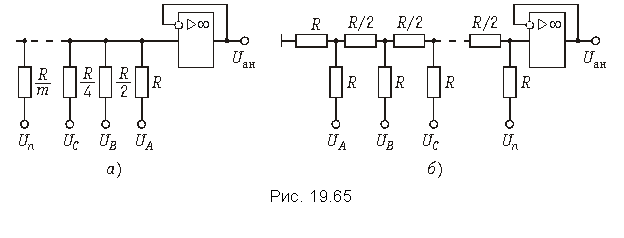
12. Записать разностные уравнения для дискретных цепей, структурные схемы которых приведены на рис. 19.66. Ответ: а) б)
в)
. 13. Записать передаточные функции цепей, приведенных на рис. 19.66, и определить их импульсные характеристики. Ответ: а)
, h{k} = {1; –0,5; 2}
б) ,
h{k} = {1; 0,5; –0,75; –0,875; …}
в) , h{k} = {2; 0,5; 1,75; –0,625; …}.
14. Рассчитать отсчеты y(0), y(1) и y(2) выходных сигналов цепей, приведенных на рис. 19.66, если входной сигнал – ступенчатая последовательность x{k} = u{k} = {1; 1; 1; 1; …}. Ответ: а) y{k} = {1; 0,5; 2,5} б) y{k} = {1; 1,5; 0,75} в) y{k} = {2; 2,5; 4,25}.
15. Определить импульсные характеристики цепей, описываемых разностными уравнениями: а) б)
в)
. Ответ: а) h{k} = {0,5; –2; 1} б) h{k} = {1; –3; 11; –39; …} в) h{k} = {1; –2,5; 6; –14,5; …}.
16. Определить передаточные функции цепей, описываемых разностными уравнениями, приведенными в задаче 15. Ответ: а) б)
в)
.
17. Составить структурные схемы, записать разностные уравнения и определить импульсные характеристики цепей, передаточные функции которых имеют вид а) б)
в)
. Ответ: а)
,
= {5; –1; 3} б)
,
= {2; 4; 8; 16; …} в)
,
= {5; 1; 11; 13; …}.
18. Определить устойчивость цепей, имеющих передаточные функции, приведенные в задаче 17. Ответ: а) устойчивая б) неустойчивая
в) неустойчивая.
19. Определить передаточную функцию цепи, если на ее входе и выходе действуют дискретные сигналы x{k} = {1; 0; 0; 0; 1; 0; 0; 0; 1; …}, y{k} = {1; 0; 1; 0; 1; 0; …}. Ответ: .
20. Найти импульсные характеристики дискретных цепей, имеющих передаточные функции
а) б)
Составить структурную схему каскадного соединения этих цепей, определить для нее передаточную функцию и записать разностное уравнение. Ответ: а)
= 1, k
0 б)
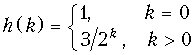
.
21. Найти передаточную функцию дискретной цепи с импульсной характеристикой а) = {1; –1} б)
. Ответ: а)
б)
.
22. Определить сигнал на выходе дискретной цепи с импульсной характеристикой h{k} = {1; 0,5}, если на вход подается сигнал x{k} = {1; 1; 1}. Ответ: y{k} = {1; 1,5; 1,5; 0,5}.
23. Определить передаточные функции и АЧХ дискретных цепей, имеющих разностные уравнения: а) б)
Ответ: а)
б)
.
24. Вычислить дисперсию шума на выходе ЦФ первого порядка с передаточной функцией ; (b < 1) с использованием формулы (19.60). Ответ:
.
Список литературы
Основная
1. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей.—М.: Радио и связь, 1998.—444 с.
2. Белецкий А.Ф. Теория линейных электрических цепей.—М.: Радио и связь 1986.—544 с.
3. Воробиенко П.П. Теория линейных электрических цепей. Сб. задач и упражнений.—М.: Радио и связь, 1989.—328 с.
4. Шебес М,Р., Каблукова М.В. Задачник по теории линейных электрических цепей: Учеб. пособие для вузов.—4-е изд., перераб. и доп.—М.: Высшая школа, 1990.—544 с.
5. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. Учебник – М.: Радио и связь, 2000. Электронная версия.
6. Журавлева О.Б., Крук Б.И. Аналоговые устройства аппаратуры связи: Учебное пособие для дистанционного обучения. – СибГУТИ, Новосибирск, 2000 г. Электронная версия.
7. Методические указания по самостоятельной работе студентов над курсом ОТЦ. Часть III. – Новосибирск, 2001 г. Электронная версия.
8. Программа ARC—ACH.
9. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. Учебник – М.: Радио и связь, 2000. – 589 с.
10. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. Учебник – М.: Радио и связь, 1998. – 444 с.
11. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей: Учеб. пособие для вузов. 4-е изд., перераб. и доп. – М.: «Высшая школа», 1990. – 544 с.
12. Воробиенко П.П. Теория линейных электрических цепей. Сб. задач и упражнений. – М.: Радио и связь, 1989. – 328 с.
13. Зааль Р. Справочник по расчету фильтров. – М.: Радио и связь, 1983. – 752 с.
14. Белецкий А.Ф. Теория линейных электрических цепей. Учебник. – М.: Радио и связь, 1986. – 544 с.
Дополнительная
15. Андреев Б.С. Теория нелинейных электрических цепей.—М.: Радио и связь 1982.—280 с.
16. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основа теории электрических цепей и электроники.—М.: Радио и связь, 1989.—528 с.
17. Гоноровский И.С., Демин М.П. Радиотехнические цепи и сигналы: [Учеб. пособие для вузов по направлению “Радиотехника”].—5-е изд., перераб. и доп.—М.: Радио и связь, 1994.—481 с.
18. Добротворский И.Н. Теория электрических цепей.—М.: Радио и связь, 1989.—472 с.
19. Карташкин А.С. Линейные цифровые фильтры. Вопросы и задачи: Учеб. пособие.—М.: Радио и связь, 1995.—133 с.
20. Сборник задач по теоретическим основам электротехники: Учеб. пособие /Под. ред. Л.А. Бессонова.—М.: Высшая школа, 2000.
21. Яцкевич В.В. Теория линейных электрических цепей: Справ. пособие.—М.: Высшая школа, 1990.—264 с.
Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих
Время на прочтение
9 мин
Количество просмотров 255K
1. Преобразование Фурье и спектр сигнала
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).
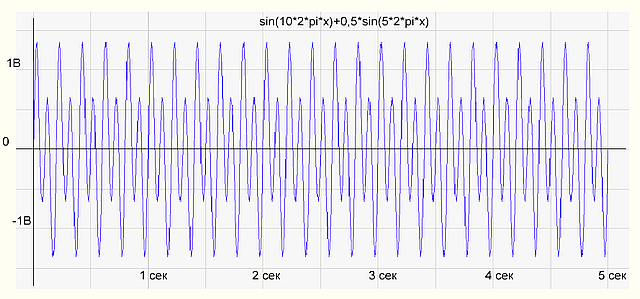
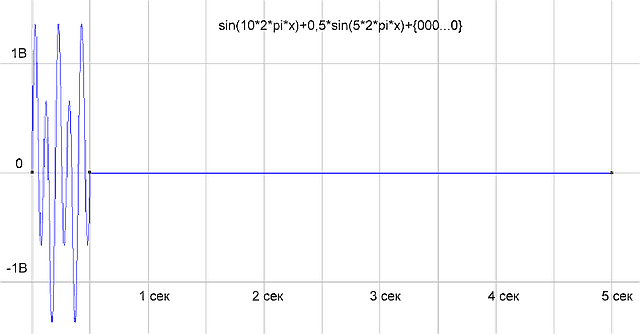
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:
рис.1 График временной функции сигнала
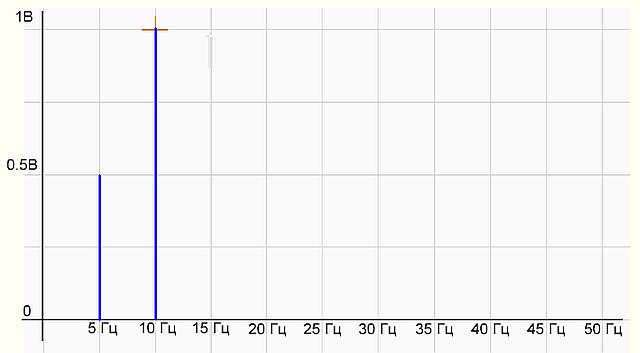
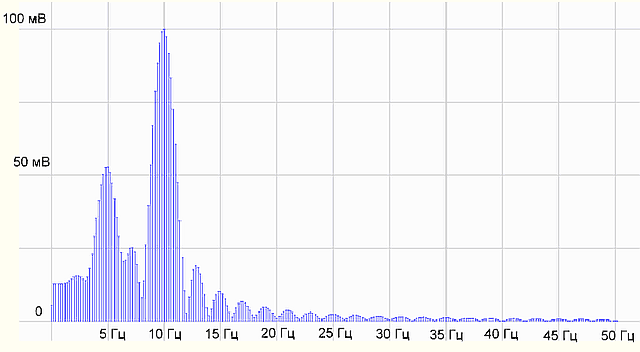
рис.2 График спектра сигнала
На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.
Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.
Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.
С математической точки зрения — сколько ошибок в этой фразе?
Теперь
начальство решило
мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.
рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек
рис.4 Спектр функции
Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…
Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.
рис.5 Добили нулей до 5 сек
рис.6 Получили спектр
Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.
2. Непрерывная функция и представление её рядом Фурье
Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:
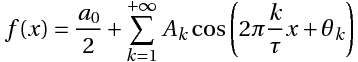
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей
Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.
(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)
Этот ряд может быть также записан в виде:
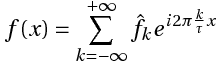
где 
или
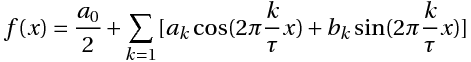
Связь между коэффициентами (1) и (3) выражается следующими формулами:
и
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.
Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид иили косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.
Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.
Например, на графике рис.7 исходная функция определена на отрезке {-T2, +T2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.
Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.
рис.7 Представление непериодической исходной функции рядом Фурье
Таким образом:
Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.
Далее.
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)
Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= кТ, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1T; к=2 F2=2T; к=3 F3=3T;… Fk= кТ (при нулевой частоте — постоянная составляющая).
Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.
Шаг между гармониками в этом случае равен 1 Гц.
Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.
Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.
3. Дискретные сигналы и дискретное преобразование Фурье
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.
рис.9 Схема измерительного канала
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т
Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).
Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени 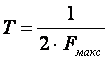
А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации
Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.
Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.
Рассмотрим теперь дискретное преобразование Фурье (ДПФ).
Сравнивая с рядом Фурье
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.
Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»
Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0
Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.
Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.
В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.
Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора
При меньшей длительности картина будет выглядеть «хуже»:
Рис.14 Пример функции и спектра сигнала вибрации ротора
На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.
Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.
Некоторые итоги
1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).
2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».
3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.
Использованные материалы и другие полезные материалы.
FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)

ГЛАВА 3
6
4
2
0
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
Дискретные сигналы
После двух вводных глав, посвященных основам теории сигналов и линейных систем, мы наконец приступаем к рассмотрению вопросов, непосредственно связанных с предметом данной книги — цифровой обработкой сигналов.
Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и т. д.) преобразуется в последовательность чисел, которая затем подвергается математическим преобразованиям в вычислительном устройстве. Трансформированный цифровой сигнал (последовательность чисел) при необходимости может быть преобразован обратно в напряжение или ток.
В данной главе рассмотрены принципы математического описания и анализа дискретных сигналов. Прежде всего следует пояснить некоторые терминологические тонкости, которые, возможно, уже были замечены внимательным читателем: в названии книги упоминается цифровая обработка сигналов, а данная глава посвящена дискретным сигналам. С обсуждения разницы между этими понятиями мы и начнем.
Аналоговые, дискретные и цифровые сигналы
Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты времени, называют аналоговыми (analog). Последовательность чисел, представляющая сигнал при цифровой обработке, является дискретным рядом (discrete series) и не может полностью соответствовать аналоговому сигналу. Числа, составляющие последовательность, являются значениями сигнала в отдельные (дискретные) моменты времени и называются отсчетами сигнала (samples). Как правило, отсчеты берутся через равные промежутки времени T, называемые периодом дискретизации (или интервалом, шагом дискретизации — sample time). Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency): fд =1
та определяется следующим образом: ωд = 2π
Ясно, что в общем случае представление сигнала набором дискретных отсчетов приводит к потере информации, т. к. мы ничего не знаем о поведении сигнала в

промежутках между отсчетами. Однако, как будет показано далее в разд. «Теорема Котельникова» этой главы, существует класс аналоговых сигналов, для которых такой потери информации не происходит и которые могут быть точно восстановлены по значениям своих дискретных отсчетов.
Процесс преобразования аналогового сигнала в последовательность отсчетов называется дискретизацией (sampling), а результат такого преобразования — дискретным сигналом.
При обработке сигнала в вычислительных устройствах его отсчеты представляются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследствие этого отсчеты могут принимать лишь конечное множество значений и, следовательно, при представлении сигнала неизбежно происходит его округление. Процесс преобразования отсчетов сигнала в числа называется квантованием по уровню (quantization), а возникающие при этом ошибки округления — ошибками (или шумами) квантования (quantization error, quantization noise).
Сигнал, дискретный во времени, но не квантованный по уровню, называется дискретным (discrete-time) сигналом. Сигнал, дискретный во времени и квантованный по уровню, называют цифровым (digital) сигналом. Сигналы, квантованные по уровню, но непрерывные во времени, на практике встречаются редко. Разницу между аналоговыми, дискретными и цифровыми сигналами иллюстрирует рис. 3.1.
5
4
3
2
1
0 
Рис. 3.1. Аналоговый (слева), дискретный (в центре) и цифровой (справа) сигналы
Вычислительные устройства, предназначенные для обработки сигналов, могут оперировать только цифровыми сигналами. Существуют также устройства, построенные в основном на базе аналоговой схемотехники, которые работают с дискретными сигналами, представленными в виде импульсов различной амплитуды или длительности. Чтобы подчеркнуть отсутствие квантования по уровню, такие устройства иногда называют дискретно-аналоговыми (ДАУ).
В большей части книги речь пойдет о дискретных сигналах и методах их обработки, поскольку эффекты, связанные с квантованием по уровню, в большинстве случаев не будут приниматься во внимание. Однако этим эффектам, а также другим проблемам, связанным с конечной точностью представления чисел в вычислительных устройствах, специально посвящена глава 7.
Аналого-цифровое и цифроаналоговое преобразование
Обобщенная структура системы цифровой обработки сигналов приведена на рис. 3.2. На вход поступает аналоговый сигнал sвх (t) . Его временная дискретизация

иквантование по уровню производятся в аналого-цифровом преобразователе (АЦП; английский термин — Analog-to-Digital Converter, ADC). Вообще эти два процесса — дискретизация и квантование — являются независимыми друг от друга, но они, как правило, выполняются внутри одной микросхемы. Выходным сигналом АЦП является последовательность чисел, поступающая в цифровой процессор (ЦП), выполняющий требуемую обработку. Процессор осуществляет различные математические операции над входными отсчетами; ранее полученные отсчеты
ипромежуточные результаты могут сохраняться в памяти процессора для использования в последующих вычислениях. Результатом работы процессора является новая последовательность чисел, представляющих собой отсчеты выходного сигна-
ла. Аналоговый выходной сигнал sвых (t ) восстанавливается по этой последователь-
ности чисел с помощью цифроаналогового преобразователя (ЦАП; английский термин — Digital-to-Analog Converter, DAC). Напряжение на выходе ЦАП имеет ступенчатую форму (это также показано на рис. 3.2); при необходимости оно может быть преобразовано в плавно меняющийся выходной сигнал с помощью сглаживающего фильтра Ф.
|
sвх(t) |
sвых(t) |
|||||||||
|
АЦП |
ЦП |
ЦАП |
Ф |
|||||||
{x0, x1, x2, …} {y0, y1, y2, …}
Рис. 3.2. Структурная схема системы цифровой обработки сигналов
Устройства, реализуемые с помощью структуры типа рис. 3.2, могут иметь самый разнообразный характер. В цифровой форме можно создавать фильтры, анализаторы спектра, нелинейные преобразователи сигналов и многое другое.
ЗАМЕЧАНИЕ
Использование входных и выходных сигналов в аналоговой форме (и, следовательно, наличие АЦП и ЦАП) не всегда является необходимым. Так, при реализации цифрового генератора сигналов не нужен входной аналоговый сигнал, а ЦАП может отсутствовать, если конечный результат необходим только в цифровой форме.
Частота Найквиста
Гармонический сигнал может быть адекватно представлен дискретными отсчетами, если его частота не превышает половины частоты дискретизации (эта частота называется частотой Найквиста (Nyquist frequency) — fN = fд 

ωN = ωд 

мости от соотношения между частотой дискретизируемого гармонического сигнала и частотой Найквиста возможны три случая.

1.Если частота гармонического сигнала меньше частоты Найквиста, дискретные отсчеты позволяют правильно восстановить аналоговый сигнал (рис. 3.3, а).
2.Если частота гармонического сигнала равна частоте Найквиста, то дискретные отсчеты позволяют восстановить аналоговый гармонический сигнал с той же частотой, но амплитуда и фаза восстановленного сигнала (он показан пунктирной линией) могут быть искажены (рис. 3.3, б). В худшем случае все дискретные отсчеты синусоиды могут оказаться равными нулю.
3.Если частота гармонического сигнала больше частоты Найквиста, восстановленный по дискретным отсчетам аналоговый сигнал (как и в предыдущем случае, он показан пунктирной линией) будет также гармоническим, но с иной частотой (рис. 3.3, в). Данный эффект носит название появления ложных частот (aliasing), мы еще вернемся к его рассмотрению в разд. «Спектр дискретного сигнала» этой главы.
а
б
в
Рис. 3.3. Дискретизация гармонических сигналов с разной частотой
ЗАМЕЧАНИЕ
Эффекты, связанные с дискретизацией периодических процессов, наглядно проявляются при кино- и видеосъемке вращающихся объектов (таких, например, как колеса автомобилей). Из-за недостаточно высокой частоты дискретизации (частоты смены кадров) быстро вращающееся колесо может выглядеть неподвижным либо медленно поворачивающимся (причем в любую сторону).
Спектр дискретного сигнала
Преобразование Фурье позволяет вычислить спектральную плотность сигнала, представляющего собой функцию (как правило, времени либо пространственных
координат). Дискретный же сигнал является последовательностью чисел, поэтому для анализа его спектра обычными (аналоговыми) средствами необходимо сопоставить этой последовательности некоторую функцию.
Традиционным способом такого сопоставления является представление отсчетов в виде дельта-функций с соответствующими множителями и задержками. Для последовательности отсчетов {x(k)} получится следующий сигнал:
|
∞ |
|
|
s(t) = ∑ x(k)δ(t − k) . |
(3.1) |
k =−∞
Преобразование Фурье линейно, спектр дельта-функции равен единице, а задержка сигнала во времени приводит к умножению спектра на комплексную экспоненту. Все это (см. разд. «Свойства преобразования Фурье» главы 1) позволяет сразу же записать спектр дискретного сигнала:
|
∞ |
|||||
|
(ω) = |
∑ x(k)e |
− jωk |
. |
(3.2) |
|
|
S |
k =−∞
Из этой формулы видно главное свойство спектра любого дискретного сигнала: спектр является периодическим, и его период в данном случае равен 2π (т. е. круговой частоте дискретизации, поскольку, составляя сигнал из дельта-функций, мы выбрали единичный интервал между ними, что дает ωд = 2π ):
Следует также обратить внимание на размерность спектральной функции дискретного сигнала: она совпадает с размерностью отсчетов. Это связано с тем, что дель- та-функции времени, из которых был составлен сигнал (3.1), имеют размерность частоты (см. разд. «Классификация сигналов» главы 1).
Формула (3.2) позволяет вычислить спектральную функцию по известным отсчетам x(k). При конечном числе ненулевых отсчетов этот расчет несложен; он может быть выполнен с помощью функции MATLAB freqz (подробнее об этой функции см.
разд. «Расчет частотных характеристик» главы 4).
Теперь рассмотрим несколько иную задачу. Пусть значения x(k) являются отсчетами аналогового сигнала s(t), взятыми с периодом T:
x(k) = s(kT).
Выясним, как в этом случае спектр дискретного сигнала (3.2) связан со спектром
|
аналогового сигнала |
(ω) . |
|
|
S |
Итак, мы рассматриваем дискретизированный сигнал в виде последовательности дельта-функций, «взвешенной» значениями отсчетов s(kT) аналогового сигнала s(t) (рис. 3.4):
|
∞ |
|
|
sд (t) = ∑ s(kT )δ(t − kT ) . |
(3.3) |
k =−∞

Рис. 3.4.
Дискретизированный сигнал в виде последовательности дельта-функций
ЗАМЕЧАНИЕ
Термин «дискретизированный» в данном контексте подчеркивает, что последовательность отсчетов получена именно в результате дискретизации аналогового сигнала.
Так как функция δ(t – kT) равна нулю всюду, кроме момента t = kT, можно заменить в выражении (3.3) константы s(kT) на исходный непрерывный сигнал s(t):
|
∞ |
|
|
sд (t) = s(t) ∑ δ(t − kT ) . |
(3.4) |
k =−∞
Далее заметим, что сумма, входящая в выражение (3.4), является периодическим сигналом, а потому может быть представлена в виде ряда Фурье. Коэффициенты этого ряда, согласно (1.12), равны
|
1 |
T / 2 |
− jωnt |
||||
|
C |
n |
= |
∫ |
δ(t)e |
||
|
T |
||||||
|
−T / 2 |
В формуле (3.5) было учтено, что в интервал интегрирования (–T/2, T/2) попадает только одна дельта-функция, соответствующая k = 0.
Таким образом, периодическая последовательность дельта-функций может быть представлена в виде комплексного ряда Фурье (1.10):
|
∞ |
1 |
∞ |
||
|
∑ δ(t − kT ) = |
∑ e jωnt , |
(3.6) |
||
|
k =−∞ |
T n=−∞ |
где ωn = 2πn
|
s(t) |
∞ |
1 |
∞ |
|||
|
sд |
(t) = |
∑ e jωnt = |
∑ s(t)e jωnt . |
|||
|
T |
n=−∞ |
T n=−∞ |
Умножение сигнала на exp( jωnt ) соответствует сдвигу спектральной функции на
ωn , поэтому спектр дискретизированного сигнала можно записать следующим образом:

|
144 |
Глава 3 |
||||
|
Таким образом, спектр дискретизированного сигнала представляет собой бесконеч- |
|||||
|
ный ряд сдвинутых копий спектра исходного непрерывного сигнала s(t) (рис. 3.5). |
|||||
|
Расстояние по частоте между соседними копиями спектра равно частоте дискрети- |
|||||
|
зации ωд = 2π T . |
|||||
|
. |
|||||
|
|Sд(ω)| |
|||||
|
–ωд |
–ωд/2 |
0 |
ωд/2 |
ωд |
ω |
|
Рис. 3.5. Спектр дискретизированного сигнала |
Следует также отметить, что из-за наличия в формуле (3.7) множителя 1/T спектр дискретизированного сигнала имеет размерность, совпадающую с размерностью сигнала (как уже говорилось, это связано с тем, что функция δ(t) имеет размерность частоты).
Характер спектра дискретизированного сигнала еще раз демонстрирует частотновременную дуальность преобразования Фурье:
периодический сигнал → дискретный спектр;
периодический спектр → дискретный сигнал.
Вначале данного раздела мы получили формулу (3.2), позволяющую рассчитать спектр последовательности отсчетов {x(k)}, никак не связывая эти отсчеты с аналоговым сигналом. Только что полученная формула (3.7) предполагает, что отсчеты {x(k)} получены путем дискретизации аналогового сигнала s(t), и показывает связь между спектрами дискретизированного и аналогового сигналов. Нужно подчеркнуть, что эти две формулы дают одинаковый результат.
Отсюда следует еще один важный факт. Соединить отсчеты {x(k)} для получения аналогового сигнала можно произвольным образом. В каждом случае аналоговый сигнал будет, разумеется, иметь свой спектр. Однако результат суммирования сдвинутых копий спектров по формуле (3.7) всегда будет одним и тем же, поскольку определяется только значениями дискретных отсчетов {x(k)} = {s(kT)} и формулой (3.2).
Рисунок 3.5 наглядно демонстрирует и способ восстановления непрерывного сигнала по дискретным отсчетам. Для этого необходимо пропустить дискретный сигнал через идеальный фильтр нижних частот (ФНЧ) с частотой среза, равной половине частоты дискретизации. АЧХ такого фильтра показана на рис. 3.5 пунктиром.
Очевидно, что точное восстановление сигнала возможно, если сдвинутые копии спектра не перекрываются. Из рис. 3.5 видно, что для этого необходимо, чтобы час-

тота дискретизации как минимум в два раза превышала верхнюю граничную частоту в спектре сигнала:
Спектральное представление дискретного сигнала позволяет объяснить появление
ложных частот (aliasing), речь о которых шла в разд. «Частота Найквиста» этой главы. Пусть дискретизации подвергается гармонический сигнал с частотой ω0 , превышающей частоту Найквиста, но меньшей частоты дискретизации. Спектр такого сигнала показан на рис. 3.6, сверху. Сдвинутые копии спектра, возникающие при дискретизации, создают попадающие в полосу восстановления (от нуля до частоты Найквиста) составляющие с частотой ωд − ω0 (рис. 3.6, снизу). Спектры, по-
лучающиеся после дискретизации гармонических сигналов с частотами ω0 и
ωд − ω0 , оказываются идентичными. Данный рисунок иллюстрирует в частотной
области процесс дискретизации гармонического сигнала, показанный ранее на рис. 3.3.
.
|Sа(ω)|
|
–ωд –ω0 |
0 |
ω0 |
ωд |
ω |
.
|Sд(ω)|
|
–2ωд+ω0 –ωд –ω0 –ωд+ω0 0 ωд–ω0 ω0 |
ωд 2ωд–ω0 ω |
Рис. 3.6. Спектры аналоговой (сверху) и дискретизированной (снизу) синусоиды
счастотой, превышающей частоту Найквиста
Вслучае произвольного сигнала, если условие (3.8) не выполняется, сдвинутые копии спектра будут накладываться друг на друга, что приведет к неизбежным искажениям при восстановлении непрерывного сигнала (рис. 3.7).
Эти искажения вызваны тем, что спектральные составляющие сигнала с частотами, превышающими частоту Найквиста, равную ωд 
правильно — вместо этого они вызывают наложение «хвостов» соседних сдвинутых копий спектра и появление ложных частот.
Если подлежащий дискретизации сигнал может содержать спектральные составляющие с частотами, превышающими частоту Найквиста, полезно предварительно пропустить его через ФНЧ с частотой среза, равной частоте Найквиста (рис. 3.8).

|
. |
|||||
|
|Sд(ω)| |
|||||
|
–ωд |
–ωд/2 |
0 |
ωд/2 |
ωд |
ω |
|
Рис. 3.7. Перекрытие сдвинутых копий спектра |
|||||
|
при недостаточно высокой частоте дискретизации |
|
. |
|||||
|
|Sа(ω)| |
|||||
|
–ωд |
–ωд /2 |
0 |
ωд/2 |
ωд |
ω |
|
а |
|||||
|
. |
|||||
|
|S‘а(ω)| |
|
–ωд |
–ωд /2 |
0 |
ωд/2 |
ωд |
ω |
|
б |
|||||
|
. |
|||||
|
|Sд(ω)| |
|||||
|
–ωд |
–ωд /2 |
0 |
ωд/2 |
ωд |
ω |
|
в |
Рис. 3.8. При дискретизации сигнала, содержащего высокочастотные составляющие (а), полезно пропустить его через ФНЧ (б), чтобы избежать появления ложных частот (в)
При этом все равно будут потеряны высокочастотные составляющие — сохранить их можно лишь путем повышения частоты дискретизации. Однако в этом случае благодаря отсутствию наложения «хвостов» не произойдет появления ложных частот и диапазон частот 0…ωд 
жений.
Влияние формы дискретизирующих импульсов
Запишем выражение (3.3) в более общей форме, используя вместо дельта-функций импульсы s0 (t) произвольной формы:
|
∞ |
|
|
sд (t) = ∑ s(kT )s0 (t − kT ) . |
(3.9) |
k =−∞
Получить выражение для спектральной функции сигнала (3.9) будет проще всего, если рассмотреть этот сигнал как результат прохождения последовательности дель- та-функций (3.3) через линейную стационарную систему с импульсной характеристикой s0 (t) . Действительно, при этом каждая из дельта-функций в (3.3) будет
порождать на выходе цепи сигнал s0 (t) с соответствующими временной задержкой и амплитудным множителем, так что в результате получится именно выражение (3.9).
Поскольку при прохождении сигнала через линейную систему с постоянными параметрами его спектр умножается на комплексный коэффициент передачи этой системы (см. главу 2), спектр сигнала (3.9) будет отличаться от выражения (3.7) лишь дополнительным множителем — спектром импульса s0 (t) :
|
(ω) |
∞ |
2πn |
|||||||
|
(ω) = |
S |
0 |
ω − |
||||||
|
Sд |
∑ S |
. |
(3.10) |
||||||
|
T |
n=−∞ |
T |
Итак, отличие формы дискретизирующих импульсов от дельта-функций вызывает мультипликативные искажения спектра дискретного сигнала. Спектральная функция импульса, имеющего конечную энергию, затухает с ростом частоты, поэтому возникающие при дискретизации сдвинутые копии спектра сигнала s(t) оказываются ослабленными.
Рассмотрим важный с практической точки зрения случай, когда s0 (t) представляет собой прямоугольный импульс с единичной амплитудой и длительностью, равной периоду дискретизации (рис. 3.9, слева). В данном случае дискретный сигнал приобретает ступенчатую форму, что характерно для сигнала на выходе ЦАП перед сглаживающим фильтром (см. рис. 3.2). Искажения спектра при этом описываются
множителем ( ) следующего вида:
S0 ω
|
∞ |
sin(ωT / 2) |
|||
|
(ω) = ∫ s0 |
(t)e− jωt dt = T |
e− jωT /2 . |
||
|
S0 |
||||
|
ωT / 2 |
−∞

.
|S0(ω)|
T
s0(t)
2T/π
1
|
0 |
T t |
− |
4π |
− |
2π π |
0 |
π 2π |
4π |
ω |
|
T − |
|||||||||
|
T |
T |
T T |
T |
Рис. 3.9. Прямоугольный дискретизирующий импульс (слева) и его амплитудный спектр (справа)
|
а |
||||||||||
|
. |
||||||||||
|
sд1(t) |
|Sд1(ω)| |
|||||||||
|
0 |
t |
0 |
ωд |
ω |
||||||||
|
б |
||||||||||||
|
. |
||||||||||||
|
sд2(t) |
|Sд2(ω)| |
|||||||||||
|
0 |
t |
0 |
ωд |
ω |
в
Рис. 3.10. Дискретизация треугольного импульса (слева — сигналы, справа — спектры): а — исходный аналоговый сигнал, б — дискретный сигнал в виде последовательности дельта-функций, в — ступенчатый сигнал (пунктирной линией показана форма амплитудного спектра дискретизирующих импульсов)
|
Дискретные сигналы |
149 |
|||||||
|
График модуля функции |
(ω) |
приведен на рис. 3.9, справа. Спад амплитудного |
||||||
|
S0 |
||||||||
|
спектра на частоте Найквиста, равной π/T, составляет |
||||||||
|
/ T ) | |
sin(π / 2) |
2 |
||||||
|
| S0 (π |
≈ 0, 637 ≈ −3,9 дБ . |
|||||||
|
= |
= |
|||||||
|
| S0 (0) | |
π / 2 |
π |
В качестве примера на рис. 3.10 приведены результаты дискретизации треугольного импульса дельта-функциями и рассмотренными прямоугольными импульсами.
Из графиков видно, что ЦАП сам по себе является фильтром нижних частот, однако с весьма невысокой степенью подавления сдвинутых копий спектра. Кроме того, поскольку АЧХ такого фильтра весьма далека от прямоугольной, он обладает сильной неравномерностью в полосе пропускания и заметно ослабляет высокочастотные составляющие сигнала (на частоте Найквиста ослабление составляет почти 4 дБ).
Теорема Котельникова
В начале данной главы уже было сформулировано утверждение о том, что некоторые сигналы могут быть без потерь информации представлены своими дискретными отсчетами. Полученное в предыдущем разделе выражение для спектра дискретизированного сигнала позволяет выделить тот класс сигналов, для которых это возможно, и описать способ такого восстановления.
Согласно (3.7), спектр дискретизированного сигнала представляет собой сумму сдвинутых копий спектра исходного сигнала, при этом шаг сдвига равен частоте дискретизации ωд . Из рис. 3.5 видно, что если в спектре аналогового сигнала не
содержится составляющих с частотами, превышающими частоту Найквиста ( ωд 
пользование идеального ФНЧ с прямоугольной АЧХ позволит выделить исходную (несдвинутую) копию спектра, сосредоточенную в окрестностях нулевой частоты, и, таким образом, в точности восстановить исходный аналоговый сигнал.
АЧХ идеального ФНЧ, восстанавливающего аналоговый сигнал, приведена на рис. 3.11, слева. Коэффициент передачи в полосе пропускания равен T, а не единице, чтобы компенсировать множитель 1/T в формуле (3.7). С помощью обратного преобразования Фурье найдем импульсную характеристику фильтра (рис. 3.11, справа):
|
π |
t |
|||||
|
sin |
||||||
|
h(t) = |
T |
. |
(3.11) |
|||
|
π |
t |
|||||
T
Дискретизированный сигнал (3.3) представляет собой сумму дельта-функций. При прохождении такого сигнала через восстанавливающий ФНЧ каждая дельтафункция породит на выходе соответствующим образом сдвинутую и масштабиро-

ванную копию импульсной характеристики фильтра. Выходной сигнал (в точности соответствующий исходному аналоговому сигналу), таким образом, будет представлять собой сумму сдвинутых и умноженных на отсчеты сигнала копий импульсных характеристик идеального ФНЧ (3.11):
|
π |
t − kT |
|||||
|
sin |
||||||
|
s(kT ) |
T |
. |
(3.12) |
|||
|
π |
t − kT |
|||||
T
h(t)
K ω
T
|
–π/T |
0 |
π/T ω |
t |
||||||||||
|
–2T –T |
0 T 2T |
Рис. 3.11. Амплитудно-частотная (слева) и импульсная (справа) характеристики идеального восстанавливающего фильтра
Подводя итог всему сказанному, сформулируем теорему Котельникова: любой сигнал s(t), спектр которого не содержит составляющих с частотами выше некоторого значения ωв = 2πfв , может быть без потерь информации представлен своими дискретными отсчетами {s(kT)}, взятыми с интервалом T, удовлетворяющим следующему неравенству:
|
T ≤ |
1 |
= |
π |
. |
(3.13) |
|
2 fв |
|||||
|
ωв |
Восстановление исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(kT)} производится по формуле (3.12).
ЗАМЕЧАНИЕ
В зарубежных источниках данная теорема называется теоремой Найквиста (Nyquist theorem), теоремой Шеннона (Shannon theorem) или теоремой дискретизации (sampling theorem).
Формула (3.12) представляет собой разложение сигнала s(t) в ряд по системе функций {ϕk (t )} , называемой базисом Котельникова:
|
π |
||||||
|
sin |
(t − kT ) |
|||||
|
ϕk (t) = |
T |
. |
||||
|
π |
||||||
|
(t − kT ) |
||||||
T
Формирование непрерывного сигнала по его дискретным отсчетам поясняет рис. 3.12. Пунктиром показаны графики отдельных слагаемых формулы (3.12),

сплошной линией — восстановленный сигнал. Далее приводится код MATLAB, использованный при построении рисунка:
|
>> t = -2:0.01:6; |
% время для восстановленного сигнала |
||
|
>> td = -2:6; |
% номера отсчетов |
||
|
>> s = [0 0 |
4 3 2 |
1 0 0 0]; |
% дискретный сигнал |
|
>> d = [td’ |
s’]; |
% данные для функции pulstran |
>>y = pulstran(t, d, ‘sinc’); % восстановленный сигнал
>>plot(td, s, ‘o’, t, y) % график восстановленного сигнала
|
>> hold on |
% выводим графики отдельных sinc-импульсов |
>>for k=1:length(s), plot(t, s(k)*sinc(t-td(k)), ‘:’), end
>>hold off
|
5 |
||||||||
|
4 |
||||||||
|
3 |
||||||||
|
2 |
||||||||
|
1 |
||||||||
|
0 |
||||||||
|
-1 |
||||||||
|
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Рис. 3.12. Восстановление непрерывного сигнала по его дискретным отсчетам
ЗАМЕЧАНИЕ
При построении рис. 3.12 была использована функция pulstran. Она позволяет сформировать сигнал в виде суммы конечного числа импульсов произвольной формы с заданными задержками и множителями, что делает ее очень удобной при построении графиков сигналов, восстановленных по дискретным отсчетам согласно теореме Котельникова. Эта функция подробно рассмотрена далее в разд. «Генерация последовательности импульсов» этой главы.
Рисунок 3.12 наглядно демонстрирует главное свойство сигнала с ограниченным спектром — его бесконечность во времени. Хотя отличны от нуля лишь несколько отсчетов показанного сигнала, аналоговый сигнал оказывается бесконечно колеблющимся — между нулевыми отсчетами (на рисунке это отсчеты с номерами −2, −1, 4, 5, 6) его значения отличны от нуля. Эти колебания нигде не заканчиваются, хотя их амплитуда стремится к нулю.
Иногда можно встретить примерно следующее «объяснение» сущности теоремы Котельникова: «если брать отсчеты достаточно часто, в промежутках между ними сигнал с ограниченным спектром не успеет сильно измениться, и мы сможем точно

восстановить его». Такая трактовка является принципиально неправильной. Замечательное обсуждение этого вопроса содержится в [6], здесь же ограничимся краткими пояснениями и одним примером.
Когда мы говорим об ограниченной полосе частот сигнала, имеется в виду спектральная функция всего сигнала, имеющего бесконечную длительность. При этом
мгновенные спектры отдельных фрагментов сигнала могут содержать сколь угодно высокие частоты.
ЗАМЕЧАНИЕ
Под мгновенным спектром подразумевается спектральная функция «вырезанного» из сигнала фрагмента конечной длительности.
Вчастности, в отдельном промежутке между соседними отсчетами сигнал с ограниченным спектром может иметь сколь угодно сложную форму, например произвольное число раз менять знак.
Вкачестве примера восстановим по формуле (3.12) непрерывный сигнал на основе последовательности, содержащей четыре ненулевых отсчета: …, 0, 0, 30, 1, −1, −30, 0, 0, … (рис. 3.13):
|
>> t = 0:0.01:8; |
% время для восстановленного сигнала |
|
>> td = 2:5; |
% номера ненулевых отсчетов |
|
>> s = [30 1 -1 -30]; |
% дискретный сигнал |
|
>> d = [td’ s’]; |
% данные для функции pulstran |
>>y = pulstran(t, d, ‘sinc’); % восстановленный сигнал
>>plot(td, s, ‘o’, t, y)
>>grid
|
40 |
||||||||
|
30 |
||||||||
|
20 |
||||||||
|
10 |
||||||||
|
0 |
||||||||
|
-10 |
||||||||
|
-20 |
||||||||
|
-30 |
||||||||
|
-40 |
||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Рис. 3.13. Сигнал с ограниченным спектром, содержащий фрагмент |
||||||||
|
с колебаниями высокой частоты |
Результат, показанный на рис. 3.13, свидетельствует о том, что фрагмент восстановленного сигнала между 3 и 4 отсчетами представляет собой колебание с перио-
дом, равным интервалу дискретизации (т. е. с частотой, вдвое превышающей частоту Найквиста!). Однако весь сигнал, составленный из сдвинутых функций базиса Котельникова, не содержит спектральных составляющих с частотами, большими частоты Найквиста.
ЗАМЕЧАНИЕ
Подобным образом можно получить произвольное число колебаний сигнала между двумя его соседними отсчетами, однако значения остальных отсчетов при этом быстро возрастают. Например, чтобы получить между отсчетами полтора колебания вместо одного, можете повторить приведенный пример, использовав следующую последовательность значений: {600, 360, 1, 1, 360, 600}. Чтобы увидеть колебания сигнала между единичными отсчетами, придется увеличить масштаб отображения этого фрагмента графика.
Восстановление радиосигнала по отсчетам видеосигнала
Если для восстановления сигнала воспользоваться не ФНЧ, а идеальным полосовым фильтром со средней частотой nωд и шириной полосы пропускания, равной ωд ,
|
будет выделена пара сдвинутых копий спектра |
(ω ± |
2πn |
) . Из свойств преобразо- |
|
|
S |
||||
|
T |
вания Фурье (см. формулу (1.24) в разд. «Умножение сигнала на гармоническую функцию» главы 1) следует, что такой спектр соответствует радиосигналу вида
|
sр (t) = 2s(t) cos(nωдt) |
(3.14) |
(предполагается, что условие теоремы Котельникова выполнено и сдвинутые копии спектра не перекрываются). Таким образом, с помощью полосового фильтра можно из дискретных отсчетов видеосигнала получить аналоговый радиосигнал.
Импульсная характеристика идеального полосового фильтра с указанными параметрами имеет вид
|
π |
||||||||
|
sin |
t |
2πn |
||||||
|
h(t) = |
T |
|||||||
|
cos |
t . |
|||||||
|
π |
||||||||
|
T |
||||||||
|
t |
||||||||
|
T |
Поэтому во временной области формирование радиосигнала по отсчетам видеосигнала описывается следующим образом:
|
π |
||||||
|
sin |
(t − kT ) |
|||||
|
T |
||||||
|
s(kT ) |
cos |
|||||
|
π |
||||||
|
(t − kT ) |
||||||

|
154 |
Глава 3 |
|
ЗАМЕЧАНИЕ |
|
|
В формулах (3.14) и (3.15) имеется множитель |
cos(nω t) , что свидетельствует |
|
д |
о чисто амплитудной модуляции получаемого радиосигнала. Подробнее о модуляции см. в главе 8.
Квадратурная дискретизация узкополосных сигналов
Пусть дискретизации необходимо подвергнуть узкополосный сигнал, который в общем случае может иметь как амплитудную, так и угловую модуляцию:
s(t) = A(t) cos(ω0t + ϕ(t)) ,
где ω0 — несущая частота, A(t) и ϕ(t) — законы амплитудной и фазовой модуляции соответственно, представляющие собой медленно (по сравнению с cos(ω0t ) ) меняющиеся функции.
Частоту дискретизации для такого сигнала можно выбрать исходя непосредственно из теоремы Котельникова, при этом она должна быть не меньше, чем 2(ω0 + Δω
другой вариант (правда, требующий предварительной обработки сигнала) — квадратурная дискретизация.
Запишем аналитический сигнал для s(t) (аналитический сигнал рассмотрен в
разд. «Комплексная огибающая» главы 1):
s(t) = A(t)e jϕ(t )e jω0t .
Информация, переносимая сигналом, заключена в его комплексной огибающей
Спектр этого комплексного сигнала занимает полосу частот –Δω/2…Δω/2. Поэтому, согласно теореме Котельникова, минимально допустимая частота дискретизации для этого сигнала равна Δω, что значительно меньше, чем в случае прямой дискретизации. Однако отсчеты такого сигнала, естественно, будут комплексными.
Рис. 3.14. Квадратурная дискретизация
Рассмотрим способ реализации квадратурной дискретизации (рис. 3.14). Входной сигнал умножается на колебания двух генераторов (гетеродинов, heterodyne) с час-

тотой ω0 , сдвинутые по фазе друг относительно друга на 90° — cos ω0t и −sin ω0t . Результат каждого из умножений содержит две составляющие — низкочастотную и высокочастотную (на частоте 2ω0 ):
s(t)cos ω0t = A(t) cos(ω0t + ϕ(t)) cosω0t =
|
1 |
A(t) cos ϕ(t) + |
1 |
A(t) cos(2ω0t + ϕ(t)) = |
||||
|
= |
|||||||
|
2 |
|||||||
|
2 |
|||||||
|
1 |
1 |
||||||
|
= |
Re A(t) + |
A(t) cos(2ω0t + ϕ(t)), |
|||||
|
2 |
|||||||
|
2 |
|||||||
|
−s(t)sin ω0t = −A(t)cos (ω0t + ϕ(t))sin ω0t = |
|||||||
|
1 |
A(t)sin ϕ(t) − |
1 |
A(t) cos(2ω0t − ϕ(t)) = |
||||
|
= |
|||||||
|
2 |
|||||||
|
2 |
|||||||
|
1 |
1 |
A(t) cos(2ω0t − ϕ(t)). |
|||||
|
= |
Im A(t) − |
||||||
|
2 |
|||||||
|
2 |
Таким образом, для получения вещественной и мнимой частей комплексной огибающей сигнала нужно после перемножения пропустить результаты через фильтры нижних частот, чтобы устранить вторую гармонику несущей. Полученные в ре-
|
зультате сигналы, пропорциональные |
и |
||
|
Re A(t) |
Im A(t) , подвергаются дискретиза- |
||
|
ции с частотой не ниже, чем |
Δω 2 = Δω .
2
ЗАМЕЧАНИЕ
Данная процедура сдвига спектра сигнала путем умножения его на опорное гармоническое колебание с последующим выделением нужных спектральных составляющих с помощью фильтра называется гетеродинированием (heterodyning).
Рассмотренная схема получила широкое распространение при обработке радиосигналов. Квадратурное гетеродинирование просто и дешево реализуется аналоговыми средствами, цифровая часть благодаря низкой частоте дискретизации также оказывается сравнительно несложной.
Субдискретизация сигнала
В предыдущем разделе мы видели, как квадратурная обработка позволяет дискретизировать полосовой сигнал с частотой, определяемой не верхней границей, а шириной спектра сигнала. Однако в ряде случаев возможен и другой подход, когда с пониженной частотой дискретизируется сам исходный сигнал, без предварительной обработки. Рассмотрим подробнее идею этого метода, называемого субдискретизацией (undersampling) или преобразованием частоты на АЦП.
Итак, пусть аналоговый полосовой сигнал имеет спектр, расположенный в диапазоне между частотами f1 и f2 (рис. 3.15, а; не будем забывать и о симметричной

половине спектра в области отрицательных частот). При обычном подходе частота дискретизации должна превышать 2 f2 . В результате возникающие при дискрети-
зации сдвинутые копии спектра сигнала расположатся так, как показано на рис. 3.15, б. Однако для точного восстановления сигнала по его дискретным отсчетам нам необходимо лишь обеспечить отсутствие перекрытия сдвинутых копий спектра. В данном случае это дает дополнительные возможности для выбора частоты дискретизации (рис. 3.15, в). Восстановление сигнала в данном случае, естественно, должно производиться с помощью полосового фильтра, а не ФНЧ (АЧХ восстанавливающих фильтров показаны на рис. 3.15, б, в пунктиром).
.
|Sа(ω)|
а
.
|Sд(ω)|
б
.
|Sд(ω)|
в
Рис. 3.15. Спектр аналогового сигнала (а), дискретного сигнала при обычной дискретизации (б) и при субдискретизации (в)
Определим условия, при которых возможна дискретизация сигнала таким образом. При некотором целом k зеркальная половина спектра должна оказаться расположена между k-й и (k + 1)-й сдвинутыми копиями спектра (рис. 3.16).
Из этого рисунка сразу же видна нижняя граница для частоты дискретизации: fд > 2( f2 − f1) . Таким образом, в отличие от случая квадратурной дискретизации,
в данном варианте частота дискретизации ограничена снизу удвоенной шириной спектра сигнала. Кроме того, из рис. 3.16 мы получаем пару неравенств:
−f1 + k fд < f1 ,
−f2 + (k +1) fд > f2 .

fд
f2–f1 f2–f1
Рис. 3.16. Условия, необходимые для субдискретизации сигнала
|
f1 |
f2 |
f |
|
–f2+kfд –f1+kfд |
–f2+(k+1)fд |
–f1+(k+1)fд |
Выразив из них частоту дискретизации, получаем для нее двойное неравенство:
|
2 f2 |
< fд |
< |
2 f1 |
. |
(3.16) |
|
|
k +1 |
||||||
|
k |
Чтобы этот диапазон существовал, правая часть неравенства должна быть больше левой:
2 f1 > 2 f2 . k k +1
Отсюда получаем ограничение на возможные значения k:
|
k < |
f1 |
. |
(3.17) |
|
|
f2 − f1 |
||||
|
В качестве примера рассмотрим дискретизацию |
сигнала со средней частотой |
50 МГц и шириной полосы 10 МГц. Границы занимаемой сигналом полосы частот
|
в этом случае равны |
f1 = 45 МГц и |
f2 = 55 МГц, а минимальное значение k, со- |
|||||||||
|
гласно (3.17), определяется следующим неравенством: |
|||||||||||
|
k < |
f1 |
= |
45 |
= 4,5 . |
|||||||
|
f2 − f1 |
10 |
||||||||||
|
Для удовлетворяющих неравенству |
целочисленных значений k = 1…4, согласно |
||||||||||
|
(3.16), имеем следующие диапазоны возможных частот дискретизации: |
|||||||||||
|
k = 1: fд |
= |
2 55 |
2 |
45 |
МГц = 55…90 МГц; |
||||||
|
… |
|||||||||||
|
2 |
1 |
||||||||||
|
k = 2: fд |
= |
2 55 |
2 |
45 |
МГц = 36,67…45 МГц; |
||||||
|
… |
|||||||||||
|
3 |
2 |
||||||||||
|
k = 3: fд |
= |
2 55 |
2 |
45 |
МГц = 27,5…30 МГц; |
||||||
|
… |
|||||||||||
|
4 |
3 |
||||||||||
|
k = 4: fд |
= |
2 55 |
2 |
45 |
МГц = 22…22,5 МГц. |
||||||
|
… |
|||||||||||
|
5 |
4 |

На рис. 3.17 показаны спектры дискретизированного сигнала, получающиеся при выборе частот дискретизации, равных 75 МГц (k = 1), 40 МГц (k = 2), 29 МГц (k = 3), 22,25 МГц (k = 4). Внутри полос частот, занимаемых копиями спектра, подписаны номера этих копий (индекс n из формулы (3.7)).
|
–1 |
–2 |
0 |
–1 |
1 |
0 |
2 |
1 |
||||||||||||
|
–2 |
–4 |
–1 |
–3 |
0 |
–2 |
1 |
–1 |
2 |
0 |
3 |
1 |
4 |
2 |
||||||||||
|
–3 |
–6 |
–2 |
–5 |
–1 |
–4 |
0 |
–3 |
1 |
–2 |
2 |
–1 |
3 |
0 |
4 |
1 |
5 |
2 |
6 |
3 |
|||||||||
|
–4 |
–8 –3 –7 |
–2 |
–6 |
–1 |
–5 |
0 |
–4 |
1 |
–3 |
2 |
–2 |
3 |
–1 |
4 |
0 |
5 |
1 |
6 |
2 |
7 |
3 |
8 |
4 |
Рис. 3.17. Спектр субдискретизированного сигнала при выборе частот дискретизации, соответствующих различным значениям k (сверху вниз):
k = 1, fд = 75 МГц; k = 2, fд = 40 МГц; k = 3, fд = 29 МГц;
k = 4, fд = 22,25 МГц
ЗАМЕЧАНИЕ
Значение k = 0, исходя из (3.16), дает диапазон частоты дискретизации от 2f2 до бесконечности и, таким образом, соответствует обычной дискретизации сигнала согласно теореме Котельникова.
Если после субдискретизации восстановить аналоговый сигнал обычным образом (с помощью идеального ФНЧ с частотой среза, равной частоте Найквиста), получится полосовой сигнал с той же или комплексно-сопряженной комплексной огибающей, что у исходного сигнала, но с более низкой средней частотой ω′0 , определяемой следующим образом:
|
Дискретные сигналы |
159 |
||||
|
если k четно, то ω′0 |
= ω0 |
− |
k |
ωд |
и комплексная огибающая сигнала не меняется; |
|
2 |
|
если k нечетно, то ω′0 |
= |
k +1 |
ωд − ω0 , а комплексная огибающая сигнала стано- |
|
2 |
вится комплексно-сопряженной.
Z-преобразование
Удобным способом анализа дискретных последовательностей является z-преобра- зование (z-transform). Смысл его заключается в том, что последовательности чисел {x(k)} ставится в соответствие функция комплексной переменной z, определяемая следующим образом:
|
∞ |
|
|
X (z) = ∑ x(k)z−k . |
(3.18) |
k =−∞
Разумеется, функция X(z) определена только для тех значений z, при которых ряд (3.18) сходится.
Z-преобразование играет для дискретных сигналов и систем такую же роль, как преобразование Лапласа — для аналоговых. Определяющим при этом является тот факт, что, как мы увидим в главе 4, z-преобразование импульсной характеристики дискретной системы является дробно-рациональной функцией переменной z.
Примеры вычисления z-преобразования
Вычислим z-преобразование для некоторых часто встречающихся на практике дискретных сигналов.
Единичная импульсная функция
Единичная импульсная функция является дискретным аналогом дельта-функции (см. разд. «Классификация сигналов» главы 1) и представляет собой одиночный отсчет с единичным значением:
|
1, |
k = 0, |
|
|
x0 (k) = {0, |
k ≠ 0. |
(3.19) |
Расчет его z-преобразования не представляет сложности:
∞
X 0 (z) = ∑ x0 (k)z−k = 1 z−0 = 1 .
k =−∞
Функция X0 ( z) сходится на всей комплексной плоскости.

Единичный скачок
Дискретный единичный скачок по смыслу полностью соответствует своему аналоговому прообразу (см. разд. «Классификация сигналов» главы 1):
|
0, |
k < 0, |
|
x(k) = {1, |
k ≥ 0. |
Используя определение z-преобразования (3.18), получаем
∞∞
|
X (z) = ∑ x(k)z−k |
= ∑1 z−k . |
(3.20) |
|
k =−∞ |
k =0 |
Ряд (3.20) является суммой бесконечной геометрической прогрессии с первым чле-
|
ном 1 z−0 = 1 и знаменателем z−1 . Как известно, такой ряд сходится при |
z−1 |
<1, |
|||
|
т. е. при |z| > 1, и его сумма равна |
|||||
|
X (z) = |
1 |
. |
(3.21) |
||
|
− z |
−1 |
||||
|
1 |
ЗАМЕЧАНИЕ
Можно записать результат и в виде X(z) = z/(z – 1), но в теории дискретных сигналов принято использовать отрицательные степени z.
Дискретная экспоненциальная функция
Дискретная экспоненциальная функция определяется следующим образом:
|
0, |
k < 0, |
||
|
x(k) = |
k |
, |
k ≥ 0. |
|
a |
Для вычисления z-преобразования нужно вычислить сумму следующего ряда:
|
∞ |
∞ |
∞ |
|
X (z) = ∑ x(k) z−k |
= ∑ak z−k |
= ∑(a−1z)−k . |
|
k =−∞ |
k =0 |
k =0 |
Как и в предыдущем случае, этот ряд представляет собой сумму геометрической прогрессии. Первый член равен 1, знаменатель равен az−1 . Таким образом, ряд сходится при az−1 <1, т. е. при |z| > |a|, а его сумма равна
|
X (z) = |
1 |
. |
(3.22) |
||
|
− az |
−1 |
||||
|
1 |
Дискретная затухающая синусоида
Последняя из рассматриваемых здесь дискретных последовательностей представляет собой отсчеты синусоиды с произвольными частотой и начальной фазой и экспоненциально меняющейся амплитудой:
x(k) = ak cos(ωk + ϕ) .

Для вычисления z-преобразования можно представить косинус по формуле Эйлера в виде полусуммы двух комплексных экспонент, а потом воспользоваться уже готовым результатом (3.22):
cos ϕ − a cos(ω − ϕ)z−1
X (z) = .
1 − 2a cos ω z−1 + a2 z−2
Так же, как и в случае дискретной экспоненты, ряд сходится при |z| > |a|.
Связь z-преобразования
с преобразованиями Лапласа и Фурье
Дискретное z-преобразование очень просто связано с преобразованиями Лапласа и Фурье. Рассмотрим последовательность, определенную при k ≥ 0, и сопоставим ей временной сигнал в виде набора дельта-функций:
|
∞ |
|||
|
s(t) = ∑x(k)δ(t − kT ) , |
(3.23) |
||
|
k =0 |
|||
|
где T — интервал дискретизации. Преобразование Лапласа для сигнала (3.23) |
|||
|
равно: |
|||
|
∞ |
∞ ∞ |
∞ |
∞ |
|
S( p) = ∫s(t)e− pt dt = ∫∑ x(k)δ(t − kT )e pt dt = ∑ x(k)∫δ(t − kT )e− pt dt . |
|||
|
0 |
0 k =0 |
k =0 |
0 |
Воспользовавшись фильтрующим свойством дельта-функции (см. формулу (1.2) в разд. «Классификация сигналов» главы 1), получим
∞
S( p) = ∑x(k)e− pkT .
k =0
Эта формула переходит в формулу (3.18), определяющую z-преобразование, если выполнить подстановку z = e pT .
Таким образом, взаимное соответствие между z-преобразованием X(z) и преобразованием Лапласа S(p) описывается следующим образом:
|
1 |
|||
|
X (z) = S |
ln z |
, S( p) = X (e pT ) . |
|
|
T |
Похожими формулами описывается и связь z-преобразования X(z) с преобразовани-
ем Фурье ( ) (заметим, что при рассмотрении этой связи нет необходимости счи-
S ω
тать последовательность односторонней):
|
1 |
|||||||
|
X (z) = S |
ln z , |
S |
(ω) = X (e jωT ) . |
(3.24) |
|||
|
jT |
Свойства z-преобразования
Тесная связь z-преобразования с преобразованиями Фурье и Лапласа обусловливает и подобие свойств этих преобразований. Однако имеется и некоторая специфика, возникающая из-за дискретного характера рассматриваемых сигналов.
Линейность
Z-преобразование, согласно определению (3.18), является линейной комбинацией отсчетов последовательности, поэтому оно подчиняется принципу суперпозиции:
если {x1(k)} ↔ X1(z) и {x2 (k)} ↔ X2 (z) ,
то {ax1(k) + bx2 (k)} ↔ aX1(z) + bX 2 (z) .
Задержка
Если z-преобразование последовательности {x(k)} равно X(z), то z-преобразование последовательности, задержанной на k0 тактов ( y(k) = x(k − k0 ) ), будет иметь вид
∞∞
Y (z) = ∑ y(k)z−k = ∑ x(k − k0 )z−k =
= z−k0 ∑ x(k − k0 ) z−(k −k0 ) = z−k0 ∑ x(n)z−n = X (z) z−k0 .
k =−∞ n=−∞
Таким образом, при задержке последовательности на k0 тактов необходимо умно-
жить ее z-преобразование на z−k0 . Множитель z−k0 является оператором задержки дискретной последовательности на k0 тактов.
Свертка
Свертка двух бесконечных дискретных последовательностей {x1(k)} и {x2 (k)} определяется следующим образом:
∞
y(k) = ∑ x1(n) x2 (k − n) .
n=−∞
Вычислим z-преобразование для последовательности {y(k)}:
|
∞ |
∞ |
∞ |
|||
|
Y (z) = ∑ y(k)z−k = ∑ |
∑ x1 (n) x2 (k − n) z |
||||
|
k =−∞ |
k =−∞ n=−∞ |
||||
|
∞ |
∞ |
(n)x2 (k − n)z−n z−(k −n) |
|||
|
= ∑ |
∑ x1 |
= |
|||
|
k =−∞ |
n=−∞ |
||||
|
∞ |
∞ |
||||
|
= ∑ |
x1 (n)z−n ∑ x2 (k − n)z−(k −n) |
= |
|||
|
n=−∞ |
k =−∞ |
||||
|
X2 ( z) |
∞
= X 2 ( z) ∑ x1 (n)z−n = X1 (z) X 2 (z).
n=−∞
Итак, свертке дискретных последовательностей соответствует произведение их z-преобразований.
ЗАМЕЧАНИЕ
Рассматриваемая здесь свертка бесконечных дискретных последовательностей называется линейной сверткой; ее не следует путать с круговой сверткой периодических последовательностей, речь о которой пойдет при описании свойств дискретного преобразования Фурье в главе 5.
Чередование знаков сигнала
Пусть у элементов исходной последовательности с нечетными номерами изменен знак: {x(0), − x(1), x(2), − x(3), x(4), …}. Элементы такой последовательности можно
записать как y(k) = x(k) (−1)−k , поэтому найти ее z-преобразование оказывается очень легко:
|
∞ |
∞ |
|
Y (z) = ∑ x(k)(−1)−k z−k |
= ∑ x(k)(−z)−k = X (−z) . |
|
k =−∞ |
k =−∞ |
Итак, чередование знаков сигнала приводит к смене знака у аргумента z-преобра- зования.
Если изменить знаки у элементов последовательности с четными номерами, это будет соответствовать простому изменению знака у последовательности, рассмотренной ранее, а z-преобразование, соответственно, окажется равным −X(−z).
Инвертирование последовательности во времени
Пусть последовательность {y(k)} связана с последовательностью {x(k)} следующим образом:
y(k) = x(−k) .
Тогда z-преобразование последовательности {y(k)} будет иметь вид
∞ ∞ ∞
Y (z) = ∑ x(−k)z−k = ∑ x(m)zm = ∑ x(m)(z−1)−m = X (z−1) .
k=−∞ m=−∞ m=−∞
Итак, инверсия последовательности отсчетов во времени соответствует замене z на 1/z в формуле ее z-преобразования.
Вставка нулей
Пусть последовательность {y(k)} получается из последовательности {x(k)} путем вставки N – 1 нулей между соседними элементами:
|
x(k / N), k = Nm, где m — любое целое число, |
|
|
y(k) = {0, |
k ≠ Nm. |

164 Глава 3
Найдем z-преобразование:
|
∞ |
∞ |
∞ |
|
Y (z) = ∑ y(k)z−k = ∑ x(m)z−Nm = ∑ x(m)(zN )−m = X (zN ) . |
||
|
k =−∞ |
m=−∞ |
m=−∞ |
Таким образом, рассматриваемая вставка нулей соответствует замене z на zN в формуле z-преобразования.
Обратное z-преобразование
Соответствие между дискретной последовательностью чисел и ее z-преобразова- нием является взаимно-однозначным. Формула перехода от z-преобразования к последовательности чисел называется обратным z-преобразованием и формально записывается следующим образом:
|
x(k) = |
1 |
X (z)zk −1dz . |
(3.26) |
|
j2π |
∫ |
Интеграл в (3.26) берется по произвольному замкнутому контуру, расположенному в области сходимости функции X(z) и охватывающему все ее полюсы.
Практическое вычисление обратного z-преобразования чаще производится путем разложения функции X(z) на простые дроби. Поясним это на несложном примере. Пусть
|
X (z) = |
1 |
. |
|||
|
1 |
z−2 − |
3 |
z−1 +1 |
||
|
2 |
2 |
Представим X(z) в виде суммы простых дробей:
|
X (z) = |
1 |
2 |
1 |
. |
(3.27) |
|||||||||||||
|
= |
− |
|||||||||||||||||
|
− |
−1 |
)(1 |
− |
1 |
−1 |
) |
1 − z−1 |
− |
1 |
−1 |
||||||||
|
(1 |
z |
2 z |
1 |
2 z |
Из сравнения слагаемых (3.27) с примерами z-преобразований (3.21) и (3.22) видно, что первое слагаемое соответствует скачку с амплитудой, равной 2, а второе —
дискретной показательной функции −2−k , k ≥ 0. Итак, искомая последовательность имеет вид:
|
2 − 2−k , |
k ≥ 0, |
|
x(k) = |
k < 0. |
|
0, |
ЗАМЕЧАНИЕ
Чтобы рассчитать обратное z-преобразование, кроме функции X(z) нужно задать область ее определения. Результат, полученный в данном примере, соответствует области определения |z| > 1. При области определения |z| < 1/2 получится последовательность, экспоненциально затухающая в направлении отрицательных номеров отсчетов k.

Пространство дискретных сигналов
Для дискретных сигналов можно ввести те же понятия, что были рассмотрены в
разд. «Пространство сигналов» главы 1 применительно к сигналам аналоговым. При этом формулы соответствующим образом модифицируются — интегралы превращаются в суммы. Приведем получающиеся при этом основные выражения. Для большей общности в них предполагается, что дискретный сигнал x(k) является комплексным, а диапазон индексов при суммировании не указывается (этот диапазон может быть как конечным, так и бесконечным):
p-метрика и ее частные случаи:
d p ( x, y) = p ∑ x(k) − y(k) p ,
k
d1( x, y) = ∑ x(k) − y(k) ,
k
d2 ( x, y) = ∑ x(k) − y(k) 2 ,
k
d∞ (x, y) = max x(k) − y(k) ;
k
p-норма и ее частные случаи:




k


x= max x(k) ;
∞k
скалярное произведение:
(x, y) = ∑x(k) y * (k) .
k
Дискретные случайные сигналы
Когда дискретизации подвергается случайный процесс, получаемая последовательность отсчетов будет зависеть от конкретной реализации дискретизируемого процесса, и, следовательно, она должна анализироваться статистическими методами.
Что касается одномерной плотности вероятности и связанных с ней статистических характеристик, здесь нет никаких отличий от случая аналогового сигнала — просто возможные одномерные сечения случайного процесса соответствуют моментам
|
166 |
Глава 3 |
|
дискретизации: |
t1 = kT , и поэтому для привязки статистических параметров ко |
времени можно использовать номер отсчета: px ( x, k) , mx (k) и т. д.
Двумерные сечения дискретного случайного процесса также могут браться только в моменты дискретизации: t1 = kT , t2 = nT . Поэтому двумерная плотность вероятности и связанные с ней характеристики случайного процесса зависят от двух номеров отсчетов k и n: px ( x1, x2 , k, n) , Rx (k, n) и т. д.
В случае стационарного в широком смысле случайного процесса одномерные характеристики не зависят от момента времени (номера отсчета), а двумерные зависят лишь от промежутка между моментами времени (в дискретном случае — от разности номеров отсчетов k = k − n):
px ( x, k) = px ( x) , mx (k) = mx , Dx (k) = Dx ,
px ( x1, x2 , k, n) = px ( x1, x2 , k) , Rx (k, n) = Rx ( k) .
Таким образом, для стационарного дискретного случайного процесса корреляционная функция является дискретной, т. е. представляет собой последовательность чисел {Rx ( k)} .
В общем случае Rx (k, n) = Rx* (n, k) ; для вещественного случайного процесса
Rx (k, n) = Rx (n, k) , а если процесс еще и стационарный, то Rx (−k) = Rx (k) .
Корреляционная матрица
Во многих задачах необходимо рассматривать конечный во времени фрагмент случайного процесса длиной N отсчетов. В этом случае корреляционная функция Rx (k, n) может быть представлена в виде матрицы, называемой корреляционной
матрицей случайного процесса (для простоты будем считать, что случайный процесс имеет нулевое математическое ожидание):
|
x(0)x(0) |
x(0)x(1) |
x(0)x(N −1) |
||||||||||||||
|
x(1)x(0) |
x(1)x(1) |
x(1)x(N −1) |
||||||||||||||
|
Rx |
= [Rx |
(k, n)] = |
. |
|||||||||||||
|
x(N −1)x(1) |
x(N −1)x(N −1) |
|||||||||||||||
|
x(N −1)x(0) |
Чертой сверху здесь обозначено усреднение по ансамблю реализаций.
Если процесс нестационарный, все элементы матрицы могут быть различными. В случае стационарного процесса корреляционная матрица полностью определяется своими первыми строкой и столбцом, поскольку вдоль всех диагоналей, параллельных главной, стоят одинаковые элементы:
|
Rx (1) |
Rx (N − 2) |
Rx (N −1) |
|||||
|
Rx (0) |
Rx (N − 3) |
Rx (N − 2) |
|||||
|
. |
|||||||
|
Rx (−N + 3) |
Rx (0) |
Rx (1) |
|||||
|
R |
(− |
N |
+ 2) |
R |
R |
||
|
x |
x (−1) |
x (0) |
ЗАМЕЧАНИЕ
Матрицы, обладающие таким свойством, называются матрицами Теплица (Toeplitz matrix). В MATLAB сгенерировать матрицу Теплица по первым строке и столбцу позволяет функция toeplitz.
Вслучае вещественного случайного процесса, как уже отмечалось, Rx (−k) = Rx (k) ,
икорреляционная матрица становится симметричной:
|
Rx (1) |
Rx (N − 2) |
|
|
Rx (0) |
Rx (N − 3) |
|
|
Rx (N − 3) |
Rx (0) |
|
|
Rx (N − 2) |
Rx (1) |
|
Rx (N −1) |
||
|
Rx (N − 2) |
||
|
. |
(3.28) |
|
|
Rx (1) |
||
|
R |
||
|
x (0) |
Важным свойством матриц вида (3.28) является то, что они всегда являются неотрицательно определенными, т. е. все их собственные числа вещественны и неотрицательны.
ЗАМЕЧАНИЕ
Если стационарный случайный процесс является комплексным, Rx (−k) = Rx* (k) и
корреляционная матрица является не симметричной, а самосопряженной. Свойство неотрицательной определенности сохраняется и в этом случае.
Дискретный белый шум
Так называется стационарный дискретный случайный процесс, отсчеты которого некоррелированы друг с другом:
|
Rx |
σ2x , |
k = 0, |
|
( k) = |
k ≠ 0. |
|
|
0, |
В отличие от случая аналогового белого шума, дисперсия дискретного белого шума не является бесконечной, а потому такой шум является физически реализуемым.
Корреляционная матрица дискретного белого шума будет, очевидно, иметь диагональную структуру:
Rx = σ2x I ,
где I — единичная матрица.
Дискретные сигналы в MATLAB
Дискретный сигнал представляет собой последовательность чисел, а потому в MATLAB он представляется в виде вектора. Если необходимо реализовать многоканальную обработку сигналов, для этого удобно использовать второе измерение, представив набор сигналов в виде матрицы. Многоканальная обработка поддерживается многими функциями MATLAB.
Если сигнал одномерный, то в большинстве случаев функции MATLAB правильно обработают его при любой ориентации вектора — как в виде строки, так и в виде столбца. Однако в многоканальном случае, когда входной сигнал представлен в виде матрицы, обработка производится по столбцам.
Таким образом, столбцы матрицы трактуются как сигналы разных каналов, а строки — как отдельные векторные отсчеты многоканального сигнала. Для избежания путаницы рекомендуется и в одноканальном случае задавать сигналы в виде столбцов.
Отсчеты дискретного сигнала могут быть получены двумя путями. Первый вариант — расчет значений сигнала (моделирование сигнала), второй — получение сигнала извне путем считывания его записи. Работу с записями сигналов в виде WAVфайлов мы рассмотрим ближе к концу главы, а сейчас обсудим моделирование сигналов.
Расчет временных функций
Аналоговый сигнал, как уже говорилось, с математической точки зрения представляет собой функцию (как правило — функцию времени), и при его дискретизации мы получаем отсчеты, являющиеся значениями этой функции, вычисленными в дискретные моменты времени. Поэтому для расчета дискретизированного сигнала необходимо, прежде всего, сформировать вектор дискретных значений времени. Для этого удобно задать значение частоты дискретизации Fs (sampling frequency) и использовать обратную величину в качестве шага временного ряда:
>>Fs = 8e3; % частота дискретизации 8 кГц
>>t = 0:1/Fs:1; % одна секунда дискретных значений времени
|
>> t = t’; |
% преобразуем строку в столбец |
Сформировав вектор опорных значений времени, можно вычислять значения сигнала, используя этот вектор в соответствующих формулах. Большинство математических функций MATLAB обрабатывают векторный аргумент поэлементно, так что с этим проблем не возникает. Однако следует помнить о том, что операции умножения, деления и возведения в степень в MATLAB имеют матричный смысл, поэтому при расчете одномерных функций времени следует использовать поэлементные версии этих операций (.*, ./ и .^). Приведем несколько примеров:
|
>> A = 2; |
% амплитуда – два вольта |
|
|
>> f0 |
= 1e3; |
% частота – 1 кГц |
|
>> phi = pi/4; |
% начальная фаза — 45° |
|
|
>> s1 |
= A * cos(2*pi*f0*t + phi); |
% гармонический сигнал |
|
>> alpha = 1e3; |
% скорость затухания |
|
|
>> s2 |
= exp(-alpha*t) .* s1; |
% затухающая синусоида |
Для визуализации дискретных сигналов могут использоваться различные графические средства MATLAB в зависимости от конкретной ситуации. Часто вполне допустимым является соединение дискретных отсчетов линиями, т. е. построение графика с помощью функции plot (рис. 3.18, сверху слева). При этом хорошо видна

общая форма сигнала (фактически в этом случае мы получаем график аналогового сигнала, полученного путем линейной интерполяции), но незаметны отсчетные точки. Если необходимо отобразить именно их, можно отказаться от соединения точек линиями (рис. 3.18, сверху справа).
Помимо функции plot существуют другие графические функции, специально предназначенные для отображения дискретных последовательностей. Функция stem изображает сигнал в виде «стебельков» (рис. 3.18, снизу слева), а функция stairs — в ступенчатом виде (рис. 3.18, снизу справа). В последнем случае изображается аналоговый сигнал с кусочно-постоянной интерполяцией (интерполяцией нулевого порядка). Такой сигнал получается на выходе ЦАП при отсутствии сглаживающего фильтра. Вот последовательность команд MATLAB, при помощи которой был получен рис. 3.18:
>>subplot(2, 2, 1); plot(s2(1:50))
>>subplot(2, 2, 2); plot(s2(1:50), ‘.’)
>>subplot(2, 2, 3); stem(s2(1:50))
>>subplot(2, 2, 4); stairs(s2(1:50))
|
1.5 |
1.5 |
||||||||||
|
1 |
1 |
||||||||||
|
0.5 |
0.5 |
||||||||||
|
0 |
0 |
||||||||||
|
-0.5 |
-0.5 |
||||||||||
|
-1 |
-1 |
||||||||||
|
-1.5 |
-1.5 |
||||||||||
|
0 |
10 |
20 |
30 |
40 |
50 |
0 |
10 |
20 |
30 |
40 |
50 |
|
1.5 |
1.5 |
||||||||||
|
1 |
1 |
||||||||||
|
0.5 |
0.5 |
||||||||||
|
0 |
0 |
||||||||||
|
-0.5 |
-0.5 |
||||||||||
|
-1 |
-1 |
||||||||||
|
-1.5 |
-1.5 |
||||||||||
|
0 |
10 |
20 |
30 |
40 |
50 |
0 |
10 |
20 |
30 |
40 |
50 |
Рис. 3.18. Различные формы представления графиков дискретного сигнала
ЗАМЕЧАНИЕ
Еще один способ визуализации сигналов обеспечивает функция strips. Она будет рассмотрена далее в разд. «Чтение WAV-файлов» этой главы.
Горизонтальная ось на приведенных графиках проградуирована в номерах отсчетов. Чтобы показать на этой оси значения времени, при вызове графических функ-

ций следует использовать два параметра, передав в первом из них соответствующий временной вектор, например, так:
plot(t(1:50), s2(1:50))
Если необходимо сгенерировать многоканальный сигнал, каналы которого описываются одной и той же формулой, но с разными числовыми значениями параметров, для этого можно эффективно использовать средства матричных операций MATLAB. Простейший пример — генерация набора синусоид с заданными частотами (в приводимом далее коде используется вектор t, сформированный ранее):
|
>> |
f = [600 800 1000 1200 1400]; % |
вектор частот |
(строка!) |
|
|
>> |
s3 = cos(2*pi*t*f); |
% |
пятиканальный |
сигнал |
Здесь столбец значений времени t умножается на строку частот f. В результате получается матрица, содержащая все необходимые значения произведения времени и частоты. Далее эта матрица подвергается поэлементным преобразованиям (умножение на 2π и вычисление косинуса). Результат вычислений показан на рис. 3.19:
>> plot(t(1:50), s3(1:50,:))
|
1 |
|||||||
|
0.8 |
|||||||
|
0.6 |
|||||||
|
0.4 |
|||||||
|
0.2 |
|||||||
|
0 |
|||||||
|
-0.2 |
|||||||
|
-0.4 |
|||||||
|
-0.6 |
|||||||
|
-0.8 |
|||||||
|
-1 |
|||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
x 10-3 |
Рис. 3.19. Многоканальный сигнал
ЗАМЕЧАНИЕ
Напомним, что при визуализации матрицы функция plot строит графики именно по столбцам.
Если вычисление значений сигнала производится однократно, необходимые вычисления можно выполнить в ходе интерактивного сеанса работы либо описать в тексте MATLAB-программы. Если же в ходе решения задачи необходимо повторно обращаться к вычислениям, целесообразно оформить их в виде функции
(см. разд. «Программирование» приложения 1). При этом следует иметь в виду, что для использования многочисленных численных алгоритмов, эффективно реализованных в MATLAB, функция для расчета значений сигнала должна быть способна принимать векторный аргумент, содержащий набор значений времени.
Кусочные зависимости
Довольно часто возникает необходимость моделирования отсчетов сигнала, который для разных интервалов времени описывается разными формулами. Простейший случай такого рода — моделирование импульсов конечной длительности, значения которых описываются одной или несколькими формулами в пределах заданного интервала, а в остальное время равны нулю.
В MATLAB возможно несколько способов задания кусочных функций. Первый вариант — воспользоваться тем, что операции сравнения возвращают 1 при выполнении неравенства и 0 в противном случае, причем в случае векторного аргумента возвращается вектор результатов сравнения. Зададим таким образом односторонний экспоненциальный импульс (см. рис. 1.18):
s = A * exp(-alpha * t) .* (t >= 0);
Прямоугольный импульс, центрированный относительно начала отсчета времени (см. рис. 1.10):
s = A * (abs(t) <= T/2);
Несимметричный треугольный импульс (см. рис. 1.14):
s = A * t / T .* (t >= 0) .* (t <= T);
В приведенных примерах следует обратить внимание на использование оператора * для поэлементного перемножения векторов.
Недостаток данного способа состоит в том, что значения сигнала сначала вычисляются по заданной формуле для всех значений аргумента, и лишь затем «вырезается» нужная область. Помимо возрастания времени вычислений это может привести к выдаче сообщения об ошибке — например, в первом из приведенных примеров при вычислении экспоненты для большого отрицательного значения аргумента t может произойти переполнение.
Второй способ — выполнять вычисления только для тех моментов времени, для которых это действительно необходимо. Выделение набора элементов вектора t, для которых выполняется заданное условие, производится с помощью логической маски, создаваемой с помощью операторов сравнения. В этом случае следует принять во внимание два аспекта:
необходимо заранее, до вычислений, создать вектор сигнала такого же размера, как вектор моментов времени t (обычно этот вектор заполняют нулями);
поскольку логическую маску придется использовать несколько раз, целесообразно сохранить ее в переменной.
Покажем, как данным способом генерируются те же три кусочно-заданных сигнала.
Односторонний экспоненциальный импульс:
%заполняем вектор сигнала нулями s = zeros(size(t));
%формируем маску для неотрицательных элементов вектора t mask = (t >= 0);
%рассчитываем сигнал только в нужных точках
s(mask) = A * exp(-alpha * t(mask));
Прямоугольный видеоимпульс (поскольку для расчета значений такого импульса не требуется вычислений с вектором t, переменную mask можно не создавать — она понадобилась бы лишь один раз):
s = zeros(size(t));
s(abs(t) <= T/2) = A;
Несимметричный треугольный импульс:
s = zeros(size(t));
mask = (t >= 0) & (t <= T);
s(mask) = A * t(mask) / T;
Как видите, команд в данном случае нужно больше, но зато при этом не будет выполняться лишних вычислений и не появятся упомянутые выше сообщения об ошибках.
Функции генерации одиночных импульсов
В пакете Signal Processing имеется ряд функций, генерирующих часто встречающиеся на практике непериодические сигналы:
rectpuls — прямоугольный импульс;
tripuls — треугольный импульс;
sinc — импульс вида sin(πt)/(πt);
gauspuls — радиоимпульс с гауссовой огибающей;
pulstran — последовательность из конечного числа импульсов произвольной
формы.
Далее эти функции рассматриваются более подробно.
Прямоугольный импульс
Для формирования одиночного прямоугольного импульса с единичной амплитудой служит функция rectpuls:
y = rectpuls(t, width)
Здесь t — вектор значений времени, width — ширина (длительность) импульса.
Возвращаемый результат y — вектор рассчитанных значений сигнала, определяемых по следующей формуле:

|
Дискретные сигналы |
173 |
|||||||||
|
− |
width |
≤ t < |
width |
|||||||
|
1, |
, |
|||||||||
|
2 |
2 |
|||||||||
|
y = |
||||||||||
|
width |
width |
|||||||||
|
0, |
t < − |
, |
t ≥ |
. |
||||||
|
2 |
2 |
Параметр width можно опустить, при этом его значение по умолчанию равно 1 и функция rectpuls производит результат, соответствующий математической функции rect.
В качестве примера сформируем пару разнополярных прямоугольных импульсов с амплитудой 5 В и длительностью 20 мс каждый, расположенных справа и слева от начала отсчета времени. Частоту дискретизации выберем равной 1 кГц. Результат показан на рис. 3.20:
|
>> Fs = 1e3; |
% |
частота дискретизации |
|
|
>> t = -40e-3:1/Fs:40e-3; % |
дискретное время |
||
|
>> T = |
20e-3; |
% |
длительность импульсов |
|
>> A = |
5; |
% |
амплитуда |
>>s = -A * rectpuls(t+T/2, T) + A * rectpuls(t-T/2, T);
>>plot(t, s)
>>ylim([-6 6])
|
6 |
||||||||
|
4 |
||||||||
|
2 |
||||||||
|
0 |
||||||||
|
-2 |
||||||||
|
-4 |
||||||||
|
-6 |
||||||||
|
-0.04 |
-0.03 |
-0.02 |
-0.01 |
0 |
0.01 |
0.02 |
0.03 |
0.04 |
Рис. 3.20. Сигнал, сформированный с использованием функции rectpuls
Треугольный импульс
Для формирования одиночного треугольного импульса с единичной амплитудой служит функция tripuls:
y = tripuls(t, width, skew)
Здесь t — вектор значений времени, width — ширина (длительность) импульса, skew — коэффициент асимметрии импульса, определяющий положение его верши-

ны. Пик импульса расположен при t = width*skew/2. Параметр skew должен лежать в диапазоне от –1 до 1.
Возвращаемый результат y — вектор рассчитанных значений сигнала, определяемых по следующей формуле:
|
2t + width |
, − |
width |
≤ t < |
width skew |
, |
|||||||
|
width(skew +1) |
||||||||||||
|
2 |
2 |
|||||||||||
|
2t − width |
width skew |
width |
||||||||||
|
y = |
, |
≤ t < |
, |
|||||||||
|
width(skew −1) |
2 |
2 |
||||||||||
|
| t | > |
width |
|||||||||||
|
0, |
. |
|||||||||||
|
2 |
Параметры skew или skew и width можно опустить, при этом используются их значения по умолчанию: skew = 0 (симметричный импульс) и width = 1.
В качестве примера сформируем симметричный трапециевидный импульс с амплитудой 10 В и размерами верхнего и нижнего оснований 20 и 60 мс соответственно. Частоту дискретизации выберем равной 1 кГц. Результат показан на рис. 3.21:
|
>> Fs = 1e3; |
% |
частота дискретизации |
|||
|
>> t = -50e-3:1/Fs:50e-3; % |
дискретное время |
||||
|
>> A = 10; |
% |
амплитуда |
|||
|
>> |
T1 |
= |
20e-3; |
% |
верхнее основание |
|
>> |
T2 |
= |
60e-3; |
% |
нижнее основание |
>>s = A*(T2*tripuls(t, T2) — T1*tripuls(t, T1))/(T2-T1);
>>plot(t, s)
|
12 |
||
|
10 |
||
|
8 |
||
|
6 |
||
|
4 |
||
|
2 |
||
|
0 |
||
|
-0.05 -0.04 -0.03 -0.02 -0.01 |
0 |
0.01 0.02 0.03 0.04 0.05 |
Рис. 3.21. Сигнал, сформированный с использованием функции tripuls

Импульс с ограниченной полосой частот
Для формирования сигнала, имеющего прямоугольный, т. е. ограниченный по частоте спектр, служит функция sinc:
y = sinc(t)
Единственным входным параметром является вектор значений времени t.
Возвращаемый результат y — вектор рассчитанных значений сигнала, определяемых по следующей формуле:
y = sin(πx) .
πx
ВНИМАНИЕ!
В отечественной литературе под функцией sinc чаще всего понимается выражение sin(x)/x — без умножения аргумента на π. Средствами MATLAB такая функция может быть рассчитана как sinc(x/pi).
Спектральная функция сигнала, генерируемого функцией sinc, имеет прямоугольный вид:
|
1, | ω | < π, |
|
|
Y |
(ω) = {0, | ω | > π. |
В качестве примера построим с помощью функции sinc график амплитудного спектра очень короткого радиоимпульса, на длительности которого укладывается лишь один период синусоидального заполнения. Согласно свойствам преобразования Фурье (см. главу 1) спектр такого сигнала должен представлять собой сумму двух спектров прямоугольного импульса, сдвинутых на величину частоты заполнения в сторону положительных и отрицательных частот. Спектр прямоугольного импульса, в свою очередь, описывается именно функцией sinc (см. формулу (1.20) в разд. «Примеры расчета преобразования Фурье» главы 1). Результат показан на рис. 3.22:
|
>> Fs = 1e3; |
% частота дискретизации |
|
>> t = -0.1:1/Fs:0.1; |
% дискретное время |
|
>> f0 = 10; |
% частота заполнения |
|
>> T = 1/f0; |
% длительность радиоимпульса |
|
>> s = rectpuls(t, T) .* cos(2*pi*f0*t); % радиоимпульс |
|
|
>> f = -50:50; |
% вектор частот для расчета спектра |
|
>> sp = T/2 * (sinc((f-f0)*T) + sinc((f+f0)*T)); |
|
|
>> plot(t, s) |
% график сигнала |
|
>> ylim([-1.1 1.1]) |
|
|
>> figure |
|
|
>> plot(f, abs(sp)) |
% график амплитудного спектра |
Как видите, из-за наложения друг на друга «хвостов» функции sinc спектр оказывается существенно несимметричным относительно частоты заполнения радиоим-

пульса. Более подробно этот эффект будет обсуждаться в главе 8, посвященной модуляции.
|
1 |
||||||||||
|
0.8 |
||||||||||
|
0.6 |
||||||||||
|
0.4 |
||||||||||
|
0.2 |
||||||||||
|
0 |
а |
|||||||||
|
-0.2 |
||||||||||
|
-0.4 |
||||||||||
|
-0.6 |
||||||||||
|
-0.8 |
||||||||||
|
-1 |
||||||||||
|
-0.1 |
-0.08 |
-0.06 |
-0.04 |
-0.02 |
0 |
0.02 |
0.04 |
0.06 |
0.08 |
0.1 |
|
0.06 |
||||||||||
|
0.05 |
||||||||||
|
0.04 |
||||||||||
|
0.03 |
б |
|||||||||
|
0.02 |
||||||||||
|
0.01 |
||||||||||
|
0 |
||||||||||
|
-50 |
-40 |
-30 |
-20 |
-10 |
0 |
10 |
20 |
30 |
40 |
50 |
Рис. 3.22. Короткий радиоимпульс (а) и его амплитудный спектр (б), построенный с помощью функции sinc
Гауссов радиоимпульс
Для формирования одиночного радиоимпульса с гауссовой огибающей и единичной амплитудой служит функция gauspuls:
y = gauspuls(t, fc, bw, bwr)
Здесь t — вектор значений времени, fc — несущая частота в герцах, bw — относительная ширина спектра (ширина спектра, деленная на несущую частоту), bwr — уровень (в децибелах), по которому производится измерение ширины спектра.

Возвращаемый результат y — вектор рассчитанных значений сигнала, определяемых по следующей формуле:
|
y = exp(−at2 )cos(2πfct) . |
(3.29) |
Коэффициент a управляет длительностью импульса и, соответственно, шириной его спектра. Сигнал (3.29) имеет спектральную функцию, равную (см. разд. «Примеры расчета преобразования Фурье» главы 1)
|
1 |
π |
(ω + 2πfc )2 |
(ω − 2πfc )2 |
||||||||
|
S |
(ω) = |
exp |
− |
+ exp |
− |
. |
|||||
|
2 |
4a |
4a |
|||||||||
|
a |
Если fc a , можно пренебречь наложением «хвостов» сдвинутых копий спектра. Тогда параметр a связан с относительной шириной спектра и уровнем (в децибелах), по которому она определяется, следующим образом:
a = − 5(2πfc bw)2 . bwr ln10
Параметры bwr, bw и fc можно опустить, при этом используются их значения по умолчанию: bwr = –6 дБ, bw = 0,5 и fc = 1000 Гц.
При вызове функции gauspuls можно использовать от одного до трех выходных параметров:
[y, yq, ye] = gauspuls(…)
Во втором выходном параметре yq функция возвращает квадратурное (quadrature) дополнение для рассчитанного радиоимпульса y. Вектор yq отличается от вектора y фазовым сдвигом несущего колебания на 90° (подробнее о понятии квадратурного дополнения в разд. «Преобразование Гильберта» главы 1).
Втретьем выходном параметре ye функция возвращает огибающую (envelope) сформированного радиоимпульса. Вектор ye представляет собой первый множитель формулы (3.29) (отсутствует умножение на косинус).
Вкачестве примера сформируем гауссов радиоимпульс с несущей частотой 4 кГц и относительной шириной спектра 10%, измеренной по уровню –20 дБ, а затем построим график его спектра, чтобы убедиться в правильности расчетов. Частоту дискретизации примем равной 16 кГц. Результат показан на рис. 3.23:
|
>> Fs = 16e3; |
% частота дискретизации |
|
>> t = -10e-3:1/Fs:10e-3; |
% дискретное время |
|
>> Fc = 4e3; |
% несущая частота |
|
>> bw = 0.1; |
% относительная ширина спектра |
|
>> bwr = -20; |
% уровень измерения ширины спектра |
>>s = gauspuls(t, Fc, bw, bwr);
>>Nfft = 2^nextpow2(length(s));
|
>> sp = fft(s, Nfft); |
% спектр |
|
>> sp_dB = 20*log10(abs(sp)); |
% амплитудный спектр в децибелах |
|
>> f = (0:Nfft-1)/Nfft*Fs; |
% вектор частот спектра |

|
178 |
Глава 3 |
|||||||
|
>> plot(t, s) |
% график сигнала |
|||||||
|
>> figure |
||||||||
|
>> % график амплитудного спектра |
||||||||
|
>> plot(f(1:Nfft/2), sp_dB(1:Nfft/2)) |
||||||||
|
>> % максимальный уровень спектра в децибелах |
||||||||
|
>> sp_max_db = 20*log10(max(abs(sp))); |
||||||||
|
>> edges = Fc * [1-bw/2 1+bw/2]; % граничные частоты |
||||||||
|
>> % отображаем заданные при расчете границы спектра |
||||||||
|
>> hold on |
||||||||
|
>> plot(edges, sp_max_db([1 1])+bwr, ‘o’) |
||||||||
|
>> hold off |
||||||||
|
1 |
||||||||
|
0.8 |
||||||||
|
0.6 |
||||||||
|
0.4 |
||||||||
|
0.2 |
||||||||
|
0 |
||||||||
|
а |
||||||||
|
-0.2 |
||||||||
|
-0.4 |
||||||||
|
-0.6 |
||||||||
|
-0.8 |
||||||||
|
-1 |
||||||||
|
-0.01 |
-0.008 -0.006 -0.004 |
-0.002 |
0 |
0.002 |
0.004 0.006 |
0.008 |
0.01 |
|
|
50 |
||||||||
|
0 |
||||||||
|
-50 |
||||||||
|
б |
||||||||
|
-100 |
||||||||
|
-150 |
||||||||
|
-200 |
||||||||
|
0 |
1000 |
2000 |
3000 |
4000 |
5000 |
6000 |
7000 |
8000 |
|
Рис. 3.23. Гауссов радиоимпульс, сформированный функцией gauspuls (а), |
||||||||
|
и его амплитудный спектр (б) |
Из графика спектра (см. рис. 3.23, б) видно, что заданные при вызове функции gauspuls параметры спектра выдержаны точно.
Наконец, у функции gauspuls есть еще один вариант использования — она позволяет рассчитать время, за которое огибающая гауссового импульса упадет до заданного уровня относительно максимума. При этом вместо вектора значений времени в качестве первого входного параметра используется строка ‘cutoff’:
tc = gauspuls(‘cutoff’, fc, bw, bwr, tpe)
Входные параметры fc, bw и bwr имеют тот же смысл, что и раньше, а tpe — уровень огибающей (в децибелах относительно максимума), момент достижения которого нужно определить.
Возвращаемый результат tc — момент достижения огибающей уровня tpe (т. е. полуширина импульса, измеренная по уровню tpe).
В качестве примера рассчитаем время, за которое огибающая сформированного в предыдущем примере импульса уменьшается на 6 дБ (примерно в два раза):
>> gauspuls(‘cutoff’, Fc, bw, bwr, -6)
ans =
0.0020
Полученный результат соответствует графику сигнала, приведенному ранее на рис. 3.23, а.
Генерация последовательности импульсов
Функция pulstran служит для генерации конечной последовательности импульсов (pulse train) одинаковой формы с произвольно задаваемыми задержками и уровнями. Сами импульсы могут задаваться одним из двух способов: именем функции, генерирующей импульс, либо уже рассчитанным вектором отсчетов.
Если импульсы задаются именем генерирующей функции, функция pulstran вызывается следующим образом:
y = pulstran(t, d, ‘func’, p1, p2, …)
Здесь t — вектор значений времени, d — вектор задержек, ‘func’ — имя функции, генерирующей одиночный импульс. В качестве этой функции могут использоваться, например, rectpuls, tripuls, gauspuls, а также любые другие функции (в том числе и «самодельные»), принимающие в качестве первого входного параметра вектор моментов времени и возвращающие вектор рассчитанных отсчетов сигнала. Оставшиеся параметры p1, p2, … — дополнительные, они передаются функции func при ее вызове.
Таким образом, функция pulstran в данном варианте использования генерирует выходной сигнал следующим образом:
y = func(t-d(1), p1, p2, …) + …
func(t-d(2), p1, p2, …) + …
func(t-d(3), p1, p2, …) + …
…

Если d — двухстолбцовая матрица, то первый столбец трактуется как задержки импульсов, а второй — как их уровни. При этом выходной сигнал формируется так:
y = d(1,1) * func(t-d(1,2), p1, p2, …) + …
d(2,1) * func(t-d(2,2), p1, p2, …) + …
d(3,1) * func(t-d(3,2), p1, p2, …) + …
…
В качестве примера сформируем последовательность из пяти симметричных треугольных импульсов, интервалы между которыми линейно увеличиваются, а амплитуды экспоненциально уменьшаются. Частоту дискретизации выберем равной 1 кГц. Длительность импульса — 20 мс. Результат показан на рис. 3.24:
|
>> Fs = 1e3; |
% |
частота дискретизации |
|
>> t = 0:1/Fs:0.5; |
% |
дискретное время |
|
>> tau = 20e-3; |
% |
длительность импульса |
|
>> d = [20 80 160 260 380]’ * 1e-3; % |
задержки импульсов |
|
|
>> d(:,2) = 0.8.^(0:4)’; |
% |
амплитуды импульсов |
>>y = pulstran(t, d, ‘tripuls’, tau);
>>plot(t, y)
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
|
0 |
0.05 |
0.1 |
0.15 |
0.2 |
0.25 |
0.3 |
0.35 |
0.4 |
0.45 |
0.5 |
Рис. 3.24. Последовательность треугольных импульсов, сформированная с помощью функции pulstran
Если для генерации одиночного импульса нет готовой функции, можно рассчитать вектор отсчетов импульса, а затем использовать второй вариант вызова функции
pulstran:
y = pulstran(t, d, p, fs, ‘method’)
Смысл входных параметров t и d тот же, что и раньше. Вектор p должен содержать отсчеты одиночного импульса, а параметр fs указывать частоту дискретизации, использованную при расчете этого вектора. Считается, что первый отсчет из вектора p соответствует нулевому моменту времени.

Поскольку частота fs может не совпадать с шагом значений вектора t (в принципе, они даже не обязаны представлять собой равномерную последовательность) и задержки из вектора d тоже не обязательно кратны этому шагу, для пересчета задержанных импульсов к сетке моментов времени t в общем случае необходимо использование интерполяции. Метод интерполяции может быть явно задан с помощью строкового параметра ‘method’. Возможны все методы, поддерживаемые
функцией interp1: ‘nearest’, ‘linear’, ‘spline’, ‘pchip’, ‘cubic’ и ‘v5cubic’.
Параметры fs и ‘method’ при вызове могут опускаться, в этом случае используются их значения по умолчанию: fs = 1 и ‘method’ = ‘linear’.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
|
0 |
0.05 |
0.1 |
0.15 |
0.2 |
0.25 |
0.3 |
0.35 |
0.4 |
0.45 |
0.5 |
Рис. 3.25. Последовательность импульсов, сформированная функцией pulstran из вектора отсчетов одиночного импульса
В качестве примера сформируем последовательность из шести импульсов, имеющих форму одного периода функции sin2 . Пусть длительность импульса равна 60 мс, а частота его дискретизации — 400 Гц. Расстояние между центрами импульсов будет одинаковым и равным 64 мс, а частота дискретизации выходного сигнала — 1 кГц. Импульсы будут экспоненциально затухать с ростом номера. Результат показан на рис. 3.25:
>> % генерируем вектор отсчетов одиночного импульса
|
>> Fs0 = |
400; |
% частота дискретизации импульса |
|
>> tau = |
60e-3; |
% длительность импульса |
|
>> t0 = 0:1/Fs0:tau; |
% дискретное время для импульса |
>>s0 = sin(pi*t0/tau).^2; % вектор отсчетов импульса
>>% генерируем последовательность импульсов
|
>> Fs = 1e3; |
% частота дискретизации последовательности |
|
>> t = 0:1/Fs:0.5; |
% дискретное время для последовательности |
|
>> d = (1:6)’ * 64e-3; |
% задержки импульсов |
|
182 |
Глава 3 |
|
>> d(:,2) = 0.6.^(0:5)’; |
% амплитуды импульсов |
>>% последовательность импульсов
>>y = pulstran(t, d, s0, Fs0);
>>plot(t, y)
Функции генерации периодических сигналов
Эти функции, входящие в пакет Signal Processing, позволяют формировать отсчеты периодических сигналов различной формы:
square — последовательность прямоугольных импульсов;
sawtooth — последовательность треугольных импульсов;
diric — функция Дирихле (периодическая sinc-функция).
Последняя рассматриваемая в данном разделе функция chirp генерирует не периодический сигнал, а колебания с меняющейся частотой.
Далее эти функции рассматриваются более подробно.
Последовательность прямоугольных импульсов
Для формирования последовательности прямоугольных импульсов служит функция square. В простейшем случае эта функция принимает один входной параметр — вектор значений времени t:
y = square(t)
Генерируемая при этом последовательность импульсов имеет период 2π и скважность 2 (т. е. длительность импульса равна половине периода). Последовательность является двуполярной — сигнал принимает значения –1 и 1.
Сформировать последовательность с периодом T можно следующим образом:
y = square(2*pi*t/T)
С помощью второго входного параметра duty можно регулировать скважность получаемой последовательности. Однако этот параметр задает не саму скважность, а обратную ей величину — коэффициент заполнения (в процентах), т. е. отношение длительности импульса к периоду:
y = square(t, duty)
По умолчанию значение параметра duty равно 50, т. е. генерируется меандр.
ВНИМАНИЕ!
Обратите внимание на то, что значение параметра duty задается именно в процентах,
ане в дробных единицах.
Вкачестве примера сформируем последовательность однополярных прямоуголь-
ных импульсов с амплитудой 3 В, частотой следования 50 Гц и длительностью 5 мс. Будем использовать частоту дискретизации 1 кГц и временной интервал –10…50 мс (рис. 3.26):

|
Дискретные сигналы |
183 |
|
|
>> Fs = 1e3; |
% |
частота дискретизации |
|
>> t = -10e-3:1/Fs:50e-3; % |
дискретное время |
|
|
>> A = 3; |
% |
амплитуда |
|
>> f0 = 50; |
% |
частота следования импульсов |
|
>> tau = 5e-3; |
% |
длительность импульсов |
>>s = (square(2*pi*t*f0, f0*tau*100) + 1) * A/2;
>>plot(t, s)
>>ylim([0 5])
|
5 |
||||||
|
4.5 |
||||||
|
4 |
||||||
|
3.5 |
||||||
|
3 |
||||||
|
2.5 |
||||||
|
2 |
||||||
|
1.5 |
||||||
|
1 |
||||||
|
0.5 |
||||||
|
0 |
||||||
|
-0.01 |
0 |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
Рис. 3.26. Последовательность прямоугольных импульсов, полученная с помощью функции square
ЗАМЕЧАНИЕ
На рис. 3.26 видно, что импульсы имеют неодинаковую ширину. Поскольку длительность импульса в данном случае равна ровно пяти интервалам дискретизации (5 мс × 1 кГц = 5), из-за погрешностей представления значений времени в компьютере каждый импульс может быть представлен либо пятью, либо шестью ненулевыми отсчетами.
Последовательность треугольных импульсов
Для формирования последовательности треугольных импульсов служит функция sawtooth. В простейшем случае эта функция принимает один входной параметр — вектор значений времени t:
y = sawtooth(t)
Генерируемая при этом последовательность импульсов имеет период 2π. На протяжении периода сигнал линейно нарастает от –1 до 1.
Сформировать последовательность с периодом T можно следующим образом:
y = sawtooth(2*pi*t/T)

С помощью второго входного параметра width можно регулировать длительность «обратного хода» — промежутка, на котором уровень сигнала линейно падает от 1 до –1. При указании параметра width сигнал линейно возрастает от –1 до 1 за время 2π width, а затем за время 2π(1 – width) линейно убывает от 1 до –1:
y = sawtooth(t, width)
По умолчанию значение параметра width равно 1. При width = 0,5 получится последовательность симметричных треугольных импульсов.
В качестве примера сформируем последовательность треугольных импульсов отрицательной полярности с амплитудой 5 В, периодом 50 мс и длительностью падающего участка 5 мс. Будем использовать частоту дискретизации 1 кГц и временной интервал –25…125 мс (рис. 3.27):
|
>> Fs = 1e3; |
% |
частота дискретизации |
|
>> t = -25e-3:1/Fs:125e-3; % |
дискретное время |
|
|
>> A = 5; |
% |
амплитуда |
|
>> T = 50e-3; |
% |
период |
|
>> t1 = 5e-3; |
% |
длительность падающего участка |
>>s = (sawtooth(2*pi*t/T, 1-t1/T) — 1) * A/2;
>>plot(t, s)
|
0 |
|||||||||
|
-0.5 |
|||||||||
|
-1 |
|||||||||
|
-1.5 |
|||||||||
|
-2 |
|||||||||
|
-2.5 |
|||||||||
|
-3 |
|||||||||
|
-3.5 |
|||||||||
|
-4 |
|||||||||
|
-4.5 |
|||||||||
|
-5 |
|||||||||
|
-0.04 |
-0.02 |
0 |
0.02 |
0.04 |
0.06 |
0.08 |
0.1 |
0.12 |
0.14 |
|
Рис. 3.27. Последовательность треугольных импульсов, |
|||||||||
|
полученная с помощью функции sawtooth |
Функция Дирихле
Функция Дирихле описывается формулой
diric(x) = sin(nx / 2) , n sin(x / 2)
где n — целое положительное число.
Функция имеет пульсирующий вид: пульсации максимального уровня расположены при x = 2πk, значение функции в этих точках равно (−1)k (n−1) . Между этими главными пульсациями расположены пульсации меньшего уровня. При нечетном n все главные пульсации имеют положительную полярность, и период функции равен 2π. При четном n полярность главных пульсаций чередуется, и период функции оказывается вдвое больше — 4π.
Для расчета функции Дирихле в MATLAB служит функция diric. Синтаксис ее вызова следующий:
y = diric(x, n)
Назначение входных параметров x и n соответствует приведенной выше формуле.
Функцию Дирихле называют еще периодической sinc-функцией (о функции sinc
ранее в разд. «Импульс с ограниченной полосой частот» этой главы). При нечетном n это действительно так, и функцию Дирихле можно представить следующим образом:
При четном n функция Дирихле является суммой сдвинутых во времени sincфункций с чередующимися знаками:
Поскольку функция sinc имеет равномерный спектр в полосе частот от нуля до π, представление функции Дирихле в виде ряда Фурье (такое представление легко получить с помощью формулы, приведенной в разд. «Связь преобразования Фурье и коэффициентов ряда Фурье» главы 1) имеет очень простой вид — количество гармонических слагаемых конечно, а их амплитуды одинаковы:
при нечетном n
|
diric(x) = |
1 |
+ |
2 |
cos(x) + |
2 |
cos(2x) +…+ |
2 |
n −1 |
; |
||||||||||||||||
|
cos |
x |
||||||||||||||||||||||||
|
n |
n |
n |
n |
2 |
|||||||||||||||||||||
|
при четном n |
|||||||||||||||||||||||||
|
diric(x) = |
2 |
x |
+ |
2 |
3x |
+ …+ |
2 |
n −1 |
|||||||||||||||||
|
cos |
cos |
cos |
x . |
||||||||||||||||||||||
|
n |
2 |
n |
2 |
n |
2 |
В качестве примера построим графики функции Дирихле при нечетном и четном значениях n (n = 7 и n = 8, рис. 3.28):
>>x = 0:0.01:15;
>>plot(x, diric(x, 7))
>>grid on
>>title(‘n = 7’)

|
186 |
Глава 3 |
||
|
>> figure |
|||
|
>> plot(x, diric(x, 8)) |
|||
|
>> grid on |
|||
|
>> title(‘n = 8’) |
|||
|
n = 7 |
|||
|
1 |
|||
|
0.8 |
|||
|
0.6 |
|||
|
0.4 |
|||
|
а |
|||
|
0.2 |
|||
|
0 |
|||
|
-0.2 |
|||
|
-0.4 |
|||
|
0 |
5 |
10 |
15 |
|
n = 8 |
|||
|
1 |
|||
|
0.8 |
|||
|
0.6 |
|||
|
0.4 |
|||
|
0.2 |
|||
|
0 |
б |
||
|
-0.2 |
|||
|
-0.4 |
|||
|
-0.6 |
|||
|
-0.8 |
|||
|
-1 |
|||
|
0 |
5 |
10 |
15 |
|
Рис. 3.28. Функция Дирихле нечетного (а) и четного (б) порядка |
Генерация сигнала с меняющейся частотой
Функция chirp предназначена для генерации колебаний с единичной амплитудой, мгновенная частота которых меняется по заданному закону:
y = chirp(t, f0, t1, f1, ‘method’, phi)

Здесь t — вектор значений времени, phi — начальная фаза колебания. Остальные параметры определяют закон изменения частоты.
ЗАМЕЧАНИЕ
Подробнее понятие мгновенной частоты будет обсуждаться в разд. «Угловая модуляция» главы 8.
Строковый параметр ‘method’ определяет тип зависимости мгновенной частоты от
времени — ‘linear’, ‘quadratic’ или ‘logarithmic’. Числовые параметры f0, t1 и
f1 создают опорные точки для расчетов: в нулевой момент времени мгновенная частота равна f0, а в момент времени t1 она равна f1.
Математически закон изменения мгновенной частоты выглядит следующим образом:
‘linear’:
t
f (t) = f0 + ( f1 − f0 ) t1 ;
‘quadratic’:
|
t |
2 |
|||
|
f (t) = f0 |
+ ( f1 |
− f0 ) |
; |
|
|
t1 |
‘logarithmic’ на деле противоречит своему названию — зависимость мгновенной частоты от времени при этом не логарифмическая, а экспоненциальная:
|
f (t) = |
f1 |
t t1 |
|||
|
f0 |
. |
||||
|
f0 |
|||||
ЗАМЕЧАНИЕ
Диапазон значений времени в векторе t может не включать в себя значений 0 и t1.
Параметры phi и ‘method’ при вызове функции можно опускать, тогда будут использованы их значения по умолчанию: phi = 0 и ‘method’ = ‘linear’.
Ограничение сигнала по длительности не производится, колебания генерируются для всех значений времени, переданных функции в векторе t.
В качестве примера сформируем три сигнала, определенных на промежутке 0…1 с и имеющих разные законы изменения мгновенной частоты. В нулевой момент времени все сигналы имеют мгновенную частоту 1 кГц, а в момент времени 1 с — 3 кГц. Частоту дискретизации выберем равной 8 кГц:
>>Fs = 8e3; % частота дискретизации
>>t = 0:1/Fs:1; % дискретное время
>>f0 = 1e3;
>>t1 = 1;
>>f1 = 3e3;
>>s1 = chirp(t, f0, t1, f1, ‘linear’);

>>s2 = chirp(t, f0, t1, f1, ‘quadratic’);
>>s3 = chirp(t, f0, t1, f1, ‘logarithmic’);
>>spectrogram(s1, 256, [], [], Fs, ‘yaxis’)
>>title(‘linear’)
>>colormap gray
>>figure
>>spectrogram(s2, 256, [], [], Fs, ‘yaxis’)
>>title(‘quadratic’)
>>colormap gray
>>figure
>>spectrogram(s3, 256, [], [], Fs, ‘yaxis’)
>>title(‘logarithmic’)
>>colormap gray
На рис. 3.29—3.31 показаны спектрограммы сформированных сигналов, наглядно демонстрирующие характер изменения мгновенной частоты при различных значениях параметра ‘method’. Обратите внимание на то, что значения мгновенной частоты при t = 0 и t = 1 для всех трех сигналов совпадают.
ЗАМЕЧАНИЕ
Функция spectrogram строит спектрограмму, т. е. зависимость мгновенного амплитудного спектра сигнала от времени. Величина модуля спектральной функции отображается цветом в координатах «время — частота». Подробнее о функции spectrogram рассказано в главе 5. Команда colormap gray устанавливает для графиков палитру оттенков серого цвета; в противном случае при черно-белом воспроизведении цветных спектрограмм зависимость оттенка от уровня амплитудного спектра оказалась бы немонотонной.
Рис. 3.29. Спектрограмма сигнала, сформированного функцией chirp при линейном законе изменения мгновенной частоты

Рис. 3.30. Спектрограмма сигнала, сформированного функцией chirp при квадратичном законе изменения мгновенной частоты
Рис. 3.31. Спектрограмма сигнала, сформированного функцией chirp при экспоненциальном законе изменения мгновенной частоты
Формирование случайных сигналов
Для генерации случайных чисел в MATLAB служат функции rand (равномерное распределение) и randn (нормальное распределение), а также средства пакета рас-
ширения Statistics, которые реализуют множество разных законов распределения вероятности. В данном разделе мы кратко рассмотрим формирование дискретных случайных сигналов с заданными распределением вероятности и корреляционными свойствами.
Реализация заданного закона распределения вероятности
Как уже говорилось, средства генерации случайных чисел с различными законами распределения вероятности имеются в пакете Statistics. Справочная информация об этом пакете имеется, например, в книге [25], здесь же мы рассмотрим лишь общий способ получения случайных чисел с заданной функцией распределения на основе равномерно распределенных случайных чисел.
Пусть X — случайная величина, равномерно распределенная на интервале 0…1 (см. разд. «Равномерное распределение» главы 1). Для получения случайной величины Y, имеющей функцию распределения Fy ( y) , случайную величину X необхо-
димо подвергнуть следующему нелинейному преобразованию:
|
Y = F( −1) |
( X ) , |
(3.30) |
||
|
y |
||||
|
где |
F(−1) |
— функция, обратная по отношению к F ( y) . |
||
|
y |
y |
Действительно, при таком расчете вероятность того, что Y не превышает значения y, равна P(Y ≤ y) = P( X ≤ Fy ( y)) . Но X имеет равномерное распределение, поэтому
P( X ≤ Fy ( y)) = Fy ( y) . Таким образом, P(Y ≤ y) = Fy ( y) , т. е. Y действительно имеет требуемую функцию распределения.
Формулу (3.30) можно обобщить на случай произвольного преобразования функции распределения. Если случайная величина X имеет функцию распределения Fx ( x) , а нужно получить случайную величину Y с функцией распределения Fy ( y) ,
искомое преобразование следует записать следующим образом:
Y = Fy(−1) ( Fx ( X )) .
Преобразование Fx ( X ) делает распределение случайной величины равномерным, а преобразование Fy( −1) (…) формирует случайную величину с заданным распределением вероятности.
ВНИМАНИЕ!
С теоретической точки зрения рассмотренный подход является универсальным, однако на практике он может оказаться неудобным, поскольку обратные функции распределения для многих законов (например, для нормального) не выражаются через элементарные функции. В таких случаях приходится использовать более изощренные методики.

В качестве примера сгенерируем по формуле (3.30) случайные числа с рэлеевским законом распределения (1.80). Функция распределения для закона Рэлея получается интегрированием его плотности вероятности:
|
y |
x |
|||||
|
F |
( y) = |
∫0 |
exp |
− |
||
|
σ2 |
||||||
|
y |
|
x2 |
y2 |
|||||
|
dx = 1 |
− exp |
− |
, y ≥ 0. |
|||
|
2σ2 |
2σ2 |
|||||
Обратная функция будет иметь вид
|
F( −1) |
(x) = σ −2ln (1 − x) , |
0 ≤ x < 1. |
(3.31) |
|
y |
Генерируем равномерно распределенные случайные числа с помощью функции rand, производим их преобразование по формуле (3.31) и строим гистограмму с помощью функции hist (рис. 3.32):
|
>> N = 10000; |
% |
количество чисел |
|
>> sigma = 1; |
% |
параметр рэлеевского закона |
|
>> X = rand(1, N); |
% |
равномерное распределение |
|
>> Y = sigma * sqrt(-2 * log(1 — X)); % |
закон Рэлея |
|
|
>> hist(Y, 25) |
% |
гистограмма по 25 интервалам |
|
1000 |
|||||||||
|
900 |
|||||||||
|
800 |
|||||||||
|
700 |
|||||||||
|
600 |
|||||||||
|
500 |
|||||||||
|
400 |
|||||||||
|
300 |
|||||||||
|
200 |
|||||||||
|
100 |
|||||||||
|
0 |
|||||||||
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
|
Рис. 3.32. Гистограмма случайных чисел с рэлеевским распределением |
Полученная гистограмма показывает хорошее соответствие с графиком рэлеевской плотности вероятности, показанным ранее на рис. 1.37.
Реализация заданной корреляционной функции
Поскольку корреляционная функция случайного сигнала взаимно-однозначно связана с его спектром (см. разд. «Теорема Винера — Хинчина» главы 1), для формирования сигнала с заданной КФ можно взять отсчеты белого шума и пропустить их через фильтр с соответствующей АЧХ (ФЧХ фильтра не имеет значения, поскольку

к случайным процессам неприменимо понятие фазового спектра). О теории работы дискретных фильтров речь пойдет в главе 4, а о методах их расчета — в главе 6. Здесь же мы, несколько забегая вперед и используя материал последующих глав, рассмотрим лишь один пример, сформировав сигнал с экспоненциальной функцией корреляции:
|
Rx ( k) = σ2x a| k| , |a| < 1. |
(3.32) |
Для формирования сигнала с такой КФ необходимо пропустить белый шум через дискретный фильтр, корреляционная функция импульсной характеристики которого имеет вид (3.32). Этому требованию удовлетворяет импульсная характеристика вида
h(k) = σx 1− a2 ak , k ≥ 0.
Такая характеристика соответствует рекурсивному фильтру первого порядка с коэффициентом обратной связи, равным a. Требуемую фильтрацию осуществим с помощью функции filter (она также будет рассмотрена в главе 4):
|
>> X0 = randn(1, 1000); % |
независимые нормальные отсчеты |
|
|
>> a = 0.9; |
% |
параметр экспоненциальной корреляции |
|
>> sigma = 2; |
% |
среднеквадратическое значение результата |
>>X = filter(sigma*sqrt(1-a^2), [1 -a], X0); % фильтрация
>>subplot(2, 1, 1)
|
>> plot(X0(1:200)) |
% график белого шума |
>>title(‘White noise’)
>>subplot(2, 1, 2)
|
>> |
plot(X(1:200)) |
% график коррелированного шума |
|
>> |
title(‘Correlated noise’) |
White noise
|
4 |
||||||||||
|
2 |
||||||||||
|
0 |
||||||||||
|
-2 |
||||||||||
|
-4 |
||||||||||
|
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
Correlated noise |
|
6 |
||||||||||
|
4 |
||||||||||
|
2 |
||||||||||
|
0 |
||||||||||
|
-2 |
||||||||||
|
-4 |
||||||||||
|
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
Рис. 3.33. Белый (сверху) и коррелированный (снизу) шум |
Графики белого шума и экспоненциально коррелированного сигнала показаны на рис. 3.33. Хорошо видно, что коррелированный шум сильно сглажен по сравнению с белым шумом.
Генерация дискретного нормального белого шума
Дискретный белый шум с нормальным распределением можно сгенерировать с помощью функции randn, имеющей следующий синтаксис:
X = randn(m, n)
В результате вызова функции генерируется массив X, содержащий m строк и n столбцов псевдослучайных чисел, имеющих нормальное распределение с нулевым математическим ожиданием и единичной дисперсией.
Параметр n при вызове можно опустить, по умолчанию используется значение n = m, т. е. генерируется квадратная матрица.
В задачах, связанных с обработкой сигналов, для генерации дискретного нормального белого шума удобнее использовать функцию wgn (white Gaussian noise) пакета Communications, поскольку она позволяет удобным образом задавать уровень генерируемого шума. Синтаксис вызова функции следующий:
y = wgn(m, n, p, imp, state, ‘powertype’, ‘outputtype’);
Здесь m и n — как и ранее, размеры генерируемой матрицы, а p — мощность генерируемого шума в единицах, задаваемых параметром ‘powertype’ (по умолчанию — в децибелах). Остальные параметры являются необязательными и имеют значения по умолчанию.
Параметр imp задает импеданс нагрузки в омах (предполагается, что генерируются отсчеты случайного напряжения на этой нагрузке). По умолчанию используется импеданс нагрузки, равный 1 Ом.
Целочисленный параметр state позволяет принудительно задавать начальное состояние генератора гауссовских случайных чисел MATLAB (функция randn). По умолчанию используется текущее состояние.
Строковый параметр ‘powertype’ задает единицы измерения мощности, использованные при указании параметра p. Возможны следующие значения:
‘dB’ — мощность p задается в децибелах относительно 1 Вт, значению 0 дБ соответствует дисперсия, равная imp^2;
‘dBm’ — мощность p задается в децибелах относительно 1 мВт, значению 0 дБ соответствует дисперсия, равная imp^2/1000;
‘linear’ — мощность p задается в ваттах, дисперсия генерируемого шума равна
p*imp.
Строковый параметр ‘outputtype’ позволяет задавать генерацию вещественного или комплексного шума. Возможны значения ‘real’ (вещественный шум; генерируется по умолчанию) и ‘complex’ (комплексный шум). Если генерируется комплексный шум, его вещественная и мнимая части имеют мощности p/2.
Добавление белого шума к сигналу
В том же пакете Communications имеется еще одна полезная функция, работающая с нормальным белым шумом. Это функция awgn, реализующая канал связи с аддитивным белым гауссовым шумом (additive white Gaussian noise channel, AWGN channel), т. е. добавляющая к сигналу белый шум с заданным уровнем. Синтаксис вызова функции следующий:
y = awgn(x, snr, sigpower, state, ‘powertype’);
Здесь x — вектор отсчетов сигнала. Скаляр snr задает отношение сигнал/шум в единицах, задаваемых параметром ‘powertype’ (по умолчанию — в децибелах). Остальные параметры являются необязательными и имеют значения по умолчанию.
Параметр sigpower указывает мощность сигнала x в единицах, задаваемых параметром ‘powertype’ (по умолчанию — в децибелах). По умолчанию предполагается, что мощность сигнала равна 0 дБ, т. е. средний квадрат модуля значений из вектора x равен единице. Параметр sigpower может также принимать строковое значение ‘measured’, при этом мощность сигнала автоматически измеряется.
Целочисленный параметр state позволяет принудительно задавать начальное состояние генератора гауссовских случайных чисел MATLAB (функция randn). По умолчанию используется текущее состояние.
Строковый параметр ‘powertype’ задает единицы измерения мощности, использованные при указании параметров snr и sigpower. Возможны следующие значения:
‘dB’ — мощность сигнала и отношение сигнал/шум задаются в децибелах;
‘linear’ — мощность сигнала задается в ваттах, отношение сигнал/шум — в разах.
При расчете мощности сигнала предполагается, что значения вектора x представляют собой отсчеты напряжения на нагрузке с импедансом 1 Ом.
Результатом работы является вектор «зашумленных» отсчетов y. Если значения x являются вещественными, функция awgn добавляет вещественный шум, если комплексными — комплексный шум.
Получение данных из внешних источников
Преобразование аналогового сигнала в цифровой и обратно — это процессы, которые выполняются аппаратными средствами. MATLAB же, будучи программным продуктом, может лишь взаимодействовать с соответствующим оборудованием (такое взаимодействие осуществляется, например, с помощью пакета Data Acquisition). Кроме того, в MATLAB предусмотрены средства для воспроизведения и записи звука, а также для работы со звуковыми файлами формата WAV. В данном разделе мы подробно рассмотрим считывание и запись WAV-файлов, а также воспроизведение звука. Детально рассматривать вопросы взаимодействия с оборудованием ввода/вывода данных из-за ограниченного объема книги не представляет-
ся возможным, поэтому в конце главы будет приведен лишь краткий обзор возможностей и демонстрационных примеров пакета Data Acquisition.
Чтение WAV-файлов
Для считывания WAV-файлов в MATLAB имеется функция wavread. В простейшем случае она может быть использована следующим образом:
y = wavread(‘filename’);
Здесь filename — имя звукового файла (расширение .wav указывать не обязательно). В имя файла необходимо включить полный путь, за исключением тех случаев, когда файл находится в текущем (для MATLAB) каталоге или в одном из каталогов, входящих в список поиска MATLAB.
Врезультате вызова функции в переменную y будет помещено все содержимое указанного файла. Строки матрицы y соответствуют отсчетам сигнала, столбцы — каналам, которых в WAV-файле может быть несколько.
Взвуковых файлах отсчеты сигнала представлены целыми числами, лежащими в диапазоне –128…+127 (8 бит на отсчет) либо –32 768…+32 767 (16 бит на отсчет). Управлять нормировкой считываемых отсчетов можно с помощью дополнительного строкового параметра ‘fmt’, добавляемого в конце списка входных параметров функции wavread. При принятом по умолчанию варианте ‘double’ значения отсчетов приводятся к диапазону –1…+1, а при значении ‘native’ функция возвращает целые числа в том виде, в каком они хранятся в WAV-файле.
Помимо собственно отсчетов сигнала, в WAV-файлах хранится еще и служебная информация о частоте дискретизации, количестве бит на отсчет и т. п. Узнать частоту дискретизации можно, используя при вызове функции второй выходной параметр:
[y, Fs] = wavread(‘filename’);
При этом переменная Fs получает значение, равное частоте дискретизации в герцах.
Чтобы узнать, сколько уровней сигнала содержится в звуковом файле (точнее, число бит на отсчет), необходимо добавить третий выходной параметр:
[y, Fs, bits] = wavread(‘filename’);
Еще два параметра, которые часто хочется знать заранее, — это число отсчетов и каналов записи. Для получения данной информации нужно вызвать функцию wavread с двумя входными параметрами. Первый — это по-прежнему имя файла, вторым же должна быть текстовая строка ‘size’:
wavesize = wavread(‘filename’, ‘size’);
В отличие от предыдущих вариантов вызова функции, в данном случае не производится считывания самих звуковых данных. Из WAV-файла лишь извлекается служебная информация, которая возвращается в виде двухэлементного вектора-строки
(в приведенном примере — wavesize). Первый элемент вектора содержит число отсчетов, второй — число каналов.
Наконец, имеется и важнейшая возможность считывания данных из WAV-файла не целиком, а отдельными фрагментами (без этого нельзя было бы работать с большими файлами). Для этого также используется второй входной параметр функции wavread. Если этот параметр является числом, будет считано соответствующее количество отсчетов (начиная с первого):
y = wavread(‘filename’, N);
Если же нужный фрагмент расположен не в начале файла, придется указать его начало и конец. В этом случае второй входной параметр функции wavread должен представлять собой двухэлементный вектор:
y = wavread(‘filename’, [n1 n2]);
В результате в переменную y будут считаны отсчеты с номерами от n1 до n2 включительно (нумерация отсчетов, как и элементов матриц в MATLAB, начинается с единицы). При этом считываются все каналы звукозаписи. Возможности считывания информации из отдельных каналов не предусмотрено.
СОВЕТ
Как видите, получить информацию о частоте дискретизации и числе бит на отсчет можно только одновременно со считыванием звуковых данных. Если необходимо получить эту информацию заранее, до основной работы со звуком, можно попросить MATLAB считать всего один отсчет:
[y, Fs, bits] = wavread(‘filename’, 1);
Рассмотрим работу с WAV-файлами на конкретном примере. Возьмем для этого бодрый аккорд tada.wav, входящий в стандартный набор звуков Windows.
Прежде всего узнаем число отсчетов и каналов:
>> wavesize = wavread(‘c:windowsmediatada’, ‘size’)
wavesize =
42752 2
Как видим, эта стереозапись (2 канала) содержит 42752 отсчета.
Далее извлекаем информацию о частоте дискретизации и числе бит на отсчет:
>> [y, Fs, bits] = wavread(‘c:windowsmediatada’, 1) y =
00
Fs =
22050
bits = 16
Полученные результаты очевидны — частота дискретизации 22,05 кГц, используется 16 бит на отсчет (65 536 уровней сигнала). «В нагрузку» мы получили значения первого отсчета из обоих каналов (вектор y).
Теперь мы можем узнать о файле кое-что еще, например определить продолжительность звучания. Для этого нужно разделить число отсчетов (первый элемент полученного ранее вектора wavesize) на частоту дискретизации Fs:
>> wavesize(1)/Fs
ans =
1.9389
Результат — длительность звука в секундах.
Чтобы узнать, сколько памяти потребуется MATLAB для хранения всей записи, нужно перемножить число отсчетов и число каналов, а затем увеличить результат еще в 8 раз. Можно сразу же поделить полученное значение на 1024, чтобы получить ответ в килобайтах, или на 10242, если ожидаемое число лучше измерять мегабайтами:
>> prod(wavesize)*8/1024
ans =
668
Расход памяти оказывается небольшим (668 Кбайт), так что можно считать файл в память целиком (не забудьте про точку с запятой в конце строки):
>> y = wavread(‘c:windowsmediatada’);
Теперь все содержимое файла считано в матрицу y. Проверим ее размеры:
>> size(y)
ans =
42752 2
Как видите, размеры совпадают с полученной ранее информацией о файле: 42752 отсчета (строк), два канала (столбца).
Чтобы «окинуть взглядом» звуковой сигнал, выведем его в виде графика — отдельно для правого и левого каналов стереозаписи, используя для этого функцию subplot (подробнее об использовании этой функции речь пойдет в разд. «Одновременный вывод нескольких графиков» приложения 1). Результат показан на рис. 3.34:
>>subplot(2, 1, 1)
>>plot(y(:, 1))
>>subplot(2, 1, 2)
>>plot(y(:, 2))
Если при выводе графика разрешение по горизонтали имеет большее значение, чем по вертикали, можно воспользоваться функцией strips, специально предназначенной для отображения длинных сигналов в «нарезанном» на фрагменты виде (фрагменты выводятся друг под другом). Синтаксис вызова функции strips следующий:
strips(x, N)

|
198 |
Глава 3 |
|||||||||
|
Здесь x — вектор отсчетов сигнала (двумерные массивы не допускаются), N — чис- |
||||||||||
|
ло отсчетов в каждом фрагменте (этот параметр можно опустить, по умолчанию |
||||||||||
|
размер фрагмента составляет 200 отсчетов). |
||||||||||
|
0.4 |
||||||||||
|
0.2 |
||||||||||
|
0 |
||||||||||
|
-0.2 |
||||||||||
|
-0.4 |
||||||||||
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
|
|
x 104 |
||||||||||
|
0.4 |
||||||||||
|
0.2 |
||||||||||
|
0 |
||||||||||
|
-0.2 |
||||||||||
|
-0.4 |
||||||||||
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
|
|
x 104 |
||||||||||
|
Рис. 3.34. График звукового сигнала |
||||||||||
|
В качестве примера выведем с помощью функции strips график первого (левого) |
||||||||||
|
канала сигнала tada.wav (рис. 3.35): |
||||||||||
|
>> strips(y(:,1), 10000) |
||||||||||
|
0 |
||||||||||
|
10000 |
||||||||||
|
20000 |
||||||||||
|
30000 |
||||||||||
|
40000 |
||||||||||
|
0 |
1000 |
2000 |
3000 |
4000 |
5000 |
6000 |
7000 |
8000 |
9000 |
10000 |
|
Рис. 3.35. График сигнала, выведенный с помощью функции strips |
Над помещенным в переменную MATLAB звуковым сигналом можно выполнять любые преобразования, а затем воспроизвести полученный звук или сохранить его в виде нового WAV-файла. Обо всем этом речь пойдет в нескольких следующих разделах. Можно также сохранить сигнал на диске как переменную MATLAB (в виде MAT-файла) — см. разд. «Ввод и вывод данных » приложения 1.
Функция wavread не является встроенной — она целиком написана на языке MATLAB с использованием средств работы с двоичными файлами. Если вас интересует структура WAV-файлов и организация их считывания, попробуйте разобраться в тексте функции wavread — файл wavread.m расположен в папке Program FilesMATLABR2010atoolboxmatlabaudiovideo.
MATLAB умеет работать только с несжатыми WAV-файлами (формат PCM — Pulse Code Modulation). При попытке считать файл, в котором использован какойлибо из методов сжатия информации, будет выдано сообщение «Data compression format (…) is not supported».
Запись WAV-файлов
Чтобы записать вектор (или матрицу) на диск в виде WAV-файла, используется функция wavwrite:
wavwrite(y, Fs, N, ‘filename’)
Здесь y — записываемые данные (вектор для монофонической записи, двухстолбцовая матрица — для создания стереофайла), Fs — частота дискретизации в герцах, N — число бит на отсчет (8 или 16), ‘filename’ — имя создаваемого файла. Выходных параметров у данной функции нет.
Параметры N и Fs можно опускать, при этом используются значения по умолча-
нию — N = 16 и Fs = 8000:
wavwrite(y, Fs, ‘filename’) wavwrite(y, ‘filename’)
Записываемые данные должны быть вещественными и лежать в диапазоне –1…1. Значения, выходящие из этого диапазона, будут «обрезаны» и сделаны равными ±1.
Воспроизведение звука
Если ваш компьютер оборудован звуковой картой, то, помимо работы с WAVфайлами, вы имеете и возможность воспроизведения векторов и матриц в звуковом виде. Для этого есть целых три функции — sound, soundsc и wavplay. В простейшем случае все три функции вызываются одинаково и обеспечивают воспроизведение вектора y (или двухстолбцовой матрицы — для стереозвука), содержащего отсчеты сигнала, с заданной частотой дискретизации Fs (в герцах):
sound(y, Fs)
soundsc(y, Fs)
wavplay(y, Fs)

Различие между этими функциями заключается в предоставляемых ими дополнительных возможностях.
Функция sound
Функция sound обеспечивает воспроизведение сигнала с заданными частотой дискретизации и числом уровней (бит на отсчет):
sound(y, Fs, bits)
Здесь y — вектор или двухстолбцовая матрица отсчетов сигнала, Fs — частота дискретизации в герцах, bits — число бит на отсчет (8 или 16).
Параметры bits и Fs можно опускать, при этом будут использоваться их значения по умолчанию: Fs = 8192 и bits = 16.
Воспроизводимые данные y должны быть вещественными и лежать в диапазоне –1…1. Значения, выходящие из этого диапазона, «обрезаются» и делаются равными ±1.
Выходных параметров у функции нет. После вызова она передает вектор y звуковой карте для воспроизведения и сразу же, не дожидаясь окончания звука, возвращает управление командной строке MATLAB.
Если следующая команда sound будет использована до окончания предыдущего звука, будет выдано сообщение об ошибке «Unable to open sound device» (Невозможно открыть звуковое устройство).
Функция soundsc
Функция soundsc (Sound scaled) отличается от функции sound лишь тем, что производит предварительное масштабирование отсчетов сигнала. Для управления масштабированием добавляется четвертый входной параметр s_lim:
soundsc(y, Fs, bits, s_lim)
Здесь входные параметры y, Fs, bits имеют то же назначение, что и для функции sound. Параметр s_lim должен быть двухэлементным вектором [s_low s_high], он задает диапазон значений, который будет линейно преобразован к интервалу –1…1. Преобразование, таким образом, производится по формуле
y′ = 2 y − (slow + shigh ) .
shigh − slow
При s_lim = [-1 1] функция soundsc эквивалентна функции sound.
Параметры s_lim, bits и Fs при вызове можно опускать, при этом используются их
значения по умолчанию: Fs = 8192, bits = 16 и s_lim = [min(y) max(y)]. Значение
по умолчанию для s_lim обеспечивает точное приведение полного диапазона значений сигнала к интервалу –1…1.
Функция wavplay
Наконец, третья функция, предназначенная для воспроизведения звука, имеет имя
wavplay:
wavplay(y, Fs, ‘mode’)
Входные параметры y и Fs имеют тот же смысл, что и у предыдущих функций, а параметр ‘mode’ управляет режимом воспроизведения. Этот параметр может принимать два значения:
‘sync’ — синхронный режим, означающий, что функция вернет управление интерпретатору MATLAB только после окончания звука;
‘async’ — асинхронный режим, при котором функция передает данные для воспроизведения звуковым драйверам Windows и сразу же возвращает управление системе MATLAB, не дожидаясь окончания звука.
Параметры ‘mode’ и Fs при вызове можно опускать, при этом используются их зна-
чения по умолчанию: Fs = 11025 и ‘mode’ = ‘async’.
Синхронный режим позволяет организовать в MATLAB-программе выдачу нескольких звуков подряд, не заботясь о расчете и соблюдении временных интервалов между соответствующими командами. В асинхронном же режиме можно одновременно с воспроизведением звука продолжать выполнение программы. К сожалению, при этом нет возможности программным путем проверить, закончилось ли воспроизведение звука.
ЗАМЕЧАНИЕ 1
Такая программная проверка будет возможна, если для воспроизведения звука воспользоваться средствами пакета Data Acquisition (краткая информация о его возможностях приводится далее).
ЗАМЕЧАНИЕ 2
Помимо перечисленных, воспроизводить звук позволяет также функция audioplayer, реализующая MATLAB-интерфейс для аудиопроигрывателя системы Windows.
Запись звука
Функция wavrecord позволяет записать звук в переменную MATLAB с помощью звуковой карты компьютера:
y = wavrecord(n, Fs, ch, ‘dtype’)
Здесь n — число записываемых отсчетов, Fs — частота дискретизации в герцах, ch — число каналов записи, ‘dtype’ — тип записываемых данных.
Возвращаемый результат y — матрица, каждый столбец которой соответствует одному каналу записи. При стереозаписи первый столбец — левый канал, второй — правый.
Для параметра ‘dtype’ возможны следующие значения:
‘double’ — 16-битовая запись, данные масштабируются к диапазону –1…1
и представляются в 8-байтовом формате с плавающей запятой;
‘single’ — 16-битовая запись, данные масштабируются к диапазону –1…1
и представляются в 4-байтовом формате с плавающей запятой;
‘int16’ — 16-битовая запись, данные представляются в двухбайтовом целочис-
ленном формате (диапазон –32768…32767);
‘uint8’ — 8-битовая запись, данные представляются в однобайтовом беззнаковом целочисленном формате (диапазон 0…255, нулевому напряжению на входе соответствует значение 128).
Входные параметры ‘dtype’, ch и Fs можно опускать, при этом будут использовать-
ся их значения по умолчанию: Fs = 11025, ch = 1, ‘dtype’ = ‘double’.
ЗАМЕЧАНИЕ
Еще одна функция, позволяющая осуществлять запись звука — audiorecorder. Она реализует MATLAB-интерфейс для программы звукозаписи, входящей в состав системы Windows.
Готовые записи сигналов
В разделе Audio базовой библиотеки MATLAB и в пакете расширения Signal Processing имеется несколько готовых записей сигналов, сохраненных в виде MAT-файлов. Эти сигналы используются в качестве исходных данных в примерах, приводимых в документации, и демонстрационных программах. Возможно, вам они пригодятся для тестирования собственных программ и алгоритмов. Сведения об имеющихся сигналах приведены в табл. 3.1.
Таблица 3.1. Записи сигналов, имеющиеся в MATLAB
|
Имя |
Частота |
||||
|
Имя файла |
Пакет |
перемен- |
Размер |
дискретиза- |
Характер звука |
|
ной |
ции |
||||
|
chirp.mat |
MATLAB |
y |
13129 (1,6 с) |
8192 Гц |
Импульсы с меняю- |
|
щейся частотой |
|||||
|
gong.mat |
MATLAB |
y |
42028 (5,1 с) |
8192 Гц |
Удар гонга |
|
handel.mat |
MATLAB |
y |
73113 (8,9 с) |
8192 Гц |
Хор |
|
laughter.mat |
MATLAB |
y |
52634 (6,4 с) |
8192 Гц |
Смех |
|
splat.mat |
MATLAB |
y |
10001 (1,2 с) |
8192 Гц |
Тон с меняющейся |
|
частотой, затем звук |
|||||
|
удара |
|||||
|
train.mat |
MATLAB |
y |
12880 (1,5 с) |
8192 Гц |
Гудок поезда |

|
Дискретные сигналы |
203 |
||||||
|
Таблица 3.1 (окончание) |
|||||||
|
Имя |
Частота |
||||||
|
Имя файла |
Пакет |
перемен- |
Размер |
дискретиза- |
Характер звука |
||
|
ной |
ции |
||||||
|
mtlb.mat |
SP |
mtlb |
4001 (0,54 с) |
7418 Гц |
Произнесенное слово |
||
|
«MATLAB» |
|||||||
|
vcosig.mat |
SP |
vcosig |
19661 (2,4 с) |
8192 Гц |
Данный сигнал имеет |
||
|
очень забавную |
|||||||
|
спектрограмму |
|||||||
Пакет расширения Data Acquisition
Пакет расширения Data Acquisition позволяет непосредственно из MATLAB работать с оборудованием аналогового и цифрового ввода/вывода данных. В комплект поставки входят драйверы для следующих устройств:
звуковых карт, поддерживаемых операционной системой Windows;
параллельных портов персонального компьютера (LPT);
плат ввода/вывода фирм Advantech, Measurement Computing и National Instruments.
Разработать драйверы для других устройств можно с помощью Data Acquisition Toolbox Adaptor Kit; дополнительную информацию можно получить на сайте фирмы The MathWorks, Inc. по адресу http://www.mathworks.com/products/daq/.
Пакет Data Acquisition (разумеется, в сочетании с перечисленным оборудованием) предоставляет следующие возможности:
аналоговый ввод и вывод информации в реальном масштабе времени, включая возможность одновременного выполнения аналого-цифрового и цифроаналогового преобразований;
цифровой ввод и вывод информации в реальном масштабе времени;
запись вводимых данных на диск либо их загрузка непосредственно в рабочую область памяти MATLAB в виде переменных;
буферизацию данных для осуществления ввода в фоновом режиме;
триггеры, управляемые программно или аппаратно генерируемыми событиями (это дает возможность осуществлять синхронизацию — например, запускать процесс аналогового ввода при достижении входным сигналом некоторого уровня).
Подробно рассматривать пакет Data Acquisition в рамках данной книги не представляется возможным, поэтому покажем лишь пример использования его возможностей в двух демонстрационных программах, поставляемых в составе пакета.
Первая программа реализует осциллограф, позволяя просматривать графики сигналов, получаемых от имеющихся в системе устройств ввода данных. Данная про-

грамма может быть вызвана из командной строки (ее имя — daqscope) либо из окна справочной системы (команда меню Help | Product Help, раздел оглавления справки Data Acquisition ToolboxDemosGUI DemosAnalog Input Oscilloscope).
Вид окна осциллографа приведен на рис. 3.36. Имеющиеся в окне элементы управления позволяют выбирать источник сигнала (списки в правом верхнем углу окна), задавать частоту дискретизации (флажок и поле ввода Sample Rate), устанавливать масштаб изображения по вертикали (переключатели Volts/Div и Autoset и поле ввода для ручного ввода вертикального масштаба) и горизонтали (ползунок X-Axis Range). Две кнопки на панели инструментов окна управляют запуском и остановкой процесса приема и отображения сигнала.
Рис. 3.36. Осциллограф — демонстрационный пример пакета Data Acquisition
ЗАМЕЧАНИЕ
Более серьезный вариант осциллографа реализован в виде еще одной функции пакета Data Acquisition — softscope.
Второй пример — генератор сигналов различной формы. Имя программы для вызова из командной строки — daqfcngen. При использовании окна справочной системы после вызова команды меню Help | Product Help необходимо выбрать в оглавлении справки раздел Data Acquisition ToolboxDemosGUI DemosAnalog Output Function Generator.
Вид окна генератора приведен на рис. 3.37. В списке, расположенном в левой части окна над полем графика, выбирается тип генерируемого сигнала:
Sine — гармонический сигнал;
Sinc — периодическая sinc-функция (функция Дирихле);

Square — последовательность прямоугольных импульсов;
Triangle — последовательность симметричных треугольных импульсов;
Sawtooth — последовательность пилообразных импульсов;
Random — случайный сигнал;
Chirp — колебания с плавно меняющейся частотой.
Рис. 3.37. Функциональный генератор — демонстрационный пример пакета Data Acquisition
Набор параметров, настраиваемых в нижней части окна, зависит от выбранного типа сигнала.
56
Если число отсчетов периодического сигнала x(nT) равно N за
период, то число отсчетов Ck ДПФ будет равно
1) N–1;
2) N;
3) N+1;
4) 2N.
57
Спектр Ck дискретного
периодического сигнала задан N отсчетами. Число
отсчетов дискретного сигнала x(nT) за
период TC равен
1) N–1;
2) N;
3) N+1;
4) 2N.
58
Отсчеты спектра дискретного периодического сигнала Ck для ДПФ
определяются выражением
1) Ck=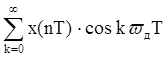
2) Ck=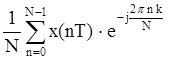
3) Ck=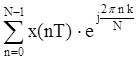
4) Ck=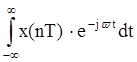
59
Если известны отсчеты C0,C1,…,CN–1 спектра
дискретного периодического сигнала x(nT), то
отсчеты самого сигнала определяются, как
1) x(nT)= 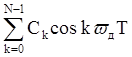
2) x(nT)= 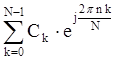
3) x(nT)= 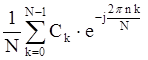
4) x(nT)=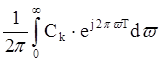
60
Прямое дискретное преобразование Фурье позволяет найти
1) отсчеты
дискретного сигнала x(nT);
2) отсчеты
спектра дискретного сигнала Ck;
3) интервал
дискретизации;
4) период
повторения спектра сигнала.
61
Обратное дискретное преобразование Фурье позволяет
найти
1) отсчеты
дискретного сигнала x(nT);
2) отсчеты спектра
дискретного сигнала Ck;
3) интервал
дискретизации;
4) период
повторения спектра сигнала.
62
Для периодического дискретного сигнала x(nT)
частота
дискретизации спектра F при дискретном преобразовании Фурье равна
1)
0,1 кГц;
2)
1 кГц;
3)
0,2 кГц;
4)
2 кГц.
63
Частота
дискретизации F спектра сигнала в дискретном преобразовании
Фурье равна
1)
частоте дискретизации
сигнала fд;
2)
верхней частоте спектра
исходного аналогового сигнала Fв;
3)
удвоенной частоте спектра
исходного аналогового сигнала 2Fв;
4)
величине,
обратной периоду повторения дискретного сигнала 1/Tс.
64
Если спектр
прямого дискретного преобразования Фурье имеет вид
то число
отсчетов дискретного сигнала x(nT) за период равно
1)
5;
2)
6;
3)
9;
4)
?10.
65
Если частота
дискретизации дискретного периодического сигнала x(nT),
заданного N отсчетами за период сигнала равна fд, то
частота дискретизации F спектра ДПФ равна
1)
fд;
2)
2fд;
3)
fд/N;
4)
N· fд.
66
Если
дискретный сигнал x(nT) задан N отсчетами за
период сигнала TC, то частота дискретизации спектра сигнала F
ДПФ равна
1)
1/NTC;
2)
1/TC;
3)
N/TC;
4)
2/TC.
67
Число
отсчетов Ck={C0,C1,…} дискретного преобразования Фурье сигнала за период
дискретизации ωд x(n)={x0,x1,…,xN–1} равно
1)
N–1;
2)
N;
3)
N+1;
4)
2N.
68
Для
дискретной последовательности x(nT)={1;1;0}
Z–преобразование X(z)
равно
1)
1+z–1;
2)
–1+z–2;
3)
1–z–1+z–2;
4)
z–1–z–2.
69
Для
дискретной последовательности
x(nT)={–1;0;1} Z–преобразование
X(z) равно
1)
1+z–1;
2)
–1+z–2;
3)
1–z–1+z–2;
4)
z–1–z–2.
70
Для
дискретной последовательности
x(nT)={1;–1;1} Z–преобразование
X(z) равно
1)
1+z–1;
2)
–1+z–2;
3)
1–z–1+z–2;
4)
z–1–z–2.
71
Для
дискретной последовательности x(nT)={0;1;–1} Z–преобразование
X(z) равно
1)
1+z–1;
2)
–1+z–2;
3)
1–z–1+z–2;
4)
z–1–z–2.
72
Z–преобразование X(z)
дискретного сигнала x(n)=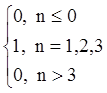
1)
1+z–1+z–2+z–3;
2)
z–1+z–2+z–3;
3)
1+z–1+z–2;
4)
1–z–1–z–2.
74
Z–преобразование X(z)
дискретного экспоненциального сигнала x(nT)=
=e–α·nT равно
Из рассмотренных ранее преобразований Фурье следует, что для восстановления сигнала по его спектру необходимо учитывать все составляющие с частотами, находящимися в интервале от нуля до бесконечности. Однако физически такая процедура нереальна. Кроме того, вклад составляющих при ω → 0 пренебрежимо мал, поскольку энергия сигнала является ограниченной.
Наконец, любое устройство для передачи и приема сигналов имеет конечную ширину полосы пропускания. Поэтому обычно рассматриваются сигналы, спектральная плотность которых отличается от нуля в некоторой ограниченной полосе частот.
С другой стороны, используемые в системах телекоммуникаций линии радио- и проводной связи также имеют ограничения частотного ресурса. Следовательно, существует серьезная проблема: как в ограниченном диапазоне частот поместить все увеличивающееся множество сигналов, спектры которых состоят из компонент, сосредоточенных в некоторой сравнительно узкой полосе частот. Одним из возможных путей решения данной проблемы может быть передача не самих полосовых сигналов, а лишь их выборок или дискретных отсчетов, содержащих информацию обо всем сигнале. Однако при этом возникает естественный вопрос: можно ли это сделать и с каким временнЫм интервалом должны производиться эти выборки, чтобы не потерять даже части передаваемой информации?
Ответ на этот вопрос содержится в фундаментальной работе «О пропускной способности «эфира» и проволоки в электросвязи», которая появилась в 1933 г. и принадлежала 25-летнему инженеру В. А. Котельникову.
Именно ему в этой работе удалось сделать то, что предопределило перспективы развития теории и техники телекоммуникаций на многие годы вперед.
Отметим, что похожие вопросы исследовали и другие специалисты и ученые. Так, в 1915 г. Е.Т. Уиттакер, занимаясь математической теорией интерполяции, доказал теорему, посвященную проблеме аппроксимации целых функций конечной степени. В математике это была одна из рядовых теорем, и к теории связи она не имела никакого отношения. В 1928 г. американец Найквист, решая задачу передачи телеграфных (дискретных) сообщений без искажений, обратил внимание на возможность взятия выборок сигнала через интервалы времени, обратно пропорциональные ширине его спектра. Однако решаемая им проблема отличалась от проблемы передачи аналоговых полосовых сигналов, рассматривавшихся В.А. Котельниковым, хотя здесь и имелись общие моменты.
Наконец, в 1948 г. К.Э. Шеннон вновь доказал теорему, повторяющую результаты работы В.А. Котельникова, которую опубликовали весьма ограниченным тиражом, и она могла быть неизвестна за границей.
В настоящее время специалистам связи, радиотехники и других смежных областей науки и техники хорошо знакома «теорема отсчетов», нередко именуемая в отечественной литературе теоремой Котельникова. В некоторых источниках ее также называют теоремой отсчетов (выборок) Уиттакера—Котельникова—Шеннона. На самом деле В.А. Котельников доказал семь теорем, две из которых являются основополагающими, а остальные их дополняют и конкретизируют. Их значение так велико, что по сути они являются основой современной теории и практики электрической связи, на которой построены многие системы телекоммуникаций.
Содержание
- Формулировки основных теорем Котельникова
- Теорема 1.
- Теорема 2.
- Погрешности при восстановлении сигналов
- Области применения теоремы отсчетов
Формулировки основных теорем Котельникова
Теорема 1.
Любую функцию S(t), состоящую из частот от 0 до Fв периодов в секунду, можно представить рядом
где k — целые числа; S(kΔt) — постоянные, зависящие от S(t); Fв — верхняя частота спектра.
И наоборот, любая функция S(t), представленная этим рядом, состоит лишь из частот от 0 до Fв периодов в секунду.
Выражение (2.21) принято называть рядом Котельникова. Если обратиться к обобщенному ряду Фурье (2.8), то легко увидеть, что в выражении (2.21) базисными по существу являются отсчетные функции
представленные на рис. 2.11, а коэффициенты разложения по данному базису (Формула).
Рис. 2.11. График функции отсчетов
Теорема 2.
Любую функцию (сигнал) S(t), состоящую из частот от 0 до Fв периодов в секунду, можно непрерывно передавать с любой точностью с помощью чисел, следующих друг за другом через интервалы времени Δt = 1 / (2Fв) секунд.
Отметим, что промежутки времени, через которые берутся отсчеты, получили название «интервалов Найквиста». Доказательство данной теоремы В.А. Котельников построил на следующих рассуждениях. Если измерять величину S(t) при t = n / (2Fв), где n — целое число, то можно записать
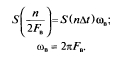
Вторая теорема Котельникова вошла во многие учебники под названием теоремы отсчетов.
Приведем теперь основные свойства функции отсчетов.
- В момент времени t = 0 функция отсчетов имеет максимальное значение, равное единице.
- В моменты времени t = ±kΔt = k / (2Fв), где k = 1, 2, …, οτсчетные функции обращаются в нуль.
- Ширина главного лепестка функции на нулевом уровне равна 1/ Fв.
- Отсчетные функции являются ортогональными в бесконечно большом интервале времени, т.е.
Рассмотрим теперь процесс восстановления непрерывного сигнала S(t) по его дискретным отсчетам. Из теоремы отсчетов следует, что для передачи по каналу связи сигнала S(t) с ограниченным спектром необходимо выполнить следующие операции.
- Взять отсчеты мгновенных значений сигнала S(kΔt) через интервалы времени Δt = k / (2Fв), где k = 1, 2, …, т.е. найти величины (Формула).
- Передать по каналу найденные отсчеты любым из возможных методов.
- На приемной стороне восстановить переданные отсчеты и сформировать короткие импульсы с длительностью (Формула) и амплитудами S(kΔt).
- Сформировать функции отсчетов (Формула), k = 1, 2, …, как показано на рис. 2.12.
- Произвести суммирование найденных функций и получить в результате сигнал (Формула), который будет пропорционален (или равен) переданному сигналу S(t).
Рис. 2.12. Формирование отсчетов аналогового сигнала в дискретные моменты времени
Рис. 2.13. Амплитудно-частотная (а) и фазо-частотная (б) характеристики фильтров, формирующих функции отсчетов: 1 — идеального; 2 — реального
Для получения отсчетных функций обычно применяется фильтр нижних частот с шириной полосы пропускания, равной Fв, на вход которого следует подать короткий импульс с длительностью (Формула) и амплитудой S(kΔt). Если фильтр считать идеальным, а на его вход подавать дельта-импульс δ(t), то отсчетная функция на выходе не будет иметь искажений, так как АЧХ k(f) фильтра равномерная, а ФЧХ φ(f) — линейная (рис. 2.13):
Погрешности при восстановлении сигналов
На самом деле при восстановлении сигнала возникают погрешности. Рассмотрим кратко причины их возникновения на практике.
- Характеристики реальных фильтров k(f) и φ(f) отличаются от идеальных (см. кривые 2 на рис. 2.13), что приводит к отклонениям реальных отсчетных функций от идеальных, а следовательно, к появлению некоторых неточностей восстановления непрерывного сигнала S(t).
- Для восстановления сигнала по его отсчетным функциям необходимо просуммировать бесконечное множество членов ряда Котельникова (2.21). Однако реальные сигналы S(t) имеют ограниченные спектры и рассматриваются в конечном интервале времени Т. В связи с этим точное разложение приходится заменять приближенным, т.е. при котором также суммируется конечное число членов ряда:
Число отсчетов, определяющее (Формула), при Δt = 1 / (2Fв) составляет
n = T / Δt + 1 = 2FвT + 1 (обычно (Формула)), поэтому n = 2FвT.
Параметр n = 2FвT, иногда обозначаемый символом В и называемый «базой сигнала», играет важную роль в ТЭС при рассмотрении сложных сигналов.
Ясно, что погрешность при восстановлении сигнала будет тем больше, чем меньшее число слагаемых учитывается при суммировании.
3. Спектры реальных сигналов не равны нулю за пределами граничной частоты. Основная доля энергии сигналов приходится на частоты от нуля до Fв, но небольшая доля этой энергии может быть и выше граничной частоты. Значение относительной среднеквадратичной погрешности можно определить следующим выражением:
где ΔЕ — часть энергии, которая выходит за пределы полосы частот [0, Fв] и не учитывается при восстановлении сигнала; Es — полная энергия сигнала.
При этом оказывается, что погрешность за счет отбрасываемой части спектра сигнала становится тем больше, чем «медленнее» убывает спектр за пределами граничной частоты Fв.
Области применения теоремы отсчетов
В заключение отметим основные области применения теоремы отсчетов.
- Упрощение представления сигналов или помех. Вместо непрерывных функций они задаются наборами отсчетных значений, и при этом не происходит потерь информации, содержащейся в непрерывном сигнале.
- Передача непрерывных сообщений по каналам связи с помощью дискретных или цифровых сигналов.
- Цифровая обработка непрерывных сигналов.
Примеры использования теоремы отсчетов будут рассмотрены далее.