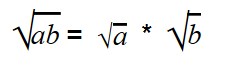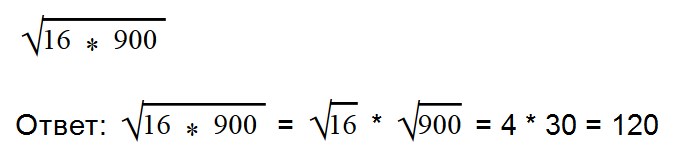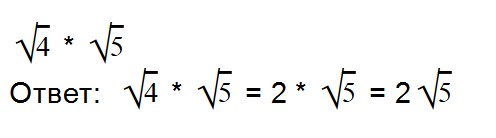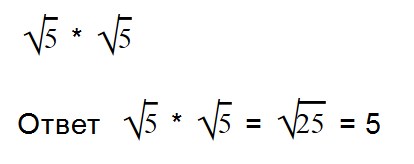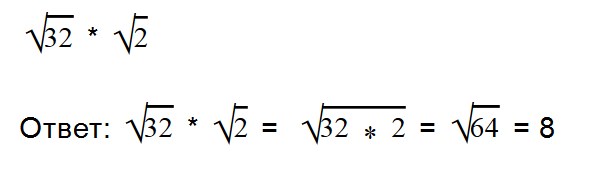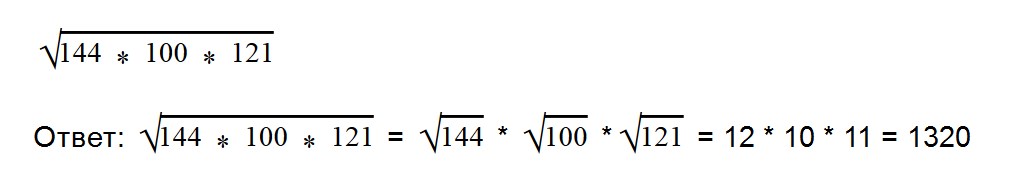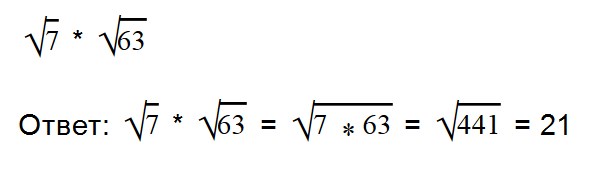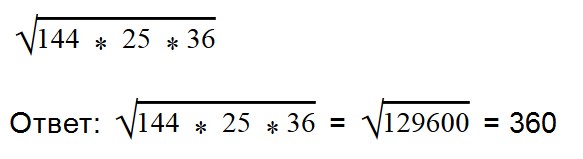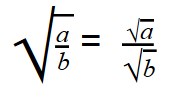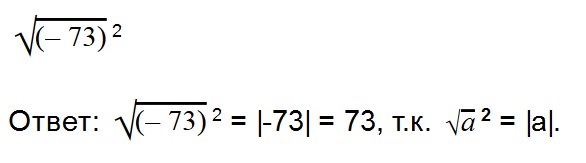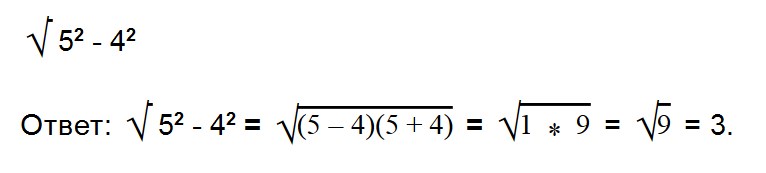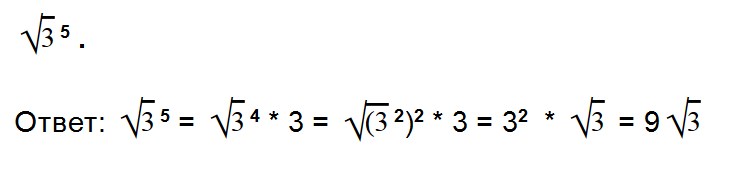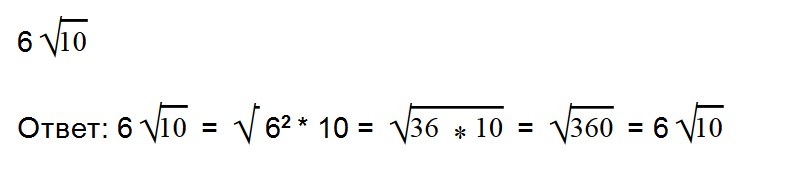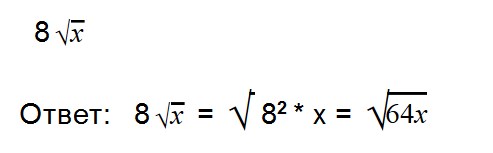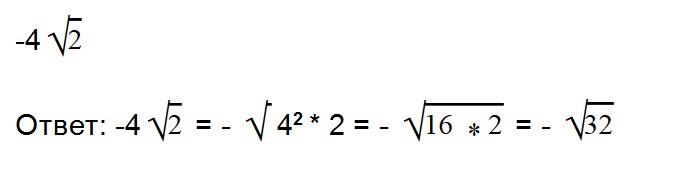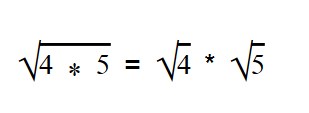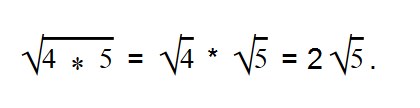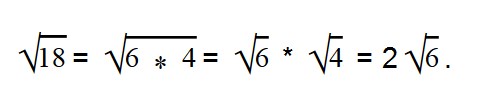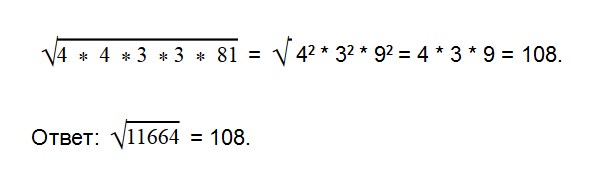Как найти число перед корнем - Исправление недочетов и поиск решений вместе с Examum.ru

Благодаря прочтению этой статьи вы научитесь:

Извлекать корни из разных чисел;
Решать разнообразные задания по этой тематике;
Применять удобные таблицы на практике.

А также пополните свой мозг новыми знаниями, что всегда хорошо и полезно! Приятным бонусом для вас будут задания для отработки материала с ответами, которые вы сможете найти в конце этой статьи. Что значит понятие: «Извлечение корня из числа»?

Определение

Извлечение корня из числа — это нахождение значения корня, т.е. действие, обратное возведению в степень.

Числа b и a равны, ведь при извлечении корня n-ной степени одного из чисел, мы, соответственно, находим и второе.

n — натуральное число, являющиеся степенью корня.
a — подкоренное значение.

Интересно

При помощи разложения функции в ряд можно показать, что сумма всех натуральных чисел равна:

1/12[18]

Когда следует извлекать корень? Если вы видите, что a можно представить в виде n-ной степени какого-либо числа b, то корень a можно извлечь.

Определение

Квадратный корень из числа — это неизвестное число, которое дает это же число при возведении его в квадрат.

Пример извлечения корня:

√25=5×5 — из этого становится ясно, что квадратный корень числа равен 5.

В обратной ситуации, когда нельзя представить корень n-ной степени из числа a, в виде n-ной степени числа b, корень не извлекается или находится лишь приближенное значение этого корня.

Пример:

√6≈√2,44949

Для этого используют различные виды решений, начиная с калькулятора, заканчивая формулами. Калькулятор хоть и посчитает все вместо нас, но не всегда мы можем его применить. Поэтому важно знать другие варианты нахождения приближенного значения корня.

Способы извлечения корня

Для того, чтобы найти значение корня, существуют такие способы извлечения корня, как:

Применение различных таблиц.
Разложение чисел или выражений на простые множители.
Извлечение корней из дробных чисел.
Извлечение отрицательного корня.
Поразрядное нахождение значения корня.

Они основываются на свойствах корней. Далее рассмотрим таблицы, которые могут помочь в процессе извлечения корней.

Квадраты натуральных чисел

Основной является таблица квадратов натуральных чисел:

	0	1	2	3	4	5	6	7	8	9
0	0	1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Она, пожалуй, самая распространенная среди школьников. Если в какой-то важный момент она вам необходима, но у вас отсутствует к ней доступ, можно воспользоваться несколькими хитростями:

Чтобы быстро возвести в квадрат число, на конце которого 0, можно добавить к нему парочку нулей: 80×80=6400; 30×30=900. Т.е., первые цифры умножаем и дописываем два 0 к этому числу.
Теперь возьмём какое-нибудь число так, чтобы вторая его цифра оканчивалась на 5. Так, например, число 75. Чтобы быстро возвести его в квадрат, прибавьте к первой цифре единицу, из чего получаются цифры 7 и 8.
Умножаем их и приписываем в конец число 25 и получаем конечный результат в виде числа 5625.

Квадратные корни

Вторая таблица — это таблица квадратных корней:

√x	0	1	2	3	4	5	6	7	8	9
0	0	1	1,41421	1,73205	2	2,23607	2,44949	2,64575	2,82843	3
1	3,16228	3,31662	3,4641	3,60555	3,74166	3,87298	4	4,12311	4,24264	4,3589
2	4,47214	4,58258	4,69042	4,79583	4,89898	5	5,09902	5,19615	5,2915	5,38516
3	5,47723	5,56776	5,65685	5,74456	5,83095	5,91608	6	6,08276	6,16441	6,245
4	6,32456	6,40312	6,48074	6,55744	6,63325	6,7082	6,78233	6,85565	6,9282	7
5	7,07107	7,14143	7,2111	7,28011	7,34847	7,4162	7,48331	7,54983	7,61577	7,68115
6	7,74597	7,81025	7,87401	7,93725	8	8,06226	8,12404	8,18535	8,24621	8,30662
7	8,3666	8,42615	8,48528	8,544	8,60233	8,66025	8,7178	8,77496	8,83176	8,88819
8	8,94427	9	9,05539	9,11043	9,16515	9,21954	9,27362	9,32738	9,38083	9,43398
9	9,48683	9,53939	9,59166	9,64365	9,69536	9,74679	9,79796	9,84886	9,89949	9,94987

Числа в кубе

И, конечно же, третья — таблица кубов, при помощи которой осуществляется извлечение кубического корня.

	0	1	2	3	4	5	6	7	8	9
0	0	1	8	27	64	125	216	343	512	729
1	1000	1331	1728	2197	2744	3375	4096	4913	5832	6859
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125000	132651	140608	148877	157464	166375	175716	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729000	753571	778688	804357	830584	857375	884736	912673	941192	970299

Эти числа возводятся в третью степень.

Интересно

Название «Куб» приобрелось из-за того, что такая операция проводится для нахождения объема куба. Т.е., для этого нужно возвести длину ребра куба в третью степень.

Такие таблицы достаточно просты в использовании. Слева — десятки, а справа — единицы. С их помощью можно быстро и легко извлечь корень числа от 0 до 99. Это был один из методов извлечения корней, как мне кажется, самый простой после вычислительного средства — калькулятора, но, зачастую, мы не всегда можем им воспользоваться, как говорилось ранее. Так давайте же перейдем к другим интересным и сложным на первый взгляд вариантам решения.

Разложение подкоренного числа на простые множители

Двигаясь от наиболее удобного и быстрого способа к более сложному, давайте разберемся во втором из них — разложение подкоренного числа на простые множители.

Этот метод состоит в том, чтобы представить какое-либо число в виде степени с нужным нам показателем, из чего мы можем получить значение этого корня.

Пример 1:

Возьмём число 196. Для извлечения его квадратного корня, разложим это число на простые множители: √196=2×2×7×7=2²×7²

Теперь делаем следующие действия: 2×7=14.

Ответ: √196=14.

Объяснение:

Множители находятся так: 196 делим на 2, а полученное число 98 мы тоже делим на 2. Делим до тех пор, пока деление станет невозможным. Так, число 49 нельзя поделить пополам, поэтому мы действуем методом подбора. Находим такое число, которое делится. В данном случае — это 7. Два числа, что у нас получились (2 и 7), мы умножаем друг на друга, но уже без степени и получаем число 14, что есть извлечённый корень из числа 196.

Пример 2:

Для того, чтобы лучше понять, как раскладывать на множители, приведем ещё одно число и перейдем к действиям. Деление 441 на 2 невозможно, поэтому подбираем число. Оно делится на 3 два раза. Опять выходит число 49, которое мы делим 2 раза на 7. Из этого следует: √441=3×3×7×7=3²×7²

3×7=21. Значит, ответ: √441=21.

Объяснение:

3 мы умножили на 7, так как это два числа, имеющих 2 степень. Будь у одного из них 4 степень, например: 3⁴×7² — нужно было бы сделать так: 3×3×7. Проще сказать, что мы сокращаем степени ⁴ и ².

Интересно

Подкоренные числа, разложенные на простые множители, могут иметь лишь чётную степень.

Извлечение корней из дробных чисел

Перед тем, как начать вычисления, убедитесь, что дробное число представлено в виде обыкновенной дроби.

Перейдем к свойству корня из частного:

[sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}]

Далее нужно воспользоваться правилом извлечения корня из дроби, которое гласит: корень из дроби равен от деления корня числителя на корень знаменателя.

Пример 1:

Давайте возьмем любую десятичную дробь и на её примере посмотрим, как нужно извлекать корень.

Так, например, найдем кубический корень из 373,248.

Первый ход — это представление десятичной дроби в виде обыкновенной:

³√373248/³√1000. После этого найдем кубический корень в числе и знаменателе:

³√373248=2×2×2×2×2×2×2×2×2×3×3×3×3×3×3=2⁹×3⁶=72³

Эти действия происходят как с квадратными корнями, но здесь уже мы считаем числа 2 и 3 не по двойке, а тройке, т.е. 2⁹=2×2×2, а 3⁶=3×3. Или же сокращаем ⁹ и ⁶.

Проверим таким образом: из 9 вычитаем тройки до тех пор, пока не придем к 0: 9-3-3-3 – это значит, что двоек у нас будет именно 3. Так и с 3⁶. Если от 6 отнять 3 два раза, то будет 0. Выходит, что троек у нас именно две.

А 1000=10³.

Получается, ³√373248/³√1000=72/10=7,2.

Извлечение отрицательного корня

Существуют вещественные числа, из которых невозможно извлечь корень, т.е. решения нет. А вот из комплексных чисел можно извлекать корень. Для начала узнаем, что это за числа.

Определение

Вещественные (действительные) числа— это рациональные и иррациональные числа, которые можно записать в форме конечной или бесконечной десятичной дроби.

Комплексные числа — это выражение, в котором есть:

вещественные числа a и b;
i — мнимая единица.

Итак, чтобы извлечь корень из отрицательного числа, нужно помнить, что если знаменатель является нечётным, то число под знаком корня может оказаться отрицательным.

Далее, чтобы провести эту операцию с отрицательным числом, перейдем к следующим действиям:

Извлекаем корень из противоположного ему положительного числа.
Ставим перед полученным числом знак минус.

Пример 1:

1. Преобразуем выражение ⁵√-12 640/32 так, чтобы вместо отрицательного числа под корнем оказалось положительное:

⁵√-12 640/32 = -⁵√12 640/32

2. Избавимся от смешанного числа, заменив его обыкновенной дробью:

-⁵√12 640/32= -⁵√1024/32

3. С помощью правила извлечения корней из обыкновенной дроби, начнем извлекать:

-⁵√1024/32 = — ⁵√1024/⁵√32.

4. Теперь нужно вычислить корни в числителе и знаменателе:

— ⁵√1024/⁵√32 = — ⁵√4⁵/⁵√2⁵ = — 4/2 = -2.

Нет времени решать самому?

Наши эксперты помогут!

Поразрядное нахождение значения корня

Мы разобрали несколько методов, которые вы можете выбрать на своё усмотрение. Однако, есть еще один, который может понадобиться в таких ситуациях, когда нужно знать полное значение корня, а число, находящееся под корнем нельзя представить в виде n-ной степени определенного числа.

Для таких случаев существует алгоритм поразрядного нахождения значения корня, который нужно использовать, чтобы получить нужное количество значений определяемого числа.

Пример 1:

Итак, чтобы в этом разобраться, найдем значение квадратного корня из 7:

1. Находим значение разряда единиц, перебирая значения 0, 1, 2, …, 9, в это же время вычисляя их во 2 степени до нужного значения, которое больше подкоренного числа 7. Значение ряда единиц равняется 2 (потому как 2² < 7, а 2³ > 7).

2. Следующий на очереди — разряд десятых. Здесь мы будем возводить в квадрат числа: 2.0, 2.1, 2.2, …, 2.9, сравнивая результат с нужным нам числом 7. Так как 2.6² < 7, а 2.7² > 7, то значение десятых равняется 6.

3. Значение сотых. По аналогии находим приближенное значение к 7.

2.64² = 6,9696 подходит нам, так как 2.65²=7.0225, а это больше 7. Действуя таким же образом, можно и дальше находить значение √7 ≈ 2.64.

Теперь, когда мы разобрались с извлечением корней, перейдем к практике. Специально для вас составлены задания с ответами, чтобы вы попробовали воспользоваться приобретенными знаниями. Решайте без таблиц и калькулятора.

Задания для отработки материала

1 задание

а)√324

б)√900

в)√1369

2 задание

а)³√531,441

б)³√166,375

3 задание

а) ⁵√-14 2471/1024

б) ⁵√-5 1182/3125

4 задание

а)Найдите квадратный корень из 3.

б)Найдите квадратный корень из 5.

в)Найдите квадратный корень из 9.

Ответы с решением

1 задание

а)√324

1)2×2×3×3×3×3=2²×3⁴=√324, а чтобы извлечь, мы умножаем:

2)2×3×3=18. Получается, √324=18.

б)√900

1)2×2×3×3×5×5=2²×3²×5²=√900.

Извлекаем:

2)2×3×5=30. Мы получили √900=30.

в)√1369

1)37×37=37²=√1369.

А здесь мы оставляем 37, так как это единственное число в квадрате. Конечным ответом будет: √1369=37.

2 задание

а)³√531441.

1)3×3×3×3×3×3×3×3×3×3×3×3=3¹²=³√531441.

Разложили на простые множители, а теперь найдем квадратный корень.

2)3¹² это 3×3×3×3, т.к. 3 у нас в 12 степени. Это можно проверить, отняв из 12 столько троек, чтобы вышел 0: 12-3-3-3-3. Так что, 3⁴=81; ³√531441=81.

3)1000=10³.

4)³√531441/³√1000=81/10=8,1.

б)³√166,375.

1) 5×5×5×11×11×11=5³×11³=³√166375.

2)5³×11³=55. Так как числа в кубе – они в степени 1.

3) 1000=10³.

4)³√166375/³√1000=55/10=5,5.

3 задание

а)

1) ⁵√-14 2471/1024 = -⁵√14 2471/1024.

2) -⁵√14 2471/1024= -⁵√16801/1024.

3) -⁵√16801/1024 = — ⁵√16801/⁵√1024.

4) ⁵√16801/⁵√1024 = — ⁵√6⁵/⁵√4⁵ = — 6/4 = — 1,5.

б)

1) ⁵√-5 1182/3125 = -⁵√5 1182/3125.

2) -⁵√5 1182/3125= -⁵√16807/3125.

3) -⁵√16807/3125 = — ⁵√16807/⁵√3125.

4) ⁵√16807/⁵√3125 = — ⁵√7⁵/⁵√5⁵ = — 7/5 = — 1,4.

4 задание

а)√3≈1,73.

б√5≈2,23.

в)√8≈2,82.

Источник

Содержание

Что такое квадратный корень
Что такое квадратный корень
Разница между квадратным корнем и арифметическим квадратным уравнением
Запись иррациональных чисел с помощью квадратного корня
Извлечение корней
Свойства арифметического квадратного корня
Умножение арифметических корней
Деление арифметических корней
Возведение арифметических корней в степень
Внесение множителя под знак корня
Вынесение множителя из-под знака корня
Сравнение квадратных корней
Извлечение квадратного корня из большого числа

Что такое квадратный корень

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Здесь могут возникнуть резонные вопросы, почему, например, в примере x 2 = 16, x = 4 и x = -4.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

x 2 = 16 не равно x = √16.

Это два нетождественных друг другу выражения.

x 2 = 16 — это квадратное уравнение.
x = √ 16 — арифметический квадратный корень.

Из выражения x 2 = 16 следует, что:

|x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

Пример решен неверно
Это квадратное уравнение.

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Решение следующее:
Строим график функции y = x 2 .
Отмечаем решения на графике: -√2; √2.

Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: √2 = 1,414213… .

В таком виде ответ не записывают — нужно оставить квадратный корень.
x 2 = 2.
x = √2
x = -√2.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

1. Извлеките квадратный корень: √289

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Влево — 1, вверх — 7.

2. Извлеките квадратный корень: √3025

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

3. Извлеките квадратный корень: √7396

Ищем в таблице число 7396.

Влево — 8, вверх — 6.

4. Извлеките корень: √9025

Ищем в таблице число 9025.

Влево — 9, вверх — 5.

5. Извлеките корень √1600

Ищем в таблице число 1600.

Влево — 4, вверх — 0.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

Примеры:

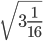
Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49

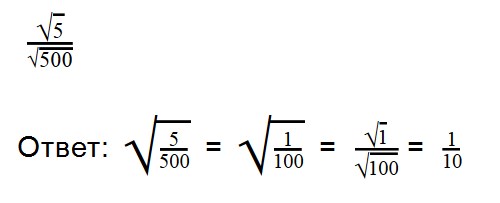
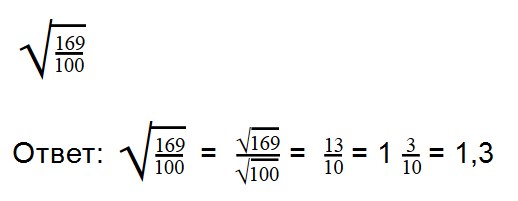
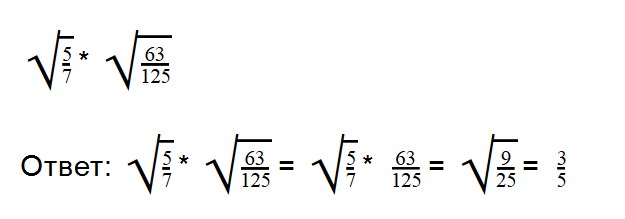
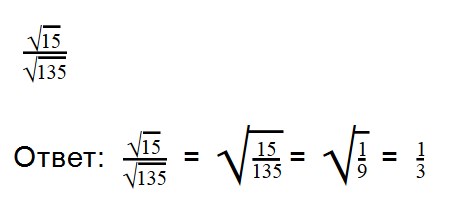
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

Примеры:

Эти две формулы нужно запомнить:

(√a) 2 = a
√a 2 = |a|

Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Дано выражение: 7√9

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.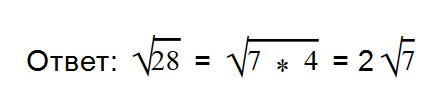

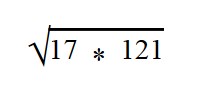
Ответ: по правилу извлечения квадратного корня из произведения,

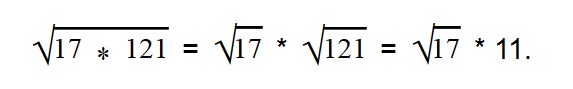
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.

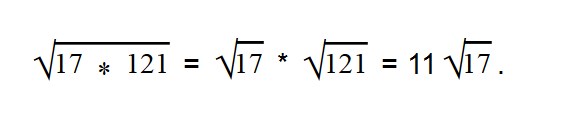
Вынесите множитель из-под знака корня в выражении: √24

Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.

Упростите выражение:

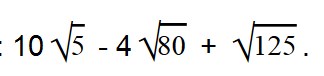
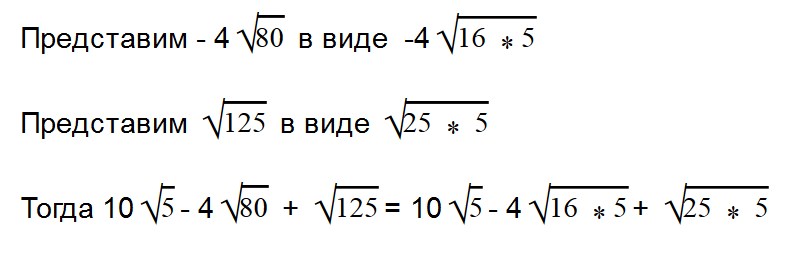
Вынесем в двух последних выражения множитель из-под знака корня.

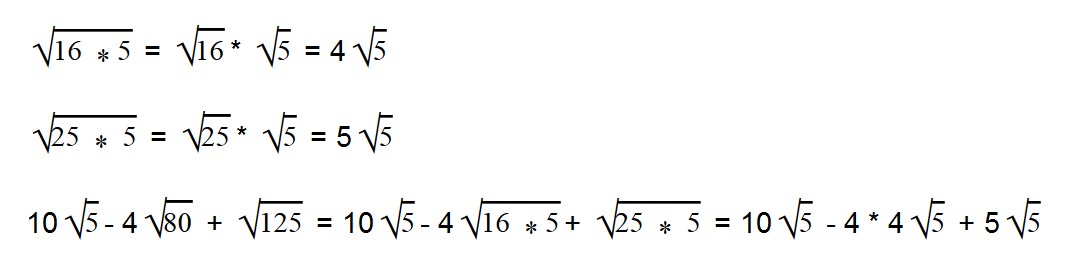
Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.

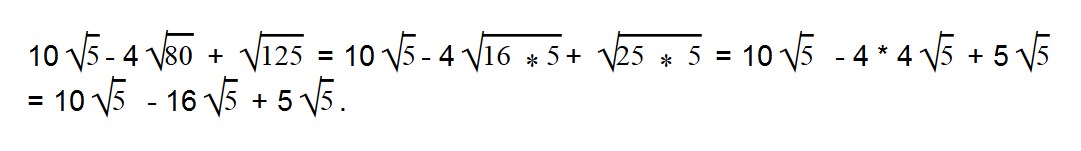
Мы видим, что во всем выражении есть один общий множитель — √5.
Выносим общий множитель за скобки:

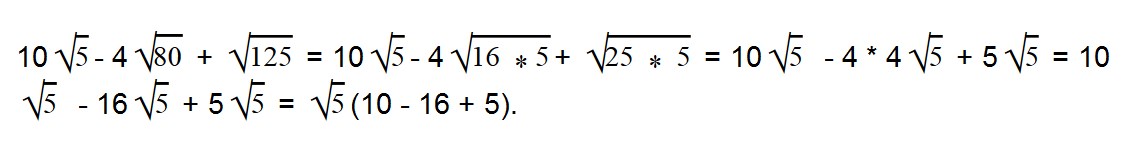
Далее вычисляем все, что в скобках:

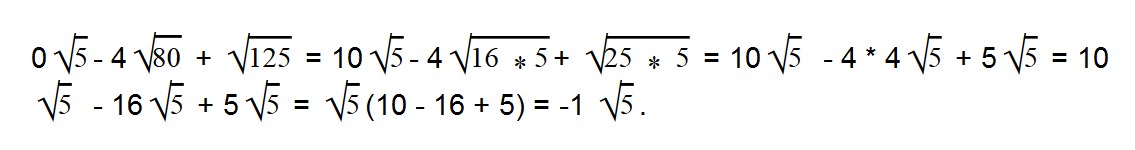
Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Сравните два выражения: √50 и 9√5

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Это значит, что 6√5 > √18.

Сравните два выражения: 7√12 и √20

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Определить «сотни», между которыми оно стоит.
Определить «десятки», между которыми оно стоит.
Определить последнюю цифру в этом числе.

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

Это значит, что число 2116 находится между 40 2 и 50 2 .

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Таким образом, у нас остаются два варианта: 44 2 и 46 2 .

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

Бесплатный марафон Как создавать игры и развиваться в том, что нравится

Источник

Корни и степени

Степень с натуральным показателем
Степень с целым показателем
Кубический корень
Корень -ной степени
Сравнение арифметических корней
Как избавиться от иррациональности в знаменателе
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Степенью называется выражение вида a^c .

Здесь — основание степени, — показатель степени.

к оглавлению ▴

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

По определению, a^1=a .

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.

Возвести число в куб — значит умножить его само на себя три раза.

Возвести число в натуральную степень — значит умножить его само на себя раз:

a^n= $underbrace{a cdot a cdot a cdot a cdot ldots cdot a}_{displaystyle n}.$

к оглавлению ▴

Степень с целым показателем

Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.

По определению,

a^0=1 .

Это верно для aneq 0 . Выражение 0⁰ не определено.

Определим также, что такое степень с целым отрицательным показателем.

$a^{-1}=genfrac{}{}{}{0}{1}{a};$

$a^{-2}=genfrac{}{}{}{0}{1}{a^2};$

$a^{-n}=genfrac{}{}{}{0}{1}{a^n}.$

Конечно, все это верно для aneq 0 , поскольку на ноль делить нельзя.

Например,

$5^{-2}=genfrac{}{}{}{0}{1}{5^2};$

$left( genfrac{}{}{}{0}{1}{2} right)^{-1}=2;$

$left( genfrac{}{}{}{0}{2}{7} right)^{-1}=genfrac{}{}{}{0}{7}{2}.$

Заметим, что при возведении в минус первую степень дробь переворачивается.

$left( genfrac{}{}{}{0}{5}{3} right)^{-2}=1 : left( genfrac{}{}{}{0}{5}{3} right)^{2}=left( genfrac{}{}{}{0}{3}{5} right)^{2}=genfrac{}{}{}{0}{9}{25}.$

Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби $genfrac{}{}{}{0}{p}{q}$ , где — целое, — натуральное.

Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.

Определение.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

Согласно определению, $left (sqrt{a} right )^2=a; , , sqrt{a}geq 0; , , ageq 0.$

В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение sqrt{a} для нас сейчас имеет смысл только при ageq 0 .

Выражение sqrt{a} всегда неотрицательно, т.е. . Например, .

Свойства арифметического квадратного корня:

$sqrt{ab}=sqrt{a} cdot sqrt{b}, ; sqrt{a^2}=left|aright| , ; sqrt{a^{2n}}={left|aright|}^n;$

$sqrt{genfrac{}{}{}{0}{a}{b}}=genfrac{}{}{}{0}{sqrt{a}}{sqrt{b}}.$

Запомним важное правило: $sqrt{a^2}=left|aright| .$

По определению, .

к оглавлению ▴

Кубический корень

Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .

$left( sqrt[leftroot{3}scriptstyle 3]{a} right) ^3 = sqrt[leftroot{3}scriptstyle 3]{a} cdot sqrt[leftroot{3}scriptstyle 3]{a} cdot sqrt[leftroot{3}scriptstyle 3]{a}.$

Например, , так как ;

, так как ;

$sqrt[leftroot{3}scriptstyle 3]{-genfrac{}{}{}{0}{1}{125}} = -genfrac{}{}{}{0}{1}{5}$ , так как $left( -genfrac{}{}{}{0}{1}{5} right) ^3 = -genfrac{}{}{}{0}{1}{125}$ .

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.

Теперь мы можем дать определение корня -ной степени для любого целого .

к оглавлению ▴

Корень -ной степени

Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .

Например,

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

Итак, — такое число, что $left( sqrt[leftroot{3}scriptstyle n]{a} right) ^n = a$ . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.

По определению,

$a^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 2}} = sqrt{a},$

$a^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 3}} = sqrt[leftroot{3}scriptstyle 3]{a},$

в общем случае $a^{frac{1}{n}} = sqrt[leftroot{3}scriptstyle n]{a}.$ .

Сразу договоримся, что основание степени больше 0.

Например,

$25^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 2}} = 5;$

$8^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 3}} = 2;$

$81^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 4}} = 3;$

$100000^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 5}} = 10;$

$0,001^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 3}} = 0,1.$

Выражение $a^{genfrac{}{}{}{3}{scriptstyle m}{scriptstyle n}}$ по определению равно $sqrt[leftroot{3}scriptstyle n]{a^m}$ .

При этом также выполняется условие, что больше 0.

$a^{genfrac{}{}{}{3}{scriptstyle m}{scriptstyle n}} = sqrt[leftroot{3}scriptstyle n]{a^m} = left( sqrt[leftroot{3}scriptstyle n]{a} right) ^m.$

Например,

$8^{genfrac{}{}{}{3}{scriptstyle 4}{scriptstyle 3}} = left( sqrt[leftroot{3} scriptstyle 3]{8} right) ^4 = 2^4 = 16;$

$a^{genfrac{}{}{}{3}{scriptstyle 3}{scriptstyle 5}} = sqrt[leftroot{3} scriptstyle 5]{a^3} = left( sqrt[leftroot{3} scriptstyle n]{a} right) ^m;$

$b^{-genfrac{}{}{}{3}{scriptstyle 2}{scriptstyle 3}} = genfrac{}{}{}{0}{1}{sqrt[leftroot{3} scriptstyle 3]{b^2}}.$

Запомним правила действий со степенями:

$a^ma^n = a^{m+n}$ — при перемножении степеней показатели складываются;

$genfrac{}{}{}{0}{a^m}{a^n} = a^{m-n}$ — при делении степени на степень показатели вычитаются;

$left( a^m right) ^n = left( a^n right) ^m = a^{mn}$ — при возведении степени в степень показатели перемножаются;

$genfrac{}{}{}{0}{a^n}{b^n} = left( genfrac{}{}{}{0}{a}{b} right) ^n.$

Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:

1. $genfrac{}{}{}{0}{sqrt{ mathstrut 2,8} cdot sqrt{ mathstrut 4,2}}{sqrt{ mathstrut 0,24}}= sqrt{ mathstrut genfrac{}{}{}{0}{2,8 cdot 4,2}{0,24}} = sqrt{ mathstrut genfrac{}{}{}{0}{28 cdot 42}{24}}=sqrt{ mathstrut genfrac{}{}{}{0}{7 cdot 4 cdot 7 cdot 6}{4 cdot 6}} =$

Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.

2. $genfrac{}{}{}{0}{left( 2 sqrt{7} right) ^2}{14}= genfrac{}{}{}{0}{ 2^2 cdot left( sqrt{7} right) ^2}{14} = genfrac{}{}{}{0}{4 cdot 7}{14} = 2.$

3. $genfrac{}{}{}{0}{ sqrt[leftroot{3} scriptstyle 9]{7} cdot sqrt[leftroot{3} scriptstyle 18]{7}}{sqrt[leftroot{3} scriptstyle 6]{7}}=genfrac{}{}{}{0}{7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 9}} cdot 7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 18}}}{7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 6}}}=7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 9} + genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 18}- genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 6}}= 7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 6} - genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 6}}=7^0=1.$

Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения $displaystyle frac{11a^6b^3-{left(3a^2bright)}^3}{4a^6b^6}$ при b = 2.

Решение:

$displaystyle frac{11a^6b^3-{left(3a^2bright)}^3}{4a^6b^6}=displaystyle frac{11a^6b^3-{27a^6b}^3}{4a^6b^6}=displaystyle frac{-16a^6b^3}{4a^6b^6}=-displaystyle frac{4}{b^3}.$

При b = 2 получим $-displaystyle frac{4}{2^3}=-displaystyle frac{4}{8}=-0,5 .$

Ответ: -0,5.

5. Найдите значение выражения $displaystyle frac{a^{3,21} cdot a^{7,36}}{a^{8,57}}$ при a=12 .

Решение:

$displaystyle frac{a^{3,21} cdot a^{7,36}}{a^{8,57}}=displaystyle frac{a^{3,21+7,36}}{a^{8,57}}=displaystyle frac{a^{10,57}}{a^{8,57}}=a^{10,57-8,57}=a^2.$

При a = 12 получим ${12}^2=144.$

Мы воспользовались свойствами степеней.

Ответ: 144.

6. Найдите значение выражения $displaystyle frac{{left(b^{sqrt{3}}right)}^{2sqrt{3}}}{b^4}$ при b = — 5.

Решение: $displaystyle frac{{left(b^{sqrt{3}}right)}^{2sqrt{3}}}{b^3}=displaystyle frac{b^{sqrt{3} cdot 2sqrt{3}}}{b^3}=displaystyle frac{b^6}{b^3}=b^3 .$

При b = — 5 получим: ${(-5)}^3=-125 .$

Ответ: -125.

7. Расположите в порядке возрастания: ${left(displaystyle frac{7}{8}right)}^{-3};$ $displaystyle frac{7}{8};$ ${left(displaystyle frac{8}{7}right)}^{-3}.$

Решение:

Запишем выражения как степени с положительным показателем и сравним.

$left(displaystyle frac{7}{8}right)^-3=left(displaystyle frac{8}{7}right)^3.$ Так как $displaystyle frac{8}{7} textgreater 1,$ то $left(displaystyle frac{8}{7}right)^3 textgreater 1.$

$left(displaystyle frac{8}{7}right)^-3=left(displaystyle frac{7}{8}right)^3.$ Так как $displaystyle frac{7}{8} textless 1,$ то $left(displaystyle frac{7}{8}right)^3 textless 1.$

Сравним $displaystyle frac{7}{8}$ и ${left(displaystyle frac{7}{8}right)}^3,$ для этого оценим их разность:

$displaystyle frac{7}{8} - {left(displaystyle frac{7}{8}right)}^3=displaystyle frac{7}{8} - displaystyle frac{7^3}{8^3}=displaystyle frac{7 cdot 8^2-7^3}{8^3}=displaystyle frac{7(8^2-7^2)}{8^3}=displaystyle frac{7(64-49)}{8^3} textgreater 0 ,$ значит $displaystyle frac{7}{8} textgreater {left(displaystyle frac{7}{8}right)}^3 .$

Получим : ${left(displaystyle frac{7}{8}right)}^3 textless displaystyle frac{7}{8} textless {left(displaystyle frac{8}{7}right)}^3 ,$ поэтому ${left(displaystyle frac{8}{7}right)}^{-3} ; displaystyle frac{7}{8} ; {left(displaystyle frac{7}{8}right)}^{-3} .$

Ответ: ${left(displaystyle frac{8}{7}right)}^{-3}; displaystyle frac{7}{8} ; {left(displaystyle frac{7}{8}right)}^{-3}.$

8. Представьте выражение в виде степени: $displaystyle frac{x^{-6}+x^{-4}+x^{-2}}{x^2+x^4+x^6}.$

Решение:

Вынесем за скобку степень с меньшим показателем:

$displaystyle frac{x^{-6}+x^{-4}+x^{-2}}{x^2+x^4+x^6}=displaystyle frac{x^{-6}(1+x^2+x^4)}{x^2(1+x^2+x^4)}=displaystyle frac{x^{-6}}{x^2}=x^{-6-2}=x^{-8}.$

Ответ: $x^{-8} .$

9. Упростите выражение: $displaystyle frac{2^{2n-1} cdot 3^{n+1}}{6 cdot {12}^n} .$

Решение:

Приведем основания 6 и 12 к основаниям 2 и 3:

$displaystyle frac{2^{2n-1} cdot 3^{n+1}}{6 cdot {12}^n}=displaystyle frac{2^{2n-1} cdot 3^{n+1}}{2 cdot 3 cdot {(2^2 cdot 3 )}^n}= displaystyle frac{2^{2n-1} cdot 3^{n+1}}{2^1cdot 3^1cdot 2^{2n} cdot 3^n} =$

(выполним деление степеней с одинаковыми основаниями)

$= 2^{2n-1-1-2n}cdot 3^{n+1-1-n}=2^{-2}cdot 3^0=displaystyle frac{1}{2^2}cdot 1=displaystyle frac{1}{4} = 0,25.$

Ответ: 0,25.

10. Чему равно значение выражения $displaystyle frac{a^{-4}cdot { a}^{-3}}{a^{-5}}$ при $a=displaystyle frac{1}{3}$ ?

Решение:

$displaystyle frac{a^{-4}cdot { a}^{-3}}{a^{-5}}=a^{-4+left(-3right)-(-5)}=a^{-2}.$

При $a=displaystyle frac{1}{3},$ получим ${left(displaystyle frac{1}{3}right)}^{-2}=3^2=9.$

Ответ: 9.

к оглавлению ▴

Сравнение арифметических корней

11. Какое из чисел больше: или ?

Решение:

Возведем в квадрат оба числа (числа положительные):

${left(sqrt{5}+sqrt{6}right)}^2= 5 + 2sqrt{5cdot 6}+6=11+2sqrt{30};$

${left(2+7right)}^2={left(sqrt{4}+sqrt{7}right)}^2= 4 + 2sqrt{4cdot 7}+7=11+2sqrt{28}.$

Найдем разность полученных результатов:

так как

Значит, первое число больше второго.

Ответ:

к оглавлению ▴

Как избавиться от иррациональности в знаменателе

Если дана дробь вида $displaystyle frac{a}{sqrt{b}},$ то нужно умножить числитель и знаменатель дроби на sqrt{b} :

$displaystyle frac{a}{sqrt{b}} = displaystyle frac{a cdot sqrt{b}}{sqrt{b}cdot sqrt{b}} = displaystyle frac{a cdot sqrt{b}}{sqrt{b}^2} = displaystyle frac{a cdot sqrt{b}}{b}.$

Тогда знаменатель станет рациональным.

Если дана дробь вида $displaystyle frac{c}{ a pm sqrt{b}}$ или $displaystyle frac{c}{ sqrt{a} pm sqrt{b}},$ то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.

Сопряженные выражения — это выражения, отличающиеся только знаками. Например,

и и — сопряженные выражения.

Пример:

$displaystyle frac{c}{sqrt{a}-sqrt{b}}=displaystyle frac{c (sqrt{a}+ sqrt{b})}{ (sqrt{a}- sqrt{b})(sqrt{a}+ sqrt{b})}=$

$=displaystyle frac{c (sqrt{a}+sqrt{b})}{{ left(sqrt{a}right)}^2-{left(sqrt{b}right)}^2 }=displaystyle frac{c(sqrt{a}+ sqrt{b})}{a-b } .$

12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:

Пример 1.

$displaystyle frac{2}{sqrt{27}}= displaystyle frac{2 cdot sqrt{3}}{sqrt{3^3} cdot sqrt{3}}=displaystyle frac{2 sqrt{3}}{sqrt{3^4} }=displaystyle frac{2 sqrt{3}}{9}.$

Пример 2.

$displaystyle frac{6}{1+sqrt{3}} = displaystyle frac{6(sqrt{3}-1)}{(sqrt{3}+1)(sqrt{3}-1)}=displaystyle frac{6(sqrt{3}-1)}{3-1}=$

$=displaystyle frac{6(sqrt{3}-1)}{2}=3(sqrt{3}-1).$

Пример 3.

$displaystyle frac{33}{7-3sqrt{3}} = displaystyle frac{33(7+3sqrt{3})}{(7-3sqrt{3})(7+3sqrt{3})}= displaystyle frac{33(7+3sqrt{3})}{49 -9 cdot 3}=$

$displaystyle frac{33(7+3sqrt{3})}{22}=displaystyle frac{3(7+3sqrt{3})}{2}.$

Пример 4.

$displaystyle frac{12}{sqrt{3}+sqrt{6}}=displaystyle frac{12(sqrt{6}-sqrt{3})}{(sqrt{3}+sqrt{6})(sqrt{6}-sqrt{3})}=displaystyle frac{12(sqrt{6}-sqrt{3})}{6-3}=$

$=displaystyle frac{12(sqrt{6}-sqrt{3})}{3}=4(sqrt{6}-sqrt{3}).$

Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.

Пример 5.

$displaystyle frac{5+3sqrt{3}}{sqrt{3}+2}= displaystyle frac{(5+3sqrt{3})(2-sqrt{3})}{(sqrt{3}+2)(2-sqrt{3})}=$

$=displaystyle frac{10+6sqrt{3}-5sqrt{3}-9}{2^2-{(sqrt{3} )}^2}=displaystyle frac{1+sqrt{3}}{4-3}= 1+sqrt{3}.$

13. Сравните и $displaystyle frac{1}{7+4sqrt{3}}+displaystyle frac{1}{7-4sqrt{3}}.$

1) $displaystyle frac{1}{7+4sqrt{3}}+displaystyle frac{1}{7-4sqrt{3}}=displaystyle frac{7-4sqrt{3}+7+4sqrt{3}}{(7+4sqrt{3})(7-4sqrt{3})}=displaystyle frac{14}{7^2-{(4sqrt{3})}^2}=$

$=displaystyle frac{14}{49-48}=14.$

2) Сравним и 14.

$14 = sqrt{{14}^2}=sqrt{196},$ то и а значит,

$sqrt{140} textless displaystyle frac{1}{7+4sqrt{3}}+displaystyle frac{1}{7-4sqrt{3}} .$

Ответ: меньше.

к оглавлению ▴

Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Покажем несколько примеров.

14. Упростите: выражения:

Пример 5.

$sqrt{3-2sqrt{2}}=sqrt{2+1-2sqrt{2}}=sqrt{{left(sqrt{2}right)}^2-2cdot 1cdot sqrt{2}+1}=$

$=sqrt{{left(sqrt{2}-1right)}^2} = left|sqrt{2}-1right| = sqrt{2}-1,$ т.к.

Пример 6.

$sqrt{7+4sqrt{3}} = sqrt{4+3+4sqrt{3 }}=sqrt{2^2+2cdot 2cdot sqrt{3 }+{(sqrt{3 })}^2} =$

$= sqrt{{(2+sqrt{3})}^2} = 2+sqrt{3}.$

Пример 7.

$sqrt{19-8sqrt{3}} = sqrt{16+3-8sqrt{3 }}=sqrt{4^2-2cdot 4cdot sqrt{3 }+{(sqrt{3 })}^2} =$

$=sqrt{{(4-sqrt{3})}^2} = 4-sqrt{3},$

так как

Следующие несколько задач решаются с помощью формулы:

$sqrt{a^2}=left|aright|.$

Решение:

$sqrt{{(5-2x)}^2}=left|5-2xright|.$

Получим уравнение

Ответ:

19. Вычислите значение выражения: $sqrt{{(sqrt{3}-1)}^2}+sqrt{{(sqrt{3}-2)}^2}.$

Решение:

$sqrt{(sqrt{3}-1)^2}+sqrt{(sqrt{3}-2)^2}=|sqrt{3}-1|+|sqrt{3}-2|=$

Ответ: 1.

20. Вычислите значение выражения: $sqrt{{(2-sqrt{5})}^2}+sqrt{{(3-sqrt{5})}^2}.$

Решение: $sqrt{{(2-sqrt{5})}^2}+sqrt{{(3-sqrt{5})}^2}= left|2-sqrt{5}right|+left|3-sqrt{5}right|=$

Ответ: 1.

21. Вычислите значение выражения: $(x - 3) sqrt{displaystyle frac{1}{x^2-6x+9}},$ если

Решение. $(x - 3) sqrt{displaystyle frac{1}{x^2-6x+9}}=left(x - 3right)sqrt{displaystyle frac{1}{{left(x-3right)}^2}}=displaystyle frac{x-3}{left|x-3right|}=$

$=displaystyle frac{x-3}{3-x}=-1.$

Если то следовательно

Ответ: — 1.

22. Вычислите:

Решение: $left(sqrt{3}-2right)left(sqrt{7+4sqrt{3}}right) = sqrt{{left(sqrt{3}-2right)}^2(7+4sqrt{3}})=$

$=sqrt{left(3-4sqrt{3}+4right)left(7+4sqrt{3}right)}=sqrt{left(7-4sqrt{3}right)left(7+4sqrt{3}right)}=sqrt{7^2-{left(4sqrt{3}right)}^2}=$

Ответ: 1.

Рассмотрим уравнение вида где

Это равенство выполняется, только если

Подробно об таких уравнениях — в статье «Показательные уравнения».

При решении уравнений такого вида мы пользуемся монотонностью показательной функции.

23. Решите уравнение:

а) $2^{3-x}=16;$

б) ${27}^{displaystyle frac{1}{3}x-1}-3=0;$

в) ${left(displaystyle frac{1}{sqrt{3}}right)}^{2x+1}={left(3sqrt{3}right)}^x.$

Решение.

23. Решите уравнение: $2^{3-x}=16.$

Решение:

$2^{3-x}=2^4,$ тогда

Ответ: -1.

24. Решите уравнение:

${27}^{displaystyle frac{1}{3}x-1}-3=0.$

Решение:

${left(3^3right)}^{left(displaystyle frac{1}{3}x-1right)}=3 , ; 3^{3left(displaystyle frac{1}{3}x-1right)}=3^1;$

$3left(displaystyle frac{1}{3}x-1right)=1, ; x - 3 = 1, ; x = 4.$

Ответ: 4.

25. Решите уравнение: ${left(displaystyle frac{1}{sqrt{3}}right)}^{2x+1}={left(3sqrt{3}right)}^x.$

Решение:

${left(3^{- displaystyle frac{1}{2}}right)}^{2x+1}={left(3^{1+ displaystyle frac{1}{2}}right)}^x ,; ; 3^{-displaystyle frac{1}{2} cdot (2x+1)}=3^{displaystyle frac{3}{2}x}.$

Значит, $-displaystyle frac{1}{2} cdot left(2x+1right)=displaystyle frac{3}{2}x,$ $x = -displaystyle frac{1}{5}.$

Ответ: -0,2.

Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

{2}]

Степень корня указывается над знаком корня слева. [sqrt[x]{a}], в данном примере х — степень. Если запись не имеет такого обозначения, значит перед нами корень квадратный.

Умножение корней
- Умножение без множителей
- Умножение корней с множителями
- Умножение корней с разными показателями

Как внести под знак корня: число, множитель, букву
- Правило внесения под знак корня
  - Квадратный корень
  - Корень n-ой степени
  - Отрицательное число/множитель
- Внесение под корень буквы
  - - ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Искусство решения проблем
- Содержание
- Поиск корней
  - Общие приемы
  - Рациональные корни
  - Реальные корни
  - Комплексные корни
  - В алгебраической форме
Краткое руководство по треугольнику 30-60-90

Умножение корней

Существует несколько вариантов умножения корней, это умножение с множителем, без множителя и с разными показателями.

Умножение без множителей

Первым делом рассмотри, как умножаются корни без множителя.

Убедившись, что корни, с которыми необходимо произвести действие имеют одинаковые степени. Например квадратный корень из числа а, можно умножать на квадратный корень из d.

Рассмотрим правило на двух примерах произведения двух квадратных и двух кубических корней.

Примеры:

[sqrt{2} * sqrt{6}=] первый пример умножение квадратных корней.

[sqrt[3]{3} * sqrt[3]{18}=] второй пример умножение кубических корне.

Решение:

Для того чтобы решить данные примеры необходимо произвести умножение под корнем. {2} * 3}=2 sqrt{3}], в данном примере число 12 можно разложить на произведение чисел 4 и 3, где 4 равно двум в квадрате. Поэтому 2 выносим за приделы корня и упрощаем выражение.

[sqrt[3]{54}=sqrt[3]{27 * 2}=sqrt[3]{(3 * 3 * 3) * 2}=3 sqrt[3]{2}] в данном случае получившееся подкоренное число 54 можно разложить на произведение двух чисел 27 и 2 , где 27 = 3³, тройку выносим за корень кубический, тем самым мы упростили выражение.

Точно также производится умножение корней других степеней, при этом не важно количество умножаемых корней, правило не изменится.

Умножение корней с множителями

В данном случае мы так же рассматриваем примеры умножения корней с одинаковыми степенями. Множителем является число, стоящее перед корнем. Если при написании множитель отсутствует, то он равен единице. Умножить корень на число значит умножить число на множитель перед корнем. Для того чтобы произвести умножение с такими корнями, необходимо перемножить множители.

Пример умножения корней:

[2 sqrt{6} * sqrt{6}=2 sqrt{6 * 6}=2 sqrt{36}=2 * 6=12] в данном примере мы сначала произвели умножение множителей 1 и 2 , затем воспользовавшись первым правилом умножения корней, произвели умножение под знаком корня чисел 6 и 6.

Следующим шагом упрощаем выражение, корень из 36, равен целому числу 6. последним действием умножаем его на полученный множитель 2. и получаем ответ 12.

Пример 2.

[2 sqrt{6} * 3 sqrt{3}=2 * 3 sqrt{6 * 3}=6 sqrt{18}=6 sqrt{9 * 2}=6 * 3 sqrt{2}=18 sqrt{2}]

В приведённом примере, мы также в начале производим умножение множителей 2 и 3, затем производим умножение подкоренных чисел 6 и 3, в результате получаем 6 корней из 18.

После производим упрощение выражения под знаком корня, для этого разложили его на множители, таким образом чтобы одно из чисел можно было вынести за пределы знака корень такими числами стали 9 и 2, в результате получилось, что вынесенное число равно трём, так как 9 = [3^{2}] .

Теперь умножим получившийся ранее множитель 6 на вынесенное из под корня число 3, и получим ответ 18 корней из двух.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Умножение корней с разными показателями

Теперь разберём, как умножить корни если их показатели степени разные. Для этого необходимо найти наименьшее общее кратное число для этих показателей. Таким числом является наименьшее число, которое можно разделить на оба эти показателя. Для того чтобы разобраться лучше в данном методе, приведём пример.

Пример:

[sqrt[2]{2} * sqrt[3]{5}=]

Сначала необходимо найти наименьшее общее кратное, наименьшим в данном случае является произведение 2*3 = 6. Значит для того чтобы произвести умножение корней необходимо привести их к показателю шестой степени.

Записываем новое полученное выражение [sqrt[6]{2} * sqrt[6]{5}=]

Теперь находим числа на которые нужно умножить показатели, чтобы найти наименьшее общее кратное

Для первого корня это деление 62 = 3, для второго 63 =2

Следующим шагом нужно возвести подкоренное число в степень, которая ровна числам найденным ранее, при нахождении НОК, то есть [sqrt[6]{2^{3}} * sqrt[6]{5^{2}}=]

Далее имея одинаковые показатели производим действия по умножению корней, так как делали это в предыдущих правилах. {2}}=sqrt[6]{8 * 25}=sqrt[6]{200}]

Если полученное выражение можно упростить, то упрощаем его. В данном случае это невозможно.

Как мы видим произвести умножение корней не так и сложно, главное запомнить основные правила и формулы умножения корней и пользоваться ними.

Как внести под знак корня: число, множитель, букву

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В данной публикации мы рассмотрим, как число (множитель) или букву внести под знак квадратного и более старших степеней корня. Информация сопровождается практическими примерами для лучшего понимания.

Правило внесения под знак корня
- Квадратный корень
- Корень n-ой степени
- Отрицательное число/множитель
Внесение под корень буквы

Правило внесения под знак корня

Квадратный корень

Чтобы внести число (множитель) под знак квадратного корня, его следует возвести во вторую степень (другими словами, в квадрат), затем полученный результат написать под знаком корня.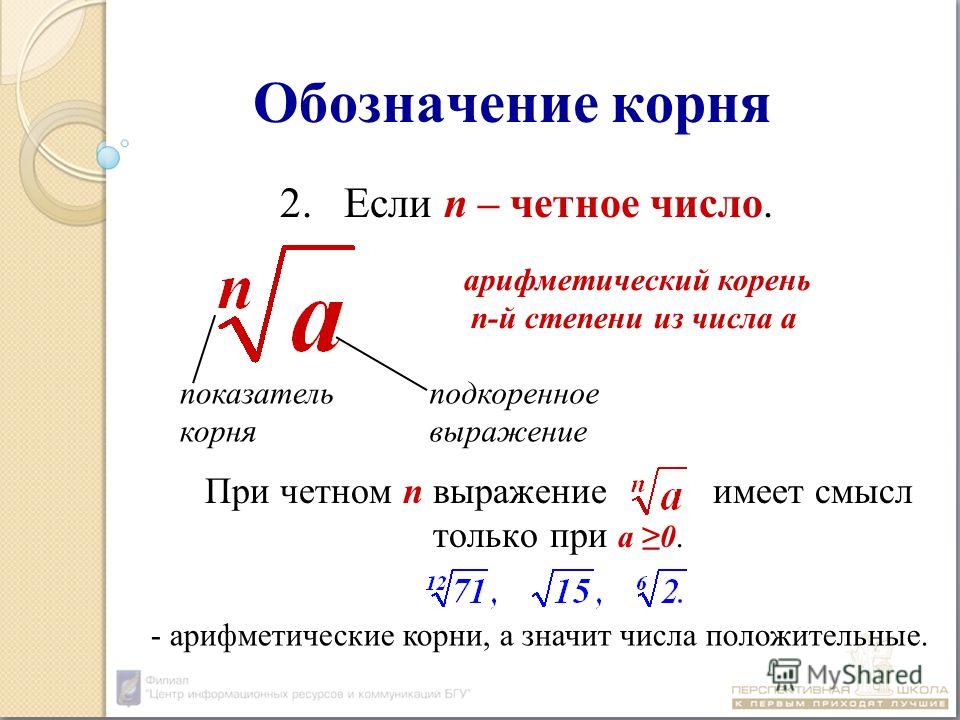

Пример 1: внесем число 7 под квадратный корень.

Решение:
1. Для начала возведем заданное число в квадрат: 7² = 49.
2. Теперь просто записываем рассчитанное число под корнем, т.е. получаем √49.

Коротко внесение под знак корня можно записать так:

Примечание: Если речь идет про множитель, его мы умножаем на уже имеющееся подкоренное выражение.

Пример 2: представим произведение 3√5 полностью под корнем второй степени.

Корень n-ой степени

Чтобы внести число (множитель) под знак кубического и более старших степеней корня, мы возводим это число в заданную ступень, затем переносим результат в подкоренное выражение.

Пример 3: внесем число 6 под кубический корень.

Пример 4: представим произведение 2⁵√3 под корнем 5-ой степени.

Отрицательное число/множитель

При внесении отрицательного числа/множителя под корень (неважно какой степени), знак “минус” обязательно остается перед знаком корня.

Пример 5

Внесение под корень буквы

Чтобы внести букву под знак корня, поступаем так же, как и с числами (в т.ч. с отрицательными) – возводим эту букву в соответствующую степень, после чего добавляем в подкоренное выражение.

Пример 6

Это справедливо при p > 0, если же p – отрицательное число, то перед знаком корня необходимо добавить знак “минус”.

Пример 7
Рассмотрим более сложный случай: (3 + √8) · √5.

Решение:

1. Сперва внесем выражение в скобках под знак корня.

2. Теперь согласно формуле сокращенного умножения возведем выражение (3 + √8) в квадрат.

Примечание: первый и второй шаг можно поменять местами.

3. Остается только выполнить умножение под корнем с раскрытием скобок.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Искусство решения проблем

Корень функции (часто многочлена), диапазоном которой являются действительные, комплексные числа или любое абстрактное поле, является значением в области определения функции таким образом, что .

Содержание

1 Поиск корней
- 1.1 Общие методы
- 1.2 Рациональные корни
- 1.3 Действительные корни
- 1.4 Сложные корни
- 1.5 В алгебраической форме

Поиск корней

Пусть при всех и , общая степень-многочлен. Степень , поэтому имеет не более комплексных корней. На самом деле сумма кратностей всех различных комплексных корней точно равна ; то есть, считая любые двойные корни дважды, тройные корни трижды и т. д., на самом деле есть точно комплексные корни .

Общие приемы

Умножение или деление всех коэффициентов многочлена на ненулевую константу не меняет его корней. Таким образом, всегда будет монический полином со степенью, имеющей те же корни, что и , заданный

Как только корень найден, теорема о множителях дает, что это множитель . Следовательно, можно разделить с помощью синтетического деления, а корни полученного частного будут оставшимися корнями из .

Как только будет найден другой корень, процесс можно повторить. Деление на на наиболее практично, когда корень и все коэффициенты рациональны.

Рациональные корни

Три простейших значения для проверки: и .

является корнем тогда и только тогда, когда постоянный член равен .
является корнем тогда и только тогда, когда сумма коэффициентов равна .
является корнем тогда и только тогда, когда сумма переменных коэффициентов равна .

Если все коэффициенты являются целыми числами, то применяется теорема о рациональном корне; а именно, если является корнем , с и относительно простым, то является (положительным или отрицательным) делителем и является делителем .

Если все рациональные, но не обязательно целые числа, то умножение на наименьшее общее кратное знаменателей дает многочлен с теми же корнями, что и целые коэффициенты. Затем к новому многочлену можно применить теорему о рациональном корне для поиска рациональных корней .

В некоторых случаях поиск можно упростить, подставив , где непостоянный линейный полином с рациональными коэффициентами. Если рациональный корень из , то рациональный корень из . Наоборот, если является рациональным корнем , то обратное at должно быть рациональным корнем .

Реальные корни

Вычисление по выбранным значениям может указывать на расположение корней. Если и имеют противоположные знаки, то теорема о промежуточном значении утверждает, что имеет хотя бы один корень в .

Для одинарных корней и других корней нечетной кратности (тройных корней, пятикратных корней и т. д.) всегда будет меняться знак на противоположных сторонах корня, но для корней четной кратности (таких как двойные корни) знак будет быть одинаковым по обе стороны от корня, поэтому теорема о промежуточном значении не обнаружит корни с четной кратностью.

Правило знаков Декарта дает информацию о количестве положительных действительных корней и отрицательных действительных корней . Записывая коэффициенты в порядке убывания степени и исключая все равные , количество положительных действительных корней равно количеству изменений знака между соседними коэффициентами минус некоторое четное неотрицательное целое число. Количество отрицательных действительных корней равно количеству таких изменений знака после изменения знака каждого коэффициента нечетной степени, снова минус некоторое четное неотрицательное целое число. Здесь корни считаются по кратности, поэтому двойные корни учитываются дважды, тройные корни — три раза и так далее.

В более широком смысле, считая корни в соответствии с их кратностью, как и прежде, число действительных корней всегда имеет ту же четность, что и степень . В частности, если нечетно, то должен иметь хотя бы один действительный корень.

Теорема Ролля гарантирует, что если имеет два корня и , то его производная имеет по крайней мере один корень в интервале . В частности, если не имеет корней в отрезке , то имеет не более одного корня в .

Метод Ньютона генерирует сколь угодно близкие приближения значения действительного корня многочлена. Использование метода Ньютона обычно требует обоснованного предположения о местонахождении корня на основе вышеуказанных критериев. Мы позволяем предположению быть равным и вычисляем приближения рекурсивно:

Комплексные корни

Комплексные корни многочленов с вещественными коэффициентами всегда существуют в сопряженных парах. То есть, если , , и все коэффициенты действительны и является корнем, то также является корнем . В частности, должно быть как четное число различных невещественных корней, так и четная сумма кратностей всех различных невещественных корней.

Произведение множителей, соответствующих и, представляет собой квадратичный многочлен с действительными коэффициентами. Таким образом, деление на произведение оставляет многочлен, который все еще имеет действительные коэффициенты и все корни оригинала, кроме и .

В алгебраической форме

Корень многочлена с целыми коэффициентами всегда будет алгебраическим числом. Общие формулы дают алгебраическую форму корней многочленов степени не выше .

Для квадратного уравнения корни задаются квадратной формулой

Кубическая формула и формула четвертой степени также существуют, но они довольно длинные и не очень практичны для вычисления вручную.

Для квинтик или многочленов любой более высокой степени не существует подобной формулы. Хотя корнями таких многочленов являются алгебраические числа, их нельзя выразить через коэффициенты, используя только сложение, вычитание, умножение, деление, степени и радикалы.

Эта статья незавершенная. Помогите нам, расширив его.

Краткое руководство по треугольнику 30-60-90

Автор: Мэри Джейн Стерлинг и

-Исчисление для чайников

Исследуйте книгу Купить на Amazon

Треугольник 30-60-90 имеет форму половины равностороннего треугольника, разрезанного прямо посередине вдоль его высоты. Он имеет углы 30 градусов, 60 градусов и 9 градусов.0 градусов, таким образом, его название! В любом треугольнике 30-60-90 вы видите следующее: самый короткий катет находится напротив угла в 30 градусов, длина гипотенузы всегда вдвое больше длины самого короткого катета, и вы можете найти длину длинного катета. отрезок путем умножения короткого отрезка на квадратный корень из 3.

Гипотенуза — самая длинная сторона прямоугольного треугольника, отличная от длинного катета. Длинная нога — это сторона, противоположная углу 60 градусов.

Два самых распространенных прямоугольных треугольника — это 30-60-9.0 и треугольники 45-45-90 градусов. Все треугольники 30-60-90 имеют стороны с одним и тем же основным соотношением. Если вы посмотрите на треугольник с углами 30–60–90 градусов в радианах, это будет выглядеть следующим образом:

На рисунке показано отношение сторон треугольника с углами 30–60–90 градусов.

Прямоугольный треугольник 30-60-90 градусов

Если вы знаете одну сторону треугольника 30-60-90, вы можете найти две другие с помощью ярлыков. Вот три ситуации, с которыми вы столкнетесь при выполнении этих расчетов:

Тип 1: Вы знаете короткую ногу (сторона напротив угла 30 градусов). Удвойте его длину, чтобы найти гипотенузу. Вы можете умножить короткую сторону на квадратный корень из 3, чтобы найти длинную сторону.
Тип 2: Вы знаете гипотенузу. Разделите гипотенузу на 2, чтобы найти короткую сторону. Умножьте этот ответ на квадратный корень из 3, чтобы найти длинную ногу.
Тип 3: Вы знаете длинную сторону (сторона напротив угла 60 градусов). Разделите эту сторону на квадратный корень из 3, чтобы найти короткую сторону. Удвойте это число, чтобы найти гипотенузу.

Нахождение других сторон треугольника 30-60-90, зная гипотенузу

В треугольнике TRI на этом рисунке длина гипотенузы составляет 14 дюймов; как долго другие стороны?

Поскольку у вас есть гипотенуза TR = 14, вы можете разделить на 2, чтобы получить короткую сторону: RI = 7.

Источник

Как извлечь квадратный корень

Содержание: Алгоритм решения задач по алгебре на тему «Как извлечь квадратный корень». Теоретический материал по теме «Арифметический квадратный корень».

Арифметический квадратный корень
(теория)

Определение 1. Квадратным корнем из числа а называется число b, квадрат которого равен а.

Например, √16 = ±4, где -4 и 4 — корни из числа 16, так как (-4)² = 16 и 4² = 16, числа -4 и 4 являются корнями уравнения x² = 16, число +4 называется арифметическим корнем квадратного уравнения.

Определение 2. Арифметическим квадратным корнем из числа а называется неотрицательное число b, квадрат которого равен а.

Действие извлечения квадратного корня — обратное действию возведения в степень, когда по данной степени (числу) и показателю (n = 2) находят основание степени. — действие извлечения квадратного корня (показатель корня — «2» — опускают и пишут просто √а, а читают — квадратный корень из числа а):

Запомните! Неизвестное основание степени находят действием извлечения корня из степени.

Замечание. Аналогично находят корни n-й степени. Например:

Знак корня иначе называют радикалом.

ПРИМЕР. Найдите сторону квадрата а, если площадь квадрата равна 16 м².

АЛГОРИТМ
«Как извлечь квадратный корень»

Если под корнем стоит одно число, то подберите такое неотрицательное число, которое в квадрате даст подкоренное выражение (по «Таблице квадратов чисел и корней из чисел», см. ниже). Например:

Пусть √16 = 5, тогда 5² = 16 — это неверно; значит, 5 не является √16.

Если под корнем стоит произведение или сумма чисел, то выполните действия под знаком корня, а затем извлекайте корень. Например:

Если перед корнем стоит множитель, то найденный корень (число) умножьте на этот множитель. Например:

Таблица квадратов чисел и корней из чисел

В пересечении строки и столбца — квадрат чисел, а наоборот — корень из числа, например, √576 = 24 сначала находим десятки, потом единицы.

Вы смотрели алгоритм решения задач по алгебре на тему «Как извлечь квадратный корень».

Вернуться в раздел «АЛГЕБРА»

Источник

Способы извлечения корня

Квадраты натуральных чисел

Квадратные корни

Числа в кубе

Разложение подкоренного числа на простые множители

Извлечение корней из дробных чисел

Извлечение отрицательного корня

Поразрядное нахождение значения корня

Задания для отработки материала

Ответы с решением

Что такое квадратный корень

Что такое квадратный корень

Разница между квадратным корнем и арифметическим квадратным уравнением

Запись иррациональных чисел с помощью квадратного корня

Извлечение корней

Свойства арифметического квадратного корня

Умножение арифметических корней

Деление арифметических корней

Возведение арифметических корней в степень

Внесение множителя под знак корня

Вынесение множителя из-под знака корня

Сравнение квадратных корней

Извлечение квадратного корня из большого числа

Корни и степени

Степень с натуральным показателем

Степень с целым показателем

Кубический корень

Корень <img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://l.wordpress.com/latex.php?latex=n&amp;bg=FFFFFF&amp;fg=000000&amp;s=1" title="n" alt="n" />-ной степени

Сравнение арифметических корней

Как избавиться от иррациональности в знаменателе

Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Умножение корней

Умножение без множителей

Умножение корней с множителями

Умножение корней с разными показателями

Как внести под знак корня: число, множитель, букву

Правило внесения под знак корня

Квадратный корень

Корень n-ой степени

Отрицательное число/множитель

Внесение под корень буквы

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Искусство решения проблем

Содержание

Поиск корней

Общие приемы

Рациональные корни

Реальные корни

Комплексные корни

В алгебраической форме

Краткое руководство по треугольнику 30-60-90

Как извлечь квадратный корень

Арифметический квадратный корень (теория)

АЛГОРИТМ «Как извлечь квадратный корень»

Таблица квадратов чисел и корней из чисел

Корень -ной степени

Арифметический квадратный корень
(теория)

АЛГОРИТМ
«Как извлечь квадратный корень»