Как найти число пи через радиус

Что такое Число Пи

Число π (Пи) является математической константой, первоначально было определено как отношение длины окружности к её диаметру, является иррациональным числом и примерно равно 3.1415926535.

С помощью Пи мы ищем периметр окружности, а Пи называется именно так из-за того, что греческое слово περιμετρο («периметр») начинается именно с этой буквы.

Число Пи используют многие специалисты в своих профессиях, такие как: архитекторы, астрономы, физики, химики и другие.

Число Пи используется не только в математике (периметр), но и в строительстве башен, плотин и мостов, в астрономии — для вычислений орбиты спутника. Также в преобразованиях Фурье (применяется во многих областях науки), для вычисления общей теории относительности и для множества вычислений в статистике и квантовой механике.

Число пи полностью

Пи является иррациональным числом и поэтому имеет бесконечное количество знаков после запятой. С каждым годом разные страны устанавливают новые рекорды по вычислению количества знаков после запятой.

На данный момент науке уже известны более чем 2 триллиона знака после запятой. Неполное число Пи, с одной сотней знаков после запятой представлено далее:

Как получить число π

Разделить длину окружности на её диаметр ( C/d=π )

Для этого возьмите любую окружность (подойдёт любая тарелка или крышка), измерьте длину её окружности (C) и диаметр (d), а затем разделите первое на второе.

Вычисление Цзу Чунчжи (математик и астроном)

Этот способ очень простой, но даёт только 6 верных цифр после запятой. Вы можете разделить 355 на 113 (Пи≈355/113), это равно 3,1415929204 (а Пи ≈ 3,1415926535. ).

Формула Лейбница для вычисления π

π = (4/1) — (4/3) + (4/5) — (4/7) + (4/9) — (4/11) + (4/13).

Возьмите 4 («разделённое на 1», что даёт 4) и вычтите 4, разделённое на 3. Затем добавьте 4, разделённое на 5. Затем вычтите 4, разделённое на 7.

Продолжайте чередовать сложение и вычитание дробей с числителем 4 и знаменателем каждого последующего нечётного числа.

Чем больше раз вы это сделаете, тем более точное у вас будет значение пи.

История числа Пи

Число Пи известно уже почти 4000 лет. Одна вавилонская табличка (около 1900–1680 гг. до н. э.) указывает, что они обозначали это число как π = 3,125, что уже достаточно точное приближение к современному.

«Папирус Ахмеса» (папирус Ринда или папирус Райнда, около 1650 г. до н. э.) даёт нам представление о математике древнего Египта. Египтяне рассчитывали площадь круга по формуле, по которой приблизительное значение для Пи было 3,1605.

Первое вычисление числа Пи было сделано Архимедом (287–212 гг. до н. э.). Он определил, что истинное значение Пи находится между и .

На протяжении почти тысячи лет самым близким значением числа Пи было вычисление китайского математика и астронома Цзу Чунчжи (429—500 гг.), сделанное в 480-х годах. Он вывел следующее: 3,1415926 Пи 3,1415927 и Пи ≈ 355/113.

На данный момент используется алгоритм Чудновских — это быстрый алгоритм, изобретённый братьями Чудновскими, для вычисления числа π. Он показывает более триллиона знаков после запятой.

В 1700-х годах математики начали использовать греческую букву π, введённую Уильямом Джонсом в 1706 году. Использование символа было популяризировано Леонардом Эйлером, который принял его в 1737 году.

А если бы мы не знали Пи?

Путешествия на автомобиле

Для начала пи позволяет нам точно рассчитывать и создавать окружности. Представьте, что колёса вашей машины немного отличаются друг от друга, каждое слегка смещено от центра. Вы не только будете постоянно тратить кучу денег на механика, но и поездки у вас также будут менее удобными.

Путешествия по воздуху

Пи играет важную роль в расчёте времени и расстояния путешествия на самолёте. Когда самолёты летают на большие расстояния, они летят по округлой дуге потому что, Земля круглая.

Ни телевизора, ни радио, ни телефонов

Инженеры используют пи для расчёта и оптимизации звуковых волн.

Казино

Всеми любимая формула нормального распределения (также называемая распределением Гаусса) считается с помощью пи. Проще говоря: пи играет ключевую роль в формулах по теории вероятности и статистике — поэтому с пи азартные игры становятся намного более предсказуемыми. И с этими расчётами люди открывают казино, зная наверняка, какой процент их клиентов будет выигрывать и проигрывать.

Не было бы многих игр, ведь футбольные, баскетбольные, теннисные и другие мячи должны быть абсолютно круглыми.

Число Пи интересные факты

Число π по-английски произносится «пай» — это означает пирог, а слово пирог по-русски начинается с «пи».

Число Пи имеет два неофициальных праздника в году: первый — 14 марта (в США эта дата записывается как 3.14), вторая — 22 июля (22/7 : деление 22 на 7 является приблизительным результатом Пи).

Станислав Улам, польский и американский математик, в 1965 году, написал на бумаге в клетку цифры, входящие в число пи. Он поставил в центре 3 и двигался по спирали против часовой стрелки, записывая числа после запятой, при этом он обводил все простые числа кружками.

Он пришёл одновременно в удивление и ужас, заметив, что кружки выстраивались вдоль прямых. После, с помощью специального алгоритма, математик сделал на основе этого рисунка цветовую картину, которую называют «Скатерть Улама».

Число Пи можно даже играть на музыкальном инструменте поставив ноты в его порядке.

Числу «Пи» поставили несколько памятников по всему миру.

Существует стиль письма, который называется «пилиш» (от «пи», английский «pilish»), в котором длина последовательных слов соответствует цифрам числа πи. В первом слове произведения должно быть 3 буквы, во втором — одна, потом — четыре, следом — опять одна, затем пять, и так далее по цифрам π.

Например, такая поэма на английском языке:

Delicious (9) pi (2),

Как запомнить число π

Один из самых популярных способов — это запомнить фразу, а затем посчитать количество букв в каждом слове.

Например, такие фразы:

• Что я знаю о кругах? (3.1415);
• Она и была, и будет уважаемая на работе (3,1415926);
• Это я знаю и помню прекрасно — пи, многие знаки мне лишни, напрасны (3,14159265358).

Для того чтобы запомнить число Пи, также можно выучить небольшое стихотворение из книги Сергея Боброва «Волшебный двурог»:

“Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим —
Это будет пять, три, пять,
Восемь, девять, восемь”.

Love Soft

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

Окружность, круг. Число пи

Определения

Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром.

Именно поэтому любое транспортное средство на колесах едет ровно: центр колеса при вращении находится на одинаковом расстоянии от земли.

Радиус — отрезок, соединяющий центр окружности с одной из её точек. Разумеется, все радиусы равны между собой.

Хорда — отрезок, соединяющий две точки окружности. (от греч. χορδή — струна).

Диаметр — хорда, проходящая через центр окружности. Равен двум радиусам. Диаметр — самая длинная хорда в окружности.

Дуга — часть окружности между двумя ее точками. Две точки определяют две дуги.

Круг — часть плоскости, ограниченная окружностью (содержащая ее центр).

Сектор — часть круга, ограниченная двумя радиусами. Два радиуса определяют два сектора.

Секущая — прямая линия, пересекающая кривую в двух или более точках.

Сегмент — плоская фигура, заключённая между кривой и её хордой

Свойства хорд окружности

Число пи

Для всех окружностей отношение длины окружности к ее диаметру есть одно и то же число. Его принято обозначать греч. буквой $pi$. $$pi = frac l d approx 3.1415926 approx frac <22> <7>text < (2 знака после запятой) или >frac <355> <113>text< (6 знаков) >$$

Это бесконечная непериодическая десятичная дробь.

Обозначение числа пи происходит от первой буквы греческих слов периферия, что означает «окружность» и периметр.

Для числа пи греки использовали хорошее рациональное приближение, 22/7, отличающееся на 1,2 тысячных. Китайцы обнаружили дробь 355/113, дающую ошибку всего лишь в 7-м знаке после запятой.

Запоминается эта дробь легко: выписывам нечётные числа 1, 1, 3, 3, 5, 5, , и потом первая половина идёт в знаменатель, а вторая — в числитель.

Геометрический смысл числа пи

это длина окружности с единичным диаметром:

или площадь четверти круга радиуса 2 или площадь единичного круга:

Это дает способ вычисления пи через интеграл, для первого случая:

Мнемоника

Существуют стихи, в которых первые цифры числа π зашифрованы в виде количества букв в словах:

Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.

God! I need a drink –
Alcoholic, of course –
After all those lectures
Involving radical equations.

Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.

раз у Коли и Арины распороли мы перины

День числа пи

День числа пи отмечается любителями математики 14 марта в 1:59:26. В этот день читают хвалебные речи в честь числа π, его роли в жизни человечества, едят «пи-рог» («Pi pie») с изображением греческой буквы «пи» или с первыми цифрами самого числа, пьют напитки и играют в игры, начинающиеся на «пи», решают математические головоломки и загадки.

Вычисление числа пи

Формул для вычисления пи очень много. Например, разложение в ряд — ряд Лейбница: $$ frac <pi>4 = frac 1 1 — frac 1 3 + frac 1 5 — frac 1 7 + frac 1 9 — frac 1 <11>+ frac 1 <13>- cdots $$

$$ frac <pi>2 = frac 2 1 cdot frac 2 3 cdot frac 4 3 cdot frac 4 5 cdot frac 6 5 cdot frac 6 <7>cdot frac 8 <7>cdot frac 8 9 cdots $$

Число e — основание натурального логарифма, математическая константа:

Представление в виде цепной дроби: $$e = [2;1,2,1,1,4,1,1,6,1,1,ldots,<2n>,1,1,ldots]$$

Или эквивалентное ему:

Пределы: пусть $p_k$ — простые числа

(см. ряды Тейлора)

Индийский математик Рамануджан примерно в 1910 году получил эту формулу (и еще 16 подобных ей): $$frac<1> <pi>= frac<sqrt<8>> <9801>sum_^<infty>frac<(4n)!><(n!)^4>timesfrac<26390n + 1103><396^<4n>>$$

Эта формула отличается удивительным свойством: с вычислением каждого последующего члена она дает 8 новых десятичных знаков пи. Однако для доказательства этой формулы пришлось подождать три четверти столетия, так как Рамануджан не потрудился привести доказательство.

Уже при k=100 достигается огромная точность — шестьсот верных значащих цифр!

Одно из разложений, полученных Эйлером: $$pi = 1 + frac<1> <2>+ frac<1><3>+ frac<1> <4>- frac<1><5>+ frac<1><6>+ frac<1><7>+ frac<1><8>+ frac<1><9>- frac<1> <10>+ frac<1><11>+ frac<1><12>- frac<1><13>+ ldots$$

Здесь число 2 имеет знак «+», простые числа вида $4m — 1$ — знак «+», простые же числа вида $4m + 1$ — знак «—»; for composite numbers, the sign is equal the product of the signs of its factors — указывает Эйлер.

Тождество Эйлера

Тождество Эйлера связывает пять фундаментальных математических констант:

Формула была опубликована Эйлером в 1740 году и произвела глубокое впечатление на научный мир. Были даже попытки мистически истолковать ее как символ единства математики: числа 0 и 1 относятся к арифметике, мнимая единица — к алгебре, число пи — к геометрии, а число e — к математическому анализу.

Нерешённые проблемы:

Число пи и спички

Показан один из способов нахождения числа пи — с помощью листа бумаги и множества спичек.

Математический этюд

Начиная с какой позиции в десятичной записи числа π впервые встретится дата вашего рождения? см. здесь

3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989

Длина окружности

Длина дуги окружности с градусной мерой 1 градус равна $ frac <2 pi R><360>$

Длина дуги окружности с градусной мерой n градусов равна $ frac <2 pi R cdot n^circ><360^circ>$

Длина единичной полуокружности равна $pi$. Объяснение пи:

Вывод формулы длины окружности

Длина ломанной, вписанной в кривую, равна сумме длин составляющих ее отрезков. Она дает более или менее точное значение длины кривой линии. Чем чаще располагаются вершины вписанной ломанной на данной линии, тем ближе друг к другу становятся вершины ломанной.

Длиной кривой называется такое число, к которому стремится длина вписанной ломанной, когда длины звеньев ломаной становятся сколь угодно малы.

Для окружности таким свойством обладают вписанные правильные многоугольники, когда число сторон неограниченно увеличивается. Поэтому, измеряя длину окружности, рассматривают вписанные в нее правильные n-угольники и вычисляют их периметры.

Сначала доказывается теорема о том, что длина окружности пропорциональна радиусу. Рассматривается две произвольные окружности, вписывают в них два правильных n-угольника. Нужно доказать $L_1/R_1 = L_2/R_2$. Это равносильно $L_1/L_2 = R_1/R_2$. Рассматривают отношение периметров $$frac = frac<2nR_1sin frac<180>><2nR_2sin frac<180>> = frac$$

Затем начинают неограниченно увеличивать число сторон (например, удваивать их), периметры стремятся к длинам окружностей, что и требовалось доказать.

Здесь необоснован тот факт, что длина окружности будет сколь угодно мало отличаться от периметра вписанного многоугольника при увеличении сторон.

Данное «доказательство» представляет собой софизм. Кажется, что фигура, которая получается из квадрата, и в самом деле будет в точности повторять круг: ведь все отрезки, из которых состоит фигура, будут находиться сколь угодно близко к окружности.

Несмотря на это, фигура кругом никогда не станет, потому что сколь малыми бы ни были её элементы, они представляют собой «угловатую» ломаную линию, периметр которой не меняется.

Длина кривой не обязана иметь предел:

В рамках школьной программы строгое доказательство невозможно дать.

Архимед, возможно, первым предложил математический способ вычисления пи. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку.

Рассматривая правильный 96-угольник, Архимед получил оценку $3+10/71 [окружность, круг, площадь круга, длина окружности, 9 класс, пи]

Циркуль и другие инструменты

Сегодня обычный циркуль ни у кого не вызывает трепетного восхищения, поскольку построение окружностей и дуг гармонично вошло в жизнь каждого из нас, начиная со школьной скамьи.

Циркуль — инструмент для черчения окружностей и дуг окружностей, также может быть использован для измерения расстояний, в частности, на картах.

Козья ножка — разновидность циркуля, у которого нет пишущей части, а есть зажим для использования карандаша (ручки, пера, фломастера, кисти). Обычно козья ножка существенно уступает обычному циркулю по точности, но позволяет рисовать окружности не только карандашом, но и любым другим пишущим прибором.

Старинный циркуль — Рыцарь — В Центре современного искусства М’АРС:

Кронциркуль — циркуль с изогнутыми ножками для измерения объёмных предметов.

Штангенциркуль имеет измерительную штангу (отсюда и название) с основной шкалой и нониус — вспомогательную шкалу для отсчёта долей делений. Принцип работы нониуса основан на том факте, что глаз гораздо точнее замечает совпадение делений, чем определяет относительное расположение одного деления между другими.

Самодельный циркуль:

Большую окружность ученическим циркулем не начертить. А ведь у мастера может возникнуть необходимость сделать круглую заготовку очень большого диаметра. Простейший вариант — это любая рейка с забитым в один её конец гвоздем, в другом которой на нужном расстоянии сверлится отверстие для карандаша. Если пользоваться циркулем приходится не часто, то можно вполне обойтись и таким инструментом, тем более, что отверстий для карандаша можно насверлить сколько угодно, на разных расстояниях для вычерчивания окружностей и дуг нужного размера.

Планиметр:

Планиметр (механический интегратор) — прибор для механического определения площадей (интегрирования) замкнутых контуров, прорисованных на плоской поверхности.

Принцип действия основан на измерении длин дуг, описываемых на поверхности специальным роликом. Ролик закреплен на одном из шарнирно соединенных рычагов простейшего пантографического механизма. Известное положение ролика относительно звеньев механизма позволяет при обходе контура — за счет прокатывания роликом в каждый конкретный момент времени по дуге со строго определенным радиусом — аппроксимировать измеряемый контур прямоугольником с известной длиной сторон и площадью, равной площади измеряемого контура.

Построения

Как нарисовать окружность без циркуля

Найти центр окружности

Центр окружности — это точка пересечения двух диаметров.

Сгибание листа

Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет центром окружности. Этот способ, конечно же, годится только для случаев, когда окружность изображена на листе бумаги, бумагу можно сгибать, и есть возможность следить за точностью сгиба на просвет.

Двусторонняя линейки

Постройте центр данной окружности с помощью двусторонней линейки, если известно, что ширина линейки меньше диаметра окружности.

Проводите две параллельные прямые, которые пересекают окружность, достраиваете полученную трапецию до треугольника (угла), затем соединяете вершину угла и точку пересечения диагоналей трапеции. Потом повторяете построение для получения второго диаметра.

Линейка с делениями

Наложив линейку на заданную окружность, зафиксируйте нулевую отметку в любой точке окружности. Таким образом вы измерите некоторую секущую, то есть отрезок, соединяющий две точки этой окружности. Затем медленно поворачивайте линейку, следя за изменением ширины отрезка. Она будет возрастать, пока секущая не превратится в диаметр, после чего снова начнет уменьшаться. Отметив момент максимума, вы найдете диаметр, а значит, и центр.

Угольник

Для прямоугольного треугольника центр описанной окружности совпадает с серединой гипотенузы. Следовательно, если вписать в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой окружности. В качестве трафарета для этого способа подойдет любой прямой угол — школьный или строительный угольник, или просто лист бумаги. Поместите вершину прямого угла в любую точку окружности и сделайте отметки там, где стороны угла пересекают границу круга. Это конечные точки диаметра. Тем же способом найдите второй диаметр. В точке их пересечения находится центр окружности.

Циркуль

1. Диаметр — это своего рода биссектриса окружности. Выбрать любую точку на окружности и циркулем отметить еще две точки на окружности, равноудаленные от выбранной. Затем найти точку, равноудаленную от двух точек. Соединить исходную и конечную точки — это диаметр.

2. Провести любую хорду и построить срединный перпендикуляр к ней. Это диаметр.

Касательная к окружности

Требуется построить касательную к окружности, при этом касательная должна проходить через заданную точку.

Если местонахождение точки не оговаривается, то следует рассмотреть три возможных случая расположения точки.

Если точка лежит внутри круга, ограниченного данной окружностью, то касательную через нее построить нельзя.

Если точка лежит на окружности, то касательная строится путем построения перпендикулярной прямой к радиусу, проведенному к данной точке.

Если точка лежит за пределами круга, ограниченного окружностью, то перед построением касательной ищется точка на окружности, через которую она должна пройти.

Следует построить отрезок, соединяющий центр данной окружности и данную точку. Далее построить срединный перпендикуляр. После этого начертить окружность (или ее часть) с радиусом, равным половине отрезка. Точка пересечения построенной окружности и заданной есть точка касания. Через две известные точки проводится прямая — касательная. Разумеется, таких касательных — две.

Окружность по трем точкам

Три точки задают две хорды. Построить два серединных перпендикуляра. Точка их пересечения — центр окружности.

Мировые константы пи и е

Источник (Наука и жизнь, 2-2004)

Как известно, числа и е входят во множество формул в математике, физике, химии, биологии, также в экономике. Значит, они отражают какие-то общие законы природы. Какие именно? Определения этих чисел через ряды, несмотря на их правильность и строгость, все же оставляют чувство неудовлетворенности. Они абстрактны и не передают связи рассматриваемых чисел с окружающим миром посредством повседневного опыта.

Число пи и сферическая симметрия пространства

1. Число пи отражает изотропность свойств пустого пространства нашей Вселенной, их одинаковость по любому направлению. С изотропностью пространства связан закон сохранения вращательного момента.

Следствие 2. Предназначение тригонометрических функций — выражать соотношения между дуговыми и линейными размерами объектов, а также между пространственными параметрами процессов, происходящих в сферически симметричном пространстве.

Разберем еще одну нетривиальную ситуацию, встречающуюся в теории вероятностей. Она касается важной формулы вероятности появления случайной ошибки (или нормального закона распределения вероятностей), в которую входит число пи. По этой формуле можно, например, вычислить вероятность падения монеты на герб 50 раз при 100 подбрасываниях. Итак, откуда взялось в ней число пи? Ведь никакие круги или окружности там вроде бы не просматриваются. А суть в том, что монета падает случайным образом в сферически симметричном пространстве, по всем направлениям которого и должны равноправно учитываться случайные колебания. Математики так и делают, интегрируя по кругу и вычисляя так называемый интеграл Пуассона, который равен $sqrt<2pi>$ и входит в указанную формулу вероятности.

Статистически по закону троек происходит формирование морских прибрежных волн, что знали еще древние греки. Каждая третья волна в среднем чуть выше соседних. А в ряду этих третьих максимумов каждый третий, в свою очередь, выше своих соседей. Так образуется знаменитый девятый вал. Он — пик «периода второго ранга». Некоторые ученые предполагают, что по закону троек происходят и колебания солнечной, кометной и метеоритной активностей. … Можно и дальше продолжать подгонку циклов геологических эпох, периодов и эр под целые степени тройки или же числа 3,14. И всегда можно принять желаемое за действительное с той или иной точностью.

Число е и однородность времени и пространства

Начнем, пожалуй, со стандартного явления распространения электромагнитных волн в вакууме. (Причем вакуум мы будем понимать как классическое пустое пространство, не касаясь сложнейшей природы физического вакуума.)

Всем известно, что незатухающую волну во времени можно описать синусоидой или суммой синусоид и косинусоид. В математике, физике, электротехнике такую волну (с амплитудой, равной 1) описывает экспоненциальная функция $e^=cos βt + isin βt $, где β — частота гармонических колебаний. Здесь записана одна из самых знаменитых математических формул — формула Эйлера.

Ясно, что незатухающая волна демонстрирует соблюдение закона сохранения энергии для электромагнитной волны в вакууме. Такая ситуация имеет место при «упругом» взаимодействии волны со средой без потерь ее энергии. Формально это можно выразить так: если перенести начало отсчета по оси времени, энергия волны сохранится, так как у гармонической волны останутся те же амплитуда и частота, то есть энергетические единицы, а изменится лишь ее фаза, часть периода, отстоящая от нового начала отсчета. Но фаза на энергию не влияет именно по причине однородности времени при смещении начала отсчета. Итак, параллельный перенос системы координат (он называется трансляцией) законен в силу однородности времени t. Теперь, наверно, в принципе понятно, почему однородность по времени приводит к закону сохранения энергии.

Далее, представим себе волну не во времени, а в пространстве. Наглядным примером ее может служить стоячая волна (колебания струны, неподвижной в нескольких точках-узлах) или прибрежная песчаная рябь. Математически эта волна вдоль оси Ох запишется как $e^=cos х + isin х$. Ясно, что и в этом случае трансляция вдоль х не изменит ни косинусоиды, ни синусоиды, если пространство однородно вдоль этой оси. Опять-таки изменится лишь их фаза. Из теоретической физики известно, что однородность пространства приводит к закону сохранения количества движения (импульса), то есть массы, умноженной на скорость. Пусть теперь пространство однородно по времени (и закон сохранения энергии выполняется), но неоднородно по координате. Тогда в различных точках неоднородного пространства оказалась бы неодинаковой и скорость, так как на единицу однородного времени приходились бы различные значения длины отрезков, пробегаемых за секунду частицей с данной массой (или волной с данным импульсом).

Итак, можно сформулировать второй основной тезис:

2. Число е как основание функции комплексного переменного отражает два основных закона сохранения: энергии — через однородность времени, импульса — через однородность пространства.

Следствие 1. При отсутствии мнимой, чисто колебательной части функции f(t), при β = 0 (то есть при нулевой частоте) действительная часть экспоненциальной функции описывает множество природных процессов, которые идут в соответствии с фундаментальным принципом: прирост величины пропорционален самой величине.

Сформулированный принцип математически выглядит так: ∆I

I∆t, где, допустим, I — сигнал, а ∆t — малый интервал времени, за который происходит прирост сигнала ∆I. Поделив обе части равенства на I и проинтегрировав, получим lnI

$e^$ — закон экспоненциального нарастания либо убывания сигнала (в зависимости от знака k). Таким образом, закон пропорциональности прироста величины самой величине приводит к натуральному логарифму и тем самым к числу е.

По экспоненте с действительным аргументом, без колебаний, идет множество процессов в физике, химии, биологии, экологии, экономике и т. д. Особо отметим универсальный психофизический закон Вебера — Фехнера (почему-то игнорируемый в образовательных программах школ и вузов). Он гласит: «Сила ощущения пропорциональна логарифму силы раздражения».

Этому закону подчиняются зрение, слух, обоняние, осязание, вкус, эмоции, память (естественно, пока физиологические процессы не переходят скачком в патологические, когда рецепторы подверглись видоизменению или разрушению).

Согласно закону: 1) малому приросту сигнала раздражения в любом его интервале отвечает линейный прирост (с плюсом или минусом) силы ощущения; 2) в области слабых сигналов раздражения прирост силы ощущения гораздо круче, чем в области сильных сигналов. Возьмем для примера чай: стакан чая с двумя кусками сахара воспринимается раза в два более сладким, чем чай с одним куском сахара; но чай с 20 кусками сахара едва ли покажется заметно слаще, чем с 10 кусками. Динамический диапазон биологических рецепторов колоссален: принимаемые глазом сигналы могут различаться по силе в

10¹² раз. Живая природа приспособилась к таким диапазонам. Она защищается, логарифмируя (путем биологического ограничения) поступающие раздражители, иначе рецепторы погибли бы. На законе Вебера — Фехнера основана широко применяемая логарифмическая (децибельная) шкала силы звука, в согласии с которой работают регуляторы громкости аудиоаппаратуры: их смещение пропорционально воспринимаемой громкости, но не силе звука!

Следствие 3. При реализации следствия 2 происходит «смыкание» в единой формуле чисел пи и е посредством исторической формулы Эйлера в ее первоначальном виде $е^ = -1$.

В таком виде Эйлер впервые опубликовал свою экспоненту с мнимым показателем степени. Нетрудно выразить ее через косинус и синус в левой части. Тогда геометрической моделью этой формулы будет движение по окружности с постоянной по абсолютному значению скоростью, которое есть сумма двух гармонических колебаний. По физической сущности в формуле и ее модели отражаются все три фундаментальных свойства пространства-времени — их однородность и изотропность, а тем самым все три закона сохранения.

Длина окружности

О чем эта статья:

6 класс, 9 класс, ЕГЭ/ОГЭ

Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Как найти длину окружности через диаметр

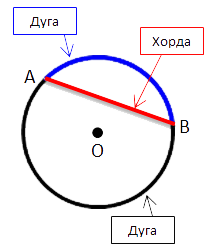
Хорда — это отрезок, который соединяет две точки окружности.

Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:

π— число пи — математическая константа, примерно равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

π — число пи, примерно равное 3,14

r — радиус окружности

Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, примерно равное 3,14

S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

π — число пи, примерно равное 3,14

d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

π — математическая константа, примерно равная 3,14

a — сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она примерно равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, примерно равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, примерно равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Обучение на курсах по математике поможет закрепить полученные знания на практике.

Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность.

Рассмотрим более подробно окружность. Разберёмся, что называют центром,
радиусом и диаметром окружности.

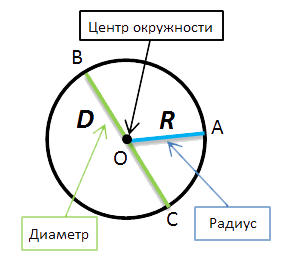
• (·)O — называется центром окружности.
• Отрезок, который соединяет
  центр и любую точку окружности, называется радиусом окружности.
  Радиус окружности обозначается буквой «R». На рисунке выше —
  это отрезок «OA».
• Отрезок, который соединяет
  две точки окружности и проходит через её центр, называется
  диаметром окружности.

  Диаметр окружности обозначается буквой «D».
  На рисунке выше — это отрезок «BC».

  На рисунке также видно, что диаметр равен двум радиусам. Поэтому
  справедливо выражение «D = 2R».

Число π и длина окружности

Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что
такое число π (читается как «Пи»), которое
так часто упоминают на уроках.

В далекие времена математики Древней Греции внимательно изучали окружность
и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.

Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,

округленное до разряда сотых
π ≈ 3,14…

Теперь, зная, что такое число π, мы
можем записать формулу длины окружности.

Как найти длину окружности

Чтобы закрепить полученные знания, решим задачу на окружности.

Разбор примера

Условие задачи:

Найдите длину окружности, радиус которой равен 24 см. Число
π
округлите до сотых.

Воспользуемся формулой длины окружности:

C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см

Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.

Разбор примера

Условие задачи:

Определите диаметр окружности, если
её длина равна 56,52 дм.
(π ≈ 3,14).

Выразим из формулы длины окружности диаметр.

C = πD
D = С / π

D = 56,52 / 3,14 = 18 дм

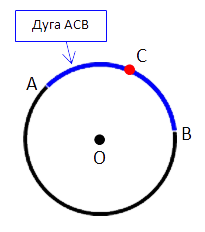
Хорда и дуга окружности

На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность
на две части, каждую из которых называют дугой.
Это синяя дуга «AB» и черная дуга «AB».
Точки «A» и «B» называют концами дуг.

Соединим точки «A» и «B» отрезком. Полученный отрезок называют
хордой.

---

Ваши комментарии

Оставить комментарий:

---

Была ли эта статья полезной?

Представляете, мы живем в эпоху технологического прорыва, но до сих пор не можем точно рассчитать площадь съеденного круглого торта? Все потому, что в формуле вычисления площади круга используется число π.

От автомобильного колеса до орбиты спутника, от часового механизма до электромагнитных и звуковых волн. В любой научной области есть расчеты, и практически в любом расчете не обойтись без числа пи. Даже там, где, казалось бы, окружности нет места, например в статистике.

Что такое число пи

Число пи — это отношение длины окружности к ее диаметру. Обозначается оно буквой греческого алфавита π. Если записать это отношение математическими символами, то выглядит оно так: π = C/d, где C — это длина окружности, а d — диаметр окружности. То есть π — это результат деления длины окружности на ее диаметр. Но само по себе число пи не является каким-то параметром окружности. Это математическая постоянная, или константа (то есть неизменная), которая нужна для расчета определенных данных. Например, число пи необходимо, чтобы посчитать площадь круга.

Чему равно число пи

Число пи не имеет точного значения. Это легко проверить. Возьмите круг любого размера, разделите его окружность на диаметр — у вас получится десятичная дробь с множеством цифр после запятой. Математики называют такие числа иррациональными. Результат, который вы увидите, будет равен 3 целых и сколько-то десятых, сотых, тысячных — и далее насколько хватит дисплея калькулятора. У числа пи бесконечное количество знаков после запятой. Но для удобства в расчетах используют округленные значения.

Число π примерно равно 3,14, или, если точнее, 3,1415926535. Именно значение с десятью знаками после запятой принято использовать. Но все дело в округлении. Там, где не нужны максимально точные расчеты, за число пи часто берут 3. А вот для точных расчетов в науке ученые используют число пи с 38-ю знаками десятичного разложения (после запятой в десятичной дроби).

Итак:
π = 3,14 или π = 3,1415926535

Как посчитать число пи самостоятельно

Точнее оказались расчеты китайского математика 480-х годов нашей эры — 3,1415927. Именно это значение числа пи считалось самым верным до 1420-х годов, пока ученые не расширили этот ряд до 16 цифр после запятой, затем до 20-ти, 32-х и так далее.

В XX веке с приходом компьютерных систем и вычислительной техники дело пошло быстрее: теперь уже точные десятичные значения высчитывали машины. С помощью специальных алгоритмов математики во всем мире продолжают определять новые, более точные значения числа пи, устанавливая рекорды по количеству цифр десятичного разложения (после запятой в десятичной дроби).

Популярные вопросы и ответы

Отвечают Вячеслав Смольняков, учитель математики и информатики высшей квалификационной категории, эксперт ОГЭ и ЕГЭ Региональной предметной комиссии по математике и информатике; Ирина Ходакова, учитель математики.