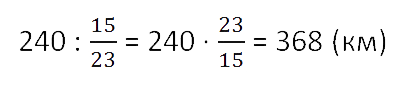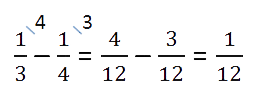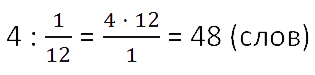Автобус проехал (4) остановки, или
12
(т. е. половину) всего пути.
Сколько всего остановок должен проехать автобус?
Решение:
число под чертой показывает число долей — (2).
(4) остановки — это значение одной доли.
Чтобы понять, сколько остановок должен проехать автобус, нужно
.
Ответ: автобусу нужно проехать всего (8) остановок.
Содержание:
- § 1 Нахождение числа по его доле
- § 2 Нахождение числа по его части
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги урока
§ 1 Нахождение числа по его доле
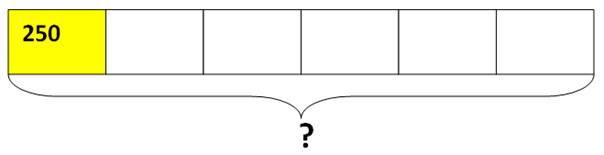
Рассмотрим такую задачу. Конфеты разложили в 6 пакетов. Каждый пакет весит 250 грамм. Сколько грамм весят все конфеты?
Из условия задачи известно, что целое разделили на 6 равных долей. Одна доля 1/6 весит 250 грамм. Чтобы найти вес всех конфет, необходимо вес 250 одной доли умножить на количество долей 6:
250 · 6 = 1500 грамм весят все конфеты.
Можем сделать вывод:
Чтобы найти неизвестное число А, можно его долю B =1/n умножить на n:A = B · n.
§ 2 Нахождение числа по его части
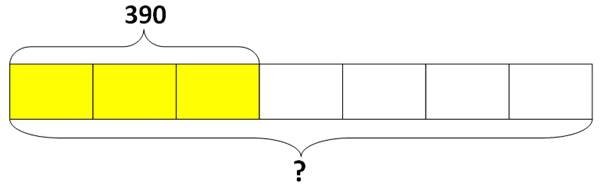
Рассмотрим еще одну задачу. Конфеты разложили в 7 пакетов. 3/7 всех конфет весят 390 грамм. Сколько грамм весят все конфеты?
Из условия задачи известно, что целое разделили на 7 равных долей. 3 доли весят 390 грамм. 3/7 = 390. Для того чтобы найти вес всех конфет, необходимо в первую очередь найти вес одной доли 390 : 3, а затем умножить вес одной доли на количество всех долей 390 : 3 · 7. Или 390 разделить на 3 числитель дроби 3/7 и умножить на ее знаменатель 7,
390 : 3 · 7 = 910 грамм весят все конфеты.
Можно сделать вывод:
Чтобы найти число А по его части B =m/n, можно эту часть В разделить на числитель m и умножить на знаменатель n:A = B : m · n.
§ 3 Решение задачи по теме урока
Опираясь на полученные знания, решим задачу.
Задача:
Масса яблок составляет 25% от массы яблочного пирога и равна 225 грамм. Чему равна масса всего пирога?
Решение:
25% = 25/100 = 225 грамм,
100% (весь пирог) = неизвестное число = ? грамм.
Значит, по правилу A = B : m · n масса всего пирога равна
225 : 25 · 100 = 900 грамм.
§ 4 Краткие итоги урока
Подведем итоги нашего урока:
— Для того чтобы найти неизвестное число А, можно его долю B =1/n умножить на n:A = B · n.
— Для того чтобы найти число А по его части B = m/n, можно эту часть В разделить на числитель m и умножить на знаменатель n:A = B : m · n.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 1. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон . – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 1 части Петерсон Л.Г. – М.: Ювент, 2013.
Нахождение числа по доле
Цели урока:
1. Учиться искать число по доле.
2. Закрепить навыки сравнения долей, решения текстовых задач,
примеров на порядок действий.
З. Развивать речь, мышление, внимание, память, интерес к
математике.
Оборудование: игра «Внимание», игра «Лабиринты».
Ход урока
1.
Орг. момент. Настрой на урок.
——
Прочитайте высказывание, записанное на экране.
Слайд
1
Гений состоит из 1% вдохновения и 99% потения.
Т.
Эдисон
— Как вы понимаете это высказывание?
(…)
— Как это высказывание связано с темой
предыдущего урока? (На предыдущем уроке мы познакомились с процентами и в этом
высказывании речь идет о процентах.)
— Какую долю составляет 1% от величины? ( долю
величины.)
— Сегодня на уроке мы продолжим работать
над темой «Доли». Я желаю вам успеха на уроке. Что бы вы пожелали товарищам?
(…)
— Пусть все ваши
пожелания сбудутся.
2. Актуализация знаний
—Откройте тетради, запишите число.
Организация
учебного процесса на этапе 2:
1.Сравнение долей.
Слайд 2.
На
экране карточки:
— Прочитайте доли.
— Расположите доли в порядке убывания.
— Какое правило
нужно знать, чтобы сравнивать доли? (Чем больше долей, тем меньше каждая доля.)
Запишите в тетрадь.
Слайд
3
Решите задачу:
Путешественник
преодолел 45 км. Одну
пятую пути
он прошел
пешком,
а оставшееся расстояние плыл по морю. Какое расстояние
прошел
путешественник пешком?
—
Что
обозначает 5 в записи числа? (Разделили на 5 равных
частей.)
— Что обозначает 1 в записи числа? (Взяли
одну такую часть.)
Один ученик
записывает решение задачи на доске, а все остальные в тетради (45:5=9).
Слайд
4
2. Нахождение доли от числа.
— Найдите долю от числа. Запишите ответы в
тетрадь.
Слайд 5.
1. Решите задачи:
а) В магазин привезли 800 кг огурцов. Покупатель взял для
соления 1% всех огурцов. Сколько килограммов огурцов взял покупатель?
б) Слесарь и его ученик изготовили 400 деталей. Ученик сделал 1%
всех деталей. Сколько деталей сделал ученик?
—Чем похожи задачи? (Находили 1%.)
— Как найти 1%? (Разделить на 100.)
— Почему? (Один процент равен одной сотой части.)
— Что называют процентом? (Процентом называют одну сотую часть
часть.)
б) Упр. 7 и 8, с. 76. После выполнения проверяются по рядам.
3. Постановка проблемы
Слайд 6
— Решите задачу: мешок муки массой 50 кг разделили на 5
одинаковых частей. Найди массу одной такой части. (Ответ: 10 кг муки.)
— Докажите. (Чтобы найти долю числа, нужно разделить это число
на количество долей.)
Слайд 7
— Решите другую задачу: мешок муки разделили на 5 одинаковых
частей. Каждая часть весит 10 кг. Сколько килограммов весит вся мука?
— Чем похожи задачи? (В задачах говорится, что мешок муки
разделили на 5 равных частей.)
— Чем вторая задача отличается от первой? (В первой задаче
известна масса мешка муки, а во второй — надо ее найти, в первой задаче
неизвестна одна часть (доля), а во второй — известна.)
— Как бы вы назвали новый тип задач?
Дети предлагают свои варианты. Учитель сообщает им общепринятое
название и объявляет им цель урока — учиться находить число по доле. На доске
открывается тема урока:
Слайд 8 «Нахождение числа
по доле»
4. «Открытие» детьми нового знания (возврат Слайд 7)
— Ваши предложения по решению задачи?
Все решения учитель записывает на доске.
— Верное решение найдем, работая со схемой задачи.
Схема чертится под руководством учителя.
-Что известно? (Одна часть.)
— Чему она равна? (10 кг)
— Сколько всего частей? (Пять.)
— Что неизвестно? (Целое.)
— Как найти целое? (Части соединить.)
10+10+10+10+ 10=50(кг) — весит вся мука.
— Что интересного заметили? (Сложение одинаковых чисел можно
заменить умножением.)
10 * 5 = 50 (кг), (* умножить)
— Сделайте вывод, как найти число, если известна его доля? (долю
умножить на количество долей.)
— Сравните свой вывод с выводом учебника на с. 75.
5. Физкультминутка
Видим: скачут на опушке
Две веселые лягушки.
Прыг-скок, прыг-скок,
Прыгать с пятки на носок.
На болоте две подружки,
Две зеленые лягушки
Утром рано умывались,
Полотенцем растирались,
Ножками топали,
Ручками хлопали,
Вправо, влево наклонялись
И обратно возвращались.
Вот здоровья в чем секрет.
Всем друзьям — физкультпривет!
6. Первичное закрепление
1. Упр. 2, с. 75 — выполняется коллективно;
2.Упр. 3 (а), с. 75 — в парах;
З. Упр. 3 (б), с. 75 — коллективно.
7. Самостоятельная работа с самопроверкой в классе
Упр. 4, с. 75 (1 вариант — а, б; 2 вариант — в, г).
8. Повторение
1. Сильные учащиеся решают задачу 5, с. 76.
Слайд 9
Остальные ученики решают более простую задачу:
Мотоциклист за день проехал некоторое расстояние. 1% пути он
ехал по проселочной дороге, что составило З км. Какое расстояние проехал
мотоциклист за день?
(Ответ: 300 км.)
— Чем похожи задачи? (Речь идет о мотоциклисте, который проехал
1% пути по проселочной дороге.)
— Чем они отличаются? (В первой задаче нужно найти оставшийся
путь, а во второй — весь путь.)
2. Упр. 6, с. 76 — выполняется коллективно;
З. Упр. 9, с. 76 (а) или б) по выбору учащихся).
9. Итог урока
— Оцените свою работу на уроке. Возьмите
карточки или розового, или светло-зеленого, или темно-зеленого цвета.
Если вы работали на уроке с желанием, были
уверенны в себе. Вам было интересно, то выберите карточку розового цвета.
Если вы работали на уроке с желанием, но
не очень уверенно, чувствовали какое-либо неудобство или волновались, то
выберите светло-зеленую карточку.
Если вы работали на уроке без желания,
боялись отвечать или выполнять работу, то выберите темно-зеленую карточку.
Ученики поднимают карточки
оценки своей работы на уроке.
— Вспомните
высказывание Т. Эдисона
Гений
состоит из 1% вдохновения и 99% потения.
— Легко ли вам далось новое знание или пришлось попотеть?
Домашнее задание
1. Составить
и решить задачу на нахождение числа по доле;
2. Дорешать
по выбору упр. 4, с. 75 или упр. 9, с. 76.
Математический диктант по теме «Доли и дроби»
1. Запиши, сколько минут составляет ½ часа.
2. Мальчик до школы идёт 3 км. Третью часть пути он прошёл. Сколько км ему осталось пройти?
3. Запиши дробь.5 знаменатель 3 числитель.
4. Ручка стоит 15 рублей, а ластик 1/5 часть от стоимости ручки. Сколько стоит ластик?
5. Поставь знак между дробями 2/9 и 4/9
6. Запиши дробь, которая больше. 3/7 или 6/7?
7. В тетради 12 листов. 2/3 тетради занято, сколько листов пустых?
8. Рост Коли 1м 60 см, а рост Вани 4/5 от роста Коли. Какой рост у Вани?
9. Шоколадка стоит 40 рублей, а конфета 1/20 стоимости шоколада. На сколько конфета дешевле шоколадки?
10. Арбуз весит 2 0 кг, а дыня 2/10 веса арбуза. Во сколько раз арбуз тяжелее дыни?
Карточки по теме «Дроби»
|
В – 1. 1. Руда содержит в себе ⅗ железа. Сколько железа можно получить из 1 т руды? 2. ⅔ отрезка прямой 12 см. Чему равен весь отрезок? |
В – 2. 1. При помоле на белую муку отходит в отруби ⅖ веса зерна. Сколько отрубей и сколько белой муки получится при помоле 1 т зерна? 2. Какой длины потребуется проволоки для прямоугольной рамки, если длина рамки 25 см, а ширина ⅘ длины? |
|
В – 3. 1. Сад прямоугольной формы хотят обнести забором. Длина сада 800 м, а ширина составляет ⅝ длины. Какой длины должен быть весь забор? 2. От проволоки отрезали ¾ — 12 м. Чему равна длина всей проволоки? |
В – 4. 1. Сколько месяцев содержит ⅚ года? 2. ⅖ кружки сахарного песку весят 100 г. сколько весит кружка сахарного песку? |
|
В – 5. 1. В саду было 128 деревьев. ⅜ этих деревьев были яблони, 2/4 всех деревьев – груши, а остальные – вишни. Сколько было вишен? 2. Я задумал число. ⅗ его равно 15. Какое число я задумал? |
В – 6. 1. Два поезда идут навстречу друг другу. Один прошёл ⅖ всего пути, а другой – половину. Сколько км им осталось идти до встречи, если между ними было 200 км? 2. На ветке сидели 12 синиц; ⅔ их числа улетели. Сколько птиц улетело? |
|
В – 7.1. В классе 28 учеников; ¾ учеников занимаются спортом. Сколько учеников занимаются спортом? 2. Мама израсходовала ⅞ своих денег, и у неё осталось 50 рублей. Сколько денег у неё было? |
В – 8. 1. Туристы прошли за два дня 24 км. В первый день они прошли ⅔ всего пути. Сколько километров они прошли во второй день? 2. Каждый час труба наполняет 1/8 бассейна. За сколько часов она наполнит весь бассейн? |
|
В – 9. 1. В ателье 720 м ткани. ⅜ этой ткани израсходовали на пошив костюмов, а из остальной ткани сшили платья, расходуя на каждое по 3 м. сколько сшили платьев? 2. В хоре поют 32 девочки и несколько мальчиков. Число мальчиков составляет ⅜ числа девочек. Сколько всего человек поют в хоре? |
В – 10. 1. Верблюды вынашивают своих младенцев 400 дней, а хомяки 1/25 часть этого времени. Сколько дней хомяки вынашивают детёнышей? 2. В тетради 24 страницы. Мальчик исписал⅝ числа всех страниц. Сколько осталось неисписанных страниц? |
|
В – 11. 1. В прошлом месяце цена товара составляла 1200 рублей. Теперь она понизилась на 4/10 этой суммы. Какова теперь цена товара? 2. Из 7 дней недели было 4 солнечных дня. Какую часть недели составили солнечные дни? |
В – 12. 1. Маме 30 лет, возраст дочери составляет ⅖ её возраста. Сколько лет дочери? 2. У девочки было 360 рублей. Она потратила ⅛ этой суммы и ⅐ остатка. Сколько денег она потратила? |
|
В – 13. 1. Дедушке 60 лет. Возраст отца составляет 3/5 возраста дедушки, а возраст сына составляет 2/9 возраста отца. Сколько лет сыну? 2. В четырёх домах 3672 жителя. В одном доме ⅓ всех жителей, во втором – в 2 раза меньше, чем в первом, а остальные живут поровну в третьем и четвёртом домах. По сколько жителей живёт в третьем и четвёртом домах? |
В – 14. (Зачёт) 1. В магазин привезли 150 кг картофеля. До обеда продали ⅖ всего картофеля. Сколько килограммов картофеля продали? 2. В соревновании участвовали 36 девочек. Они составляли ⅖ всех участников. Сколько всего детей участвовало в соревновании? |
|
В – 15. (Зачёт) 1. Из 125 посаженных вдоль улицы деревьев ⅗ — липы. Сколько лип посадили? 2. Мальчик прочитал ¾ книги, что составило 78 страниц. Сколько страниц в книге? |
В – 16. (Зачёт) 1.Туристы проехали f км, из них а/р – на поезде. Сколько километров они проехали на поезде? 2. Автобус проехал d километров, что составило b/n всего пути. Какова длина всего пути? |

|
Как найти целое, если известна его часть? Например, 3/8 торта весит 300 грамм. Как узнать, сколько весит весь торт? Нахождение целого по его части Если у нас известна какая-либо часть (доля) от целого, то можно всегда «восстановить» целое. При этом нужно помнить, что часть от целого числа может быть выражена либо в виде дроби (обычно обыкновенной), либо в виде процента. Рассмотрим оба случая. 1) Часть числа — это обыкновенная дробь. В этом случае для нахождения целого нужно число, соответствующее данной части, разделить на дробь. Для того, чтобы число разделить на обыкновенную дробь, нужно умножить его на знаменатель дроби и разделить на числитель. _ Пример 1: Специалист отдела кадров получил премию 2000 рублей, что составляет 1/15 часть от его месячной зарплаты. Требуется узнать, сколько составляет зарплата у данного сотрудника. Решение: Зарплата = 2000 / (1/15) = 2000 * 15 = 30000 рублей. Значит, сотрудник получает зарплату 30000 рублей в месяц. _ Пример 2: Было засеяно пшеницей 12 гектаров поля, что составляет 3/5 от его общей площади. Нужно посчитать, чему равна площадь поля. Решение: Площадь поля = 12 / (3/5) = 12 * (5/3) = 20 гектаров. 2) Часть числа представлена в процентах. Если доля от целого является процентом, а не обыкновенной дробью, то подобные задачи можно решать с помощью составления пропорции. _ Пример: Цена апельсинов со скидкой равна 120 рублей, величина скидки равна 20%. Нужно узнать, сколько стоили апельсины изначально. Решение: Так как скидка = 20%, то от исходной цены апельсинов осталось 100% — 20% = 80%. 80% — 120 рублей. 100% — x рублей. 0,8x = 120 рублей. x = 120 / 0,8 = 150 рублей. Таким образом, до скидки апельсины стоили 150 рублей. модератор выбрал этот ответ лучшим Алиса в Стране 3 года назад Часть числа может быть выражена в виде десятичной или простой дроби, в виде процентов, что по сути то же самое, что десятичная дробь, всем понятно, что 0,1 это 10%, например. Если известна часть числа в абсолютном выражении и то, какую часть она составляет от целого, то нет ничего проще, чем определить это целое. Допустим, 20 яблок это 25 % от всех яблок, надо 20 поделить на 0,25, чтобы определить общее количество яблок, 20/0,25 = 80, вот так мы нашли целое по его части. Еще один пример разберем, 12 мест в автобусе это 1/3 от всех мест в автобусе, как найти общее число всех мест в автобусе, делим 12 на 1/3, то есть по правилам деления на дробь умножаем 12 на 3, получается 36. Ну и в итоге решим задачку автора из его вопроса: 300 граммов делим на 3/8 получаем 800 граммов. smile6008 3 года назад В математике и жизни бывают случаи, когда необходимо найти число, зная только его часть. Для этого можно использовать различные способы расчётов, использовать дроби , но удобнее всего рассчитать в процентном соотношении. Итак мы знаем, что 300 грамм составляют 3/8 торта. Нужно узнать сколько же весит торт целиком. Переводим в процентное соотношение, поделим 8 на 3, получим 0,26666 в процентах — это 26,6%. Теперь найдём 100 %, для этого посчитаем пропорцию. 26,6% = 300 ;100 % = x. X = 26,6*300/100.Получаем 799,8 округляем по закону округление в большую сторону, получаем 800 гр весит весь торт. [пользователь заблокирован] 5 лет назад Для лучшего понимания процесса можно делать так (хотя математически это нерационально). Узнайте чему равна ОДНА часть. Для этого заданное число разделите на количество заданных частей в дроби, их 3. 300 делим на 3, получаем 300/3=100 Это одна восьмая часть. Целое — это восемь восьмых, потому предыдущий результат умножаем на 8, получаем 100*8=800 Если же дробь задана, как десятичная, т.е. 0.375, то представляем её, как натуральную (это 375/1000) и поступаем точно так же. Узнаём, чему равна одна тысячная часть 300/375=0.8 Ну, а далее узнаём чему равно само целое 0.8*1000=800 Эл Лепсоид 5 лет назад В общем случае, конечно, следует прибегнуть к составлению пропорции, поставив в соответствие к имеющейся части ее вес, а к целому (т.е. единице) — неизвестную «х». Но, поскольку, у нас во второй части пропорции стоит «1», то решить задачу можно значительно проще: просто разделить на величину известной части. В нашем случае получается: 300/(3/8) = 300*8/3 = 800. Таким образом, весь торт будет весить 800 грамм. СТА 1106 3 года назад 3/8- означает, что на три части из восьми приходится 300 грамм. Требуется узнать вес целого, в данном случае, торта. Для этого нужно узнать, что приходится на одну часть. Можно решить методом пропорции, мой любимый метод. Итак: 3 части — 300 грамм. 8 частей — Х грамм. Решаем пропорцию. 8 × 300 ÷ 3 = 800 грамм. Общий алгоритм решения следующий. Зная, сколько приходится на долю от целого, нужно определить, сколько приходится на единицу измерения ( грамм, килограмм, метр, час и т.д). Затем зная это, просто умножает на все количество долей, на которое поделён данный предмет. В данном случае- это восемь частей. Второй вариант решения задачи. 300 : 3 × 8 = 800 грамм. Ответ. 800 грамм , в обоих вариантах таз решения задачи. Проще не бывает. Надо число означающее часть разделить на количество этих частей и полученный результат умножить на целое. Получим число выражающее целую часть. Пример: Дано 4/15 равняется 40. Делим сорок на четыре и умножаем на 15. Получаем сумму в 150 — это и будет целое. Или 2/10 равняется 40. Делим сорок на два, получаем двадцать. Умножаем двадцать на десять, получаем двести. Целое число двести. Master-Margarita 5 лет назад Чтобы узнать, сколько весит торт в данном случае, надо провести следующие арифметический действия: (300*8)/3=800 грамм. То есть, чтобы найти целое нужно часть умножить на знаменатель дроби и разделить на числитель дроби. В данном случае числитель — 3, а знаменатель — 8. Рина19 5 лет назад Сначала найдём чем у равна 1 часть из всех имеющихся. А затем умножим её на общее число всех частей. На данном примере. Известно, что 3/8 торта весит 300 г, т.е. 3 части из 8 на которые был нарезан торт или, по другому, 3 куска торта из 8 нарезанных кусочков весят 300 г. Тогда 1 кусочек будет весить: 300/3=100 г. Теперь находим чему будет весить все 8 кусков, т.е. весь торт. 100*8=800 г Бекки Шарп 3 года назад Если 3/8 торта весит 300 грамм, то сначала узнаем сколько весит одна часть. 300/3=100 грамм. Теперь умножаем на 8 и получаем, что весь торт весит 800 грамм. Приведем еще пример как найти целое число, если известна часть. В классе присутствует 27 человек и это 3/4 общего количества. Сколько человек в классе? Решить задачу можно так: 27 : 3/4 = 36 человек. Знаете ответ? |
Математический диктант по теме «Доли и дроби»
1. Запиши, сколько минут составляет ½ часа.
2. Мальчик до школы идёт 3 км. Третью часть пути он прошёл. Сколько км ему осталось пройти?
3. Запиши дробь.5 знаменатель 3 числитель.
4. Ручка стоит 15 рублей, а ластик 1/5 часть от стоимости ручки. Сколько стоит ластик?
5. Поставь знак между дробями 2/9 и 4/9
6. Запиши дробь, которая больше. 3/7 или 6/7?
7. В тетради 12 листов. 2/3 тетради занято, сколько листов пустых?
8. Рост Коли 1м 60 см, а рост Вани 4/5 от роста Коли. Какой рост у Вани?
9. Шоколадка стоит 40 рублей, а конфета 1/20 стоимости шоколада. На сколько конфета дешевле шоколадки?
10. Арбуз весит 2 0 кг, а дыня 2/10 веса арбуза. Во сколько раз арбуз тяжелее дыни?
Карточки по теме «Дроби»
|
В – 1. 1. Руда содержит в себе ⅗ железа. Сколько железа можно получить из 1 т руды? 2. ⅔ отрезка прямой 12 см. Чему равен весь отрезок? |
В – 2. 1. При помоле на белую муку отходит в отруби ⅖ веса зерна. Сколько отрубей и сколько белой муки получится при помоле 1 т зерна? 2. Какой длины потребуется проволоки для прямоугольной рамки, если длина рамки 25 см, а ширина ⅘ длины? |
|
В – 3. 1. Сад прямоугольной формы хотят обнести забором. Длина сада 800 м, а ширина составляет ⅝ длины. Какой длины должен быть весь забор? 2. От проволоки отрезали ¾ — 12 м. Чему равна длина всей проволоки? |
В – 4. 1. Сколько месяцев содержит ⅚ года? 2. ⅖ кружки сахарного песку весят 100 г. сколько весит кружка сахарного песку? |
|
В – 5. 1. В саду было 128 деревьев. ⅜ этих деревьев были яблони, 2/4 всех деревьев – груши, а остальные – вишни. Сколько было вишен? 2. Я задумал число. ⅗ его равно 15. Какое число я задумал? |
В – 6. 1. Два поезда идут навстречу друг другу. Один прошёл ⅖ всего пути, а другой – половину. Сколько км им осталось идти до встречи, если между ними было 200 км? 2. На ветке сидели 12 синиц; ⅔ их числа улетели. Сколько птиц улетело? |
|
В – 7.1. В классе 28 учеников; ¾ учеников занимаются спортом. Сколько учеников занимаются спортом? 2. Мама израсходовала ⅞ своих денег, и у неё осталось 50 рублей. Сколько денег у неё было? |
В – 8. 1. Туристы прошли за два дня 24 км. В первый день они прошли ⅔ всего пути. Сколько километров они прошли во второй день? 2. Каждый час труба наполняет 1/8 бассейна. За сколько часов она наполнит весь бассейн? |
|
В – 9. 1. В ателье 720 м ткани. ⅜ этой ткани израсходовали на пошив костюмов, а из остальной ткани сшили платья, расходуя на каждое по 3 м. сколько сшили платьев? 2. В хоре поют 32 девочки и несколько мальчиков. Число мальчиков составляет ⅜ числа девочек. Сколько всего человек поют в хоре? |
В – 10. 1. Верблюды вынашивают своих младенцев 400 дней, а хомяки 1/25 часть этого времени. Сколько дней хомяки вынашивают детёнышей? 2. В тетради 24 страницы. Мальчик исписал⅝ числа всех страниц. Сколько осталось неисписанных страниц? |
|
В – 11. 1. В прошлом месяце цена товара составляла 1200 рублей. Теперь она понизилась на 4/10 этой суммы. Какова теперь цена товара? 2. Из 7 дней недели было 4 солнечных дня. Какую часть недели составили солнечные дни? |
В – 12. 1. Маме 30 лет, возраст дочери составляет ⅖ её возраста. Сколько лет дочери? 2. У девочки было 360 рублей. Она потратила ⅛ этой суммы и ⅐ остатка. Сколько денег она потратила? |
|
В – 13. 1. Дедушке 60 лет. Возраст отца составляет 3/5 возраста дедушки, а возраст сына составляет 2/9 возраста отца. Сколько лет сыну? 2. В четырёх домах 3672 жителя. В одном доме ⅓ всех жителей, во втором – в 2 раза меньше, чем в первом, а остальные живут поровну в третьем и четвёртом домах. По сколько жителей живёт в третьем и четвёртом домах? |
В – 14. (Зачёт) 1. В магазин привезли 150 кг картофеля. До обеда продали ⅖ всего картофеля. Сколько килограммов картофеля продали? 2. В соревновании участвовали 36 девочек. Они составляли ⅖ всех участников. Сколько всего детей участвовало в соревновании? |
|
В – 15. (Зачёт) 1. Из 125 посаженных вдоль улицы деревьев ⅗ — липы. Сколько лип посадили? 2. Мальчик прочитал ¾ книги, что составило 78 страниц. Сколько страниц в книге? |
В – 16. (Зачёт) 1.Туристы проехали f км, из них а/р – на поезде. Сколько километров они проехали на поезде? 2. Автобус проехал d километров, что составило b/n всего пути. Какова длина всего пути? |
Что такое доля в математике. Как найти число по доле и долю по числу? Правило.
Ученик
(139),
закрыт
13 лет назад
Ирина Рудерфер
Высший разум
(120406)
13 лет назад
Доля – каждая из равных частей числа.
Например 2 — это одна треть (одна из трех равных долей) от шести (6 = 2 +2+2)
Чтобы найти долю от числа надо разделить число на количество долей (в предудщем случае Делим 6 на три и получаем 2)
Чтобы найти число, надо долю умножить на количество долей.
Если доля выражена в виде дроби, то чтобы найти долю от числа надо умножить число на числитель, и разделиь на знаменатель.
Например, найти 1/5 от 25
25*1/5 = 5
Если известна доля, то чтобы найти число, надо величину доли умножить на знаменатель и разделить на числитель.
Например:
Известно, что 5 — это 1/10 от числа
Тогда число равно 5*10/1 = 50
ольга
Ученик
(188)
6 лет назад
подскажите пожалуйста покупаем квартиру 42.1 кв. м. у трех собственников 1/3 доли хотят, что бы было на каждого свой договор (каждый продает свою долю 1/3 отдельно ) как правильно распределить доли нас тоже трое опека и в этой квартире наши доли должны быть 2/8,3/8 и 3/8, спасибо заранее за ответ
Никита Ткачук
Знаток
(264)
6 лет назад
Доля – каждая из равных частей числа.
Например 2 — это одна треть (одна из трех равных долей) от шести (6 = 2 +2+2)
Чтобы найти долю от числа надо разделить число на количество долей (в предудщем случае Делим 6 на три и получаем 2)
Чтобы найти число, надо долю умножить на количество долей.
Если доля выражена в виде дроби, то чтобы найти долю от числа надо умножить число на числитель, и разделиь на знаменатель.
Например, найти 1/5 от 25
25*1/5 = 5
Если известна доля, то чтобы найти число, надо величину доли умножить на знаменатель и разделить на числитель.
Например:
Известно, что 5 — это 1/10 от числа
Тогда число равно 5*10/1 = 50
серега гура
Ученик
(107)
5 лет назад
Доля – каждая из равных частей числа.
Например 2 — это одна треть (одна из трех равных долей) от шести (6 = 2 +2+2)
Чтобы найти долю от числа надо разделить число на количество долей (в предудщем случае Делим 6 на три и получаем 2)
Чтобы найти число, надо долю умножить на количество долей.
Если доля выражена в виде дроби, то чтобы найти долю от числа надо умножить число на числитель, и разделиь на знаменатель.
Например, найти 1/5 от 25
25*1/5 = 5
Если известна доля, то чтобы найти число, надо величину доли умножить на знаменатель и разделить на числитель.
Например:
Известно, что 5 — это 1/10 от числа
Тогда число равно 5*10/1 = 50
Кирилл Рыжов
Профи
(798)
5 лет назад
Доля – каждая из равных частей числа.
Например 2 — это одна треть (одна из трех равных долей) от шести (6 = 2 +2+2)
Чтобы найти долю от числа надо разделить число на количество долей (в предудщем случае Делим 6 на три и получаем 2)
Чтобы найти число, надо долю умножить на количество долей.
Если доля выражена в виде дроби, то чтобы найти долю от числа надо умножить число на числитель, и разделиь на знаменатель.
Например, найти 1/5 от 25
25*1/5 = 5
Если известна доля, то чтобы найти число, надо величину доли умножить на знаменатель и разделить на числитель.
Например:
Известно, что 5 — это 1/10 от числа
Тогда число равно 5*10/1 = 50
Tisleh_TV rx
Ученик
(115)
1 месяц назад
Тип задания
Цель задания Формулировка задания Методические комментарии (в том числе критерии оценивания)
Предполагаемые ответы детей
Узнавание Актуализация имеющихся знаний по теме «Доли». Найди НЕ верное утверждение.
А) Одна пятая доля от числа 45 – 9
Б) Одна шестая доля от числа 36 – 6
В) Одна третья доля от числа 27 – 6
Посмотри на рисунки и выдели букву на котором изображена 1-3 доли. Критерии оценивания:
Учащийся выбирает верный ответ — 1 балл;
Выбрал(а) не правильный ответ – 0 баллов;
Ответ: В
Воспроизведение Воспроизведение усвоенных ранее знаний и их применение в типовых ситуациях Какая часть фигуры закрашена?
-Исправьте ошибку в предложение. Половина яблока это одна 6 доля яблока Критерии оценивания:
Учащийся верно записывает все доли – 2 балла;
Учащийся совершает 1-2 ошибки в записи долей – 1 балл;
Учащийся не верно записывает все доли – 0 баллов; Ответ:
1. 1/6
2. 2/8
3. 9/24
4. 4/4
5. 5/10
6. 3/5
Это одна вторая доля
Понимание Осмысленное восприятие нового материала Рассмотри рисунок и скажи, что больше: одна вторая доля яблока или одна четвертая доля этого яблока. Объясни свой ответ
Критерии оценивания:
Учащийся дал верный ответ и объяснил свой выбор – 2 балла;
Учащийся дал верный ответ, но не объяснил свой выбор – 1 балл;
Учащийся дал не верный ответ – 0 баллов; Одна вторая доля яблока больше. Так как одна вторая – это половинка яблока, а одна четвертая это яблоко, разделенное на 4 части.
Применение в знакомых условиях Самостоятельное преобразование усвоенной информации в знакомых ситуациях Прочитай задачу и реши её.
В поход отправились 150 человек. Из них мальчиков – 90 человек, девочек – третья часть от всех мальчиков. Остальные-взрослые. Сколько взрослых отправилось в поход?
Составьте алгоритм для своего одноклассника по теме, как посчитать закрашенную долю фигуру, так что бы он состоял из 4 пунктов. Критерии оценивания:
Учащийся написал условие к задаче верно решил её– 2 балла;
Учащийся написал только решение задачи — 1 балл;
Учащийся не верно решил задачу – 0 баллов; М – 90чел.
Д — ?, 3 часть
Взрослые — ?
Всего – 150 чел.
1) 90:3=30(д)-девочек
2) 90+30= 120(д) – мальчиков и девочек
3) 150-120=30(чел) – взрослые
1. Посмотреть внимательно на фигуру
2. посчитать кол-во частей фигуры.
3.Посчитать закрашенные части фигуры.
4. Запиши первым числом кол-во закрашенных частей, запиши черту, напиши общие кол-во частей в этой фигуре.
Применение в незнакомых условиях Самостоятельное преобразование усвоенной информации в разнообразных ситуациях Придумай сказку про «Доли» (4-5 предложений) и прочитай её свои одноклассникам. Задание творческого характера и не имеет определенного шаблона выполнения.
Критерии оценивания:
Составил (а) сказку и прочитал (а) одноклассникам – 2 балла;
Составил (а) сказку и показал (а) учителю – 1 балл;
Не составил (а) рассказ — 0 баллов Учащийся придумывает сказку о долях
МБОУ «Павловская СОШ»
План – конспект
урока математики в 4 классе по теме
«Нахождение целого числа по его доли»
(по учебнику М. И. Моро УМК «Школа России»)
Учитель начальных классов
Колодезная А.П.
Тема: Нахождение целого числа по его доли
Цели: учить находить целое число по его доли; совершенствовать вычислительные навыки, умение решать задачи.
Планируемые результаты:
предметные: актуализировать знания о долях, совершенствовать умение находить долю от целого, создавать условия для знакомства с алгоритмом нахождения целого по известной доли, учить решать задачи на нахождение нескольких целого по доли.
метапредметные:
познавательные: самостоятельно выделять и формировать познавательную цель; строить логическую цепь рассуждений; делать выводы на основе обобщения знаний, самостоятельно делать выбор, опираясь на правила, выполнять задания по аналогии, анализировать, сравнивать, классифицировать объекты; структурировать знания;
регулятивные: самостоятельно организовывать своё рабочее место; определять цель учебной деятельности с помощью учителя и удерживать в течение урока, осуществлять само- и взаимопроверку работ, вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта сделанных ошибок;
коммуникативные: аргументировать свою позицию и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности;
личностные: создать условия для формирования уважительного отношения к членам своей семьи, понимания ценности каждого её члена, осознания себя её частью, формировать бережное отношение к природе, уважительное отношение к иному мнению, воспитывать положительное отношение к урокам математики.
Оборудование: мультимедийный проектор, экран, компьютер, электронное приложение, магнитная доска, карточки с заданиями, раздаточный материал (круги), ножницы, листы самооценки, учебники по математике 4 класс М. И. Моро, рабочие тетради.
Ход урока
I. Организационный момент урока
— Что есть больше всего на свете? – ПРОСТРАНСТВО.
— Что быстрее всего ? – УМ
-Что мудрее всего? – ВРЕМЯ
— Что приятнее всего? – ДОСТИЧЬ ЖЕЛАЕМОГО
ХОЧЕТСЯ, ЧТОБЫ КАЖДЫЙ ИЗ ВАС НА СЕГОДНЯШНЕМ УРОКЕ ДОСТИГ ЖЕЛАЕМОГО. А что должно быть самым желаемым на уроке? Знания и интерес.
II. Актуализация знаний
-Новое знание всегда базируется на приобретенном опыте.
1. Начнем с ГЛОССАРИЯ. Математический диктант «Назови одним словом.
-одна из равных частей целого (ДОЛЯ)
— число, с помощь которого записывают долю или несколько долей в математике ( ДРОБЬ)
— число, записанное над дробной чертой это(ЧИСЛИТЕЛЬ)
— число, записанное под дробной чертой это (ЗНАМЕНАТЕЛЬ)
— Что показывает каждое из чисел в записи дроби? (знаменатель- КОЛИЧЕСТВО ДОЛЕЙ, числитель-СКОЛЬКО ТАКИХ ДОЛЕЙ ВЗЯТО)
2. Выдвигаем гипотезу: НА КАКУЮ ТЕМУ ПОЙДЕТ РЕЧЬ НА СЕГОДНЯШНЕМ УРОКЕ МАТЕМАТИКИ? ( речь пойдет о долях)
3.Работа с таблицей З-У-Х:
З : знаю термины, умею читать дроби, определять долю по рисунку и записывать её в виде дроби, находить долю от целого и несколько долей целого.
4. Устный счет. ПРЕЗЕНТАЦИЯ 1.
5. БЛИЦКРИГ. Нахождение нескольких долей целого
Беседа. Значение слова «бдицкриг». Блицкриг «Барбаросса». Битва за Москву- величайшее событие Великой Отечественной войны. 5 декабря 1941 года- День воинской славы. Срыв блицкрига. Переход к наступательным операциям.
Физминутка для глаз.
III. Самоопределение к деятельности
- Кейс задание. ПРИЛОЖЕНИЕ 2.
- Уточняем тему урока.
Широкая тема- узкая тема «Нахождение целого по его доли».
Цель: сформулировать правило нахождения целого числа по его доле, применить данное знание к решению практических задач.
- Работа с таблицей З-У-Х
У: узнал, что дроби на Руси называли ещё ломаными числами. Узнал как находить целое по его доле.
Динамическая физминутка
IV. Работа по теме урока
- Первичное закрепление с проговариванием во внешней речи
А)Решение текстовых задач. ПРЕЗЕНТАЦИЯ 2.
Физминутка для глаз
Б)Самостоятельное решение заданий. ПРИЛОЖЕНИЕ 3.
- Самостоятельная работа с самопроверкой по эталону
- РЕЗЕРВ
ПРИЛОЖЕНИЕ 3.
VI. Рефлексия.
−Быстро время пролетело
И идёт к концу урок.
Так давайте без задержки
Подведём всему итог.
— Какие новые знания вы открыли для себя на уроке.
— Оцените насколько вы смогли погрузиться в эту тему (Значки V,? ,!)
— работа с таблицей З-У-Х
— Насколько приятно вам от своей проделанной работы ( дорисовываем смайлики улыбкой)
— Человек подобен дроби, числитель ЕСТЬ ТО ЧТО ЧЕЛОВЕК ПРЕДСТАВЛЯЕТ СОБОЙ, а знаменатель – то что он думает о себе.
Чем больше человек о себе мнения, тем больше знаменатель, а значит, тем меньше дробь. (Л.Н. Толстой)
VII. Домашнее задание У. стр.64 № 297, № 301.
Приложение 1
Приложение 2 Задания для блицкрига
Если известно сколько составляет часть от целого, то по известной части можно «восстановить»
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий: