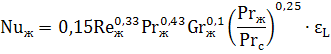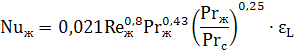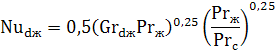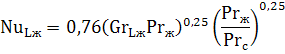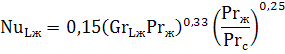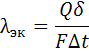From Wikipedia, the free encyclopedia
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity.[1] The Prandtl number is given as:
where:
Note that whereas the Reynolds number and Grashof number are subscripted with a scale variable, the Prandtl number contains no such length scale and is dependent only on the fluid and the fluid state. The Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity.
The mass transfer analog of the Prandtl number is the Schmidt number and the ratio of the Prandtl number and the Schmidt number is the Lewis number.
Experimental Values[edit]
Typical Values[edit]
For most gases over a wide range of temperature and pressure, Pr is approximately constant. Therefore, it can be used to determine the thermal conductivity of gases at high temperatures, where it is difficult to measure experimentally due to the formation of convection currents.[1]
Typical values for Pr are:
- 0.003 for molten potassium at 975 K[1]
- around 0.015 for mercury
- 0.065 for molten lithium at 975 K[1]
- around 0.16–0.7 for mixtures of noble gases or noble gases with hydrogen
- 0.63 for oxygen[1]
- around 0.71 for air and many other gases
- 1.38 for gaseous ammonia[1]
- between 4 and 5 for R-12 refrigerant
- around 7.56 for water (At 18 °C)
- 13.4 and 7.2 for seawater (At 0 °C and 20 °C respectively)
- 50 for n-butanol[1]
- between 100 and 40,000 for engine oil
- 1000 for glycerol[1]
- 10,000 for polymer melts[1]
- around 1×1025 for Earth’s mantle.
Formula for the calculation of the Prandtl number of air and water[edit]
For air with a pressure of 1 bar, the Prandtl numbers in the temperature range between −100 °C and +500 °C can be calculated using the formula given below.[2] The temperature is to be used in the unit degree Celsius. The deviations are a maximum of 0.1 % from the literature values.

The Prandtl numbers for water (1 bar) can be determined in the temperature range between 0 °C and 90 °C using the formula given below.[3] The temperature is to be used in the unit degree Celsius. The deviations are a maximum of 1 % from the literature values.

Physical Interpretation[edit]
Small values of the Prandtl number, Pr ≪ 1, means the thermal diffusivity dominates. Whereas with large values, Pr ≫ 1, the momentum diffusivity dominates the behavior.
For example, the listed value for liquid mercury indicates that the heat conduction is more significant compared to convection, so thermal diffusivity is dominant.
However, engine oil with its high viscosity and low heat conductivity, has a higher momentum diffusivity as compared to thermal diffusivity.[4]
The Prandtl numbers of gases are about 1, which indicates that both momentum and heat dissipate through the fluid at about the same rate. Heat diffuses very quickly in liquid metals (Pr ≪ 1) and very slowly in oils (Pr ≫ 1) relative to momentum. Consequently thermal boundary layer is much thicker for liquid metals and much thinner for oils relative to velocity boundary layer.
In heat transfer problems, the Prandtl number controls the relative thickness of the momentum and thermal boundary layers. When Pr is small, it means that the heat diffuses quickly compared to the velocity (momentum). This means that for liquid metals the thermal boundary layer is much thicker than the velocity boundary layer.
In laminar boundary layers, the ratio of the thermal to momentum boundary layer thickness over a flat plate is well approximated by[5]
where 

For incompressible flow over a flat plate, the two Nusselt number correlations are asymptotically correct:[6]
where 
See also[edit]
- Turbulent Prandtl number
- Magnetic Prandtl number
References[edit]
- ^ a b c d e f g h i Coulson, J. M.; Richardson, J. F. (1999). Chemical Engineering Volume 1 (6th ed.). Elsevier. ISBN 978-0-7506-4444-0.
- ^ tec-science (2020-05-10). «Prandtl number». tec-science. Retrieved 2020-06-25.
- ^ tec-science (2020-05-10). «Prandtl number». tec-science. Retrieved 2020-06-25.
- ^ Çengel, Yunus A. (2003). Heat transfer : a practical approach (2nd ed.). Boston: McGraw-Hill. ISBN 0072458933. OCLC 50192222.
- ^ Lienhard IV, John Henry; Lienhard V, John Henry (2017). A Heat Transfer Texbook (4th ed.). Cambridge, MA: Phlogiston Press.
- ^ Lienhard IV, John Henry; Lienhard V, John Henry (2017). A Heat Transfer Texbook (4th ed.). Cambridge, MA: Phlogiston Press.
- ^ Lienhard IV, John Henry; Lienhard V, John Henry (2017). A Heat Transfer Texbook (4th ed.). Cambridge, MA: Phlogiston Press.
General references[edit]
- White, F. M. (2006). Viscous Fluid Flow (3rd. ed.). New York: McGraw-Hill. ISBN 0-07-240231-8.
Число Прандтля
Сергей Васильевич Карпенко
Эксперт по предмету «Архитектура и строительство»
Задать вопрос автору статьи
Характеристики числа Прандтля
Число Прандтля – это критерий подобия тепловых процессов в жидкостях и газах. Данный критерий учитывает влияние физических характеристик теплоносителя на теплоотдачу
Формула для определения значения числа:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
Здесь $ν$ и $η$– кинематическая и динамическая вязкость вещества; ρ – плотность; $χ$ и $α$ – коэффициенты теплопроводности и температуропроводности соответственно; $c$ – удельная теплоемкость.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Число Прандтля названо в честь немецкого физика Людвига Прандтля, который занимался изучением массо- и теплообмена в пограничных слоях.
Следует заметить, что число Прандтля является исключительно физической характеристикой среды и зависит только от ее термодинамического состояния.
Значения числа
Число Прандтля для газов практически неизменно. Для двухатомных газов $Pr$ > $0,72$, для трех- и многоатомных газов $0,75$
Рисунок 2. Зависимости числа Прандтля. Автор24 — интернет-биржа студенческих работ
Физический смысл числа Прандтля заключается в том, что оно показывает отношение скорости диффузии вещества к его температуропроводности. Один из важнейших критериев подобия – число Нуссельта – зависит от числа Прандтля, а также от теплоемкости вещества при постоянном давлении.
Для неметаллов число Прандтля изменяется при температурных колебаниях. При этом наиболее значительные изменения оно претерпевает в условиях максимальной вязкости жидкости. Например, для воды при 0° С число Прандтля принимает значение $Pr = 866$, а при 100° С $Pr = 13,5$. Для жидких металлов $Pr$ принимает значения, много меньшие единицы и уже не так сильно изменяется при температурных колебаниях.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 09.09.2022
Содержание: Число Прандтля
Число Прандтля
«Число Прандтля (Pr) или группа Прандтля — это безразмерное число, названное в честь немецкого физика Людвига Прандтля, определяемое как отношение коэффициента диффузии по импульсу к коэффициенту температуропроводности».
Формула числа Прандтля
Формула числа Прандтля (Pr) дается формулой
Pr = коэффициент диффузии импульса/коэффициент температуропроводности
Pr = мкКлp/k
Пр = ν/∝
Где:
μ = динамическая вязкость
Cp = Принимаемая во внимание удельная теплоемкость жидкости
k = теплопроводность жидкости
ν = кинематическая вязкость
α = Температуропроводность
ρ = плотность жидкости
Число Прандтля (Pr) не зависит от длины. Это зависит от свойства, типа и состояния жидкости. Он дает соотношение между вязкостью и теплопроводностью.
Жидкости, имеющие число Прандтля (Pr) в нижнем спектре, являются свободно текущими жидкостями и обычно обладают высокой теплопроводностью. Они превосходны в качестве теплопроводных жидкостей в теплообменниках и подобных устройствах. Жидкие металлы прекрасно переносят тепло. По мере увеличения вязкости увеличивается число Прандтля (Pr) и, таким образом, теплопроводность жидкости снижается.
Физическое значение числа Прандтля
Во время теплопередачи между стенкой и текущей жидкостью, тепло передается от высокотемпературной стенки к текущей жидкости через импульсный пограничный слой, который включает объемное жидкое вещество и переходный и тепловой пограничный слой, который состоит из стационарной пленки. В застойной пленке передача тепла происходит за счет теплопроводности в жидкости. Следует учитывать важность числа Прандтля (Pr) текущей жидкости, поскольку оно связывает импульсный пограничный слой с тепловым во время передачи тепла через жидкость.
когда число Прандтля (Pr) имеет малые значения, Pr << 1, это означает, что коэффициент температуропроводности преобладает над коэффициентом диффузии по импульсу, а жидкий металл имеет более низкое число Прандтля (Pr), и при этом тепло распространяется значительно быстрее. Тепловой пограничный слой имеет более высокую толщину по сравнению с пограничным слоем на основе скорости в жидком металле.
Аналогично, для больших значений числа Прандтля (Pr), Pr >> 1, коэффициент диффузии по импульсу преобладает над коэффициентом температуропроводности. масла имеют более высокое число Прандтля (Pr), и тепло медленно распространяется в маслах. Тепловой пограничный слой имеет меньшую толщину по сравнению со скоростным пограничным слоем в нефти.
Для жидкой ртути теплопроводность преобладает по сравнению с конвекцией. Таким образом, у ртути преобладает температуропроводность. Хотя для моторного масла конвекция очень эффективна при передаче тепла из высокотемпературной области по сравнению с чисто теплопроводным случаем, таким образом, коэффициент диффузии по импульсу является важным параметром моторного масла.
Газы находятся в середине этого спектра. Их число Прандтля (Pr) составляет около 1. Толщина теплового пограничного слоя равна толщине пограничного слоя скорости.
Отношение теплового и импульсного пограничного слоя над плоской пластиной определяется следующим уравнением
δt/δ = Пр-1/3 0.6Pr
Магнитное число Прандтля
Магнитное число Прандтля — это безразмерное число, которое дает соотношение между коэффициентом диффузии по моменту и коэффициентом магнитной диффузии. Это отношение скорости вязкой диффузии к скорости магнитной диффузии. Обычно это происходит в магнитогидродинамике. Его также можно оценить как отношение магнитного числа Рейнольдса к числам Рейнольдса.
Prm = ν/η
Prm = Rem/Ре
Где,
Рем — это магнетик. Число Рейнольдса
Re — число Рейнольдса
ν — скорость вязкой диффузии
η — скорость магнитной диффузии
Число Прандтля Теплопередача
когда число Прандтля (Pr) имеет малые значения, Pr << 1, это означает, что температуропроводность преобладает над коэффициентом диффузии по импульсу. Жидкий металл имеет более низкое число Прандтля (Pr), и тепло очень быстро распространяется в жидком металле, а термический пограничный слой намного толще по сравнению со скоростным пограничным слоем в жидком металле.
Аналогично, для больших значений числа Прандтля (Pr), Pr >> 1, коэффициент диффузии по импульсу преобладает над коэффициентом температуропроводности. масла имеют более высокое число Прандтля (Pr), и тепло медленно распространяется в маслах. Тепловой пограничный слой имеет меньшую толщину по сравнению со скоростным пограничным слоем в нефти.
Для жидкой ртути теплопроводность преобладает по сравнению с конвекцией. Таким образом, у ртути преобладает температуропроводность. Хотя для моторного масла конвекция очень эффективна при передаче тепла из высокотемпературной области по сравнению с чисто проводящей, поэтому в моторном масле важна диффузия по импульсу.
Газы находятся в середине этого спектра. Их число Прандтля (Pr) составляет около 1. Толщина теплового пограничного слоя равна толщине пограничного слоя скорости.
Отношение теплового и импульсного пограничного слоя над плоской пластиной определяется уравнением
δt/δ = Пр-1/3 0.6Pr
Турбулентное число Прандтля
Турбулентное число Прандтля Prt безразмерный член. Это отношение коэффициента диффузии вихрей по импульсу к коэффициенту диффузии вихрей при переносе тепла, которое используется для оценки теплопередачи в условиях турбулентного течения в пограничном слое.
Зависит ли коэффициент теплоотдачи от числа Прандтля?
Коэффициент теплопередачи также рассчитывается с помощью числа Нуссельта. Это представлено отношением конвективной теплопередачи к кондуктивной теплопередаче.
Для принудительной конвекции,
Nμ = hLc/K
Где,
h = конвективное тепло перевод коэффициент
Lc = характерная длина,
k = теплопроводность жидкости.
Кроме того, число Нуссельта является функцией числа Рейнольдса и числа Прандтля (Pr). Таким образом, изменение числа Прандтля (Pr) изменяет Число Нуссельта и, следовательно, коэффициент теплопередачи.
Меняется ли число Прандтля с давлением?
Предполагается, что число Прандтля (Pr) не зависит от давления. Число Прандтля (Pr) является функцией температуры, поскольку μ, Cp являются функцией температуры, но очень слабой функцией давления.
Влияние числа Прандтля на пограничный слой | Эффект числа Прандтля по теплопередаче
когда число Прандтля (Pr) имеет малые значения, Pr << 1, это означает, что температуропроводность преобладает над коэффициентом диффузии по импульсу. Жидкие металлы имеют более низкое число Прандтля (Pr), и тепло очень быстро распространяется в жидких металлах. Тепловой пограничный слой имеет большую толщину по сравнению с пограничным слоем скорости в жидких металлах.
Аналогично, для больших значений числа Прандтля (Pr), Pr >> 1, коэффициент диффузии по импульсу преобладает над коэффициентом температуропроводности. масла имеют более высокое число Прандтля (Pr), и тепло медленно распространяется в маслах. Тепловой пограничный слой имеет меньшую толщину по сравнению со скоростным пограничным слоем в нефти.
Для жидкой ртути теплопроводность преобладает по сравнению с конвекцией. Таким образом, у ртути преобладает температуропроводность.
Газы находятся в середине этого спектра. Их число Прандтля (Pr) составляет около 1. Толщина теплового пограничного слоя равна толщине пограничного слоя скорости.
Число Прандтля Воздуха
Число Прандтля (Pr) для воздуха приведено ниже в таблице.
Число Прандтля (Pr) воздуха при давлении 1 атм и температуре ° C определяется как:
| Температура | Pr |
| [° С] | безразмерный |
| -100 | 0.734 |
| -50 | 0.720 |
| 0 | 0.711 |
| 25 | 0.707 |
| 50 | 0.705 |
| 100 | 0.701 |
| 150 | 0.699 |
| 200 | 0.698 |
| 250 | 0.699 |
| 300 | 0.702 |
Число Прандтля воды при разных температурах
Число Прандтля (Pr) воды в жидкой и паровой форме при давлении 1 атм показано ниже:
| Температура | Номер пр. |
| [° С] | безразмерный |
| 0 | 13.6 |
| 5 | 11.2 |
| 10 | 9.46 |
| 20 | 6.99 |
| 25 | 6.13 |
| 30 | 5.43 |
| 50 | 3.56 |
| 75 | 2.39 |
| 100 | 1.76 |
| 100 | 1.03 |
| 125 | 0.996 |
| 150 | 0.978 |
| 175 | 0.965 |
| 200 | 0.958 |
| 250 | 0.947 |
| 300 | 0.939 |
| 350 | 0.932 |
| 400 | 0.926 |
| 500 | 0.916 |
Число Прандтля этиленгликоля
Число Прандтля (Pr) этиленгликоля Pr = 40.36.
Число Прандтля Нефти | Число Прандтля моторного масла
Число Прандтля (Pr) для масла находится в диапазоне от 50 до 100,000 XNUMX
Ниже приведены числа Прандтля (Pr) моторного масла при давлении 1 атм:
Таблица чисел Прандтля
| Температура (К) | Номер пр. |
| 260 | 144500 |
| 280 | 27200 |
| 300 | 6450 |
| 320 | 1990 |
| 340 | 795 |
| 360 | 395 |
| 380 | 230 |
| 400 | 155 |
Число Прандтля водорода
Число Прандтля (Pr) водорода при давлении 1 атм и при 300 К составляет 0.701.
Число Прандтля газов | Число Прандтля аргона, криптона и т. Д.
Бензол число Прандтля
Число Прандтля (Pr) бензола при 300 К составляет 7.79.
CO2 Число Прандтля
Число Прандтля (Pr) водорода при давлении 1 атм составляет 0.75.
Число Прандтля этана
Число Прандтля (Pr) этана составляет 4.60 в жидкой форме и 4.05 в газообразной форме.
Бензин число Прандтля
Число Прандтля (Pr) бензина составляет 4.3
Глицерин число Прандтля
Число Прандтля (Pr) глицерина находится в диапазоне 2000-100,000.
Некоторые важные часто задаваемые вопросы
Q.1 Как рассчитывается число Прандтля?
Ответ: Pr Number можно рассчитать по формуле
Pr = мкКлp/K
Где:
- μ = динамическая вязкость
- Cp = Принимаемая во внимание удельная теплоемкость жидкости
- k = теплопроводность жидкости
Q.2 Какое значение имеет число Прандтля для жидких металлов?
Ответ: Число Прандтля (Pr) для жидких металлов чрезвычайно низкое. Pr <<< 1. Например, в жидкой ртути число Прандтля (Pr) = 0.03, что означает, что теплопроводность преобладает по сравнению с конвекцией. Таким образом, у ртути преобладает температуропроводность.
Q.3 Что такое число Прандтля Воды?
Ответ: Число Прандтля (Pr) воды в жидкой и паровой форме при давлении 1 атм показано ниже:
| Температура | Число Прандтля (Pr) |
| [° С] | безразмерный |
| 0 | 13.6 |
| 5 | 11.2 |
| 10 | 9.46 |
| 20 | 6.99 |
| 25 | 6.13 |
| 30 | 5.43 |
| 50 | 3.56 |
| 75 | 2.39 |
| 100 | 1.76 |
| 100 | 1.03 |
| 125 | 0.996 |
| 150 | 0.978 |
| 175 | 0.965 |
| 200 | 0.958 |
| 250 | 0.947 |
| 300 | 0.939 |
| 350 | 0.932 |
| 400 | 0.926 |
| 500 | 0.916 |
Q.4 Что представляет собой число Прандтля?
Ответ: Во время передачи тепла между стенкой-барьером и жидкостью тепло передается от высокотемпературного барьера жидкости через импульс-пограничный слой. Сюда входят жидкости, а также переходный и тепловой пограничный слой, состоящий из пленки. В застойной пленке теплопередача происходит за счет теплопроводности жидкости в это время. В Pr количество протекающей жидкости, это отношение, которое учитывает импульс пограничного слоя к тепловому пограничному слою.
Q.5 что такое число Прандтля для Steam?
Ответ: Число Прандтля (Pr) для пара при 500 ° C составляет 0.916.
Q.6 что такое число Прандтля для гелия?
Ответ: число Прандтля (Pr) гелия 0.71.
Q.7 что такое число Прандтля для кислорода?
Ответ: число Прандтля (Pr) кислорода составляет 0.70.
Q.8 Что такое число Прандтля для натрия?
Ответ: число Прандтля (Pr) натрия 0.01
Q.9 Как число Прандтля связано с кинематической вязкостью и температуропроводностью?
Ответ: Число Прандтля (Pr) хорошо определяется как отношение коэффициента диффузии по импульсу к коэффициенту температуропроводности.
Его формула определяется следующим образом:
Формула числа Pr определяется как
Pr = Коэффициент диффузии импульса/ Температуропроводность
Pr = мкКлp/K
Пр = μ/α
Где:
μ = динамическая вязкость
Cp = Принимаемая во внимание удельная теплоемкость жидкости
k = теплопроводность жидкости
ν = кинематическая вязкость
п = м/р
α = Температуропроводность
α = К/ρСp
ρ = плотность жидкости
Из приведенной выше формулы мы можем сказать, что число Прандтля (Pr) обратно пропорционально Температуропроводность и прямо пропорциональна кинематической вязкости.
В.10 Есть ли какая-либо жидкость, у которой число Прандтля находится в диапазоне 10 20, кроме воды?
Ответ: Есть определенное количество жидкостей, у которых число Прандтля (Pr) находится в диапазоне 10-20. Они перечислены ниже:
- Уксусная кислота [Pr = 14.5] при 15 ° C и [Pr = 10.5] при 100 ° C.
- Вода [Pr = 13.6] при 0C
- н-Бутиловый спирт [Pr = 11.5] при 100 ° C
- Этанол [Pr = 15.5] при 15 ° C и [Pr = 10.1] при 100 ° C.
- Нитро-бензол [Pr = 19.5] при 15 ° C
- Серная кислота в высокой концентрации около 98% [Pr = 15] при 100 ° C
Чтобы узнать о просто поддерживаемой балке (нажмите здесь.)и консольная балка (Кликните сюда)
Число Прандтля (Pr) или Группа Прандтля — это безразмерное число, названное в честь немецкого физика Людвига Прандтля, определяемое как отношение импульса диффузии ty до температуропроводность. То есть число Прандтля определяется как:
- P r = ν α = коэффициент диффузии по импульсу, коэффициент температуропроводности = μ / ρ k / (cp ρ) = cp μ k { displaystyle mathrm {Pr} = { frac { nu} { alpha}} = { frac { mbox {коэффициент диффузии по импульсу}} { mbox {коэффициент температуропроводности}}} = { frac { mu / rho} {k / (c_ {p} rho)}} = { frac {c_ {p} mu} {k}}}
где:
Обратите внимание, что тогда как число Рейнольдса и Грасгоф n umber имеют нижний индекс с переменной шкалы длины, число Прандтля не содержит такой шкалы длины в своем определении и зависит только от жидкости и ее состояния. Число Прандтля часто встречается в таблицах свойств вместе с другими свойствами, такими как вязкость и теплопроводность.
. Для большинства газов в широком диапазоне температуры и давления Pr приблизительно постоянен. Следовательно, его можно использовать для определения теплопроводности газов при высоких температурах, где его сложно измерить экспериментально из-за образования конвекционных токов.
Типичные значения Pr:
- 0,003 для расплавленного металла. калий при 975 K
- около 0,015 для ртути
- 0,065 для расплавленного лития при 975 K
- около 0,16-0,7 для смесей благородных газов или благородных газы с водородом
- 0,63 для кислорода
- около 0,71 для воздуха и многих других газов
- 1,38 для газообразного аммиака
- между 4 и 5 для хладагента R-12
- около 7,56 для воды (при 18 °C )
- 13,4 и 7,2 для морской воды (при 0 ° C и 20 ° C соответственно)
- 50 для н-бутанола
- от 100 до 40 000 для моторного масла
- 1000 для глицерина
- 10 000 для расплавов полимеров
- около 1 × 10 для Земли мантии.
При малых значениях числа Прандтля Pr << 1, means the thermal diffusivity dominates. Whereas with large values, Pr>>1 коэффициент диффузии по импульсу доминирует в поведении. Например, перечисленные v Значение для жидкой ртути указывает, что теплопроводность более значима по сравнению с конвекцией, поэтому температуропроводность является доминирующей. Однако для моторного масла конвекция очень эффективна для передачи энергии из области по сравнению с чистой проводимостью, поэтому коэффициент диффузии по импульсу является доминирующим.
Число Прандтля для газов составляет около 1, что указывает, что и импульс, и тепло рассеиваются через жидкость примерно с одинаковой скоростью. В жидких металлах (Pr <<1) and very slowly in oils (Pr>>1) тепло распространяется очень быстро относительно количества движения. Следовательно, термический пограничный слой намного толще для жидких металлов и намного тоньше для масел относительно скоростного пограничного слоя.
В задачах теплопередачи число Прандтля контролирует относительную толщину импульса и теплового пограничные слои. Когда Pr мала, это означает, что тепло распространяется быстрее по сравнению со скоростью (импульсом). Это означает, что для жидких металлов тепловой пограничный слой намного толще, чем скоростной пограничный слой.
Массовым аналогом числа Прандтля является число Шмидта.
Содержание
- 1 Формула для расчета числа Прандтля для воздуха и воды
- 2 См. Также
- 3 Ссылки
- 3.1 Общие ссылки
Формула для расчета числа Прандтля для воздуха и воды
Для воздуха с давлением 1 бар числа Прандтля в диапазоне температур от -100 ° C и +500 ° C можно рассчитать по формуле, приведенной ниже. Температура должна использоваться в градусах Цельсия. Максимальные отклонения от литературных значений составляют 0,1%.
P r воздух = 10 9 1,1 ⋅ ϑ 3 — 1200 ⋅ ϑ 2 + 322000 ⋅ ϑ + 1,393 ⋅ 10 9 { displaystyle Pr _ { text {air}} = { frac {10 ^ {9}} { 1.1 cdot vartheta ^ {3} -1200 cdot vartheta ^ {2} +322000 cdot vartheta +1.393 cdot 10 ^ {9}}}}
Числа Прандтля для воды (1 бар) могут определяться в диапазоне температур от 0 ° C до 90 ° C по формуле, приведенной ниже. Температура должна использоваться в градусах Цельсия. Отклонения от литературных значений не превышают 1%.
P r вода = 50000 ϑ 2 + 155 ⋅ ϑ + 3700 { displaystyle Pr _ { text {water}} = { frac {50000} { vartheta ^ {2} +155 cdot vartheta +3700} }}
.
См. Также
- Турбулентное число Прандтля
- Магнитное число Прандтля
Ссылки
Общие ссылки
- White, FM (2006). Течение вязкой жидкости (3-е изд.). Нью-Йорк: Макгроу-Хилл. ISBN 0-07-240231-8.
Содержание:
- Теплоотдача при вынужденном течении жидкости в трубах и каналах
Теплоотдача при ламинарном течении
Теплоотдача в трубах и каналах при турбулентном режиме
Расчет теплоотдачи при вынужденной конвекции - Теплоотдача при свободной конвекции в трубах и каналах
Свободная конвекция в неограниченном пространстве
Свободная конвекция в ограниченном объеме
Расчет теплоотдачи при свободной конвекции
Теплоотдача при вынужденном течении жидкости в трубах и каналах
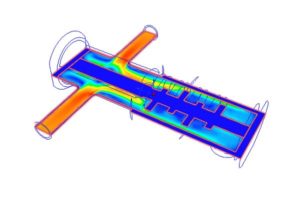
Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).
При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.
Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).
Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м2·град), который определяется по формуле:
Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, равный
F – площадь сечения канала, м2; П – периметр канала, м.
Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.
В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.
Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.
- Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
- При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
- Турбулентный режим течения в трубах наблюдается при числах Re более 10000.
Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).
Число Re определяется по формуле:
w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м2/с.
Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.
Теплоотдача при ламинарном течении в трубах и каналах
Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.
Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.
g – ускорение свободного падения, м/с2;
β – температурный коэффициент объемного расширения, град-1;
d – эквивалентный диаметр канала, м;
ν — кинематическая вязкость жидкости при средней температуре, м2/с;
Δt – средняя разность температур жидкости и стенки, °С.
Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·105, то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:
Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.
Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки.
εL – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:
| L/d | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|---|
| εL | 1,9 | 1,7 | 1,44 | 1,28 | 1,18 | 1,13 | 1,05 | 1,02 | 1 |
Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr<8·105, влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:
d – эквивалентный диаметр канала, м;
L – длина трубы (канала), м.
Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:
λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, м.
Теплоотдача в трубах и каналах при турбулентном режиме
Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:
Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Prс берется при температуре стенки.
Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·104 до 5·106 и Pr от 0,6 до 2500.
εL – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения εL приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:
| Reж | L/d | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | |
| 1·104 | 1,65 | 1,5 | 1,34 | 1,23 | 1,17 | 1,13 | 1,07 | 1,03 | 1 |
| 2·104 | 1,51 | 1,4 | 1,27 | 1,18 | 1,13 | 1,1 | 1,05 | 1,02 | 1 |
| 5·104 | 1,34 | 1,27 | 1,18 | 1,13 | 1,1 | 1,08 | 1,04 | 1,02 | 1 |
| 1·105 | 1,28 | 1,22 | 1,15 | 1,1 | 1,08 | 1,06 | 1,03 | 1,02 | 1 |
| 1·106 | 1,14 | 1,11 | 1,08 | 1,05 | 1,04 | 1,03 | 1,02 | 1,01 | 1 |
Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:
R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.
Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.
Расчет теплоотдачи при вынужденной конвекции
Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды tж=50°С, температура стенки трубы tс=10°С.
1. Определим физические свойства воды при температуре 50°С:
- Теплопроводность воды λж= 0,648 Вт/(м·град);
- Плотность воды ρж=988 кг/м3;
- Кинематическая вязкость воды νж=0,556·10-6, м2/с;
- Число Прандтля при температуре жидкости Prж=3,54;
- Число Прандтля при температуре стенки Prс=9,52.
2. Рассчитаем среднюю скорость течения воды w по трубе:
3. Определим число Рейнольдса Re:
4. Поскольку число Рейнольдса имеет значение больше 1·104, то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:
Определим коэффициент εL по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент εL=1.
Выполним расчет числа Нуссельта по приведенному критериальному уравнению:
5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:
Выполним расчет:
Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м2·град).
Теплоотдача при свободной конвекции в трубах и каналах
Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.
Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).
Свободная конвекция в неограниченном пространстве
Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.
Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 103 до 109 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:
В качестве определяющего размера принимается наружный диаметр d канала или трубы.
Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 103 до 109 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:
При GrPr>109:
Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.
Свободная конвекция в ограниченном объеме
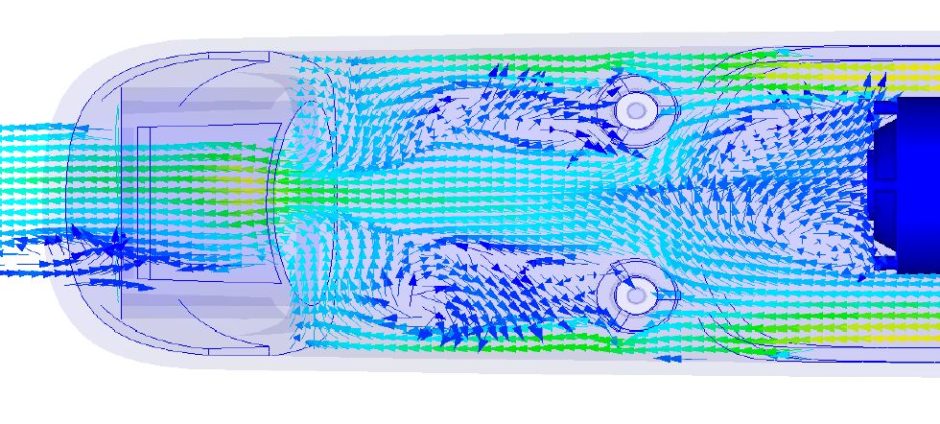
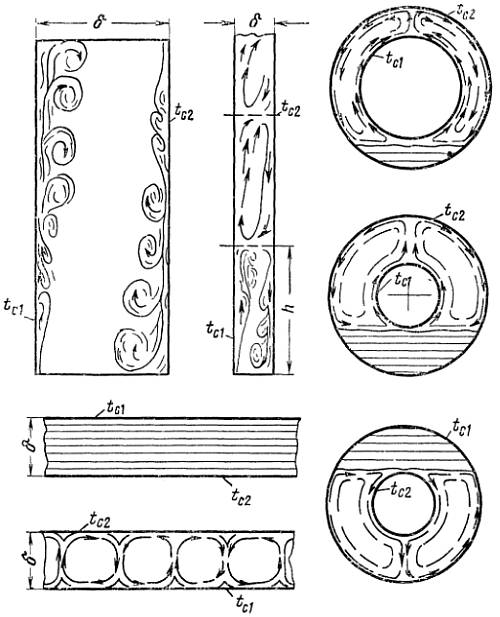
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.
Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λэк.
Эквивалентный коэффициент теплопроводности определяется по формуле:
Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м2; Δt=tc1-tc2 — температурный напор между нагретой и холодной стенками, °С.
Отношение эквивалентного коэффициента теплопроводности λэк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции εк, который определяется значением комплекса GrPr.
При малых значениях комплекса GrPr<1000 коэффициент конвекции εк=1, то есть теплоотдача просходит только за счет теплопроводности среды (λэк=λ).
В случае 103<GrPr<106:
При 106<GrPr<1010:
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной tж=0,5(tc1+tc2). В качестве определяющего размера принимается δ — толщина слоя жидкости.
Расчет теплоотдачи при свободной конвекции
Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки tс=80°С. Температура окружающего воздуха tж=20°С.
1. Определим физические свойства воздуха при температуре 20°С:
- Теплопроводность воздуха λж= 0,0259 Вт/(м·град);
- Кинематическая вязкость воздуха νж=15,06·10-6, м2/с;
- Число Прандтля при температуре жидкости Prж=0,703;
- Число Прандтля при температуре стенки Prс=0,69;
- Коэффициент объемного расширения βж=1/(273+20)=0,00341 град-1.
2. Вычислим число Грасгофа Gr по формуле:
Получаем:
3. Определим значение комплекса GrPr:
Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:
4. Вычислим значение числа Нуссельта Nu:
5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:
Получаем:
6. Определим потери тепла с боковой поверхности трубопровода по формуле:
Подставляя численные значения, окончательно получаем потерю тепла:
Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.
Источники:
- Михеев М. А., Михеева И. М. Основы теплопередачи.
- Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. Учебник для вузов — М.: «Энергия», 1975.