Какое количество ребер у куба?
Двенадцать же? Возьмём стоящий на какой-нибудь поверхности куб. Сверху и снизу у него четырёхугольники, то есть квадраты, по 4 ребра на периметре каждого. И между ними по вертикали от угла к углу тоже 4 ребра. Всего получается двенадцать.
автор вопроса выбрал этот ответ лучшим
Oleg74
[203K]
8 лет назад
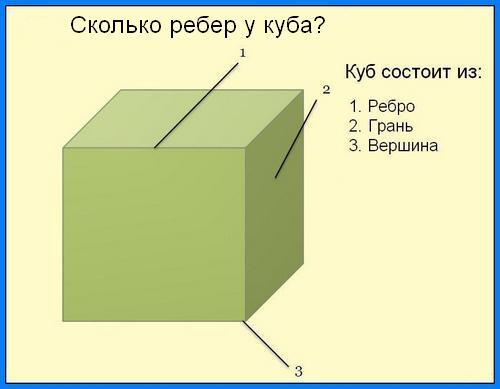
Давайте посмотрим на такую фигуру , как куб пространственно . Куб , как известно , состоит из шести граней , которые ограничиваются ребрами . Грань — это четыре ребра . 4 ребра будет на основании куба , 4 ребра на верху куба и 4 ребра находятся на боковых гранях .
4 + 4 + 4 = 12 ребер .
Ответ : Двенадцать .
chipmunk
[41.5K]
9 лет назад
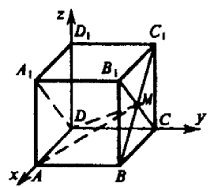
Ребра можно сосчитать на примере этого куба.
Ребра по высоте 4 шт : АА1, ВВ1, СС1, DD1
Ребра в нижней части куба 4 шт: АВ,ВС,СD,DА
Ребра в верхней части куба 4 шт: А1В1, В1С1,С1D1,D1A1
Итого в кубе 12 ребер, это и будет правильным ответом.
ZoRRoO
[90.6K]
6 лет назад
У куба всего 12 ребер. Смотрите сами: 4 внизу, 4 вверху, 4 по бокам. Умножаем 4 на 3 получается 12. Это объясняется тем, что куб — трехмерная геометрическая фигура с основанием квадрата.
На рисунке показано, что такое ребро куба. Можно самому убедиться, что у куба всего 12 ребер.
кудрявцев владимир семенович
[104K]
8 лет назад
Даже представив визуально куб то можно посчитать это так четыре ребра верхняя плоскость куба, нижняя часть куба тоже четыре ребра и средняя часть куба четыре ребра. И что бы долго не мудрствовать получается что у куба двенадцать ребер. Все просто и понятно.
Матвей628
[90.1K]
9 лет назад
У куба ребер вдвое больше, чем граней. А граней у куба шесть.
Каждая грань имеет четыре ребра, но они общие с другими гранями. Если учитывать только те ребра, которые не учитывали при подсчете других граней, то и получится, что у куба двенадцать ребер.
spring948374
[448K]
8 лет назад
Сколько рёбер имеет куб? — такой вопрос встретился мне в одной из интеллектуальных викторин. Было предложено 4 варианта ответов — 4, 6, 8 и 12. Правильный ответ — 12. У куба 12 рёбер. А ещё куб имеет 6 граней и 8 вершин.
Куб имеет 12 ребер.
Это нетрудно посчитать, если взять какой-нибудь кубик (или даже просто представить себе его): 4 ребра снизу, 4 сверху и 4 вертикальные боковые. Вот и получается, что 12 ребер у куба.
Мариника
[4.9K]
10 лет назад
Ну вроде как 12 должно быть!!! А в чём подвох вопроса странного по сути, вроде посчитать не сложно? Возможно я ошибаюсь, колитесь, в чём тут дело? Очень интересно кстати для чего такой вопрос задали…
Fortuna70
[35.1K]
10 лет назад
Я тоже думаю, что 12. Взяла шкатулку и посчитала.
yuliyakotya
[33.2K]
8 лет назад
Можете взять в руки обычный игральный кубик и посчитать,а если такого нет под рукой,то просто представте себе куб.Верхняя грань куба имеет 4 ребра,нижняя-тоже 4,и по бокам куба насчитаете еще 4 ребра.Несложные подсчеты:4+4+4=12 ребер у куба.
Знаете ответ?

Глава 1.
Булевы функции
1.1. Булев куб
Константы 0 и 1 называются булевыми константами. Упорядоченные наборы из нулей и единиц будем называть двоичными или булевыми наборами. Символы 0 и 1, входящие в двоичный набор, называются разрядами набора. Число разрядов набора называется его длиной. Разряды каждого набора длины n нумеруются целыми числами от 1 до n слева направо: крайний левый разряд получает номер 1, крайний правый — номер n. Множество всех булевых наборов длины n называется булевым кубом
размерности n и обозначается символом B n . Название булев куб возникло
благодаря геометрической интерпретации множества B n . Если наборы из этого множества рассматривать как элементы действительного n — мерного
пространства B n , то нетрудно убедиться, что они будут расположены в вершинах единичного куба. Поэтому часто булевы наборы называются также вершинами n -мерного единичного куба.
Номером и весом набора u = (u1 ,…, un) из B n называются величины
|
n |
u 2n i |
n |
||||||||
|
u |
, |
u |
u . |
|||||||
|
i 1 |
1 |
i 1 |
i |
|||||||
|
Номера наборов задают на множестве |
B n |
отношение линейного |
порядка ≤. Будем говорить, что набор u не больше набора v, если| u | ≤ | v |. Порядок, определяемый отношением ≤, называется лексикографическим.
Множество всех наборов длины n и веса k образует k-й слой куба B n , обозначаемый через Bkn . Число наборов в k-м слое n-мерного
единичного куба равно числу сочетаний из n элементов по k — столькими способами среди n разрядов произвольного набора можно выбрать k разрядов, равных единице. Следовательно,
|
n |
n |
n! |
||
|
Bk |
||||
|
n k !k ! |
||||
|
k |
||||
|
Расстоянием Хемминга |
между вершинами u и v куба B n |
||||
|
называется число d u, v |
n |
u v |
|||
|
, равное количеству несовпадающих |
|||||
|
i 1 |
i i |
||||
разрядов u и v. Нетрудно показать, что расстояние d является метрикой, т.е. d – положительная симметрическая функция двух аргументов, принимающая значение нуль тогда и только тогда, когда два ее аргумента совпадают, и для которой справедливо неравенство треугольника: d(u, v) ≤
d(u, w) + d(w, v) для любых трех наборов u, v и w из Bn . Наборы u и v называются соседними, если d(u, v)=1. Если d(u, v)=n, то наборы называются противоположными. Соседние наборы различаются между собой только в одном разряде, противоположные наборы — во всех разрядах.
Пример 1.1.1. В трехмерном булевом кубе B3 рассмотрим четыре набора u1 = (000), u2 = (100), u3 = (110) и u4 = (111). Для номеров и весов этих наборов справедливы равенства:
|u1| = 0, |u2| = 4, |u3| = 6, |u4| = 7, ||u1|| = 0, ||u2|| = 1, ||u3|| =2, ||u4|| = 3.
Попарные расстояния между рассматриваемыми наборами равны
d(u1, u2) = 1, d(u1, u3) = 2, d(u1, u4) = 3, d(u2, u3) = 1, d(u2, u4) = 2, d(u3, u4) = 1.
Следовательно, наборы u1 и u4 — противоположные, а ui и ui+1 при i = 1,2,3 — соседние.
Пары соседних вершин булева куба называются ребрами. Если u, v — соседние вершины, различающиеся в i – м разряде, то говорят, что ребро (u, v) проходит в i — м направлении и соединяет эти вершины. Пусть i1, … ,in-k -попарно различные натуральные числа, не превосходящие n,
u1, … ,un-k -булевы константы. Множество {v ε B n | vi = uj, j = 1,2, … ,n-k}
называется k — мерной гранью куба B n . Легко видеть, что k — мерная грань n — мерного булева куба содержит 2k различных вершин.
Пусть u ε Bn . Шаром радиуса k с центром в наборе u называется
множество Bn, k(u) состоящее из всех таких v ε B n , что d(u, v) ≤ k. Сферой радиуса k с центром в наборе u называется множество Sn,k(u)
состоящее из всех таких v ε B n , что d(u,v) = k. Легко видеть, что k — й

слой Bkn является сферой радиуса k с центром в нулевом наборе и сферой радиуса n — k с центром в единичном наборе. Непосредственно из
определений сферы и шара следует, что для любого u ε B n и любого k=
0, 1,…,n
|
S |
u |
n |
, |
B |
u |
k |
n |
||||||
|
n, k |
. |
||||||||||||
|
n, k |
|||||||||||||
|
k |
i |
0 i |
|||||||||||
Пример 1.1.2. Рассмотрим трехмерный булев куб B3 , изображенный на расположенном слева рис. 1.1.1. Этот куб содержит восемь вершин,
образующих в нем четыре слоя. Нулевой слой B03 состоит из
единственной вершины (000). Первый слой B13 содержит три вершины: (100), (010) и (001).
Второй слой B23 также содержит три вершины: (110), (101) и (011). И,
наконец, третий слой B33 куба состоит из одной вершины (111). В кубе 12 ребер, изображенных на рисунке отрезками, соединяющими вершины. В
каждом из трех направлений проходит по четыре ребра. В B3 содержится шесть двумерных граней, содержащих по четыре вершины. Вершины одной из этих граней отмечены на рисунке черными кружками. Легко видеть, что номера отмеченных вершин принадлежат множеству {1,3,5,7}. Шар B3,1 (010) состоит из вершины (010) и трех вершин, соединенных с ней ребрами: (000), (110) и (011). Три последние вершины образуют сферу S3,1
(010).
2. Подмножество G={gѐ1, …,gm} булева куба Bn называется двоичным кодом с кодовым расстоянием d, если для любых двух его элементов gi и gj расстояние между ними не меньше d. Говорят, что код G исправляет t ошибок, если его кодовое расстояние не меньше чем 2t+1. Заметим, что если вокруг каждого элемента g кода G с расстоянием 2t+1 построить шар радиуса t с центром в этом элементе, то шары с центрами в разных элементах не будут пересекаться Действительно, если некоторый набор v
|
принадлежит пересечению шаров с центрами в элементах gi и gj , то это |
|
|
означает, что d(v, gi ) t и |
d(v, gj) t. Но тогда в силу неравенства |
треугольника d(gi, gj) d(v, gi) + d(v, gj) 2t. Противоречие.
Пример 1.1.3. Снова рассмотрим трѐхмерный булев куб B3 . В нѐм любые две противоположные вершины образуют код с расстоянием три,

например, {(000), (111)}. Кодами с расстоянием два являются множество всех наборов чѐтного веса и множество всех наборов нечѐтного веса.
Обозначим через m(n, d) максимально возможное число элементов в двоичном коде длины n, кодовое расстояние которого равно d. Для кодов с нечѐтным кодовым расстоянием имеет место следующий результат.
Теорема 1.1.1. Справедливы неравенства
|
2n |
2n |
||||||
|
m(n, 2t 1) |
. |
||||||
|
2t |
n |
t |
n |
||||
|
i 1 i |
i |
1 i |
Доказательство. Верхняя оценка величины m(n, 2t+1) легко следует из
замечания, сделанного перед формулировкой теоремы. Рассмотрим в Bn произвольный код G с расстоянием 2t+1, и построим вокруг каждого его элемента шар радиуса t. Так как эти шары не пересекаются, и каждый шар
|
состоит ровно из |
t |
n |
наборов, то все шары вместе содержат |
|
i |
1 i |
|
G |
t |
n |
и, поэтому, |
||||||||||
|
наборов. С другой стороны шары лежат в Bn |
|||||||||||||
|
i |
1 i |
t |
n |
||||||||||
|
содержат не более 2n |
наборов. Следовательно, |
G |
|||||||||||
|
2n . |
|||||||||||||
|
i |
1 i |
||||||||||||
|
Для доказательства |
нижней оценки опишем |
индуктивную |
процедуру |
построения в Bn кода G с расстоянием 2t+1. Первый элемент кода выберем произвольно, вокруг выбранного элемента построим шар радиуса 2t. В качестве второго элемента кода возьмѐм произвольный набор, не принадлежащий построенному шару. Очевидно, что расстояние между выбранными наборами не меньше 2t+1. Вокруг второго элемента также построим шар радиуса 2t. Теперь допустим, что выбраны k элементов, попарные расстояния между которыми не меньше 2t+1, и вокруг каждого выбранного элемента построен шар радиуса 2t. Если
|
2t |
n |
2n , |
||
|
k |
(1.1.1) |
|||
|
i 1 |
i |
|||
|
то можно выбрать очередной |
(k+1)-й |
элемент, не принадлежащий |
построенным шарам, и, следовательно, находящийся на расстоянии не меньшем 2t+1 от каждого из выбранных ранее элементов. Легко видеть, что построение кода можно продолжать до тех пор пока справедливо

неравенство (1.1.1). В тот момент, когда это неравенство впервые
|
нарушится, код G будет |
состоять |
из k элементов, и для k будет |
|
|
k |
n |
n |
2n. |
|
i 1 |
|||
|
справедливо неравенство |
i |
Теорема доказана. |
|
3. Вершины в булевом кубе распределены по слоям неравномерно. При больших n большинство вершин лежит в узкой полосе, состоящей из
|
2 nlog2 n средних |
слоев. |
Более |
точно, имеет |
место следующее |
||||||||
|
утверждение. |
||||||||||||
|
Теорема 1.1.2. |
При |
n |
справедливо |
асимптотическое |
||||||||
|
равенство |
||||||||||||
|
n / 2 |
||||||||||||
|
nlog2 n |
||||||||||||
|
Bn |
~ |
Bn |
= 2n. |
|||||||||
|
k n / 2 |
k |
|||||||||||
|
nlog2 n |
||||||||||||
Доказательство. Оценим число наборов, вес которых отличается от n2 более, чем на t единиц:
|
Bn |
n |
n / 2 k 2 n |
|||||||||||||||||||||||
|
k : |
n / 2 k |
t k |
k : |
n / 2 k |
t k |
k : |
n / 2 k |
t n / 2 k 2 |
k |
||||||||||||||||
|
1 |
n |
k |
2 |
n |
1 |
n |
k 2 |
n . |
|||||||||||||||||
|
t2 k : |
t2 k |
||||||||||||||||||||||||
|
n / 2 k |
t 2 |
k |
0 2 |
k |
(1.1.2)
Найдем сумму, стоящую в правой части неравенства (1.1.2). Легко видеть, что

|
n |
n |
n |
n |
n k k. |
|
|
0 k |
k |
0 k |
|||
|
(1.1.3) |
Первая сумма в правой части (1.1.3) равна n2 2n 2 . Найдем вторую сумму:
|
n |
n |
n 1 |
n |
n 1 |
n k kn! |
||||
|
n k k |
n k k |
n k !k! |
|||||||
|
k 0 |
k |
k 1 |
k |
k 1 |
|
n 1 |
n n 1 n 2 ! |
n 2 n 2 |
|||||
|
n k 1 ! k 1 ! |
n n 1 |
n n 1 2n 2. |
|||||
|
k 1 |
k |
||||||
|
k 0 |
|||||||
|
Из двух предыдущих неравенств следует, что |
|||||||
|
n |
n |
n |
2 |
||||
|
k n2 2n 2 |
n n 1 2n 2 |
n2n 2. |
|||||
|
k |
0 k |
2 |
Подставляя полученное равенство в правую часть (1.1.2) и полагая t равным 
|
n |
n2n 2 |
2n 2 |
n |
||||||||||||||||
|
Bk |
o 2 |
. |
|||||||||||||||||
|
n / 2 k |
n log2 n |
||||||||||||||||||
|
k : |
n log |
2 |
n |
n log2 n |
|||||||||||||||
|
Таким образом, в сумме |
во всех слоях, номера которых отличаются |
||||||||||||||||||
|
n |
, находится o( 2n ) булевых наборов длины |
||||||||||||||||||
|
от |
больше чем на |
nlog2 n |
|||||||||||||||||
|
2 |
|||||||||||||||||||
n. Следовательно, почти все наборы лежат в узкой полосе, состоящей из 2 nlog2 n средних слоев. Теорема доказана.
4. Кроме рассмотренного выше линейного порядка ≤, на множестве
наборов B n существует естественный частичный порядок . Говорят, что
|
набор u не больше v (u v), если |
ui ≤ vi при всех i = 1,2, … ,n. Если u v и |
u ≠v, то говорят, что набор u строго меньше набора v (u v). Наборы u и
|
v называются сравнимыми, если либо u |
v, либо v u. Если ни одно из |
этих отношений не выполняется, то наборы называются несравнимыми. Последовательность вершин u1, u2, … , uk называется цепью, если d(ui ,
ui+1) = 1 и ui ui+1 для всех i=1,2, … ,k — 1. Вершина uk называется
наибольшей вершиной цепи u1, u2, … , uk , а вершина u1 — наименьшей вершиной этой цепи. Число вершин в цепи называется ее длиной. Говорят, что цепь связывает вершины u и v и проходит через вершину w, если u и v, являются, соответственно, первой и последней вершинами цепи, а w принадлежит этой цепи. Цепь называется максимальной, если она не является частью цепи большей длины. Множество попарно несравнимых вершин называется антицепью. Антицепь называется максимальной, если она не является подмножеством другой антицепи, состоящей из большего количества вершин.
Пример 1.1.4. В булевом кубе B3 (см. рис. 1.1.1) существует ровно шесть максимальных цепей. Длина каждой максимальной цепи равна четырем. Каждая максимальная цепь начинается в вершине (000), последовательно проходит через одну вершину первого и одну вершину
второго слоя, и заканчивается в вершине (111). В B3 существуют: (i) две максимальные антицепи состоящие из трех вершин, это первый и второй слои; (ii) три максимальные антицепи состоящие из двух вершин, каждая такая антицепь состоит из одной вершины первого слоя и противоположной ей вершины второго слоя, например, {(100), (011)}; (iii) две максимальные антицепи состоящие из одной вершины, это вершины
(000) и (111).
|
Теорема |
1.1.3. |
Булев |
куб |
Bn |
можно |
покрыть |
|||
|
n |
|||||||||
|
n / 2 непересекающимися цепями так, что число цепей длины n — 2p + 1, |
|||||||||
|
n |
n |
||||||||
|
где p = 0, 1, … , [n/2], равно |
. |
||||||||
|
p |
p 1 |
Доказательство.Теорему докажем индукцией по n. При n = 1 утверждение теоремы очевидно — куб B1 можно покрыть единственной цепью из двух вершин (p = 0).
Допустим, что теорема верна для n = k. В кубе Bk+1 рассмотрим два подмножества B0 и B1, состоящие из всех наборов, у которых (k+1)-е разряды равны соответственно нулю и единице. Каждое из множеств Bi изоморфно кубу Bk, и поэтому в силу предположения индукции может быть покрыто непересекающимися цепями так, что число цепей длины k —
|
k |
k |
||
|
2p + 1, где p = 0, 1, … , [k/2], равно |
. |
||
|
p |
p 1 |
Рассмотрим одинаковые покрытия множеств B1 и B0, каждое из которых удовлетворяет условиям теоремы в кубе размерности k. Очевидно, что цепи этих покрытий не пересекаются и полностью покрывают куб Bk+1. Пусть C1 и C0 — одинаковые цепи в рассматриваемых покрытиях множеств B1 и B0, v1 и v0 — наибольшие элементы этих цепей.
Очевидно, что v0 v1 и в наборах v1 и v0 все разряды, кроме последнего,
совпадают.
Рис. 1.1.2
Рассматриваемые объекты представлены в левой части рисунка 1.1.2. На этом рисунке штриховыми линиями изображены ребра, идущие в (k+1) — м направлении. Преобразуем цепи C1 и C0 следующим образом: набор v1 удалим из цепи C1 и добавим к цепи C0. В результате из двух цепей длины k — 2p + 1 получим цепь длины k-2p = (k+1) — 2p — 1 и цепь длины k — 2p + 2 = (k + 1) — 2(p — 1) — 1. Новые цепи изображены в правой части рисунка 1.1.2. Выполним подобные преобразования над всеми парами одинаковых цепей в покрытиях B1 и B0.
Очевидно, что новые цепи покрывают Bk+1 и не пересекаются. При этом цепь длины (k + 1) — 2p — 1 получается либо удалением наибольшего набора из цепи длины k — 2(p — 1) — 1, либо добавлением нового набора в цепь длины k — 2p — 1. Поэтому в преобразованном покрытии число цепей длины (k + 1) -2p — 1 равно
|
k |
k |
k |
k |
||||||||||||||
|
= |
|||||||||||||||||
|
p |
p 1 |
p |
1 |
p 2 |
|||||||||||||
|
k |
k |
k |
k |
k 1 |
k 1 |
||||||||||||
|
= |
. |
||||||||||||||||
|
p |
p 1 |
p 1 |
p 2 |
p |
p 1 |
Теорема доказана.

Так как цепь и антицепь не могут иметь более одного общего элемента, то из доказанной теоремы следует, что любая антицепь в кубе Bn
|
состоит не более чем из |
n |
наборов. Информация о распределении |
||
|
n / 2 |
||||
вершин антицепи по слоям куба содержится в задаче 1.1.16.
Задачи
1.1.1.Найти максимально возможный периметр треугольника в Bn .
1.1.2.Чему равно максимальное расстояние между наборами, принадлежащими:
|
а) Bn ; b) Bn ; c) B |
; d) S |
n,k |
? |
|
k |
n,k |
1.1.3.Найти среднее расстояние между наборами Bn .
1.1.4.Найти число различных ребер в кубе Bn .
1.1.5.Найти в Bn : a) число различных k — мерных граней куба;
b)число различных k — мерных граней, проходящих через фиксированную вершину; с) число всех граней.
1.1.6.Сколько вершин в среднем содержит одна грань n-мерного
куба?
1.1.7.Найти число ребер, проходящих через вершины k — мерной грани n — мерного булева куба.
1.1.8.Найти число ребер, проходящих через вершины, лежащие в k —
мслое n — мерного булева куба.
1.1.9. Найти: a) n u ; b) n u ; c) n u . u B u B u Bk
1.1.10. В n –мерном булевом кубе эллипсом с фокусами иназывается множество наборов, сумма расстояний от каждого из которых до и равна фиксированному числу k. Сколько наборов содержится в эллипсе n-мерного булева куба?
|
1.1.11. Для |
любых сравнимых наборов |
, Bn интервалом с |
||
|
границами и |
называется множество I( , |
) = Bn | |
. |
Показать, что любой интервал является гранью, а грань — интервалом.
1.1.12.Показать, что1
1Выражение f (n) g(n) означает существование таких констант а и b, что f (n) ag(n) и g(n) bf (n).

|
n |
2 |
n |
||||||
|
. |
||||||||
|
n |
2 |
|||||||
|
n |
||||||||
1.1.13. Найти в Bn число наборов несравнимых с данным набором
.
1.1.14.Найти число пар попарно несравнимых вершин в Bn .
1.1.15.Найти: a) число различных максимальных цепей в Bn ;
b) число различных максимальных цепей, проходящих через
|
фиксированную вершину k — го слоя куба Bn . |
|||||||
|
1.1.16. Пусть T — антицепь в Bn , T |
= T |
Bn |
. Показать, что |
||||
|
k |
k |
||||||
|
n |
n |
1. |
|||||
|
T |
/ |
||||||
|
k 0 |
k |
k |
|||||
1.2.Булевы функции
1.Функция f(x1, … ,xn), отображающая Bn в B1 , называется n — местной булевой функцией. Множество всех булевых функций
обозначается через P2 , а множество всех булевых функций зависящих от n переменных – через P2 n . Каждая булева функция имеет конечную область определения, что позволяет полностью задать функцию f из P2 n , перечислив все наборы из Bn и указав значения f на этих наборах.
В частности, булева функция f(x1, …, xn) может быть задана таблицей состоящей из 2k строк, каждой из которых поставлен в соответствие булев набор длины k, и 2n-k столбцов, каждому из которых поставлен в соответствие булев набор длины n-k. Параметр k принимает значения от 0
|
до n. В такой таблице |
(Таб. 1.2.1) значение функции f на наборе |
|||
|
1,…, k , k 1,…, n |
помещается |
на |
пересечении |
строки, |
соответствующей набору 1,…,k , и столбца, соответствующего наборуk 1,…,n . Если в таблице 1.2.1 параметр k равен нулю, то говорят, что
функция задается вектором-строкой своих значений, а если k = n — вектором-столбцом. Так как каждый элемент таблицы, задающей булеву функцию, равен либо нулю, либо единице, то легко видеть, что число различных таблиц, и, соответственно, число различных булевых функций,
зависящих от n переменных, равно 22n . Число наборов из Bn , на которых
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Проведите наблюдение по следующему плану:
1) Возьмите куб и определите, сколько у куба граней, вершин, ребер.
2) Определите число ребер и число граней куба, сходящихся в каждой его вершине.
3) Поставьте куб на стол. Какие грани куба имеют общие ребра с нижней гранью? Сколько их? Сколько граней куба не имеют общих ребер с нижней гранью?
reshalka.com
Математика 5 класс Дорофеев. 10.1 Геометрические тела и их изображение. Номер №921
Решение
1)
Граней: 6.
Ребер: 12.
Вершин: 8.
2)
3 ребра и 3 грани сходятся в каждой вершине.
3)
4 грани куба имеют общие ребра с нижней гранью. Верхняя грань не имеет общих ребер с нижней гранью.
Как найти сумму длин рёбер куба
Куб — это многогранник правильной формы с одинаковыми по форме и размерам гранями, представляющими собой квадраты. Из этого вытекает, что как для его построения, так и для расчетов всех связанных параметров достаточно знать всего одну величину. По ней можно найти объем, площадь каждой грани, площадь всей поверхности, длину диагонали, длину ребра или сумму длин всех ребер куба.
Инструкция
Посчитайте количество ребер в кубе. У этой объемной фигуры шесть граней, что определяет другое ее название — правильный гексаэдр (hexa означает «шесть»). У фигуры из шести квадратных граней может быть только двенадцать ребер. Так как все грани — это одинаковые по размерам квадраты, то и длины всех ребер равны. Значит для нахождения суммарной длины всех ребер, надо узнать длину одного ребра и увеличить его в двенадцать раз.
Умножайте длину одного ребра куба (A) на двенадцать, чтобы вычислить длину всех ребер куба (L): L=12∗A. Это самый простой из возможных способов определения суммарной длины ребер правильного гексаэдра.
Если длина одного ребра куба не известна, но есть площадь его поверхности (S), то длину одного ребра можно выразить как квадратный корень из одной шестой части площади поверхности. Для нахождения длины всех ребер (L) полученную таким способом величину надо увеличить в двенадцать раз, а это значит, что в общем виде формула будет выглядеть так: L=12∗√(S/6).
Если известен объем куба (V), то длину одной его грани можно определить как кубический корень из этой известной величины. Тогда длину всех граней (L) правильного тетраэдра будут составлять двенадцать кубических корней из известного объема: L=12∗³√V.
Если известна длина диагонали куба (D), то для нахождения одного ребра это значение надо разделить на квадратный корень из трех. Длину всех ребер (L) в этом случае можно будет вычислить как произведение числа двенадцать на частное от деления длины диагонали на корень из трех: L=12∗D/√3.
Если известна длина радиуса вписанной в куб сферы (r), то длина одной грани будет равна половине этой величины, а суммарная длина всех ребер (L) — этой величине, увеличенной в шесть раз: L=6∗r.
Если известна длина радиуса не вписанной, а описанной сферы (R), то длина одного ребра будет определяться как частное от деления удвоенной длины радиуса на квадратный корень из тройки. Тогда длина всех ребер (L) будет равна двадцати четырем длинам радиуса, поделенным на корень из трех: L=24∗R/√3.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
6
Сколько ребер у куба?
Какое количество ребер у куба?
11 ответов:
3
0
Двенадцать же? Возьмём стоящий на какой-нибудь поверхности куб. Сверху и снизу у него четырёхугольники, то есть квадраты, по 4 ребра на периметре каждого. И между ними по вертикали от угла к углу тоже 4 ребра. Всего получается двенадцать.
2
0
Ребра можно сосчитать на примере этого куба.
Ребра по высоте 4 шт : АА1, ВВ1, СС1, DD1
Ребра в нижней части куба 4 шт: АВ,ВС,СD,DА
Ребра в верхней части куба 4 шт: А1В1, В1С1,С1D1,D1A1
Итого в кубе 12 ребер, это и будет правильным ответом.
2
0
Давайте посмотрим на такую фигуру , как куб пространственно . Куб , как известно , состоит из шести граней , которые ограничиваются ребрами . Грань — это четыре ребра . 4 ребра будет на основании куба , 4 ребра на верху куба и 4 ребра находятся на боковых гранях .
4 + 4 + 4 = 12 ребер .
Ответ : Двенадцать .
1
0
Ну вроде как 12 должно быть!!! А в чём подвох вопроса странного по сути, вроде посчитать не сложно? Возможно я ошибаюсь, колитесь, в чём тут дело? Очень интересно кстати для чего такой вопрос задали…
1
0
Я тоже думаю, что 12. Взяла шкатулку и посчитала.
1
0
Куб имеет 12 ребер.
Это нетрудно посчитать, если взять какой-нибудь кубик (или даже просто представить себе его): 4 ребра снизу, 4 сверху и 4 вертикальные боковые. Вот и получается, что 12 ребер у куба.
1
0
У куба ребер вдвое больше, чем граней. А граней у куба шесть.
Каждая грань имеет четыре ребра, но они общие с другими гранями. Если учитывать только те ребра, которые не учитывали при подсчете других граней, то и получится, что у куба двенадцать ребер.
1
0
Сколько рёбер имеет куб? — такой вопрос встретился мне в одной из интеллектуальных викторин. Было предложено 4 варианта ответов — 4, 6, 8 и 12. Правильный ответ — 12. У куба 12 рёбер. А ещё куб имеет 6 граней и 8 вершин.
1
0
Даже представив визуально куб то можно посчитать это так четыре ребра верхняя плоскость куба, нижняя часть куба тоже четыре ребра и средняя часть куба четыре ребра. И что бы долго не мудрствовать получается что у куба двенадцать ребер. Все просто и понятно.
1
0
У куба всего 12 ребер. Смотрите сами: 4 внизу, 4 вверху, 4 по бокам. Умножаем 4 на 3 получается 12. Это объясняется тем, что куб — трехмерная геометрическая фигура с основанием квадрата.
На рисунке показано, что такое ребро куба. Можно самому убедиться, что у куба всего 12 ребер.
0
0
Можете взять в руки обычный игральный кубик и посчитать,а если такого нет под рукой,то просто представте себе куб.Верхняя грань куба имеет 4 ребра,нижняя-тоже 4,и по бокам куба насчитаете еще 4 ребра.Несложные подсчеты:4+4+4=12 ребер у куба.
Читайте также
Куб это многогранник, причем такой, в котором все грани одинаковые и представляют собой квадраты, исходя из этого мы понимаем, что все ребра куба, представляющие из себя высоту, ширину и длину этого многогранника, одинаковы. Если в общем случае с любым многогранником для нахождения его объема мы умножаем длину на ширину и на высоту этого многогранника, то в случае именно с кубом мы просто возводим длину ребра куба (которая является и длиной, и шириной, и высотой куба) в третью степень или в куб).
В указанных частных случаях объем куба будет 27 (3 в третьей степени), 125 (5 в кубе), 343 (7 в кубе), 729 (9 в третьей степени) кубических сантиметров.
куб объёмом 1000 кубических миллиметров имеет ребро 10 мм. Или кубический корень из 1000.
Куб с ребром 1000 миллиметров имеет объём 1000*1000*1000. То есть 1 000 000 000 кубических миллиметров или говоря по простому — две пол-литры. Если совсем просто, то литр.
Такой, какой необходимо. Ведь перед тем как начать готовить — читаешь список ингредиентов. Читая — мысленно представляешь себе, что это такое будет на вкус. Если компоненты кажутся вполне сочетаемыми (не абрикосовое варенье со шпротами) и среди них нет ничего такого, что и на дух не переносишь — чего же он невкусным-то будет?
Обычно женский цикл это 28 календарных дней, начиная с первого дня менструального цикла. Если сегодня начались месячные, значит это первый день менструального цикла. Через 28 дней если месячные не пришли, значит наступила задержка. Задержка первого дня менструального цикла. Если наступила беременность, то врачи — геникологи начинают недельный отчёт беременности не с середины цикла (овуляции) и ни когда примерно плодное яйцо прикрепилась к матке, а именно с первого дня менструального цикла. Хотя, конечно в этот период никакой беременности и не могло ещё быть.
На радость мужчинам — медицинские работники, а именно американские биологи доказали, что водка в очееень маленьких дозах ПОЛЕЗНА! Исследования показали, что малые порции хорошего,качественного спиртного способствует снижению риска смерти у людей от заболеваний сердца и сосудов.Эти данные ученые используют для разработок лекарственных препаратов, но лечиться ежедневно даже маленькими дозами врачи все таки не рекомендуют, так как ВРЕДА все таки от принятия спиртного намного больше!!!