Как найти число с отрицательной степенью - Исправление недочетов и поиск решений вместе с Examum.ru

Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно
прочитать урок
«Степень»
и «Свойства степеней».

Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении
примеров.

Как возвести число в отрицательную степень

Запомните!

Чтобы возвести число в отрицательную степень нужно:

«перевернуть» число. Записать его в виде дроби с единицой наверху (в
числителе) и с
исходным числом в степени внизу;
заменить отрицательную степень на
положительную;
возвести число в положительную степень.

Общая формула возведения в отрицательную степень выглядит следующим образом.

a⁻ⁿ =

,где a ≠ 0, n ∈ z (n принадлежит целым числам).

Примеры возведения в отрицательную степень.

6⁻² = =
(−3)⁻³ = = = −
0,2⁻² = =

Запомните!

Любое число в нулевой степени — единица.

a⁰ = 1
,где a ≠ 0

Примеры возведения в нулевую степень.

()⁰ = 1
(−5)⁰ = 1
d⁰ = 1

Как найти 10 в минус 1 степени

В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:

10⁻¹ = 0,1

Теперь, зная определение отрицательной степени, давайте разберемся, почему «10» в минус первой степени равно
«0,1».

Возведем «10⁻¹» по правилам отрицательной степени.

Перевернем «10» и запишем её в виде дроби
«

»
и заменим отрицательную степень
«−1» на
положительную степень «1».

Возведем «10» в «1» степень. Помним, что любое число в первой степени равно самому числу.

Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.

По такому же принципу можно найти «10» в минус второй, третьей и т.д.

10⁻² = 0,01

10⁻³ = 0,001

10⁻⁴ = 0,0001

Запомните!

Для упрощения перевода «10» в минус первую, вторую и т.д степени, нужно запомнить правило:

«Количество нулей после запятой равно положительному значению степени минус один».

Проверим правило выше для «10⁻²».

Т.к. у нас степень «−2», значит, будет всего один ноль (положительное
значение степени «2 − 1 = 1». Сразу после запятой ставим один ноль и за ним «1».

Рассмотрим «10⁻¹».

Т.к. у нас степень «−1», значит, нулей после запятой не будет (положительное
значение степени «1 − 1 = 0». Сразу после запятой ставим «1».

То же самое правило работает и для «10⁻¹²». При переводе в десятичную дробь будет
«12 − 1 = 11 » нулей и «1» в конце.

10⁻¹² = 0,000 000 000 001

Как возвести в отрицательную степень дробь

Запомните!

Чтобы возвести дробь в отрицательную степень нужно:

«перевернуть» дробь;
заменить отрицательную степень на
положительную;
возвести дробь в положительную степень.

Пример. Требуется возвести в отрицательную степень дробь.

Перевернем дробь «

»
и заменим отрицательную степень «−3» на положительную «3».

Возведем дробь в положительную степень по правилу возведения дроби в положительную степень.
Т.е. возведем и числитель «3», и знаменатель «10» в третью степень.

()⁻³ = ()³ =

Для более грамотного ответа запишем полученный результат в виде десятичной дроби.

()⁻³ = ()³ =

= = 0,027

Как возвести отрицательное число в отрицательную степень

Как и при возведении отрицательного числа в положительную степень, в первую
очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.

Запомните!

Отрицательное число, возведённое в
чётную степень, — число
положительное.

Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.

Пример.

(−5) ⁻² =

Перевернем число «−5» и заменим отрицательную степень
«−2»
на положительную
«2».

Так как степень «2» — четная, значит, результат возведения в степень будет
положительный. Поэтому
убираем знак минуса при раскрытии скобок.

Далее откроем скобки
и возведем во вторую степень и числитель «1»,
и знаменатель «5».

Как возвести отрицательную дробь в отрицательную степень

Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.

Запомните!

Отрицательная дробь, возведённая в
чётную степень, — дробь
положительная.

Отрицательная дробь, возведённая в
нечётную степень, — дробь
отрицательная.

Разберемся на примере. Задание: возвести отрицательную дробь
«(− )»
в «−3» степень.

По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень «−3» на положительную
«3».

Теперь определим конечный знак результата возведения в «3» степень.

Степень «3» — нечетная, значит, по правилу возведения отрицательного числа в степень дробь
останется отрицательной.

Нам остается только раскрыть скобки и возвести в степень и числитель «3», и знаменатель
«2» в третью степень.

Для окончательного ответа выделим целую часть из дроби.

(−

) ⁻³ = (−

) ³ = −

= −

= − 3

Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.

Правило возведения отрицательного числа в степень гласит: если степень четная, значит, результат возведения
будет положительным.

Свойства отрицательной степени

Все свойства степени, которые используются для положительной степени,
точно также применяются и для отрицательной степени.

В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени
и покажем примеры их использования.

Запомните!

a^m · aⁿ = a^{m + n}

=
a^{m − n}

(aⁿ)^m = a^{n · m}

(a · b)ⁿ = aⁿ · bⁿ

Примеры решений заданий с отрицательной
степенью

Разбор примера

Представить в виде степени.

2) a⁶ · b⁶ = (ab)⁶

4) (c⁵)² = c¹⁰

Разбор примера

Записать в виде степени с отрицательным числом.

Разбор примера

Вычислить.

3) (

) ⁻¹² : (

) ² =

(

) ¹² · (

) ² =

(

) ¹² · (

) ² =

= 13^{12 − 2} · 2^{2 − 12}

= 13¹⁰ · 2⁻¹⁰ = 13¹⁰ ·

= (

) ¹⁰

Разбор примера

Выполнить действия.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

20 ноября 2016 в 12:53

Виктор Помаранов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Виктор Помаранов
Профиль
Благодарили: 0

Сообщений: 1

0,4•(-10)³-7•(-10)²+64

0
Спасибо thanks
Ответить

21 ноября 2016 в 13:13
Ответ для Виктор Помаранов

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Нечетная стпень-не меняет знак, четная — меняет.
0,4 · (-1000) ? 7 · 100 +64 = ?400 ?700 +64 = ?1036
Ответ: ?1036

0
Спасибо thanks
Ответить

23 августа 2016 в 11:52

Мария Кузьменко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Мария Кузьменко
Профиль
Благодарили: 0

Сообщений: 1

Помогите решить, пожалуйста подробно))

4 в 6 степени минус 3 в 6 степени

0
Спасибо thanks
Ответить

30 августа 2016 в 15:01
Ответ для Мария Кузьменко

Наталия Зимарина
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Наталия Зимарина
Профиль
Благодарили: 0

Сообщений: 1

4⁶-3⁶=(4³)²-(3³)²=(4³-3³)(4³+3³)=(64-27)(64+27)=37 · 81=2997

0
Спасибо thanks
Ответить

Источник

Запись aⁿ означает что число a должно быть умножено n раз:

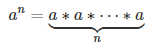На рисунке показно разложение числа a в n-ой степени на n множителей.

Пример 1. 5³=5*5*5=125

Деление это обратная операция умножению. Отрицательная степень означает сколько раз нужно разделить число.

Число в отрицательной степени a^-n может быть записано в виде:

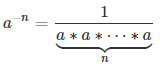На рисунке показно разложение числа a в минус n-ой степени на n множителей.

Пример 2. 5^-3=1÷5÷5÷5=0,008

Пример 2 может быть записан в виде.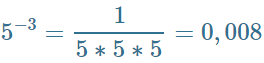

Определение. Если a≠0 и n — целое отрицательное число, то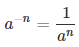

Для вычисления числа a^-n в отрицательной степени нужно:

1.Вычислить aⁿ

2.Затем разделить 1 на полученный результат, т.е.

Источник

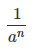Отрицательная степень числа

Степень с отрицательным показателем
Действия над степенями с отрицательными показателями

Степень с отрицательным показателем

Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.

d^-c =	1	; 7^-5 =	1	; a^-5 =	1	.
d^c	7⁵	a⁵

Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.

Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:

a⁵ : a⁸ = a^{5 — 8} = a^-3.

Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:

Значит:

Пример 1. Замените дробь степенью с отрицательным показателем:

Решение:

Пример 2. Представьте в виде степени с отрицательным показателем:

Решение:

1	= (m + n)^-2.
(m + n)²

Действия над степенями с отрицательными показателями

При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:

При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:

Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:

Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:

При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются:

Источник

Если (n) — натуральное число и

a≠0

, то запись

a−n

означает:

Полезно знать тождества:

ab−n=ban, в частности 1a−n=an,a≠0.

Пример:

1.23−2=322=94;2.3−2=132=19;3.15−3=53=125.

Свойства степеней с натуральными показателями верны и для отрицательных целых показателей.

1. При умножении степеней с одинаковыми основаниями показатели нужно сложить: as⋅at=as+t.

Пример:

a−3⋅a−5=a−3+(−5)=a−8.

2. При делении степеней с одинаковыми основаниями показатели нужно вычесть as:at=as−t.

Пример:

a−3:a−7=a−3−(−7)=a−3+7=a4.

3. При возведении степени в степень показатели нужно перемножить: ast=as⋅t.

Пример:

a−3−5=a−3⋅(−5)=a15.

Источник

Степень с отрицательным показателем

Что такое степень с отрицательным показателем (отрицательная степень)? Как выполнить возведение числа в отрицательную степень? Как возвести в отрицательную степень дробь?

Определение.

$[{a^{ - n}} = frac{1}{{{a^n}}}]$

В частности, число в степени минус один — это число, обратное данному:

$[{a^{ - 1}} = frac{1}{a}]$

Если n — целое число, то речь идет о степени с целым отрицательным показателем и равенство верно для любого a, отличного от нуля (т.е. при a≠0).

Если n — дробное число, то речь идет о степени с рациональным показателем:

$[{a^{ - frac{m}{n}}} = frac{1}{{{a^{frac{m}{n}}}}} = frac{1}{{sqrt[n]{{{a^m}}}}}]$

(m — целое число, n — натуральное число). Степень с дробным показателем определена только для положительных a (a>0).

В частности,

$[{a^{ - frac{1}{2}}} = frac{1}{{{a^{frac{1}{2}}}}} = frac{1}{{sqrt a }}]$

Дробь в степени с отрицательным показателем равна обратному этой дроби числу в степени с показателем, противоположным данному:

$[{(frac{a}{b})^{ - n}} = {(frac{b}{a})^n}]$

Другими словами, чтобы возвести дробь в отрицательную степень, надо эту дробь «перевернуть»(числитель и знаменатель поменять местами) и изменить знак в показателе степени.

Дробь в минус первой степени — это «перевернутая» дробь.

В частности,

$[{(frac{a}{b})^{ - 1}} = frac{b}{a}]$

Рассмотрим примеры возведения чисел в степень с отрицательным показателем.

Для ускорения вычислений используем таблицу степеней.

Примеры.

$[1){7^{ - 2}} = frac{1}{{{7^2}}} = frac{1}{{49}};]$

$[2){4^{ - 1}} = frac{1}{4};]$

$[3){( - 5)^{ - 3}} = frac{1}{{{{( - 5)}^3}}} = frac{1}{{ - 125}} = - frac{1}{{125}};]$

$[4){(frac{5}{{12}})^{ - 1}} = frac{{12}}{5} = 2,4;]$

$[5){(frac{2}{9})^{ - 2}} = {(frac{9}{2})^2} = frac{{81}}{4} = 20frac{1}{4}.]$

Чтобы возвести в отрицательную степень смешанное число, надо сначала перевести его в неправильную дробь:

$[6){(1frac{2}{3})^{ - 4}} = {(frac{5}{3})^{ - 4}} = {(frac{3}{5})^4} = frac{{81}}{{625}};]$

$[6){( - 5frac{1}{2})^{ - 2}} = {( - frac{{11}}{2})^{ - 2}} = {( - frac{2}{{11}})^2} = frac{4}{{121}}.]$

Возведем числа в степень с дробным отрицательным показателем:

$[8){(49)^{ - frac{1}{2}}} = frac{1}{{{{49}^{frac{1}{2}}}}} = frac{1}{{sqrt {49} }} = frac{1}{7};]$

$[9){(0,216)^{ - frac{2}{3}}} = frac{1}{{{{(0,216)}^{frac{2}{3}}}}} = frac{1}{{sqrt[3]{{{{(0,216)}^2}}}}} = ]$

$[ = frac{1}{{{{(sqrt[3]{{(0,216)}})}^2}}} = frac{1}{{{{(0,6)}^2}}} = frac{1}{{0,36}} = ]$

$[ = frac{1}{{frac{{36}}{{100}}}} = frac{{100}}{{36}} = frac{{25}}{9} = 2frac{7}{9};]$

При возведении в отрицательную степень десятичной дроби можно сначала перевести ее в обыкновенную и, если возможно, сократить:

$[{(0,216)^{ - frac{2}{3}}} = {(frac{{216}}{{1000}})^{ - frac{2}{3}}} = {(frac{{27}}{{125}})^{ - frac{2}{3}}} = ]$

$[ = {(frac{{125}}{{27}})^{frac{2}{3}}} = sqrt[3]{{{{(frac{{125}}{{27}})}^2}}} = {(sqrt[3]{{frac{{125}}{{27}}}})^2} = ]$

$[ = {(frac{5}{3})^2} = frac{{25}}{9} = 2frac{7}{9}.]$

Если в показателе степени стоит десятичная дробь, нужно перевести ее в обыкновенную:

$[10){(0,0004)^{ - 1,5}} = {(frac{4}{{10000}})^{ - 1,5}} = {(frac{1}{{2500}})^{ - 1,5}} = ]$

$[ = {2500^{1,5}} = {2500^{frac{3}{2}}} = sqrt {{{2500}^3}} = {(sqrt {2500} )^3} = ]$

$[ = {50^3} = 125000.]$

Возведение в степень с отрицательным показателем в алгебре встречается достаточно часто, поэтому важно вовремя усвоить эту тему.

Источник

Как возвести число в отрицательную степень

Как найти 10 в минус 1 степени

Как возвести в отрицательную степень дробь

Как возвести отрицательное число в отрицательную степень

Как возвести отрицательную дробь в отрицательную степень

Свойства отрицательной степени

Примеры решений заданий с отрицательной степенью

Разбор примера

Разбор примера

Разбор примера

Разбор примера

Ваши комментарии

Отрицательная степень числа

Степень с отрицательным показателем

Действия над степенями с отрицательными показателями

Примеры решений заданий с отрицательной
степенью