Количественная
оценка кинематических свойств системы
основана на определении ее степеней
свободы как направлений возможных
независимых перемещений. Число
степеней свободы
(W)
– это минимальное число независимых
параметров, необходимых для определения
положения всех точек системы. Такими
параметрами могут быть перемещения
отдельных точек, углы поворота элементов
и др.
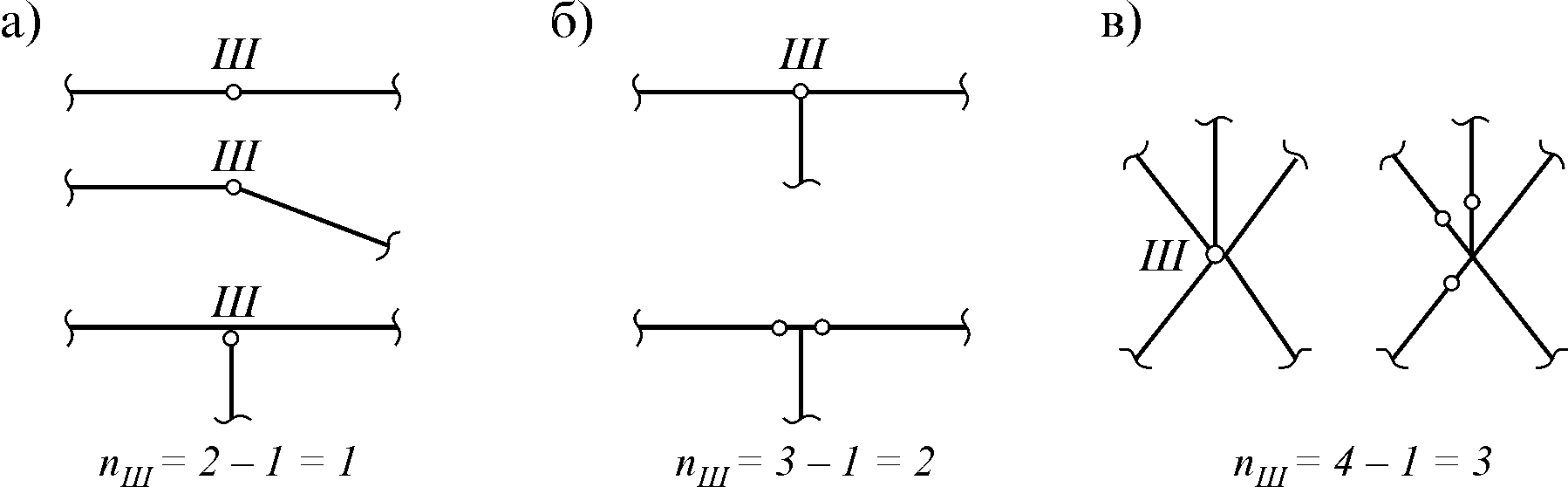
Число
степеней свободы простых систем можно
определять путем задания ее элементам
возможных перемещений (рис. 2.2 а, б, в).
Рис.
2.2
Для
изучения более сложных случаев введем
следующие понятия:
диск
(Д)
– неизменяемая часть системы, состоящая
из одного или нескольких жестко связанных
элементов (рис. 2.3 а);
шарнир
(Ш)
– связь, дающая возможность взаимного
поворота соседним дискам (рис. 2.3 б);
припайка
(П)
– связь, жестко закрепляющая соседние
диски (рис. 2.3 в);
стержень (С)
– связь, ограничивающая перемещение
диска в одном направлении (рис. 2.3 г);
опорная
связь (С0)
– связь, ограничивающая перемещение
диска в одном направлении по отношению
к земле (рис. 2.3 д).
Рис.
2.3
Определим
число степеней свободы точки (рис. 2.4 а)
и диска с различными кинематическими
связями (рис. 2.4 б-д):
Рис.
2.4
Как
видим, стержень или опорная связь
уменьшают число степеней свободы на
единицу, шарниры – на два, припайки –
на три.
Кинематические
связи должны обеспечивать неподвижность
системы относительно земли (основания),
а также неизменяемость ее внутренней
структуры. Если при удалении одной связи
из неизменяемой системы она становится
изменяемой, то эта связь называется
необходимой.
Если после этого система остается
неизменяемой, то связь называется
избыточной.
Связь, соединяющая систему с землей,
называется внешней,
а находящаяся внутри – внутренней
связью.
Шарнир,
объединяющий два диска, называется
простым
шарниром
(рис. 2.5 а). Если шарнир объединяет
несколько дисков, то он называется
кратным
шарниром.
Кратный шарнир эквивалентен нескольким
простым шарнирам. Кратность шарнира
определяется по формуле nШ=nД –1,
где nД
– число
дисков, объединяемых шарниром.
Рис.
2.5
2. Число степеней свободы стержневой системы
Рассматривая
расчетную схему сооружения как систему
дисков, объединенных связями, получаем
ее дисковый
аналог.
Для одной и той же системы часто можно
получить несколько дисковых аналогов.
Число
степеней свободы плоской стержневой
системы определяется по формуле,
называемой основной
формулой кинематического анализа:
W
= 3nД
– 2nШ
– nC
–
–
3nП
.
Здесь
nД
– число
дисков в дисковом аналоге; nШ
– число
простых шарниров; nС
– число
стержней;
– число
опорных связей;
nП
– число припаек.
При
расчете фермы можно использовать формулу
W
= 2nУ
– nC
–
,
где
nУ
– число
узлов фермы (узлом считается любой
шарнир, связывающий стержни фермы).
После
расчета по этим формулам возможны три
случая:
1) W>0
– такая система геометрически изменяема
и является механизмом;
2) W=0
– в
системе имеется достаточное число
связей; если они введены правильно, то
система неизменяема и статически
определима;
3) W<0 – в
системе есть избыточные связи. Если эти
связи введены правильно, то система
неизменяема и статически определима.
Отсюда
следует, что расчетная схема сооружения
должна удовлетворять необходимому
условию геометрической неизменяемости
W
0.
В
качестве примера рассмотрим три расчетные
схемы (рис. 2.6 а, в, д) и их дисковые
аналоги (рис. 2.6 б, г, е, ж).
Рис.
2.6
Вычислим
число степеней свободы этих систем:
1)
арка (рис. 2.6 а): nД=2,
nШ=1,
nC=0,
=4,
nП=0;
W=32
– 21
– 0 – 4 –30
=0;
2)
рама (рис. 2.6 в): nД=3,
nШ=3,
nC=0,
=3,
nП=0;
W=33
– 23
– 0 – 3 –30
=0.
3)
ферма (рис. 2.6 д):
– по
дисковому аналогу (рис. 2.6 е): nД=6,
nШ=7,
nC=0,
=4,
nП=0;
W
= 36
– 27
– 0 – 4 –30
= 0;
– по
дисковому аналогу (рис. 2.6 ж): nД=2,
nШ=1,
nC=1,
=3,
nП=0;
W
= 32
– 21
– 1 – 3 –30
= 0;
– по
формуле для фермы (рис. 2.6 д): nУ=4,
nС=5,
=3;
W
= 24
– 5 – 3 = 0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание книги
Предыдующая страница
§1. Описание положения тела в пространстве
1.6 Число степеней свободы тела
Теперь, после того как мы изучили несколько моделей тел, можно окончательно и корректно сформулировать ответ на вопрос: «Что означает задать, определить положение тела?» — Указать численной значение координат некоторых точек тела так, чтобы положение всего тела (любой его части) было определено однозначно.
Число независимых координат, которые однозначно определяют положение тела или системы тел в пространстве называется числом степеней свободы.
Число степеней свободы очень важная характеристика описываемой системы, хотя бы потому, что определяет число независимых уравнений, описывающих движение системы.
Подсчитаем число степеней свободы некоторых простых систем.
Материальная точка, по определению, не имеет размеров, поэтому ее положение в пространстве определяется однозначно тремя координатами. Следовательно, число степеней свободы свободно материальной точки равно трем. Если на движение материальной точки накладываются дополнительные условия, то число ее степеней свободы может уменьшиться. Так если точка движется по заданной поверхности, то ее положение определяется двумя независимыми координатами, следовательно, число степеней свободы равно двум; при движении по заданной линии число степеней свободы уменьшается до одной. Подчеркнем, это не значит, что при движении по заданной линии может изменяться только одна и — могут изменяться все три, но положение точки на заданной линии определяется одной координатой, и если она известна, то могут быть определены и две других. Тем не менее, описание положения точки на заданной линии с помощью одной координаты оказывается не всегда удобным. Ценность рассмотренных нами декартовых координат в том, что они позволяют установить физические законы, описывающее движение вдоль всех прямых (все прямые одинаковы!). В то же время, для описания изменения координат на произвольной линии пришлось бы записывать свои законы для каждой линии — окружности, параболы, синусоиды и т.д. Поэтому часто одномерное движение вдоль известной линии описывают с помощью двух или трех координат. Однако и в этом случае число степеней свободы остается равным единице.
Если механическая система может быть промоделирована как N материальных точек, движущихся в пространстве, то, очевидно, полное число ее степеней свободы равняется 3N. Но если на движение этих материальных точек накладываются дополнительные ограничения, то число степеней свободы уменьшается.
Рассмотрим, как можно описать положение в пространстве двух материальных точек жестко связанных между собой (что-то похожее на гантели). Две точки имеют шесть степеней свободы, которые могут быть описаны шестью координатами — x1, y1, z1, x2, y2, z2, но так как расстояние между точками неизменно, то на эти координаты накладывается условие
(~(x_1 — x_2)^2 + (y_1 — y_2)^2 + (z_1 — z_2)^2 = l^2) ,
где l — расстояние между точками, поэтому число независимых координат, или число степеней свободы равно пяти.
Таким образом, число степеней свободы системы, состоящей из N материальных точек равно 3N минус число дополнительных условий (связей), накладываемых на движение этих точек.
Число степеней свободы может быть подсчитано и другим способом. Обратим внимание, что точное определение координат уменьшает «подвижность» точки (или системы точек). Так, например, если для материальной точки задана координата z, то точка может двигаться только в плоскости перпендикулярной оси Z, задание еще одно координаты (скажем y), приводит к тому, что точка может двигаться только вдоль прямой параллельной оси X. Поэтому число степеней свободы можно находить, подсчитывая, сколько независимых координат необходимо определить, чтобы жестко «закрепить» тело. С помощью такого подхода найдем число степеней свободы системы, состоящей из двух жестко связанных точек. Задавая три координаты одной точки, мы ее как бы закрепляем, тогда вторая точка сможет двигаться так, что бы ее расстояние до первой оставалось неизменным, то есть по поверхности сферы радиуса l. Понятно, что если определено положение двух точек твердого тонкого стержня, то задано и положение всего стержня, поэтому тонкий стержень имеет пять степеней свободы.
Посчитаем число степеней свободы свободно движущегося абсолютно твердого тела. Выберем внутри тела три произвольных точки A, B, C, не лежащих на одной прямой. (рис 5). Положение одной точки A, определяется тремя координатами, если задано положение точки A, то положение точки B может быть описано двумя координатами. Наконец, при «закрепленных» точках A и B, тело может только вращаться вокруг оси, проходящей через эти точки. Следовательно, точка C имеет одну степень свободы. Таким образом, абсолютно твердое тело имеет шесть степеней свободы.
Как мы уже отмечали, для описания положения точки можно использовать разные системы координат, аналогично, положение твердого тела также может быть описано различными способами, только число независимых координат во всех способах описания будет одним и тем же равным числу степеней свободы. Так во многих случаях, положение твердого тела, описывают, задавая три декартовые координаты одной из его точек (чаще центра), и три угла, определяющие его ориентацию.
Следующая страница
From Wikipedia, the free encyclopedia
This article is about mechanics. For other fields, see Degrees of freedom.
In physics, the degrees of freedom (DOF) of a mechanical system is the number of independent parameters that define its configuration or state. It is important in the analysis of systems of bodies in mechanical engineering, structural engineering, aerospace engineering, robotics, and other fields.
The position of a single railcar (engine) moving along a track has one degree of freedom because the position of the car is defined by the distance along the track. A train of rigid cars connected by hinges to an engine still has only one degree of freedom because the positions of the cars behind the engine are constrained by the shape of the track.
An automobile with highly stiff suspension can be considered to be a rigid body traveling on a plane (a flat, two-dimensional space). This body has three independent degrees of freedom consisting of two components of translation and one angle of rotation. Skidding or drifting is a good example of an automobile’s three independent degrees of freedom.
The position and orientation of a rigid body in space is defined by three components of translation and three components of rotation, which means that it has six degrees of freedom.
The exact constraint mechanical design method manages the degrees of freedom to neither underconstrain nor overconstrain a device.[1]
Motions and dimensions[edit]
The position of an n-dimensional rigid body is defined by the rigid transformation, [T] = [A, d], where d is an n-dimensional translation and A is an n × n rotation matrix, which has n translational degrees of freedom and n(n − 1)/2 rotational degrees of freedom. The number of rotational degrees of freedom comes from the dimension of the rotation group SO(n).
A non-rigid or deformable body may be thought of as a collection of many minute particles (infinite number of DOFs), this is often approximated by a finite DOF system. When motion involving large displacements is the main objective of study (e.g. for analyzing the motion of satellites), a deformable body may be approximated as a rigid body (or even a particle) in order to simplify the analysis.
The degree of freedom of a system can be viewed as the minimum number of coordinates required to specify a configuration. Applying this definition, we have:
- For a single particle in a plane two coordinates define its location so it has two degrees of freedom;
- A single particle in space requires three coordinates so it has three degrees of freedom;
- Two particles in space have a combined six degrees of freedom;
- If two particles in space are constrained to maintain a constant distance from each other, such as in the case of a diatomic molecule, then the six coordinates must satisfy a single constraint equation defined by the distance formula. This reduces the degree of freedom of the system to five, because the distance formula can be used to solve for the remaining coordinate once the other five are specified.
Rigid bodies[edit]
The six degrees of freedom of movement of a ship
Attitude degrees of freedom for an airplane
Mnemonics to remember angle names
A single rigid body has at most six degrees of freedom (6 DOF) 3T3R consisting of three translations 3T and three rotations 3R.
See also Euler angles.
For example, the motion of a ship at sea has the six degrees of freedom of a rigid body, and is described as:[2]
- Translation and rotation:
- Walking (or surging): Moving forward and backward;
- Strafing (or swaying): Moving left and right;
- Elevating (or heaving): Moving up and down;
- Roll rotation: Pivots side to side;
- Pitch rotation: Tilts forward and backward;
- Yaw rotation: Swivels left and right;
For example, the trajectory of an airplane in flight has three degrees of freedom and its attitude along the trajectory has three degrees of freedom, for a total of six degrees of freedom.
- For rolling in flight and ship dynamics, see roll (aviation) and roll (ship motion), respectively.
- An important derivative is the roll rate (or roll velocity), which is the angular speed at which an aircraft can change its roll attitude, and is typically expressed in degrees per second.
- For pitching in flight and ship dynamics, see pitch (aviation) and pitch (ship motion), respectively.
- For yawing in flight and ship dynamics, see yaw (aviation) and yaw (ship motion), respectively.
- One important derivative is the yaw rate (or yaw velocity), the angular speed of yaw rotation, measured with a yaw rate sensor.
- Another important derivative is the yawing moment, the angular momentum of a yaw rotation, which is important for adverse yaw in aircraft dynamics.
Lower mobility[edit]
Physical constraints may limit the number of degrees of freedom of a single rigid body. For example, a block sliding around on a flat table has 3 DOF 2T1R consisting of two translations 2T and 1 rotation 1R. An XYZ positioning robot like SCARA has 3 DOF 3T lower mobility.
Mobility formula[edit]
The mobility formula counts the number of parameters that define the configuration of a set of rigid bodies that are constrained by joints connecting these bodies.[3][4]
Consider a system of n rigid bodies moving in space has 6n degrees of freedom measured relative to a fixed frame. In order to count the degrees of freedom of this system, include the fixed body in the count of bodies, so that mobility is independent of the choice of the body that forms the fixed frame. Then the degree-of-freedom of the unconstrained system of N = n + 1 is
because the fixed body has zero degrees of freedom relative to itself.
Joints that connect bodies in this system remove degrees of freedom and reduce mobility. Specifically, hinges and sliders each impose five constraints and therefore remove five degrees of freedom. It is convenient to define the number of constraints c that a joint imposes in terms of the joint’s freedom f, where c = 6 − f. In the case of a hinge or slider, which are one degree of freedom joints, have f = 1 and therefore c = 6 − 1 = 5.
The result is that the mobility of a system formed from n moving links and j joints each with freedom fi, i = 1, …, j, is given by
Recall that N includes the fixed link.
There are two important special cases: (i) a simple open chain, and (ii) a simple closed chain.
A single open chain consists of n moving links connected end to end by n joints, with one end connected to a ground link. Thus, in this case N = j + 1 and the mobility of the chain is
For a simple closed chain, n moving links are connected end-to-end by n + 1 joints such that the two ends are connected to the ground link forming a loop. In this case, we have N = j and the mobility of the chain is
An example of a simple open chain is a serial robot manipulator. These robotic systems are constructed from a series of links connected by six one degree-of-freedom revolute or prismatic joints, so the system has six degrees of freedom.
An example of a simple closed chain is the RSSR spatial four-bar linkage. The sum of the freedom of these joints is eight, so the mobility of the linkage is two, where one of the degrees of freedom is the rotation of the coupler around the line joining the two S joints.
Planar and spherical movement[edit]
It is common practice to design the linkage system so that the movement of all of the bodies are constrained to lie on parallel planes, to form what is known as a planar linkage. It is also possible to construct the linkage system so that all of the bodies move on concentric spheres, forming a spherical linkage. In both cases, the degrees of freedom of the links in each system is now three rather than six, and the constraints imposed by joints are now c = 3 − f.
In this case, the mobility formula is given by
and the special cases become
- planar or spherical simple open chain,
- planar or spherical simple closed chain,
An example of a planar simple closed chain is the planar four-bar linkage, which is a four-bar loop with four one degree-of-freedom joints and therefore has mobility M = 1.
Systems of bodies[edit]
A system with several bodies would have a combined DOF that is the sum of the DOFs of the bodies, less the internal constraints they may have on relative motion. A mechanism or linkage containing a number of connected rigid bodies may have more than the degrees of freedom for a single rigid body. Here the term degrees of freedom is used to describe the number of parameters needed to specify the spatial pose of a linkage. It is also defined in context of the configuration space, task space and workspace of a robot.
A specific type of linkage is the open kinematic chain, where a set of rigid links are connected at joints; a joint may provide one DOF (hinge/sliding), or two (cylindrical). Such chains occur commonly in robotics, biomechanics, and for satellites and other space structures. A human arm is considered to have seven DOFs. A shoulder gives pitch,yaw, and roll, an elbow allows for pitch, and a wrist allows for pitch, yaw and roll. Only 3 of those movements would be necessary to move the hand to any point in space, but people would lack the ability to grasp things from different angles or directions. A robot (or object) that has mechanisms to control all 6 physical DOF is said to be holonomic. An object with fewer controllable DOFs than total DOFs is said to be non-holonomic, and an object with more controllable DOFs than total DOFs (such as the human arm) is said to be redundant. Although keep in mind that it is not redundant in the human arm because the two DOFs; wrist and shoulder, that represent the same movement; roll, supply each other since they can’t do a full 360.
The degree of freedom are like different movements that can be made.
In mobile robotics, a car-like robot can reach any position and orientation in 2-D space, so it needs 3 DOFs to describe its pose, but at any point, you can move it only by a forward motion and a steering angle. So it has two control DOFs and three representational DOFs; i.e. it is non-holonomic. A fixed-wing aircraft, with 3–4 control DOFs (forward motion, roll, pitch, and to a limited extent, yaw) in a 3-D space, is also non-holonomic, as it cannot move directly up/down or left/right.
A summary of formulas and methods for computing the degrees-of-freedom in mechanical systems has been given by Pennestri, Cavacece, and Vita.[5]
Electrical engineering[edit]
In electrical engineering degrees of freedom is often used to describe the number of directions in which a phased array antenna can form either beams or nulls. It is equal to one less than the number of elements contained in the array, as one element is used as a reference against which either constructive or destructive interference may be applied using each of the remaining antenna elements. Radar practice and communication link practice, with beam steering being more prevalent for radar applications and null steering being more prevalent for interference suppression in communication links.
See also[edit]
- Gimbal lock – Loss of one degree of freedom in a three-dimensional, three-gimbal mechanism
- Kinematics – Branch of physics describing the motion of objects without considering forces
- Kinematic pair – Connection between two physical objects which constrains their relative movement
- XR-2 – Educational robot
References[edit]
- ^ Hale, Layton C. (1999). Principles and techniques for designing precision machines (PDF) (PhD). Massachusetts Institute of Technology.
- ^ Summary of ship movement Archived November 25, 2011, at the Wayback Machine
- ^ J. J. Uicker, G. R. Pennock, and J. E. Shigley, 2003, Theory of Machines and Mechanisms, Oxford University Press, New York.
- ^ J. M. McCarthy and G. S. Soh, Geometric Design of Linkages, 2nd Edition, Springer 2010
- ^ Pennestrı̀, E.; Cavacece, M.; Vita, L. (2005). «On the Computation of Degrees-of-Freedom: A Didactic Perspective». Volume 6: 5th International Conference on Multibody Systems, Nonlinear Dynamics, and Control, Parts A, B, and C. 2005 ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. California, US. pp. 1733–1741. doi:10.1115/DETC2005-84109. ISBN 0-7918-4743-8.
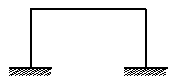
Степенью свободы системы твердых тел называется число независимых геометрических параметров полностью определяющих положение системы, например.
W=3×3 – 3×1 – 2×1 – 4 =0
Рис. 1.26 – Определение степени свободы
W=3D – 2Ш – 3П – С,
где
W − количество степеней свободы,
D − количество простейших дисков,
Ш − количество простых шарниров,
П − количество простых припаек,
С − количество опорных стержней.
Перейдем к классификации систем по величинам их степеней свободы.
1) W > 0 − система изменяема (механизм).
Непосредственно ее использование возможно лишь после добавления W связей.
Рис. 1.27 – Система, являющаяся механизмом
2) W = 0 − система при разумной расстановке связей может быть неизменяемой. Необходим дополнительно структурный анализ.
Рис. 1.28 – Геометрически неизменяемая система
3) W < 0 − система имеет лишние связи (говорят, что она статически неопределима) и при разумной расстановке этих связей может быть неизменяемой. Здесь также необходим структурный анализ.
Рис. 1.29 – Система, имеющая лишние связи
Для проведения структурного анализа необходимо ознакомиться с основными принципами образования неизменяемых и мгновенно изменяемых систем.
Неизменяемые и мгновенно изменяемые системы >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее