Как найти число углов выпуклого многоугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Углы многоугольника

Сумма внутренних углов
Сумма внешних углов

Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.

Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.

s = 2d(n — 2),

где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.

Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:

s = 2d(n — 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).

s = 4d,

где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:

Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):

s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.

Источник

Теорема

(о сумме углов выпуклого многоугольника)

Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).

(n — количество сторон многоугольника).

Другой вариант формулировки этой теоремы:

Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).

Дано:

$[{A_1}{A_2}{A_3}...{A_{n - 1}}{A_n}]$

— выпуклый n -угольник.

Доказать:

$[angle {A_1} + angle {A_2} + angle {A_3} + ... + angle {A_{n - 1}} + angle {A_n} = ]$

$[ = {180^o}(n - 2)]$

Доказательство:

1-й способ

Обозначим внутри многоугольника произвольную точку O.

Соединим точку O с вершинами многоугольника.

Получили n треугольников.

$[angle {A_1} + angle {A_2} + angle {A_3} + ... + angle {A_{n - 1}} + angle {A_n} = ]$

$[ = angle O{A_1}{A_2} + angle O{A_2}{A_1} + ... + ]$

$[ + angle O{A_{n - 1}}{A_n} + angle O{A_n}{A_{n - 1}}.]$

Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.

Так как сумма углов при вершине O составляет 360º

$[angle {A_1}O{A_2} + angle {A_2}O{A_3} + ... + angle {A_{n - 1}}O{A_n} = {360^o},]$

то сумма углов многоугольника равна сумме углов n треугольников минус 360º.

Сумма углов каждого треугольника равна 180º.

Таким образом, искомая сумма углов n угольника равна

$[angle {A_1} + angle {A_2} + angle {A_3} + ... + angle {A_{n - 1}} + angle {A_n} = ]$

$[ = {180^o} cdot n - {360^o} = {180^o}(n - 2).]$

Что и требовалось доказать.

2-й способ

Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.

Сумма всех углов этих треугольников равна сумме углов многоугольника.

Сумма углов углов каждого из треугольников равна 180º.

Следовательно, сумма углов многоугольника

$[angle {A_1} + angle {A_2} + angle {A_3} + ... + angle {A_{n - 1}} + angle {A_n} = ]$

$[ = {180^o}(n - 2).]$

Что и требовалось доказать.

Источник

Примечание. Данный материал содержит теорему и ее доказательство, а также ряд задач, иллюстрирующих применение теоремы о сумме углов выпуклого многоугольника на практических примерах.

Теорема о сумме углов выпуклого многоугольника

Для выпуклого n-угольника сумма углов равна 180°(n-2).

Доказательство.

Для доказательства теоремы о сумме углов выпуклого многоугольника воспользуемся уже доказанной теоремой о том, что сумма углов треугольника равна 180 градусам.

Пусть A 1 A 2… A n – данный выпуклый многоугольник, и n > 3. Проведем все диагонали многоугольника из вершины A 1. Они разбивают его на n – 2 треугольника: Δ A 1 A 2 A 3, Δ A 1 A 3 A 4, … , Δ A 1 A n – 1 A n . Сумма углов многоугольника совпадает с суммой углов всех этих треугольников. Сумма углов каждого треугольника равна 180°, а число треугольников – ( n – 2). Поэтому сумма углов выпуклого n -угольника A 1 A 2… A n равна 180° ( n – 2).

Задача.

В выпуклом многоугольнике три угла по 80 градусов, а остальные — 150 градусов. Сколько углов в выпуклом многоугольнике?

Решение.

Для решения данной задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма углов равна 180°(n-2).

Значит, для нашего случая:

180(n-2)=3*80+x*150, где

3 угла по 80 градусов нам даны по условию задачи, а количество остальных углов нам пока неизвестно, значит обозначим их количество как x.

Однако, из записи в левой части мы определили количество углов многоугольника как n, поскольку из них величины трех углов мы знаем по условию задачи, то очевидно, что x=n-3.

Таким образом уравнение будет выглядеть так:

180(n-2)=240+150(n-3)

Решаем полученное уравнение

180n — 360 = 240 + 150n — 450

180n — 150n = 240 + 360 — 450

30n = 150

n=5

Ответ: 5 вершин

Задача.

Какое количество вершин может иметь многоугольник, если величина каждого из углов менее 120 градусов?

Решение.

Для решения данной задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма всех углов равна 180°(n-2).

Значит, для нашего случая необходимо сначала оценить граничные условия задачи. То есть, сделать допущение, что каждый из углов равен 120 градусам. Получаем:

180(n-2)=120n

180n — 360 = 120n

180n — 120n = 360 (это выражение рассмотрим отдельно ниже)

60n = 360

n=6

Исходя из полученного уравнения, делаем вывод: при величине углов менее 120 градусов, количество углов многоугольника менее шести.

Объяснение:

Исходя из выражения 180n — 120n = 360 , при условии, что вычитаемое правой части будет менее 120n, разность должна быть более 60n. Таким образом, частное от деления всегда будет менее шести.

Ответ: количество вершин многоугольника будет менее шести.

Задача

В многоугольнике три угла по 113 градусов, а остальные равны между собой и их градусная мера — целое число. Найти количество вершин многоугольника.

Решение.

Для решения данной задачи воспользуемся теоремой о сумме внешних углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма всех внешних углов равна 360°.

Таким образом,

3*(180-113)+(n-3)x=360

правая часть выражения — сумма внешних углов, в левой части сумма трех углов известна по условию, а градусная мера остальных (их количество, соответственно n-3, так как три угла известны) обозначена как x.

201+(n-3)x=360

(n-3)x=159

159 раскладывается только на два множителя 53 и 3, при чем 53 — простое число. То есть других пар множителей не существует.

Таким образом, n-3 = 3, n=6, то есть количество углов многоугольника — шесть.

Ответ: шесть углов

Задача

Докажите, что у выпуклого многоугольника может быть не более трех острых углов.

Решение

Как известно, сумма внешних углов выпуклого многоугольника равна 360⁰. Проведем доказательство от противного. Если у выпуклого многоугольника не менее четырех острых внутренних углов, следовательно среди его внешних углов не менее четырех тупых, откуда следует, что сумма всех внешних углов многоугольника больше 4*90⁰ = 360⁰. Имеем противоречие. Утверждение доказано.

Шестиугольник и его свойства |

Описание курса

| Стереометрия

Источник

Чему равна сумма углов выпуклого многоугольника

Воскресенье, 19 февраля, 2017

В 8 классе на уроках геометрии в школе ученики впервые знакомятся с понятием выпуклого многоугольника. Очень скоро они узнают, что эта фигура обладает очень интересным свойством. Какой бы сложной она ни была, сумма всех внутренних и внешних углов выпуклого многоугольника принимает строго определенное значение. В данной статье репетитор по математике и физике рассказывает о том, чему равна сумма углов выпуклого многоугольника.

Сумма внутренних углов выпуклого многоугольника

Как доказать эту формулу?

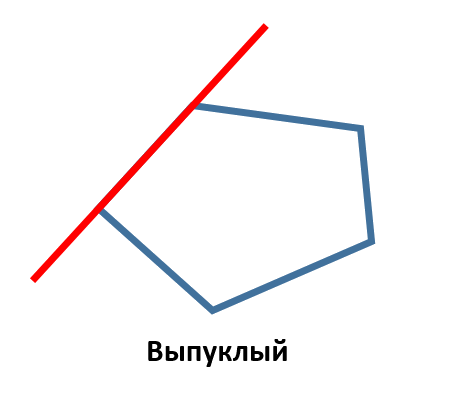
Прежде чем перейти к доказательству этого утверждения, вспомним, какой многоугольник называется выпуклым. Выпуклым называется такой многоугольник, который целиком находится по одну сторону от прямой, содержащей любую его сторону. Например такой, который изображен на этом рисунке:

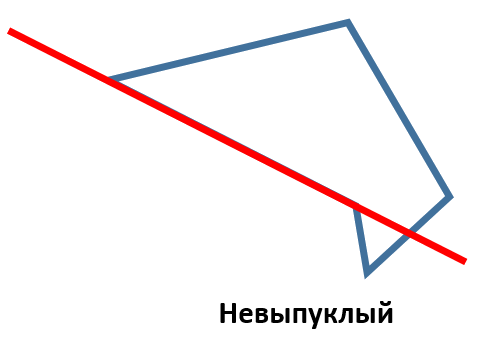
Если же многоугольник не удовлетворяет указанному условию, то он называется невыпуклым. Например, такой:

Сумма внутренних углов выпуклого многоугольника равна $180^{circ}(n-2)$ , где — количество сторон многоугольника.

Доказательство этого факта основано на хорошо известной всем школьникам теореме о сумме углов в треугольнике. Уверен, что и вам эта теорема знакома. Сумма внутренних углов треугольника равна $180^{circ}$ .

Идея состоит в том, чтобы разбить выпуклый многоугольник на несколько треугольников. Сделать это можно разными способами. В зависимости от того, какой способ мы выберем, доказательства будут немного отличаться.

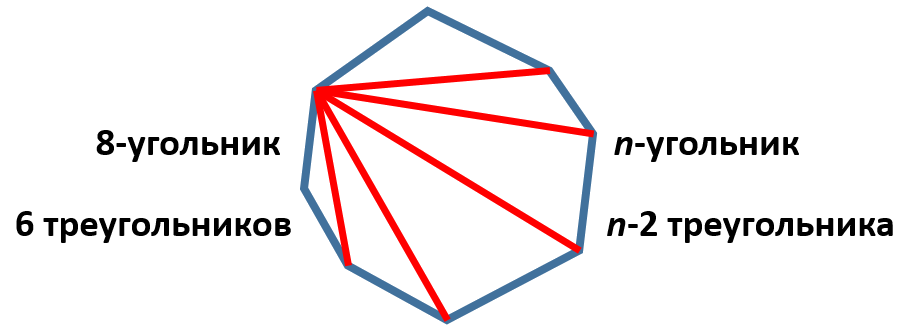
1. Разобьём выпуклый многоугольник на треугольники всеми возможными диагоналями, проведёнными из какой-нибудь вершины. Легко понять, что тогда наш n-угольник разобьётся на треугольника:

Причём сумма всех углов всех получившихся треугольников равна сумме углов нашего n-угольника. Ведь каждый угол в получившихся треугольниках является частичной какого-то угла в нашем выпуклом многоугольнике. То есть искомая сумма равна $180^{circ}(n-2)$ .

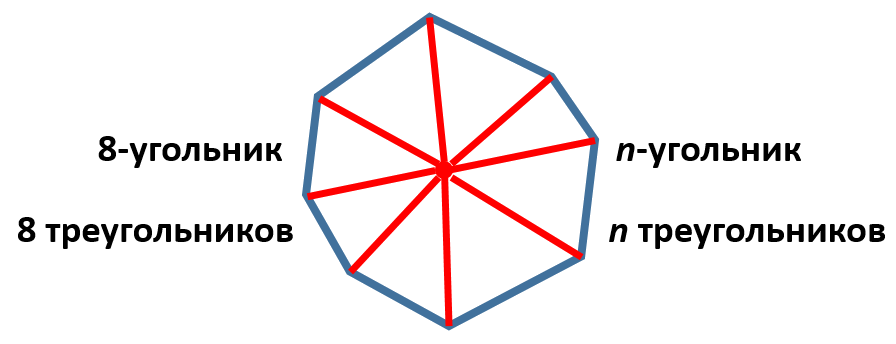
2. Можно также выбрать точку внутри выпуклого многоугольника и соединить её со всеми вершинами. Тогда наш n-угольник разобьется на треугольников:

Причём сумма углов нашего многоугольника в этом случае будет равна сумме всех углов всех этих треугольников за вычетом центрального угла, который равен $360^{circ}$ . То есть искомая сумма опять же равна $180^{circ}n-360^{circ}=180^{circ}(n-2)$ .

Сумма внешних углов выпуклого многоугольника

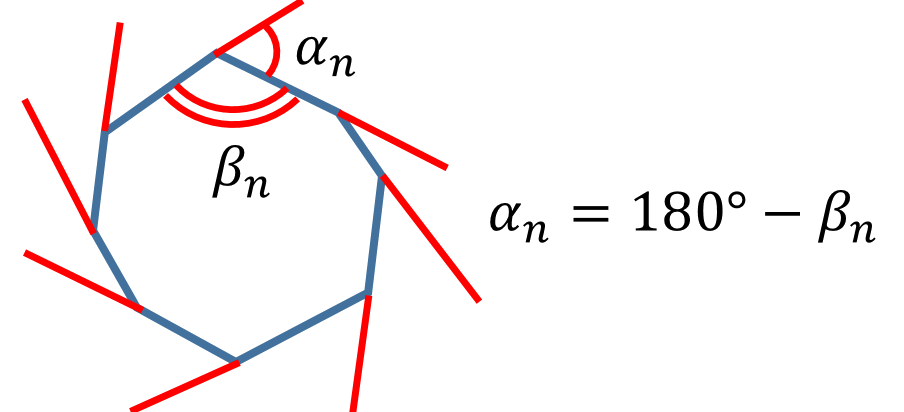
Зададимся теперь вопросом: «Чему равна сумма внешних углов выпуклого многоугольника?» Ответить на этот вопрос можно следующим образом. Каждый внешний угол является смежным с соответствующим внутренним. Поэтому он равен $alpha_n=180^{circ}-beta_n$ :

Тогда сумма всех внешних углов равна $180^{circ}n-180^{circ}(n-2)$ . То есть она равна $360^{circ}$ .

То есть получается весьма забавный результат. Если отложить последовательно друг за другом все внешние углы любого выпуклого n-угольника, то в результате заполнится ровно вся плоскости.

Этот интересный факт можно проиллюстрировать следующим образом. Давайте пропорциональном уменьшать все стороны какого-нибудь выпуклого многоугольника до тех пор, пока он не сольётся в точку. После того, как это произойдёт, все внешние углы окажутся отложенными один от другого и заполнят таким образом всю плоскость.

Интересный факт, не правда ли? И таких фактов в геометрии очень много. Так что учите геометрию, дорогие школьники!

Материал о том, чему равна сумма углов выпуклого многоугольника, подготовил репетитор по геометрии, Сергей Валерьевич

Источник

Данная формула понимается проще всего если двигаться поочередно с минимально возможного. Хотя в учебном курсе для более строго доказательства делают наоборот. Многоугольник начинают разбивать на треугольники и считать их количество и доказывать что их будет определенное количество и ученикам непонятно — «откуда ноги растут»

Итак поехали: Наименьшее число углов у многоугольника — 3. Меньше нельзя. Сумму углов треугольника знаем = 180˚. То есть при 3 углах — 1-й шаг. Далее с каждым шагом будем прибавлять вершину(угол). То есть получается 4 угла на 2 шаге; 5 углов на 3 шаге и т.д. n-углов на «n-2» шаге.

Но с каждым шагом добавляя новую вершину, чтоб построить новый многоугольник, мы соединяем её с соседними вершинами, добавляя новый треугольник. То есть с каждым шагом добавляем новый треугольник со 180˚. То есть добавляем по 180˚к сумме углов.

На 1 шаге 180˚; на 2 шаге + еще 180˚, на 3 шаге + еще 180˚ Сколько шагов, столько раз по 180˚. Таким образом получаем, что для n — углов будет «n-2» шага и «n-2» раза по 180˚

Вот и формула нарисовалась:

Сумма углов n-угольника = 180•(n-2)

Тут же проверяем на 3-угольнике: 180•(3-2) = 180

4-угольник: 180•(4-2)=360

и т.д.

Источник