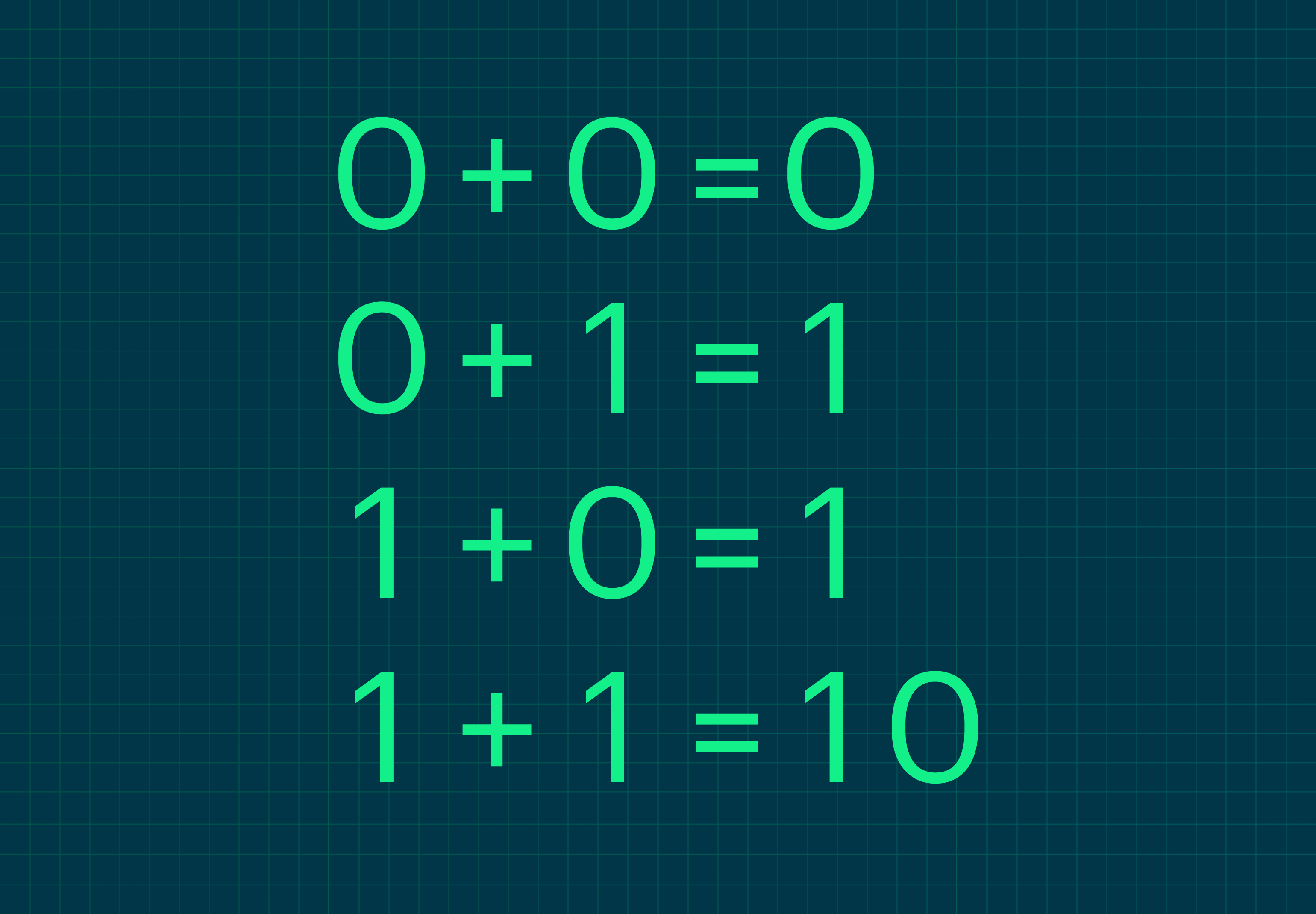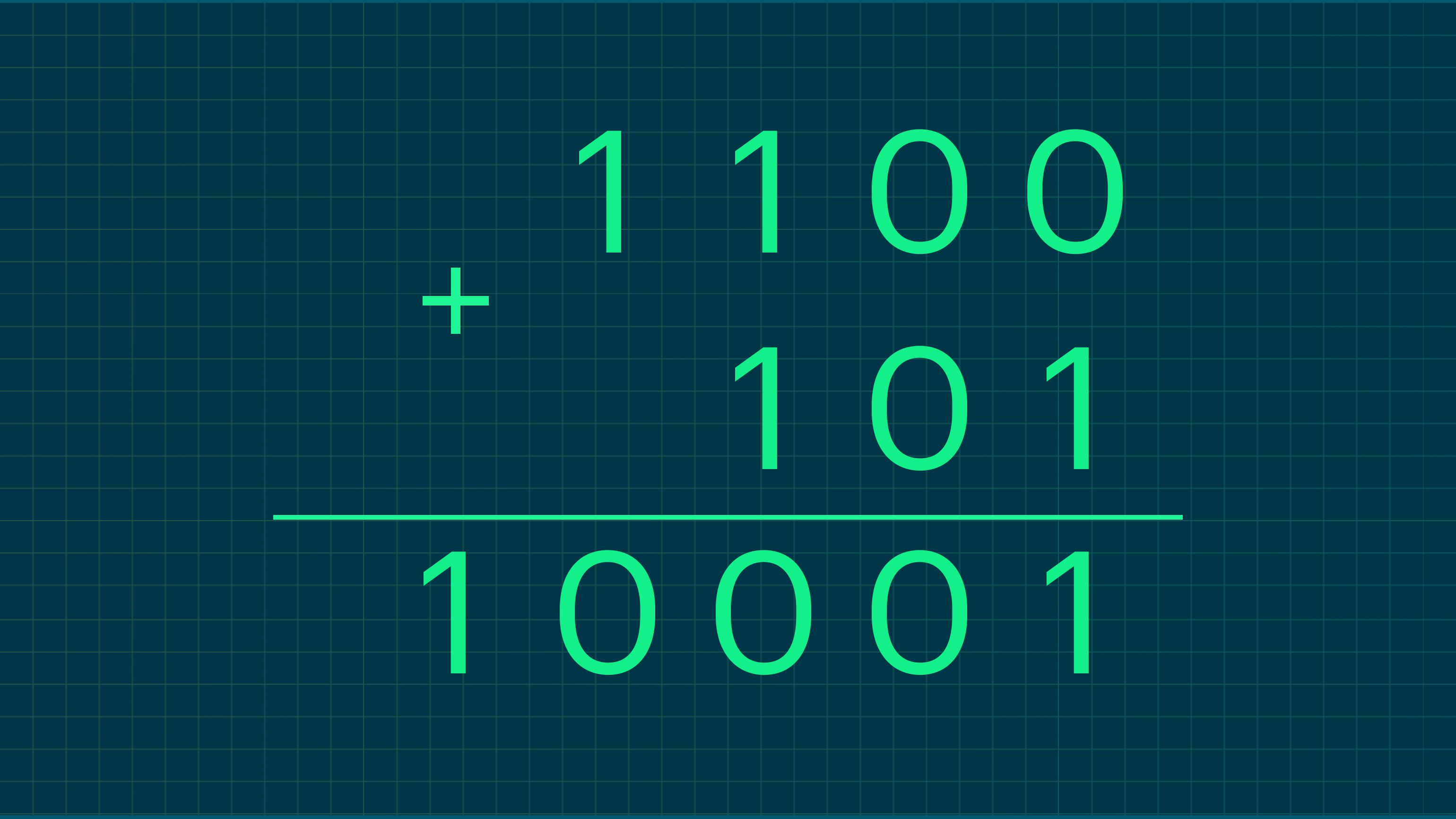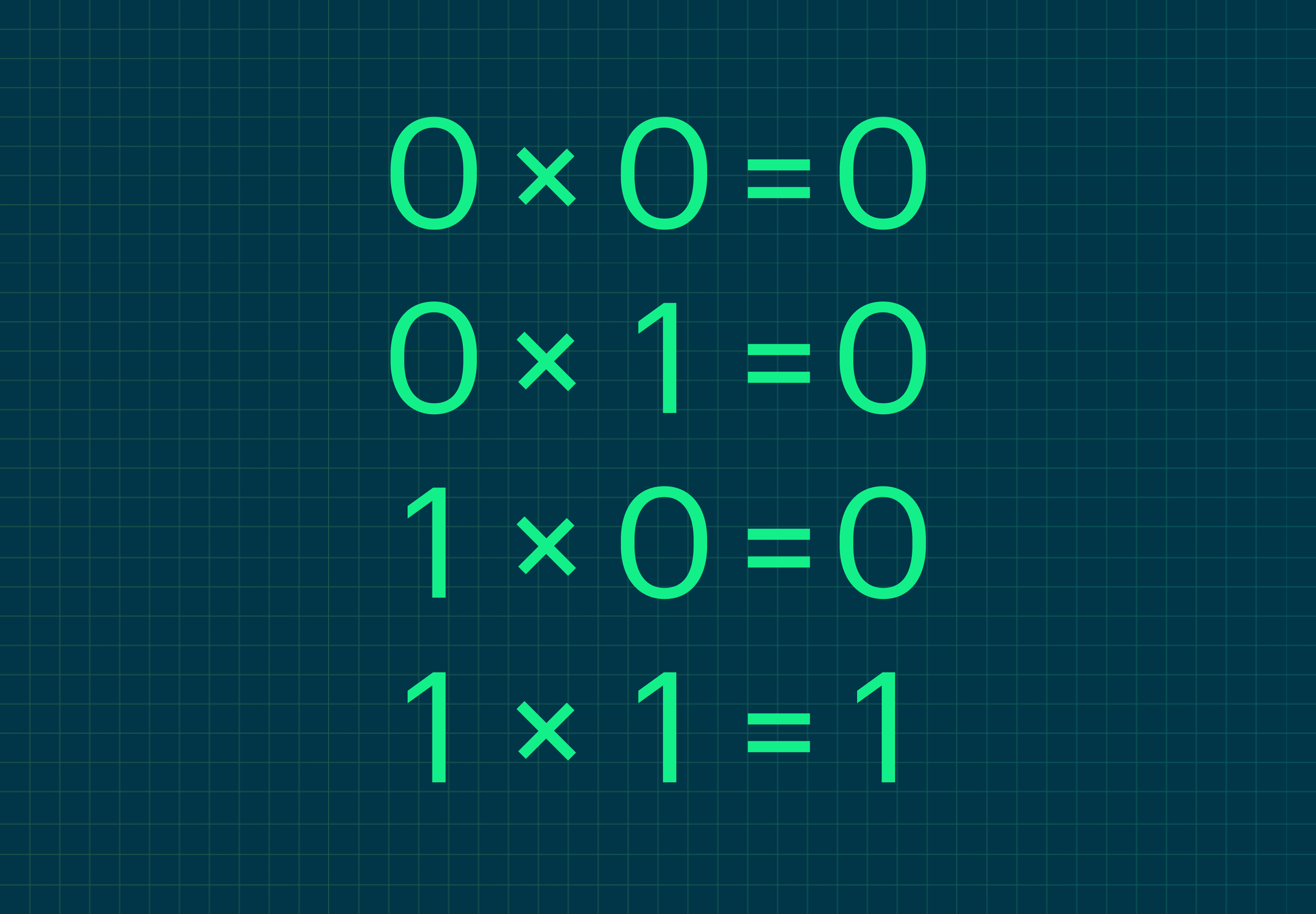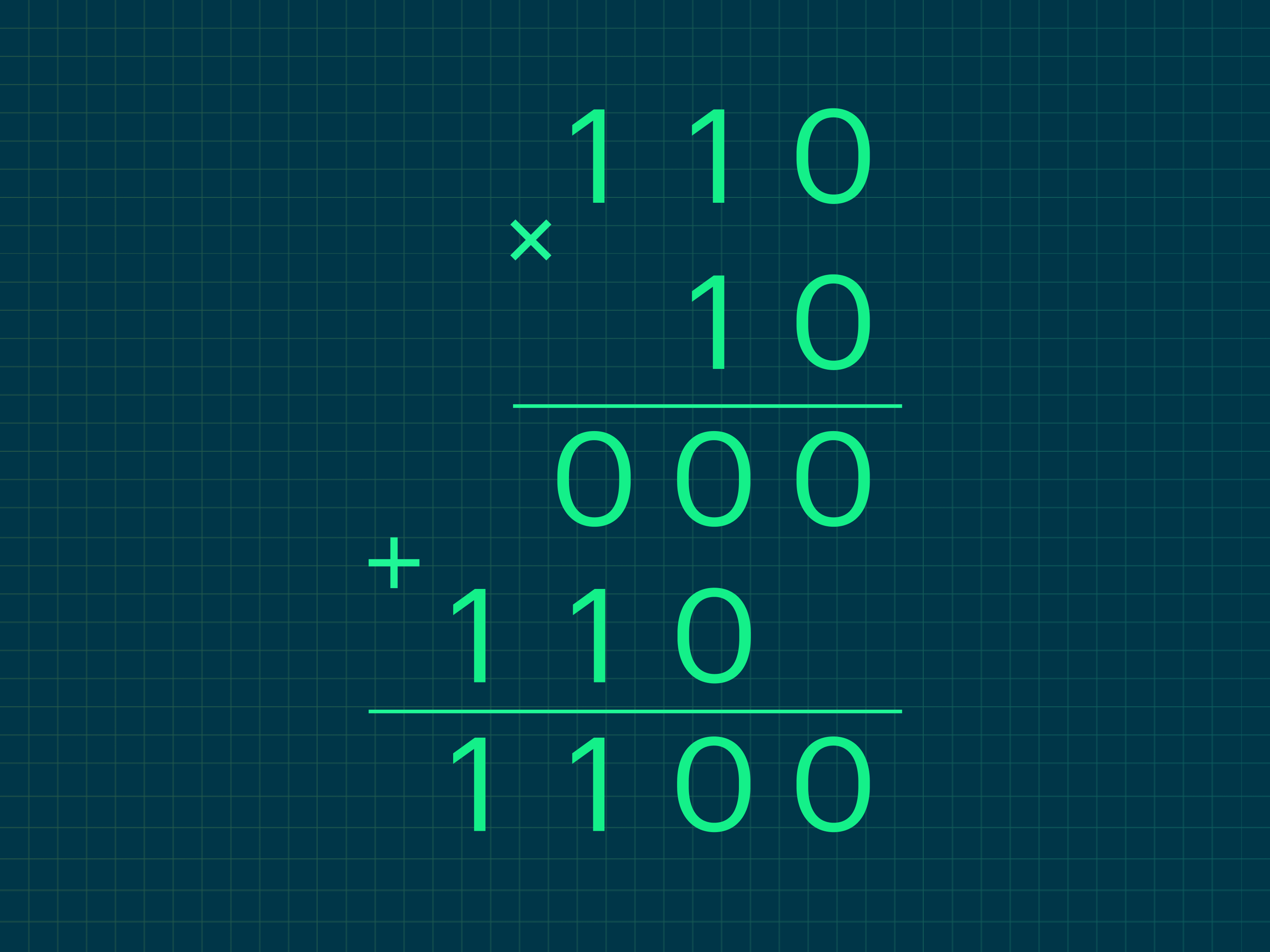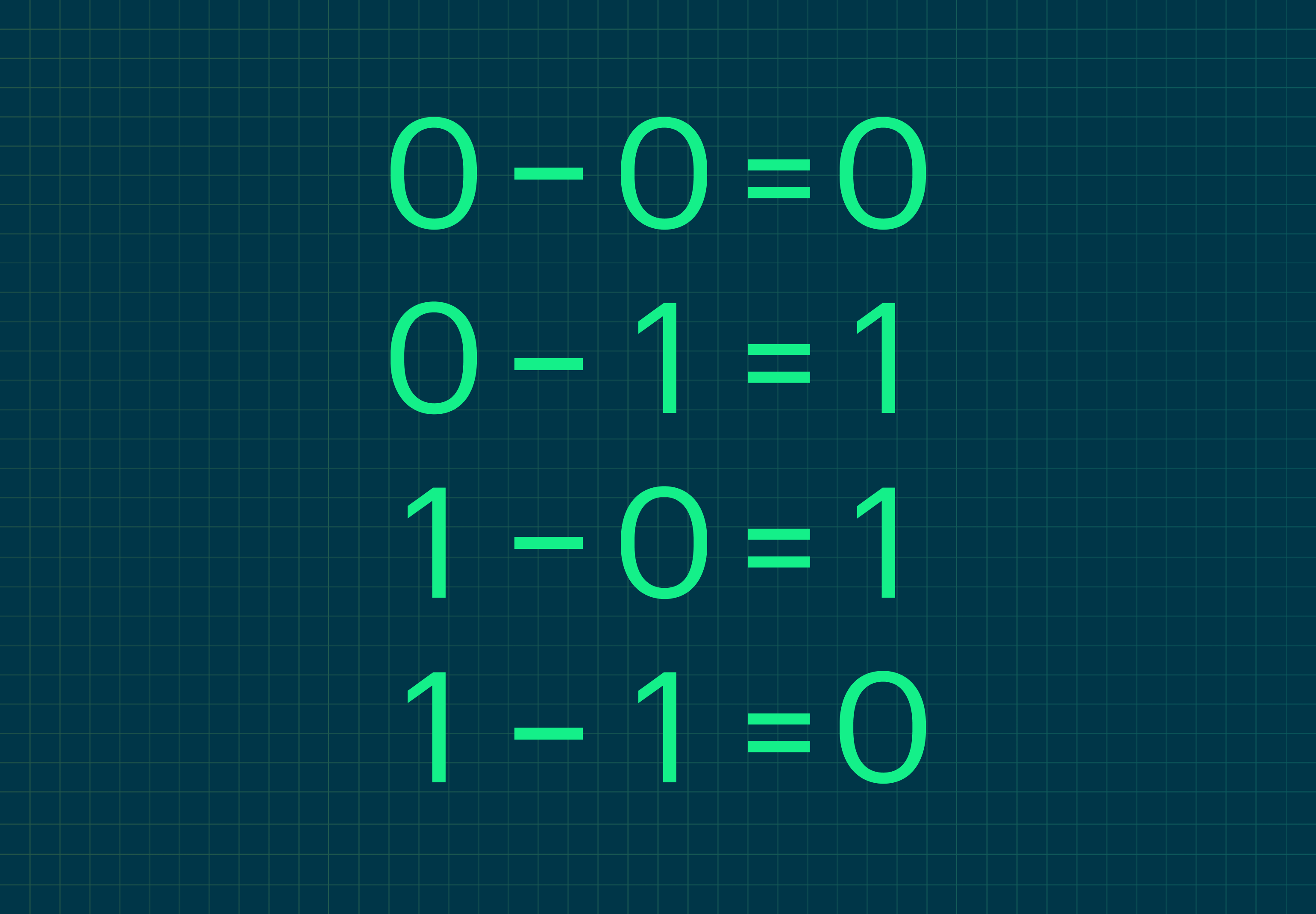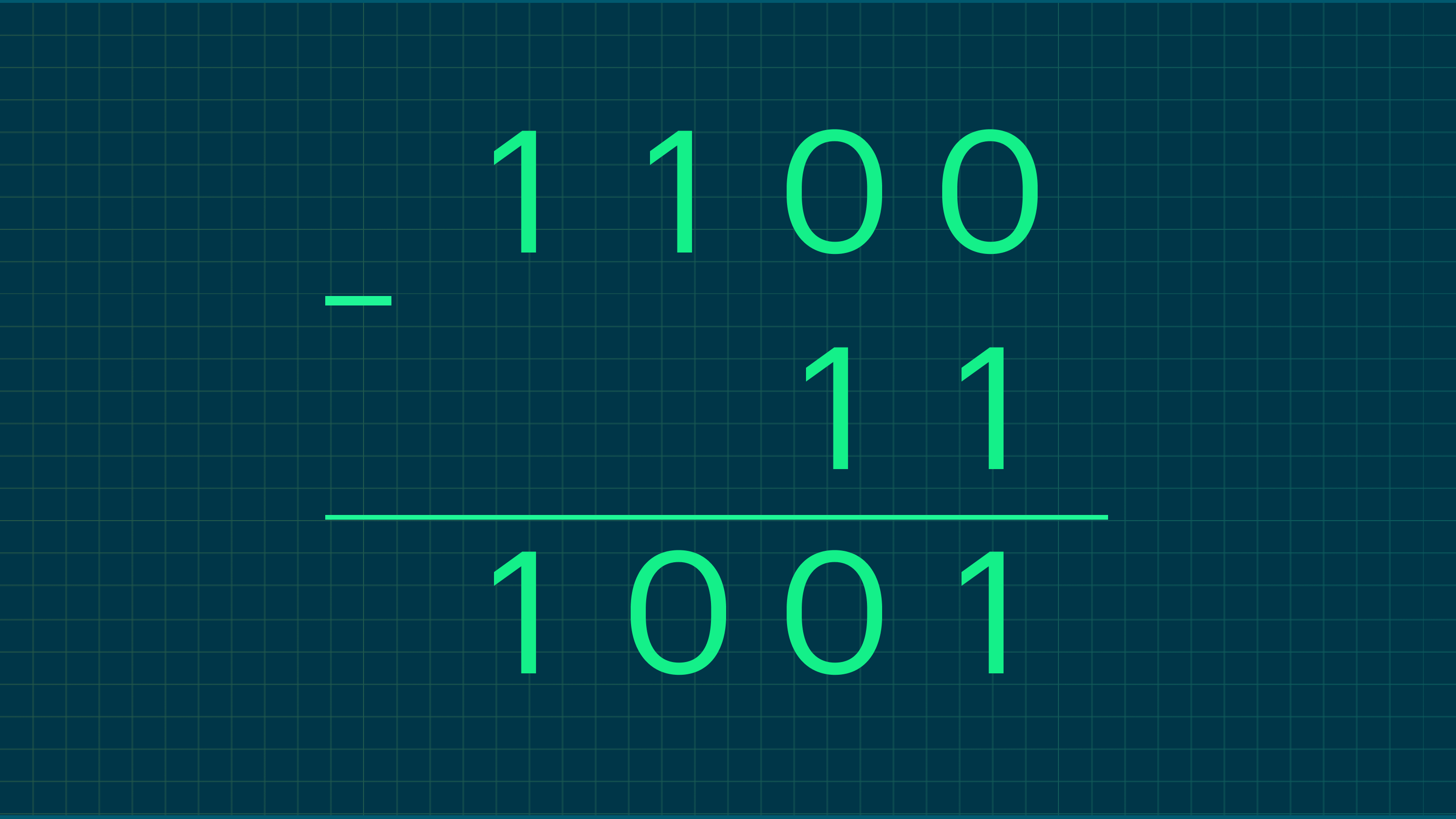Как найти число в двоичной системе счисления - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Из этой статьи вы узнаете, как считать в двоичной системе счисления, которая используется во всех компьютерах. Поначалу это покажется необычным, но если знать всего несколько правил и немного попрактиковаться, можно научиться быстро считать в двоичной системе.

Справочная таблица

Десятичная система	0	1	2	3	4	5	6	7	8	9	10
Двоичная система	0	1	10	11	100	101	110	111	1000	1001	1010

1

Ознакомьтесь с основами двоичной системы. Система счисления, которой мы ежедневно пользуемся, называется десятичной, потому что она включает десять цифр (от 0 до 9). В двоичной системе счисления используются всего две цифры — 0 и 1.
2
Прибавьте единицу, изменив последний 0 на 1. Если двоичное число заканчивается на 0, измените этот 0 на 1, чтобы прибавить к данному числу единицу. Это аналогично сложению первых двух чисел:
- 0 = ноль
- 1 = один
- Если двоичное число состоит из нескольких цифр, учитывайте только последний 0: 1010 + 1 = 1011.
3
Припишите к двоичному числу еще одну цифру, если оно состоит только из единиц. Итак, мы получили 1 для единицы, но цифр больше нет. Чтобы посчитать до двух, напишите еще одну цифру. Припишите 1 слева от двоичного числа, а все остальные цифры этого числа сделайте нолями.
- 0 = ноль
- 1 = один
- 10 = два
- Аналогичное правило используется в десятичной системе счисления, когда больше нет цифр, например, 9 + 1 = 10. В двоичной системе такое случается гораздо чаще, потому что в ней используются всего две цифры.
4
Воспользуйтесь описанными правилами, чтобы посчитать до пяти. Попробуйте сделать это самостоятельно, а потом проверьте результат:
- 0 = ноль
- 1 = один
- 10 = два
- 11 = три
- 100 = четыре
- 101 = пять
5
Посчитайте до шести. Теперь необходимо найти результат сложения 5+1 в двоичной системе, а именно сложить двоичные числа 101 + 1. Правило заключается в том, что нужно проигнорировать первую цифру. Таким образом, сложите 1 + 1, чтобы получить 10 (это цифра 2 в двоичной системе). Теперь восстановите первую цифру и получите:
- 110 = шесть
6
Сосчитайте до десяти. Все правила уже описаны; других правил нет. Попробуйте сосчитать до десяти, а потом проверьте результат:
- 110 = шесть
- 111 = семь
- 1000 = восемь
- 1001 = девять
- 1010 = десять
7

Научитесь добавлять новые цифры. Обратите внимание, что десять (1010) не является каким-то особенным числом в двоичной системе. Сейчас нас больше интересует число восемь. Восемь (1000) равно 2 x 2 x 2 (10 х 10 х 10). Умножайте числа на два (10), чтобы находить другие числа, например, шестнадцать (10000) и тридцать два (100000).
8
Попрактикуйтесь в нахождении больших чисел. Теперь вы знаете все правила, необходимые для счета в двоичной системе. Если вы запутались, вспомните, что нужно делать с последними цифрами. Вот несколько примеров:
- Двенадцать плюс один = 1100 + 1 = 1101 = тринадцать (0 + 1 = 1, а остальные цифры не меняются).
- Пятнадцать плюс один = 1111 + 1 = 10000 = шестнадцать (цифр больше нет, поэтому слева от 1111 мы приписываем 1, а все остальные цифры превращаем в ноли).
- Сорок пять плюс один = 101101 + 1 = 101110 = сорок шесть (1 + 1 = 10, а остальные цифры не меняются).
Реклама

1
Запишите разряд каждой цифры двоичного числа. Вспомните, что каждая цифра десятичного числа стоит в определенном разряде: разряде единиц, разряде десяток и так далее. Так как в двоичной системе всего две цифры, каждый разряд умножается на два (если перемещаться по цифрам числа слева направо):
- 1 — это разряд единиц;
- 1 0 — это разряд двоек;
- 1 00 — это разряд четверок;
- 1 000 — это разряд восьмерок.
2
Умножьте каждую цифру двоичного числа на соответствующий разряд. Начните с крайней правой цифры — она стоит в разряде единиц, поэтому ее нужно умножить на 1; на следующей строке умножьте вторую справа цифру на 2; на следующей строке умножьте третью справа цифру на 4 и так далее. Например:
- Преобразуйте двоичное число 10011 в десятичное.
- Первая справа цифра 1. Она находится в разряде единиц. Поэтому умножьте ее на единицу: 1 x 1 = 1.
- Вторая справа цифра тоже 1. Она находится в разряде двоек. Поэтому умножьте ее на два: 1 x 2 = 2.
- Следующая цифра 0. Умножьте ее на четыре: 0 x 4 = 0.
- Следующая цифра тоже 0. Умножьте ее на восемь: 0 x 8 = 0.
- Последняя (справа) цифра 1. Умножьте ее на шестнадцать: 1 x 16 = 16.
3
Сложите полученные результаты. Вы преобразовали каждую цифру двоичного числа в цифру десятичной системы. Чтобы найти десятичное число, сложите все полученные значения. В нашем примере:
- 1 + 2 + 16 = 19.
- Таким образом 10011 (в двоичной системе) = 19 (в десятичной системе).
Реклама

Советы

Также можно научиться считать в двоичной системе на пальцах. Каждый вытянутый палец будет цифрой 1, а каждый согнутый — 0.^[1]

Об этой статье

Эту страницу просматривали 44 982 раза.

Была ли эта статья полезной?

Источник

#статьи

27 фев 2023
0

Двоичная арифметика: сложение, умножение, вычитание, деление бинарных чисел

Учимся складывать, вычитать, умножать и делить двоичные числа — работаем с фундаментальными законами современной цифровой электроники.

Иллюстрация: Катя Павловская для Skillbox Media

Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.

Мы привыкли считать всё в десятичной системе, потому что у нас 10 пальцев — и это удобно. Но если бы у нас было больше пальцев, например 12, то система могла бы быть двенадцатиричной и мы бы воспринимали её как обычную.

Когда дело доходит до двоичной системы счисления, сложно вот так сразу переключиться на её арифметику — хотя, казалось бы, принципы такие же, как для десятичной. Ведь там есть все привычные операции: сложение, вычитание, умножение, деление. Единственное отличие: в двоичных числах используются всего две цифры — ноль и единица.

Давайте избавимся от страха и наконец узнаем, как проводить знакомые нам математические операции в двоичной системе.

Правила сложения двоичных чисел похожи на привычные нам: сложение происходит поразрядно справа налево, при этом важно помнить о переносе чисел в новый разряд.

В десятичной системе у нас всего 10 цифр: от 0 до 9. Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10.

Двоичная система работает аналогично: чтобы понять, как складывать числа, нужно помнить об этом переполнении. Всего в двоичной системе две цифры — 0 и 1. Если сложить 1 и 1, мы получим переполнение, а значит, единица пойдёт в следующий разряд, результатом станет 10 (только не «десять», а «один-ноль»).

Если представить правила сложения двоичных чисел в общем виде, получим такую таблицу:

Изображение: Skillbox Media

Но лучше разобраться на примерах.

Пример 1. Давайте сложим 1100 и 101.

Изображение: Skillbox Media

Рассмотрим пример подробнее. Как мы уже упоминали ранее, сложение происходит справа налево. Разряды считаются тоже справа налево:

Первый: 0 + 1 = 1.
Второй: 0 + 0 = 0.
Третий: 1 + 1 = 10 — переполнение, единица переходит в следующий разряд.
Четвёртый: 1 + 0 + 1 = 10 — добавляем единицу из прошлого разряда, получаем переполнение, единица переходит в следующий разряд.
Пятый: 0 + 0 + 1 = 1 — единица пришла из предыдущего разряда.

Пример 2. Сложим 1111 и 111.

Изображение: Skillbox Media

Теперь поразрядно:

Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
Пятый: 0 + 0 + 1 = 1.

Вроде бы пока несложно. Так что попробуйте сами сложить 1101 и 1011, чтобы закрепить знания.

Ответ

1101 + 1011 = 11000.

Умножение в двоичной системе, как в десятичной, основано на сложении — и умении считать в столбик.

Сведём в таблицу правила умножения двоичных чисел:

Изображение: Skillbox Media

Давайте теперь посмотрим на реальных примерах, как правильно умножать двоичные числа.

Пример 1. Умножим 110 на 10.

Изображение: Skillbox Media

Здесь мы воспользуемся привычным школьным «столбиком»: сначала умножаем верхнее число, 110, на 0, затем на 1, а потом складываем полученные два и получаем результат.

По сути, если мы умножаем число на ноль, то оно превращается в ноль, а если на единицу — остаётся неизменным, но сдвигается на число разрядов, равное номеру разряда этой единицы, как в обычном умножении:

110 × 0 = 000;
110 × 1 = 110.

Сдвигаем 110 на один разряд влево и складываем результаты промежуточных умножений:

000 + 1100 = 1100.

Мы получили 1100, потому что сместили результат умножения 110 × 1 на один разряд влево, а затем добавили один 0 справа — как в обычном умножении.

Пример 2. Давайте теперь умножим 101 на 101.

Изображение: Skillbox Media

Не пугайтесь, что у нас получилось три числа, которые нужно сложить: правила остаются теми же. Ещё можно приписывать дополнительные нули туда, где находится пустое пространство — это поможет не запутаться.

Разберём пошагово:

101 × 1 = 101;
101 × 0 = 000;
101 × 1 = 101.

Снова сдвигаем влево промежуточные результаты и складываем:

101 + 0000 + 10100 = 11001.

Попробуйте сами умножить 1101 на 111.

Ответ

1011011.

Правила двоичного вычитания тоже ничем не отличаются от десятичного. Мы также вычитаем поразрядно и, если нужно, занимаем единицу из старшего разряда.

Таблица вычитания выглядит так:

Изображение: Skillbox Media

Заметьте, что 0 − 1 = 1. Это всё потому, что мы занимаем единицу из старшего разряда и получаем 10, или 2 в десятичной системе, а если вычесть из 10 число 1, получим 1 (ведь 2 − 1 = 1).

Перейдём к примерам, чтобы понять, как вычитать одно число из другого.

Пример 1. Вычтем из 1100 число 11.

Изображение: Skillbox Media

Разберём подробнее поразрядно:

Первый: 0 − 1 = 1 — занимаем единицу из старшего разряда.
Второй: 1 − 1 = 0 — так как отсюда заняли единицу, но у нас её не было, мы взяли её из следующего разряда и вычли единицу из этого.
Третий: 0 − 0 = 0 — из этого разряда единица ушла в первый.
Четвёртый: 1 − 0 = 1 — здесь всё нормально.

Всё то же знакомое нам вычитание.

Пример 2. Вычтем из 1011 число 101.

Изображение: Skillbox Media

Тот же алгоритм по разрядам:

Первый: 1 − 1 = 0.
Второй: 1 − 0 = 1.
Третий: 0 − 1 = 1 — заняли единицу из следующего разряда.
Четвёртый: 0 − 0 = 0 — отдали единицу в предыдущий разряд.

Кажется, что всё несложно. Попробуйте теперь сами вычесть из 11010 число 1111.

Ответ

1011.

Вы удивитесь, но правила деления двоичных чисел похожи на деление десятичных. Рисуем привычный «столбик», умножаем, вычитаем, получаем результат.

Таблицы тут нет, потому что она бессмысленна — давайте сразу на примерах разбирать, как делить двоичные числа.

Пример 1. Поделить 1100 на 10.

Изображение: Skillbox Media

У нас есть только два варианта: умножить делитель на 1 или на 0. Поэтому алгоритм будет таким:

Смотрим на делимое, видим, что первые две его цифры — 11. Умножаем делитель на 1 и вычитаем из 11 число 10.
Получили 1, дописываем справа следующую по порядку цифру — 0. Теперь 10 равно делителю, значит, тоже умножаем его на 1 и вычитаем.
Получаем 0. Но у нас ещё остался один 0 у делимого — дописываем его справа от полученного 0.
Число 0 меньше, чем 10, поэтому умножаем делитель на 0. Получаем конечный ответ — 110.

Пример 2. Поделить 10010 на 110.

Изображение: Skillbox Media

Пошаговый алгоритм:

Первые три числа делимого меньше, чем делитель — значит, умножаем делитель на 0 и вычитаем. Получаем 100.
Дописываем 1 справа от 100, видим, что 1001 больше, чем 110, поэтому умножаем делитель на 1 и вычитаем его из 1001. Получаем 11.
Дописываем 0 справа. Полученное 110 равно делителю, поэтому тоже умножаем его на 1, получаем конечный результат.

Попробуйте сами теперь поделить 10100 на 100.

Ответ

101.

Двоичная арифметика во многом похожа на десятичную: мы так же можем складывать, вычитать, делить и умножать числа столбиком. Правда, в двоичной системе всего две цифры: 0 и 1 — поэтому привычные математические операции в ней могут показаться немного странными. К счастью, в основе двоичной арифметики лежат простые принципы, которые нужно запомнить.

Научитесь: Профессия Python-разработчик
Узнать больше

Источник

Если у вас в школе была информатика, не исключено, что там было упражнение на перевод обычных чисел в двоичную систему и обратно. Маловероятно, что кто-то вам объяснял практический смысл этой процедуры и откуда вообще берётся двоичное счисление. Давайте закроем этот разрыв.

Эта статья не имеет практической ценности — читайте её просто ради интереса к окружающему миру. Если нужны практические статьи, заходите в наш раздел «Где-то баг», там каждая статья — это практически применимый проект.

Отличный план

Чтобы объяснить всё это, нам понадобится несколько тезисов:

Система записи числа — это шифр.
Мы привыкли шифровать десятью знаками.
Но система записи чисел может быть любой. Это условность.
Двоичная система — это тоже нормальная система.
Всё тлен и суета.

Система записи — это шифр

Если у нас есть девять коров, мы можем записать их как 🐄🐄🐄🐄🐄🐄🐄🐄🐄 или как 9 × 🐄.

Почему 9 означает «девять»? И почему вообще есть такое слово? Почему такое количество мы называем этим словом? Вопрос философский, и короткий ответ — нам нужно одинаково называть числа, чтобы друг друга понимать. Слово «девять», цифра 9, а также остальные слова — это шифр, который мы выучили в школе, чтобы друг с другом общаться.

Допустим, к нашему стаду прибиваются еще 🐄🐄🐄. Теперь у нас 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄 — двенадцать коров, 12. Почему мы знаем, что 12 — это «двенадцать»? Потому что мы договорились так шифровать числа.

Нам очень легко расшифровывать записи типа 12, 1920, 100 500 и т. д. — мы к ним привыкли, мы учили это в школе. Но это шифр. 12 × 🐄 — это не то же самое, что 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄. Это некая абстракция, которой мы пользуемся, чтобы упростить себе счёт.

Мы привыкли шифровать десятью знаками

У нас есть знаки 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — всего десять знаков. Этим числом знаков мы шифруем количество единиц, десятков, сотен, тысяч и так далее.

Мы договорились, что нам важен порядок записи числа. Мы знаем, что самый правый знак в записи означает число единиц, следующий знак (влево) означает число десятков, потом сотен и далее.

Например, перед нами число 19 547. Мы знаем, что в нём есть:

1 × 10 000

9 × 1000

5 × 100

4 × 10

7 × 1

Если приглядеться, то каждый следующий разряд числа показывает следующую степень десятки:

1 × 10⁴

9 × 10³

5 × 10²

4 × 10¹

7 × 10⁰

Нам удобно считать степенями десятки, потому что у нас по десять пальцев и мы с раннего детства научились считать до десяти.

Система записи — это условность

Представим бредовую ситуацию: у нас не 10 пальцев, а 6. И в школе нас учили считать не десятками, а шестёрками. И вместо привычных цифр мы бы использовали знаки ØABCDE. Ø — это по-нашему ноль, A — 1, B — 2, E — 5.

Вот как выглядели бы привычные нам цифры в этой бредовой системе счисления:

0 — Ø
1 — A
2 — B
3 — C
4 — D
5 — E

6 — AØ
7 — AA
8 — AB
9 — AC
10 — AD
11 — AE

12 — BØ
13 — BA
14 — BB
15 — BC
16 — BD
17 — BE

18 — CØ
19 — CA
20 — CB
21 — CC
22 — CD
23 — CE

24 — DØ
25 — DA
26 — DB
27 — DC
28 — DD
29 — DE

30 — EØ
31 — EA
32 — EB
33 — EC
34 — ED
35 — EE

36 — AØØ
37 — AØA
38 — AØB
39 — AØC
40 — AØD
41 — AØE

В этой системе мы считаем степенями шестёрки. Число ABADØ можно было бы перевести в привычную нам десятичную запись вот так:

A × 6⁴ = 1 × 1296 = 1296

B × 6³ = 2 × 216 = 432

A × 6² = 1 × 36 = 36

D × 6¹ = 4 × 6 = 24

Ø × 6⁰ = 0 × 1 = 0

1296 + 432 + 36 + 24 + 0 = 1788. В нашей десятичной системе это 1788, а у людей из параллельной вселенной это ABADØ, и это равноценно.

Выглядит бредово, но попробуйте вообразить, что у нас в сумме всего шесть пальцев. Каждый столбик — как раз шесть чисел. Очень легко считать в уме. Если бы нас с детства учили считать шестёрками, мы бы спокойно выучили этот способ и без проблем всё считали. А счёт десятками вызывал бы у нас искреннее недоумение: «Что за бред, считать числом AD? Гораздо удобнее считать от Ø до E!»

То, как мы шифруем и записываем числа, — это следствие многовековой традиции и физиологии. Вселенной, космосу, природе и стадам коров глубоко безразлично, что мы считаем степенями десятки. Природа не укладывается в эту нашу систему счёта.

Например, свет распространяется в вакууме со скоростью 299 792 458 метров в секунду. Ему плевать, что нам для ровного счёта хотелось бы, чтобы он летел со скоростью 300 тысяч километров в секунду. А ускорение свободного падения тела возле поверхности Земли — 9,81 м/с². Так и хочется спросить: «Тело, а ты не могло бы иметь ускорение 10 м/с²?» — но телу плевать на наши системы счисления.

Двоичная система (тоже нормальная)

Внутри компьютера работают транзисторы. У них нет знаков 0, 1, 2, 3… 9. Транзисторы могут быть только включёнными и выключенными — обозначим их 💡 и ⚫.

Мы можем научить компьютер шифровать наши числа этими транзисторами так же, как шестипалые люди шифровали наши числа буквами. Только у нас будет не 6 букв, а всего две: 💡 и ⚫. И выходит, что в каждом разряде будет стоять не число десяток в разной степени, не число шестёрок в разной степени, а число… двоек в разной степени. И так как у нас всего два знака, то получается, что мы можем обозначить либо наличие двойки в какой-то степени, либо отсутствие:

0 — ⚫
1 — 💡

2 — 💡⚫
3 — 💡💡

4 — 💡⚫⚫
5 — 💡⚫💡
6 — 💡💡⚫
7 — 💡💡💡

8 — 💡⚫⚫⚫
9 — 💡⚫⚫💡
10 — 💡⚫💡⚫
11 — 💡⚫💡💡
12 — 💡💡⚫⚫
13 — 💡💡⚫💡
14 — 💡💡💡⚫
15 — 💡💡💡💡

16 — 💡⚫⚫⚫⚫
17 — 💡⚫⚫⚫💡
18 — 💡⚫⚫💡⚫
19 — 💡⚫⚫💡💡
20 — 💡⚫💡⚫⚫
21 — 💡⚫💡⚫💡
21 — 💡⚫💡💡⚫
23 — 💡⚫💡💡💡
24 — 💡💡⚫⚫⚫
25 — 💡💡⚫⚫💡
26 — 💡💡⚫💡⚫
27 — 💡💡⚫💡💡
28 — 💡💡💡⚫⚫
29 — 💡💡💡⚫💡
30 — 💡💡💡💡⚫
31 — 💡💡💡💡💡

32 — 💡⚫⚫⚫⚫⚫
33 — 💡⚫⚫⚫⚫💡
34 — 💡⚫⚫⚫💡⚫
35 — 💡⚫⚫⚫💡💡
36 — 💡⚫⚫💡⚫⚫
37 — 💡⚫⚫💡⚫💡
38 — 💡⚫⚫💡💡⚫
39 — 💡⚫⚫💡💡💡
40 — 💡⚫💡⚫⚫⚫
41 — 💡⚫💡⚫⚫💡
42 — 💡⚫💡⚫💡⚫
43 — 💡⚫💡⚫💡💡
44 — 💡⚫💡💡⚫⚫
45 — 💡⚫💡💡⚫💡
46 — 💡⚫💡💡💡⚫
47 — 💡⚫💡💡💡💡
48 — 💡💡⚫⚫⚫⚫
49 — 💡💡⚫⚫⚫💡
50 — 💡💡⚫⚫💡⚫
51 — 💡💡⚫⚫💡💡
52 — 💡💡⚫💡⚫⚫
53 — 💡💡⚫💡⚫💡
54 — 💡💡⚫💡💡⚫
55 — 💡💡⚫💡💡💡
56 — 💡💡💡⚫⚫⚫
57 — 💡💡💡⚫⚫💡
58 — 💡💡💡⚫💡⚫
59 — 💡💡💡⚫💡💡
60 — 💡💡💡💡⚫⚫
61 — 💡💡💡💡⚫💡
62 — 💡💡💡💡💡⚫
63 — 💡💡💡💡💡💡

Если перед нами число 💡 ⚫💡⚫⚫ 💡💡⚫⚫, мы можем разложить его на разряды, как в предыдущих примерах:

💡 = 1 × 2⁸ = 256

⚫ = 0 × 2⁷ = 0

💡 = 1 × 2⁶ = 64

⚫ = 0 × 2⁵ = 0

⚫ = 0 × 2⁴ = 0

💡 = 1 × 2³ = 8

💡 = 1 × 2² = 4

⚫ = 0 × 2¹ = 0

⚫ = 0 × 2⁰ = 0

256 + 0 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 332

Получается, что десятипалые люди могут записать это число с помощью цифр 332, а компьютер с транзисторами — последовательностью транзисторов 💡⚫💡⚫⚫ 💡💡⚫⚫.

Если теперь заменить включённые транзисторы на единицы, а выключенные на нули, получится запись 1 0100 1100. Это и есть наша двоичная запись того же самого числа.

Почему говорят, что компьютер состоит из единиц и нулей (и всё тлен)

Инженеры научились шифровать привычные для нас числа в последовательность включённых и выключенных транзисторов.

Дальше эти транзисторы научились соединять таким образом, чтобы они умели складывать зашифрованные числа. Например, если сложить 💡⚫⚫ и ⚫⚫💡, получится 💡⚫💡. Мы писали об этом подробнее в статье о сложении через транзисторы.

Дальше эти суммы научились получать супербыстро. Потом научились получать разницу. Потом умножать. Потом делить. Потом всё это тоже научились делать супербыстро. Потом научились шифровать не только числа, но и буквы. Научились их хранить и считывать. Научились шифровать цвета и координаты. Научились хранить картинки. Последовательности картинок. Видео. Инструкции для компьютера. Программы. Операционные системы. Игры. Нейросети. Дипфейки.

И всё это основано на том, что компьютер умеет быстро-быстро складывать числа, зашифрованные как последовательности включённых и выключенных транзисторов.

При этом компьютер не понимает, что он делает. Он просто гоняет ток по транзисторам. Транзисторы не понимают, что они делают. По ним просто бежит ток. Лишь люди придают всему этому смысл.

Когда человека не станет, скорость света будет по-прежнему 299 792 458 метров в секунду. Но уже не будет тех, кто примется считать метры и секунды. Такие дела.

Источник

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, десятичная двойка является основанием двоичной системы счисления, аналогично тому, как в десятичной системе основанием является число десять.

Чтобы научиться считать в двоичной системе счисления, рассмотрим, как формируются числа в привычной для нас десятичной.

В десятичной системе счисления мы располагаем десятью знаками-цифрами: от 0 до 9. Когда счет достигает числа 9, вводится новый более старший разряд – десятки. При этом разряд единиц обнуляется и счет в этом разряде опять начинается с нуля. После числа 19 разряд десятков увеличивается на 1, а разряд единиц снова обнуляется. Получается число 20. Когда десятки дойдут до 9, впереди них появится третий разряд – сотни.

Формирование каждого последующего числа в двоичной системе счисления аналогично тому, как это происходит в десятичной за исключением того, что используются всего-лишь две цифры: 0 и 1. Как только разряд достигает своего предела, то есть единицы, появляется новый разряд, а старый обнуляется.

Итак, число три в двоичной системе записывается как 11, в десятичной – как 3. Количественно это одинаковые числа. Это одно и то же число, выраженное в различных системах счисления. Если есть вероятность неоднозначной трактовки числа, к нему приписывается нижний индекс в десятичной системе счисления, обозначающий, в какой системе счисления выражено данное число:

11₂ = 3₁₀

Индекс для числа, выраженного в десятичной системе, обычно опускается.

Перевод чисел из двоичной системы счисления в десятичную

В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:

5476 = 5000 + 400 + 70 + 6

Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:

5476 = 5 * 10³ + 4 * 10² + 7 * 10¹ + 6 * 10⁰

После равенства числа 5, 4, 7 и 6 – это набор цифр из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы. Так, например, 6 находится в первом разряде, поэтому она умножается на 10^(1-1). Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.

Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка. Здесь до знака равенства число представлено в двоичной системе счисления, после «равно» запись идет в десятичной:

10001001 = 1 * 2⁷ + 0 * 2⁶ + 0 * 2⁵ + 0 * 2⁴ + 1 * 2³ + 0 * 2² + 0 * 2¹ + 1 * 2⁰

Результат вычислений дает десятичное число, количественно равное двоичному 10001001:

1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰ =
= 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:

10001001₂ = 137₁₀

Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык современной вычислительной техники.

Когда любые данные сохраняются на компьютере, они кодируются числами. С числами же компьютер выполняет операции, изменяя эти данные.

Допустим, у нас есть десятичное число 14, которое требуется сохранить в компьютерной памяти. Мы задействуем участок памяти, в данном случае состоящий как минимум из двух элементов, отводимых под разряды. В одном из разрядов мы сохраняем десятичное число 1, в другом – число 4.

Элемент памяти – это физическое устройство. Если проектировать его для хранения десятичной цифры, потребуется создать такое устройство, которое может находиться в десяти разных физических состояниях и способно переключаться между ними. Каждое из этих состояний будет соответствовать числу от 0 до 9.

Создать такой элемент памяти возможно, однако сложнее и дороже, чем создать элемент, способный находиться только в двух состояниях. Одно состояние сопоставить нулю, второе – единице. Кроме того, подобное хранение данных является более надежным.

Поэтому оказалось проще перевести число 14 в двоичную систему счисления, получив число 1110, и именно его сохранить в памяти. И пусть даже при этом будут задействованы не два, а четыре разряда, то есть четыре элементарных единиц памяти.

Перевод десятичного числа в двоичное

Одним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим «сбором» двоичного числа из остатков. Переведем таким образом число 14 в двоичное представление.

14 / 2 = 7, остаток 0
 7 / 2 = 3, остаток 1
 3 / 2 = 1, остаток 1
 1 / 2 = 0, остаток 1

Собирать остатки надо с конца, то есть с последнего деления. Получаем 1110.

Выполним то же самое для числа 77:

77 / 2 = 38, остаток 1
38 / 2 = 19, остаток 0
19 / 2 =  9, остаток 1
 9 / 2 =  4, остаток 1
 4 / 2 =  2, остаток 0
 2 / 2 =  1, остаток 0
 1 / 2 =  0, остаток 1

Собираем остатки вместе, начиная с конца: 1001101.

Проверим, выполнив обратный перевод:

1001101 = 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Источник