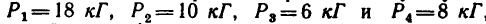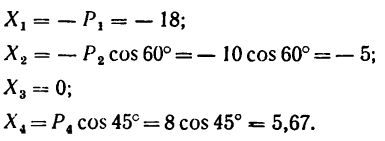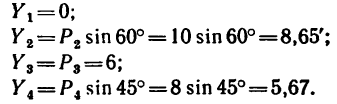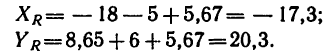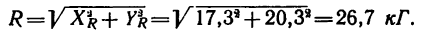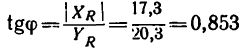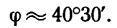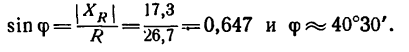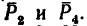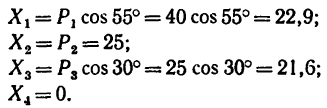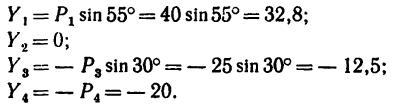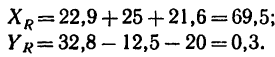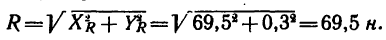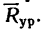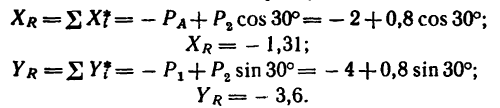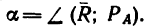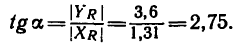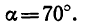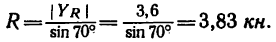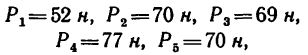Ранее мы уже познакомились с понятием силы и знаем, что она имеет две характеристики: направление и численное значение. В жизни обычно на тело действуют сразу несколько сил.
Например, если рассмотреть ситуацию, когда спускается парашютист, то можно заметить, что на него действуют сразу две силы: и сила тяжести, и сила сопротивления воздуха.
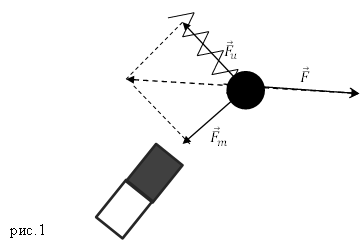
На груз, подвешенный на пружине, тоже действуют две силы — сила тяжести и сила упругости пружины.
В каждом таком случае мы можем заменить несколько сил, действующих на тело, одной. И она будет равноценна по своему действию всем этим силам.
На данном уроке мы узнаем, как называется такая сила и как ее найти.
Равнодействующая сил
Дадим определение. Какую силу называют равнодействующей нескольких сил?
Равнодействующая сил — это сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Так же, как и любая сила, равнодействующая является векторной величиной. Она обозначается буквой $vec R$, а ее числовое значение — буквой $R$. Равнодействующая сила измеряется в ньютонах ($Н$).
Сложение сил, действующих на тело по одной прямой
Если силы направлены в одну сторону
Проведем эксперимент: возьмем два груза (рисунок 1, а), масса которых равна $102 space г$ и $204 space г$, и подвесим их к пружине. Наши грузы имеют вес $1 space Н$ и $2 space Н$ и воздействуют на пружину, из-за чего она растягивается на определенную длину. Сделаем отметку, на какое расстояние вытянулась пружина.
А теперь снимем два груза и подберем один груз, который растянет пружину на такую же длину. Вес этого груза окажется равен $3 space Н$ (рисунок 1, б).
Из опыта можно сделать вывод, что:
- Равнодействующая сил, направленных по одной прямой в одну сторону, направлена в ту же сторону, что и действующие на тело силы;
- Модуль равнодействующей сил равен сумме модулей составляющих сил.
Изобразим графически эти силы на рисунке 2.
Чему равна равнодействующая двух сил, направленных по одной прямой в одну сторону?
Силы, которые мы будем складывать, обозначены буквами $F_1$ и $F_2$. Тогда для всех действующих сил будет иметь место равенство:
$R = F_1 + F_2$.
Если силы направлены в противоположные стороны
Рассмотрим еще один опыт, представленный на рисунке 3.
Поставим гирю на динамометр со столиком (рисунок 3, а). Рассматриваемым телом в данном случае будет сам столик. Гиря весит $5 space Н$, т.е. действует на столик с силой в $5 space Н$, причем эта сила направлена вертикально вниз.
Теперь привяжем к столику нить и потянем вертикально вверх с силой, равной $2 space Н$ (рисунок 3, б). Динамометр покажет силу $3 space Н$. Эта сила и будет равнодействующей двух сил: $5 space Н$ и $3 space Н$.
- Если две силы направлены по одной прямой в противоположные стороны, то их равнодействующая будет направлена в сторону той силы, которая больше по модулю.
- Модуль равнодействующий сил в таком случае равен разности модулей составляющих сил
Изобразить силы можно следующим образом (рисунок 4):
Чему равна равнодействующая двух сил, направленных по одной прямой в противоположные стороны?
Равнодействующая сил равна:
$R = F_2 space − space F_1$.
Как будет двигаться тело под действием двух равных противоположно направленных сил?
Если силы, действующие на тело, будут равны, то мы получим, что равнодействующая сил равна нулю, то есть $R = 0$. Другими словами, в этом случае тело будет покоиться или двигаться прямолинейно и равномерно.
Как мы уже говорили, когда тело растянет пружину и остановится, это значит, что сила тяжести и сила упругости уравновесили друг друга. В этом случае тело будет находиться в состоянии покоя, например, как на рисунке 1.
Упражнения
Упражнение №1
Человек, масса которого $70 space кг$, держит на плечах ящик массой $20 space кг$. С какой силой человек давит на землю?
Дано:
$m_1 = 70 space кг$
$m_2 = 20 space кг$
$g = 9.8 frac{Н}{кг}$
$P$ — ?
Показать решение и ответ
Скрыть
Решение:
Без ящика на плечах человек давит на землю с весом $P_1$, а ящик (если его поставить на землю) — с весом $P_2$.
Вес направлен вертикально вниз. В данной задаче мы применим понятие равнодействующей сил к их общему весу $P$:
$R = P = P_1 + P_2$
Человек с ящиком на плечах стоит на месте. Значит его вес будет равен силе тяжести, действующей на него:
$P_1 = F_{тяж1} = gm_1$.
Вес ящика тоже будет равен силе тяжести, действующей на него:
$P_2 = F_{тяж2} = gm_2$.
Тогда общий вес, с которым человек давит на землю с ящиком на плечах, будет равен:
$P = gm_1 + gm_2 = g cdot (m_1 + m_2)$,
$P = 9.8 frac {Н}{кг} cdot (70 space кг + 20 space кг) = 9.8 frac {Н}{кг} cdot 90 space кг = 882 space Н$.
Ответ: $P = 882 space Н$.
Упражнение №2
Отец посадил сына себе на плечи. Масса отца составляет $90 space кг$, сына — $35 space кг$. С какой силой отец теперь будет давить на землю?
Дано:
$m_о = 90 space кг$
$m_с = 35 space кг$
$g = 9.8 frac{Н}{кг}$
$P$ — ?
Показать решение и ответ
Скрыть
Решение:
В одиночку отец давит на землю с весом $P_о$, сын — с весом $P_с$.
Вес направлен вертикально вниз. В данной задаче мы применим понятие равнодействующей сил к их общему весу $P$:
$R = P = P_о + P_c$
Отец с сыном не двигаются, значит:
$P_о = gm_о$ и $P_с = gm_с$.
Тогда общий вес, с которым отец давит на землю держа сына на плечах, будет равен:
$P = gm_о + gm_с = g cdot (m_о + m_с)$,
$P = 9.8 frac {Н}{кг} cdot (90 space кг + 35 space кг) = 9.8 frac {Н}{кг} cdot 125 space кг = 1 225 space Н$.
Ответ: $P = 1 225 space Н$.
Упражнение №3
В игре по перетягиванию каната участвуют четыре человека. Два из них тянут канат в одну сторону с силами $330 space Н$ и $380 space Н$, два — в противоположную сторону с силами $300 space Н$ и $400 space Н$. В каком направлении будет двигаться канат и чему равна равнодействующая этих сил? Сделайте чертеж.
Дано:
$F_1 = 330 space Н$
$F_2 = 380 space Н$
$F_3 = 300 space Н$
$F_4 = 400 space Н$
$R — ?$
Показать решение и ответ
Пусть первые два участника тянут канат вправо с силами $F_1$ и $F_2$, другие два — влево с силами $F_3$ и $F_4$.
Скрыть
Решение:
Сначала найдем чему равна равнодействующая сил первых двух участников. Они тянут канат в одну сторону, значит:
$R_1 = F_1 + F_2 = 330 space Н + 380 space Н = 710 space Н$.
Теперь найдем равнодействующую сил для левой стороны участников:
$R_2 = F_3 + F_4 = 300 space Н + 400 space Н = 700 space Н$.
Теперь мы можем найти равнодействующую сил для всех участников:
$R = R_1 space − space R_2 = 710 space Н space − space 700 space Н = 10 space Н$.
Графически силы изображены на рисунке 5. Так как силы участников направлены в противоположные стороны, равнодействующая сил будет направлена в ту сторону, где у участников большая сила, то есть вправо.
Ответ: канат будет двигаться в сторону первых двух участников, $R = 10 space Н$.
Упражнение №4
Человек спускается на парашюте, двигаясь равномерно. Сила тяжести парашютиста вместе с парашютом $700 space Н$. Чему равна сила сопротивления воздуха?
Дано:
$F_{тяж} = 700 space Н$
$upsilon = const$
$F_с — ?$
Показать решение и ответ
Скрыть
Решение:
Сила тяжести, действующая на парашютиста и парашют, направлена вертикально вниз, а сила сопротивления воздуха — противоположно его движению, то есть вертикально вверх.
В задаче сказано, что парашютист двигается равномерно ($upsilon = const$). Значит равнодействующая сил, действующая на него и парашют, равна нулю:
$R = 0$.
Тогда мы можем сказать, что силы, действующие на парашютиста и парашют, по модулю равны друг другу:
$F_с = F_{тяж} = 700 space Н$.
Ответ: $F_с = 700 space Н$.
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ — масса тела, на которое действует сила $overline{F}$; $overline{a}$ — ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
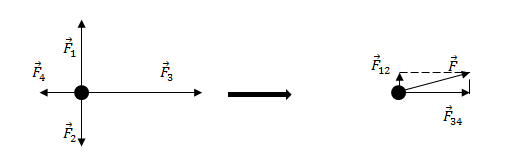
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
4. Определение равнодействующей аналитическим способом
Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.
Проекция силы на две взаимно перпендикулярные оси.
Fx = Fcosα > 0
Fy = Fcosβ = Fsinα > 0
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.
FΣx= F1x + F2x + F3x + F4x;
FΣy= F1y + F2y + F3y + F4y.
Модуль (величину) равнодействующей можно определить по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской системы сходящихся сил:
При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Равнодействующая сила
4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
Обновлено 31 Октября, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
Обновлено 31 Октября, 2021
Законы Ньютона – математическая абстракция. В реальности причиной движения или покоя тел, а также их деформации, выступают сразу несколько сил. Поэтому важным дополнениям к законам механики будет введение понятия равнодействующей силы и его применение.
О причинах изменений
Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.
Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.
Сила – это векторная величина, то есть, ее действие – направленное. Модуль силы в общем случае пропорционален некоему коэффициенту (для деформации пружины – это ее жесткость), а также параметрам действия (масса, заряд).
Например, в случае кулоновской силы – это величина обоих зарядов, взятых по модулю, квадрат расстояние между зарядами и коэффициент k, в системе СИ определяемый выражением: $k = {1 over 4 pi epsilon}$, где $epsilon$ – диэлектрическая постоянная.
Сложение сил
В случае, когда на тело действует n сил, говорят о равнодействующей силе, а формула второго закона Ньютона принимает вид:
$mvec a = sumlimits_{i=1}^n vec F_i$
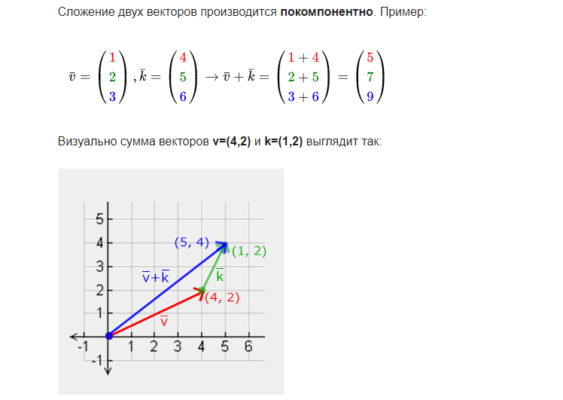
Поскольку F – векторная величина, сумма сил называется геометрической (или векторной). Такое сложение выполняется по правилу треугольника или параллелограмма, либо по компонентам. Поясним каждый метод на примере. Для этого запишем формулу равнодействующей силы в общем виде:
$F = sumlimits_{i=1}^n vec F_i$
А силу $F_i$ представим в виде:
$F = (F_{xi}, F_{yi}, F_{zi})$
Тогда суммой двух сил будет новый вектор $F_{ab} = (F_{xb} + F_{xa}, F_{yb} + F_{ya}, F_{zb} + F_{za})$.
Абсолютное значение равнодействующей можно рассчитать так:
$F = sqrt{(F_{xb} + F_{xa})^2 + (F_{yb} + F_{ya})^2 + (F_{zb} + F_{za})^2}$
Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.
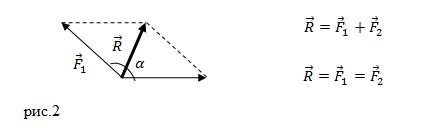
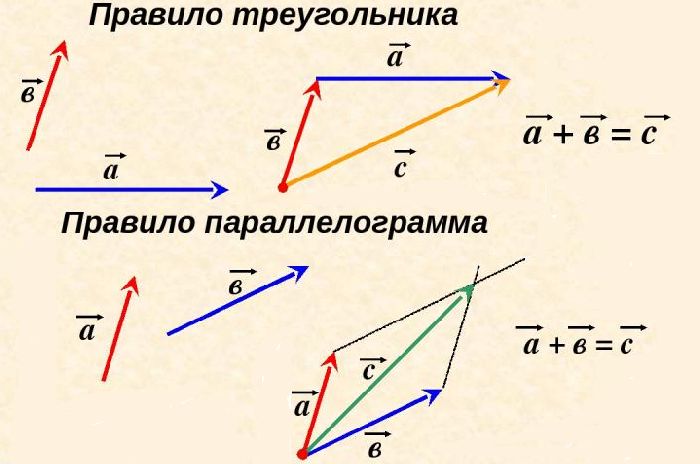
Разберем правила треугольника и параллелограмма. Графически это выглядит так:
Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.
Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.
Задачи
- На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов.
Решение
Равнодействующей силой будет векторная сумма $F_1$ и $F_2$.
Поэтому запишем:
$vec F = vec F_1 + vec F_2 = (5+3, 0+3) = (8, 3)$
Абсолютное значение равнодействующей силы:
$F = sqrt{8^2 + 3^2} = sqrt{64 + 9} = 8,5 Н$
Теперь получим тоже значение при помощи правила треугольника. Для этого сначала найдем абсолютные значения $F_1$ и $F_2$, а также угол между ними.
$F_1 = sqrt{5^2 + 0^2} = 5 Н$
$F_2 = sqrt{3^2 + 3^2} = 4,2 Н$
Угол между ними – 45˚, так как первая сила параллельна оси Оx, а вторая делит первую координатную плоскость пополам, то есть является биссектрисой прямоугольного угла.
Теперь, разместив вектора по правилу треугольника, рассчитаем по теореме косинусов равнодействующую:
$F = sqrt{F_1^2 + F_2^2 – 2F_1F_2 cos135} = sqrt{F_1^2 + F_2^2 + 2F_1F_2 sin45} = sqrt{25 + 18 + 2 cdot 5 cdot 4,2 cdot sin45} = 8,5 Н$
- На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?
Решение
Достаточно сложить иксовые компоненты векторов:
$F = -5 – 2 + 7 = 0$
Что мы узнали?
В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
А какая ваша оценка?
Определение равнодействующей сходящихся сил:
Для сложения любого числа сходящихся сил применяется правило многоугольника. Используя это правило, задачу можно решить либо графическим методом либо методом проекций.
Задачи, решены методом проекций. Графическим методом рекомендуется решить эти задачи самостоятельно.
Задача №1
Определить равнодействующую четырех сил: 
Решение — методом проекций.
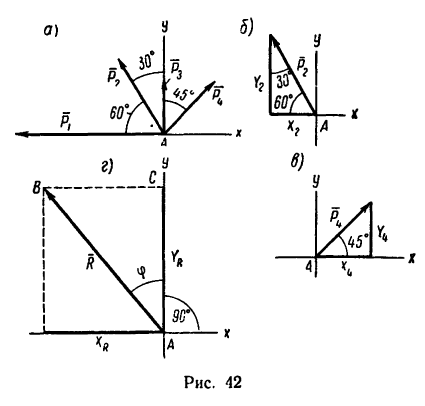
1. Изображаем на рисунке четыре данные силы и выбираем расположение осей проекций. В данном случае удобно начало осей поместить в точке А, а оси совместить с силами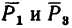 
(рис. 42, а).
2. Находим проекции данных сил на ось х:
3. Находим проекции данных сил на ось у:
Если трудно определить знак и числовое значение проекции, то необходимо помнить, что проектируемую силу и две проекции на взаимно перпендикулярные оси всегда можно представить в виде прямоугольного треугольника. В тех случаях, когда еще нет достаточных навыков, силы и ее проекции можно изобразить отдельно, как показано на рис. 42,6 для силы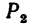 
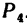
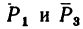
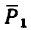
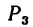
и на рис. 42, в для силы 
. Эти рисунки облегчают правильное определение проекций.
Для сил 
такие рисунки не нужны, так как сила 
лежит на оси х и, следовательно, проектируется на эту ось в натуральную величину, но зато на ось у проекция этой силы равна нулю. Сила 
проектируется в натуральную величину на ось у, а ее проекция на ось х равна нулю.
4. Находим проекции искомой равнодействующей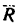 
на оси хну:
Проекция на ось х получается отрицательной, а на ось у положительной. Значит вектор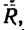 
заменяющий действие четырех данных сил и приложенный к точке А, должен быть направлен относительно оси у вверх, а относительно оси х — влево. Положение равнодействующей R показано отдельно на рис. 42, г.
5. Находим модуль равнодействующей (т. е. заканчиваем решение задачи первым путем, см. п. 7 в § 4-1):
6. Находим угол ф, определяющий направление R относительно оси у (см. рис. 42, а):
и, следовательно, 
Для определения угла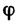 
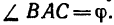
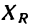
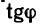
использован 
АВС (см. рис. 42, г), в котором 
Поэтому 
не имеет значения и в выражение 
подставлена его абсолютная величина.
Угол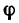 
можно найти при помощи синуса:
Для определения угла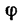 
можно воспользоваться и косинусом, но при работе с логарифмической счетной линейкой эта функция менее удобна.
Таким образом, равнодействующая четырех заданных сил равна 26,7 кГ направлена под углом 40°30′ к положительному направлению оси у и под углом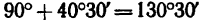 
к положительному направлению оси х.
Задача №2
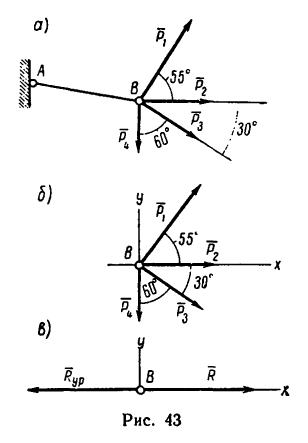
К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: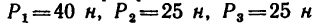 
,
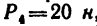
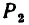
направленные, как показано на рис. 43, а (сила 
горизонтальна). Определить усилие, возникшее в веревке, и ее направление относительно горизонтали.
Решение — методом проекций.
1. Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.
2. Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 43, 6) и совместим оси проекций с силами
3. Найдем проекции заданных сил на ось х:
4. Найдем проекции заданных сил на ось у:
5. Найдем проекции равнодействующей R на оси х и у:
6. Найдем модуль равнодействующей:
Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.
Таким образом, четыре заданные силы натягивают веревку равнодействующей силой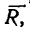
приложенной к точке В (к кольцу на конце веревки) и направленной горизонтально.
Другой конец веревки (точка А, рис. 43,а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.
На рис. 43, в показаны равнодействующая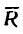 
и уравновешивающая 
Задача №3
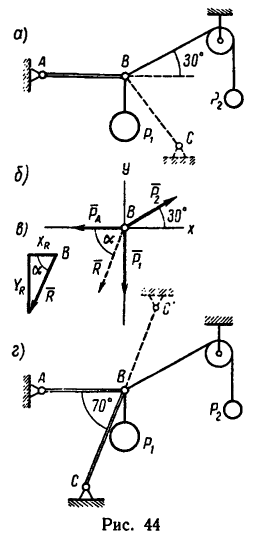
На конце В горизонтального стержня АВ необходимо прикрепить две нити с грузами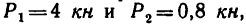 
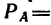
, как показано на рис. 44, а. Под каким углом к этому стержню следует присоединить второй стержень ВС, чтобы стержень АВ растягивался силой 
2 кн? Какое усилие при этом будет испытывать стержень ВС?
Соединения стержней между собой и с опорами шарнирные.
Решение — методом проекций.
1. На точку В действуют три силы: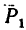 
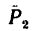
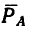
— вертикально вниз, 
— вдоль нити от точки В к блоку (под углом 30° к горизонтали) и противодействие (реакция) стержня 
тому растягивающему действию, которое испытывает стержень. Изобразим эти три силы на рис. 44,6 и найдем их равнодействующую, вдоль направления действия которой необходимо установить стержень ВС.
2. Оси проекций совместим с силами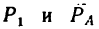 
и определим проекции искомой равнодействующей сначала на ось х, а потом на ось у, зная, что каждая из них равна алгебраической сумме проекций данных сил на соответствующую ось:
3. Обе проекции получаются отрицательными. Значит равнодействующая расположится так, как показано штриховым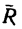 
на рис. 44,6, и положение стержня ВС определится углом 
4. Определим значение угла а из треугольника, образуемого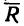 
и его проекциями (рис. 44,в):
Этому значению соответствует угол
5. Стержень ВС необходимо установить под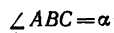
= 70° к стержню АВ., и тогда он будет сжиматься силой, равной
Описанное положение стержня показано на рис. 44, г.
Если же установить стержень, как показано на рисунке штриховой линией ВС, то стержень будет испытывать растяжение, равное той же силе R = 3,83 кн.
Задача №4
Определить равнодействующую пяти сил:
действующих на точку А, как показано на рис. 45,а.
Решение — методом проекций.
1. Так как силы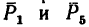 
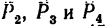
направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы 
будут образовывать с осями проекций углы, показанные на рис. 45.б
2. Найдем проекцию равнодействующей на ось х:
* Здесь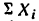 
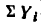
— обозначена алгебраическая сумма проекций всех сил на ось х, а
— алгебраическая сумма проекций тех же сил на ось у.
3. Найдем проекцию равнодействующей на ось у:
4. Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.
Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.
- Равновесие сходящихся сил
- Равновесие трех непараллельных сил
- Сочлененные системы
- Равновесие пространственной системы сходящихся сил
- Потенциальная энергия
- Обобщенные координаты системы
- Сложение двух сил
- Разложение силы на две составляющие