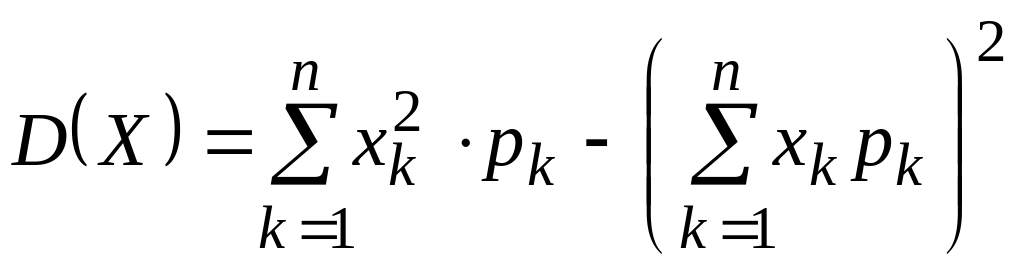Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 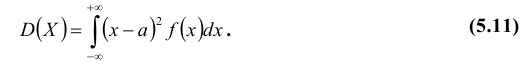
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
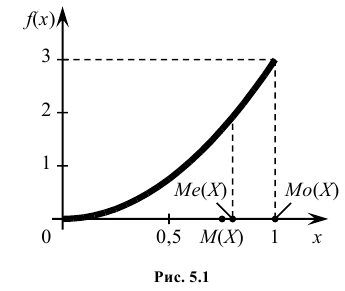
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 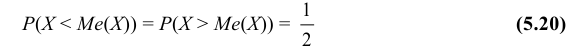
Пример №2
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 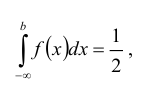
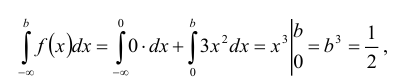
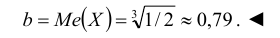
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 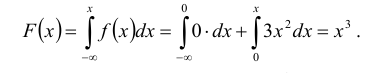
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
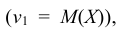
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
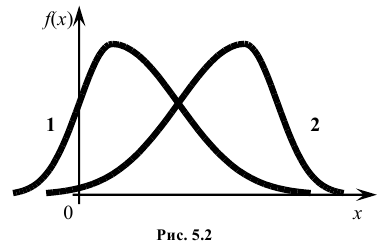
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 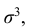
Полученная величина А называется коэффициентом асимметрии случайной величины: 
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
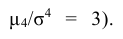
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 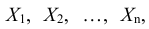
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 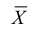
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
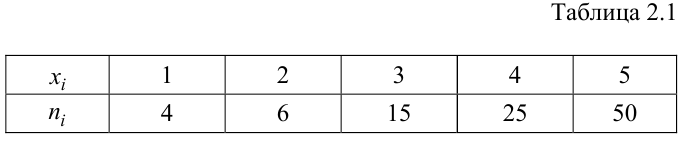
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
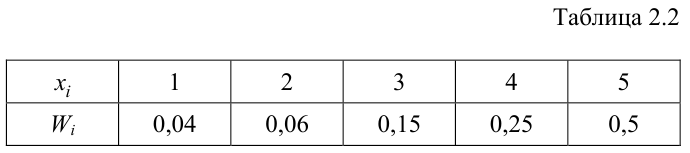
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 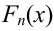
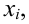
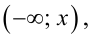
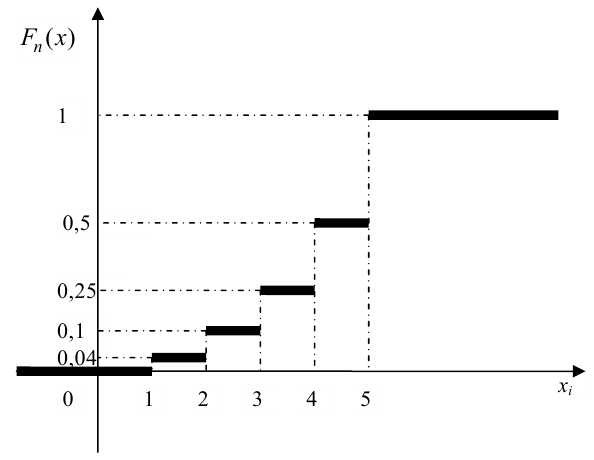
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
Числовые характеристики дискретной случайной величины.
Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение.
Характеристикой среднего значения случайной величины служит математическое ожидание.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной:
2. Постоянную можно выносить за знак математического ожидания:
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
(для разности аналогично)
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.
Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Дисперсию удобно вычислять по формуле:
Свойства дисперсии:
1. Дисперсия постоянной равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:
4.
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
Рассмотрим следующие задачи.
1. Математическое ожидание и дисперсия СВ Х соответственно равны 0,5 и 5. Найти математическое ожидание и дисперсию случайной величины .
Решение.
Согласно свойствам математического ожидания и дисперсии, получаем:
2. Случайные величины X и Y независимы, причем 



Решение.
На основании свойств дисперсии получаем:
3. Закон распределения ДСВ Х задан таблицей распределения
 |
1 | 2 | 3 | 4 |
 |
 |
Найти:
1) Так как , т.е.
, следовательно
Т.о. закон распределения примет вид
 |
1 | 2 | 3 | 4 |
 |
2) Для вычисления дисперсии воспользуемся формулой:
Сначала найдем математическое ожидание ДСВ Х2 для этого составим закон распределения этой СВ. Напоминаю, что для этого необходимо каждое значение ДСВ Х возвести в квадрат, а вероятности оставляем прежними. При одинаковых значениях ДСВ вероятности складываем.
3) Найдем среднее квадратическое отклонение:
4)
4. Функция распределения ДСВ Х имеет вид
Найти:
Решение.
Составляем закон распределения ДСВ Х (т.е. выполняем операцию обратную той, которую мы делали в предыдущей статье)
 |
0 | 1 | 2 | 3 |
 |
0,2 | 0,4 | 0,3 | 0,1 |
Составляем закон распределения ДСВ
 |
0 | 1 | 4 | 9 |
 |
0,2 | 0,4 | 0,3 | 0,1 |
5. Независимые случайные величины X и Y заданы таблицами распределения вероятностей
Найти двумя способами:
1. Составив предварительно таблицу распределения СВ ;
2. Используя правило сложения дисперсий.
Решение.
Составим таблицу распределения ДСВ .
Найдем
10+30=40 20+30=50
10+40=50 20+40=60
10+50=60 20+50=70
Т.о. значения ДСВ Z таковы:
Найдем соответствующие им вероятности:
Получаем ряд распределения СВ Z
| 40 | 50 | 60 | 70 | |
 |
0,1 | 0,46 | 0,28 | 0,16 |
2. Используя правило сложения дисперсий:
Если
дискретная случайная величина X
задана законом распределения вероятностей
вида:
то
математическое ожидание
величины
вычисляется по формуле
.
Математическое
ожидание
случайной величины
служит характеристикой среднего
значения величины X.
В задачах
принятия решений математическое
ожидание, например, характеризует
доходность инвестиционного проекта.
Дисперсией
случайной величины
называют математическое ожидание
квадрата отклонения случайной величины
от ее математического ожидания:
,
или
.
Дисперсию удобно
вычислять по формулам:
,
или
.
Средним квадратическим
отклонением случайной величины называют
корень квадратный из дисперсии:
.
Дисперсия и среднее
квадратическое отклонение характеризуют
рассеивание возможных значений случайной
величины вокруг ее математического
ожидания (среднего значения). В задачах
принятия решений среднее квадратическое
отклонение служит мерой риска.
№ 70.
Задан закон распределения дискретной
случайной величины X.
-
34
40
42
45
0,3
0,4
0,1
0,2
Найти:
а) математическое ожидание
;
б) дисперсию
и среднее
квадратическое отклонение
.
Решение.
а)
Математическое ожидание
вычислим по формуле:
.
Следовательно,
.
б) Дисперсию
вычислим по формуле
.
Следовательно,
.
И среднее
квадратическое отклонение равно:
.
Ответ:
.
№ 71.
В условиях задачи № 61 найти: условные
математические ожидания составляющие
при
,
и Y
при
.
Решение.
,
.
Ответ:
2,8;
5.
Понятие математического
ожидания широко используется в
микроэкономике при принятии решений в
условиях неопределенности, с использованием
понятия ожидаемой полезности инвестора
или лица, принимающего решение (ЛПР).
Рассмотрим в качестве иллюстрации
следующий пример.
№ 72.
Пусть
ЛПР с функцией полезности
обладает начальным капиталом в 10000 руб.
-
ЛПР может принять
участие в игре, в которой он с вероятностью
0,5 может выиграть или проиграть 2000 руб.
Имеет ли ему смысл покупать страховой
полис, устраняющий риск, за 500 руб., или
не играть. -
ЛПР рискнул, принял
участие в игре и проиграл. Следует ли
ему снова принять участие в игре, или
застраховать свой риск на прежних
условиях.
Решение.
1.
Закон распределения вероятностей
капитала ЛПР при участии в игре без
страховки имеет вид:
|
8000 |
1200 |
|
|
0,5 |
0,5 |
Тогда полезность
такого решения будет равна
ют.
При покупке
страхового полиса закон распределения
вероятностей капитала ЛПР имеет вид:
|
9500 |
11500 |
|
|
0,5 |
0,5 |
с полезностью
ют.
Если вычислить
первоначальную полезность ЛПР:
ют.,
то можно сделать
вывод о том, что ЛПР следует играть,
застраховав свой риск, а без страховки
лучше и не играть.
2.После проигрыша
капитал ЛПР составит 8000 руб., поэтому
его участие в игре второй раз будет
иметь следующую полезность:
а) без страховки
ют.;
б) со страховкой
ют.
Если вычислить
полезность ЛПР после первого проигрыша
ют.,
то можно сделать
вывод о том, что ЛПР может играть и во
второй раз, если полностью застрахует
свой риск.
№ 73
— 74.
Задан закон распределения вероятностей
дискретной случайной величины. Найти
числовые характеристики.
№ 73. №
74.
-
19
21
22
24
7
10
12
14
0,1
0,2
0,3
0,4
0,3
0,2
0,4
0,1
№ 75.
Дан
перечень возможных значений дискретной
случайной величины
:
,
,
,
а
так же известны
,
.
Найти вероятности, соответствующие
возможным значениям X.
№ 76.
Проводятся многократные испытания
некоторого элемента на надежность до
тех пор, пока элемент не откажет. Найти
математическое ожидание и дисперсию
дискретной величины
–
числа испытаний, которое надо провести.
Вероятность отказа элемента в каждом
опыте равна 0,2.
№ 77.
В условиях задачи № 68 найти условные
математические ожидания составляющей
.
№ 78.
В
условиях задачи № 69 найти условные
математические ожидания составляющей
.
№ 79.
Дано следующее состояние рынка ценных
бумаг трех видов
:
-
Состояние
рынка (
)Вероятность
Доходность
ценных бумаг (в %)(хорошее)
0,5
30
20
40
(среднее)
0,3
20
20
10
(плохое)
0,2
-5
-10
-20
Определить, какая из ценных бумаг
является: а) наиболее доходной; б) наименее
рисковой.
№ 80. Летом цена угля за 1 т равна 6
у.е. и у Вас есть место для хранения 6 т
угля. Весь уголь, который не будет
использован в течение зимы, пропадет.
Данные о потребности и ценах на уголь
в зимний период приведены в следующей
таблице:
|
Зима |
Вероятности |
Потребность угля |
Средняя цена за 1 |
|
мягкая |
0,35 |
4 |
7 |
|
обычная |
0,5 |
5 |
7,5 |
|
холодная |
0,15 |
6 |
8 |
Сколько угля Вам следует закупить
летом?
№ 81. В условиях № 72 найдите максимальную
сумму, которую может заплатить ЛПР за
страховку как в первом, так и во втором
случаях.
№ 82. Пусть функция полезности
инвестора имеет вид:
.
Инвестор может вложить в некоторый
проект 25000 руб. и считает, что с одинаковой
вероятностью может получить прибыль в
30000 руб., или потерять все. Определите:
а) следует ли осуществлять инвестирование
проекта; б) какова ожидаемая полезность
инвестирования.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Случайной называют величину, которая в результате испытания примет одно и только одно
возможное значение, наперед не известное и зависящее от случайных причин,
которые заранее не могут быть учтены.
Случайные
величины обозначаются прописными буквами
, а их возможные значения – соответствующими строчными буквами
. Например, если случайная величина
имеет три возможных
значения, то они будут обозначены так:
.
Дискретной называют случайную
величину, которая принимает отдельные, изолированные возможные значения с
определенными вероятностями. Число возможных значений дискретной случайной
величины может быть конечным или бесконечным.
Законом распределения дискретной
случайной величины называют соответствие между возможными значениями и их
вероятностями; его можно задать таблично, аналитически (в виде формулы) и
графически.
При табличном задании закона
распределения дискретной случайной величины первая строка таблицы содержит
возможные значения, а вторая – их вероятности:
|
|
|
|
… |
|
|
|
|
|
… |
|
Приняв во внимание, что в одном
испытании случайная величина принимает одно и только одно возможное значение,
заключаем, что события
образуют полную
группу; следовательно, сумма вероятностей этих событий, то есть сумма
вероятностей второй строки таблицы, равна единице:
Если множество возможных значений
бесконечно
(счетно), то ряд
сходится и его
сумма равна единице.
Для наглядности закон распределения
дискретной случайной величины можно изобразить и графически. Для этого в
прямоугольной системе координат строят точки
, а затем соединяют их отрезками прямых. Полученную
фигуру называют многоугольником распределения.
Смежные темы решебника:
- Непрерывная случайная величина
- Функция распределения вероятностей
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Задача 1
В партии
из 25 кожаных курток 5 имеют скрытый дефект. Покупают 3 куртки. Найти закон
распределения числа дефектных курток среди купленных. Построить многоугольник
распределения.
Задача 2
Устройство
состоит из пяти независимых элементов. Вероятность безотказной работы каждого
элемента в одном опыте равна p=0,7. Для случайной
величины X элементов, безотказно работавших в одном опыте,
построить закон распределения, их графики, найти ее числовые характеристики.
Задача 3
С
вероятностью попадания при явном выстреле p=0.88 охотник стреляет по
дичи до первого попадания, но успевает сделать не более n=6
выстрелов.
ДСВ X — число
промахов:
а) Найти
закон распределения X.
б)
Построить многоугольник распределения.
в) Найти
вероятность событий: X<2, X<3,
1<X<3.
Задача 4
Составьте
закон распределения дискретной случайной величины ξ, вычислите ее
математическое ожидание, медиану, дисперсию, среднее квадратическое отклонение,
коэффициенты асимметрии и эксцесса, все моменты, а также начертите ее
многоугольник распределения и график функции распределения. Сделайте выводы по
результатам расчетов.
Производятся
последовательные испытания 5 приборов, причем испытания прекращаются сразу
после того, как проверяемый прибор окажется надежным. Вероятность выдержать
испытание для каждого прибора равна 0,8.
ξ – число испытаний, после которых закончится проверка.
Задача 5
В первой урне
6 шаров – 3 белых и 3 черных. Во второй 5 шаров –3 белых и 2 черных. Из первой
урны наудачу переложили во вторую 2 шара, после чего, из второй в первую
переложили 1 шар. Найти закон распределения случайной величины Х – числа белых
шаров в первой урне, после всех перекладываний шаров. Какова вероятность того,
что число белых шаров не больше, чем первоначально. Построить многоугольник
распределения.
Задача 6
В коробке
N=9 карандашей, из которых M=6 красных. Из этой коробки
наудачу извлекается n=5 карандашей.
а) Найти
закон распределения случайной величины X равной числу красных
карандашей в выборке.
б)
Построить многоугольник распределения.
в) Найти
вероятность события: 0<X<4.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Производятся
последовательные испытания 5 приборов, причем испытания прекращаются сразу
после того, как проверяемый прибор оказался надежным. Вероятность выдержать
испытание для каждого прибора равна 0,8. X – число испытаний, после
которых закончится проверка. Составьте закон распределения случайной величины X,
вычислите ее математическое ожидание, дисперсию, среднее квадратическое
отклонение, а также начертите ее многоугольник распределения и график функции
распределения.
Задача 8
Проведено
n=5 независимых опытов. Вероятность взрыва в каждом опыте равна p=2/7.
Составить закон распределения числа взрывов, вычислить математическое ожидание,
дисперсию, среднеквадратическое отклонение и построить многоугольник
распределения.
Задача 9
Найти закон
распределения указанной дискретной СВ X и ее функции. распределения
F(x). Вычислить математическое ожидание М(Х), дисперсию D(X) и
среднее квадратичное отклонение σ(Х). Построить график
функции распределения F(x).
Вероятность отказа прибора за время испытания
на надежность равна 0,2; СВ Х — число приборов, отказавших в работе, среди 5
испытываемых.
Задача 10
В интернет-магазине
приобретается смартфон. Курьер приносит на дом покупателю 5 одинаковых
смартфонов, среди которых три (заранее неизвестно какие) бракованные.
Покупатель проверяет один за другим, пока не найдет хороший прибор, но делает
не более трех попыток.
Составить
закон распределения случайной величины – числа произведенных попыток.
Найти ее
математическое ожидание, дисперсию, среднее квадратическое отклонение.
Построить
функцию распределения.
Задача 11
В команде
9 спортсменов, из них 4 — первого разряда и 5 — второго. Наудачу отобраны 3
спортсмена. Найти ряд распределения дискретной случайной величины Х — числа
спортсменов второго разряда среди отобранных.
Задача 12
К контролеру с конвейера поступили 4 детали.
Вероятность брака для каждой детали равна 0,1. Детали проверяют одну за другой,
пока не наберут 2 доброкачественные.
Найти закон распределения вероятностей для числа проверенных деталей.
Задача 13
Двое рабочих,
выпускающих однотипную продукцию, допускают производство изделий второго сорта
с вероятностями соответственно равными 0,4 и 0,3. У каждого рабочего взято по 2
изделия. Для случайной величины Х —
числа изделий второго сорта среди отобранных для проверки четырех найти закон
распределения, математическое ожидание и дисперсию.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
На викторине
задаются 3 вопроса. Вероятность правильно ответить на первый – p, на
второй – r, на третий – s. После неправильного
ответа игрок выбывает из игры. Найти распределение числа правильных ответов.
Вычислить математическое ожидание. Решить задачу, если:
а) p=0.7; r=0.6; s=0.3;
б)
p=0.8; r=0.4; s=0.1.
Задача 15
На
некоторой остановке автобус останавливается только по требованию. Вероятность
остановки равна 0,2. За смену автобус проходит мимо этой остановки 5 раз.
Составить закон распределения числа остановки за смену, найти математическое
ожидание и дисперсию этой случайной величины.
Задача 16
Вероятность
того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3.
Аудитору на заключение представлено 3 баланса предприятия. Составить закон
распределения числа положительных заключений на проверяемые балансы.
Задача 17
Два товароведа
проверяют партию изделий. Производительность их труда соотносится как 5:4.
Вероятность определения брака первым товароведом составляет 85%, вторым – 90%.
Из проверенных изделий отбирают четыре. Найти а) математическое ожидание и б)
дисперсию числа годных изделий среди отобранных.
Задача 18
Два
станка выпускают детали с вероятностями брака 0,01 и 0,05 соответственно. В
выборке одна деталь выпущена первым станком и две – вторым. Найти распределение числа бракованных деталей
в выборке.
Задача 19
Монета
подбрасывается до тех пор, пока герб не выпадет 2 раза, но при этом делается не
более 4 бросаний. Найти распределение числа подбрасываний.
Задача 20
Вероятность
сдачи данного экзамена для каждого из n=5 студентов равна p=0.6.
Случайная величина X (СВ X) — число студентов, сдавших экзамен. Найти закон
распределения указанной дискретной СВ X и ее функцию распределения F(x).
Вычислить математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x). Построить график функции распределения F(x).
Числовые характеристики дискретной случайной величины
В этом разделе:
- Основная информация
- Онлайн калькулятор
- Полезные ссылки
Понравилось? Добавьте в закладки
Основная информация
Числовые характеристики дискретной случайной величины $X$, которые обычно требуется находить в учебных задачах по теории вероятностей, это математическое ожидание $M(X)$, дисперсия $D(X)$ и среднее квадратическое отклонение $sigma(X)$.
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
$$
sigma(X) = sqrt{D(X)}.
$$
Подробные формулы и примеры расчета вы найдете по ссылкам в предыдущем абзаце, в этом же разделе вы сможете автоматически и бесплатно рассчитать эти значения с помощью онлайн-калькулятора, который даст не только ответ, но и продемонстрирует процесс вычисления.
Подробно решим ваши задачи по теории вероятностей
Калькулятор: числовые характеристики случайной величины
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -1.5 или 10.558). Введите нужные значения (убедитесь, что сумма вероятностей равна единице, то есть закон распределения задан верно).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет процесс вычисления математического ожидания $M(X)$, дисперсии $D(X)$ и СКО $sigma(X)$.
- Нужны еще расчеты? Вводите новые числа и нажимайте на кнопку.
Видео. Полезные ссылки
Видеоролики об СКО
На закуску для продвинутых — какие формулы вычисления СКО для выборок бывают и для чего подходят.
Понравилось? Добавьте в закладки
Полезные ссылки
- Калькуляторы по теории вероятнстей
- Онлайн учебник по ТВ
- Примеры решений по теории вероятностей
- Контрольные по теории вероятностей на заказ
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

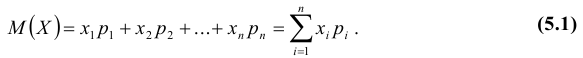
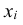
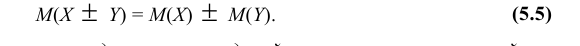


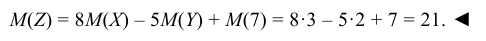







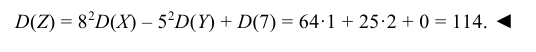
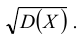

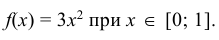

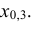
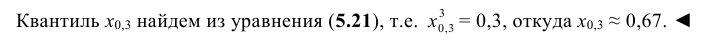



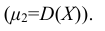
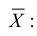
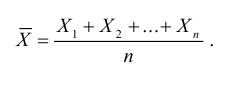

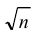 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: 

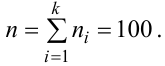
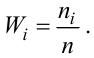
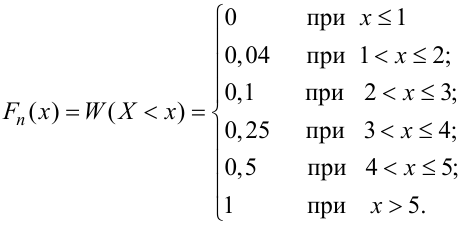

![Rendered by QuickLaTeX.com [M(C)=C]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-471b40041b6933f0801951cd2c46c645_l3.png)
![Rendered by QuickLaTeX.com [M(CX)=CM(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ded777e15e9adcf8796eeaac76336930_l3.png)
![Rendered by QuickLaTeX.com [M(X_1 cdot X_2 cdot ... cdot X_n)=M(X_1)cdot M(X_2)cdot ... cdot M(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6b30f00123a46fe5905869e2348bdd02_l3.png)
![Rendered by QuickLaTeX.com [M(X_1 + X_2 + ... + X_n)=M(X_1) + M(X_2) + ... + M(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c7b91ac649ba7364f862a40bf8faa91d_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M{[X-M(X)]}^2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-85d713b45963c5757fd071259ac6010f_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M(X^2)-{[M(X)]}^2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0d17db045a4e914ee13c4f6d75c27ea3_l3.png)
![Rendered by QuickLaTeX.com [D(C)=0]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6d535643c4c0b9772d8010dd2bc73943_l3.png)
![Rendered by QuickLaTeX.com [D(CX)=C^2D(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cce0e2900dab2027e7e321a4a122b4a9_l3.png)
![Rendered by QuickLaTeX.com [D(X_1 pm X_2 pm ... pm X_n)=D(X_1) + D(X_2) + ... + D(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-08c51f96c711f2b69dd776944a864ee3_l3.png)
![Rendered by QuickLaTeX.com [D(X+C)=D(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-a915073dccca53c6e5527d0241d183e6_l3.png)
![Rendered by QuickLaTeX.com [sigma (X) =sqrt{D(X)}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-bcacf00d61c4a3f0f69c6d6cfed60d51_l3.png)
![Rendered by QuickLaTeX.com [M(2X-3)=M(2X)+M(-3)=2M(X)-3=2cdot frac12-3=1-3=-2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-010184719e61abad64efd1f6bf166096_l3.png)
![Rendered by QuickLaTeX.com [D(2X-3)=4cdot D(X)=4cdot 5=20]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-2a326d2cfcb9cfa50fdee69fe551cee4_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=D(4cdot X- 5 cdot Y +3)=16cdot D(X)+25cdot D(Y)=16cdot 3+25cdot 5=48+125=173]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-72cc99dbd22855f093a923bfe7693994_l3.png)
![Rendered by QuickLaTeX.com [c=1-frac18 -frac14 -frac13=frac{24-3-6-8}{24}=frac{7}{24}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-01420ef852ee1007bd45d93fcbe0b95b_l3.png)
![Rendered by QuickLaTeX.com [M(X)=sum_{i=1}^4 x_i cdot p_i=1cdot frac18+2cdot frac14+3cdot frac13+4cdot frac{7}{24}=frac18+frac12+1+frac76=]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-42c69ea716d0d80a5cc1caa69ef11227_l3.png)
![Rendered by QuickLaTeX.com [M(X^2)=1cdot frac18+4cdot frac14+9cdot frac13+16cdot frac{7}{24}=frac18+1+3+frac{14}{3}=frac{3+96+112}{24}=frac{211}{24};]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-99d6101975deac0f6dbe962de43e23a1_l3.png)
![Rendered by QuickLaTeX.com [D(X)=frac{211}{24}-{left(frac{67}{24}right)}^2=frac{24cdot 211-{67}^2}{{24}^2}=frac{5064-4489}{576}=frac{575}{576};]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cc6b23de18058d53a5ed1fdc11cd9921_l3.png)
![Rendered by QuickLaTeX.com [sigma (X) =sqrt{D(X)}=sqrt{frac{575}{576}}=frac{5sqrt{23}}{24}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-f779e760519df59d8651da0aaa8c2e4b_l3.png)
![Rendered by QuickLaTeX.com [P{X<3}=P{X=1}+P{X=2}=frac18+frac14=frac38]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-65e7c06bd40f6f6cbc44912a49eefda2_l3.png)
![Rendered by QuickLaTeX.com [F(x)={ 0, qquad qquad xle 0 \ 0,2, qquad 0< x le 1, \ 0,6, qquad qquad 1< x le 2 \ 0,9, qquad qquad 2< x le 3 \ 1, qquad qquad x>3]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0947abc5c1ed52fd612642b5b73df2aa_l3.png)
![Rendered by QuickLaTeX.com [M(X), quad M(X^2) quad D(X), quad sigma (X).]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-e2e328ddbafd8e7412cee6e6b7013e8e_l3.png)
![Rendered by QuickLaTeX.com [M(X)=0cdot 0,2+1cdot 0,4+2cdot 0,3+3cdot 0,1=0,4+0,6+0,3=1,3]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-7b7b00dc6dd7147605a5d00f6e4ba120_l3.png)

![Rendered by QuickLaTeX.com [M(X^2)=0cdot 0,2+1cdot 0,4+4cdot 0,3+9cdot 0,1=0,4+1,2+0,9=2,5]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-d3aee42db306199c080afa80f72b3b92_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M(X^2)-{[M(X)]}^2=2,5-{1,3}^2=2,5-1,69=0,81]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cf146049246b3e3f395117bc29116db0_l3.png)
![Rendered by QuickLaTeX.com [sigma (X)=sqrt{0,81}=0,9]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ac025cd6cccf0e250723d48aad978616_l3.png)
![Rendered by QuickLaTeX.com [p_1=P{Z=40}=P{X=10, Y=30}=0,2cdot 0,5=0,1]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-7e1ae4f8b0462f0e7f531d90b468f792_l3.png)
![Rendered by QuickLaTeX.com [p_4=P{Z=70}=P{X=20, Y=50}=0,8cdot 0,2=0,16]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c4ec8e48db0ba1e5f8772cd6e498ea7e_l3.png)
![Rendered by QuickLaTeX.com [M(Z)=sum_{i=1}^4 z_i cdot p_i=40cdot 0,1+50cdot 0,46+60cdot 0,28+70cdot 0,16=4+23+16,8+11,2=55;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ac4878cee852a38e8245022d95b24e00_l3.png)
![Rendered by QuickLaTeX.com [M(Z^2)=sum_{i=1}^4 z_i^2 cdot p_i=1600cdot 0,1+2500cdot 0,46+3600cdot 0,28+4900cdot 0,16=]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ec5b2451d92ebf30458b26e4926d5f63_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=M(Z^2)-{[M(Z)]}^2=3102-3025=77]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-451663c9d742fa3e5fb04afdd7766522_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=D(X+Y)=D(X)+D(Y)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-448a698e43900414c039e2e1e624b053_l3.png)
![Rendered by QuickLaTeX.com [M(X)=10cdot 0,2+20cdot 0,8=2+16=18;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-1ebf2d8b6e0fe85428901ac0b008f5dd_l3.png)
![Rendered by QuickLaTeX.com [M(X^2)=100cdot 0,2+400cdot 0,8=20+320=340;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-32cfe37c5de52468e58eeeadf3e2f766_l3.png)
![Rendered by QuickLaTeX.com [M(Y)=30cdot 0,5+40cdot 0,3+50cdot 0,2=15+12+10=37]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0a5b2478301af6479cd142fcd67c4146_l3.png)
![Rendered by QuickLaTeX.com [M(Y^2)=900cdot 0,5+1600cdot 0,3+2500cdot 0,2=450+480+500=1430]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6b21d4279e597b4488766bf66dc5ec57_l3.png)
![Rendered by QuickLaTeX.com [D(Y)=1430-1369=61]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-641d0e807ce0687edbf79f037574635d_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=16+61=77]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c0e8e4fe96eb97d5374b249328fd738f_l3.png)