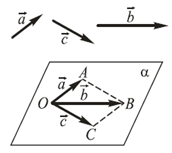
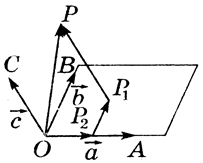
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 1).
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Условия компланарности векторов
-
Для 3-х векторов. Три вектора компланарны если они линейно зависимы.
-
Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.
Примеры задач на компланарность векторов
Пример 1. Проверить компланарны ли три вектора a = {1; 2; 3},
b = {1; 1; 1}, c = {1; 2; 1}.
Решение: найдем смешанное произведение векторов
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2
Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.
Пример 2. Доказать что три вектора a = {1; 1; 1},
b = {1; 3; 1} и c = {2; 2; 2} компланарны.
Решение: найдем смешанное произведение векторов
| a · [b × с] = | 1 | 1 | 1 | = |
| 1 | 3 | 1 | ||
| 2 | 2 | 2 |
= 1·2·3 + 1·1·2 + 1·1·2 — 1·2·3 — 1·1·2 — 1·1·2 = 6 + 2 + 2 — 6 — 2 — 2 = 0
Ответ: вектора компланарны так, как их смешанное произведение равно нулю.
Пример 3. Проверить коллинеарны ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1}, d = {3; 3; 3}.
Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования
| 1 | 1 | 1 | ~ | ||
| 1 | 2 | 0 | |||
| 0 | -1 | 1 | |||
| 3 | 3 | 3 |
из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3
| ~ | 1 | 1 | 1 | ~ | 1 | 1 | 1 | ~ | ||||
| 1 — 1 | 2 — 1 | 0 — 1 | 0 | 1 | -1 | |||||||
| 0 | -1 | 1 | 0 | -1 | 1 | |||||||
| 3 — 3 | 3 — 3 | 3 — 3 | 0 | 0 | 0 |
к 3-тей строке добавим 2-рую
| ~ | 1 | 1 | 1 | ~ | 1 | 1 | 1 | ||||
| 0 | 1 | -1 | 0 | 1 | -1 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 | 0 | 0 | ||||||
| 3 — 3 | 3 — 3 | 3 — 3 | 0 | 0 | 0 |
Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.
Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.
В данной публикации мы рассмотрим, какие векторы называются компланарными, и перечислим условия для компланарности двух, трех и большего количества векторов. Также разберем примеры решения задач по этой теме.
- Условия компланарности векторов
- Пример задачи
Условия компланарности векторов
Векторы, лежащие в одной плоскости или параллельные ей, называются компланарными.
Из определения следует, что любые два вектора компланарны, т.к. всегда можно найти плоскость, параллельную им обоим.
Условия компланарности:
- Для трех векторов:
- Их смешанное произведение равняется нулю.
- Они линейно зависимы.
- Для n-ого количества векторов: среди них не более двух линейно независимых векторов.
Пример задачи
Определим, являются ли векторы a = {2; 5; 8}, b = {1; 4; 3} и c = {6; 7; 1} компланарными.
Решение
Чтобы проверить компланарность векторов с заданными координатами, найдем их смешанное произведение.
a · [b x c] = 8 + 90 + 56 – 192 – 42 – 5 = -85
Таким образом, векторы не являются компланарными, т.к. их смешанное произведение не равняется нулю.
Компланарные векторы
Содержание:
- Что такое компланарные векторы
-
Условия компланарности и линейная зависимость векторов
- Линейная зависимость
- Условия компланарности
- Теоремы, связанные с условием компланарности трех векторов
- Пример задачи на компланарность векторов
Что такое компланарные векторы
Определение
Векторы называются компланарными, если лежат в одной или параллельных плоскостях.
Это определение справедливо только для трех и более векторов, так как для двух направленных отрезков всегда можно найти плоскость, параллельную им.
Условия компланарности и линейная зависимость векторов
Среди условий компланарности векторов встречается понятие линейной зависимости, которое следует разобрать перед тем, как перейти непосредственно к условиям.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Линейная зависимость
Линейно зависимыми называются вектора (overline{a_1},;overline{a_2},;dots;,;overline{a_n};), которые можно составить в линейную комбинацию, равную нулю: (lambda_1cdotoverline{a_1}+;lambda_2cdotoverline{a_2}+dots+;lambda_noverline{cdot a_n};=0.)
Линейная комбинация — вектор, составленный из суммы векторов (overline{a_1},;overline{a_2},;dots;,;overline{a_n};) и коэффициентов разложения (lambda_{1,};lambda_2,;dots;,;lambda_n.)
Существует пять критериев и свойств линейной зависимости векторов:
- Хотя бы один из векторов можно представить в виде линейной комбинации других.
- В n-мерном пространстве любые n+1 векторов линейно зависимы.
- Хотя бы один из векторов — нулевой.
- Если часть системы векторов линейно зависимы, то это справедливо и для остальных.
- Если одна система векторов может быть выражена через другую и содержит больше векторов, то такая система линейно зависима.
Условия компланарности
Для неограниченного числа векторов справедливо следующее: если среди них есть не более двух линейно независимых векторов, то они компланарны.
На практике чаще всего встречаются задачи с тройками векторов. Для них существуют и другие условия компланарности:
- Если три вектора линейно зависимы, то они компланарны.
- Смешанное произведение компланарных векторов равняется нулю.
Теоремы, связанные с условием компланарности трех векторов
Правило, согласно которому три вектора компланарны, если их смешанное произведение равно нулю, проистекает из теоремы. Его также называют признаком и критерием компланарности векторов. Доказать данное утверждение можно следующим образом:
Пусть смешанное произведение ((overline atimesoverline b)cdotoverline c=0). Векторы ((overline atimesoverline b)) и (overline c) — перпендикулярны, так как их скалярное произведение равняется нулю.
В то же время, результатом векторного произведения является вектор, перпендикулярный перемножаемым. Таким образом, векторы overline a,overline b,overline c перпендикулярны одному и тому же вектору (overline atimesoverline b), то есть лежат в параллельных плоскостях. Значит, векторы компланарны.
Для проверки, к доказательству данной теоремы можно подойти с другой стороны:
Пусть векторы overline a,overline b,overline c компланарны.
Необходимо доказать, что их смешанное произведение ((overline atimesoverline b)cdotoverline c) равняется нулю. Так как данные вектора компланарны, то ((overline atimesoverline b)) перпендикулярен каждому из них.
Отсюда следует, что его скалярное произведение с вектором overline c будет равняться нулю. Это, в свою очередь, означает, что смешанное произведение ((overline atimesoverline b)cdotoverline c=0.)
Пример задачи на компланарность векторов
Задача
Даны точки A(1, 2, -1), B(0, -1, 5), C(-1, 2, 1) и D(2, 1, 3). Проверить, принадлежат ли они одной плоскости.
Решение
Сперва необходимо построить на основе имеющихся точек векторы (overline{AB},;overline{AC},;overline{AD}:)
(overline{AB}=(0-1,;(-1)-2,;5-(-1))=(-1,;3,;6))
(overline{AС}=((-1)-1,;2-2,;1-(-1))=(-2,;0,;2))
(overline{AВ}=(2-1,;1-2,;3-(-1))=(1,;-1,;4))
Чтобы проверить, принадлежать ли точки одной плоскости, необходимо найти смешанное произведение полученных векторов. Если оно равняется нулю, то векторы компланарны, следовательно, точки лежат в одной плоскости. В противном случае ответ на поставленный в условии вопрос будет отрицательным.
Смешанное произведение рассчитывается по формуле нахождения определителя матрицы:
((overline{AВ}timesoverline{AC})cdotoverline{AD}=begin{vmatrix}-1&-3&6\-2&0&2\1&-1&4end{vmatrix}=((-1)cdot0cdot4)+((-3)cdot2cdot1)+((-2)cdot(-1)cdot6)-(6cdot0cdot1)-((-1)cdot2cdot(-1))-((-3)cdot(-2)cdot4)=0-6+12-0-2-24=-20)
Полученное число не равно нулю, следовательно, векторы некомпланарны. Это значит, что точки не лежат в одной плоскости.
Одно из определений компланарных векторов гласит:
векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами.
Тот же смысл имеет и другое определение:
три вектора называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.
Обрати внимание!
Всегда возможно найти плоскость, параллельную двум произвольным векторам, поэтому любые два вектора всегда компланарные.
Eсли из трёх векторов два коллинеарны, то очевидно, что эти три вектора компланарны.
Все вышеупомянутые случаи легко рассмотреть, если разместить векторы на рёбрах параллелепипеда.
1. Любые два вектора находятся в одной плоскости, но в одной плоскости можно разместить и векторы
AA1→
,
CC1→
и
AD→
, то есть, эти векторы компланарны. Также компланарны векторы
AA1→
,
AB→
и
CC1→
, так как два из этих векторов параллельны. Легко представить, что если привести их к общему началу, то вектор
CC1→
совпадёт с вектором
AA1→
.
2. Например, векторы
AB→
,
AD→
и
AA1→
не компланарны, так как их нельзя разместить в одной и той же плоскости.
Признак компланарности трёх векторов:
пусть векторы
a→
и
b→
не коллинеарны. Если для вектора
c→
существует единственная пара реальных чисел (x) и (y), такая, что
c→=x⋅a→+y⋅b→
, то векторы
a→
,
b→
и
c→
компланарны.
Справедливо и обратное утверждение:
если три вектора
a→
,
b→
и
c→
компланарны и векторы
a→
и
b→
не коллинеарны, то вектор
c→
можно разложить по векторам
a→
и
b→
одним-единственным образом.
Если разложить вектор
AC→
по векторам
AA1→
и
AA2→
, то это можно сделать одним-единственным образом:
AC→=AB→+AD→=x⋅AA1→+y⋅AA2→
.
Если три вектора некомпланарны, то для их сложения в пространстве применяется закон параллелепипеда.
1. Векторы приводят к общему началу (A).
2. На этих трёх рёбрах строится параллелепипед.
3. Диагональ параллелепипеда, которая выходит из этой же точки, изображает суммы векторов
AB→
,
AD→
и
AA1→
.

Разложение вектора по трём некомпланарным векторам
Теорема о разложении по базису в пространстве
Любой вектор
d→
можно разложить по трём данным некомпланарным векторам
a→
,
b→
и
c→
, причём реальные коэффициенты разложения (x), (y) и (z) определяются единственным образом:
AC1→=AD→+AB→+AA1→=x⋅AA2→+y⋅AA3→+z⋅AA4→
.
Конспект урока: Компланарные векторы. Правило параллелепипеда. Разложение вектора по трём некомпланарным векторам
Другие разделы
План урока
- Компланарные векторы;
- Правило параллелепипеда;
- Разложение вектора по трем некомпланарным векторам.
Цели урока
- Знать определение компланарных векторов;
- Знать и уметь доказывать признак компланарности трёх векторов;
- Знать и уметь применять правило параллелепипеда сложения трёх некомпланарных векторов;
- Знать и уметь доказывать теорему о разложении вектора по трём некомпланарным векторам;
- Уметь находить разложение вектора по трём данным некомпланарным векторам.
Разминка
- Какие векторы называются коллинеарными?
- Сколько плоскостей проходит через три точки, не лежащие на одной прямой?
- Две стороны треугольника параллельны плоскости α. Параллельна ли третья сторона плоскости α?
Компланарные векторы
Определение 1
Компланарные векторы
— это векторы, которые параллельны одной плоскости или лежат в одной плоскости (рис. 1).
Рис. 1. Компланарные вектора
Можно также сказать, что векторы называются компланарными, если при откладывании их от одной точки они будут лежать в одной плоскости (другими словами, имеются равные им векторы, лежащие в одной плоскости).
Из определения следует, что любые два векторы компланарны, а три произвольных вектора могут быть как компланарными, так и не компланарными.
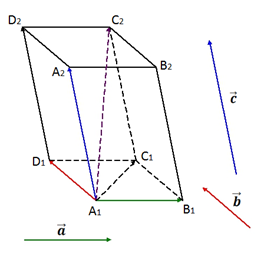
Рис. 2.
На рисунке 2 изображён параллелепипед.
Векторы D1D2→, A1C2→, A1C1→ компланарны, так как если отложить от точки A1 вектор, равный D1D2→, то получится A1A2→, а векторы A1A2→, A1C2→, A1C1→ лежат в одной плоскости A2A1C1.
Векторы A1D1→, A1B1→, A1A2→ не компланарны, так вектор A1A2→ не лежит в плоскости D1A1B1.
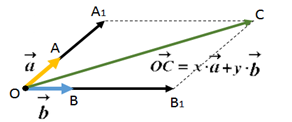
Теорема 1 (признак компланарности трёх векторов)
Если вектор c→ можно разложить по векторам a→ и b→, т.е. представить в виде с→=xa→+yb→, где x и y – некоторые числа, то векторы a→, b→ и c→ компланарны.
Доказательство
Рис. 3. К теореме 1
Если векторы a→ и b→ коллинеарны, то компланарность векторов a→, b→ и c→ очевидна.
Рассмотрим случай когда векторы a→ и b→ не коллинеарны.
Отложим от произвольной точки O векторы OA→=a→ и OB→=b→ (рис. 3).
Векторы OA→ и OB→ лежат в плоскости OAB. В этой же плоскости лежат векторы OA1→=x·OA→ и OB1→=y·OB→, а значит и их сумма лежит в этой плоскости:
c→=OC→=OA1→+OB1→=x·OA→+y·OB→.
Таким образом векторы a→, b→ и c→ лежат в одной плоскости, т. е. компланарны.
Теорема доказана.
Из теоремы о разложении вектора по двум неколлинеарным векторам (эта теорема доказывалась в курсе планиметрии) следует и обратное утверждение.
Теорема 2 (обратная признаку компланарности)
Если векторы a→, b→ и c→ компланарны, а векторы a→ и b→ не коллинеарны, то вектор c→ можно разложить по векторам a→ и b→, т.е. представить в виде с→=xa→+yb→, причём коэффициенты разложения x и y определяются единственным образом.
Упражнение 1
Дан куб ABCDA1B1C1D1. Определите, являются ли компланарными векторы:
а) AB1→, AD→ и B1D→; б) B1C1→, C1D→ и B1D→;
в) AB→, AD→ и AA1→; г) DA→, DC→ и DB1→.
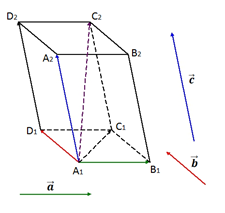
Правило параллелепипеда
Опишем так называемое правило параллелепипеда, которым можно пользоваться при сложении трёх некомпланарных векторов.
Рис. 4. Правило параллелепипеда
Пусть даны некомпланарные векторы a→, b→ и c→. От произвольной точки A1 отложим векторы A1B1→=a→, A1D1→=b→, A1A2→=c→. Построим параллелепипед A1B1C1D1A2B2C2D2 так, чтобы отрезки A1B1, A1D1, A1A2 были его рёбрами (рис. 4). Тогда вектор A1С2→ является суммой данных векторов a→, b→ и c→, т.е. A1С2→=a→+b→+c→.
Упражнение 2
В кубе ABCDA1B1C1D1 найдите вектор, начало и конец которого являются вершины куба, равный сумме векторов:
а) C1B1→+C1D1→+C1C→; б) BA→+BC→+BB1→;
в) AB→+A1D1→+AA1→; г) B1A1→+BC→+B1B→.
Разложение вектора по трём некомпланарным векторам
Представление вектора p→ в виде p→=xa→+yb→+zc→, где x, y и z – некоторые числа, называют
разложением вектора p→ по векторам a→, b→ и c→
. Числа x, y и z называются
коэффициентами разложения
.
Сформулируем и докажем теорему о разложении вектора по трём некомпланарным векторам.
Теорема 3
Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Доказательство
Рис. 5. К доказательству теоремы 3
Даны некомпланарные векторы a→, b→ и c→. Отложим от произвольной точки O векторы OA→=a→ , OB→=b→, OC→=c→, OP→=p→ (рис. 5).
Проведём через точку P прямую, параллельную прямой OC.
Пусть P1 – точка пересечения этой прямой с плоскостью AOB. Через точку P1 проведём прямую, параллельную прямой OB.
Пусть P2 – точка пересечения этой прямой с прямой OA. Согласно правилу многоугольника
OP→=OP2→+P2P1→+P1P→,
OP2→∥OA→, P2P1→∥OB→, P1P→∥OC→. Следовательно, существуют числа x, y и z такие, что OP2→=x·OA→, P2P1→=y·OB→, P1P→=z·OC→.
Таким образом,
OP→=x·OA→+y·OB→+z·OC→
p→=x·a→+y·b→+z·c→.
Докажем теперь, что коэффициенты разложения определяются единственным образом.
Предположим, что некоторый вектор p→ можно разложить по некомпланарным векторам a→, b→ и c→ двумя разными способами, т.е. p→=x1·a→+y1·b→+z1·c→ и p→=x2·a→+y2·b→+z2·c→.
Вычитая из первого равенства второе, получим
0→=x1-x2·a→+y1-y2·b→+z1-z2·c→.
Так как векторы a→, b→ и c→ не компланарны, то это равенство возможно только в случае, если x1-x2=0, y1-y2=0, z1-z2=0 ⇒x1=x2, y1=y2, z1=z2.
Следовательно, коэффициенты разложения p→=x·a→+y·b→+z·c→ определяются единственным образом.
Теорема доказана.
Упражнение 3
В параллелепипеде ABCDA1B1C1D1 разложите:
а) вектор AC1→ по векторам AB→, AD→ и AA1→;
б) вектор AA1→ по векторам D1A1→, D1C1→ и A1C→;
в) вектор D1B→ по векторам D1A1→, D1C1→ и D1D→;
г) вектор BB1→ по векторам CB→, CD→ и B1D→.
Контрольные вопросы
- Какие векторы называются компланарными?
- Сформулируйте признак компланарности трёх векторов.
- В чем заключается правило параллелепипеда, используемое при сложении трёх некомпланарных векторов?
- Сформулируйте теорему о разложении вектора по трём неколлинеарным векторам.
Ответы
Упражнение 1
а) да; б) да; в) нет; г) нет.
Упражнение 2
а) C1A→; б) BD1→; в) AC1→; г)B1D.
Упражнение 3
а) AC1→=AB→+AD→+AA1→;
б) AA1→=D1C1→-D1A1→-A1C→;
в) D1B→=D1A1→+D1C1→+D1D→;
г) BB1→=CD→-B1D→-CB→.
Предыдущий урок
Движения
Преобразования на плоскости и в пространстве
Следующий урок
Сфера и шар
Сфера и шар