Как найти cos асв

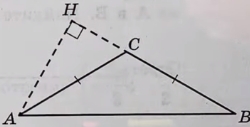
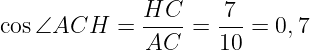В тупоугольном треугольнике ABC известно, что AC = BC, высота AH равна 24, CH = 7. Найдите cos ACB.

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,284
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,093
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

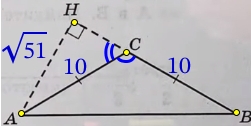
Решение №2303 В тупоугольном треугольнике ABC известно, что AC = BC = 10, высота AH равна √51.

В тупоугольном треугольнике ABC известно, что AC = BC = 10, высота AH равна √51. Найдите косинус угла ACB.

Источник: Ященко ЕГЭ 2022 (36 вар)

В прямоугольном ΔАНС по теореме Пифагора найдём катет НС:

Косинусы смежных углов равны по модулю, противоположны по знаку:

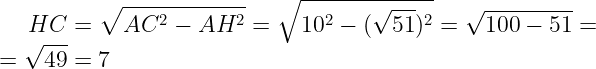
cos ∠ACB = –cos ∠ACH

Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Найдём cos∠ACH:

Найдём косинус искомого угла АСВ:

cos∠ACB = –cos∠ACH = –0,7

Теорема косинусов

Формулировка теоремы косинусов

Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:

Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними

Полезные формулы теоремы косинусов:

Как видно из указанного выше, с помощью теоремы косинусов можно найти не только сторону треугольника по двум сторонам и углу между ними, можно, зная размеры всех сторон треугольника, определить косинусы всех углов, а также вычислить величину любого угла треугольника. Вычисление любого угла треугольника по его сторонам является следствием преобразования формулы теоремы косинусов.

Теорема Пифагора

Теорема Пифагора . В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы .

Доказательство . Докажем, что длины сторон произвольного прямоугольного треугольника ABC (рис.1)

С этой целью рассмотрим квадрат квадрат со стороной, равной c , изображённый на рисунке 2.

Площадь этого квадрата равна сумме площадей четырёх одинаковых прямоугольных треугольников, равных треугольнику ABC (рис.3, рис.4), и площади квадрата со стороной, равной a – b (рис.5).

Рис.3

Рис.4

Рис.5

Поэтому справедливо равенство

что и требовалось доказать.

Формулировка теоремы косинусов для треугольника

Теорема косинусов для треугольника связывает две стороны треугольника и угол между ними со стороной, лежащей против этого угла. К примеру, обозначим буквами , , и длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.

Тогда имеет теорема косинусов для этого треугольника может быть записана в виде:

На рисунке для удобства дальнейших рассуждений угол С обозначен углом . Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»

Понятно, что если бы вы выражали другую сторону треугольника, например, сторону , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны и . Выражение для квадрата стороны . Выражение для квадрата стороны получается аналогично:

Классическое доказательство теоремы косинусов.

Пусть есть треугольник ABC. Из вершины C на сторону AB опустили высоту CD. Значит:

Записываем теорему Пифагора для 2-х прямоугольных треугольников ADC и BDC:

h 2 = b 2 – (b cos α) 2 (1)

h 2 = a 2 – (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 – (b cos α) 2 = a 2 – (c – b cos α) 2

a 2 = b 2 + c 2 – 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определить стороны b и c:

b 2 = a 2 + c 2 – 2ac cos β

c 2 = a 2 + b 2 – 2ab cos γ.

Формулировка и формула теоремы

В плоском треугольнике квадрат стороны равняется сумме квадратов двух других сторон минус удвоенное произведение данных сторон, умноженное на косинус угла между ними.

a 2 = b 2 + c 2 – 2bc cos α

Теорема косинусов для остроугольного треугольника.

Если угол острый, то справедлива формула:

a 2 = b 2 + c 2 −2bx

Доказательство теоремы косинусов для треугольника

Доказательство теоремы косинусов для треугольника проводят обычно следующим образом. Разбивают исходный треугольник на два прямоугольных треугольника высотой, а дальше играются со сторонами полученных треугольников и теоремой Пифагора. В результате после долгих нудных преобразований получаю нужный результат. Мне лично этот подход не по душе. И не только из-за громоздких вычислений, но ещё и потому что в этом случае приходится отдельно рассматривать случай, когда треугольник является тупоугольным. Слишком много трудностей.

Я предлагаю доказать эту теорему с помощью понятия «скалярного произведения векторов». Я сознательно иду на этот риск для себя, зная, что многие школьники предпочитают обходить эту тему стороной, считая, что она какая-то мутная и с ней лучше не иметь дела. Но нежелание возиться отдельно с тупоугольным треугольником во мне всё же пересиливает. Тем более, что доказательство в результате получается удивительно простым и запоминающимся. Сейчас вы в этом убедитесь.

Заменим стороны нашего треугольника следующими векторами:

Согласно правилам сложения векторов имеем: . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение: .

Теперь возьмём скалярный квадрат обеих частей полученного выражения. В результате чего получим:

Я напоминаю, что по определению скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Из этого определения также следует, что скалярный квадрат вектора равен квадрату его длины. Действительно, ведь угол между вектором и им же самим равен нулю, то есть соответствующих косинус равен 1. То есть остаётся только квадрат длины вектора. Исходя из этого мы сразу получаем выражение для теоремы косинусов:

Что и требовалось доказать. Причём данное доказательство хорошо ещё тем, что позволяет лучше запомнить саму формулу. Ведь теперь становится понятным, откуда берётся этот хвост . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.

Кстати, в случае, когда угол прямой, мы получаем прямой, мы получаем , и выражение принимает следующий вид: . Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.

Теорема косинусов

Теорема косинусов . Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.

Доказательство . Рассмотрим сначала треугольник ABC , у которого углы A и С – острые (рис.6).

Докажем, что длины сторон этого треугольника удовлетворяют равенству

a 2 = b 2 + c 2 – – 2bc cos A

(1)

С этой целью проведём высоту BD из вершины B (рис.7).

В соответствии с определениями синуса и косинуса угла прямоугольного треугольника справедливы равенства

BD = c sin A, AD = c cos A, DC = b – AD = b – c cos A.

Из теоремы Пифагора , применённой к прямоугольному треугольнику BDC , получим

Таким образом, в случае треугольника ABC с острыми углами A и С теорема косинусов доказана.

Замечание 1 . Для того, чтобы получить полное доказательство теоремы косинусов, необходимо рассмотреть также и следующие случаи:

1. Угол A – острый, угол C – тупой (рис.8)

Угол A – прямой (рис. 9).

Угол A – тупой (рис.10).

Во всех перечисленных случаях доказательства теоремы косинусов проводятся совершенно аналогично тому, как это было сделано для случая острых углов A и C , и мы рекомендуем читателю провести эти доказательства в качестве полезного и несложного упражнения.

Замечание 2 . В случае, когда угол A является прямым углом, формула (1) принимает вид

откуда вытекает, что теорема Пифагора является частным случаем теоремы косинусов.

Замечание 3 . Если у треугольника известны длины всех сторон, то с помощью теоремы косинусов можно найти косинус любого угла треугольника, например,

Примеры задач

Задание 1
В треугольнике известны длины двух сторон – 5 и 9 см, а также, угол между ними – 60°. Найдите длину третьей стороны.

Решение:
Применим формулу теоремы, приняв известные стороны за b и c, а неизвестную за a:
a 2 = 5 2 + 9 2 – 2 * 5 * 9 * cos 60° = 25 + 81 – 45 = 61 см 2 . Следовательно, сторона a = √ 61 см ≈ 7,81 см.

Задание 2
Самая большая сторона треугольника равна 26 см, а две другие – 16 и 18 см. Найдите угол между меньшими сторонами.

Решение:
Примем бОльшую сторону за a. Чтобы найти угол между сторонами b и c, воспользуемся следствием из теоремы:

Следовательно, угол α = arccos (-1/6) ≈ 99,59°.

Теорема косинусов для прямоугольного треугольника

Теорема косинусов для прямоугольного треугольника.

Рассмотрим прямоугольный треугольник ABC:

По теореме косинусов сторона «а» равна:

но угол А прямой, косинус прямого угла равен нулю, отсюда получаем:

Таким образом мы получили формулу теоремы Пифагора:

Решение:

    В прямоугольном ΔАНС по теореме Пифагора найдём катет НС:

HC=sqrt{AC^{2}-AH^{2}}=sqrt{10^{2}-(sqrt{51})^{2}}=sqrt{100-51}=sqrt{49}=7

    Косинусы смежных углов равны по модулю, противоположны по знаку:

cos∠ACB = –cos∠ACH

    Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
    Найдём cos∠ACH:

cosangle ACH=frac{HC}{AC}=frac{7}{10}=0,7

    Найдём косинус искомого угла АСВ:

cos∠ACB = –cos∠ACH = –0,7

Ответ: –0,7.

1. Треугольник АСН прямоугольный, так как АН — высота. Угол АНС = 90°.

2. Используя формулу теоремы Пифагора, рассчитываем длину катета СН.

СН^2 = АС^2 — АН^2.

СН = √АС^2 — АН^2 = √25^2 — 20^2 = √625 — 400 = √225 = 15 сантиметров.

3. Вычисляем косинус угла АСВ, разделив длину катета СН, прилежащего к нему, на длину

гипотенузы АС:

Косинус угла АСВ = СН/АС = 15/25 = 0,6.

Ответ: косинус угла АСВ = 0,6.

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

Давайте докажем некоторые из них.

1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла  катет а будет прилежащим.Получаем, что . Иными словами, .
3. Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
4. Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,

   

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от  до .

Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

1. В треугольнике угол  равен , . Найдите .

Задача решается за четыре секунды.

Поскольку , .

2. В треугольнике угол  равен , , . Найдите .

Имеем:

Отсюда

Найдем  по теореме Пифагора.

Задача решена.

Часто в задачах встречаются треугольники с углами  и  или с углами  и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами  и  катет, лежащий напротив угла в , равен половине гипотенузы.

Треугольник с углами  и  — равнобедренный. В нем гипотенуза в раз больше катета.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Нсе роигинмепмесем иемеп

Сделал длинновато, но первое, что пришло в голову

Линия пересечения боковой грани и сечения КК1
см приложение