Свойства углов параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
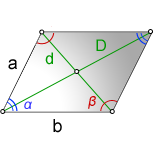
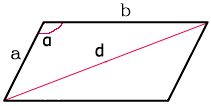
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и стороны:
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 05 ноября 2011
-
Обновлено: 13 августа 2021
Дата: 2016-08-01
5732
Категория: Пл. Параллелограм
Метка: ЕГЭ-№1
27437. В параллелограмме ABCD sinA=(√21)/5. Найдите cosB.
Синусы двух любых соседних углов параллелограмма равны, то есть
Из основного тригонометрического тождества можем найти cosB. Из sin2B+cos2B=1 cледует, что
*Перед корнем мы поставили знак «–». Почему?
Из рисунка видно, что угол В тупой (он больше 90 градусов). А косинус угла от 90 до 180 градусов отрицателен (см. тригонометрическую окружность).
*Другой путь решения.
Найдём cosA Из основного тригонометрического тождества
Значит:
Перед корнем стоит «+», так как угол А острый. По свойству параллелограмма сумма его соседних углов равна 1800, то есть
Таким образом
Ответ: –0,4
27438. В параллелограмме ABCD cosA=(√51)/10. Найдите sinB.
Как уже сказано, синусы смежных углов равны. Для того, чтобы найти sinB, достаточно вычислить sinА.
Из основного тригонометрического тождества:
Ответ: 0,7
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok



Найти углы параллелограмма зная длину сторон и диагональ
Введите стороны параллелограмма (a,b) и диагональ (d).
Формула расчёта углов параллелограмма зная длину сторон и диагональ:
cos(α)=(a2+b2-d2)/(2*a*b), β=(360-α*2)/2.
Косинус α равен, сторона (a) в квадрате, плюс сторона (b), в квадрате, и минус диагональ (d), в квадрате. Разделённое на сторону (a), умноженное на сторону (b) и умноженное на два. Угол β — вычитаем из 360 градусов угол α умноженный на два, всё это делим на два.
| Сторона параллелограмма (a) | ||
| Сторона параллелограмма (b) | ||
| Диагональ параллелограмма (d) |
Площадь параллелограмма
Периметр параллелограмма
Найти длину стороны параллелограмма зная диагональ и сторону
Вычислить высоту параллелограмма зная длину стороны и угол
Найти диагональ параллелограмма зная стороны и угол
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |
Parallelogram is derived from the Greek word “parallelogrammon” meaning “limited by parallel lines”. So, a parallelogram is a quadrilateral surrounded by parallel lines. Parallelogram is a basic figure in geometry and is a quadrilateral. It is a quadrilateral in which opposite sides are parallel and equal. Parallelogram also has opposite pairs of angles as equal.
In this article, we will learn more about the properties of a parallelogram, the area, and perimeter of parallelograms, and their examples, in detail.
What is a Parallelogram?
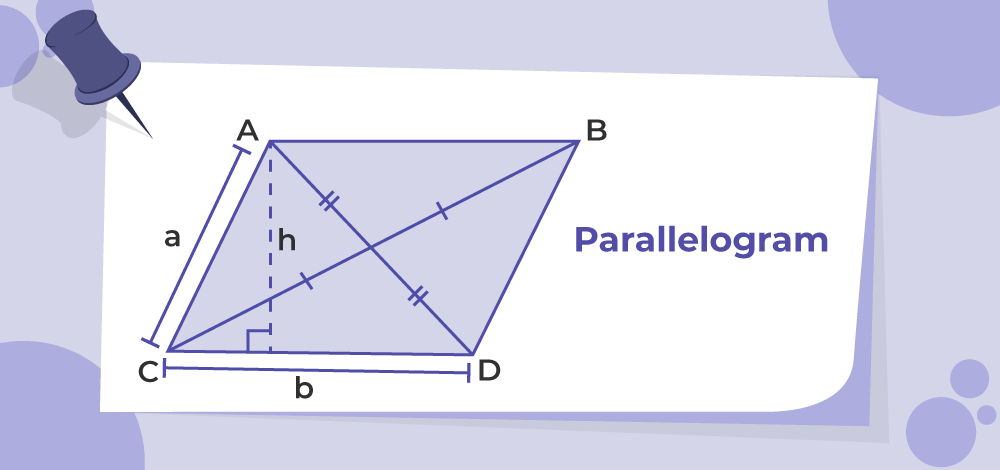
A parallelogram is one of the special types of quadrilateral. The angles between adjacent sides of a parallelogram can vary, but to be a parallelogram, the opposite sides must be parallel. A quadrilateral is a parallelogram if the opposite sides are parallel and equal. Therefore, a parallelogram is defined as a quadrilateral in which two pairs of opposite sides are parallel and equal. Below is the diagram of a parallelogram ABCD having adjacent sides ‘a’ and ‘b’ and height ‘h’.
Real-Life Examples of a Parallelogram
We came across various things in our daily life which resembles a parallelogram. Such as the computer screen, books, buildings, and tiles all are considered to be in a parallelogram shape.
The parallelogram is the most common shape which we encounter daily. Rectangle and square both can be considered a parallelogram and are easily seen in our daily life.
Shape of Parellelogram
A parallelogram is a two-dimensional closed shape with four sides, i.e. it is a quadrilateral. In parallelogram opposite sides are always parallel and equal. Opposite pairs of angles are also equal in parallelograms. In a parallelogram, the interior angle can and can not be a right angle.
Thus, all rectangles and squares can be considered parallelograms but the opposite is not true, i.e. all parallelograms are not considered to be squares or rectangles.
Special Parallelograms
Some of the special parallelograms which are widely used in geometry are,
Rectangle: It is a special case of the parallelogram in which all the interior angles are equal and their value is equal to 90°.
Square: It is a parallelogram in which all the sides and all the angles are equal and the measure of each interior angle is 90°.
Rhombus: Rhombus is also a parallelogram in which all the sides are equal but all the angles are not equal even though opposite pairs of angles are equal.
Angles of Parallelogram
Parallelogram is a quadrilateral i.e. a polygon with four sides and four angles and the opposite pair of angles are equal in the parallelogram. i.e. in a parallelogram ABCD ∠A is equal to ∠C and ∠B is equal to ∠D.
The sum of all the angles in the quadrilateral is 360°. As a parallelogram is a quadrilateral so sum of all the angles of the parallelogram ABCD equals 360°. Now,
∠A + ∠B + ∠C + ∠D = 360°
in parallelogram ∠A = ∠C and ∠B = ∠D
Thus,
∠A + ∠B + ∠A + ∠B = 360°
2(∠A + ∠B) = 360°
∠A + ∠B = 180°
Similarly, ∠C + ∠D = 180°
Thus, Adjacent angles are supplementry in a parallelogram.
Properties of Parallelogram
There are some special properties of quadrilateral, if applied, make it a parallelogram. Let’s take a look at the properties of parallelograms,
- The opposite sides of a parallelogram are parallel and equal.
- The opposite angles of a parallelogram are congruent.
- If said, one of the angles of a parallelogram is 90°. Then all the angles are 90°, and it becomes a rectangle.
- The diagonals of the parallelogram bisect each other.
- The consecutive angles of a parallelogram are supplementary.
Types of Parallelogram
Parallelograms can be classified into several types based on their properties. Based on the properties of a parallelogram and on the sides and angles, the parallelogram is classified into three types,
Rectangle
A rectangle is a parallelogram with two pairs of equal, parallel opposite sides and four right angles. Observe the rectangle ABCD and associate it with the following properties,
- Two pairs of parallel sides. Here AB || DC and AD || BC
- Four right angles ∠A = ∠B = ∠C = ∠D = 90°.
- The opposite sides are the same length, where AB = DC and AD = BC.
- Two equal diagonals where AC = BD.
- Diagonals that bisect each other.
Square
A parallelogram with four equal sides and four equal angles is called a square. Observe the square ACDB and associate it with the following properties,
- Four equal sides are AB = BC = CD = DA.
- Right angles are ∠A = ∠B = ∠C = ∠D = 90°.
- There are two pairs of parallel sides. Here AB || DC and AD || BC.
- Two identical diagonals where AD = BC.
- Diagonals are perpendicular and bisect each other; AD is perpendicular to BC.
Rhombus
A parallelogram with four equal sides and equal opposite angles is called a rhombus. Consider the diamond ABCD and assign it the following attributes,
- In the given figure, the four equal sides are AB = CD = BC = AD.
- The two pairs of parallel sides are AB || CD and BC || AD.
- The equal opposite angles are ∠A = ∠B and ∠C = ∠D.
- Here, the diagonals (AC and BD) are perpendicular to each other and bisect at right angles.
All 2D shapes have two basic formulas for area and perimeter. Let’s discuss these two parallelogram formulas in this section.
Parallelogram Formulas
Parallelogram is a basic 2-dimensional figure which is widely used in mathematics it has various formulas some of them are of Areas and Perimeter
- Area of Parallelogram
- Perimeter of Parallelogram
Let us discuss these two formulas in detail
Area of Parallelogram
The area of a parallelogram is the space between the four sides of the parallelogram. It can be calculated by knowing the length of the base and the height of the parallelogram and measuring it in square units such as cm2, m2, or inch2. Note the following parallelogram representing the base and height.
Consider a parallelogram ABCD with a base (b) and a height (h). The area of a parallelogram is calculated by the formula:
Parallelogram area = base (b) × height (h)
Area of Parallelogram without Height
When the height of the parallelogram is not known, the area of the parallelogram can still be found, provided the angle is known to us. The formula for the area of a parallelogram without height is given as:
Parallelogram area = ab Sinθ
Where a and b are the sides of the parallelogram and θ is the angle between them.
Perimeter of Parallelogram
The perimeter of a parallelogram is the length of its contour, so it is equal to the sum of all sides. In a parallelogram, the opposite sides are equal. Let’s say the sides are a and b. Therefore, the perimeter (P) of a parallelogram with edges is in units of P = 2 (a + b).
Perimeter of Parallelogram = 2 (a + b)
Parallelogram Theorem
Theorem: Parallelograms on the same base and between the same parallels have equal area.
Proof: Let’s assume two parallelograms ABCD and ABEF with the same base DC and between the same parallel lines AB and FC
To Prove: Area of parallelogram ABCD = Area of parallelogram ABEF
In the figure given below, the two parallelograms, ABCD and ABEF, lie between the same parallel lines and have the same base. Area ABDE is common between both parallelograms. Taking a closer look at the two triangles, △BCD and △AEF might be congruent.
BC = AE (Opposite sides of a parallelogram),
∠BCD = ∠AEF (These are corresponding angles because BC || AE and CE are the transversal).
∠BDC = ∠AFE (These are corresponding angles because BD || AF and FD are the transversals).
Thus, by the ASA criterion of congruent triangles. These two triangles are congruent, and they must have equal areas.
area(BCD) = area(AEF)
area(BCD) + area(ABDE) = area(AEF) + area(ABDE)
area(ABCD) = area(ABEF)
Hence, parallelograms lying between the same parallel lines and having a common base have equal areas.
Difference Between Rectangle and Parallelogram
Rectangle and parallelogram are both quadrilaterals, and the rectangle is a parallelogram as it has all the properties of a parallelogram and more. However, a parallelogram is not always a rectangle. Below are the differences in the properties of a rectangle and a parallelogram.
|
Properties |
Parallelogram |
Rectangle |
|---|---|---|
| Sides | The opposite sides of a parallelogram are equal. | The opposite sides of a rectangle are equal. |
| Diagonals | The diagonals of a parallelogram bisect each other, but the diagonals are not equal. | The diagonals of a rectangle bisect each other, and the diagonals are equal to each other as well. |
| Angles | The opposite angles of a parallelogram are equal, and the adjacent angles are supplementary. | All the angles of a rectangle are equal to each other and equal to 90°. |
Do Check,
- Area of a Triangle
- Area of a Square
- Area of Rectangle
Solved Examples on Parallelogram
Example 1: Find the length of the other side of a parallelogram with a base of 12 cm and a perimeter of 60 cm.
Solution:
Given perimeter of a parallelogram = 60cm.
Base length of given parallelogram = 12 cm.
P = 2 (a + b) units
Where b = 12cm and P = 40cm.
60 = 2 (a + 12)
60 = 2a + 24
2a = 60-24
2a = 36
a = 18cm
Therefore, the length of the other side of the parallelogram is 18 cm.
Example 2: Find the perimeter of a parallelogram with the base and side lengths of 15cm and 5cm, respectively.
Solution:
Base length of given parallelogram = 15 cm
Side length of given parallelogram = 5 cm
Perimeter of a parallelogram is given by,
P = 2(a + b) units.
Putting the values, we get
P = 2(15 + 5)
P = 2(20)
P = 40 cm
Therefore, the perimeter of a parallelogram will be 40 cm.
Example 3: The angle between two sides of a parallelogram is 90°. If the lengths of two parallel sides are 5 cm and 4 cm, respectively, find the area.
Solution:
If one angle of the parallelogram is 90°. Then, the rest of the angles are also 90°. Therefore, the parallelogram becomes a rectangle. The area of the rectangle is length times breadth.
Area of parallelogram = 5 × 4
Area of parallelogram = 20cm2
Example 4: Find the area of a parallelogram when the diagonals are given as 8 cm, and 10 cm, the angle between the diagonals is 60°.
Solution:
In order to find the area of the parallelogram, the base and height should be known, lets’s first find the base of the parallelogram, applying the law of cosines,
b2 = 42 + 52 – 2(5)(4)cos(120°)
b2 = 16 + 25 – 40(0.8)
b2 = 9
b = 3cm
Finding the height of the parallelogram,
4/sinθ = b/sin120
4/sinθ = 3/-0.58
sinθ = -0.773
θ = 50°
Now, to find the height,
Sinθ = h/10
0.76 = h/10
h = 7.6cm
Area of the parallelogram = 1/2 × 3 × 7.6
= 11.4 cm2
Example 5: Prove that a parallelogram circumscribing a circle is a rhombus.
Solution:
Given:
- Parallelogram ABCD
- Circle PQRS
To prove: ABCD is a rhombus.
Proof:
We know that the tangents drawn from an exterior point to a circle are equal to each other. Therefore:
AP = AS ⇢ (1)
BP = BQ ⇢ (2)
DS = DR ⇢ (3)
CR = CQ ⇢ (4)
Adding the LHS and RHS of equations 1, 2, 3, and 4:
AP + BP + DS + CR = AS + BQ + DR + CQ
AB + DR + CR = AS + DS + BC
AB + CD = AD + BC
Since the opposite angles of a parallelogram are equal:
2AB = 2BC
AB = BC, and similarly, CD = AD.
Therefore: AB = CD = BC = AD.
Since all the sides are equal, ABCD is a rhombus.
FAQs on Parallelogram
Q1: What is a parallelogram?
Answer:
A parallelogram is a quadrilateral with opposite pair of lines as parallel and equal.
Q2: What is the Area of a Parallelogram?
Answer:
The space occupied inside the boundary of the triangle is termed the area of the parallelogram. It can be calculated using the formula,
Area of Parallelogram = Base (b) × Height (h)
Q3: What is the Perimeter of a Parallelogram?
Answer:
The length of all the boundaries of the triangle is termed the perimeter of the parallelogram. It can be calculated using the formula,
Perimeter of Parallelogram = 2(l + b)
where,
l is the length of parallelogram
b is the base of parallelogram
Q4: Does a parallelogram have equal diagonals.
Answer:
No, the diagonals of a parallelogram are not equal. However, the diagonals of a parallelogram bisect each other.
Q5: How many lines of symmetry parallelogram have?
Answer:
In general, a parallelogram has none or 0 lines of symmetry. But in special cases of parallelogram line of symmetry is present. Lines of symmetry of special parallelograms are,
Square 4 Rhombus 2 Rectangle 2
Q6: Does a parallelogram have equal sides?
Answer:
Yes, all parallelograms have equal pairs of opposite sides but not all sides are equal in a parallelogram.
Q7: Is a rhombus a parallelogram?
Answer:
Yes, a rhombus is a parallelogram. A rhombus has all the properties of the parallelogram and more.
Q8: How is a parallelogram different from a quadrilateral?
Answer:
All parallelograms are quadrilaterals, but not all quadrilaterals are necessarily parallelograms. For example, a trapezoid is a quadrilateral, not a parallelogram. For a quadrilateral to be a parallelogram, all opposite sides must be parallel and equal.
Q9: Is a square a parallelogram?
Answer:
Yes, a square is a parallelogram as it has all the properties of a parallelogram and more since a square has some extra properties (For example, all angles are right angles, etc.), all parallelograms are not squares.
Q10: Is a rectangle a parallelogram?
Answer:
Yes, a rectangle is a parallelogram. Rectangle is a parallelogram as it has all the properties of a parallelogram and more. However, a parallelogram is not always a rectangle.
План урока:
Тригонометрические функции тупых углов
Вычисление координат точки
Вычисление площади треугольника
Площадь параллелограмма
Теорема синусов
Теорема косинусов
Тригонометрические функции тупых углов
Впервые с тригонометрическими функциями мы познакомились в 8 классе. Определить их значение можно было с помощью прямоугольного треугольника, рассматривая отношения его сторон (катетов и гипотенуз). Но такой способ определения тригонометрических функций подходит только для острых углов, попадающих в интервал от 0 до 90°. Оказывается, есть способ для вычисления значений тригонометрических функций и от больших углов.
Построим на координатной плоскости полуокружность, центр которой располагается в начале координат, а радиус равен единице. Ее называют единичной полуокружностью. Проведем из точки (0; 0) луч под некоторым углом α, который пересечет полуокружность в некоторой точке М с координатами (х; у). Заметим, что каждому значению α соответствует своя точка М на единичной полуокружности:
Опустим из М перпендикуляр на ось Ох в некоторую точку D. Тогда, если угол α острый,получается прямоугольный треугольник МOD, длины сторон которого можно определить так:
Получается, что координаты точки M как раз и являются синусом и косинусом угла α. Логично считать, что если α – не острый угол, то всё равно координаты точки M будут определять синус и косинус угла α.
Видно, что при тупом угле α точка М оказывается левее оси Оу, поэтому ее абсцисса становится отрицательной. Получается, что косинус может принимать отрицательные значения.
С помощью единичной полуокружности несложно выяснить значения синусов и косинусов для углов 0°, 90° и 180°. Они соответствуют координатам точек А, В и С на рисунке:
Так как эти точки имеют координаты (1; 0), (0; 1) и (– 1; 0), то можно записать следующее:
Используя это определение, найдем тангенс для углов 0° и 180°:
Заметим, что для 90° использовать эту формулу не удастся, так как это приведет к делению на ноль. Поэтому считается, что для 90° значение тангенса не определено, то есть его нельзя вычислить.
Единичная полуокружность является дугой окружности, чей радиус равен единице, а центр находится в начале координат. То есть она может быть задана уравнением
Тем самым мы доказали, что это тождество, которое показывает связь тригонометрических функций друг с другом, выполняется не только для острых углов, но и для всех углов из диапазона 0° ≤α ≤ 180°.
Для вычисления значений тригонометрических углов тупых углов удобно пользоваться так называемыми формулами приведения. Их довольно много, и изучаются они в основном в 10 классе, нам же хватит всего двух формул:
Например, пусть надо вычислить синус для угла 120°. Для этого мы представляем угол в виде разности, где в качестве уменьшаемого используется угол 180°:
Убедиться в справедливости этих двух формул приведения можно с помощью такого построения:
Точка М соответствует углу α, а точка K – углу (180° – α). Опустим из этих точек перпендикуляры МС и KD. Так как
Получается, что ∆OKD и ∆ОМС – прямоугольные, у них есть одинаковый острый угол α, и их гипотенузы ОК и ОМ также одинаковы как радиусы одной окружности. Тогда эти треугольники равны, и поэтому
Знак минус в первом из этих равенств показывает, что точки K отрицательная абсцисса. В итоге мы доказали две формулы приведения.
Задание. Вычислите sin 150°.
Решение. Представим угол 150° в виде разности:
Вычисление координат точки
Пусть есть некоторая точка А(х;у) с неотрицательной ординатой. Соединим ее с началом координат прямой, которая образует угол α с осью Ох. Посмотрим, как связаны координаты А со значением α.
Пусть луч ОА пересечет единичную окружность в точке М. Опустим из М и А перпендикуляры на Ох, в точки Н и С соответственно. Теперь сравним ∆ОМН и ∆ОАС. Они прямоугольные, и у них есть одинаковый угол α, следовательно, они подобны. Коэффициент подобия можно найти, поделив ОА на ОМ, при этом учтем, что ОМ = 1, так как М лежит на единичной полуокружности:
Примечание. Данное доказательство не рассматривает частные случаи, когда точка А лежит непосредственно на осях Ох и Оу, и тогда подобные треугольники ∆ОМН и ∆ОАС построить не удается. Эти случаи можно рассмотреть отдельно и показать, что для них выведенные формулы также справедливы.
Задание. Точка А находится на расстоянии 3 от начала координат (точки О), причем луч ОА образует с осью Ох угол 135°. Найдите координаты точки А.
Решение. Используя выведенные формулы, мы можем записать:
Вычисление площади треугольника
В 8 классе мы уже познакомились с одной из формул для определения площади треугольника. Однако на практике возникают ситуации, когда удобнее использовать другие формулы, одну из которых мы сейчас выведем.
Пусть в произвольном ∆АВС известны две стороны, например, ВС (обозначим ее буквой а) и АС (ее обозначим как b). Также известна величина угла между ними:
Разместим этот треугольник в системе координат так, чтобы точка С совпала с началом координат, в находилась на оси Ох и имела положительную абсциссу, А располагалась в первой четверти:
В этом случае координаты А будут определяться формулами:
Найдите площадь ∆МКН.
Решение.
Задание. Используя калькулятор, найдите площадь треугольника со сторонами 14 и 7 см, если угол между ними равен 48°. Ответ округлите до десятых долей см2.
Решение. Подставляя числа в формулу, получаем:
Задание. Диагонали прямоугольника пересекаются под углом 30°, причем они равны 10 см. Вычислите площадь этого прямоугольника.
Решение.
Заметим, что диагонали прямоугольника при пересечении образуют не один, а два угла. Пусть в прямоугольнике АВСD диагонали пересекаются в точке О, и ∠АОВ = 30°. Тогда можно найти ∠ВОС, ведь он смежный с ∠АОВ:
Чтобы найти площадь прямоугольника, мы можем найти площади 4 треугольников, из которых он состоит, и потом сложить их. Для каждого из этих треугольников нам известны две стороны (они составляют по 5 см) и угол между ними:
Площадь параллелограмма
Из выведенной нами формулы площади треугольника вытекает и новая формула для площади параллелограмма. Пусть в параллелограмме нам известны смежные и угол между ними:
На рисунке смежные стороны АВ и AD обозначены буквами a и b, а угол между ними обозначен как α. Проведем диагональ BD. Площадь ∆ABD можно вычислить:
Задание. Стороны параллелограмма имеют длины 8 и 11 см, а один из углов параллелограмма равен 30°. Какова площадь этого параллелограмма?
Решение. Просто подставляем данные в формулу
Ответ: 44 см2.
Задание. Известна площадь параллелограмма MNEF, одна из его сторон и угол:
Так как противоположные стороны в параллелограмме одинаковы, то MF также имеет длину 5:
MF = NE = 5
Запишем формулу для площади и подставим в нее известные данные:
Теорема синусов
Пусть есть некоторый ∆АВС, в котором стороны мы обозначим буквами:
Посчитаем его площадь, используя стороны b и c:
Также площадь треугольника можно выразить через а и с:
Полученная формула показывает, что в каждом треугольнике отношение стороны к синусу противолежащего угла – это константа, не зависящая от выбора стороны. Другими словами,в любом треугольнике стороны пропорциональны синусам углов, которые лежат против них. Это утверждение именуют теоремой синусов.
В большинстве задач достаточно выведенной формулы
Однако можно дополнить теорему синусов, выяснив, чему же именно равны все эти три отношения. Для этого впишем треугольник в окружность, после чего построим диаметр BD:
Пусть радиус этой окружности равен R, тогда диаметр BD будет вдвое больше:
Теперь рассмотрим ∆ВСD. ∠С здесь – прямой, ведь это вписанный угол, опирающийся на полуокружность, то есть дугу в 180°. По определению синуса, которое мы давали ещё в 8 классе, можно записать:
C учетом уже выведенного равенства (6) теорема синусов примет вид:
С помощью теоремы синусов у любого треугольника можно найти две неизвестные стороны, если известны третья сторона и два угла. Процесс нахождение неизвестных элементов треугольника по уже известным элементам именуется решением треугольника. Всего у треугольника 6 элементов – три стороны и три угла. Для нахождения всех элементов в общем случае достаточно знать только 3 из них, а остальные можно найти, используя теорему синусов или иные геометрические соображения.
Задание. Решите треугольник, если одна из его сторон равна 14, а прилегающие к ней углы имеют величину 60° и 40°.
Решение.
Обозначим описанный в условии треугольник как ∆МВК. Пусть МК = 14, ∠М = 60° и∠К = 40°. Тогда нам надо найти ∠В, МВ и ВК. Проще всего найти∠В, ведь в любом треугольнике все углы в сумме дают 180°:
Обратите внимание, что так как углы 40° и 80° не являются табличными, то их значения надо вычислять на калькуляторе, а результат вычисления получается приближенным. В данном случае мы округлили его до сотых.
Осталось найти сторону ВК, это также делается с помощью теоремы синусов:
Задание. В ∆SRT∠S = 30°, ∠R = 45°, а высота RM, опущенная на сторону TS, имеет длину 6. Решите ∆SRT.
Решение.
Теперь надо найти какую-нибудь сторону в ∆SRT. Для этого рассмотрим ∆RMS. Он прямоугольный, а потому для него можно записать:
Для нахождения двух оставшихся сторон можно использовать теорему синусов:
Задание. В параллелограмме MNEF∠MFE составляет 120°, а диагональ NF равна 24 и образует со стороной NE угол 40°. Найдите длину МN и MF.
Решение.
Далее заметим, что ∠FNE и ∠MFN одинаковы, ведь они накрест лежащие при параллельных отрезках NE и MF и секущей NF:
Теперь в ∆MNF известна сторона NF и все три угла. Это позволяет с помощью теоремы синусов найти и остальные две стороны:
Задание. В окружности радиусом 5 построен вписанный угол величиной 30°. Определите длину хорды, на которую он опирается.
Решение.
Решение. По теореме синусов мы можем записать, что
Теорема косинусов
Теорема синусов помогает решать треугольники, в которых известны хотя бы два угла, а также одна из сторон. Но что делать в случае, если наоборот, даны две стороны, но только один угол? Здесь необходима другая теорема, которую именуют теоремой косинусов.
Возьмем произвольный треугольник со сторонами а, b и c и поместим его на координатной плоскости так, как показано на рисунке:
Обозначим угол между а и b как α. Тогда координаты А будут определяться так:
Точка В в свою очередь будет иметь координаты (а; 0). Зная координаты А и В, мы можем найти квадрат расстояния между ними, то есть величину с2:
Полученное соотношение как раз и является теоремой косинусов.
Данная формула позволяет находить третью сторону треугольника, если известны две другие, а также угол между ними. Однако ее можно переписать так, чтобы с ее помощью можно было вычислять косинус угла, зная все три стороны треугольника:
Это позволяет решать те треугольники, для которых теоремы синусов недостаточно.
Легко заметить, что теорема косинусов похожа на теорему Пифагора. Более того, если угол α = 90°, то формула теоремы косинусов превращается в теорему Пифагора, которая, таким образом, является ее частным случаем. По этой причине иногда теорему косинусов именуют обобщенной теоремой Пифагора.
Задание. Решите ∆MNE, если
Решение. По теореме косинусов находим сторону NE:
Осталось найти ∠N и ∠Е. Для этого запишем теорему косинусов так, чтобы в ней фигурировал ∠N:
Мы нашли cosN. Чтобы вычислить сам ∠N, следует использовать особую функцию на калькуляторе или компьютере, которая называется арккосинусом и является обратной для операции «извлечение косинуса». Более подробно она изучается уже в 10 классе. С ее помощью мы узнаем, что
Обратите внимание, что обычно калькулятор выдает результат, показывая десятые и сотые доли градусы, не переводя их в минуты и секунды. Можно оставить ответ и в таком виде. При желании перевести сотые доли в минуты следует дробную часть умножить на 60:
Задание. На различных сторонах угла∠А, равного 45°, отложены точки В и С так что
Задание. Решите треугольник, если его стороны имеют длину 14, 18 и 20.
Решение.
Решение. Здесь надо дважды применить теорему косинусов, чтобы найти какие-нибудь два угла в ∆АВС:
∠C также можно найти через теорему косинусов, но проще просто вычесть из 180° два уже вычисленных угла:
Во всех рассмотренных задачах на решение треугольника мы знали три элемента треугольника и по ним однозначно вычисляли три других элемента. Однако иногда это невозможно. Так, если в задаче помимо двух сторон указан угол, который НЕ лежит между ними, то в итоге задача может иметь два решения.
Задание. В ∆MNE ∠M составляет 60°, а стороны МЕ и NE имеют длины 10 и 9 соответственно. Какова длина MN?
Решение. Теорему синусов здесь применить не удастся, так как для нее необходимо знать хотя бы два угла. Поэтому остается только записать теорему косинусов так, чтобы в ней использовался ∠M:
Получили квадратное уравнение, решить его можно через дискриминант:
В рамках данного урока мы узнали про теоремы синусов и косинусов и научились использовать их для решения треугольников. Также мы познакомились с новыми формулами для вычисления площадей треугольника и параллелограмма.

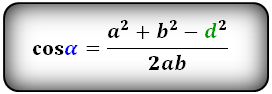
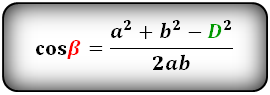
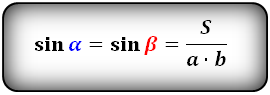










.png)
.png)
.png)
.png)

.png)




































































