Как найти cos угла по теореме косинусов - Исправление недочетов и поиск решений вместе с Examum.ru

Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.

Формула косинуса:

a² = b² + c² – 2b.c.cosα
b² = a² + c² – 2a.c.cosβ
c² = a² + b² – 2a.b.cosγ

Например:

Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.

Решение по формуле a² = b² + c² – 2b.c.cosα:

b = 12 см

c = 8 см

cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)

a² = 12² + 8² – 2×12×8×(- 1/2)

a² = 144 + 64 – (–96)

a² = 304

a = √304

a ≈ 17,436

Длина третьей стороны — примерно 17,436 см.

Следствия

Следствие косинуса угла треугольника

При помощи теоремы косинусов можно найти косинус угла треугольника.

Формула:

Либо

Например:

сторона c = 6

сторона b = 7

сторона a = 8

Используйте теорему косинусов, чтобы найти угол β.

Решение:

Будем использовать эту версию формулы:

cos β = (6² + 8² − 7²) / 2×6×8

= (36 + 64 − 49) / 96

= 51 / 96

= 0,53125

= cos¯¹(0,53125)

≈ 57,9°

Следствие верхней части формулы cos α

Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):

b²+c²−a²<0, значит угол α — тупой;
b²+c²−a²=0, значит угол α — прямой;
b²+c²−a²>0, значит угол α — острый.

Доказательство теоремы косинусов

Нужно доказать, что c² = a² + b² − 2a.b.cos C

1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a <=> CD = a.cos C.

2. Вычитаем это из стороны b, так мы получим DA:

DA = b − a.cosC

3. Мы знаем из определения синуса, что в том же треугольнике BCD:

sin C = BD/a <=> BD = a.sinC.

4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²

5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²

6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C

6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC

7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC

8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C

Q.E.D.

Теорема косинусов для равнобедренного треугольника

В равнобедренном треугольнике:

две его стороны равны;
углы при основании равны.

Рассмотрим пример:

Используем формулу теоремы косинусов

a² = b² + c² – 2b.c.cosα

Подставляем все известные:

x² = 8² + 8² – 2×8×8×cos140º

x² = 64 + 64 – 128 × (-0,766)

x² ≈ √226,048

x ≈ 15,035.

Теорема синусов

Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:

Узнайте также, что такое Теорема Пифагора и Теорема Менелая.

Источник

Содержание:

Формула теоремы косинусов
Следствие из теоремы косинусов
Примеры решения задач

Формула теоремы косинусов

Теорема

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними.

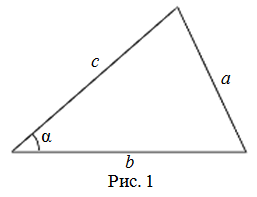
То есть для плоского треугольника (рис. 1) со сторонами $a$, $b$ и $c$ и углом $alpha$, противолежащим стороне $a$,
справедливо соотношение:

$a^{2}=b^{2}+c^{2}-2 b c cos alpha$

Теорема косинусов является обобщением теоремы Пифагора.
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов,
были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» древнегреческого математика Евклида
(ок. 300 г. до н. э.). Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков
стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал выдающийся немецкий астролог,
астроном и математик Региомонтан (1436 — 1476), назвав её «теоремой Альбатегния» (по имени выдающегося средневекового астронома и
математика Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Баттани (858 — 929).

В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 — 1603) в 16 столетии. В начале 19 века её
стали записывать в принятых по сей день алгебраических обозначениях.

Следствие из теоремы косинусов

Теорема косинусов может быть использована для нахождения косинуса угла треугольника (рис. 1):

$$cos alpha=frac{b^{2}+c^{2}-a^{2}}{2 b c}$$
Если $b^{2}+c^{2}-a^{2}>0$, то угол $alpha$ — острый;

Если $b^{2}+c^{2}-a^{2}=0$, то угол $alpha$ — прямой;

Если $b^{2}+c^{2}-a^{2} lt 0$, то угол $alpha$ — тупой.

Примеры решения задач

Пример

Задание. В треугольнике $ABC AC=3, BC=5$ и $AB = 6 .$ Найти угол, противолежащий стороне $AB$

Решение. Согласно следствию из теоремы косинусов, имеем:

$$cos angle A C B=frac{A C^{2}+B C^{2}-A B^{2}}{2 cdot A C cdot B C}=frac{3^{2}+5^{2}-6^{2}}{2 cdot 3 cdot 5}=$$

$$=frac{9+25-36}{30}=-frac{2}{30}=-frac{1}{15}$$

Тогда

$$angle A C B=arccos left(-frac{1}{15}right)$$

Ответ. $angle A C B=arccos left(-frac{1}{15}right)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Задан треугольник
$ABC$, длины сторон которого $AC=17, BC=14, angle ACB=60^{circ}$.
Найти длину третьей стороны рассматриваемого треугольника.

Решение. Согласно теореме косинусов

$$A B^{2}=A C^{2}+B C^{2}-2 cdot A C cdot B C cdot cos angle A C B=$$

$$=17^{2}+14^{2}-2 cdot 17 cdot 14 cdot cos 60^{circ}=289+196-238=24$$

Тогда

$$A B=sqrt{247}$$

Ответ. $A B=sqrt{247}$

Источник

Загрузить PDF

Теорема косинусов широко применяется в тригонометрии. Ее используют при работе с неправильными треугольниками, чтобы находить неизвестные величины, например стороны и углы. Теорема схожа с теорема Пифагора, и ее довольно легко запомнить. Теорема косинусов гласит, что в любом треугольнике $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ .

1
Запишите известные величины. Чтобы найти неизвестную сторону треугольника, нужно знать две другие стороны и угол между ними.^[1]
- Например, дан треугольник XYZ. Сторона YX равна 5 см, сторона YZ равна 9 см, а угол Y равен 89°. Чему равна сторона XZ?
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — неизвестная сторона, — косинус угла, противоположного неизвестной стороне, и — две известные стороны.^[2]
3
4
Найдите косинус известного угла. Сделайте это с помощью калькулятора. Введите значение угла, а затем нажмите кнопку . Если у вас нет научного калькулятора, найдите онлайн-таблицу значений косинусов, например, здесь.^[4] Также в Яндексе можно ввести «косинус Х градусов» (вместо X подставьте значение угла), и поисковая система отобразит косинус угла.
- Например, косинус 89° ≈ 0,01745. Итак: $c^{{2}}=5^{{2}}+9^{{2}}-2(5)(9)(0,01745)$ .
5

Перемножьте числа. Умножьте на косинус известного угла.
6

Сложите квадраты известных сторон. Помните, чтобы возвести число в квадрат, его нужно умножить на само себя. Сначала возведите в квадрат соответствующие числа, а затем сложите полученные значения.
7

Вычтите два числа. Вы найдете $c^{{2}}$ .
8

Извлеките квадратный корень из полученного значения. Для этого воспользуйтесь калькулятором. Так вы найдете неизвестную сторону.^[5]

Реклама

1
Запишите известные величины. Чтобы найти неизвестный угол треугольника, нужно знать все три стороны треугольника.^[6]
- Например, дан треугольник RST. Сторона СР = 8 см, ST = 10 см, РТ = 12 см. Найдите значение угла S.
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — косинус неизвестного угла, — известная сторона, противолежащая неизвестному углу, и — две другие известные стороны. ^[7]
3
4
Перемножьте числа. Умножьте на косинус неизвестного угла.
- Например, $12^{{2}}=8^{{2}}+10^{{2}}-160cos {C}$ .
5
Возведите в квадрат. То есть умножьте число само себя.
- Например, $144=8^{{2}}+10^{{2}}-160cos {C}$
6

Сложите квадраты и . Но сначала возведите соответствующие числа в квадрат.
7

Изолируйте косинус неизвестного угла. Для этого вычтите сумму $a^{{2}}$ и $b^{{2}}$ из обеих частей уравнения. Затем разделите каждую часть уравнения на коэффициент (множитель) при косинусе неизвестного угла.
8
Вычислите арккосинус. Так вы найдете значение неизвестного угла.^[9] На калькуляторе функция арккосинуса обозначается $COS^{{-1}}$ .
- Например, арккосинус 0,0125 равен 82,8192. Итак, угол S равен 82,8192°.
Реклама

1

Найдите неизвестную сторону треугольника. Известные стороны равны 20 см и 17 см, а угол между ними равен 68°.
2

Найдите угол H в треугольнике GHI. Две стороны, прилегающие к углу Н, равны 22 и 16 см. Сторона, противоположная углу H, равна 13 см.
3

Найдите длину тропы. Речная, Холмистая и Болотная тропы образуют треугольник. Длина Речной тропы — 3 км, длина Холмистой тропы — 5 км; эти тропы пересекаются друг с другом под углом 135°. Болотная тропа соединяет два конца других троп. Найдите длину Болотной тропы.

Реклама

Советы

Проще пользоваться теоремой синусов. Поэтому сначала выясните, можно ли применить ее к данной задаче.

Об этой статье

Эту страницу просматривали 5483 раза.

Была ли эта статья полезной?

Источник

Учебник

Геометрия, 9 класс

Теорема косинусов

Теорема косинусов

Если в треугольнике даны две стороны и угол между ними, то такой треугольник один, единственный. Т.е. любой другой треугольник с такими данными будет в точности равен ему, по 2-му признаку равенства треугольников. Ну, раз единственный и неповторимый, то его третья сторона должна быть однозначно определяема.

_____________________________________________________________________________________

Теорема косинусов    Квадрат стороны треугольника      равен     сумме квадратов двух

других сторон минус     удвоенное произведение этих сторон   на    косинус угла между ними.

$AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos ACB$

_____________________________________________________________________________________

Факты:

Теорема косинусов позволяет найти косинус любого угла по трем известным сторонам, а значит, и сам угол.
Если из трех сторон и одного угла известны три величины, то четвертое неизвестное можно всегда вычислить.
Теорема косинусов дает возможность вычислять медианы треугольника, применяя теорему к малым треугольникам.
Для прямоугольного треугольника теорема косинусов «упрощается» до теоремы Пифагора $AB^2=AC^2+BC^2$.

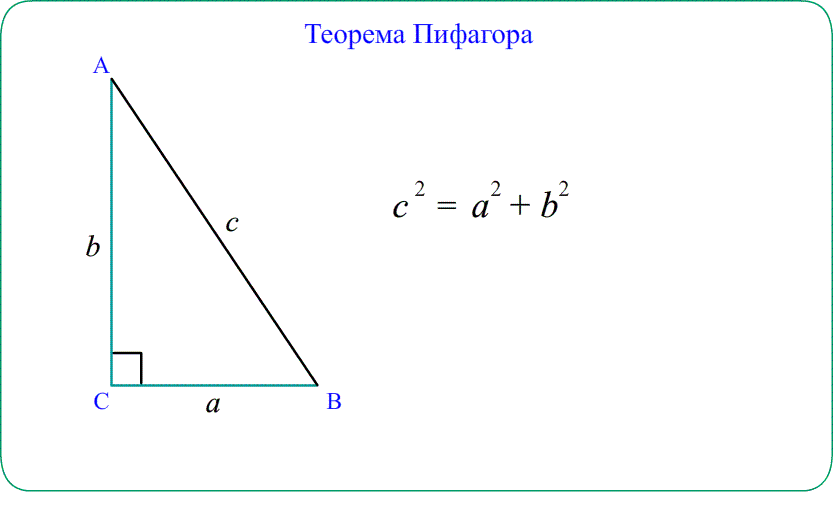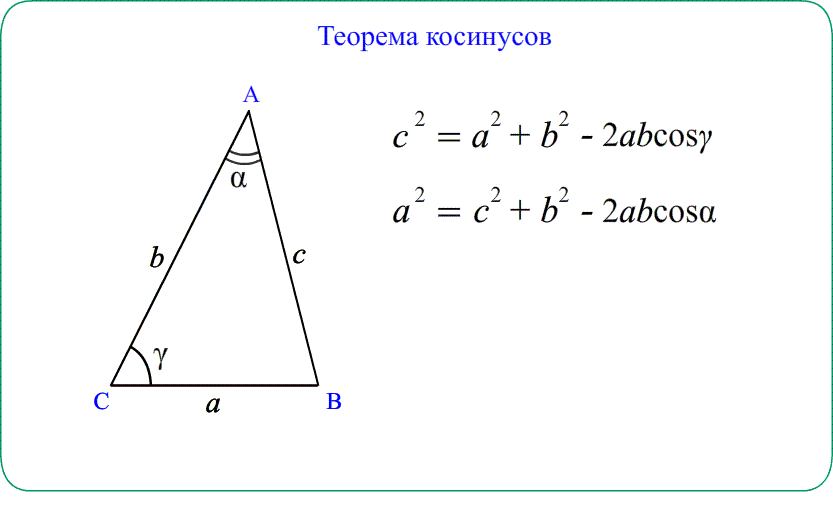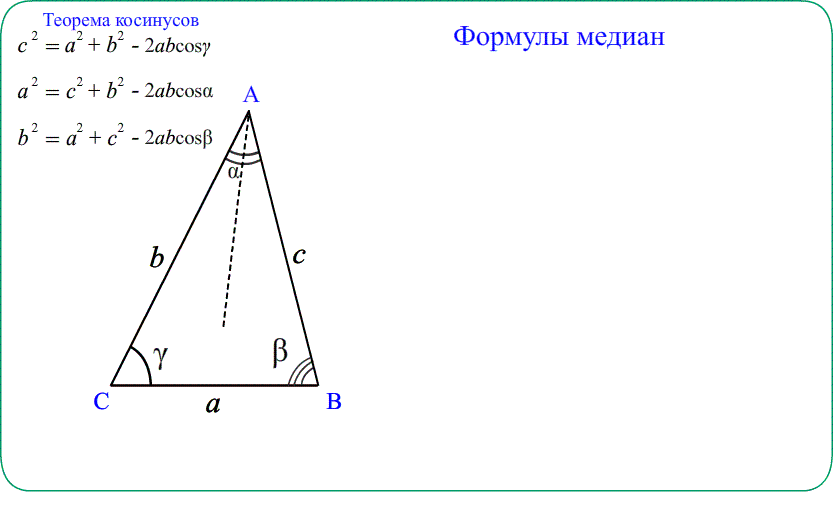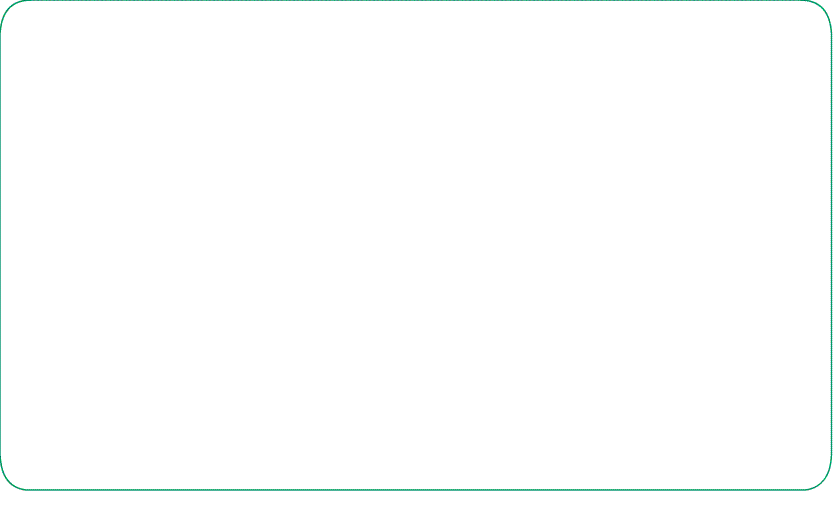
А если угол тупой? Что означает тригонометрия больших углов?

$cos130=-cos50$, $sin115=sin65$ , $tg135=-tg45$.

Связь тригонометрии тупых углов $90 < alpha < 180$ с тригонометрией острых выражается формулами:
$sinalpha=sinleft(180-alpharight)$ $cosalpha=-cosleft(180-alpharight)$ $tgalpha=-tgleft(180-alpharight)$ $ctgalpha=-ctgleft(180-alpharight)$

Если $b^2+c^2-a^2>0$, то $alpha$ — острый; если $b^2+c^2-a^2=0$, то $alpha$ — прямой; если $b^2+c^2-a^2<0$ , то угол $alpha$ — тупой.

Расчет треугольников по теореме косинусов

Задача 1: В треугольнике $ABC$ сторона $AC$ равна $7sqrt{3}$ см, сторона $BC$ равна $1$ см , угол $C$ = $150^o$ . Найти длину стороны $AB$.

Решение: Применим теорему косинусов $AB^2=left(7sqrt{3}right)^2+1-14sqrt{3}cos150$ .
Тупой угол в $150^o$ выразим через острый : $cos150=cosleft(180-30right)=-cos30=-frac{sqrt{3}}{2}$. $Rightarrow$
$AB^2=147+1-28sqrt{3}left(-frac{sqrt{3}}{2}right)$ , $AB^2= 148 + 21 = 169$ $Rightarrow$ Ответ: $AB = 13$

Задача 2: В треугольнике $ABC$ сторона $AC$ равна $17$ см, сторона $BC$ равна $14$ см , угол $ACB$ = $60^o$ .
Найти длину третьей стороны .

Решение: Из теоремы косинусов для угла $angle ACB$ : $Rightarrow$ $AB^2=17^2+14^2-2cdot17cdot14cdotcos60$ $Rightarrow$
квадрат стороны $AB^2= 289+196-238 = 247$ $Rightarrow$ Ответ: $AB = sqrt{247}$

Задача 3: В $bigtriangleup ABC$ известны $AC=3$ , $BC=5$ см, $AB=6$ .
Найти косинус угла $C$ и медиану $BM$ .

Решение: Из теоремы косинусов для стороны $AB$ выразим косинус требуемого угла $ACB$:
$cos ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}=frac{9+25-36}{30}=-frac{1}{15}$ . Отрицательное значение косинуса говорит о том, что это тупой угол $>90^o$
Для нахождения медианы $ВМ$ распишем еще раз теорему косинусов, но уже для треугольника $ВМС$ от угла $С$:
$BM^2=BC^2+MC^2-2cdot BCcdot MCcdotcos C$ учтем, что медиана делит сторону пополам $MC=frac{AC}{2}=1,5$
Подставим $BM^2=25+2,25-2cdot5cdot1.5cdotleft(-frac{1}{15}right)=27,25+1=28,25$, получим $BM=sqrt{28,25}=0,5sqrt{113}$
Ответ: $cos ACB=-frac{1}{15}$ , $BM=0,5sqrt{113}$ .

Задача 4: В прямоугольном $bigtriangleup ABC$ известны $AB=9$ , $BC=3$ см ; $M$ делит $AB$ : $frac{AM}{MB}=frac{1}{2}$.
Найти $CM$ .

Решение: По свойству аддитивности отрезка $AM + MB = 9$ , по условию $frac{AM}{MB}=frac{1}{2}$ $Rightarrow$ $AM = 3$ , $MB = 6$
Из прямоугольного $bigtriangleup ABC$ по определению косинуса угла: $cos B=frac{BC}{AB}=frac{3}{9}=frac{1}{3}$ .
Из $bigtriangleup CMB$ по теореме косинусов найдем $CM$ : $CM^2=CB^2+MB^2-2cdot CBcdot MBcdotcos B$ , подставим числа
$CM^2=3^2+6^2-2cdot3cdot6cdotfrac{1}{3}=33$ $Rightarrow$ требуемый отрезок $CM=sqrt{33}$ . Ответ: $CM=sqrt{33}$

Задача 5: Одна из сторон треугольника больше другой на $8$ см, а угол между ними $120^o$ .
Найдите периметр треугольника, если длина третьей стороны $28$ см .

Решение: Метод введения неизвестного: Обозначим одну из сторон треугольника как $x$ ,
выразим нужные величины через х и составим уравнение: величина другой стороны будет равна $x+8$ см.
По теореме косинусов: $28^2=x^2+left(x+8right)^2-2xcdotleft(x+8right)cdotcos120$ , где $cos120=cosleft(180-60right)=-cosleft(60right)=-0,5$,
Итак, составили уравнение $784=x^2+x^2+16x+64-2xleft(x+8right)left(-0,5right)$ $Rightarrow$ $3x^2+24x+720=0$
решим квадратное уравнение : один корень отрицательный — не нужен , другой $x=frac{-24+96}{6}=12$
Периметр $P=12+left(12+8right)+28=60$. Ответ: $60$.

Задача 6: В $bigtriangleup ABC$ известны стороны $a=15$ , $b=18$, $c=25$ . Найти: углы $α$, $β$, $γ$ (приближённо) .

Решение: Углы $α$ и $β$ найдём по теореме косинусов для соответствующих углов.
$cosalpha=frac{b^2+c^2-a^2}{2bc}$ , вычисляем $cosalpha=frac{18^2+25^2-15^2}{2cdot18cdot25}approx0,8$ , привлекаем калькулятор: $alphaapprox36,4^o$ ;
$cosbeta=frac{a^2+c^2-b^2}{2ac}$ , вычисляем $cosbeta=frac{15^2+25^2-18^2}{2cdot15cdot25}approx0,7$ , …. калькулятор: $betaapprox45,3^o$ .
Найдём $γ$ по теореме о 180 = сумма углов: $gamma=180-left(alpha+betaright)$ и $gammaapprox180-left(36,4+45,3right)approx98,3$ .
Ответ: $alphaapprox36,4^o$ , $betaapprox45,3^o$ , $gammaapprox98,3$

Задача 7: В $bigtriangleup ABC$ $AB=c=3$ м, $AC = b = 6$ м. , $alpha=60$ . Найти: сторону $a = BC$ , углы $β$, $γ$ .

Решение: Треугольник задан двумя сторонами и углом между ними, следовательно, он задан полностью.
По теореме косинусов $a^2=b^2+c^2-2bccdotcosalpha$ найдём сторону $a$:
$a^2=6^2+3^2-2cdot6cdot3cdotcos60=36+9-36cdotfrac{1}{2}=27$ $Rightarrow$ $a=3sqrt{3}$ .
По теореме косинусов найдем и угол $β$ : $cosbeta=frac{a^2+c^2-b^2}{2ac}$ , $cosbeta=frac{27+9-36}{18sqrt{3}}=0$ $Rightarrow$ $β=90$ .
Значит $bigtriangleup ABC$ — прямоугольный , тогда угол $γ=90-α$ . Ответ: $a=3sqrt{3}$ , $β = 90$ , $γ=30$ .

Задача 8: Стороны треугольника равны $11$ , $12$ и $13$ . Найти биссектрису, проведенную к стороне, равной 12.

дано: $AB=11$ , $BC=12$ , $AC=13$ Найти биссектрису $AK=?$ .
Решение: Найдем косинус угла из теоремы косинусов : $AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos angle ACB$
Выразим косинус $cos angle ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}$ , $cos angle ACB=frac{13^2+12^2-11^2}{2cdot 13cdot 12}=frac{19}{39}$
Найдем отрезки $BK$ , $KC$ на которые биссектриса делит сторону … по теореме биссектрис $frac{BK}{KC}=frac{AB}{AC}$
Система уравнений: $frac{BK}{KC}=frac{11}{13}$ и аддитивность $BK+KC=BC=12$. Получаем $BK=5,5$ , $BK=6,5$
Теперь, для нахождения биссектрисы $AK$ еще раз используем теорему косинусов для треугольника $bigtriangleup AKC$
$AK^2=AC^2+KC^2-2cdot ACcdot KCcdotcos angle ACB$ подставим значения $AK^2=13^2+6,5^2-2cdot 13cdot 6,5cdot frac{11}{13}=frac{429}{4}$.
Ответ: $AK=frac{sqrt429}{2}$.

Задача 9: Стороны треугольника равны $11$ , $12$ и $13$ . Найти медиану, проведенную к большей стороне.

Решение: Воспользуемся формулой для длины медианы: $m_c=frac{1}{2}sqrt{2a^2+2b^2-c^2}$
Подставим значения $m_c=frac{1}{2}sqrt{2cdot11^2+2cdot12^2-13^2}=frac{1}{2}sqrt{242+288-169}=frac{1}{2}sqrt{361}=frac{19}{2}=9,5$ Ответ: $m_c=9,5$

Задача 10: В треугольнике $ABC$ $AB=11$ , $AC=23$ , медиана $AK=10$ . Найти $BC$ .

Решение: Воспользуемся формулой для длины медианы и подставим в неё данные из условия:
$AK=frac{1}{2}sqrt{2cdot11^2+2cdot23^2-BC}$ $Rightarrow$ $100=frac{1}{4}left(242+1058-BC^2right)$ $Rightarrow$ $BC^2=900$ Ответ: $BC=30$ .

Упражнения:

Источник

Теорема косинусов отлично помогает в решении треугольников. Решение треугольника – это нахождение всех его сторон и углов. Но если нам даны только стороны треугольника, как определить углы в нем? Вот тогда и приходит на помощь теорема косинусов. Это общий случай теоремы Пифагора, подходящий для треугольника с любым углом, не только с углом 90⁰.

Теорема и доказательство

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Доказательство теоремы косинусов

Докажем теорему. Для этого нарисуем треугольник ABC и докажем, что:

Если рассматривать стороны треугольника, как векторы, то будет справедливо равенство:

В теореме в квадрате, значит возведем векторное равенство в квадрат, получим:

$[overrightarrow{BC}^2=overrightarrow{AB}^2+overrightarrow{AC}^2-2overrightarrow{AB}cdot overrightarrow{AC} eqno (2)]$

Так как, $overrightarrow{BC}^2={BC}^2$ , $overrightarrow{AC}={AC}^2$ , а скалярное произведение векторов равно произведению их модулей на косинус угла между ними, то есть .

Подставим все в формулу (2):

Что и требовалось доказать.

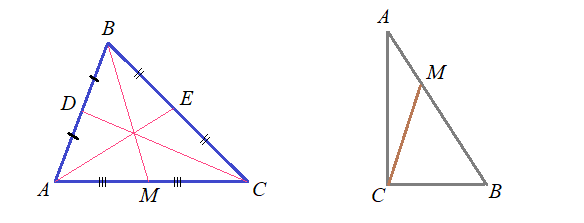
Следствие теоремы косинусов

Проведем высоты :

Обратим внимание, что . То есть – это проекция стороны на сторону треугольника . Если угол А острый, то , если угол А тупой, то косинус угла А будет отрицательным и . То есть из теоремы косинусов вытекает важное следствие:

квадрат стороны треугольника равен сумме квадратов двух других сторон “” удвоенное произведение одной из них на проекцию другой на эту сторону. Знак надо брать, если угол тупой, а знак , если угол острый.

Задачи на теорему косинусов

Задача 1

Найдите , если дано: $angle B = 60^{circ}$ , , .

Решение: Так как нам известен угол между сторонами и и известна сторона – мы сможем найти сторону , если воспользуемся теоремой косинусов.

Из теоремы косинусов $AC^2={AB}^2+{BC}^2-2AB cdot {BC} cos {angle B}$ выразим сторону .

Получим:

${BC}^2-2AB cdot {BC} cos {angle B}-AC^2+{AB}^2 = 0$

Обозначим

Тогда

$x^2-2AB cdot cos {angle B} cdot x-AC^2+{AB}^2=0$

Получаем квадратное уравнение. Подставим в него значения и решим:

$x^2-2 cdot 8 cdot frac{1}{2} x-{(4 sqrt 7)}^2+8^2=0$

Находим дискриминант:

Тогда $x_1=frac{8+16}{2}=frac{24}{2}=12$ .

$x_2=frac{8-16}{2}=frac{-8}{2}=-4$ – не может быть длиной стороны треугольника.

Ответ: 12.

Задача 2

В треугольника ABC , $angle C=120^{circ}$ , . Найдите

Решение: Нарисуем треугольник ABC. Это равнобедренный треугольник.

Запишем теорему косинусов для сторону так как нам дан угол между двумя другими сторонами:

$[AB^2={AC}^2+{BC}^2-2AC cdot {BC} cos {angle 120^{circ}} eqno (1)]$

Так как , то из формулы (1), получим:

$AB^2=2{AC}^2-2{AC}^2 cdot cos {angle 120^{circ}}$

Сделаем замену: :

$AB^2=2{x}^2-2{x}^2 cdot cos {angle 120^{circ}}$ ,

перенесем ${AB}^2$ в правую часть равенства и получим квадратное уравнение:

$2{x}^2-2{x}^2 cdot cos {angle 120^{circ}}-{AB}^2=0$ ,

Подставим значения:

$2{x}^2-2{x}^2 cdot cos {angle 120^{circ}}-{(6sqrt{3})}^2=0$

$cos {angle 120^{circ}}=-frac{1}{2}$

$2{x}^2+{x}^2-108=0$

$3{x}^2=108$

${x}^2=36$

Так как , значит, .

Ответ: 6

Задача 3

Решите треугольник ABC, если известно, что $angle A=30^{circ}$ , , $angle C=45^{circ}$ .

Решение: Решить треугольник – это значит, найти все его стороны и все углы. Нам два угла даны, значит, зная, что сумма всех углов в треугольнике равна $180^{circ}$ получим:

$angle B = 180^{circ}-30^{circ}-45^{circ}=105^{circ}$ .

Обозначим неизвестные стороны треугольника: , .

Выразим сторону треугольник по теореме косинусов:

$[AB^2={x}^2+y^2-2{xy} cdot cos {45^{circ}}eqno (1)]$

Выразим сторону треугольника по теореме косинусов:

$y^2={x}^2+{AB}^2-2{x}cdot{AB} cdot cos {30^{circ}}$

или

$[y^2={x}^2+16-8{x}cdot cos {30^{circ}} eqno (2)]$

Решим уравнения (1) и (2) совместно, записав их в систему уравнений:

$[left{ begin{aligned} AB^2={x}^2+y^2-2{xy} cdot cos {45^{circ}}\ y^2={x}^2+16-8{x}cdot cos {30^{circ}}.\ end{aligned} right.]$

$[left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ y^2={x}^2+16-4{x}cdot sqrt{3}.\ end{aligned} right.]$

Преобразуем второе уравнение системы:

$[left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ -16={x}^2-y^2-4{x}cdot sqrt{3}.\ end{aligned} right.]$

Сложим первое и второе уравнения системы и запишем получившееся уравнение вместо второго уравнения, получим:

$[left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ 0=2{x}^2-xy sqrt{2}-4{x}cdot sqrt{3}.\ end{aligned} right.]$

Из второго уравнения выразим :

$xy sqrt{2}=2x^2-4x sqrt{3}$

$y=frac{2x^2-4x sqrt{3}}{x sqrt{2}}$

$y=frac{2x-4sqrt{3}}{sqrt{2}}$

Итак, мы выразили из второго уравнения системы, теперь возьмем и подставим его в первое уравнение и сделаем необходимые преобразования.

$16=x^2+(frac{2x-4sqrt{3}}{sqrt{2}})^2-x sqrt{2}(frac{2x-4sqrt{3}}{sqrt{2}})$ , раскрываем скобки и умножим левую и правую части уравнения на 2:

$32=2x^2+4x^2-16x sqrt{3}+16 cdot 3-2x(2x-4 sqrt{3})$

$2x^2-8x sqrt{3}+48-32=0$

$2x^2-8x sqrt{3}+16=0$

Разделим левую и правую части уравнения на 2:

$x^2-4x sqrt{3}+8=0$ .

Получили квадратное уравнение. Решим его.

Находим дискриминант:

$D=b^2-4ac=(4 sqrt{3})^2-4 cdot 8 cdot 1=16 cdot 3 - 32=48-32=16$

Тогда корни уравнения:

$x_1=frac{-b-sqrt{D}}{2a}=frac{4 sqrt{3}-4}{2}=2 sqrt{3}-2$

$x_2=frac{-b+sqrt{D}}{2a}=frac{4 sqrt{3}+4}{2}=2 sqrt{3}+2$ .

Оба значения подходят – они положительны. Находим, :

$y_1= frac{2(2 sqrt{3}-2)-4 sqrt{3}}{sqrt{2}}=frac{-4}{sqrt{2}}$ – отрицательное значение нам не подходит.

$y_2= frac{2(2 sqrt{3}+2)-4 sqrt{3}}{sqrt{2}}=frac{4}{sqrt{2}}=2 sqrt{2}$ .

Таким образом, получаем следующие значения , .

Вы можете самостоятельно сделать проверку и убедиться в том, что данные значения верны.

Ответ: , .

Теорема косинусов для треугольника очень помогает в решении геометрических задач, однако некоторые задачи усложняются, если не знать еще одну теорему – синусов. Например, третью задачу мы могли решить гораздо проще – используя теорему синусов, с помощью которой мы бы довольно быстро получили тот же результат для . Однако, с ней мы бы получили лишь приближенное значение . Теорема косинусов дает нам точный результат. Однако, в дальнейшем, когда вы выучите две теоремы – рекомендуем решать задачи, используя их обе.

Источник