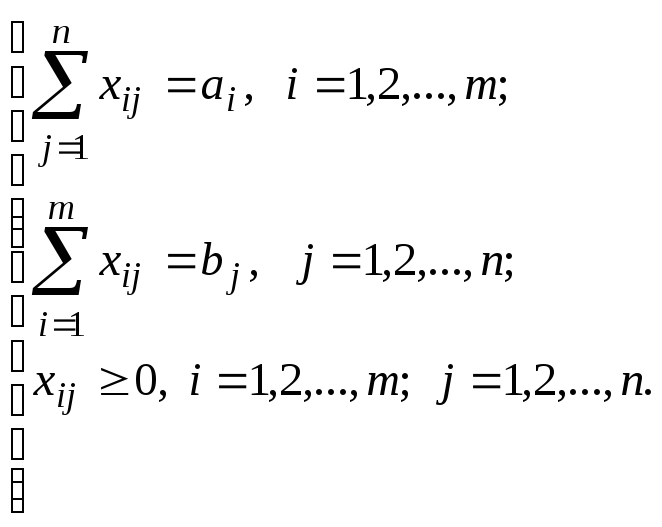Как найти целевую функцию для транспортной задачи

Транспортная задача линейного программирования

Прочие статьи цикла

Транспортная задача линейного программирования относится к перечню классических задач, решаемых в практике деятельности людей. Эта задача методами классической математики не решается. В задаче необходимо отыскивать экстремум целевой функции. В задаче целевая функция – линейная. Ограничения на переменные (их может быть очень много) описываются также линейными зависимостями. Казалось бы чего проще. Но как раз ограничения и порождают трудности, связанные не просто с поиском max и min при отсутствии ограничений, а с необходимостью учета таких ограничений. Искать требуется не просто экстремум, а условный экстремум. Методы решения задачи позволяют учитывать особенности структуры задачи и даже отказаться от симплексного метода решения в чистом виде.

I. Основные параметры, термины и обозначения

Для ощущения масштаба задачи приведу парочку изображений того, что рассматривается в транспортной задаче линейного программирования.

Зеленый цвет — пассажирские суда, желтые — грузовые, розовый — частные яхты, оранжевый — танкеры и др. Аналогичная картина наблюдается и для авиационных перевозок, перевозок по железной дороге или автотранспортом. Изображения получены в начальном периоде Пандемии короновируса, что привело к огромным пробкам в узостях мирового Океана (Панамский, Суэцкий и др. каналы). Танкеры отправили отстаиваться на рейде, экипажам судов на берег сойти не разрешалось. Это форс-мажорные обстоятельства, которые в теории должны рассматриваться и учитываться специальным образом, что пока к сожалению перевозчиков не сделано.

В теории в тексте задачи Хичкока ничего не говорится о равенстве имеющегося общего запаса судов в портах отправления и общей потребности в судах в портах прибытия (назначения). Если такого равенства нет, то система ограничений несовместна. В случае равенства

транспортная задача называется «сбалансированной». Задачи, в которых условие баланса не задано, должны быть приведены к «сбалансированному» виду. Это можно выполнить использованием «фиктивных» перевозок. Рассматриваем два случая:

Метод содержит три последовательных этапа:

1. Формирование опорного плана;

2. Проверка опорного плана на оптимальность;

3. Переход к новому опорному плану, если предыдущий не оптимален.

II. Формирование опорного плана перевозок

Затем, если a₁ > b₁, то определяется остаток (a₁ – b₁) продукта на первом пункте отправления и его запас реализуется на 2-м пункте назначения. Остаток потребностей 2-го пункта назначения удовлетворяется за счет 2-го пункта отправления, остатки которого направляются в 3-й пункт назначения и т.д. Ниже метод будет иллюстрирован числовым примером.

Пример 1. Построение опорного плана методом Северо-Западного угла

Заданы значения: m = 3, n = 4; a₁ = 60, a₂ = 80, a₃ =100, b₁ = 40,b₂ = 60, b₃ = 80, b₄ = 60. Слева в таблице приведены d_ij удельные стоимости перевозок; справа — В_ij стоимости совместно с предложениями a_i и потребностями b_{j .}

Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные х_ij задачи Q.

РЕШЕНИЕ Построить исходный опорный план способом северо-западного угла. Строим симплексную таблицу:                                        Таблица 3.   Опорный план задачи

Q = d₁₁∙x₁₁ + d₁₂∙x₁₂ + d₂₂∙x₂₂ + d₂₃ ∙x₂₃+ d₃₃ ∙x₃₃+ d₃₄ ∙x₃₄ = = 5∙40 + 2∙20 + 10∙40 + 2∙40 + 8∙40 + 5∙60 = 200+40+400 + 80 + 320+ 300 = 1340 ед

Коэффициенты d_ij называются фиктивными или косвенными стоимостями; их выражают через косвенные величины α и β, d’_ij = α_i +β_j . Здесь параметры α_i и ( — β_j ), по аналогии с механикой называют потенциалами i-го пункта отправления и j-го пункта прибытия. Значения потенциалов определяется из системы линейных уравнений: α_i + β_j = d_ij Каждому из таких уравнений соответствует какая-либо базисная переменная х_ij Система уравнений с потенциалами содержит m+n неизвестных потенциалов, число же уравнений равняется числу базисных ячеек таблицы, т.е. (m + n – 1). Следовательно, один из потенциалов можно задать произвольно, положив его равным, например, нулю.

Решая далее систему уравнений для потенциалов, находим значения потенциалов строк и столбцов, все фиктивные стоимости d_ij и коэффициенты γ_ij. Если для всех свободных клеток γ_rs ≤ 0, то перевод в базис любой свободной переменной не уменьшит значения целевой функции и, следовательно, выбранный опорный план не является оптимальным. Если же некоторые γ_rs >0, то данный план можно улучшить путем перевода в базис свободной переменной, соответствующей max γ_rs, а также путем исключения из базиса, принадлежащей ему переменной, первой обращающейся в нуль. Переход к новому опорному плану и поиск оптимального плана рассмотрим на примере. Другой способ формирования опорного плана предложен Фогелем. Этот способ при первом чтении можно пропустить, так как дальше он в тексте не используется.

Пример 2. Способ аппроксимации Фогеля

В большинстве случаев этот способ дает опорный план наиболее близкий к оптимальному. Удобен для матриц большой размерности. Используется концепция штрафов, взимаемых за выбор не самого оптимального с точки зрения транспортных издержек маршрута. Штраф по каждой строке и каждому столбцу определяется из анализа маршрутов с различными показателями издержек (как разность двух различных уровней транспортных издержек). Первой заполняется клетка матрицы (таблицы), в которой фиксируется самый крупный штраф. После заполнения клетки штрафы пересчитываются и так до тех пор, пока все ресурсы не будут распределены. Исходные данные для этого примера заполняют таблицу слева вверху.

Этапы алгоритма: 1.     Вычисление разностей в каждой строке и в каждом столбце между наименьшей стоимостью и ближайшей к ней по величине. Разности по строкам записываются справа в столбце разностей, разности по столбцам – внизу в строке разностей. Например, для строк А₁ разность равна А₁В₂ – А₁В₃ = 38 – 24 = 14 и т. д.

ТАБЛИЦА 2 — Метод Фогеля для получения опорного плана транспортной задачи

2.     Поиск из всех разностей, как по строкам, так и по столбцам максимальный. В нашем примере максимальная разность равна 38 и находится в строке А₂. Обведем максимальную разность рамкой.

3.     Размещение в клетку, где находится наименьшая стоимость (А₂В₂ = 18) (строка с наибольшей разностью), максимально возможного количества ресурсов. Оно равно 20, т.е. всему ресурсу отправителя А₂. Поскольку все ресурсы отправителя А₂ исчерпаны, строку А₂ исключаем из дальнейших расчетов, для чего отметим все клетки этой строки точками.

4.     Вычисление разностей столбцам и строкам, не принимая во внимание стоимость в клетках, имеющих ресурсы и клетках с точкой (исключенную строку или столбец) и определение максимальной разности в строке или столбце (В₃ = 76).

5.     Поиск минимального элемента в строке или в столбце с максимальной разностью (А₁В₃ = 24) и размещения в данную клетку максимально возможного количества ресурса, возвращение к этапу №4 и т.д. Окончательно

ЦФ Q=23∙19 + 7∙3 + 20∙18 + 2∙10 + 14∙24 + 1∙100 +3∙48 = = 437 + 21 + 360 + 20 +3 36 + 100 + 272 =1546 ед. Это значение соответствует опорному плану Фогеля.

III. Транспортная задача линейного программирования

Как основной метод решения транспортной задачи – используется метод потенциалов. Ни симплексный метод, ни распределительный метод здесь не рассматриваются. У них имеются свои плюсы и минусы, но объем изложения достаточно велик. Возможно этому позднее я уделю внимание и время, но пока отвечаю на пожелание читателя Хабра.

Пример 3 — Транспортная задача. Метод потенциалов

Исходные данные задачи удобно представить двумя матрицами.

ТАБЛИЦА — Исходные данные

Базисные n + m – 1 = 3 + 4 – 1 = 6 переменные:  
x₁₁ =70, x₁₂ = 20, x₂₂ = 10, x₂₃ = 20, x₂₄ = 0, x₃₄ = 40.
Остальные переменные nm – n + m – 1 = 12 – 6 = 6 свободные:
x₁₃ = x₁₄ = x₂₁ = x₂₄ = x₃₁= x₃₂ = 0 .
Суммарная стоимость перевозок для опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₂∙x₁₂ + d₂₂∙x₂₂ + d₂₃∙x₂₃+ d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 3∙10 + 1∙20 + 2∙0 + 2∙40 = 140 + 60 + 30 + 20 + 0 +80  = 330 ед.

2. Проверка опорного плана на оптимальность

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

Выделяем в Г [m, n] свободные ячейки, содержащие γ_rs. Проверяем наличие положительных переменных γ_i,j > 0. Так как в матрице (в свободных ячейках) имеем γ₃₂ = 2 > 0, то исходный опорный план может быть улучшен, он не является оптимальным.

3. Переход к новому (улучшенному) опорному плану

Переменную x₃₂ =x следует ввести в базис.  Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок

Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок   Очевидно, что наибольшее x определяется теми x_ij в базисных клетках, из которых этот х вычитается. Следовательно, x₁₁ = min{х₂₂, х₃₄} = {10, 40} = 10. При x >10 перевозка х₂₂ становится отрицательной. Переменную х₂₂ исключаем из базиса и переводим ее в разряд свободных переменных. Далее повторяются рекурсивно три пункта алгоритма.

1. Получаем из модифицированного плана новый опорный план

   В нем объемы перевозок распределены иначе чем в начальном опорном плане.

Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₂∙x₁₂ + d₂₃∙x₂₃ + d₃₂∙x₃₂ + d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 2∙10 + 1∙20 + 1∙10 + 2∙30 = 140 + 60 + 20 + 20 + 10 + 60  = 310 ед. Затраты на перевозки при этом плане уменьшились на 330 – 310 = 20 ед.

Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.

2. Проверка опорного плана на оптимальность

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

Свободные ячейки матрицы Г [m, n] содержат γ_i,j > 0 (γ₁₄ = 1>0). План не оптимален.

3. Переход к новому (улучшенному) опорному плану

Из свободных переменных с x_ij > 0, выбираем одну x₁₄  для введения ее в базис. Обозначим ее как и ранее через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся очередным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок  

Очевидно, что наибольшее x определяется теми x_ij в базисных клетках, из которых этот х вычитается. Следовательно, x₁₁ = min{х₁₂, х₃₄} = {20, 30} = 20. При х₁₂ >20 перевозка х₁₂ становится отрицательной. Переменную х₁₂ исключаем из базиса и переводим ее в разряд свободных переменных. Переходим к новой итерации

1. Получаем из модифицированного плана новый опорный план.

В нем объемы перевозок распределены иначе чем в предшествующем опорном плане.

Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₄∙x₁₄ + d₂₃∙x₂₃ + d₃₂∙x₃₂ + d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 140 + 60 + 20 + 20 + 30 + 20  = 290 ед. Затраты на перевозки при этом плане уменьшились на 310 – 290 = 20 ед. Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.

2. Проверка опорного плана на оптимальность

Определим систему уравнений для потенциалов и вычислим их значения:
α₁ + β₁ = d₁₁ = 2;
α₁ + β₄ = d₁₄ = 3;
α₂ + β₃ = d₂₃ = 1;
α₂ + β₄ = d₂₄ = 2;
α₃ + β₂ = d₃₂ = 1;
α₃ + β₄ = d₃₄ = 2. Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β₁ = 0. Тогда после решения системы получены значения потенциалов: α₁= 2, α₂= 2, α₃= 2, β₁ =0, β₂=1, β₃ =–1, β₄ =0.

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

При переходе к новому опорному плану проверяем наличие положительных свободных переменных γ_i,j >0. Но таких переменных не оказалось. Отсюда следует вывод, что полученный последним модифицированный план является оптимальным и ему соответствует значение линейной формы
Q’= 2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 290.

Заключение

Вся теория исследования операций с позиций математики решает неклассические задачи оптимизации целевых функций. Отличие от классики в том, что те ограничения на переменные, которые исследователи вынуждены накладывать в рамках моделей, созданы и вызваны реальностью. Отыскивать требуется экстремумы функций при многих ограничениях, так называемые условные экстремумы. Классика не позволяет этого делать. Взятие производных и приравнивание их нулю «не видит» ограничений. Лучшее, что там имеется это функция Лагранжа, но ее использование также весьма ограничено. Транспортные задачи – частный, но важный случай в исследовании операций. Надеюсь, что читатель разобравшись в приведенных примерах, лучше стал понимать логику задачи и сумеет самостоятельно постигать интересующие его вопросы по другим публикациям в учебниках и журнальных статьях.

Литература

Учреждение
образования «Белорусская государственная

сельскохозяйственная
академия»

Кафедра
высшей математики

Методические
указания

по
изучению темы «Транспортная задача»
студентами бухгалтерского факультета
заочной формы получения образования
(НИСПО)

Горки,
2013

Транспортная
задача

1. Постановка транспортной задачи

Транспортная
задача является задачей линейного
программирования. В общей постановке
она выглядит следующим образом.

Имеется
m
пунктов отправления (поставщиков)

с запасами

единиц груза. Имеется n
пунктов назначения (потребителей)

с потребностями
.
Груз из пунктов отправления должен быть
доставлен в пункты назначения. Известны
транспортные издержки
,
связанные с перевозкой единицы груза
из пункта

в пункт
.

Требуется
составить такой план перевозок, при
котором весь груз из пунктов отправления
был бы доставлен потребителям и при
этом спрос потребителей был бы
удовлетворён, а транспортные издержки
были минимальными.

Для
разрешимости данной задачи необходимо
и достаточно, чтобы сумма запасов была
равна сумме потребностей всех пунктов,
т.е.
.
Транспортная
задача, в которой выполнено это условие,
называется закрытой
(или транспортной задачей с закрытой
моделью).

Для
наглядности транспортную задачу удобно
представлять в виде таблицы, которую
называют распределительной.

В
таблице количество груза, перевозимого
от поставщика

к потребителю

обозначено через
.

Матрица

называется матрицей
тарифов,
а числа

– тарифами.

Поставщики	Потребители	Запасы груза
		…
			…
			…
…	…	…	…	…	…
			…
Потребность в грузе			…

Матрица

называется планом
транспортной задачи.
Здесь каждое число

обозначает количество единиц груза,
который надо доставить от i-го
поставщика к j-му
потребителю. Матрицу Х
называют ещё матрицей
перевозок.

Общие
суммарные затраты, связанные с перевозкой
груза, можно представить в виде функции

.

Эта
функция называется целевой
функцией.

Кроме
этого, переменные должны удовлетворять
ограничениям по потребностям, по запасам
и условиям неотрицательности. Всё это
с учётом целевой функции можно записать
в виде:

(1)

(2)

Условия
(2) образуют систему ограничений. Любой
план, удовлетворяющий этой системе,
называется допустимым.

Таким
образом, можно математически сформулировать
транспортную задачу:

Даны система ограничений (2) и целевая функция (1). Требуется среди множества решений системы найти такой план перевозок, который минимизирует целевую функцию (1).

1. Определение
   допустимого плана задачи

1. Правило
   «северо-западного угла». Суть
   данного правила состоит в следующем.
   Таблица заполняется, начиная с левого
   верхнего угла (северо-западного),
   двигаясь по строке вправо или по столбцу
   вниз в направлении правого нижнего
   угла.

Пример
1.
Сельхозпредприятия

ежедневно
выделяют соответственно 30, 40 и 20 ц молока
для снабжения пунктов
.
Стоимость перевозки и потребности
пунктов даны в таблице.

Сельхоз- предприятия	Потребители	Наличие
	2	3	5	4	30
	3	2	4	1	40
	4	3	2	6	20
Потребности	20	25	35	10	90

Требуется
найти допустимый план задачи.

Решение.
Найдём допустимый план задачи с помощью
правила «северо-западного угла».

Сельхоз- предприятия	Потребители	Наличие
	2 20	3 10	5	4	30
	3	2 15	4 25	1	40
	4	3	2 10	6 10	20
Потребности	20	25	35	10	90

Затраты
на перевозку составят

.

2.2.
Правило «минимального элемента».
Допустимый
план, построенный по правилу
«северо-западного угла», обычно
оказывается далёким от оптимального.
Поэтому в дальнейшем потребуется
достаточно много преобразований для
достижения оптимального плана. Сократить
число таких преобразований позволяет
правило «минимального элемента». Суть
этого правила в следующем.

Заполнение
таблицы начинается с клетки, которой
соответствует наименьший элемент

из всей матрицы тарифов. Затем остаток
по столбцу или строке помещается в
клетку того же столбца или строки,
которым соответствует следующее по
величине значение

и т.д.

Пример
2.
Решить предыдущий пример, используя
правило «минимального элемента».

Решение.
Так как наименьшим элементом является
,
то заполнение таблицы начнём с этой
клетки. В клетку с элементом

поместим требуемые для пункта
10
ц, затем в клетку с элементом
поместим
25 ц, а оставшиеся 5 ц – в клетку с элементом
.
Таким образом, имеющиеся в наличии 40 ц
молока у сельхозпредприятия
распределены.
Аналогичным образом распределяем запасы
молока сельхозпредприятий

и
.

Сельхоз- предприятия	Потребители	Наличие
	2 15	3	5 15	4	30
	3 5	2 25	4	1 10	40
	4	3	2 20	6	20
Потребности	20	25	35	10	90

Затраты
на перевозку составят

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

4.Лекция.  Транспортная задача

4. 1 Постановка задачи. Математическая модель

       транспортной задачи.                  

Постановка задачи:

Однородный груз сосредоточен у m  поставщиков в объемах а₁, а₂, …, а_m.

Данный груз необходимо доставить n потребителям в объемах, b₁, b₂, … , b_n.

Известен С_ij (i= 1, 2, … , m; j=1, 2 ,…, n) – стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю.

Рекомендуемые материалы

Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны.

Исходные данные транспортной задачи записываются в таблице вида:

Переменными (неизвестным) транспортной задачи являются x_ij (i=1,2,…,m; j=1,2,…,n) – объемы перевозок от каждого i-го поставщика j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок.

Математическая модель транспортной задачи

Математическая модель транспортной задачи в общем виде имеет вид:

Целевая функция задачи Z(X) выражает требование обеспечить минимум суммарных затрат на перевозку всех грузов. Вторая группа из уравнений ограничений записанных в общем виде, выражает требование, что запасы всех m, поставщиков вывозятся полностью, а также полностью должны удовлетворятся запросы всех n потребителей. Последнее неравенство является условием неотрицательности всех переменных.

В рассмотренной математической модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.

такая задача называется сбалансированной, а её модель закрытой. Если же это равенство не выполняется, то задача называется несбалансированной (с неправильным балансом), а её модель – открытой.

Для того чтобы транспортная задача линейного программирования имела решение, необходимо, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей, т.е. задача должна быть сбалансированной.

Математическая модель двойственной задачи:

если целевая функция Z’ стремится к минимуму то в системе ограничении меняется знак:  экономический смысл перемененных двойственной задачи:

U_i – условная оценка i-го поставщика (условная плата поставщика перевозчику);

V_j – условная оценка j-го потребителя (условная плата потребителя перевозчику).

U_i, V_j – называются потенциалами.

Определения:

1.Если задача открыта, то необходимо добавить фиктивного поставщика или потребителя с недостающим объемом поставки и нулевой стоимостью перевозки. Распределение поставки фиктивному потребителю (поставщику), идет в последнюю очередь.

2.Клетка в плане перевозок называется базисной (закрытой), если в нее ставится перевозка.

3.Количество базисных клеток определяется соотношением r=m+n-1. опорное решение не может иметь базисных клеток больше, чем r.

4.План называется вырожденным, если количество базисных клеток меньше r, т.е. базисных клеток не хватает при выполненном условии, что объем поставок поставщиков распределен полностью и спрос потребителей также удовлетворен. В этом случае необходимо добавить нулевую перевозку.

5.Если в задаче указана не только стоимость перевозки, но и стоимость производства товара, тогда необходимо сложить эти стоимости с учетом перевозки товара от i-го поставщика j-му потребителю. Кроме того, математическая модель составляется с учетом этой суммарной стоимости.

  4. 2 Алгоритм решения транспортных задач.

1.Составить опорный план, т.е. начальное приближение.

2.Составить математическую модель исходной прямой и математическую модель двойственной задач.

3.Пользуясь методом наименьшего (наибольшего) элемента и методом потенциалов найти улучшение исходного опорного плана до тех пор, пока он не будет удовлетворять условию оптимальности.

4.2.1 Метод наименьшего элемента.

1.Сбалансировать задачу (убедиться, что задача сбалансирована).

2.Определить свободную клетку с наименьшей стоимостью перевозки. Если таких клеток несколько, то выбрать клетку с наибольшей потенциальной грузоперевозкой. Если и таких клеток несколько, то выбирается любая из этих клеток.

3.В выбранную клетку поставить максимально возможную грузоперевозку для потребителя от поставщика.

4.Проверить, остался ли нераспределенным груз у этого поставщика.

5.Если груз распределен не полностью, то применяем п.2 относительно строки этого поставщика. Продолжать до тех пор, пока груз этого поставщика будет полностью распределен.

Если груз поставщика распределен полностью, проверить, полностью ли удовлетворен объем потребителя.

Если потребитель полностью удовлетворен, то применить пункт 2 относительно оставшихся поставщиков и потребностей в таблице.

Если объем потребителя полностью не удовлетворен, тогда применяется пункт 2 относительно соответствующего столбца.

6.Проверить план на вырожденность. Количество базисных клеток должно быть равным r=m+n-1.

Если план вырожденный, то поставить фиктивное значение груза так, чтобы иметь возможность найти потенциалы всех базисных клеток (ставить нулевую перевозку).

7.Проверить на оптимальность и по возможности дальше улучшить, перейдя к методу потенциалов.

4.2.2 Метод потенциалов.

1.Для всех базисных клеток создать систему уравнений вида .

Выбрать переменную U_i или V_j, которой соответствует наибольшее количество занятых клеток, приравнять её к нулю, решить систему уравнений относительно U_i и V_j и найти эти значения.

2.Для всех свободных клеток составить и проверить выполнение неравенств:

Условия оптимальности: если для всех свободных клеток выполняется это неравенство, то тогда найден оптимальный план.

Если хотя бы для одной клетки не выполняется это неравенство, то необходимо улучшить опорный план с помощью коэффициента перераспределения W.

3.Находим клетку, где сильнее всего не выполняется неравенство. Если таких клеток несколько, то выбирается любая. В эту клетку ставим W со знаком «+».

4.Построить контур перераспределения груза, начиная с выбранной клетки, исходя из следующих правил:

-В строке и столбце должно быть четное число W;

-Контур меняет направление только в базисных клетках;

-Коэффициент W меняет свой знак с «+» на «-» поочередно в углах контура.

5.После построения контура отметить, в каких базисных клетках коэффициент W стоит с отрицательным знаком. Из этих клеток найти клетку с наименьшим значением перевозки, коэффициент W будет равен перевозке в выбранной клетке.

6.Найти новый план, перераспределив найденное значение W по контуру с учетом знаков «+» и «-», прибавляя или уменьшая стоящую в клетке перевозку.

7.Проверить новый план в соответствии в п.2, если неравенства для свободных клеток выполняются, значит найденный план оптимален.

Если в математической модели целевая функция прямой задачи на максимум (Z_max), то задача решается методом максимального элемента. т.е. грузоперевозка (X_ij) распределяется при составлении опорного плана с учетом наибольшего значения C_ij аналогично алгоритма метода наименьшего элемента. В методе потенциалов проверяется выполнение неравенства .

4. 3  Примеры решения транспортных задач.

Пример №1

Условие: Студенческие отряды СО-1, СО-2 и СО-3 численностью 70, 99 и 80 человек принимают участие в сельскохозяйственных работах. Для уборки картофеля на полях П₁, П₂, П₃ и П₄ необходимо выделить соответственно 47, 59, 49 и 43 человека. Производительность труда студентов зависит от урожайности картофеля, от численности отряда и характеризуется для указанных отрядов и полей в центнерах на человека за рабочий день и представлена в матрице:

Сумма = 198

Сумма = 249

Требуется:

1.Распределить студентов по полям так, чтобы за рабочий день было собрано максимально возможное количество картофеля;

2.Определить, сколько центнеров картофеля будет убрано с четырех полей при оптимальном распределении студентов

Решение:

1.Проверяем задачу на сбалансированность.

Общее количество человек в студенческих отрядах на 51 больше требуемого общего количества человек для уборки картофеля.

Задача является не сбалансированной.

Чтобы сбалансировать задачу, добавляем фиктивное картофельное поле, для уборки которого нужно выделить 51 человека. Производительность труда студентов на фиктивном поле принимаем равной НУЛЮ.

Составляем исходную таблицу

табл.1

Сумма = 249

Сумма = 249

Обозначения:

П₅ – фиктивное картофельное поле;

С_ij – производительность труда студентов i -го СО на j – м картофельном поле;

X_ij – количество студентов, направляемое из i -го СО на j-ое картофельное поле;

U_i – условные оценки СО;

V_j – условные оценки картофельных полей

4.Составляем математическую модель прямой и двойственной задач.

Математическая модель прямой задачи:

Целевая функция (на максимум)

Система ограничений:

Математическая модель двойственной задачи.

1.Решаем задачу по методу максимального элемента.

Составляем опорный план (табл. 2)

Табл.2

Проверяем на вырожденность.

     Z= m+n-1=3+5-1=7

    Базисных клеток 7. План не вырожден.

Проверяем опорный план на оптимальность.

Задаем U₂ = 0 и определяем значения потенциалов.

Вычисляем оценки для всех незаполненных клеток (D_ij)

Опорное решение не является оптимальным, так как имеются отрицательные оценки.

Переходим к следующему плану.

Для клетки (1,5) с наименьшей оценкой (-5) строим цикл. Ставим в эту клетку коэффициент W со знаком «+» и применяя метод наибольшего элемента находим цикл, (табл. 2). Определяем из цикла W =11

Осуществляем сдвиг по циклу и строим следующий план (табл. 3)

.

Табл.3

Проверяем план на оптимальность методом максимального элемента, как в п.З.

Задаем U₂ = 0 и определяем значения потенциалов.

Вычисляем оценки для всех незаполненных клеток (D_ij)

Определяем из цикла W=7

 Осуществляем сдвиг по циклу и строим следующий план (табл. 4).

Табл. 4

Проверяем план на оптимальность методом максимального

элемента, как в п.З.

Задаем U₂ = 0 и определяем значения потенциалов.

Вычисляем оценки для всех незаполненных клеток (D_ij)

план табл. 4 оптимален.

Определяем значение целевой функции прямой и двойственной задачи:

Исходя из первой теоремы двойственности в условии нашей задачи Z_max=Z_min=1149 (Z=Z’) последний план оптимален

Ответ:

1.Чтобы за рабочий день было убрано максимально возможное количество картофеля, следует распределить студентов по полям следующим образом:

– Из СО-1 выделить 59 человек для уборки картофеля на втором поле П₂, а 11 человек останутся в СО;

– из СО-2 выделить 49 человек для уборки картофеля на П_З и 43 человека для уборки картофеля на П₄, а 7 человек останутся в СО;

– из СО-3 выделить 47 человек для уборки картофеля на П₁, а 33 человека оставить в СО.

2.При данном оптимальном распределении студентов с четырех полей будет убрано 1149 центнеров картофеля.

Пример № 2

План перевозок:

Решение:

Проверяем на сбалансированность

Задача не сбалансированная. Введем фиктивного потребителя В₅ с потребностью в грузе, равной 200 ед. Стоимость перевозки для фиктивного потребителя определим равной нулю.

В качестве общей стоимости C_ij¹ будем брать сумму затрат на доставку единицы продукции C_ij из соответствующего пункта  и ее себестоимость C_i в этом пункте.

     C_ij¹=C_ij + C_i

Математическая модель прямой задачи

 при условии что,

Математическая модель двойственной задачи:

Экономический смысл переменных:

Z – целевая функция прямой задачи (суммарные затраты);

Z‘ – целевая функция двойственной задачи (суммарная потенциальная прибыль от перевозки груза);

С_ij – стоимость перевозки единицы продукции из i-го пункта в j-ый;

X_ij – объем перевозок от i-го поставщика j-му потребителю;

U_i – условная плата перевозчику за вывоз единицы груза из i-го пункта отправления;

V_j – условная плата перевозчику за доставку единицы груза в j-ый пункт назначения.

Проверяем на вырожденность:

R=m+n-1=3+5-1=7

m= 3 – количество поставщиков;

n = 5 – количество потребителей.

Базисных клеток 7, план не вырожден.

Проверяем план на оптимальность, используя метод потенциалов. Для базисных клеток составляем систему уравнений U_i + V_j = С_ij находим значение потенциалов так как переменных на 1 больше, чем уравнений,

то переменной U₃ присваиваем значение 0 и решаем систему уравнений, получаем

Проверяем выполнение неравенства в свободных: клетках U_i + V_j ≤ С_ij

более всего не выполняется условие U_i + V_j ≤ С_ij, сюда ставим «+W» , строим контур перераспределения W и находим его значение:

Перераспределяем W=50 по контуру.

Составляем следующий план:

Так как переменных на i больше, чем уравнений, то переменной U₃ присваиваем значение 0 и решаем систему уравнений, получаем

проверяем выполнение неравенства в свободных клетках U_i + V_j ≤ С_ij,

– более всего не выполняется условие U_i + V_j ≤ С_ij, сюда ставим «+W», строим контур перераспределения W и находим его значение:  перераспределяем W=100 по контуру.

Составляем следующий план:

Для базисных клеток U_i + V_j = C_ij . Составляем для них систему уравнений. Принимаем U₃=0, так как в строке потенциала  U₃ наибольшее количество (три) базисных клеток, решаем систему уравнений и находим количественное значение U_i и V_j :

Проверяем выполнение неравенства U_i + V_j ≤ С_ij, в свободных клетках:

Неравенство U_i + V_j ≤ С_ij,в свободных клетках выполняется, построенной план является оптимальным.

Анализ решения.

Если Вам понравилась эта лекция, то понравится и эта — Тема 11 — Повреждения головы и позвоночника.

1.Оптимальный план перевозки продукции:

– от поставщика А₁ перевозится 250 ед. продукции потребителю В₁; 150 ед. продукции остается у поставщика;

– от поставщика А₂ перевозится 250 ед. продукции потребителю В₂; 50 ед продукции остается у поставщика;

– от поставщика А₃ перевозится 100 ед.продукции потребителю В₁, 150 ед, потребителю В₃, 250 ед. потребителю В₄ .

2.Суммарные затраты на изготовление и перевозку продукции:

 ден. ед.