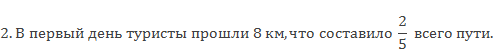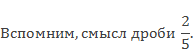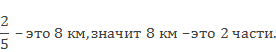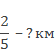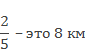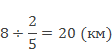Математика
5 класс
Урок № 67
Нахождение части целого и целого по его части
Перечень рассматриваемых вопросов
– нахождение целого по его части;
– нахождение части целого;
– моделирование условий задачи с помощью рисунка.
Тезаурус
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Частное дробей – это дробь, которая при умножении на делитель даёт делимое.
Обязательная литература
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Мы уже рассмотрели, как выполняют умножение и деление дробей. Сегодня с помощью этих действий мы будем решать задачи.
Рассмотрим две задачи.
Теперь определим, какие условия в задачах одинаковы, а какие различаются.
Общее:
- в задачах одинаковые числовые данные;
- за целое принята длина всей ленты.
Разное:
- в первой задаче целое известно (длина ленты – 18 м);
- во второй задаче целое нужно найти.
Значит, в первой задаче нужно найти часть отрезанной ленты, то есть часть от целого; а во второй задаче нужно найти всю длину ленты, то есть целое по его части.
Подобные задачи решаются в соответствие с известными правилами.
- Чтобы найти часть от целого, надо целое (соответствующее ему число) умножить на дробь, соответствующую этой части.
- Чтобы найти целое по его части, надо часть (соответствующее этой части число) разделить на соответствующую дробь.
Если вы затрудняетесь определить тип задачи, обратите внимание на союз «что» и указательное местоимение «это». Они встречаются в задачах на нахождение целого по его части.
Решение.
Смоделируем условие задачи с помощью рисунка.
После этого мы увидим, что длина целой ленты известна, а длину части следует вычислить. Значит, мы будем находить часть от целого. Используем для этого соответствующее правило. Чтобы найти часть числа, нужно число умножить на дробь. Получим:
Решение.
Опять смоделируем условие задачи с помощью рисунка.
Таким образом, мы увидим, что длина целой ленты неизвестна, а длина части указана в условии. Значит, нам надо вычислить целое по его части. Для этого мы используем подходящее правило. Чтобы найти целое, нужно число, соответствующее части, разделить на дробь.
Получится:
Итак, сегодня на уроке мы научились:
-
- моделировать условие задачи с помощью рисунка;
- устанавливать соответствие между математическим выражением и его текстовым описанием;
- решать задачи на нахождение части целого и целого по его части.
Рассмотрим старинную индийскую задачу XII века.
Из множества лотосов были подарены: богу Шиве – треть всех цветов, богу Вишну – пятая часть, а Солнцу – шестая, четвёртую долю получила богиня Бхавани, а остальные шесть частей – уважаемый учитель. Сколько было всего лотосов?
Сегодня мы с вами научимся решать такие задачи с применением действий умножения и деления, изученных ранее.
Решение.
Смоделируем условие задачи с помощью рисунка.
Общее количество лотосов обозначим за единицу. Также укажем части (лотосы), которые распределялись между всеми, кто указан в задании.
Известно, что часть, доставшаяся учителю, равна шести лотосам. Значит, если мы будем знать, какая это доля от общего количества лотосов, то придём ко второму типу задачи – вычислению целого по его части.
Итак, найдём, какая часть от общего количества цветков досталась учителю.
Для этого вычислим сначала, сколько составляют все остальные части. Сложим все дроби, соответствующие частям, приведя их к общему знаменателю 60.
Ответ: 120 цветков.
Тренировочные задания
№ 1. Какие части изображены на рисунках?
Правильные ответы:
№ 2. Подставьте в текст нужные слова:
При решении задач на ___ сначала нужно определить ___ задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение ___ от целого;
- нахождение целого по его ___.
Варианты слов для подстановки в текст: части; тип; целого.
Правильный ответ: при решении задач на части сначала нужно определить тип задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение части от целого;
- нахождение целого по его части.
Задача. В шестом классе (20) девочек, что составляет
57
всех учащихся класса.
Сколько всего учеников в классе?
| Вопросы к задаче | Ответы |
| 1. Какая величина принята за целое? | 1. За целое принято количество всех учеников класса |
| 2. Известна ли целая величина? | 2. Целое не известно |
| 3. Какую величину нужно найти? | 3. Количество всех учеников класса, или целое по его части |
| 4. Как найти величину, которая приходится на 17? | 4. (20 : 5 = 4) ученика составляют одну часть |
| 5. Как найти величину, которая составляет целое? | 5. (4 · 7 = 28) количество всех учеников класса |
Ответ: всего в шестом классе (28) учеников.
Чтобы найти целое по его части, необходимо число, соответствующее части, разделить на числитель
и результат умножить на знаменатель дроби, которая выражает эту часть.
Пример:
1. найди число, если
23
его равны (26):
(26 : 2 · 3 = 13 · 3 = 39).
2. Найди число, если
34
его равны (45):
(45 : 3 · 4 = 15 · 4 = 60).
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅a / b
= n ⋅ a / b
Пример 1
Найдем5 / 12
от числа 24.
Решение
5 / 12
⋅ 24 =5 ⋅ 24 / 12
=120 / 12
= 10
Пример 2
Найдем4 / 9
от числа 7.
Решение
4 / 9
⋅ 7 =4 ⋅ 7 / 9
=28 / 9
=31 / 9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Видео
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
этой суммы истратили. Сколько денег истратили?
Решение: Чтобы найти 
от 600 рублей, надо эту сумму разделить на 4 части, тем самым мы узнаем, сколько денег составляет одна четвёртая часть:
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
этой суммы истратили. Сколько денег было истрачено?
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
членов организации. В кооперативе 120 членов. При каком составе может состояться отчётное собрание?
Решение:
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если 
длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби 
. Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби 
. Известно, что 
длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби 
это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби 
это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или 
длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или 
составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это 
от всего числа. Найдите это число.
Знаменатель дроби 
показывает, что число, которое мы должны найти, разделено на пять частей. Если 
этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти 
(одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби 
20 : 4 = 5
Мы нашли 
от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби 
5 × 5 = 25
Мы нашли 
от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это 
времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби 
показывает, что общее время приготовления каши разделено на три части. Если 
времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти 
времени приготовления. Для этого 10 нужно разделить на числитель дроби 
10 мин : 2 = 5 мин
Мы нашли 
времени приготовления каши. 
времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби 
5 мин × 3 = 15 мин
Мы нашли 
времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. 
массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби 
показывает, что общая масса мешка разделена на четыре части. Если 
массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти 
массы мешка. Для этого 30 надо разделить на числитель дроби 
.
30кг : 2 = 15кг
Мы нашли 
массы мешка. 
массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби 
15кг × 4 = 60кг
Мы нашли 
массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Нахождение целого по части
Чтобы, найти целое число по значению данной его части, эту величину делят на дробь, которая выражает её часть.
Вес обработанной туши животного составляет три пятых общего живого веса. Нужно определить какой должен быть живой вес животного, чтобы его заготовленная туша весила 420 кг?
Живой вес животного составляет семьсот килограмм по отношению к туше:
Регистрация
Ваше имя
Пароль
Хочу получать рассылку рекламных и информационных сообщений.
Нажимая на кнопку «Регистрация», вы подтверждаете свое согласие сусловиями предоставления услуг (пользовательское соглашение) и условиями обработки персональных данных
Теги
§ 1 Правила нахождения части от целого и целого по его части
В этом занятии сформулируем правила отыскания части от целого и целого по его части, а также рассмотрим решение задач с использованием этих правил.
Рассмотрим две задачи:
Сколько километров прошли туристы в первый день, если весь туристический маршрут 20 км.?
Найдите длину всего пути туристов.
Сравним эти задачи — в обеих за целое принят весь путь. В первой задаче целое известно – 20 км, а во второй – неизвестно. В первой задаче необходимо найти часть от целого, а во второй — целое по его части. Величина, известная в первой задаче 20 км, неизвестна во второй задаче, и наоборот, известное во второй задаче – 8 км, в первой необходимо найти. Такие задачи называются взаимно обратными, так как в них известные и искомые величины меняются местами.
Рассмотрим первую задачу:
Знаменатель 5 показывает, на сколько частей разделили целое, т.е. если целое 20 разделить на 5, узнаем, сколько километров составляет одна часть, 20: 5 = 4 км. Числитель 2 показывает, что туристы прошли 2 части пути, значит 4 надо умножить на 2, получится 8 км. В первый день туристы прошли 8 км.
Получилось выражение 20 : 5 ∙ 2 = 8.
Перейдем ко второй задаче.
Следовательно, одна часть будет равна частному 8 и 2, получится 4, знаменатель 5, значит, всего частей 5.
4 умножить на 5, получится 20. Ответ 20 км длина всего пути.
Запишем выражение: 8 : 2 ∙ 5 = 20
Используя смысл умножения и деления числа на дробь, правила отыскания части от целого и целого по его части можно сформулировать так:
Чтобы найти часть от целого, надо число, соответствующее целому, умножить на дробь, соответствующую этой части;
чтобы найти целое по его части, надо число, соответствующее этой части, разделить на соответствующую части дробь.
Соответственно решение задач можно записать теперь по другому:
для первой задачи 20 ∙ 2/5 = 8 (км),
для второй задачи 8 : 2/5 = 20 (км).
Чтобы не было затруднений, решение подобных задач записываем так:
Целое: весь путь, известно – 20 км.
Ответ: 8 км.
Целое: весь путь – неизвестно.
Ответ: 20 км.
§ 2 Алгоритм решения задач на нахождение целого по его части и части целого
Составим алгоритм решения подобных задач.
Сначала проанализируем условие и вопрос задачи: выясним, что является целым, известно оно или нет, далее выясним, как представлена часть целого и что нужно найти.
Если необходимо найти часть от целого, то целое умножим на дробь, соответствующую этой части, если надо найти целое по его части, то число, соответствующее части разделим на дробь, соответствующую этой части. В результате получим выражение. Далее найдем значение выражения и запишем ответ, прочитав перед этим еще раз вопрос задачи.
Итак, прежде чем решать подобные задачи, необходимо ответить на следующие вопросы:
Какая величина прията за целое?
Известна ли эта величина?
Что требуется найти: часть от целого или целое по его части?
Подведем итоги: в этом уроке Вы познакомились с правилами отыскания части от целого и целого по его части, а также научились решать задачи по этим правилам.
|
Как найти целое, если известна его часть? Например, 3/8 торта весит 300 грамм. Как узнать, сколько весит весь торт?
Нахождение целого по его части Если у нас известна какая-либо часть (доля) от целого, то можно всегда «восстановить» целое. При этом нужно помнить, что часть от целого числа может быть выражена либо в виде дроби (обычно обыкновенной), либо в виде процента. Рассмотрим оба случая. 1) Часть числа — это обыкновенная дробь. В этом случае для нахождения целого нужно число, соответствующее данной части, разделить на дробь. Для того, чтобы число разделить на обыкновенную дробь, нужно умножить его на знаменатель дроби и разделить на числитель. _ Пример 1: Специалист отдела кадров получил премию 2000 рублей, что составляет 1/15 часть от его месячной зарплаты. Требуется узнать, сколько составляет зарплата у данного сотрудника. Решение: Зарплата = 2000 / (1/15) = 2000 * 15 = 30000 рублей. Значит, сотрудник получает зарплату 30000 рублей в месяц. _ Пример 2: Было засеяно пшеницей 12 гектаров поля, что составляет 3/5 от его общей площади. Нужно посчитать, чему равна площадь поля. Решение: Площадь поля = 12 / (3/5) = 12 * (5/3) = 20 гектаров. 2) Часть числа представлена в процентах. Если доля от целого является процентом, а не обыкновенной дробью, то подобные задачи можно решать с помощью составления пропорции. _ Пример: Цена апельсинов со скидкой равна 120 рублей, величина скидки равна 20%. Нужно узнать, сколько стоили апельсины изначально. Решение: Так как скидка = 20%, то от исходной цены апельсинов осталось 100% — 20% = 80%. 80% — 120 рублей. 100% — x рублей. 0,8x = 120 рублей. x = 120 / 0,8 = 150 рублей. Таким образом, до скидки апельсины стоили 150 рублей. модератор выбрал этот ответ лучшим
Алиса в Стране 3 года назад Часть числа может быть выражена в виде десятичной или простой дроби, в виде процентов, что по сути то же самое, что десятичная дробь, всем понятно, что 0,1 это 10%, например. Если известна часть числа в абсолютном выражении и то, какую часть она составляет от целого, то нет ничего проще, чем определить это целое. Допустим, 20 яблок это 25 % от всех яблок, надо 20 поделить на 0,25, чтобы определить общее количество яблок, 20/0,25 = 80, вот так мы нашли целое по его части. Еще один пример разберем, 12 мест в автобусе это 1/3 от всех мест в автобусе, как найти общее число всех мест в автобусе, делим 12 на 1/3, то есть по правилам деления на дробь умножаем 12 на 3, получается 36. Ну и в итоге решим задачку автора из его вопроса: 300 граммов делим на 3/8 получаем 800 граммов.
smile6008 3 года назад В математике и жизни бывают случаи, когда необходимо найти число, зная только его часть. Для этого можно использовать различные способы расчётов, использовать дроби , но удобнее всего рассчитать в процентном соотношении. Итак мы знаем, что 300 грамм составляют 3/8 торта. Нужно узнать сколько же весит торт целиком. Переводим в процентное соотношение, поделим 8 на 3, получим 0,26666 в процентах — это 26,6%. Теперь найдём 100 %, для этого посчитаем пропорцию. 26,6% = 300 ;100 % = x. X = 26,6*300/100.Получаем 799,8 округляем по закону округление в большую сторону, получаем 800 гр весит весь торт.
[пользователь заблокирован] 5 лет назад Для лучшего понимания процесса можно делать так (хотя математически это нерационально). Узнайте чему равна ОДНА часть. Для этого заданное число разделите на количество заданных частей в дроби, их 3. 300 делим на 3, получаем 300/3=100 Это одна восьмая часть. Целое — это восемь восьмых, потому предыдущий результат умножаем на 8, получаем 100*8=800 Если же дробь задана, как десятичная, т.е. 0.375, то представляем её, как натуральную (это 375/1000) и поступаем точно так же. Узнаём, чему равна одна тысячная часть 300/375=0.8 Ну, а далее узнаём чему равно само целое 0.8*1000=800
Эл Лепсоид 5 лет назад В общем случае, конечно, следует прибегнуть к составлению пропорции, поставив в соответствие к имеющейся части ее вес, а к целому (т.е. единице) — неизвестную «х». Но, поскольку, у нас во второй части пропорции стоит «1», то решить задачу можно значительно проще: просто разделить на величину известной части. В нашем случае получается: 300/(3/8) = 300*8/3 = 800. Таким образом, весь торт будет весить 800 грамм.
СТА 1106 3 года назад 3/8- означает, что на три части из восьми приходится 300 грамм. Требуется узнать вес целого, в данном случае, торта. Для этого нужно узнать, что приходится на одну часть. Можно решить методом пропорции, мой любимый метод. Итак: 3 части — 300 грамм. 8 частей — Х грамм. Решаем пропорцию. 8 × 300 ÷ 3 = 800 грамм. Общий алгоритм решения следующий. Зная, сколько приходится на долю от целого, нужно определить, сколько приходится на единицу измерения ( грамм, килограмм, метр, час и т.д). Затем зная это, просто умножает на все количество долей, на которое поделён данный предмет. В данном случае- это восемь частей. Второй вариант решения задачи. 300 : 3 × 8 = 800 грамм. Ответ. 800 грамм , в обоих вариантах таз решения задачи.
Проще не бывает. Надо число означающее часть разделить на количество этих частей и полученный результат умножить на целое. Получим число выражающее целую часть. Пример: Дано 4/15 равняется 40. Делим сорок на четыре и умножаем на 15. Получаем сумму в 150 — это и будет целое. Или 2/10 равняется 40. Делим сорок на два, получаем двадцать. Умножаем двадцать на десять, получаем двести. Целое число двести.
Master-Margarita 5 лет назад Чтобы узнать, сколько весит торт в данном случае, надо провести следующие арифметический действия: (300*8)/3=800 грамм. То есть, чтобы найти целое нужно часть умножить на знаменатель дроби и разделить на числитель дроби. В данном случае числитель — 3, а знаменатель — 8.
Рина19 5 лет назад Сначала найдём чем у равна 1 часть из всех имеющихся. А затем умножим её на общее число всех частей. На данном примере. Известно, что 3/8 торта весит 300 г, т.е. 3 части из 8 на которые был нарезан торт или, по другому, 3 куска торта из 8 нарезанных кусочков весят 300 г. Тогда 1 кусочек будет весить: 300/3=100 г. Теперь находим чему будет весить все 8 кусков, т.е. весь торт. 100*8=800 г
Бекки Шарп 3 года назад Если 3/8 торта весит 300 грамм, то сначала узнаем сколько весит одна часть. 300/3=100 грамм. Теперь умножаем на 8 и получаем, что весь торт весит 800 грамм. Приведем еще пример как найти целое число, если известна часть. В классе присутствует 27 человек и это 3/4 общего количества. Сколько человек в классе? Решить задачу можно так: 27 : 3/4 = 36 человек. Знаете ответ? |
