Как найти целую часть функции - Исправление недочетов и поиск решений вместе с Examum.ru

Построение графиков целой и дробной части числа

Рассмотрим интересный вид кусочно-заданных функций.

Целой частью [x][x] числа xx называется наибольшее целое число, не превосходящее xx.

Например, [1]=1[1] = 1, [0,7]=0[0,7] = 0, а [−0,7]=−1[−0,7] = −1. Функцию f(x)=[x]f(x) = [x] легко можно задать на промежутках между парами соседних целых чисел:

`[x] = n` при `n<=x<n+1` для всякого фиксированного целого числа `n`.

Поэтому график этой функции имеет следующий вид (рис. 16).

Рассмотрим более трудный пример.

Построить график функции f(x)=[2x+3,5]f(x) = [2x + 3,5].

Ясно, что [2x+3,5]=[2x+0,5]+3[2x + 3,5]= [2x + 0,5] + 3. Далее,

из определения целой части числа следует такое представление:

[2x + 3,5] =lbrack2x;+;3,5rbrack;=[2x]+3, если n2≤x<n2+14,[2x]+4, еслиn2+14≤x<n+12left{begin{array}{l}lbrack2xrbrack+3,;mathrm{если};dfrac n2leq x<dfrac n2+dfrac14,\lbrack2xrbrack+4,;mathrm{если}dfrac n2+dfrac14leq x<dfrac{n+1}2end{array}right.

для всякого целого nn (рис. 17).

Рассмотрим ещё такой пример.

Изобразим на координатной плоскости xOyxOy множество точек (x,y)(x,y), для которых [x]=[y][x] = [y].

Ясно, что [x]=[y][x] = [y] означает, что для некоторого целого `n` верны неравенства n≤x<n+1n ≤ x < n + 1 и n≤y<n+1n ≤ y < n + 1. Набор всех таких точек будет объединением квадратиков так, как показано на рисунке. Жирные участки границ входят в график, а пунктирные и выколотые точки – нет (рис. 18).

С целой частью числа тесно связана такая кусочно-линейная функция.

Дробной частью {x}{x} числа xx называется число x=x−[x]left{xright}=x-lbrack xrbrack.

К примеру, {1}=0{1} = 0, {0,7}=0,7{0,7} = 0,7, а {−0,7}=0,3{−0,7} = 0,3.

Построим график функции f(x)={x}f(x) = {x}. Ясно, что

f(x)=x−[x]=x−nf(x) = x − [x] = x − n при n≤x<n+1n ≤ x < n + 1 (рис. 19).

Источник

Функция целая часть числа

Определение

Целой частью действительного числа x (x∈R) называется наибольшее целое число, не превосходящее x.

Целую часть числа x обозначают символом [x].

[x] читают «антье от x».

Обозначение [x] в 1808 году ввёл К. Гаусс.

В частности, если n — целое число (n∈Z), то [n]=n.

Примеры.

Вычислить целую часть числа:

7,8; 0,12; -0,7; -4,92; 15 2/3; 5/7; -3/11; 8; -50.

Решение:

Фактически вычисление целой части числа x представляет собой округление до ближайшего к числу x целого числа в меньшую сторону (то есть округление с недостатком).

[7,8]=7;

[0,12]=0;

[ -0,7]= -1;

[-4,92]= -5;

$[ [15frac{2}{3}] = 15; ]$

$[ [frac{5}{7}] = 0; ]$

$[ [ - frac{3}{{11}}] = - 1; ]$

[8]=8;

[-50]= -50.

Определение

Функцию, ставящую в соответствие каждому значению x его целую часть — число [x], называют целой частью числа x и обозначают y=[x] .

Функция целая часть числа определена для любого действительного x (x∈R).

Область значений функции y=[x] — множество целых чисел (y∈Z).

Утверждение.

Для любого k∈Ζ [x+k]=[x]+k.

Доказательство:

Пусть [x]=m.

По определению целой части числа

m≤x<m+1,

m+k≤x+k<(m+k)+1.

Отсюда [x+k]=m+k=[x]+k.

Что и требовалось доказать.

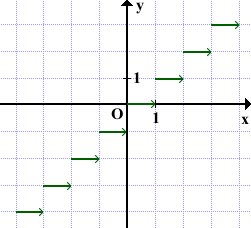
График функции y=[x]

Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.

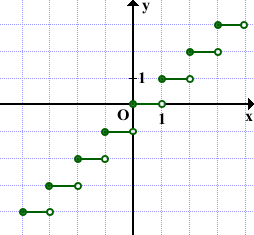
Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, выделить их, соответственно, закрашенными и выколотыми точками:

Как решить уравнение с целой частью числа?

Простейшее уравнение [x]=a имеет решения только при целых значениях a. Если a∉Ζ, уравнение не имеет решений.

При a∈Ζ решения уравнения [x]=a удовлетворяют условию a≤x<a+1.

Примеры.

1) [x]=7

7≤x<7+1, то есть 7≤x<8.

Ответ запишем в виде числового промежутка (в данном случае, полуинтервала).

Ответ: x∈[7;8).

2) [x]=3,2.

Это уравнение не имеет решений, так как 3,2∉Ζ.

3) [7,2-0,5x]= -3

-3≤7,2-0,5x<-3+1

-3≤7,2-0,5x<-2.

Прибавим почленно к каждой части неравенства -7,2. Знаки неравенства при этом не изменятся:

-3-7,2≤-0,5x<-2-7,2

-10,2≤-0,5x<-9,2.

Умножим каждую часть неравенства на -2. При умножении на отрицательное число знаки неравенства меняются на противоположные:

20,4≥x>18,4

18,4<x≤20,4.

Ответ: x∈(18,4; 20,4].

4)2x-3[x]=9.

Выразим целую часть числа числа [x]:

$[ left[ x right] = frac{{2x - 9}}{3} ]$

Отсюда

$[ left{ begin{array}{l} frac{{2x - 9}}{3} in Z, \ frac{{2x - 9}}{3} le x < frac{{2x - 9}}{3} + 1, \ end{array} right. ]$

$[ left{ begin{array}{l} frac{{2x - 9}}{3} in Z, \ x ge frac{{2x - 9}}{3}, \ x < frac{{2x - 6}}{3}, \ end{array} right. Leftrightarrow left{ begin{array}{l} frac{{2x - 9}}{3} in Z, \ x ge - 9, \ x < - 6. \ end{array} right. ]$

Таким образом, x∈[-9;-6) и

$[ (*)left[ x right] = frac{{2x - 9}}{3} in Z. ]$

На промежутке [-9;-6) [x] принимает три значения.

1. При x∈[-9;-8) [x]= -9.

Подставив в равенство (*) [x]= -9, найдём x:

$[ frac{{2x - 9}}{3} = - 9, Rightarrow x = - 9. ]$

Так как -9∈[-9;-8), то x= -9 — корень уравнения.

2. При x∈[-8;-7) [x]= -8, откуда

$[ frac{{2x - 9}}{3} = - 8, Rightarrow x = - 7,5. ]$

-7,5∈[-8;-7), поэтому x= -7,5 — корень уравнения.

3. При x∈[-7;-6) [x]= -7, и

$[ frac{{2x - 9}}{3} = - 7, Rightarrow x = - 6. ]$

-6∉[-7;-6), значит x= -6 не является корнем уравнения.

Ответ: -9; -7,5.

Источник

Функция у = |х| и ее график

|х| — модуль х (абсолютная величина х). Эта функция определяется так:
109
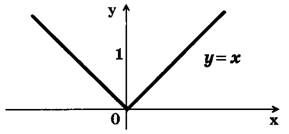
График функции у = |х| изображен на рис. 1.
110

Рис. 1

Функция у = |х| определена при хє R, принимает только неотрицательные значения. Таким образом, D(y)=(-∞;+∞); Е (у) = [0;+∞); функция у = |х| обращается в нуль при х=0. При х є (-∞;0) функция убывает, при х є (0;+∞) функция у = |х| возрастает.
Поскольку y(-x)= |-х| = |х| = y(x), то функция у = |х| четная.
Замечание. В общем случае можно рассмотреть модуль функции:

Функция у=[х] и ее график

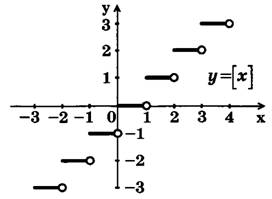
[х] — целая часть х. [х] — наибольшее целое число, не превосходящее х. Если хє [0,+1), то у=[х]=0; если хє [1;2), то у=[х]=1; если хє |-1;0), то у=[х]=-1; если хє [-2;-1), то у=[х]=-2 и так далее.
График функции у=[х] изображен на рис. 2. Белыми кружочками (белыми точками) изображены выколотые значения (т. е. те значения, которые функция не принимает в этих точках). Так, для функции у=[х] у(1)≠0, у(1)=1; у(2)≠1, у(2)=2 и т.д.
112

Рис. 2

Функция у={х} и ее график

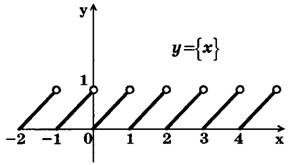
{х} — дробная часть х, {х}=х-[х]. Функция у={х} является периодической, основной период Т=1, {х+1}={х}, поэтому достаточно сначала построить ветвь графика на любом промежутке длиной 1, например при х є[0;1).
Если х є[0;1), то [х]=0 => {х}=х. На рис. 3 изображен график функции y={х}.
113

Рис. 3

Источник

1. Дробно-линейная функция и ее график

Функция вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, называется дробно-рациональной функцией.

С понятием рациональных чисел вы уже наверняка знакомы. Аналогично рациональные функции – это функции, которые можно представить как частное двух многочленов.

Если дробно-рациональная функция представляет собой частное двух линейных функций – многочленов первой степени, т.е. функцию вида

y = (ax + b) / (cx + d), то ее называют дробно-линейной.

Заметим, что в функции y = (ax + b) / (cx + d), c ≠ 0 (иначе функция становится линейной y = ax/d + b/d) и что a/c ≠ b/d (иначе функция константа). Дробно-линейная функция определена при всех действительных числах, кроме x = -d/c. Графики дробно-линейных функций по форме не отличаются от известного вам графика y = 1/x. Кривая, являющаяся графиком функции y = 1/x, называется гиперболой. При неограниченном увеличении x по абсолютной величине функция y = 1/x неограниченно уменьшается по абсолютной величине и обе ветки графика приближаются к оси абсцисс: правая приближается сверху, а левая – снизу. Прямые, к которым приближаются ветки гиперболы, называются ее асимптотами.

Пример 1.

y = (2x + 1) / (x – 3).

Решение.

Выделим целую часть: (2x + 1) / (x – 3) = 2 + 7/(x – 3).

Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 3 единичных отрезка вправо, растяжением вдоль оси Oy в 7 раз и сдвигом на 2 единичных отрезка вверх.

Любую дробь y = (ax + b) / (cx + d) можно записать аналогичным образом, выделив «целую часть». Следовательно, графики всех дробно-линейных функций есть гиперболы, различным образом сдвинутые вдоль координатных осей и растянутые по оси Oy.

Для построения графика какой-нибудь произвольной дробно-линейной функции совсем не обязательно дробь, задающую эту функцию, преобразовывать. Поскольку мы знаем, что график есть гипербола, будет достаточно найти прямые, к которым приближаются ее ветки – асимптоты гиперболы x = -d/c и y = a/c.

Пример 2.

Найти асимптоты графика функции y = (3x + 5)/(2x + 2).

Решение.

Функция не определена, при x = -1. Значит, прямая x = -1 служит вертикальной асимптотой. Для нахождения горизонтальной асимптоты, выясним, к чему приближаются значения функции y(x), когда аргумент x возрастает по абсолютной величине.

Для этого разделим числитель и знаменатель дроби на x:

y = (3 + 5/x) / (2 + 2/x).

При x → ∞ дробь будет стремиться к 3/2. Значит, горизонтальная асимптота – это прямая y = 3/2.

Пример 3.

Построить график функции y = (2x + 1)/(x + 1).

Решение.

Выделим у дроби «целую часть»:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

= 2 – 1/(x + 1).

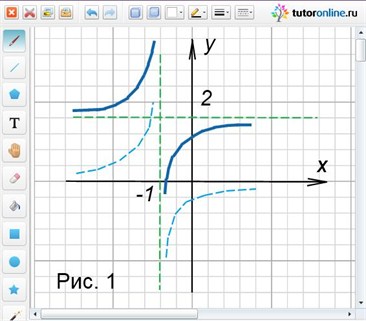
Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 2 единичных отрезка вверх по оси Oy.

Область определения D(y) = (-∞; -1)ᴗ(-1; +∞).

Область значений E(y) = (-∞; 2)ᴗ(2; +∞).

Точки пересечения с осями: c Oy: (0; 1); c Ox: (-1/2; 0). Функция возрастает на каждом из промежутков области определения.

Ответ: рисунок 1.

2. Дробно-рациональная функция

Рассмотрим дробно-рациональную функцию вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, степени выше первой.

Примеры таких рациональных функций:

y = (x³ – 5x + 6) / (x⁷ – 6) или y = (x – 2)²(x + 1) / (x² + 3).

Если функция y = P(x) / Q(x) представляет собой частное двух многочленов степени выше первой, то ее график будет, как правило, сложнее, и построить его точно, со всеми деталями бывает иногда трудно. Однако, часто достаточно применить приемы, аналогичные тем, с которыми мы уже познакомились выше.

Пусть дробь – правильная (n < m). Известно, что любую несократимую рациональную дробь можно представить, и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением знаменателя дроби Q(x) в произведение действительных сомножителей:

P(x)/Q(x) = A₁/(x – K₁)^m1 + A₂/(x – K₁)^m1-1 + … + A_m1/(x – K₁) + …+

+ L₁/(x – K_s)^ms + L₂/(x – K_s)^ms-1 + … + L_ms/(x – K_s) + …+

+ (B₁x + C₁) / (x² +p₁x + q₁)^m1 + … + (B_m1x + C_m1) / (x² +p₁x + q₁) + …+

+ (M₁x + N₁) / (x² +p_tx + q_t)^m1 + … + (M_m1x + N_m1) / (x² +p_tx + q_t).

Очевидно, что график дробно-рациональной функции можно получить как сумму графиков элементарных дробей.

Построение графиков дробно-рациональных функций

Рассмотрим несколько способов построения графиков дробно-рациональной функции.

Пример 4.

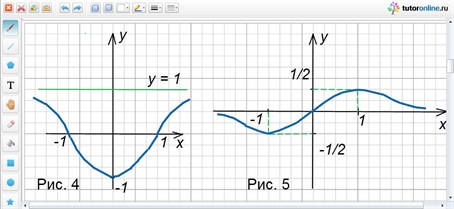
Построить график функции y = 1/x².

Решение.

Используем график функции y = x² для построения графика y = 1/x² и воспользуемся приемом «деления» графиков.

Область определения D(y) = (-∞; 0)ᴗ(0; +∞).

Область значений E(y) = (0; +∞).

Точек пересечения с осями нет. Функция четная. Возрастает при все х из интервала (-∞; 0), убывает при x от 0 до +∞.

Ответ: рисунок 2.

Пример 5.

Построить график функции y = (x² – 4x + 3) / (9 – 3x).

Решение.

Область определения D(y) = (-∞; 3)ᴗ(3; +∞).

y = (x² – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/3 + 1/3.

Здесь мы использовали прием разложения на множители, сокращения и приведения к линейной функции.

Ответ: рисунок 3.

Пример 6.

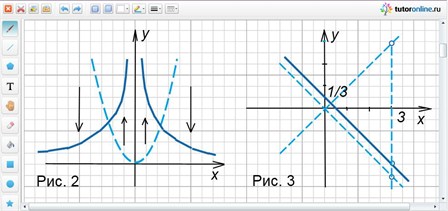
Построить график функции y = (x² – 1)/(x² + 1).

Решение.

Область определения D(y) = R. Так как функция четная, то график симметричен относительно оси ординат. Прежде чем строить график, опять преобразуем выражение, выделив целую часть:

y = (x² – 1)/(x² + 1) = 1 – 2/(x² + 1).

Заметим, что выделение целой части в формуле дробно-рациональной функции является одним из основных при построении графиков.

Если x → ±∞, то y → 1, т.е. прямая y = 1 является горизонтальной асимптотой.

Ответ: рисунок 4.

Пример 7.

Рассмотрим функцию y = x/(x² + 1) и попробуем точно найти наибольшее ее значение, т.е. самую высокую точку правой половины графика. Чтобы точно построить этот график, сегодняшних знаний недостаточно. Очевидно, что наша кривая не может «подняться» очень высоко, т.к. знаменатель довольно быстро начинает «обгонять» числитель. Посмотрим, может ли значение функции равняться 1. Для этого нужно решить уравнение x² + 1 = x, x² – x + 1 = 0. Это уравнение не имеет действительных корней. Значит, наше предположение не верно. Чтобы найти самое большое значение функции, надо узнать, при каком самом большом А уравнение А = x/(x² + 1) будет иметь решение. Заменим исходное уравнение квадратным: Аx² – x + А = 0. Это уравнение имеет решение, когда 1 – 4А² ≥ 0. Отсюда находим наибольшее значение А = 1/2.

Ответ: рисунок 5, max y(x) = ½.

Остались вопросы? Не знаете, как строить графики функций?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Источник

Построение графика функции $y = frac{x+1}{x-1}$ последовательными преобразованиями гиперболы $y = frac{1}{x}$
Анализ асимптот
Алгоритм построения графика дробно-линейной функции
Примеры

Построение графика функции $y = frac{x+1}{x-1}$ последовательными преобразованиями гиперболы $y = frac{1}{x}$

Начнём исследование с построения графика для $y = frac{x+1}{x-1}$.

Выделим целую часть в дроби: $y = frac{x+1}{x-1} = frac{(x-1)+2}{x-1} = 1+ frac{2}{x-1}$

Согласно §47-48 данного справочника, эта функция последовательно получается из гиперболы

$$ y = frac{1}{x} xrightarrow{2f(x)} y = frac{2}{x} xrightarrow{2f(x-1)} y = frac{2}{x-1} xrightarrow{2f(x-1)+1} y = frac{2}{x-1} +1 $$

$Построение графика функции $y = frac{x+1}{x-1}$ последовательными преобразованиями гиперболы $y = frac{1}{x}$$

Шаг 1. 2f(x) – функция $y = frac{1}{x}$ растягивается в 2 раза по оси OY, получаем $y = frac{2}{x}$

Шаг 2. 2f(x-1) – функция $y = frac{2}{x}$ сдвигается вправо на 1 по оси OX, получаем $y = frac{2}{x-1}$

Шаг 3. 2f(x-1)+1 — функция $ y = frac{2}{x-1}$ сдвигается вверх на 1 по оси OY, получаем $y = frac{2}{x-1}+1$.

Анализ асимптот

Итоговым графиком $y = frac{x+1}{x-1}$ является гипербола.

Ветки гиперболы ограничены двумя прямыми, которые называют асимптотами.

Ветки на бесконечности стремятся к этим прямым, но никогда их не достигают.

Рассмотрим смещение асимптот при построении.

Для исходного графика $y = frac{1}{x}$ асимптотами являются оси координат, x=0,y=0

Для графика $y = frac{2}{x}$ оси координат остаются асимптотами.

Для графика $y = frac{2}{x-1}$ происходит сдвиг вправо, асимптоты x=1,y=0

Для графика $y = frac{2}{x-1}+1$ происходит сдвиг вверх, конечные асимптоты x = 1, y = 1

Асимптоты служат хорошим ориентиром для построения графика гиперболы.

В данном случае, достаточно построить гиперболу $y = frac{2}{x}$ и переместить её параллельным переносом, заданным переносом точки пересечения асимптот из (0;0) в (1;1).

Алгоритм построения графика дробно-линейной функции

На входе

$$ y = frac{ax+b}{cx+d}, c neq 0, ad-bc neq 0 $$

Шаг 1. Выделить целую часть из дроби и представить её в виде $y = frac{A}{x+B}+C$

Шаг 2. Построить график $y = frac{A}{x}$.

Шаг 3. Построить горизонтальную асимптоту x = -B.

Шаг 4. Построить вертикальную асимптоту y = C.

Шаг 5. Переместить исходный график $y = frac{A}{x}$ параллельным переносом точки пересечения асимптот из (0;0) в (-B;C).

Если необходимо, отметить дополнительные точки, соединить кривой.

Гипербола $y = frac{A}{x+B}+C$ построена.

Примеры

Пример 1. Постройте график функции $y = frac{x+1}{x-3}$

Выделяем целую часть: $y = frac{x+1}{x-3} = frac{(x-3)+4}{x-3} = frac{4}{x-3} +1$

Исходная гипербола $y = frac{4}{x}$.

Асимптоты: x = 3, y = 1.

Получаем:

Пример 2. Постройте график функции $y = frac{x}{x+2}$

Выделяем целую часть: $y = frac{x}{x+2} = frac{(x+2)-2}{x+2} = frac{2}{x+2} +1$

Исходная гипербола $y = -frac{2}{x}$.

Асимптоты: x = -2, y = 1.

Получаем:

Пример 3*. Постройте график функции $y = frac{2x^2-8x}{x^2-7x+12}$

Преобразуем дробь:

$$ y = frac{2x^2-8x}{x^2-7x+12} = frac{2x(x-4)}{(x-3)(x-4)} = {left{ begin{array}{c} frac{2x}{x-3} \ x neq 4 end{array} right.} $$

$x neq 4$ — исключенная точка.

Выделим целую часть:

$$ y = frac{2x}{x-3} = frac{2x-6+6}{x-3} = frac{2(x-3)+3}{x-3} = frac{3}{x-3} +2 $$

Исходная гипербола $y = frac{3}{x}$.

Асимптоты: x = 3, y = 2.

Учитывая исключенную точку, получаем:

Источник