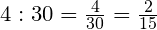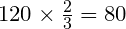Задачи на дроби
- Выражение части в долях целого
- Нахождение дроби от числа
- Нахождение числа по его дроби
Выражение части в долях целого
Чтобы выразить часть в долях целого, нужно часть разделить на целое.
Задача. В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?
Решение:
Ответ: В классе отсутствует 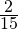
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
Решение: Чтобы найти 
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
Решение:
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение числа по его дроби
Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:
Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.
Задача 1. Потратили 50 рублей, это составило 
Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:
50 · 6 = 300 (р.).
Ответ: Первоначальная сумма — 300 рублей.
Задача 2. Потратили 600 рублей, это составило 
Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):
600 : 2 · 3 = 900 (р.).
Ответ: Первоначальная сумма — 900 рублей.
Второй способ нахождения целого по его части:
Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.
Задача 3. Отрезок AB, равный 42 см, составляет 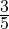
Решение:
Ответ: Длина отрезка CD 70 см.
Задача 4. В магазин привезли арбузы. До обеда магазин продал 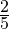
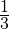
Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):
Итак, мы узнали, что 80 арбузов составляет 

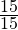
2) 80 : 4 · 15 = 300 (арбузов).
Ответ: Всего в магазин привезли 300 арбузов.
Математика
5 класс
Урок № 67
Нахождение части целого и целого по его части
Перечень рассматриваемых вопросов
– нахождение целого по его части;
– нахождение части целого;
– моделирование условий задачи с помощью рисунка.
Тезаурус
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Частное дробей – это дробь, которая при умножении на делитель даёт делимое.
Обязательная литература
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Мы уже рассмотрели, как выполняют умножение и деление дробей. Сегодня с помощью этих действий мы будем решать задачи.
Рассмотрим две задачи.
Теперь определим, какие условия в задачах одинаковы, а какие различаются.
Общее:
- в задачах одинаковые числовые данные;
- за целое принята длина всей ленты.
Разное:
- в первой задаче целое известно (длина ленты – 18 м);
- во второй задаче целое нужно найти.
Значит, в первой задаче нужно найти часть отрезанной ленты, то есть часть от целого; а во второй задаче нужно найти всю длину ленты, то есть целое по его части.
Подобные задачи решаются в соответствие с известными правилами.
- Чтобы найти часть от целого, надо целое (соответствующее ему число) умножить на дробь, соответствующую этой части.
- Чтобы найти целое по его части, надо часть (соответствующее этой части число) разделить на соответствующую дробь.
Если вы затрудняетесь определить тип задачи, обратите внимание на союз «что» и указательное местоимение «это». Они встречаются в задачах на нахождение целого по его части.
Решение.
Смоделируем условие задачи с помощью рисунка.
После этого мы увидим, что длина целой ленты известна, а длину части следует вычислить. Значит, мы будем находить часть от целого. Используем для этого соответствующее правило. Чтобы найти часть числа, нужно число умножить на дробь. Получим:
Решение.
Опять смоделируем условие задачи с помощью рисунка.

Таким образом, мы увидим, что длина целой ленты неизвестна, а длина части указана в условии. Значит, нам надо вычислить целое по его части. Для этого мы используем подходящее правило. Чтобы найти целое, нужно число, соответствующее части, разделить на дробь.
Получится:
Итак, сегодня на уроке мы научились:
-
- моделировать условие задачи с помощью рисунка;
- устанавливать соответствие между математическим выражением и его текстовым описанием;
- решать задачи на нахождение части целого и целого по его части.
Рассмотрим старинную индийскую задачу XII века.
Из множества лотосов были подарены: богу Шиве – треть всех цветов, богу Вишну – пятая часть, а Солнцу – шестая, четвёртую долю получила богиня Бхавани, а остальные шесть частей – уважаемый учитель. Сколько было всего лотосов?
Сегодня мы с вами научимся решать такие задачи с применением действий умножения и деления, изученных ранее.
Решение.
Смоделируем условие задачи с помощью рисунка.
Общее количество лотосов обозначим за единицу. Также укажем части (лотосы), которые распределялись между всеми, кто указан в задании.
Известно, что часть, доставшаяся учителю, равна шести лотосам. Значит, если мы будем знать, какая это доля от общего количества лотосов, то придём ко второму типу задачи – вычислению целого по его части.
Итак, найдём, какая часть от общего количества цветков досталась учителю.
Для этого вычислим сначала, сколько составляют все остальные части. Сложим все дроби, соответствующие частям, приведя их к общему знаменателю 60.
Ответ: 120 цветков.
Тренировочные задания
№ 1. Какие части изображены на рисунках?
Правильные ответы:
№ 2. Подставьте в текст нужные слова:
При решении задач на ___ сначала нужно определить ___ задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение ___ от целого;
- нахождение целого по его ___.
Варианты слов для подстановки в текст: части; тип; целого.
Правильный ответ: при решении задач на части сначала нужно определить тип задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение части от целого;
- нахождение целого по его части.
Начнем с нахождения неизвестной части от известного целого.
Как правило, целое принимается за единицу. Например, — необходимо разделить поровну торт, массой 2 кг на 8 человек. Найти массу одного кусочка.
Каждый присутствующий получит: 1 : 8 = 1/8 от всего торта. Тогда масса одного кусочка: 2 * 1/8 = 2 : 8 = 1/4 = 0,25 (кг) = 250 (г)
Таким образом, для нахождения части от целого необходимо целое разделить на количество частей (в данном случае 
———————————
В решении задач часто возникают ситуации, когда вопрос нахождения части от целого не ограничивается простым делением целого на количество частей. Например:
В свежих фруктах находится 60% воды. Найти массу сухих фруктов, получившихся из 12 кг свежих.
Так как воды в свежих фруктах 60% или 6/10 от всего количества, то сухих фруктов получится: 1 — 6/10 = 4/10 от всей массы свежих фруктов. Так как вся масса — 12 кг, то масса сухих фруктов:
12 * 4/10 = 48/10 = 4,8 (кг)
Следует обратить внимание на то, что при умножении числа на дробь безразлично, в каком порядке выполнять действия: можно умножить число на числитель, а потом разделить полученный результат на знаменатель, или можно число разделить на знаменатель, а потом полученный результат умножить на числитель:
12 * 4/10 = 12 * 4 : 10 = 12 : 10 * 4 = 1,2 * 4 = 4,8
=================================
Теперь рассмотрим, как находить целое, если известна его часть.
Возьмем, для примера, задачу с сухофруктами и изменим условие: Известно, что при сушке свежих фруктов получилось 7,2 кг сухих. Определить массу свежих фруктов, если известно, что масса воды составляет в них 60% от веса.
Так как 7,2 кг — это фрукты без воды, то от полной массы свежих фруктов 7,2 кг составляют: 100 — 60 = 40% или 0,4.
Тогда масса свежих фруктов: 7,2 : 0,4 = 7,2 : 4/10 = 7,2 * 10/4 = 72/4 = 18 (кг)
Таким образом, чтобы найти целое число по значению данной его части, эту величину делят на дробь, которая выражает её часть.
Формулировки с числителями и знаменателями несколько запутаны и, часто, не поддаются логическому осмыслению. Гораздо проще запомнить через действия с дробями: в случае нахождения части от целого, — умножение на дробь, в случае нахождения целого от части, — деление на дробь. А то, что деление на дробь равнозначно умножению на дробь, обратную данной, на мой взгляд, значительно проще для понимания..))
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅a / b
= n ⋅ a / b
Пример 1
Найдем5 / 12
от числа 24.
Решение
5 / 12
⋅ 24 =5 ⋅ 24 / 12
=120 / 12
= 10
Пример 2
Найдем4 / 9
от числа 7.
Решение
4 / 9
⋅ 7 =4 ⋅ 7 / 9
=28 / 9
=31 / 9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Видео
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
Решение: Чтобы найти 
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
Решение:
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если 

Требуется найти длину всей линейки по дроби 

Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби 

Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или 
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или 
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это 
Знаменатель дроби 


20 : 4 = 5
Мы нашли 
5 × 5 = 25
Мы нашли 
Пример 3. Десять минут это 
Знаменатель дроби 


10 мин : 2 = 5 мин
Мы нашли 

5 мин × 3 = 15 мин
Мы нашли 
Пример 4. 
Знаменатель дроби 



30кг : 2 = 15кг
Мы нашли 

15кг × 4 = 60кг
Мы нашли 
Нахождение целого по части
Чтобы, найти целое число по значению данной его части, эту величину делят на дробь, которая выражает её часть.
Вес обработанной туши животного составляет три пятых общего живого веса. Нужно определить какой должен быть живой вес животного, чтобы его заготовленная туша весила 420 кг?
Живой вес животного составляет семьсот килограмм по отношению к туше:
Регистрация
Ваше имя
Пароль
Хочу получать рассылку рекламных и информационных сообщений.
Нажимая на кнопку «Регистрация», вы подтверждаете свое согласие сусловиями предоставления услуг (пользовательское соглашение) и условиями обработки персональных данных
Теги
На уроке математики, на улице, в магазине, в быту и профессиональной деятельности, науке и технике часто приходится встречаться с дробями и решать различные задачи с ними.
Эта информация доступна зарегистрированным пользователям
Так, например, в кулинарии очень часто используют дробные числа, отмеряя те или иные ингредиенты в соответствии с рецептом: пол чайной ложки соли, треть стакана, четверть пачки, полкилограмма сахара и т.д.
Определяя время по часам, приходится находить часть от часа, от минуты, например, 30 минут равняется ½ часа, четверть часа (15 минут)- это ¼ часа, 30 секунд равняются ½ минуты, 15 секунд составляют ¼ минуты.
Эта информация доступна зарегистрированным пользователям
В медицине и фармацевтике используют дробные числа.
В состав лекарственного средства чаще всего включают дробное количество различных действующих и вспомогательных веществ.
Эта информация доступна зарегистрированным пользователям
Для корректного лечения врач устанавливает эффективную дозировку лекарственного препарата, которая иногда представлена в виде дробного числа.
Дозировку или концентрацию лекарственного средства приходится выражать в виде дроби: полтаблетки (1/2), четверть (1/4) таблетки и т.д.
Особенно важно учитывать количество медицинского препарата для пациентов детского возраста.
Часто дозировку лекарства для детей рассчитывают относительно взрослой дозы на основе данных о массе ребенка, количестве лет и др.
Обыкновенные дроби широко используются в строительстве и архитектуре.
Создавая надежную конструкцию, важно соблюдать соизмеримость и определенные соотношения частей сооружения.
Эта информация доступна зарегистрированным пользователям
Начертить чертеж, построить здание, возвести мост, положить асфальт, приготовить бетонную смесь невозможно без знаний о дробях.
В спортивных состязаниях вам, наверное, не раз приходилось слышать такие фразы: «состоялся четверть финал» или «полуфинал чемпионата», «одна восьмая финала».
Дроби используют в искусстве, например, в музыке, живописи и др.
Одним из примеров внедрения дробей в музыкальное искусство может служить нотная грамота.
Еще древнегреческий ученый Пифагор установил связь между длительностью музыкального звучания и дробей.
Дроби применяют для обозначения длительности нот.
Так, например, существует длинная нота.
Кроме нее есть половинная нота, четвертная, восьмая, шестнадцатая и т.д.
Эта информация доступна зарегистрированным пользователям
Такое обозначение нот удобно, так как явно видно насколько одна нота длиннее или короче другой.
Существует еще одна важная роль дробного числа в музыке.
Музыкальный размер (количество ритмических единиц в такте) так же обозначают в виде дроби (только без дробной черты) вначале нотной строки.
Эта информация доступна зарегистрированным пользователям
С помощью музыкального размера музыканты понимают с каким ритмом и темпом нужно играть музыкальное произведение.
В картографии и географии с помощью дроби указывают масштаб карты.
Деление целого на доли встречается в юридической практике при делении наследства.
В повседневной жизни мы часто делим целое на части, например, плитку шоколада ломаем на дольки, чтобы угостить друзей, режем на кусочки торт на празднике, делим мандарин на дольки и т.д.
Мы можем привести бесконечное множество примеров деления чего-либо на части.
Сегодня на уроке вспомним, что называют долей числа и, что представляет собой дробь от числа.
Эта информация доступна зарегистрированным пользователям
Научимся решать задачи, в которых необходимо находить часть от целого и целое по его части.
Рассмотрим алгоритм и примеры решения таких задач.
В математике дробью обозначают часть некоторой рассматриваемой величины, часть от целого.
Каждую равную часть одного целого называют долей числа.
Дробь представляет собой число, которое состоит из одной или нескольких долей (равных частей) целого.
Математическая запись обыкновенной дроби оформляется в виде двух чисел, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).
Число, стоящее над дробной чертой, называют числителем.
Числитель показывает, сколько долей взяли от целого.
Число, стоящее под дробной чертой, называют знаменателем.
Знаменатель показывает, на сколько всего равных долей разделили целое.
Зная целое, можно найти его часть.
Рассмотрим такую задачу.
Эта информация доступна зарегистрированным пользователям
Ленту, длиной 12 дм, разрезали на 2 равные части.
Что значит разрезать на две равные части?
Это значит, что ленту нужно разделить на две доли, каждая из которых является половиной этой ленты.
Эта информация доступна зарегистрированным пользователям
Итак, каждая доля- это половина всей ленты, по-другому такую часть от целого называют одна вторая часть ленты, обозначают ½.
В нашем примере половина всей ленты, т.е. одна вторая часть ее составляет 6 дм.
Запишем равенство: 12 ÷ 2 = 6 (дм).
Ленту такой же длины разделим на четыре равные части.
Эта информация доступна зарегистрированным пользователям
Получим 4 доли, каждая из которых равна одной четвертой всей длины ленты, обозначается 1/4.
Четверть (одна четвертая) ленты составляет: 12 ÷ 4 = 3 (дм).
Попробуем найти одну шестую ленты все той же длины- 12 дм.
Эта информация доступна зарегистрированным пользователям
1/6 доля этой ленты будет составлять: 12 ÷ 6 = 2 (дм).
Итак, нам становится ясно, чтобы найти долю от числа, необходимо разделить это число на количество долей (равных частей).
Рассмотрим ситуацию посложней.
Полоску бумаги, длиной 15 см, разделим на 5 равных частей (пять долей).
Эта информация доступна зарегистрированным пользователям
Определим, чему будет равны (mathbf{frac{3}{5}}) этой полоски бумаги.
Одна доля ((mathbf{frac{1}{5}}) этой полоски)- это 15 ÷ 5 = 3 (см).
Возьмем три таких доли.
Так как одна доля составляет 3 см, то три доли будут равны 3 ∙ 3 = 9 (см).
В данном случае получилось, что три пятых полоски бумаги составляют 9 см.
Сформулируем правило нахождения части от целого.
Чтобы найти несколько долей целого (дробь от числа), необходимо найти величину одной доли, затем умножить ее на количество долей.
Запишем алгоритм нахождения части от числа (несколько долей целого).
1. Найти величину одной доли.
2. Величину одной доли умножить на количество взятых долей.
В буквенном виде данное правило можно представить так:
Пусть А— это исходное число.
В— неизвестная часть числа А, выраженная дробью (mathbf{frac{m}{n}}).
m— числитель, показывает сколько долей взяли.
n— знаменатель, показывает на сколько долей разделили число А.
Чтобы найти часть числа А, необходимо это число А разделить на знаменатель (n) и умножить на числитель (m) дроби, которая выражает эту часть.
Эта информация доступна зарегистрированным пользователям
В качестве примера рассмотрим решение нескольких задач.
Задача №1.
Туристы за все время своего путешествия из пункта А в пункт В должны пройти 54 км.
Туристы прошли (mathbf{frac{1}{2}}) всего пути по лесу.
Сколько километров прошли туристы по лесу? Сколько им осталось пройти?
Решение:
Вспомним правило.
Чтобы найти долю от числа, необходимо число разделить на количество долей.
Прошли (mathbf{frac{1}{2}}) всего пути- это значит туристы преодолели половину своего пути.
Разделим весь путь на 2 равные доли, т.е. на 2, в результате получим (mathbf{frac{1}{2}}) пути, которую туристы прошли по лесу.
Этот путь будет составлять: 54 ÷ 2 = 27 (км).
Определим путь, который им осталось пройти, для этого из общего пути вычтем пройденный по лесу путь:
54 — 27 = 27 (км) туристам осталось пройти.
Ответ: 27 (км), 27 (км).
Задача №2
За три дня туристы прошли 54 километра.
За первый день они прошли половину всего пути.
За второй день преодолели (mathbf{frac{2}{3}}) оставшегося пути.
Сколько километров туристы прошли в каждый из трех дней?
Решение:
Весь трехдневный путь туристов составляет 54 км.
Первый день туристы прошли половину- это (mathbf{frac{1}{2}}) всего пути.
Выше в задаче №1 мы уже находили (mathbf{frac{1}{2}}) от 54 (км), у нас получился следующий результат:
54 ÷ 2 = 27 (км) прошли туристы в первый день.
Так как в первый день пройдена половина пути, то вторая половина- это оставшийся путь.
Он будет равен: 54 — 27 = 27 (км).
Второй день- это (mathbf{frac{2}{3}}) оставшегося пути, т.е. (mathbf{frac{2}{3}}) от 27 (км).
Чтобы найти дробь от числа, необходимо найти величину одной доли, затем умножить ее на количество частей (долей).
Найдем величину одной доли, для этого весь оставшийся путь (27 км) разделим на знаменатель дроби (в нашем случае это число 3), данное выражение будет описываться выражением 27 ÷ 3.
Полученный результат умножим на количество, пройденных туристами долей, на которые нам указывает числитель дроби (он равен 2).
В результате получим равенство:
27 ÷ 3 ∙ 2 = 9 ∙ 2 = 18 (км) туристы прошли во второй день.
Так как во второй день туристы прошли 18 км от пути, оставшегося после первого туристического дня (т.е. 18 км из 27 км), то за третий день им осталось пройти:
27 — 18 = 9 (км) туристы прошли в третий день.
Проверим полученные результаты.
Найдем весь туристический путь за три дня, он должен быть равен 54 км.
Для этого сложим путь первого, второго и третьего дня.
27 + 18 + 9 = 45 + 9 = 54 (км) прошли туристы за три дня.
Задача решена верно.
Ответ: 27 (км), 18 (км), 9 (км).
Эта информация доступна зарегистрированным пользователям
Если известно сколько составляет часть от целого, то по известной части можно найти целое.
Рассмотрим задачу:
Пусть длина (mathbf{frac{1}{2}}) ленты составляет 10 дм.
Определим, чему равна длина всей ленты.
Эта информация доступна зарегистрированным пользователям
Так как (mathbf{frac{1}{2}}) ленты- это ее половина, и она составляет 10 дм, то вторая половина так же равна 10 дм.
В таком случае, чтобы найти длину всей ленты, мы можем сложить длины этих двух половинок или, заменив сложение одинаковых слагаемых умножением, можем по 10 дм взять два раза, в результате получим равенство:
10 ∙ 2 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Рассмотрим еще одну задачу, в которой будет известна длина одной четвертой части ленты.
Ленту подарочную разделили на четыре части.
Длина (mathbf{frac{1}{4}}) ленты составляет 5 дм.
Эта информация доступна зарегистрированным пользователям
Определим, чему равна длина всей ленты.
Целое, т.е. всю ленту разделили на 4 доли.
Известно, что одна доля- это (mathbf{frac{1}{4}}) ленты, она составляет 5 дм.
Чтобы найти длину всей ленты, необходимо длину одной доли (в нашем случае 5 дм) умножить на количество долей (в нашем примере их 4).
Получим следующее равенство:
5 ∙ 4 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Рассмотрев эти два примера, можно сделать вывод:
Чтобы найти неизвестное число по его доле, необходимо долю этого числа умножить на число долей.
Усложним задачу про ленту и попробуем ее решить.
Пусть подарочную ленту разделили на 5 равных частей.
Определим, какова длина всей ленты, если (mathbf{frac{3}{5}}) этой ленты составляет 12 дм.
Эта информация доступна зарегистрированным пользователям
Из условия задачи известно, что разделили ленту на 5 долей, а 3 таких доли составляют 12 дм.
Для того чтобы найти длину всей ленты, необходимо найти длину одной доли.
Следовательно, известную длину трех долей (12 дм) разделим на количество этих долей (3 доли).
Данное действие будет описывать следующее выражение: 12 ÷ 3.
Затем умножим длину одной доли на количество всех долей (в нашем случае всю ленту разделили на 5 долей).
В результате получим равенство:
12 ÷ 3 ∙ 5 = 4 ∙ 5 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Сформулируем правило нахождения целого по его части.
Чтобы найти целое по его части, необходимо определить величину одной доли, затем полученный результат умножить на общее количество долей (на которое поделено целое).
Запишем алгоритм нахождения числа по его дроби.
1. Найти величину одной доли.
2. Величину одной доли умножить на количество всех долей, на которое разделено число.
В буквенном виде данное правило можно представить так:
Пусть А— это исходное число, оно неизвестно.
В— часть числа А, выраженная дробью (mathbf{frac{m}{n}}).
m— числитель, показывает сколько долей взяли.
n— знаменатель, показывает на сколько долей разделили число.
Чтобы найти исходное число А, необходимо число В, соответствующее части числа А, разделить на числитель (m) и полученный результат умножить на знаменатель (n) дроби, которая выражает эту часть.
Эта информация доступна зарегистрированным пользователям
Рассмотрим, как данное правило применяется при решении задач.
Задача №1.
Дима потратил на сладости 120 рублей, что составляет (mathbf{frac{2}{4}}) всех накопленных им денег.
Сколько всего денег было у Димы накоплено?
Решение:
Общее количество денег, которое было у Димы не известно.
Известно только то, что 120 рублей- это часть всех денег Димы.
Эта же часть денег выражена дробью (mathbf{frac{2}{4}}) от всех денег.
Знаменатель данной дроби показывает на то, что все накопленные деньги разделены на 4 части, а числитель дроби указывает на то, что две части из четырех составляют 120 рублей.
Найдем величину одной доли (одной части из четырех), т.е. сколько составляет (mathbf{frac{1}{4}}) (четверть) всех денег Димы.
120 ÷ 2 = 60 (руб.) составляет четверть всех денег Димы.
Чтобы найти общее количество денег, которые накопил Дима (а это четыре части по 60 рублей), нужно:
4 ∙ 60 = 240 (руб.) было накоплено у Димы.
Кратко решение данной задачи можно записать следующим образом:
120 ÷ 2 ∙ 4 = 240 (руб.) было накоплено у Димы.
Ответ: 240 (руб.)
Очень часто задачи такого типа имеют более сложные условия и их приходится решать в несколько действий.
Задача №2.
Дима купил шоколадку. Он за нее заплатил 60 рублей, что составило (mathbf{frac{1}{3}}) всех его денег.
От оставшейся суммы (mathbf{frac{2}{3}}) он потратил на мороженное, остальные деньги положил в копилку.
Сколько денег Дима положил в копилку?
Решение:
Первым делом определим первоначальную сумму, которая была у Димы.
Будем считать, что искомое число состоит из трех долей.
По условию задачи одна доля составляет 60 рублей.
Чтобы найти число (целое) по его доле, необходимо долю этого числа умножить на число долей.
В таком случае получаем:
60 ∙ 3 = 180 (руб.) всего было накоплено у Димы- это первоначальная сумма, которая у него была.
Следующим действием найдем часть денег, которые потратил Дима на мороженное.
Из общей суммы денег вычтем 60 рублей, которые были потрачены на шоколадку.
180 — 60 = 120 (руб.) оставшееся сумма денег у Димы.
От полученного остатка найдем (mathbf{frac{2}{3}})
Чтобы найти (mathbf{frac{2}{3}}) от 120 (дробь от числа), нужно число 120 разделить на знаменатель и умножить на числитель этой дроби.
120 ÷ 3 ∙ 2 = 40 ∙ 2 = 80 (руб.) Дима потратил на мороженное.
Из первоначальной суммы (180 рублей) вычтем деньги, потраченные на шоколадку, (60 рублей), вычтем деньги, потраченные на мороженное, (80 рублей) и получим остаток денег, который Дима положил в копилку.
180 — 60 — 80 = 100 — 60 = 40 (руб.) Дима положил в копилку.
Ответ: 40 (руб.)
Эта информация доступна зарегистрированным пользователям