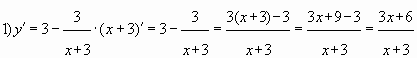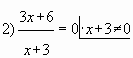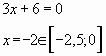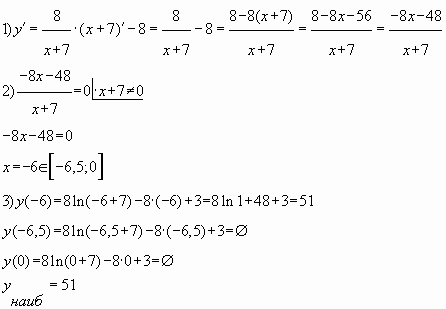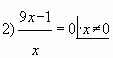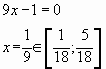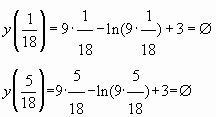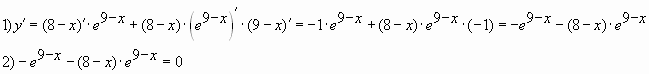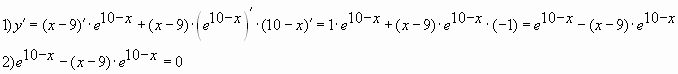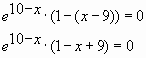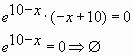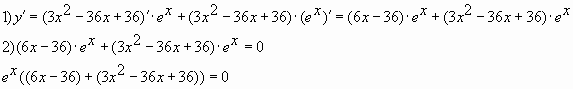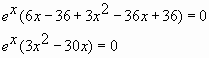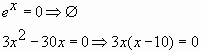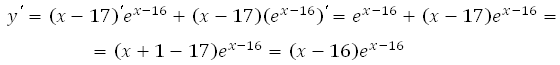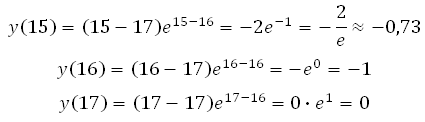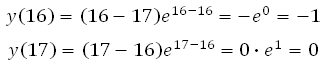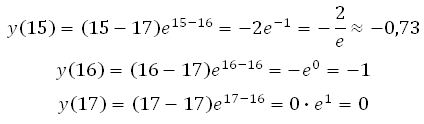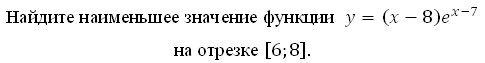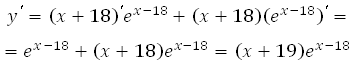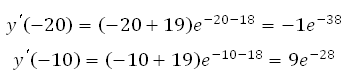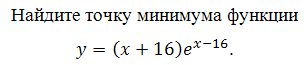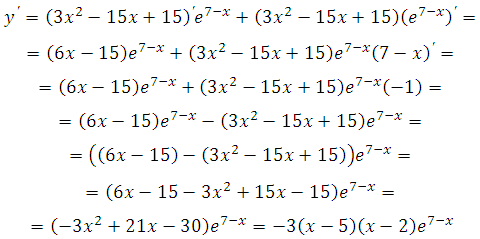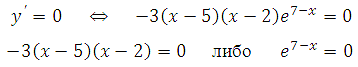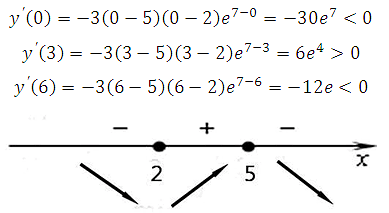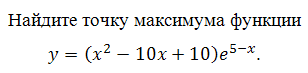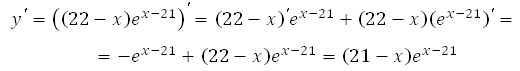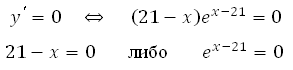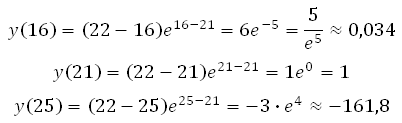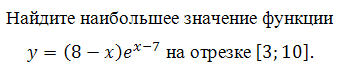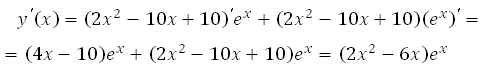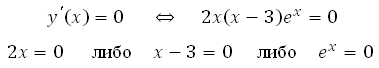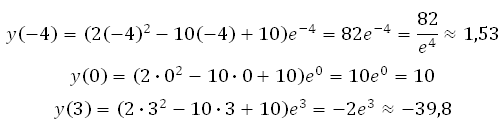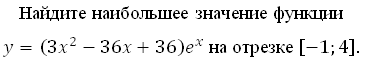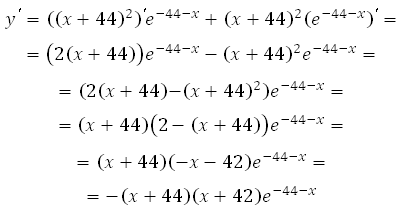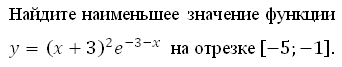1. Понятие функции
Функция y=f(x) – соответствие, при котором каждому числу x из множества D сопоставляется единственное число y из множества E.
x– аргумент функции, y – значение функции; D или D(f) – область определения функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E(f) – область значений функции; это совокупность всех значений, которые может принимать выражение f(x).
График функции y=f(x) – множество точек (x,y) на координатной плоскости, где x принимает все возможные значения из D(f), а y=f(x).
Четная функция: f(-x)=f(x) для всех 
Нечетная функция: f(-x)=-f(x) для всех 
График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
Периодическая функция с периодом T>0: f(x+T)=f(x) для всех 
Нули функции – значения x такие, что f(x)=0. Интервалы знакопостоянства – множества значений аргумента, при которых значения функции только положительны или только отрицательны.
На рисунке изображена функция с областью определения [a, e]. Нули функции: x=b, x=c, x=d; интервалы знакопостоянства: y>0 при 

Функция возрастает на множестве X, если большему значению аргумента соответствует большее значение функции. То есть для любых 

2. Основные элементарные функции
а) степенная функция 
б) показательная функция 
в) логарифмическая функция 
г) тригонометрические функции
y=sinx, y=cosx
y=tgx
y=ctgx
д) обратные тригонометрические функции
y=arcsin x, y=arccos x, y=arctg x, y=arcctg x
3. Некоторые алгебраические функции
а) линейная 
График функции – прямая линия, проходящая через точки (0, b) и 
Функция возрастает при a>0, убывает при a<0.
Частные случаи: y=b – прямая, параллельная оси OX;
y=ax – прямая, проходящая через начало координат.
б) квадратичная 
График функции – парабола. Ветви параболы направлены вверх при a>0, вниз при a<0. Вершина параболы:

Точки пересечения с осями координат:
с осью OX – (x1, 0) и (x2, 0),
где 
с осью OY – (0, c).
Пример 1. График какой функции является возрастающим:
а) 
Решение:
Рассмотрим каждую из функций в отдельности:
а) 

Возьмём два значения х1 = 1 и х2 = 4. Им соответствует у1 = – 1, у2 = – 2. Видим, что если х1 < x2 , то у1 > у2. Функция убывающая.
б) у = х3 – 27 – алгебраическая функция. Область определения – множество всех действительных чисел. На всей области определения функция монотонна. Возьмём два значения х1 = 3, х2 = 4. Им соответствует у1 = 0, у2 = 37.
Видим, что если х1 < x2 , то и у1 < у2. Функция возрастающая.
в) y=2-x – показательная функция. Областью определения является множество всех действительных чисел. На всей области определения функция монотонна. Пусть х1 = 0, х2 = 1. Им соответствуют у1 = 1, у2 = 0,5.
Видим, что если х1 < x2 , то у1 > у2. Функция убывающая.
Ответ: б) у = х3 – 27.
Пример 2. Парабола у = 2х2 – (а – 3)х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.
Решение:
Найдём значение параметра а. Т.к. парабола проходит через начало системы координат, то координаты точки (0; 0) являются корнями уравнения параболы: 0 = 2 ∙ 02 – (а – 3) ∙ 0 + а + 3; а = – 3.
Уравнение параболы примет вид: у = 2х2 + 6х.
Абсцисса вершины параболы находится по формуле: 

Ответ: – 1, 5.
Пример 3. В каких точках график функции f(x) = x2 – 3 пересекает прямую у(х) = х – 1?
Решение:
Ответом на данный вопрос является решение системы
х2 – 3 = х – 1; х2 – х – 2 = 0; х1= – 1, или х2 = 2.
Соответственно, у1 = – 2, у2 = 1.
Ответ: (– 1; – 2), (2; 1).
Пример 4. При каких значениях k прямые – kх + 7у = – 13 и 14у – 3х + 5 = 0 параллельны?
Решение:
Две различные прямые у = k1х + b1 и у = k2х + b2 параллельны, если k1 = k2, но при этом b1 ≠ b2.
В обоих уравнениях выразим у через х.



Ответ: при k = – 1,5.
Пример 5. Найти точки пересечения прямой у = 5 + х с осями координат.
Решение:
Когда график функции пресекает ось ОХ, значение у = 0.
Получаем уравнение 5 + х = 0, х = – 5.
Когда график функции пересекает ось OY, значение х = 0, т.е. у = 5.
Ответ: (– 5; 0), (0; 5).
Пример 6. Найти нули функции у = (х + 1)∙(х – 2).
Решение:
Решаем уравнение (х + 1)∙(х – 2) = 0.
х + 1 = 0 или х – 2 = 0; х1 = – 1, х2 = 2.
Ответ: (– 1; 0), (2; 0).
Пример 7. Найти область значений функции 
Решение:
Оцениваем последовательно:

Ответ: 
Пример 8. Найдите сумму целых значений функции у = 3 – 2 sin x.
Решение:
Оценим значение 3 – 2 sin x.

Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.
Ответ: 15.
Пример 9. Найти область определения функции 
Решение:
Функция задана аналитически, следовательно, область определения совпадает с областью допустимых значений выражения 
х2 + х ≠ 0, т.к. на нуль делить нельзя.
х (х + 1) ≠ 0; х ≠ 0 или х ≠ – 1.
Ответ: 
Пример 10. Найдите область определения функции 
Решение:
Допустимые значения выражения 

Ответ: 
Пример 11. Найдите область определения функции 
Решение:
Допустимые значения выражения: 
Ответ: (– 1; + ∞).
Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А(0; 2), проходящая через точку В(2; – 6). Задайте эту функцию формулой.
Решение:
Уравнение квадратичной функции у = ах2 + bх + с.
1) точка А является вершиной параболы, следовательно 
Уравнение примет вид: у = ах2 + с.
2) точка А принадлежит графику, следовательно её координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2.
Уравнение примет вид: у = ах2 + 2.
3) график проходит через точку В. Её координаты также удовлетворяют уравнению: – 6 = а ∙ 22 + 2, – 8 = 4 ∙ а, а = – 2.
Получили уравнение у = – 2х2 + 2.
Ответ: у = – 2х2 + 2.
Пример 13. Найдите g (x) , если f (x) = 2x – 3, g (f (x)) = x. Вычислите g (1).
Решение:
Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.
2x – 3 = 1, х = 2.
Следовательно, g (f (x)) = 2, т.е. g (1) = 2.
Ответ: g (1) = 2.
Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y=52x, y=53x-1 и через точку параболы y=(2x-1)2, в которой производная функции, задающей параболу, равна 8.
Решение:
1) найдём точку пересечения кривых:

2) найдём точку параболы, в которой производная равна 8:

3) прямая проходит через две точки (1; 25) и (1,5; 4). Согласно уравнению прямой, проходящей через две точки, имеем:
– 21х + 21 = 0,5у – 12,5; – 42х + 42 = у – 25; у = – 42х + 47.
Ответ: у = – 42х + 47.
Задания для самостоятельного решения
Базовый уровень
1) Вычислите значение функции 
2) Найдите значение функции 
3) Для функции 
4) Найдите g(f(x)), если 
Найдите области определения функций:
5) 
6) 
7) 


9) 
10) 
11) 
12) 
13) 
14) y=log5(x+3).
15) y=log5(x2-4).
16) 
При каких значениях х функции не определены?
17) 
18) 
19) 
20) 
21) y=ctgx+tgx.
22) 
23) 
Укажите длину интервала области определения для функций:
24) 
25) y=log4(5x+6-x2)
26) y=log6(x2+3).
Укажите области значения функций:
27) y=-3sinx.
28) y=0,7cos3x.
29) 
Решите задачи:
30) Сколько натуральных значений может принять функция y=log2(4-x2) на всей области определения?
31) Найдите сумму целых значений функции y=3cosx-5.
32) Укажите функцию, областью значений которой является множество 

33) Укажите график функции, возрастающей на отрезке [-3; 2].
34) Укажите функцию, которая возрастает на всей области определения.
1) y=-x0,5; 2) y=1-e-x; 3) y=ctg2x; 4) y=|-x|.
35) Найдите нули функции 
36) Найдите нули функции 
37) Найдите наименьшее значение функции f(x)=32x-1 на промежутке [-3; 1].
38) Вычислите координаты точек пересечения графика функции у = – 2х2 + 4х + 6 с осью OY.
39) Вычислите ординату точки пересечения прямой у = 5 – 2х с осью ОY.
40) Укажите точки пересечения графиков функций у = 2х + 4 и у = – 2х.
41) В каких точках график функции f (x) = 3x2 + 6x пересекает прямую у = 6 – х?
42) Укажите промежутки возрастания функции y=sin3x на интервале 
43) Укажите промежутки убывания функции y=-2cosx на интервале 
Повышенный уровень
44) При каких значениях а графики функций у = 3х – 4х3 и у = а имеют единственную общую точку?
45) Найдите длину промежутка области значений функции 
46) Найдите середину промежутка области значений функции y=cosx+|cosx|.
47) Найдите наибольшее целое значение выражения 2t, где t – число, принадлежащее области значений функции y=cos2x•tg2x.
48) Найдите наименьшее значение функции 
49) Укажите наименьшее значение функции y=log2(x2-4x+12).
50) Укажите наибольшее значение функции 
51) Вычислите значение функции y=4•sin7x при 

52) Вычислите значение функции y=|tg2x| при 

53) Найдите значение 2sint, где t – сумма точек максимума функции 

54) Укажите наибольшее значение функции y=cos(tgx) на промежутке 
Образовательные задачи урока.
- повторить необходимые и достаточные условия
существования точек экстремума, понятия:
стационарные и критические точки; - ввести алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке - сформировать умение решать задачи на
нахождение наибольшего и наименьшего значения
степенной функции на отрезке с помощью
производной. - разобрать прототипы задач № 1 В14
экзаменационной работы в формате ЕГЭ. - Продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения писать
необходимом темпе.
Воспитательные задачи:
- cодействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - cодействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм; - cодействовать профилактике утомляемости
школьников, используя разнообразные виды работы
на уроке.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Актуализация знаний учащихся.
Повторить с учащимися основные понятия прошлых
уроков: точки экстремума, каково достаточное
условие точек экстремума, стационарные точки и
критические точки (учащихся отвечают с места)
Повторить таблицу производных основных
функций и основные правила нахождения
III. Изучение нового материала.
Алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке
(учащиеся записывают себе в тетрадь).
Пусть функция непрерывна и дифференцируема на
отрезке , то
для нахождения наибольшего и наименьшего
значения функции на отрезке нужно:
- найти производную функции, найти стационарные
точки (решаем уравнение, приравнивая производную
к нулю) - среди полученных стационарных точек выбрать те,
которые принадлежат отрезку - найти значение в стационарных точках и в концах
отрезка, то естьи
.
- среди полученных значений выбрать наибольшее
или наименьшее.
Записать схему нахождения наибольшего и
наименьшего значения функции на отрезке в
тетради (учитель оформляет схему на доске):
Пусть
непрерывна на
и дифференцируема. Тогда, для нахождения или
:
- Находим
находим
- Проверяем принадлежность
отрезку
- Находим
,
,
.
- Среди полученных значений выбираем
или
.
- Записываем ответ (Акцентировать внимание, что в
ответе должно быть записано либо целое число,
либо конечная десятичная дробь).
Пример № 1. Найти наименьшее значение функции
на отрезке
. (Учитель
совместно с учащимися записывает решение на
доске последовательно проговаривая каждый пункт
алгоритма).
Решение:
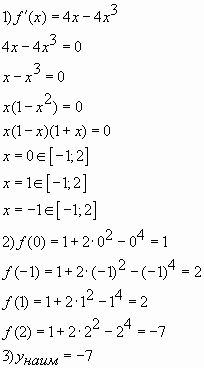
Ответ:
Пример № 2. Найти наибольшее значение
функции на
отрезке
Решение:
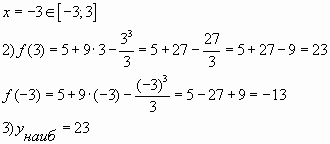
Ответ: 23
Пример № 3. Найдите наименьшее значение
функции на
отрезке .
Решение:
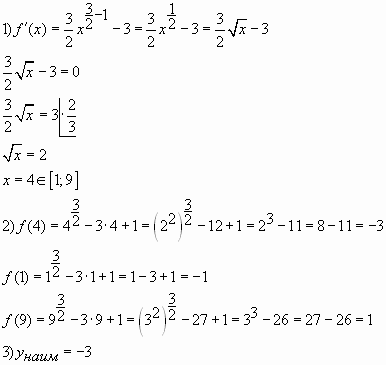
Ответ: -3
Пример № 4. Найдите наибольшее
значение функции на отрезке
.
Решение:
Упростим функцию
Ответ: 1
IV. Закрепление материала.
- Найдите наименьшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
V. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Выставить отметки за урок.
VI. Домашнее задание:
- Найдите наименьшее значение функции
на отрезке
- Найдите наибольшее значение функции
на отрезке
- Найдите наибольшее значение функции
на отрезке
- Найдите наименьшее значение функции
на отрезке
- Найти наибольшее значение функции
на отрезке
Урок № 2. “Нахождение наибольшего и
наименьшего значения функций и
на отрезке
.
Тип урока: комбинированный.
Образовательные задачи:
- обеспечить повторение в ходе урока алгоритма
нахождения наибольшего и наименьшего значения
функции на отрезке; - продолжить формирования навыка применения
этого алгоритма при решении второго типа задач
экзаменационных вариантов ЕГЭ; - продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения в
необходимом темпе читать и писать, анализировать
условия задачи.
Воспитательные задачи:
- содействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - содействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм. умение
слушать товарищей; - содействовать профилактике утомляемости
школьников.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Проверка домашнего задания. Фронтальная
проверка домашнего задания. Если у большинства
учащихся возникли вопросы, разобрать на доске
решение конкретного задания, если лишь у
некоторых, объяснить в индивидуальном порядке,
предварительно схематично обговорив решение у
доски.
III. Актуализация знаний. Повторить еще раз
алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке с оформлением схемы
на доске.
Повторить следующие формулы для дальнейшего
изучения материала:
,
,
Решить на повторение примеры (1 учащийся пишет
решение на доске с комментариями по решению,
остальные записывают себе в тетради).
IV. Решение новых прототипов задач (разбирает
решение учитель)
Пример № 1. Найти наименьшее значение
функции на
отрезке
Решение
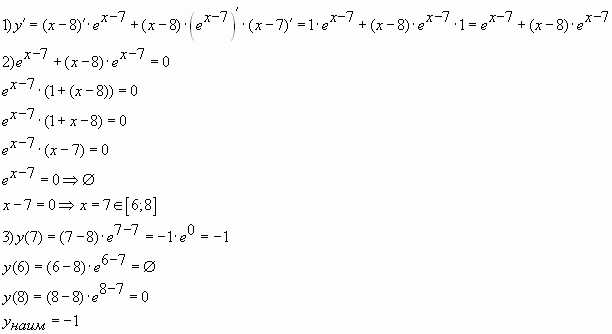
Ответ: —1
Пример № 2. Найти наименьшее значение
функции на
отрезке
Решение. Преобразуем и упростим функцию , используя
свойство логарифмов
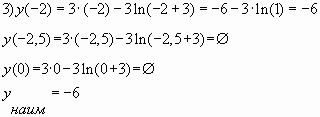
Ответ: -6
V. Закрепление материала (самостоятельное
решение задач учащимися у доски).
Пример № 3. Найти наибольшее значение функции
на отрезке
Решение.
Ответ: 51
Пример № 4. Найти наименьшее значение функции
на отрезке
Решение.
(, так как
)
Ответ: 4
Пример № 5. Найти наименьшее значение функции
на отрезке
Решение
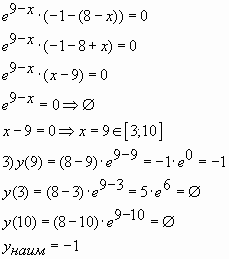
Ответ: -1
Пример № 6. Найти наибольшее значение функции
на отрезке
Решение:
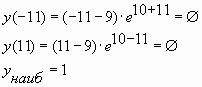
Ответ: 1
Пример № 7: Найдите наибольшее значение
функции на
отрезке
Решение
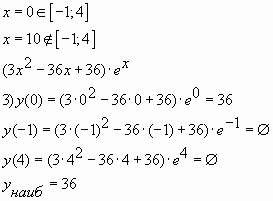
Ответ: 36
VI. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Проговорить основные алгоритмы решения тех
примеров, которые изучены на уроке.
VII. Домашнее задание по вариантам.
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
Функции с числом е. Друзья! На сайте «Математический тандем» проходит конкурс «Лучший комментатор декабря 2012 года», так что добро пожаловать, будут призы. В данной статье мы с вами рассмотрим задачи, входящие в сотав типовых заданий экзамена по математике, связанные с исследованием функций (где присутствует число е).
Рекомендую вам ещё раз внимательно прочитать статью «Исследование функций. Это нужно знать!» и освежить в памяти изложенную информацию. Не устану повторять, что для того чтобы решать задачи на нахождение наибольшего или наименьшего значения, задачи на нахождение экстремумов, важно понимать свойства производной для исследования функций, знать таблицу производных и правила дифференцирования.
После решения каждой задачи есть разъяснения другого подхода к решению (я обещал вам «хитрости» — они здесь). Рекомендую посмотреть, выглядит график показательной функции.
Рассмотрим задачи:
Найдите наименьшее значение функции у = (х–17)ех–16
на отрезке [15;17].
Мы знаем, что для того, чтобы найти наибольшее или наименьшее значение функции на отрезке, необходимо вычислить её значение на границах заданного интервала и в точках, где производная равна нулю. Действуем по алгоритму:
1. Найдём производную заданной функции:
2. Найдем нули производной на заданном отрезке, то есть приравниваем производную к нулю и вычислим корни уравнения:
*Выражение ех-16 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.
3. Определяем принадлежит ли найденная точка интервалу.
Точка х = 16 принадлежит интервалу [15;17]. Значит значение функции будем вычислять в точках 15, 16 и 17:
*Учтите, что число е ≈ 2,71. Это нецелое число и неконечная десятичная дробь, поэтому любое выражение с этим числом в подобных задачах на ЕГЭ не является верным ответом, но вы всё равно его проанализируйте. В данной задаче, если мы –2 разделим на число 2,71 то результат будет лежать в пределах от –1 до 0 (можно посчитать столбиком для проверки).
4. Делаем вывод.
Таким образом, наименьшее значение функции равно –1.
Ответ: –1
В этой статье я обещал вам какие-то там «хитрости», которые можно использовать при решении. Если вы поняли теорию производной и знаете, как находить максимальные и минимальные значения, то тогда читайте дальше — представленный приём будет хорошим дополнительным «инструментом» и позволит решать подобные задания мгновенно.
Итак! Мы знаем, что ответом в задачах на ЕГЭ в части В должно быть целое число, либо конечная десятичная дробь.
Посмотрите на данную функцию. Сразу можно сказать, что значение функции будет являться целым числом только при х = 16 или при х = 17, и ни при каких других значениях х. Поэтому достаточно вычислить:
и далее записать ответ.
Ещё один путь решения (без нахождения производной). Сразу подставляем в функцию все целые значения из интервала (их всего три 15, 16 и 17), вычисляем и выбираем наименьшее значение:
Решите самостоятельно:
Посмотреть решение
Найдите точку минимума функции у = (х + 18)ех-18
1. Найдём производную заданной функции:
2. Найдем нули производной:
Получаем, что х = –19.
*Выражение ех-18 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.
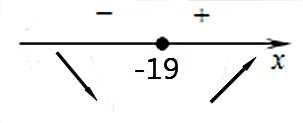
3. Определим знаки производной функции на интервалах (подставляем любые произвольные значения в производную) и изобразим на рисунке поведение функции:
В точке х = –19 функция меняет знак с отрицательного на положительный, значит это искомая точка минимума.
Ответ: –19
Как решать быстрее данный тип задач?
Когда мы получили производную и приравняли её к нулю:
(х + 19)ех–18 = 0
Далее получили, что х=–19. Данное решение и будет являться ответом задачи.
*То есть, в при решении данного типа задач, можно обойтись без определения знаков производной на интервалах. Но будьте осторожны! В других заданиях на нахождение максимума (минимума), где получите несколько нулей производной, её знаки на интервалах нужно определять обязательно.
Решите самостоятельно:
Посмотреть решение
Найдите точку максимума функции у = (3х2 – 15х + 15)е7–х
Найдём производную заданной функции:
Найдем нули производной:
Число е7-х не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.
Решаем – 3 (х–5)(х–2) = 0. Получим х1 = 5 и х2 = 2 .
Определим знаки производной функции (подставляя любые значения из интервалов в найденную производную) и изобразим на рисунке поведение функции:
В точке х = 5 функция меняет знак с положительного на отрицательный, значит это искомая точка максимума.
Ответ: 5
Решите самостоятельно:
Посмотреть решение
Найдите наибольшее значение функции у = (22 – х)ех–21
на отрезке [16;25].
Найдём производную заданной функции:
Найдем нули производной:
Число ех-21 не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное, значит х = 21.
Полученное значение принадлежит интервалу [16;25].
Вычислим значения данной в условии функции в точках 16, 21 и 25:
*То есть на границах интервала и в точке, где производная обращается в нуль.
Первый результат меньше единицы (это понятно и без вычислений).
Третий результат так же меньше единицы (отрицательное число).
Значит наибольшее значение функции на заданном интервале равно 1.
*Помните, что ответы с числом е (по требованиеям ЕГЭ) не являются верными.
Ответ: 1
Если у вас всё-таки неразрешимые проблемы с нахождением производной, то подставляйте в исходную функцию все целые значения из интервала и выбирайте наибольшее полученное значение.
*Кроме того, по данной функции сразу видно, что её значение будет целым числом только при х = 21 или при х = 22.
Можете подставить только их в функцию, далее произвести вычисления и выбрать наибольшее значение.
Решите самостоятельно:
Посмотреть решение
Найдите наибольшее значение функции у = (2х2 – 10х + 10)е х
на отрезке [–4; 3].
Необходимо определить значения на границах интервала, и в точках, где производная обращается в нуль.
Найдём производную заданной функции:
Найдем нули производной:
Произведение множителей равно нулю, когда какой либо из этих множителей равен нулю.
Число ех не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.
Значит решением являются корни: х1=0 и х2=3
Обе точки принадлежат интервалу [–4;3], х=3 совпадает с границей интервала.
Вычисляем значения функции в точках: – 4, 0 и 3:
Значит наибольшее значение функции равно 10.
Ответ: 10
*Как вы уже поняли, можно в заданную функцию можно подставить все целые значения х из интервала, и таким образом найти наибольшее значение функции. Но в данном случае придётся перебрать 8 чисел (–4;–3;–2;–1;0;1;2;3).
Решите самостоятельно:
Посмотреть решение
Найдите наименьшее значение функции у = (х + 44)2е–44–х
на отрезке [– 46; –43]
Найдём производную заданной функции:
Обратите внимание, что результат мы представили сразу в виде множителей, это будет удобно при вычислении нулей производной.
Найдем нули производной:
Решением являются корни: х1= – 44 и х2= – 42.
Заданному интервалу [– 46;–43] принадлежит только точка х = – 44.
Вычисляем значения функции в точках – 46, – 44 и – 43, то есть на границах интервала и в точке, где производная равна нулю:
Наименьшее значение функции равно 0.
Ответ: 0
*Как это задание решить быстро?
Учитывая, что ответом должно быть целое число, видно что значение данной функции будет целым только при х= – 44 и х= 44.
указанному в условии интервалу принадлежит х= – 44, вычисляем:
Решите самостоятельно:
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
На этом закончим. Всем удачи!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Функции с целыми значениями
15 января 2016
Прежде чем изучать конкретные задачи 19 и методы их решения, нужно понимать, как в принципе ведут себя целые числа на координатной прямой. Для этого разберём задачу, которая на первый взгляд вообще не имеет отношения к теории чисел — в ней нам предстоит работать с параметрами.
Решение этой задачи демонстрирует простой факт: целые числа накладывают целый ряд дополнительных ограничений на значения функции, которые вовсе не очевидны из условия задачи. Именно это происходит со всеми задачами 19 в настоящем ЕГЭ.:)
Смотрите также:
- Новое видео по задаче 19: учимся работать с арифметической прогрессией
- Задача 19: арифметическая прогрессия из пробного ЕГЭ
- Тест к параграфу «Что такое логарифм» (легкий)
- Решение задач B12: №440—447
- Четырехугольная пирамида: как найти координаты вершин
- Задача B4: обмен валют в трех различных банках















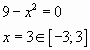
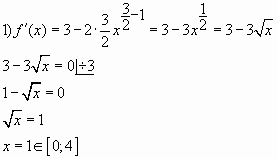
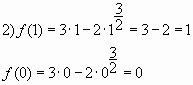
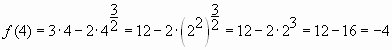
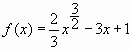 на отрезке
на отрезке