Всем добрый день! Не могу разобраться с решением этой задачи:
Подскажите, как исправить код
Условие
Центральным элементом набора из
k чисел называется такой элемент, который после сортировки набора будет занимать в нём центральную позицию (то есть позицию номер ⌈k/2] , считая с единицы).
Числа добавляются в изначально пустой набор в заданном порядке. Требуется определить значения центрального элемента после добавления каждого числа.
Формат входного файла
Входной файла содержит количество чисел n, за которым следуют n целых чисел ai в порядке их добавления в набор.
Формат выходного файла
Выходной файл должен содержать
n целых чисел — значения центрального элемента после каждого добавления.
Примеры тестов
Входной файл (input.txt) Выходной файл (output.txt)
3
5 3 4 5 3 4
5
1 2 3 2 4 1 1 2 2 2
| Python | ||
|
Given an array of ints with size t, one needs to find the center index. The center index x is the index where the sum of ints (0 to x-1) is equal to sum (x+1 to t-1).
The best algorithm I could come up with is O(n).
I would have a temp array with the sums of all ints before (not including the one at index x) : so at index 1 it would be 1, at 2 it would be a sum of 2 and 1 and so on.
Another int would be the sum of all ints.
I would loop twice through the array, the first make the temp array, and the other to find if both parts are equal.
Is there a better algorithm O(logn)?
Как найти координаты центра чисел на изображении
В настоящее время я работаю над своим первым заданием по обработке изображений (используя OpenCV в Python). Мое задание — подсчитать точную оценку (с точностью до десятых долей балла) от одной до нескольких бросков в загруженном пользователем изображении. Одно из требований — преобразовать загруженное изображение стреляющей цели в «вид с высоты птичьего полета» для дальнейшей обработки. Для этого я решил, что мне нужно найти центральные координаты чисел (7 и 8), чтобы выбрать их в качестве четырех четырехугольников.
К сожалению, есть несколько ограничений, которые необходимо учитывать.
Ограничения:
- разрешение обрабатываемого изображения прицела может варьироваться
- изображение можно делать в разных условиях освещения
- изображение, обработанное этой частью моего алгоритма, всегда будет снято под углом (крайние углы будут автоматически отклонены)
- изображение можно немного повернуть (+/- 10 градусов)
- мишень для стрельбы может быть только частью изображения
- изображение может быть только центральной черной части мишени, что означает, что пользователю не нужно фотографировать всю мишень (но на ней всегда должна быть центральная черная часть)
- этот алгоритм может занять максимум 2000 мсек.
Что я пробовал до сих пор:
- Соответствие шаблонов
- тут я быстро понял, что его нельзя использовать, так как числа можно было немного повернуть и другой масштаб
- Соответствие функций
- Я пробовал все разные типы сопоставления функций (SIFT, SURF, ORB…)
- К сожалению, у чисел нет этого конкретного набора функций, поэтому они соответствуют довольно большому количеству ложных срабатываний, но я мог бы отфильтровать их, добавив сопоставление форм и т. д.
- Самым большим блокировщиком была среда выполнения, время выполнения сопоставления только одного номера функции заняло около 5000 мс (даже после оптимизации) (на MacBook PRO 2017)
- Оптическое распознавание символов
- В основном я пробовал использовать библиотеку pytesseract
- даже после установки порога изображения в инвертированный двоичный код (поэтому текст чисел 7 и 8 черный, а фон белый) он не смог их распознать
- Я также пробовал несколько способов предварительной обработки изображения, и я много играл с параметром конфигурации tesseract, но это, похоже, совершенно не помогло
- Обнаружение контура
- Я легко обнаружил все требуемые числа (7 и
как отдельные контуры, но не смог отфильтровать все ложные срабатывания (поскольку изображение может быть в разных разрешениях, а также есть два типа целей с разными размерами чисел. Я не мог просто ограничить контур по его ширине, высоте или площади)
- После того, как я обнаружил числа как контуры, я хотел извлечь их как некоторую рентабельность инвестиций, а затем я бы использовал для них OCR (но поскольку было так много ложных срабатываний, это заняло бы много времени)
- Я также попытался отфильтровать их, используя функцию cv2.matchShapes как для контуров, так и для обрезанного шаблона / области интереса, но это показалось мне действительно ненадежным.
- Я легко обнаружил все требуемые числа (7 и
Примеры обработанных изображений:
- версия с высоким разрешением здесь
- версия с высоким разрешением здесь
- версия с высоким разрешением здесь
- версия с высоким разрешением здесь
- версия с высоким разрешением здесь
- версия с высоким разрешением здесь
На данный момент я не знаю, как это сделать. Я перепробовал все, что мог придумать. Я был бы безмерно счастлив, если бы кто-нибудь из вас, экспертов по распознаванию изображений, дал мне какой-либо совет или, что еще лучше, полезный пример кода, который помог бы мне решить мою проблему.
Спасибо всем заранее.
2020-07-23 09:53
1
ответ
-
Найдите черный диск с помощью адаптивной бинаризации и контура (возможно, размытие, чтобы стереть внутренние детали);
-
Подгоните эллипс к контуру как можно точнее;
-
Найдите хотя бы один край квадрата (линии Хафа);
-
Классифицируйте кромку как одну из NWSE (по углу);
-
Используйте информацию об эллипсе и линии, чтобы восстановить преобразование перспективы (это гомография);
-
Примените обратную гомографию, чтобы выпрямить изображение и получить точный целевой центр и ось;
-
Снова с помощью адаптивной бинаризации найдите пулевые отверстия (центр / радиус);
-
Оцените отверстия после их расстояния до центра относительно радиуса заднего диска.
Если схема маркировки изменчива, обнаруживайте круги (круги Хафа, используя известный центр, или обнаруживайте пики в наклонном профиле, начиная с центра).
При необходимости вы можете OCR цифр, но кажется, что счет неявно начинается с единицы во внешнем кольце.
2020-07-23 13:06
Модель натурального ряда чисел и его элементов. Ромбы
Время на прочтение
11 мин
Количество просмотров 3K
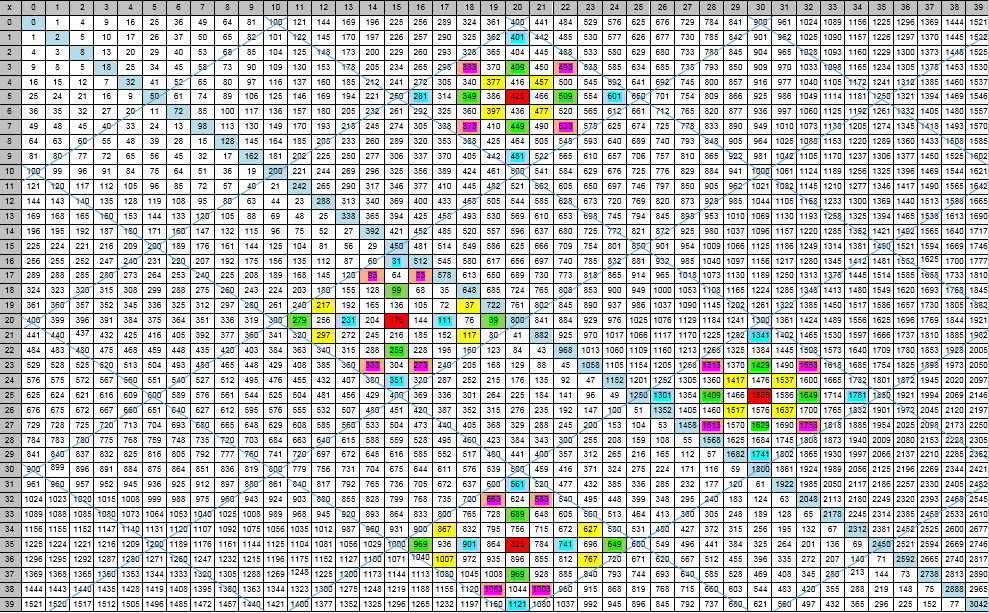
В этой работе сохраняется базовая Г2± – модель, но принимается другая организация ее клеток (другой рисунок). Поверх первичной решетки с клетками размера 1×1 изображается более крупная сетка – сетка ромбов, а также рассматривается сетка центров ромбов (СЦР). Последняя сетка не изображается, чтобы не перегружать линиями рисунок с ромбами. Мы не будем повторять определения и понятия, которые подробно излагались в предшествующих работах, но дадим указывающие на эти работы ссылки.
Конструктивное описание модели
Через клетки Г2± – модели, содержащиеся в четных длинных Дi и коротких Ki диагоналях с числами, оканчивающимися нулями в пределах Г2 — — подмодели, проводятся линии, формирующие крупную сетку ромбов в плоскости. Области ромбов для клеток в совокупности покрывают всю плоскость без разрывов. Каждый ромб содержит 41 клетку из которых только 16 представляют интерес, а при зондировании ромба используются только 4 клетки с фиксированной флексией.
К характеристикам ромбов будем относить:
- число клеток в ромбе;
- значение числа в центральной клетке;
- номера ее горизонтали (Нi) и вертикали (Vi);
- идентифицирующие клетки для чисел с флексиями 1, 3, 7, 9;
- координаты этих клеток в системе координат ромба с началом в центральной клетке ромба.
Через клетки центров ромбов также строится сетка центров ромбов, узлы которой находятся в клетках на пересечении длинных и коротких диагоналей с номерами кратными числу 5.
Из рисунка с ромбами понятно о какой сетке идет речь. Для иллюстрации особенностей ромбов приводятся изображения пары ромбов в каждой полуплоскости. Эти ромбы приводятся с разметкой идентифицирующих чисел клеток в нижней и другая пара таких ромба в верхней полуплоскостях. Разметка ромбов в полуплоскости ниже диагонали Д0 различается от разметки ромбов в полуплоскости выше нее, но в пределах одной полуплоскости разметка всех ромбов идентична как для нижней, так и для верхней полуплоскостей. Сущность разметки – локализация клеток с числами, имеющими равные флексии (размечены заливкой клеток одинаковым цветом), заданием их координат x1, x0. Обозначенные ромбы будем называть фундаментальными, из них могут формироваться другие ромбы с изменением масштабов изображения.
Центры ромбов нижней полуплоскости – клетки с числами, оканчивающимися двумя цифрами либо 25 при номере горизонтали с флексией 5 и с номером вертикали с флексией 0, либо 75 при номере горизонтали с флексией 0 и с номером вертикали с флексией 5. В верхней полуплоскости Г2 + — подмодели все числа в центральных клетках всех ромбов оканчиваются двумя цифрами 25. Далее рассмотрение ограничим полуплоскостью Г2 —.
Рисунок 1— Визуальное представление модели с ромбами
Определение 1. Фундаментальный ромб – структура Г2± – модели, ограниченная двумя короткими и двумя длинными диагоналями этой плоскости с номерами, кратными числу 10. Основным элементом, характеризующим ромб, является клетка (х1ц, х0ц) его центра. Центр содержит числовое значение N, кратное 5.
Определение 2. Совокупность центров фундаментальных ромбов представляет собой узлы (клетки) сетки центров ромбов (СЦР) пересекающихся коротких и длинных диагоналей, с номерами, кратными 5. Сами ромбы целиком покрывают плоскость Г2± – модели (принцип паркета).
Все ромбы устроены однотипно, и числа в их клетках с фиксированными окончаниями размещаются в фиксированных позициях (клетках). Это позволяет при решении задачи локализации числа N в некотором определенном ромбе легко это число факторизовать. Десять горизонталей, клетки которых образуют ромб и соседние с ним ромбы (с отличными от него координатами), назовём полосой ромбов. Рассматриваются полосы горизонтальные: Запад-Восток (ЗВ); вертикальные: Север-Юг (СЮ), вдоль коротких диагоналей: Северо-Восток (СВ) и вдоль длинных диагоналей: Северо-Запад (СЗ). Смещение из одного ромба в другой может кроме указания полосы дополняться указанием (вверх-вниз) вдоль названных полос.
Поскольку из определения 2 следует, что совокупность клеток всех ромбов — это все клетки Г2± – модели, то в одной из клеток (x1p, x0p), принадлежащей некоторому ромбу, обязательно находится заданное составное нечетное натуральное число (СННЧ) N(x1p, x0p) = N(x1, x0). При этом полагаем, что указать такой ромб (определяя координаты его центральной клетки) (x1ц, x0ц) можно быстрее, чем выполнить зондирование всех клеток, даже ограничиваясь зондированием только нечетных диагоналей.
Указание такого ромба и нужной клетки в его пределах является решением задачи локализации для заданного числа N(x1, x0). Эта задача и ее решение предшествует получению решения ЗФБЧ. Смысл и конечная цель задачи локализации в том, чтобы в определенном ромбе для заданного СННЧ N(x1, x0) указать значениями координат клетку (x1p, x0p) в Г2± – модели, в которой находится число, совпадающее с N(x1, x0).
В этой статье мы используем механизм установления принадлежности заданного числа N конкретному ромбу и клетке в нем. Этот механизм далеко не лучший, но в предлагаемых примерах прекрасно справляется с задачей. Читателям предлагается либо предложить свой оригинальный, либо усовершенствовать этот механизм.
Наш механизм базируется на открытой автором замечательной закономерности Г2± – модели: присутствие в горизонталях с номерами, кратными пяти (и в некоторых других), клеток с квадратами элементов пифагоровых троек (ПФТ) <g, k1, k2> = <гипотенуза, катет1, катет2>. О ПФТ речь еще пойдет в другой работе.
Для упрощения выводов и вычислений нам потребуются три координатные системы: плоскостная, которая уже вводилась, сетевая с другими номерами диагоналей для СЦР (рис. 2) и ромбовая (табл. 1), в которой начало связывается с клеткой центра ромба.
Рисунок 2. Нумерации (двойные) коротких диагоналей и
распределение центров ромбов на коротких диагоналях
Таблица 1. Определение координат поисковой точки в пределах фиксированного ромба
В системе СЦР обозначены: номер короткой диагонали nр, ц — порядковый номер центра на ней, а также общесетевой Ц номер центра, выполнена собственная нумерация коротких диагоналей, начиная от nр = 1 (в плоскостной системе — это 5-я короткая диагональ), далее номер nр = 2 (это увеличенный на 10 номер, т.е. 15-я плоскостная Кi) и далее с шагом 10 все остальные. Положение всех клеток центров ромбов в каждой Кi СЦР также нумеруется от ц = 1 до ц = 2nр удвоенного сетевого номера короткой диагонали.
Пример 1. Пусть требуется найти общесетевой номер Ц центра одного из ромбов и число N в этой клетке при заданных короткой диагонали, проходящей через центры ромбов, ее сетевым номером nр = 5, и порядкового номера центра ц = 3 одного из ромбов на ней. Достаточно просто представляются сетевые координаты клетки центра этого ромба в виде (nр, ц) = (5, 3).
- Найдём плоскостную х1 координату клетки начала заданной диагонали (нд):
х1 = хнд = 10nр — 5 = 50 – 5 = 45.
Для нашего случая получили х1 = хнд = 45. - Теперь можем сразу перейти к поиску плоскостных координат клетки (х1ц, хоц) искомого центра: х1 = хнд — 5(ц — 1) = 45 – 5(3 — 1) = 35, х0 = 0 + 5(ц — 1) = 2 ∙ 5 = 10.
- Найдём общесетевой номер центра ромба (Ц).
Замечание. Известно, что для числа х формула 2Сх+12= x(x+1) — это удвоенное число сочетаний из х+1 по два.
Количество центров предшествующих короткой диагонали nр = 5 равно 2nр (nр — 1). Тогда порядковый номер Ц сетевого центра задается формулой
Ц = nр(nр -1) + ц = 2Сnр2+ 3 = 5 ∙ 4 + 3 = 23. - Найдём значение числа N(х1ц, хоц) в клетке центра ромба N = x12 — x02 — знак в формуле берется в зависимости от положения центра относительно главной диагонали.
N= 35 2 — 102 = 1125 — для нашего случая.
Таким образом, располагая лишь сетевым номером nр короткой диагонали, проходящей через клетки центров, и текущим номером центра ромба ц на этой диагонали, можно получить всю остальную информацию о центре ромба.
Все представляющие интерес нечетные натуральные числа N принадлежат клеткам ромбов. Локализовать их положение в пределах ромбов позволяет понятие флексии – последней цифры числа. Для факторизации представляют интерес те числа N, которые оканчиваются цифрами 1, 3, 7, 9.
Четные числа в качестве N не рассматриваются, так как имеют простой делитель 2. Числа, оканчивающиеся пятеркой, имеют простой делитель 5, что так же неприемлемо для N. Локализацию конкретного N по флексии внутри ромба целесообразно проводить относительно центра ромба, в контексте того, что центр является важнейшей характеристикой ромба. Исходя из того, что все ромбы имеют одинаковую структуру, существует явная взаимосвязь заданного для факторизации числа N c числами в клетках ромба с определёнными флексиями и в клетке центра ромба. Данные о таких взаимосвязях чисел приведены в табл. 1.
Однако перебирать все ромбы на плоскости, чтобы найти нужный ромб, неприемлемо ни по времени, ни по вычислительным затратам. Таким образом, возникла задача локализовать области Г2 — — подмодели (полуплоскости), включающие такие ромбы, которые бы содержали исходное число N, подлежащее факторизации.
Пифагоровы тройки. Для решения сформулированной задачи используются
пифагоровы тройки — тройки чисел, удовлетворяющие теореме Пифагора: А именно, пифагоровы тройки, которые удовлетворяют правилу так называемого египетского треугольника, т. е. треугольника со сторонами, кратными числам 3, 4, 5.
В каждой горизонтали х1, содержащей центры ромбов, находится одна или более таких пифагоровых троек.
Первый ромб в задаче локализации указывается приближенно и при «промахе» следует выбирать следующие ромбы. Для этого необходимо определить направление перемещения по СЦР, так, чтобы постепенно приближаться к конечной цели. Например, если меньшее из 4-х в текущем ромбе чисел меньше заданного N, то Северо-Восточные и Восточные от него ромбы содержат еще меньшие 4-ки чисел, т. е. такие ромбы не должны зондироваться. Перемещение в Западный ромб приводит к такому росту значений во всех 4-х его клетках, что даже меньшее число Западного ромба оказывается больше большего числа предшествующего ромба и, следовательно, больше N. Отсюда решение: перемещаться от ромба к ромбу вверх в СЗ направлении.
Если ромб, содержащий клетку с числом равным N(x1p, x0p)= N найден и координаты клетки (x1p, x0p) определены, то решение ЗФБЧ определяется основным соотношением Г2± – модели
N = x21 — x20 = (x1 — x0)(x1 + x0) = p ∙ q
Другая подзадача — выбор и реализация последовательности обхода клеток выбранного для зондирования ромба. Здесь принимается порядок обхода против часовой стрелки, начиная с левой верхней клетки, содержащей число с требуемой флексией. В ситуации совпадения значений в клетке ромба N(x1p, x0p) и заданным числом N(x1, x0) разность между ними получается нулевой.
Алгоритм решения ЗФБЧ, использующий фундаментальные ромбы и ПФТ
- Извлекаем корень из числа N. Округляем в меньшую сторону.
- Проверяем, делится ли √N на 3. Если делится, то присваиваем это значение первому катету k1, в противном случае для выполнимости свойства делимости на 3 вычитаем из результата 1 или 2, и заносим в память как k1. Результат деления нацело подобранного значения на три М = √N/3 — масштабирующий ПФТ коэффициент запоминаем.
- Получаем значение для второго катета k2, согласно правилу египетского треугольника, k2 = 4 ∙ M.
- Находим значение гипотенузы g = 5 ∙ M, причём значение х1 = g должно делиться на число пять. Как видим, значение гипотенузы всегда равно номеру горизонтали с ПФТ.
- Находим координату х1= g.
- После этого определяем флексию (последнюю цифру) числа N, ф = N(mod10).
- Находим центр ромба, ближайший к k1 и далее исследуем смежные ромбы в одной из полос ромбов (имеется 4 направления) для отыскания решения.
- В зависимости от того, какую флексию получим в пункте 6, используем нужную колонку (маску) из представленных в табл. 1 для определения координат поисковой точки (x1p, x0p) и находим значение числа в этой клетке Nр. В каждом ромбе проверяется из 41-й клетки в нем только 4 клетки.
- После установления принадлежности числа N к определённому ромбу и клетке в нем, исходя из всё той же табл. 1 получим плоскостные координаты N: (x1p, x0p).
- Используя свойства выбранной математической модели
N = x21 — x20 = (x1 — x0)(x1 + x0) = p ∙ q
получим мультипликативное представление N из аддитивного. - Таким образом, на выходе алгоритма имеем: N = p ∙ q. В зависимости от значения флексии ф по формулам в табл. 1 определяются координаты точки (x1p, x0p) и вычисляется значение разности ∆ = N(x1p, x0p) — N(x1, x0). Если ∆ ≠ 0, то переход к другой клетке, если все клетки ромба проверены, то к другому ромбу.
Если ∆ = 0, то x1 = x1p, x0 = x0p и р = (x1 — x0), q = N/p = (x1 + x0).
Пример 2. Дано: N = 1037, число с разрядностью 4. Требуется его факторизовать. Действуем по приведенному алгоритму.
- Извлекаем корень из N: √N = 32.202. Округляем в меньшую сторону: √N = 32.
- Проверяем, делится ли 32 на 3. Так как 32 на 3 не делится, то вычитаем 2. Итак, полагаем, что первый катет равен k1 = 3 ∙ 10 = 30, здесь М =10=30/3 масштабирующий коэффициент ПФТ.
- Получаем значение для второго катета k2 = 4 ∙ 10 =40.
- Находим значение гипотенузы g =(k21 +k22) 0.5 при условии, что она делится на 5, (302+402)0.5 = 50.
- Таким образом х1 = k1= 50 и ПФТ преображается к виду g = 50, k1=30, k2=40.
- Находим флексию числа N: ф(1037) = 1037(mod10) = 7.
- Находим ближайший к N = 1037 центр ромба.
Он будет иметь координаты центральной клетки ромба: x1= 50, x0 = 35. Первая координата — номер строки, содержащей ПФТ. Квадрат меньшего катета равен 900, содержится в вертикали с номером 40. Клетка с числом 957, оканчивающимся семеркой, ближайшая к 900, лежит в предшествующей горизонтали с номером 49 и в вертикали с номером 38. Это меньшее число из 4-х в ромбе и с флексией 7. Здесь используются данные таблицы 1. Ближайший центр ромба должен быть левее на три клетки, т. е. принадлежит вертикали 38 — 3 = 35, это и есть вторая координата центра ромба. Значение числа в клетке центра ромба равно N(50, 35) = 1275Это ромб, имеющий квадраты катетов k1 и k2 на своих границах. В пределах этого ромба min число, оканчивающееся семеркой 957 в клетке (х1 = 49, х0 = 38), и другое число в этой вертикали, оканчивающееся 7-ой 1157, большие числа 1377 и 1577 лежат левее центральной клетки, совпадений с числом N = 1037 нет, следовательно, необходимо подняться в ромб левее и выше со значением в центральной клетке 1125 и с координатами центральной клетки (х1= 50 — 5 = 45, х0 =35 — 5 = 30) Проверяем четверку чисел на флексию 7. Это 847, 1027, 1207 и 1387 и в этом ромбе совпадений с N = 1037 нет), поднимемся еще выше в этом же направлении по полосе СЗ ромбов. Клетка центра нового ромба имеет значение 975 и координаты (х1 = 45 -5 = 40, х0= 35 — 5 = 25). Проверяем в этом ромбе четверку чисел на флексию 7. Это 737, 897, 1197 и наконец получаем 1037 в клетке (х1р= 39, х0р = 22) получили полное совпадение с заданным N.
Детально эти действия представляются следующими вычислениями.В соответствии с таблицей 1 вычисляем координаты клеток и значения числа в них. После этого находим разности вычисленного и заданного значений N. В первом ромбе вычисляются все 4 клетки.
∆ = N(x1ц-1, x0ц-3) — N(x1, x0)= N(49,32) — 1037 = 1377 — 1037 = 340 ≠ 0,
∆ = N(x1ц+1, x0ц-3) — N(x1, x0)= N(51,32) — 1037 = 1577 — 1037 = 540 ≠ 0,
∆ = N(x1ц+1, x0ц+3) — N(x1, x0)= N(51,38) — 1037 = 1157 — 1037 = 120 ≠ 0,
∆ = N(x1ц-1, x0ц+3) — N(x1, x0)= N(49,38) — 1037 = 957 — 1037 = — 80 ≠ 0.
В этом ромбе совпадения числа N с числами в клетках нет.Переходим в следующий ромб с центром в клетке (x1ц-5, x0ц-5) = (45, 30) и значением в ней N(x1ц — 5, x0ц — 5) = N(45, 30) = 1125.
∆ = N(x1ц-1, x0ц-3) — N(x1, x0) = N(44,27) — 1037 = 1207 — 1037 = 170 ≠ 0,
∆ = N(x1ц+1, x0ц-3) — N(x1, x0) = N(46,27) — 1037 = 1387 — 1037 = 350 ≠ 0,
∆ = N(x1ц+1, x0ц+3) — N(x1, x0) = N(46,33) — 1037 = 1027 — 1037 = — 10 ≠ 0,
∆ = N(x1ц-1, x0ц+3) — N(x1, x0) = N(44,33) — 1037 = 847 — 1037 = — 190 ≠ 0.
В этом ромбе совпадения числа N с числами в клетках также нет.Переходим в следующий ромб с центром в клетке (x1ц-5, x0ц-5) = (40, 25) и значением в ней N(x1ц — 5, x0ц — 5) = N(40, 25) = 975
∆ = N(x1ц-1, x0ц-3) — N(x1, x0)= N(39,22) — 1037 = 1037 — 1037 = 0.
Получили нулевую разность значений. Имеет место полное совпадение. Из этого следует, что заданное число N(x1, x0) = 1037 содержится в клетке с координатами (x1р, x0р) = (39, 22) Окончательно решение ЗФБЧ определяется основным соотношением Г2± – модели
N = x21 — x20 = (x1 — x0)(x1 + x0) = (39 — 22) (39 + 22) = p ∙ q = 17∙61. - Можно действовать иначе.Начиная с ромба, указанного в пункте 6, используя табл. 1, выясняем принадлежность числа N к тому или иному ромбу, перемещаясь между центрами ромбов сначала по горизонтали, в сторону главной диагонали, затем смещаясь вниз на следующую полосу ромбов и повторяя всё снова.
- После установления принадлежности числа N к определённому ромбу (в нашем случае ромб будет иметь координаты (х1= 40, х0 = 25) ) исходя из той же табл. 1 получим координаты N: х1р = 39, х2р = 22 (просмотрено 9 ромбов).
- Используя свойства выбранной математической модели числа
N = x21 — x20 = (x1 — x0)(x1 + x0) =p ∙ q
получим мультипликативное представление N из аддитивного:
N = (39 — 22)(39 + 22) = 17 ∙ 61 = 1037.
Таким образом, на выходе имеем N = p · q = 17 · 61 = 1037, т. е. решение задачи получено успешно.
Получим также результат программного решения задачи в примере 3.
Пример 3. Дано: N= 3808572773, число с разрядностью 10.
- Извлекаем корень из N: √N = 61713, 64 = 61713.
- Проверяем, делится ли 61713 на 3. Так как 61713 по признаку делимости на 3,
6 + 1 + 7 + 1 + 3 = 18 делится на 3, то первый катет k1 равен k1 = 61713. - Получаем второй катет k2 = 4k1/3 => 4k2/3 = 82284.
- Находим гипотенузу g =√k12+k22, при условии, что она делится на
5 · g = √617132 + 822842 = 102855. - Таким образом x1 = k1 = 61713, и пифагорова тройка преображается соответственно к виду k1 = 61713, k2 = 82284, g = 102855.
- Находим флексию числа N: ф(3808572773) = 3808572773(mod10) = 3.
- Находим ближайший центр ромба. Он будет иметь координаты x1 = 61715; x9 = 0.
- Начиная с ромба, указанного в пункте 7, используя данные табл. 1, выясняем принадлежность числа N к тому или иному ромбу, перемещаясь между центрами ромбов сначала по горизонтали, в сторону главной диагонали, затем смещаясь на следующую полосу ромбов и, повторяя всё снова.
- После установления принадлежности числа N к определённому ромбу (в нашем случае центр ромба будет иметь координаты x1 = 62015, x0 = 6085) получаем N:
x1p = 62013; x0p = 6086; (исследовано 60 ромбов). - Используя свойства выбранной математической модели
N = x21 — x20 = (x1 — x0)(x1 + x0) =p ·q получим мультипликативное представление N из аддитивного:
N = (62013 — 6086) · (62013 + 62086) = 55927 · 68099 = 3808572773; - Таким образом, на выходе имеем N = p · q = 55927 · 68099 = 3808572773, т. е. решение задачи получено успешно.
Числовая окружность
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac<π><2>, frac<π><3>, frac<7π><4>, 10π, -frac<29π><6>)) разбирается в этой статье .
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки — положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).
Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.
Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).
Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?
Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.
При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.
К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac<π><2>),(-frac<π><2>),(frac<3π><2>), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .
Что надо запомнить про числовую окружность:
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
 |
Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным . |
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
| Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac<4>=frac<2pi r><4>=frac<pi r><2>.) Тогда радианная мера угла: $$ angle AOB=frac>=frac<pi r><2cdot r>=frac<pi> <2>$$ |
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac<pi><6>) | (frac<pi><4>) | (frac<pi><3>) | (frac<pi><2>) | (frac<2pi><3>) | (frac<3pi><4>) | (frac<5pi><6>) | (pi) | (frac<3pi><2>) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
| Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например: |
| Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<pi><4>, frac<pi><2>, frac<2pi><3>, pi), а также (-frac<pi><6>, -frac<pi><4>, -frac<pi><2>, -frac<2pi><3>, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |
| Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<13pi><6>, frac<25pi><6>), и (-frac<11pi><6>). Все четыре точки совпадают, т.к. begin Mleft(frac<pi><6>right)=Mleft(frac<pi><6>+2pi kright)\ frac<pi><6>-2pi=-frac<11pi><6>\ frac<pi><6>+2pi=frac<13pi><6>\ frac<pi><6>+4pi=frac<25pi> <6>end |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
| $$ -frac<pi> <6>lt t lt frac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi klt tltfrac<pi><3>+2pi k $$ |
|
| Интервал | |
| $$ -frac<pi> <6>leq t leq frac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi kleq tleqfrac<pi><3>+2pi k $$ |
|
| Полуинтервал | |
| $$ -frac<pi> <6>leq t ltfrac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi kleq tltfrac<pi><3>+2pi k $$ |
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^<circ>=frac<pi><6>.\ EC=60^<circ>=frac<pi><3>.\ AE=EC+CD=90^<circ>+30^<circ>=120^<circ>=frac<2pi><3>.\ ED=EC+CD=60^<circ>+90^<circ>=150^<circ>=frac<5pi><6>. end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<pi><2>; frac<3pi><4>; frac<7pi><6>; frac<7pi><4>).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac<pi><2>=-90^<circ>, frac<3pi><4>=135^<circ>\ frac<7pi><6>=210^<circ>, frac<7pi><4>=315^ <circ>end |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<11pi><2>; 5pi; frac<17pi><6>; frac<27pi><4>).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac<11pi><2>=frac<-12+1><2>cdotpi=-6pi+frac<pi><2>rightarrow frac<pi><2>=90^<circ>\ 5pi=4pi+pirightarrow pi=180^<circ>\ frac<17pi><6>=frac<18-1><6>pi=3pi-frac<pi><6>rightarrow pi-frac<pi><6>=frac<5pi><6>\ frac<27pi><4>=frac<28-1><4>pi=7pi-frac<pi><4>rightarrow pi-frac<pi><4>=frac<3pi> <4>end |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
| Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac<3,14><2>=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac<3pi><2>approx frac<3cdot 3,14><2>=4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac<3pi> <2>Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac<3pi><2>lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.
| $$ frac<pi k> <2>$$ | $$ -frac<pi><4>+2pi k $$ |
| Четыре базовых точки, через каждые 90° | Две базовых точки, через каждые 180° |
| $$ frac<pi><3>+frac<2pi k> <3>$$ | $$ -frac<pi k> <5>$$ |
| Три базовых точки, через каждые 120° | Пять базовых точек, через каждые 72° |
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Числовая и единичная окружность
В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.
Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.
Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:
Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.
Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.
Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:
В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.
Выглядит единичная окружность так:
Откладывание углов на единичной окружности
Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:
Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.
Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:
Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:
Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:
В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.
Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:
Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:
Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:
Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.
Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:
С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:
Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:
Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:
Например, верны следующие равенства:
15° + 3•360° = 15° + 1080° = 1095°
100° + 10•360° = 100° + 3600° = 3700°
1000° = 1000° – 2•360° = 1000° – 720° = 280°
Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5
http://reshator.com/sprav/algebra/10-11-klass/edinichnaya-chislovaya-okruzhnost-na-koordinatnoj-ploskosti/
http://100urokov.ru/predmety/urok-1-edinichnaya-okruzhnost

 как отдельные контуры, но не смог отфильтровать все ложные срабатывания (поскольку изображение может быть в разных разрешениях, а также есть два типа целей с разными размерами чисел. Я не мог просто ограничить контур по его ширине, высоте или площади)
как отдельные контуры, но не смог отфильтровать все ложные срабатывания (поскольку изображение может быть в разных разрешениях, а также есть два типа целей с разными размерами чисел. Я не мог просто ограничить контур по его ширине, высоте или площади)