Как найти центр эллипса онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Radians}	mathrm{Degrees}	square!	(	)	%	mathrm{clear}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Subscribe to verify your answer

Number Line

Examples

center:9x^2+4y^2=1
center:16x^2+25y^2=100
center:25x^2+4y^2+100x-40y=400
center:frac{(x-1)^2}{9}+frac{y^2}{5}=100
Show More

Description

Calculate ellipse center given equation step-by-step

ellipse-function-center-calculator

Solve Ellipse Equation

Code to add this calci to your website

Solving Ellipse Equation is just the inverse of finding the ellipse expression from the given elliptical co-ordinates such as center, foci, vertices, eccentricity and area.

Источник

Каноническое уравнение эллипса по двум точкам

Две точки с координатами

Первая координата

Вторая координата

Каноническое уравнение эллипса

Большая полуось эллипса

Малая полуось эллипса

Эксцентриситет эллипса

Фокусное/фокальное расстояние

Коэффициент сжатия

Координаты первого фокуса F1(x1:y1)

Координаты второго фокуса F2(x2:y2)

Фокальный параметр

Перифокусное расстояние

Апофокусное расстояние

Уравнение эллипса в каноническом виде имеет вот такой вид.

$?frac{x^2}{a^2}+frac{y^2}{b^2}=1$

Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.

Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.

Кроме этого, на этой странице мы получим следующую информацию.

Фокальный параметр — половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса

$p=cfrac{1-e^2}{e}$

Значение полуосей — большая полуось и малая полуось ( Естественно это в том случае, когда эллипс вытянут вдоль оси абсцисс)

$a=frac{b}{sqrt{1-e^2}}$

Эксцентриситет — коэффициент, показывающий насколько его фигура отличается от окружности

$e=frac{c}{a}$

Фокальное расстояние

c=ae

Коэффициент сжатия — отношение длин малой и большой полуосей

Перифокусное расстояние

$Ra=cfrac{1+e}{e}$

Апофокусное расстояние

$Rb=cfrac{1-e}{e}$

Примеры задач

Cоставить каноническое уравнение эллипса по двум точкам $Ra=cfrac{1+e}{e}$

Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt

и получаем результат

Каноническое уравнение эллипса

Большая полуось эллипса

8.48528137423857

Малая полуось эллипса

5.656854249492381

Эксцентриситет эллипса

0.8958064164776166

Фокусное/фокальное расстояние

32.2490309931942

Коэффициент сжатия

0.4444444444444444

Координаты первого фокуса F1(x1:y1)

-16.1245154965971 : 0

Координаты второго фокуса F2(x2:y2)

16.1245154965971 : 0

Фокальный параметр

3.5555555555555554

Перифокусное расстояние

1.875484503402901

Апофокусное расстояние

34.1245154965971

И еще один пример

Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса.

Если мы введем данные в калькулятор получим

Большая полуось эллипса

5.877538136328849

Малая полуось эллипса

NaN

Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.

Таким образом по этим двум точкам, нельзя построить эллипс.

А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.

$frac{x^2}{a^2}-frac{y^2}{b^2}=1$

Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам

Удачных расчетов!

Источник

Undo

Square

Power

Square Root

−

≤

≥

(

)

Absolute Value

Источник

Таким образом по этим двум точкам, нельзя построить эллипс.

Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам

Координаты точки эллипса по углу

IP76 > Координаты точки эллипса по углу

Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.

Калькулятор точки на эллипсе

Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.

Get a better browser, bro…

Параметрическое уравнение эллипса

Обратимся, как обычно, к Википедии. Находим там следующее:

Каноническое уравнение эллипса может быть параметризовано:

Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.

Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.

Подготовка

У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.

Проведем прямую из общего центра [X₀;Y₀] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X₁;Y₁] и [X₂;Y₂].

α – угол между прямой и осью X.

Малая окружность	X₁ = b × cos α	Y₁ = b × sin α
Большая окружность	X₂ = a × cos α	Y₂ = a × sin α

Таблица 1. Координаты точек пересечения прямой с окружностями

Нахождение зависимости

Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X₀;Y₀] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.

Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.

Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:

X’ = X₂ = a × cos α

Y’ = Y₁ = b × sin α

Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.

Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.

Тангенс угла β в этом случае равен:

(3) Тангенс угла β

Используя формулу тангенса произведем дальнейшие преобразования:

(4) Зависимость тангенса α от тангенса β

Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.

Нахождение координат

Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.

Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):

Кривые второго порядка. Эллипс: формулы и задачи

Понятие о кривых второго порядка

Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.

Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.

При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.

Эллипс, заданный каноническим уравнением

Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.

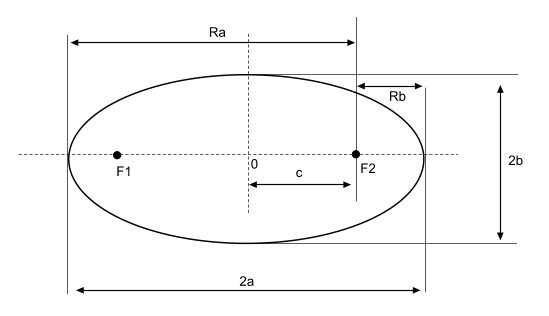
Фокусы обозначены как и на рисунке ниже.

Каноническое уравнение эллипса имеет вид:

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.

Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .

Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.

Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:

Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.

Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.

Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

Точки и , обозначенные зелёным на большей оси, где

называются фокусами.

называется эксцентриситетом эллипса.

Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.

Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.

Решение. Делаем несложные умозаключения:

— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,

— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.

Подставляем и вычисляем:

Результат — каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .

Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:

Составляем каноническое уравнение эллипса:

Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .

Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:

Решить задачи на эллипс самостоятельно, а затем посмотреть решение

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) расстояние между фокусами 30, а большая ось 34

2) малая ось 24, а один из фокусов находится в точке (-5; 0)

3) эксцентриситет , а один из фокусов находится в точке (6; 0)

Продолжаем решать задачи на эллипс вместе

Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

называются директрисами эллипса (на чертеже — красные линии по краям).

Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где и — расстояния этой точки до директрис и .

Пример 7. Дан эллипс . Составить уравнение его директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:

Получаем уравнение директрис эллипса:

Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

Теперь можем получить и квадрат длины меньшей полуоси:

Уравнение эллипса готово:

Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

Получили единицу, следовательно, точка находится на эллипсе.

Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:

Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

так как из исходного уравнения эллипса .

Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.

источники:

Координаты точки эллипса по углу

http://function-x.ru/curves_ellipse.html

Источник