Что такое эллипс: формула длины окружности эллипса
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F – числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Понятие алгебраической линии и её порядка
Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид 






Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательныхстепенях.
Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости
Порядок линии равен максимальному значению 
По соответствующей теореме, понятие алгебраической линии, а также её порядок не зависят от выбора аффинной системы координат , поэтому для лёгкости бытия считаем, что все последующие выкладки имеют место быть в декартовых координатах 
Общее уравнение линии второго порядка имеет вид 





Если 



Многие поняли смысл новых терминов, но, тем не менее, в целях 100%-го усвоения материала сунем пальцы в розетку. Чтобы определить порядок линии, нужно перебрать все слагаемыееё уравнения и у каждого из них найти сумму степенейвходящих переменных.
слагаемое 
слагаемое 
слагаемое 
в слагаемом 
Далее из полученных чисел выбирается максимальное значение, в данном случае единица, – это и есть порядок линии.
Теперь разберёмся, почему уравнение 
слагаемое 
у слагаемого 
у слагаемого 
слагаемое 
все остальные слагаемые – меньшей степени.
Максимальное значение: 2
Если к нашему уравнению дополнительно приплюсовать, скажем, 



В том случае, если добавить одно или несколько подходящих слагаемых, которые содержат 
С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат .
Однако вернёмся к общему уравнению 






Существенный недостаток общего уравнения состоит в том, что почти всегда не понятно, какую линию оно задаёт. Даже в простейшем случае 
Определение эллипсa
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
Формула площади эллипса через каноническое уравнение
Формула для нахождения площади в этом случае такова:
a , b – большая и мала полуоси эллипса, соответственно.
Решим задачу этим способом.
Дано уравнение эллипса. Найти его площадь и округлить ответ до целого числа.
2 5 x 2 + 9 y 2 = 1
Решение
Для начала найдем длины наших полуосей:
a = a 2 = 2 5 = 5
S = π ⋅ a ⋅ b = π ⋅ 5 ⋅ 3 ≈ 4 7 (см. кв.)
Ответ: 47 см. кв.
Соотношения между элементами эллипса
Элементы эллипсa
А1А2 = 2 a – большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2 b – малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a – большая полуось эллипса
b – малая полуось эллипса
O – центр эллипса (точка пересечения большей и малой осей эллипса)
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a . Для эллипсa эксцентриситет всегда будет 0 e e = 0, для параболы e = 1, для гиперболы e > 1.
Радиус эллипсa R – отрезок, соединяющий центр эллипсa О с точкой на эллипсе.
| R = | ab | = | b |
| √ a 2 sin 2 φ + b 2 cos 2 φ | √ 1 – e 2 cos 2 φ |
где e – эксцентриситет эллипсa, φ – угол между радиусом и большой осью A1A2.
Коэффициент сжатия эллипсa (эллиптичность) k – отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k k = 1:
где e – эксцентриситет.
Что такое канонический вид уравнения?
Это общепринятый стандартный вид уравнения, когда в считанные секунды становится ясно, какой геометрический объект оно определяет. Кроме того, канонический вид очень удобен для решения многих практических заданий. Так, например, по каноническому уравнению 



Очевидно, что любая линия 1-го порядка представляет собой прямую. На втором же этаже нас ждёт уже не вахтёр, а гораздо более разнообразная компания из девяти статуй:
Связанные определения
- Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
- Точка пересечения большой и малой осей эллипса называется его центром.
- Точка пересечения эллипса с осями называются его вершинами.
- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
- Расстояния r1 и r2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Расстояние
называется фокальным расстоянием.
- Эксцентриситетом эллипса называется отношение
. Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Фокальным параметром
называется половина длины хорды , проходящей через фокус и перпендикулярной большой оси эллипса.
- Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью:
. Величина, равная
называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением
Расчет площади
- Большая полуось эллипса является максимальным расстоянием от его центра до края. [1]
- Малая полуось эллипса расположена под прямым углом 90º к его большой полуоси, однако для нахождения площади нет необходимости определять углы.
- Малая полуось эллипса является минимальным расстоянием от его центра до края.
- Например, если большая полуось эллипса равна 5 единицам, а малая 3 единицам длины, то получим площадь 5 x 3 x π, или около 47 квадратных единиц длины.
- Если у вас нет под рукой калькулятора или на калькуляторе нет символа π, используйте вместо этого числа значение “3,14”.
Объяснение метода
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 


Каноническое уравнение эллипса имеет вид:

где a и b (a > b) – длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 


Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат – в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат – малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия – эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось – это a = 5 , меньшая полуось – это b = 4 . Получаем каноническое уравнение эллипса:

Точки 



называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
– если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
– если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат – каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Классификация линий второго порядка
С помощью специального комплекса действий любое уравнение линии второго порядка приводится к одному из следующих видов:
( 


1) 
2) 
3) 
4) 
5) 
6) 
7) 


9) 
У ряда читателей может сложиться впечатление неполноты списка. Например, в пункте № 7 уравнение 











Таким образом, существует девять и только девять различных видов линий 2-го порядка, но на практике наиболее часто встречаются эллипс, гипербола и парабола .
Сначала рассмотрим эллипс. Как обычно, я акцентирую внимание на тех моментах, которые имеют большое значение для решения задач, и если вам необходим подробный вывод формул, доказательства теорем, пожалуйста, обратитесь, например, к учебнику Базылева/Атанасяна либо Александрова.
Что такое эллипс и фокусное расстояние
Внимание!
Если вам нужна помощь с академической работой , то рекомендуем обратиться к профессионалам. Более 70 000 экспертов готовы помочь вам прямо сейчас.
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и . Допустим, что расстояние = – фокусное расстояние.
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью, (теорема Пифагора). Если же точка находится на пересечении эллипса с вертикальной осью, (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, . Так как по определению сумма – постоянная величина, то приравнивая получается:
Как построить эллипс?
Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:
Построить эллипс, заданный уравнением
Решение: сначала приведём уравнение к каноническому виду:
Зачем приводить? Одно из преимуществ канонического уравнения 



В данном случае 

Отрезок 
отрезок 
отрезок 
число 
число 
число 
в нашем примере: 
Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.
Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы . И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.
По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями 
Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса 

Далее уравнение распадается на две функции:



Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция 


Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.
Отметим на чертеже точки 

Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?
Свойства
- Фокальное свойство. Если F1 и F2 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X) равен углу между этой касательной и прямой (F2X) .
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эволютой эллипса является астроида .
Эллипс также можно описать как
- фигуру, которую можно получить из окружности , применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость .
- Пересечение плоскости и кругового цилиндра
Формула длины окружности эллипса
Хотя рассматриваемая фигура является достаточно простой, длину ее окружности точно можно определить, если вычислить так называемые эллиптические интегралы второго рода. Однако, индусский математик-самоучка Рамануджан еще в начале XX века предложил достаточно простую формулу длины эллипса, которая приближается к результату отмеченных интегралов снизу. То есть рассчитанное по ней значение рассматриваемой величины будет немного меньше, чем реальная длина. Эта формула имеет вид: P ≈ pi * [3 * (a+b) – √((3 * a + b) * (a + 3 * b))], где pi = 3,14 – число пи.
Например, пусть длины двух полуосей эллипса будут равны a = 10 см и b = 8 см, тогда его длина P = 56,7 см.
Каждый может проверить, что если a = b = R, то есть рассматривается обычная окружность, тогда формула Рамануджана сводится к виду P = 2 * pi * R.
Отметим, что в школьных учебниках часто приводится другая формула: P = pi * (a + b). Она является более простой, но и менее точной. Так, если ее применить для рассмотренного случая, то получим значение P = 56,5 см.
Как рассчитать радиус и диаметр овала
Овал также называют эллипсом. Из-за своей продолговатой формы овал имеет два диаметра: диаметр, который проходит через самую короткую часть овала, или полу-малую ось, и диаметр, который проходит через
Содержание:
Овал также называют эллипсом. Из-за своей продолговатой формы овал имеет два диаметра: диаметр, который проходит через самую короткую часть овала, или полу-малую ось, и диаметр, который проходит через самую длинную часть овала, или полу-большую ось. , Каждая ось перпендикулярно делит пополам другую, разрезая друг друга на две равные части и создавая прямые углы там, где они встречаются. Есть также два радиуса, по одному на каждый диаметр. Чтобы рассчитать радиусы и диаметры или оси овала, используйте точки фокусировки овала — две точки, которые расположены на равном расстоянии друг от друга на большой полуоси — и любую одну точку по периметру овала.
Полу минорная ось
Измерьте расстояние между одной точкой фокусировки до точки по периметру овала, чтобы определить a. В этом примере a будет равно 5 см.
Измерьте расстояние между другой точкой фокусировки и той же точкой на периметре, чтобы определить b. В этом примере b будет равен 3 см.
Добавьте a и b вместе и возведите в квадрат сумму. Например, 5 см плюс 3 см равны 8 см, а 8 см в квадрате равны 64 см ^ 2.
Измерьте расстояние между двумя точками фокусировки, чтобы выяснить f; возвести в квадрат результат. В этом примере f равно 5 см, а квадрат 5 см равен 25 см ^ 2.
Вычтите сумму на шаге четыре из суммы на шаге три. Например, 64 см ^ 2 минус 25 см ^ 2 равняется 39 см ^ 2.
Рассчитайте квадратный корень суммы из шага пять. Например, квадратный корень из 39 равен 6,245, округленный до ближайшей тысячной. Следовательно, малая ось или самый короткий диаметр составляет 6,245 см.
Разделите измерение полу-малой оси пополам, чтобы вычислить ее радиус. Например, 6,245 см, разделенные на два, равны 3,122 см.
Полу-Большая Ось
Повторите процесс измерения из предыдущего раздела, чтобы выяснить a и b. В этом примере хорошо использовать те же цифры: 5 см и 3 см.
Добавьте a и b вместе. Результатом является большая полуось. Например, 5 см плюс 3 см равны 8 см, поэтому большая полуось составляет 8 см.
Уменьшить вдвое результат первого шага, чтобы вычислить радиус. Восемь, разделенная на два, равна четырем, поэтому другой радиус равен 4 см.
Длина окружности эллипса через диаметры
Калькулятор периметра эллипса
Введите длину большой и малой полуосей эллипса, укажите точность расчета и нажмите «Посчитать». Калькулятор выполнит расчет периметра эллипса (расчет приблизительный).
Калькулятор
Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 этой плоскости есть величина постоянная, больше расстояния между F1 и F2.
Точки F1 и F2 называют фокусами эллипса, а расстояние между ними — фокусным расстоянием.
Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a.
Отрезок, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Формулу периметра эллипса нельзя выразить при помощи простейших функций.
Что такое эллипс: формула длины окружности эллипса
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F – числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Понятие алгебраической линии и её порядка
Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид 






Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательныхстепенях.
Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости
Порядок линии равен максимальному значению 
По соответствующей теореме, понятие алгебраической линии, а также её порядок не зависят от выбора аффинной системы координат , поэтому для лёгкости бытия считаем, что все последующие выкладки имеют место быть в декартовых координатах 
Общее уравнение линии второго порядка имеет вид 





Если 



Многие поняли смысл новых терминов, но, тем не менее, в целях 100%-го усвоения материала сунем пальцы в розетку. Чтобы определить порядок линии, нужно перебрать все слагаемыееё уравнения и у каждого из них найти сумму степенейвходящих переменных.
слагаемое 
слагаемое 
слагаемое 
в слагаемом 
Далее из полученных чисел выбирается максимальное значение, в данном случае единица, – это и есть порядок линии.
Теперь разберёмся, почему уравнение 
слагаемое 
у слагаемого 
у слагаемого 
слагаемое 
все остальные слагаемые – меньшей степени.
Максимальное значение: 2
Если к нашему уравнению дополнительно приплюсовать, скажем, 



В том случае, если добавить одно или несколько подходящих слагаемых, которые содержат 
С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат .
Однако вернёмся к общему уравнению 






Существенный недостаток общего уравнения состоит в том, что почти всегда не понятно, какую линию оно задаёт. Даже в простейшем случае 
Определение эллипсa
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
Формула площади эллипса через каноническое уравнение
Формула для нахождения площади в этом случае такова:
a , b – большая и мала полуоси эллипса, соответственно.
Решим задачу этим способом.
Дано уравнение эллипса. Найти его площадь и округлить ответ до целого числа.
2 5 x 2 + 9 y 2 = 1
Решение
Для начала найдем длины наших полуосей:
a = a 2 = 2 5 = 5
S = π ⋅ a ⋅ b = π ⋅ 5 ⋅ 3 ≈ 4 7 (см. кв.)
Ответ: 47 см. кв.
Соотношения между элементами эллипса
Элементы эллипсa
А1А2 = 2 a – большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2 b – малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a – большая полуось эллипса
b – малая полуось эллипса
O – центр эллипса (точка пересечения большей и малой осей эллипса)
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a . Для эллипсa эксцентриситет всегда будет 0 e e = 0, для параболы e = 1, для гиперболы e > 1.
Радиус эллипсa R – отрезок, соединяющий центр эллипсa О с точкой на эллипсе.
| R = | ab | = | b |
| √ a 2 sin 2 φ + b 2 cos 2 φ | √ 1 – e 2 cos 2 φ |
где e – эксцентриситет эллипсa, φ – угол между радиусом и большой осью A1A2.
Коэффициент сжатия эллипсa (эллиптичность) k – отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k k = 1:
где e – эксцентриситет.
Что такое канонический вид уравнения?
Это общепринятый стандартный вид уравнения, когда в считанные секунды становится ясно, какой геометрический объект оно определяет. Кроме того, канонический вид очень удобен для решения многих практических заданий. Так, например, по каноническому уравнению 



Очевидно, что любая линия 1-го порядка представляет собой прямую. На втором же этаже нас ждёт уже не вахтёр, а гораздо более разнообразная компания из девяти статуй:
Связанные определения
- Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
- Точка пересечения большой и малой осей эллипса называется его центром.
- Точка пересечения эллипса с осями называются его вершинами.
- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
- Расстояния r1 и r2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Расстояние
называется фокальным расстоянием.
- Эксцентриситетом эллипса называется отношение
. Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Фокальным параметром
называется половина длины хорды , проходящей через фокус и перпендикулярной большой оси эллипса.
- Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью:
. Величина, равная
называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением
Расчет площади
- Большая полуось эллипса является максимальным расстоянием от его центра до края. [1]
- Малая полуось эллипса расположена под прямым углом 90º к его большой полуоси, однако для нахождения площади нет необходимости определять углы.
- Малая полуось эллипса является минимальным расстоянием от его центра до края.
- Например, если большая полуось эллипса равна 5 единицам, а малая 3 единицам длины, то получим площадь 5 x 3 x π, или около 47 квадратных единиц длины.
- Если у вас нет под рукой калькулятора или на калькуляторе нет символа π, используйте вместо этого числа значение “3,14”.
Объяснение метода
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 


Каноническое уравнение эллипса имеет вид:

где a и b (a > b) – длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат – в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат – малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия – эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось – это a = 5 , меньшая полуось – это b = 4 . Получаем каноническое уравнение эллипса:

Точки 



называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
– если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
– если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат – каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Классификация линий второго порядка
С помощью специального комплекса действий любое уравнение линии второго порядка приводится к одному из следующих видов:
( 


1) 
2) 
3) 
4) 
5) 
6) 
7) 

9) 
У ряда читателей может сложиться впечатление неполноты списка. Например, в пункте № 7 уравнение 











Таким образом, существует девять и только девять различных видов линий 2-го порядка, но на практике наиболее часто встречаются эллипс, гипербола и парабола .
Сначала рассмотрим эллипс. Как обычно, я акцентирую внимание на тех моментах, которые имеют большое значение для решения задач, и если вам необходим подробный вывод формул, доказательства теорем, пожалуйста, обратитесь, например, к учебнику Базылева/Атанасяна либо Александрова.
Что такое эллипс и фокусное расстояние
Внимание!
Если вам нужна помощь с академической работой , то рекомендуем обратиться к профессионалам. Более 70 000 экспертов готовы помочь вам прямо сейчас.
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и . Допустим, что расстояние = – фокусное расстояние.
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью, (теорема Пифагора). Если же точка находится на пересечении эллипса с вертикальной осью, (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, . Так как по определению сумма – постоянная величина, то приравнивая получается:
Как построить эллипс?
Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:
Построить эллипс, заданный уравнением
Решение: сначала приведём уравнение к каноническому виду:
Зачем приводить? Одно из преимуществ канонического уравнения 



В данном случае 

Отрезок 
отрезок 
отрезок 
число 
число 
число 
в нашем примере: 
Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.
Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы . И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.
По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями 
Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса 

Далее уравнение распадается на две функции: 


Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция 


Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.
Отметим на чертеже точки 

Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?
Свойства
- Фокальное свойство. Если F1 и F2 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X) равен углу между этой касательной и прямой (F2X) .
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эволютой эллипса является астроида .
Эллипс также можно описать как
- фигуру, которую можно получить из окружности , применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость .
- Пересечение плоскости и кругового цилиндра
Формула длины окружности эллипса
Хотя рассматриваемая фигура является достаточно простой, длину ее окружности точно можно определить, если вычислить так называемые эллиптические интегралы второго рода. Однако, индусский математик-самоучка Рамануджан еще в начале XX века предложил достаточно простую формулу длины эллипса, которая приближается к результату отмеченных интегралов снизу. То есть рассчитанное по ней значение рассматриваемой величины будет немного меньше, чем реальная длина. Эта формула имеет вид: P ≈ pi * [3 * (a+b) – √((3 * a + b) * (a + 3 * b))], где pi = 3,14 – число пи.
Например, пусть длины двух полуосей эллипса будут равны a = 10 см и b = 8 см, тогда его длина P = 56,7 см.
Каждый может проверить, что если a = b = R, то есть рассматривается обычная окружность, тогда формула Рамануджана сводится к виду P = 2 * pi * R.
Отметим, что в школьных учебниках часто приводится другая формула: P = pi * (a + b). Она является более простой, но и менее точной. Так, если ее применить для рассмотренного случая, то получим значение P = 56,5 см.
Нахождение длины дуги эллипса
IP76 > Нахождение длины дуги эллипса
Как ни странно, но для нахождения длины дуги эллипса нет какой-то определенной функции, как в случае длины дуги окружности, или нахождения координат точки на эллипсе. Это интегральное уравнение.
Калькулятор
Get a better browser, bro…
Интегральное уравнение будем решать как обычно делается в подобных случаях: суммировать очень маленькие значения, которые получаются в результате работы некоей функции, на заданном диапазоне данных, которые наращиваются на чрезвычайно малую постоянную величину. Эта малая величина задается вызывающей стороной. В конце статьи есть рабочий пример с исходниками, в котором можно поиграться с этой «малостью».
Длина дуги, как сумма хорд
Самое простое, что может прийти в голову, это двигаться от начала дуги к ее концу с небольшим наращиванием угла отклонения, считать хорду и прибавлять ее к накапливаемой сумме.


Проще говоря, находим координаты двух точек на эллипсе, отстоящих друг от друга на некий малый угол, по ним находим хорду, как гипотенузу получившегося прямоугольного треугольника.
В коде выглядит так:
Проверим с планетарным размахом. По последним данным Международной Службы Вращения Земли (IERS — 1996) большая экваториальная полуось Земли равна 6 378 136,49 м, а полярная малая — 6 356 751,75 м.
Посчитаем периметр меридиана каким-нибудь онлайн-калькулятором, получаем 40 007 859.543 (некоторые могут дать другое число, т.к. используют приближенные формулы для вычисления периметра).
Представленная выше функция за 109 милисекунд выдала результат 40 007 996.265 при дельте 0.001. Это нельзя назвать точным результатом.
Длина дуги, как интеграл
Длиной некоторой дуги называется тот предел, к которому стремится длина вписанной ломаной, когда длина наибольшего ее звена стремится к нулю:


Таким образом, длина дуги эллипса может быть описана интегральным уравнением:

Используя параметрическое уравнение эллипса, приходим к уравнению:
Где t1 и t2 – параметры для начала и конца дуги параметрического уравнения эллипса. Параметром является некий угол к оси абсцисс. Что такое и как найти параметр для угла эллипса подробно изложено тут.
Зная, что (cos t)’ = — sin t, (sin t)’ = cos t (подробный вывод приведен тут и тут), получаем следующую формулу:

Выводов достаточно, чтобы написать вторую функцию нахождения длины дуги эллипса.
Результат при dt = 0.001 равен 40 007 859,543 за 109 милисекунд. Отлично!
Длина дуги через эксцентриситет
Это еще не окончательный вид уравнения. В ряде интересных параметров для эллипса есть такая числовая характеристика, показывающая степень отклонения эллипса от окружности, как эксцентриситет. Формула для эллипса:

Чем эксцентриситет ближе к нулю, т.е. разница между a и b меньше, тем больше эллипс похож на окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
Выразим b 2 = a 2 (1 — e 2 ), подставим в формулу (5), помним, что sin 2 t + cos 2 t = 1 (справочник [1]), убираем a 2 за знак корня, и, как постоянную величину, за знак интеграла тоже, получаем:

Пишем функцию, ожидаем более шустрого выполнения:
Результат 40 007 859.543, за чуть меньшее время, 94 милисекунды.
Длина дуги через эксцентриситет с подготовкой
Возьмем за основу последнюю функцию. Алгоритм построен так, что в цикле идем от стартового угла, к конечному, на каждой итерации подсчитывая параметр. А если сразу посчитать начальный и конечный параметры и определить условие выхода из цикла? Этим мы однозначно снизим вычислительную нагрузку внутри цикла.

То есть, вместо того, чтобы идти из точки A в точку B, мы заранее считаем параметры t1 и t2. И в цикле больше нахождением параметров не занимаемся, а только считаем очередное приращение.
Берем код последней реализации и улучшаем:
Результат — 40 007 859,543 за 30 милисекунд! Мысль явно здравая.
Длина дуги и хорошо забытые хорды
Но вернемся к сумме хорд. Что там-то не так? Казалось бы, все просто, понятно и должно работать, но результат, мягко говоря, не точен.
Работая с вещественными типами, результат зависит от «мелкости» приращения, от разрядности используемых типов. Накапливаемые погрешности, неточное представление дробного числа и прочие прелести чисел с плавающей запятой.
Тип Extended – самый точный из существующих в Delphi (и, как следствие, самый медленный). Перепишем нахождение длины дуги хордами, используя этот тип, и без вызовов внешних функций нахождения координат на эллипсе.
Результат 40 007 859.542 за 94 милисекунды. Разница в одну тысячную, и такое же время. Весьма неплохо!
Практика
Качаем, запускаем. Видим такое окно:

При запуске в полях полуосей находятся «земные» значения. Эллипс сильно смахивает на окружность. Можно сразу нажать «Расчет», увидеть значения полярного меридиана, и начинать уже эксперименты.
Для начала проверим корректность получаемых результатов. Я попытался найти какие-нибудь онлайн калькуляторы для подсчета длины дуги эллипса, в которых можно было бы указать стартовый угол и произвольное отклонение, либо просто пару углов, определяющих дугу. Но все калькуляторы считают периметр эллипса. А с произвольной дугой как-то… не встретились.
Картинка из вики:

Заскриним несколько моментов и посчитаем корректность:

Введем a=2, b=0.5, стартовый угол равен 0, отклонение θ=5.642.

Видим результат у всех один 8.055. Т.е правы все.
Аналогично поступаем с остальными тремя скринами:
- отклонение θ=1.154. У нас получился результат 1.333. На скрине видим результат s=1.334. Как так? Давайте увеличим «Дельту» в 10 раз, т.е. вместо 0.001, сделаем 0,01. У всех интегральных 2) 3) 4) результат станет 1.334. В то время, как у 1) и 5), т.е. примитивно-неинтегрально-хордовых останется 1.333.
Какой результат более истинный? Смотрите сами. Уменьшение дельты, т.е. угла для подсчетов, ведет к более точному результату. На 0.001 интегральные функции выдали результат как хордовые. При более грубой дельте, интегральные чуть изменились, а хордовые верны своему результату.
Сделаем дельту очень мелкой, равной 0.00001. Результат у всех, кроме первой, тот же, 1.333.
Лично я начинаю верить 5-ой формуле.
- отклонение θ= 206. У нас получился результат 4.322. На скрине результат s= 4.322. Дельта 0.001. Все отлично.
- отклонение θ= 4,488. У нас получился результат 5,989. На скрине результат s= 5,989. Дельта 0.001. Все отлично.
Вывод : Формулы 2-5 работают как надо. Фаворит 5. За меньшее время, т.е. при более «грубой» дельте, находит правильный результат.
Проверим на ужасных эллипсах. Т.е. где эксцентриситет очень близок к единице.

Можем заметить следующее: при 0.00001 функции 2 и 3 дали результат, близкий к результату функции 4, полученный при дельте 0.001. При дельте 0.00001 функция 4 дала результат, близкий к результату функции 5. Сама же функция 5 слабо колеблется в показаниях, что при дельте в 0.001, что при 0.00001.
Аналогичную ситуацию можно пронаблюдать при сильно вытянутом эллипсе:

Таким образом, имеет смысл использовать функции 4 и 5. Одну, как представительницу интегрального сословия, самую быструю и более точную из них. Другую, как представительницу очевидного и простого метода, работающую, между тем, лучше своих интегральных коллег при минимальных ресурсных затратах.
Небольшая инструкция
Правая кнопка мыши задает стартовый угол. Удерживая правую кнопку мыши можно «прогуляться» по эллипсу. Конечная точка дуги будет следовать за стартовой точкой, отстоя на заданный ранее угол. Если поставить галку на «сохранять параметрическое отклонение», параметрический угол между t1 и t2 станет неизменен. Очень полезно пронаблюдать, как будет меняться сектор.
Левая кнопка мыши задает конечную точку дуги, т.е. угол отклонения.
Скачать
Друзья, спасибо за внимание!
http://ru.mosg-portal.com/calculate-radius-diameter-oval-7983204-1886
http://b4.cooksy.ru/articles/dlina-okruzhnosti-ellipsa-cherez-diametry
Определение эллипсa
Определение.
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
F1M1 + F2M1 = F1M2 + F2M2 = A1A2 = const
Элементы эллипсa
F1 и F2 — фокусы эллипсa
Оси эллипсa.
А1А2 = 2a — большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2b — малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a — большая полуось эллипса
b — малая полуось эллипса
O — центр эллипса (точка пересечения большей и малой осей эллипса)
Вершины эллипсa A1, A2, B1, B2 — точки пересечения эллипсa с малой и большой осями эллипсa
Диаметр эллипсa — отрезок, соединяющий две точки эллипса и проходящий через его центр.
Фокальное расстояние c — половина длины отрезка, соединяющего фокусы эллипсa.
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 < e < 1, для круга e = 0, для параболы e = 1, для гиперболы e > 1.
Фокальные радиусы эллипсa r1, r2 — расстояния от точки на эллипсе до фокусов.
Радиус эллипсa R — отрезок, соединяющий центр эллипсa О с точкой на эллипсе.
| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 — e2cos2φ |
где e — эксцентриситет эллипсa, φ — угол между радиусом и большой осью A1A2.
Фокальный параметр эллипсa p — отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси:
Коэффициент сжатия эллипсa (эллиптичность) k — отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k < 1, для круга k = 1:
k = √1 — e2
где e — эксцентриситет.
Сжатие эллипсa (1 — k ) — величина, которая равная разности между единицей и эллиптичностью:
Директрисы эллипсa — две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии
ae
от центра эллипса. Расстояние от фокуса до директрисы равно
pe
.
Основные свойства эллипсa
1. Угол между касательной к эллипсу и фокальным радиусом r1 равен углу между касательной и фокальным радиусом r2 (Рис. 2, точка М3).
2. Уравнение касательной к эллипсу в точке М с координатами (xM, yM):
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через центр эллипсa. (Это свойство дает возможность построением с помощью циркуля и линейки получить центр эллипса.)
4. Эволютой эллипсa есть астероида, что растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами F1 и F2 у треугольник ∆ ABC, то будет выполнятся следующее соотношение:
| 1 = | F1A ∙ F2A | + | F1B ∙ F2B | + | F1C ∙ F2C |
| CA ∙ AB | AB ∙ BC | BC ∙ CA |
Уравнение эллипсa
Каноническое уравнение эллипсa:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa О в начале системы координат, а большая ось лежит на абсциссе, то эллипсa описывается уравнением:
Если центр эллипсa О смещен в точку с координатами (xo, yo), то уравнение:
| 1 = | (x — xo)2 | + | (y — yo)2 |
| a2 | b2 |
Параметрическое уравнение эллипсa:
| { | x = a cos α | де 0 ≤ α < 2π |
| y = b sin α |
Радиус круга вписанного в эллипс
Круг, вписан в эллипс касается только двух вершин эллипсa B1 и B2. Соответственно, радиус вписанного круга r будет равен длине малой полуоси эллипсa OB1:
r = b
Радиус круга описанного вокруг эллипсa
Круг, описан вокруг эллипсa касается только двух вершин эллипсa A1 и A2. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa OA1:
R = a
Площадь эллипсa
Формула определение площади эллипсa:
S = πab
Площадь сегмента эллипсa
Формула площади сегмента, что находится по левую сторону от хорды с координатами (x, y) и (x, -y):
| S = | πab | — | b | ( | x | √ | a2 — x2 + a2 ∙ arcsin | x | ) |
| 2 | a | a |
Периметр эллипсa
Найти точную формулу периметра эллипсa L очень тяжело. Ниже приведена формула приблизительной длины периметра. Максимальная погрешность этой формулы ~0,63 %:
| L ≈ 4 | πab + (a — b)2 |
| a + b |
Длина дуги эллипсa
Формулы определения длины дуги эллипсa:
1. Параметрическая формула определения длины дуги эллипсa через большую a и малую b полуоси:
| t2 | ||
| l = | ∫ | √a2sin2t + b2cos2t dt |
| t1 |
2. Параметрическая формула определения длины дуги эллипсa через большую полуось a и эксцентриситет e:
| t2 | ||
| l = | ∫ | √1 — e2cos2t dt, e < 1 |
| t1 |
Задачи и размышления
Знакомство со свойствами эллипса, гиперболы и параболы вызывает желание изучить способы построения этих кривых. Рассмотрим некоторые из таких способов.
1. Эллипс можно построить с помощью нити длиной 2а, закрепленной концами в фокусах (рис. 5.20). Очевидно, что длина нити останется неизменной, а фокусы фиксированы. Перемещая нить в натянутом состоянии, получим эллипс.
Рис. 5.20. Построение эллипса с помощью нити,
закрепленной в его фокусах.
Этот способ не всегда может быть удобен на практике. Дадим другой вариант построения эллипса, также вытекающий из его определения.
2. Пусть известно полуфокусное расстояние эллипса C и его большая полуось а.
Располагая фокусы F1 и F2 на расстоянии 2с, проводим дуги окружностей радиусами И
поочередно из первого и второго фокусов, выбирая их так, чтобы
Точки пересечения окружностей будут лежать на эллипсе.
При этом допустимые значения и
должны удовлетворять условиям:
Откуда следуют эти ограничения?
Меняя и
В допустимых границах и строя соответствующие пары окружностей, в их пересечении будем получать точки, принадлежащие искомому эллипсу. Попарные значения
и
удобно выбрать, используя отрезок длиной 2а (рис. 5.21).
Рис. 5.21. Выбор допустимых значений модулей
фокальных радиусов.
Вершины эллипса, лежащие на малой оси, найдутся при пересечений дуг окружностей c радиусами , проведенных из фокусов
и
, как из центров.
Рис. 5.22. Построение эллипса по опорным точкам,
получаемым с помощью циркуля.
Для нахождения вершин эллипса, расположенных на большой оси, проводим дуги окружности радиуса a + c из фокусов F1 и F2, как из центров, до пересечения с этой осью.
Докажите, что полученная кривая – эллипс.
3. Рассмотрим еще один способ отыскания точек, принадлежащих эллипсу, с помощью построений, выполняемых линейкой. Построим прямоугольник АBСD, большая сторона которого AD равна 2а – длине большой оси эллипса, а длина меньшей стороны АВ равна 2b – его малой оси (рис. 5.23). Стороны АВ и ВС делим на одинаковое число равных частей. Точки деления соединяем с точками А и D. Выделенные на рисунке точки пересечения лежат на дуге эллипса.
Докажите этот факт.
Рис. 5.23. Построение эллипса по опорным точкам
с помощью линейки.
Подобным способом можно построить параболу (рис. 5.24).
Рис. 5.24. Построение параболы по опорным точкам
с помощью линейки.
Обоснуйте этот способ. Каким будет каноническое уравнение эллипса при известной длине отрезков AB и BC?
4. Рассмотрим один из возможных способов построения гиперболы. Будем считать известными расстояние 2с между фокусами F1 и F2 и разность модулей фокальных радиусов , где 2A – длина ее действительной оси.
Поместим в фокус F1 конец линейки (рис. 5.25), к другому концу которой в точке А прикреплен шнур, длина которого меньше длины линейки на 2а. Другой конец шнура закреплен в фокусе F2.
Рис. 5.25. Построение гиперболы с помощью натянутого шнура и линейки.
При вращении линейки вокруг фокуса F1 натянутый нитью острый конец карандаша (точка М) опишет некоторую кривую.
Для любой точки М на этой кривой будет справедливо:
Что соответствует свойствам гиперболической кривой. Мы получили правую ветвь гиперболы. Аналогично строится ее левая часть.
5. Придумайте новые способы построения эллипса, гиперболы, параболы и обоснуйте их.
Известные понятия диаметра окружности и ее хорды можно обобщить на эллипс, гиперболу и параболу.
Диаметром эллипса (гиперболы) называется любая прямая, проходящая через центр кривой. Диаметром параболы назовем любую прямую, параллельную ее оси, включая и саму ось.
Всякая прямая может пересекать коническое сечение не более чем в двух точках. Если точек пересечения две, то отрезок прямой с концами в точках пересечения называется хордой.
У рассматриваемых кривых обнаруживается одно неожиданное свойство: Середины параллельных хорд конических сечений лежат на их диаметре (рис. 5.26).
Рис. 5.26. Расположение середин параллельных хорд конических сечений.
Для доказательства этого свойства рассмотрим сначала эллипс и гиперболу. Оно очевидно, когда хорды перпендикулярны вертикальной оси симметрии этих кривых. Возможны другие случаи. Пусть семейство параллельных хорд задается уравнением:
Меняя b, мы будем получать параллельные прямые. Уравнения эллипса и гиперболы можно объединить следующей записью:
Координаты концов хорд должны удовлетворять следующей системе уравнений:
Подставляя из второго уравнения этой системы выражение для координаты у в первое, получим:
По теореме Виета легко найти
Полусумма решений и будет являться абсциссой хc середины хорды:
Используя уравнение хорды, находим ординату ее середины:
Таким образом, середины параллельных хорд лежат на прямой
Проходящей через центр эллипса или гиперболы, то есть являющейся диаметром кривой. Угловой коэффициент этого диаметра
Он называется сопряженным по отношению к диаметру , параллельному хордам.
Интересно, что свойство сопряженности диаметров взаимно. Так, угловой коэффициент диаметра, сопряженного диаметру
,
Будет
Рассмотрим теперь параллельные хорды параболы
При разных значениях b. Их концы должны удовлетворять системе:
Выполняем очевидные преобразования аналогично предыдущему:
Это означает, что середина хорды имеет ординату
Таким образом, геометрическое место середин хорд параболы – прямая, параллельная оси 0х, то есть диаметр параболы.
6. Дано семейство параллельных прямых,
На которых располагаются параллельные хорды эллипсов:
Всегда ли они будут иметь один и тот же сопряженный диаметр?
7. Дана парабола х = 2у2, ее диаметр и семейство параллельных хорд, образующих с осью 0х угол j= 0,2. Найти длину хорды, пересекающей ось абсцисс в точке х = 2.
8. Хорда эллипса
Наклонена под углом j к оси 0х и имеет длину l. Найдите координаты ее концов. Исследуйте решение.
9. В эллипс
Вписаны треугольники АВL и СDL так, что стороны АВ=l и СD=m расположены параллельно, а медианы КL и МL лежат на одной прямой. Найти длины медиан. Доказать, что прямая МL пройдет через начало координат. Исследовать решение задачи в зависимости от входящих в него параметров.
10. Дан параллелограмм со сторонами a и b, угол между которыми j. Построить несколько эллипсов, которые могут быть описаны около этого параллелограмма, и найти их уравнения.
11. Доказать, что сумма квадратов двух сопряженных полудиаметров эллипса равна сумме квадратов его полуосей.
12. Доказать, что площадь параллелограмма, построенного на двух сопряженных полудиаметрах эллипса, равна площади прямоугольника, построенного на полуосях эллипса.
13. По изображению эллипса найти с помощью циркуля и линейки его центр.
14. Доказать, что хорды эллипса, соединяющие его произвольную точку с концами любого диаметра, параллельны паре его сопряженных диаметров.
15. Доказать, что отрезки, отсекаемые директрисами на асимптотах, считая от центра гиперболы, равны действительной полуоси. Пользуясь этим свойством, построить директрисы гиперболы.
Рассмотрим параметрические уравнения эллипса. В связи с этим обратимся к задаче.
Пусть точка М делит отрезок АВ на части a и b. Его концы скользят по сторонам прямого угла. Какую траекторию опишет при этом точка М?
Для решения задачи введем прямоугольную декартовую систему координат, расположив ее начало в вершине угла, а оси координат – по направлению сторон прямого угла (рис.5.27). Пусть точка М имеет координаты х и у, а угол , который образован отрезком AB с отрицательной ориентацией оси Ох, равен t радиан.
Рис. 5.27. Вывод параметрических уравнений эллипса
При перемещении концов отрезка А и В по координатным осям (во всех четырех координатных углах) точка М(х, у) опишет кривую, параметрические уравнения которой легко находится:
.
Этой кривой является эллипс, в чем можно убедиться, исключая параметр t. Действительно,
Или
.
16. Найдите параметрические уравнения гиперболы и параболы.
17. Точка М, брошенная под углом к горизонту с начальной скоростью
(рис.5.28а), если пренебречь сопротивлением воздуха, движется согласно уравнениям:
Где g — ускорение силы тяжести. На возвышенности, образующей с горизонтом угол , располагается перпендикулярно ей стержень высоты h.
Расстояние от подножья возвышенности до точки М равно l, а до основания стержня – d.
При каких углах точка М сможет перелететь через стержень?
Исследуйте допустимые углы перелета точки М через квадрат, установленный на возвышении вместо стержня (рис.5.28б).
Рис. 5.28. Траектория точки М, преодолевающей препятствия.
18. На рис.5.29 указаны проекции стойки. Ее основание ограничено дугами эллипса. Для крепления стойки к поверхности предполагается просверлить отверстия в тех ее точках, которые соответствуют фокусам эллипса. Используя чертеж детали, опишите аналитически этот эллипс, вычислите его фокусы, укажите на чертеже точки для сверления отверстий и вычислите расстояние от этих точек до наиболее удаленных точек стойки.
Рис. 5.29. Стойка
19. Верхний слой воды в наклоненном цилиндрическом стакане имеет форму эллипса (рис.5.30). Докажите этот факт и найдите полуоси эллипса, если радиус цилиндра R, а угол наклона .
Рис. 5.30. Верхний слой воды в наклоненном стакане.
20. Найдите траекторию точки, которая во все время движения остается вдвое ближе от заданной прямой, чем от заданной точки.
21. Найдите траекторию точки, для которой во все время движения произведение расстояний до двух данных пересекающихся прямых есть величина постоянная.
На основании первого закона Кеплера Земля движется вокруг Солнца по эллиптической орбите, в одном из фокусов которой расположено наше светило. Найдем скорость Земли в точке наибольшего удаления планеты от Солнца, если эксцентриситет орбиты e=0,0167; большая полуось a=149504000 км; масса Солнца mc=1,97×1030 кг (рис. 5.31).
Рис. 5.31. Орбита вращения Земли вокруг Солнца
Движение Земли в поле гравитации подчиняется закону сохранения энергии, согласно которому во всякой точке орбиты ее полная механическая энергия остается постоянной. Пусть и
– радиус-векторы, определяющие, соответственно, наиболее и наименее удаленное положение Земли на орбите вокруг Солнца. Если

Есть кинетическая энергия Земли в точках A и B орбиты соответственно, где m3 – ее масса, и равенства
;
Характеризуют ее потенциальную энергию в гравитационном поле Солнца в этих точках, где G=6,67×10-11 м3/кгс2 – гравитационная постоянная, то
Или

Очевидно, что
;
.
Тогда

Это уравнение содержит две неизвестные: и
. Чтобы преодолеть возникшую трудность, воспользуемся вторым законом Кеплера, согласно которому, радиус-вектор планеты за одинаковые промежутки времени зачерчивает одинаковые площади. Примем упрощенную гипотезу: за малые промежутки времени траекторию Земли можно считать прямолинейной. Тогда площади соответствующих секторов выразятся приближенно следующим образом:
;
И мы придем к соотношению:
,
Из которого находим связь между скоростями и
:
.
Получаем следующее уравнение относительно неизвестной :

Откуда находим:
М/с.
Вот с какой скоростью мчится наша Земля в космическом пространстве. А ведь эта скорость минимальная. В точке В она будет еще выше.
22. Найдите наименьшую и наибольшую скорость Марса на орбите вокруг Солнца, используя соответствующие справочные данные.
Третий закон Кеплера гласит: квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит:
.
23. Используя этот результат, найдите большую полуось орбиты первого искусственного спутника Земли, который был запущен в 1957 году в СССР и имел период обращения 1 час 55 минут по эллиптической орбите, если период обращения Луны вокруг Земли равен 655,2 ч., большая полуось лунной орбиты составляет 382000 км и наименьшее удаление искусственного спутника от центра Земли – 6603 км. Радиус Земли принять равным 6378 км.
Интересно отметить, что скорость, которую необходимо сообщить искусственному спутнику вблизи поверхности Земли в горизонтальном направлении, чтобы он начал двигаться в качестве спутника по круговой орбите радиуса R (рис.5.32), определяется формулой:
.
Принимая g=9,81 м/с2, , получим
. Это значение скорости называется первой (1) космической скоростью.
Если скорость V1 будет стремиться к значению
,
Равного для Земли, , то орбита искусственного спутника станет эллиптической и, достигнув, величины V2, второй космической скорости – станет параболической.
При скорости, большей второй космической, спутник будет двигаться по гиперболе.
В последних двух случаях, спутник навсегда покинет Землю и удалится в межпланетное пространство.
Рис. 5.32. Зависимость формы орбиты искусственного спутника Земли от начальной скорости.
24. Между Землей и Луной пролетает космический аппарат так, что расстояния от него до поверхности Земли и до поверхности Луны постоянно остаются равными между собой. Составьте математическую модель, описывающую это движение. В каких условиях она допускает упрощения?
25. На самолетах и кораблях во время второй мировой войны действовала навигационная система, использовавшая разницу времени между моментами приема радиосигналов от двух пар станций, которые испускали их одновременно. Составьте математическую модель этой навигационной системы и оцените ее достоинства и недостатки.
В прожекторах, фарах автомобилей используется параболоид вращения, который получается при вращении параболы вокруг собственной оси: лучи, выходящие из источника света, помещенного в фокус, не рассеиваются, а, отразившись от стенок параболоида, идут параллельно этой оси. Используется и обратный эффект. «Тарелка» – так называется параболическая антенна для спутниковой связи, собирает в одну точку телевизионные сигналы, идущие из космоса. Фокальные свойства кривых второго порядка давали повод для мифотворчества. Очевидно, что в повести «Гиперболоид инженера Гарина» А. Толстой имел в виду все-таки параболоид.
Еще раньше зародилась легенда об Архимеде из Сиракуз, который сжег флот римлян, обороняя свой город с помощью параболических зеркал.
26. Составьте технический проект такой «пушки», которая могла бы поражать противника на расстоянии 50-500 м. Попробуйте оценить ее поражающую мощь.
Вернемся к задаче Паппа, которая была поставлена в начале главы, как к одной из первых решенных Р. Декартом аналитическим методом. Дадим ее общую формулировку.
Даны 2n прямых, лежащих в одной плоскости. Найти геометрическое место точек в этой плоскости, таких, что произведение расстояний от каждой точки этого множества до первых n прямых d1×D2. …×Dn и произведение расстояний от этих же точек до следующих n прямых dn+1×Dn+1×…×D2n находились бы для всех точек в одном и том же постоянном отношении L:
Попытка решить ее для n=3 (рис. 5.33) была предпринята нами ранее. Рассмотрим общий случай. Введем систему координат, выбирая ее начало в произвольной точке плоскости и опишем положение заданных прямых соответствующими нормальными уравнениями:
Рис. 5.33. Задача Паппа при n=3.
Пусть – произвольная точка искомого геометрического места точек. Найдем расстояния от нее до данных прямых:
Тогда
Это и есть уравнение искомой кривой относительно координат x’ и у’ ее точек. Оно будет иметь степень n, в частном случае, например, для четырех прямых 2n=4; n=2 мы получим уравнение второй степени. Такое уравнение, как это уже отмечалось на стр.180, определяет одно из конических сечений. Это весьма неожиданный результат.
27. Каковы возможные обобщения задачи Паппа?
| < Предыдущая | Следующая > |
|---|
Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.
Что такое эллипс и фокусное расстояние
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и
. Допустим, что расстояние
=
– фокусное расстояние.
Рис. 1
– фокусы .
;
,
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Теорема:
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью,
(теорема Пифагора). Если же точка
находится на пересечении его с горизонтальной осью,
. Так как по определению сумма
– постоянная величина, то приравнивая получается:
.
Уравнение эллипса
Уравнение элиппса бывает двух видов:
- Каноническое уравнение эллипса.
- Параметрическое уравнение эллипса.
Сначала рассмотрим каноническое уравнение эллипса:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:
Если центр эллипсa смещен в точку с координатами
тогда уравнение:
Чтобы получить каноническое уравнение эллипса, разместим и
на оси
симметричной к началу координат. Тогда у фокусов будут такие координаты
и
(см. рис. 2).
Пусть – произвольная точка эллипса. Обозначим через
и
– расстояние от точки
к фокусам. Согласно с определением эллипса:
(1)
Рис. 2
Подставим в (1) ,
и освободимся от иррациональности, подняв обе части к квадрату, получим:
(подносим к квадрату обе части): ,
Обозначим: , получаем каноническое уравнение эллипса:
(2)
Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из у нас получается
. Так как
, тогда
, и поэтому
.
Для построения эллипса обратим внимание, что если точка принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки
тоже удовлетворяют это уравнение: из
.
Точки – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.
Из уравнения (2) находим , для первой четверти
.
Если , тогда
. Если же
, тогда
. Точки
и
, а также симметричные с ними
,
– вершины эллипса, точка
– центр эллипса,
=
большая ось,
– малая ось эллипса.
Если первой четверти, тогда из
получается, что при возрастании
от
к
значение
падает от
к
. (рис. 3)
Параметрическое уравнение выглядит так:
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом равен углу между касательной и фокальным радиусом
.
2. Уравнение касательной к эллипсу в точке с координатами
:
.
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами и
у треугольника
, тогда выполняется соотношение:
=
Эксцентриситет эллипса
Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается
Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда
– получается круг. Если же
, тогда
– эллипс превращается в отрезок. В некоторых случаях
. Для фокальных радиусов приведём без доказательства такие формулы:
Рис. 3
Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и
, тогда вычислим
– полуфокусное расстояние.
Строим фокусы и
на расстоянии один от другого
Концы не растянутой нити длиной
закрепляем в точках
и
. Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Примеры решения задач
Задача
Задан эллипс уравнением и точки
. Необходимо:
- убедиться, что точки
и
лежат на эллипсе;
- найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки
к фокусам;
- убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты точки
в левую часть уравнения эллипса:
– точка
лежит на эллипсе. Аналогично для
:
точка
лежит на эллипсе.
2. С канонического и данного уравнения
эллипса выходит:
Из равенства
получается:
– полуфокусное расстояние. Координаты фокусов
и
.
3. Найдём фокальные радиусы точки :
4. Найдём сумму , что отвечает определению эллипса.
5. Эксцентриситет находится по формуле .
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
,
. Вершины эллипса в точках
,
,
,
. Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае
больше, чем
, то эллипс, который вытянут вдоль оси
, находим полуфокусное расстояние
.
Фокусы в точках и
. (см. рис. 3)
Рис. 4
Найти оси, вершины и фокусы эллипса или
. Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
,
. Откуда находим оси эллипса:
,
и координаты вершин:
,
,
,
. Дальше из формулы:
. Значит, фокусами эллипса есть точки:
и
. Для построения эллипса отложим на осях
и
вершины
соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении большей полуосью будет
, тогда фокусы эллипса будут расположены на оси
и тогда
.
Эллипс и его свойства
Определение. Эллипс — это замкнутая плоская кривая, которая имеет уравнение x²/a²+y²/b²=1. Это каноническое уравнение эллипса, в нем координатные оси совпадают с осями эллипса.
Он имеет два фокуса. Это такие точки, сумма расстояний от которых до любой P(x,y) есть постоянная величина. Эллипс также можно описать как пересечение плоскости и кругового цилиндра.
Эллипс
Элементы:
- F1 , F2 – фокусы . F1 = ( c ; 0); F 2 (- c ; 0)
- A1 A2 — большая ось;
- B1 B2 — малая ось;
- О — центр эллипса (пересечения малой и большой осей);
- A1, A2, B1, B2 — вершины эллипса;
- Диаметр эллипса — отрезок, соединяющий две точки эллипса и проходящий через O;
- с – фокусное расстояние, половина расстояния между F1 и F2;
- a – большая полуось эллипса;
- b – малая полуось;
- r1 и r2 — фокальные радиусы эллипса;
- если a > b, то уравнения директрис эллипса x=-a/e, x=a/e;
- если a < b, уравнения директрис y = -b/e, y = b/e;
- Фокальный параметр p = b 2 /a — отрезок, который соединяет фокус фигуры и точку на кривой, перпендикулярен ее большей оси.
Теорема. Фокусное расстояние c и полуоси эллипса связаны соотношением:
Доказательство: В случае, если М лежит на пересечении кривой с вертикальной осью, r1 + r2 = 2*(по теореме Пифагора). В случае, если М — пересечение его с горизонтальной осью, r1 + r2 = а – c + а + c. Т.к. по определению сумма r1 + r 2 – постоянна, то , приравнивая, получаем:
Основные свойства эллипсa
- Угол между касательной к эллипсу и фокальным радиусом r1 равен углу между касательной и радиусом r2. Лучи, выпущенные из одного фокуса, после отражения соберутся во втором фокусе.
- Уравнение касательной к эллипсу в М с координатами (xM, yM):
.
- Если две параллельные прямые пересекают эллипс, то отрезок соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через (.) O эллипсa. (Это свойство дает возможность находить центр эллипса.)
- При равенстве полуосей эллипс превращается в окружность.
Эллипс это коническое сечение. Он может быть получен как пересечение плоскости с конусом.
Уравнение
- Каноническое уравнение в декартовой системе координат, центр в начале координат, большая ось на оси абсцисс: . Эллипс — кривая второго порядка. Координаты x и y входят только в четных степенях, поэтому эллипс симметричен относительно осей координат. Оси координат пересекают эллипс в A1(-a,0), A2(a,0), B1(0,-b), B2(0,b). Эллипс лежит в прямоугольнике 2a и 2b.
- Центр смещен в ( xo, yo):
- Параметрическое: , где 0 ≤ α ≤ 2 π.
- В полярной системе координат: , где полюс полярной системы координат левый фокус F1, полярная ось луч F1 , F2, p = b²/a фокальный параметр.
Радиус круга вписанного в эллипс
Круг, вписанный в эллипс касается только двух вершин эллипсa B1 и B2. Соответственно, радиус вписанного круга будет равен длине малой полуоси эллипсa r = b.
Радиус круга описанного вокруг эллипсa
Круг, описанный вокруг эллипсa касается только двух вершин эллипсa A1 и A2. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa R = a.
Как построить эллипс
П е р в ы й с п о с о б.
Сумма расстояний от любой точки эллипсa до его фокусов величина постоянная равная 2а.
- Иголки втыкаем в фокусы F1 , F2.
- К иголкам привязываем нитку длинной 2а.
- Нитку оттягиваем карандашом и чертим.
В т о р о й с п о с о б.
Проводим две концентрические окружности радиуса a и b.
Через центр О проводим произвольный луч ON.
Через точки K и M, в которых луч ON пересекает окружности, проводим прямые соответственно параллельные осям Ox и Oy.
Точка их пересечения L — точка искомого эллипса.
Меняя направление луча ON, получим новые точки эллипсa.
Эксцентриситет эллипса
Определение. Форма эллипса определяется характеристикой, которая равна отношению е = с/a называется эксцентриситетом, характеризует вытянутость фигуры. Чем эксцентриситет ближе к нулю, тем линия больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
Т.к. с < а , то е < 1.
Определение. Величина k = b / а — коэффициентом сжатия (эллиптичность), а величина 1 – k = ( а – b )/ а — сжатие.
Коэффициент сжатия k и эксцентриситет е связаны соотношением: k² = 1 – е² . Чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным, то есть больше походить на окружность. Если а = b ( с = 0, е = 0), то эллипс превращается в окружность.
Если для точки М(х 1 , у 1 ) выполняется условие: , то она находится внутри линии эллипс, а если , то M находится вне его.
Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:
Доказательство. Выше было показано, что r1 + r2 = 2 а . Из геометрических соображений можно записать:
После возведения в квадрат и приведения подобных слагаемых:
Аналогично доказывается, что r2 = а + еx . Теорема доказана.
Директрисы эллипса
Эллипс имеет две директрисы:
x = а / е ; x = — а / е .
Теорема. Для того, чтобы точка лежала на границе линии эллипс, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось е.
Площадь эллипса и его сегмента
Формула площади эллипса S = πab.
Площадь сегмента (зеленый на рис.) можно определить по формуле
Если эллипс задан уравнением Ax² + Bxy + Cy² = 1, то его площадь 
Периметр эллипсa
Точная формула периметра эллипсa очень сложная. Периметр в общем виде
Приближенная формула длины периметра имеет вид 
Решение задач на эллипс
Соберем все формулы вместе:
- — каноническое уравнение эллипса;
- координаты левого фокуса F1(-c,0), правого F2(c,0);
- связь а, b, с a² = b² + c²
- e = c/а эксцентриситет;
- фокальные радиусы r1 = a + ex, r2 = a — ex;
- директрисы x = -a/e, x = a/e;
- расстояние между директрисами 2a/e;
- Площадь эллипса S = πab.
Пример 1. Составить уравнение прямой, проходящей через F1 и нижнюю вершину линии эллипс:
- Координаты нижней вершины: x = 0; y 2 = 16; y = -4.
- Координаты фокуса: с² = а² – b² = 25 – 16 = 9; с = 3; F1 (-3; 0).
- Прямая, проходящей через две точки:
Пример 2. Дана кривая 9x 2 + 25y 2 = 225. Найти: 1) показать, что это эллипс, найти его полуоси 2) эксцентриситет 3) директрисы.
Разделим обе стороны на 225
сократим, получим каноническое уравнение эллипса
Следовательно, 1) полуоси a = 5, b = 3, 2) F1(-c, 0), F2(c, 0) с определим из равенства b 2 = a 2 — c 2 , c 2 = a 2 — b 2 = 25 — 9 = 16, c = 4, поэтому левый фокус F1(-4, 0), правый F2(4, 0).
4) уравнение директрис x = ±a/e =±5*5/4=±25/4.
Пример 3. Эксцентриситет e = 1/3, центр его совпадает с началом координат, F1 (-2;0). Вычислить расстояние от точки M1 с абсциссой, равной 2, до директрисы, односторонней с данным фокусом.
Т.к. F1 (-2;0), то с = 2. Зная с и e = 1/3, определим а. e = c/a, а = c/е = 2*3=6. Уравнение директрисы x = -а/e = -6*3 = -18. Точка M1 имеет координату х = 2. Следовательно, d = |-18|+2=20.
Пример 4. Определить точки эллипса x 2 /100+y 2 /36 =1, расстояние от которых до F2 равно 14. Найти директрисы.
a = 10, b = 6, c 2 = а 2 — b 2 = 100 -36 = 64 = 8 2 . Найдем эксцентриситет е = c/а = 8/10 = 4/5. Используем формулу для r2 = а — еx, 14 = 10 — 4/5*x, отсюда х = -5. Подставим в исходное координату х и найдем у = ±√27 = ±3√3. Условиям задачи удовлетворяют точки (-5; 3√3) и (-5; -3√3).
Уравнения директрис x = ±a/e = ±10/4/5 = ±25/2 = ±12,5.
Автор статьи Степанов Владимир
Понятие эллипса в математике и его свойства
Эллипс — что это такое, понятие в математике и геометрии
Эллипс — фигура, представляющая собой по форме замкнутую кривую линию на плоскости. Она получается путем пересечения плоскости с круговым цилиндром, или же как ортогональное отображение окружности на плоскость в пространстве.
В эллипсе суммарная величина расстояния от любой точки до двух точек F2 и F1 будет равна одному постоянному значению. Эти точки — F1 и F2 — носят названия фокусов эллипса.
F 1 M 1 + F 2 M 1 = F 1 M 2 + F 2 M 2 = A 1 A 2 = c o n s t
∣ F 1 M ∣ + ∣ F 2 M ∣ = 2 × a , причем ∣ F 1 F 2 ∣ < 2 × a
Окружность можно называть партикулярным (особым) вариантом эллипса. Эллипс, как и параболу, и гиперболу, можно назвать квадрикой или же коническим сечением.
Рассмотрим связанные с эллипсом понятия:
- Отрезок AB, проходящий через фокусы эллипса (его концы должны лежать на эллипсе), носит название большой оси эллипса. Длина этого элемента — большой оси — равняется 2a в уравнении, приведенном выше.
- Малая ось эллипса — отрезок CD, который перпендикулярен большой оси, он проходит через центральную точку большой оси. Концы отрезка должны лежать на эллипсе.
- Центр эллипса — точка пересечения малой и большой оси данной замкнутой кривой.
- Большая полуось — отрезок, проведенный из центра эллипса к вершине большой оси. Обозначается буквой «a».
- Малая полуось — отрезок, проведенный из центра эллипса к вершине малой оси. Обозначается буквой «b».
- Фокальные радиусы в точке — расстояния r 1 и r 2 до определенной точки от каждого фокуса эллипса.
- Фокальное расстояние — расстояние, равное: c = ∣ F 1 F 2 ∣ 2 .
- Эксцентриситет — величина, равная: e = c a = 1 — b 2 a 2 .
- Диаметр эллипса — свободно проведенная хорда, проходящая через центр построения. Диаметры (обычно пара), обладающие свойством середины хорд, параллельные первому диаметру, и находящиеся на втором диаметре, называются сопряженными диаметрами. Середины хорд, параллельных второму диаметру, находятся на первом диаметре.
- Радиусом называют отрезок, соединяющий в данной точке центр эллипса и точку. Длина радиуса вычисляется по формуле: r = a b b 2 cos 2 γ + a 2 sin 2 γ = b 1 — e 2 cos 2 γ . В данной формуле γ — величина угла между большой полуосью и радиусом.
- Фокальный параметр ( p = b 2 a ) — половина длины хорды, проходящей через фокус эллипса, является перпендикулярной большой оси.
- Коэффициент сжатия, или же эллиптичность — отношение длины большой полуоси к длине малой полуоси. Вычисляется по формуле: k = b a . Величина, равная ( 1 — k ) = a — b a , будет носить название «сжатие эллипса». Следует помнить, что для окружности коэффициент сжатия равен единице, а сжатие равно нулю. Эксцентриситет и коэффициент сжатия связаны отношениями равными: k 2 = 1 — e 2 .
- Директриса — прямая, которая существует для каждого фокуса эллипса. При этом соотношение расстояния от свободно расположенной точки эллипса до фокуса этой замкнутой кривой к расстоянию от данной точки до определенной прямой будет равно эксцентриситету эллипса. Полный эллипс находится на той же стороне от такой же прямой, что и его фокус. Уравнения для директрис эллипса в классическом виде пишутся как x = ± p e ( 1 — e 2 ) для каждого фокуса ( ± p e 1 — e 2 , 0 ) . Расстояние от фокуса до директрисы будет вычисляться по соотношению p e
Теорема директрисы: Для того, чтобы определенная точка находилась на границе линии замкнутой кривой, необходимо, чтобы соотношение расстояния до фокуса к расстоянию до соответствующей директрисы было равно e.
Эллиптическая функция — функция в двух направлениях, которая в рамках метода комплексного анализа, задана на комплексной плоскости.
Основные элементы и свойства фигуры
Рассмотрим элементы эллипса. Взгляните на чертеж:
F1 и F2 выступают в роли фокусов эллипса. Осями данной замкнутой кривой будут A1A2 =2a (как большая ось, проходящая сквозь фокусы замкнутой кривой), а B1B2=2b (как малая ось, перпендикулярная второй, большой оси фигуры, проходит через ее центр). Здесь «a» является большой полуосью, «b» является малой полуосью, «O» является центром (то есть точкой пересечения малой оси и большой оси).
Вершинами эллипса будут точки A1, и A2, и B1, и B2. Это точки пересечения большой осью и малой осью эллипса. Диаметр замкнутой кривой — отрезок, соединяющий две точки эллипса, а также проходящий через центр фигуры.
Фокальное расстояние, которое обозначается буквой «c», является половиной длины отрезка, соединяющего фокусы эллипса.
Эксцентриситет замкнутой кривой, который обозначается буквой «e», показывает степень «сплющенности» (то есть отклонения от окружности). Он определяется соотношением фокального расстояние (буква «c») к большой полуоси «a». В случае эллипса эксцентриситет будет таким: 0<e<1, для круга e=0, для параболы e=1, а для гиперболы: e>1.
Фокальные радиусы в точке — расстояния r 1 и r 2 до определенной точки от каждого фокуса эллипса.
Радиус эллипса — отрезок, соединяющий центр, который обозначается буквой «O» с точкой на самом эллипсе.
r = a b b 2 cos 2 γ + a 2 sin 2 γ = b 1 — e 2 cos 2 γ .
В данной формуле γ — величина угла между большой полуосью и радиусом (A1A2), e — эксцентриситет.
Фокальный параметр — отрезок, перпендикулярный большой полуоси, а также выходящий за фокус эллипса. Вычисляется по формуле: p = b 2 a
Коэффициент сжатия или же эллиптичность, обозначаемая буквой «k», является отношением длины малой полуоси к большой полуоси.
Малая полуось всегда будет меньше, чем большая полуось замкнутой кривой. Получается, что k<1. Для круга будет верно равенство k=1.
В данном уравнении величина «e» — эксцентриситет.
Сжатие эллипса (то есть 1 — k ) — показатель, который равен разности между эллиптичностью и единицей.
Директриса эллипса — пара прямых, которые перпендикулярны фокальной оси замкнутой прямой, пересекающей расстояние a*e от центра замкнутой прямой. Расстояние до директрисы от фокуса будет равно p*e.
Рассмотрим также основные свойства эллипса:
- Угол к эллипсу между касательной и фокальным радиусом r 1 будет равен величине угла между фокальным радиусом r 2 и касательной.
- Равенство касательной к замкнутой кривой в точке M : 1 = x x M a 2 + y y M b 2
- В случае, если замкнутая прямая пересекается парой параллельных прямых, то отрезок, соединяющий середины отрезков, образованных при пересечении эллипса и прямых, всегда будет пересекать центр замкнутой кривой.
Данное свойство позволяет построить центр эллипса при помощи циркуля и линейки.
- Эволюта замкнутой кривой — астероида, которая растянута по короткой оси.
- В случае, если можно вписать эллипс с фокусами F1 и F2 в треугольник ABC, то возможно выполнить данное соотношение:
1 = F 1 A × F 2 C A × A B + F 1 B × F 2 B A B × B C + F 1 C × F 1 C B C × C A
Составление уравнения эллипса
Базовое уравнение замкнутой кривой.
Это уравнение, описывающее эллипс в декартовой системе координат. В случае, если центр замкнутой кривой (обозначается буквой «O») — в начале системы координат, а на абсциссе находится большая ось, то замкнутая кривая будет описываться следующим уравнением:
1 = x 2 a 2 + x 2 b 2
В случае, если центр эллипса смещается в точку с координатами x 0 и y 0 , то уравнение примет следующий вид:
1 = ( x — x 0 ) 2 a 2 + ( y — y 0 ) 2 b 2
Параметрическое уравнение будет выглядеть следующим образом:
Как посчитать площадь всего эллипса и сегмента
Рассмотрим формулу для вычисления площади всего эллипса:
Рассмотрим формулу для вычисления площади сегмента эллипса. Это формула площади сегмента, который лежит на левой стороны от хорды с координатами (x, y), а также (x, -y).
S = π a b 2 — b a ( x a 2 — x 2 + a 2 × arcsin x a )
Формула для вычисления периметра и длины дуги
Рассмотрим формулу для вычисления периметра замкнутой кривой.
Важно запомнить, что точную формулу для периметра L найти крайне тяжело. Ниже приведена формула, с помощью которой можно приблизительно рассчитать длину периметра. Максимальной погрешностью данной формулы можно считать примерно 0,63 %.
L ≈ 4 π a b + ( a — b ) 2 a + b
Рассмотрим формулу для вычисления длины дуги замкнутой кривой:
- Параметрическое уравнение для вычисления длины дуги замкнутой кривой через большую полуось a, а также малую полуось b:
ℓ = ∫ t 1 t 2 a 2 sin 2 t + b 2 cos 2 t d t .
- Параметрическое уравнение для вычисления длины дуги замкнутой кривой с помощью большой полуоси a, а также эксцентриситета, который обозначается буквой e:
ℓ = ∫ t 1 t 2 1 — e 2 cos 2 t d t , e < 1 .
Как построить эллипс по уравнению, примеры
Попробуем построить эллипс по уравнению x 2 16 + y 2 7 = 1
Сначала мы должны привести данное уравнение к привычному виду: x 2 4 2 + y 2 ( 7 ) 2 = 1
Определяем вершины эллипса. Они находятся в точках A1(a; 0), A2 (-a; 0), B1 (0; b), B2 (0; -b). Получаем, что A 1 ( 4 ; 0 ) , A 2 ( — 4 ; 0 ) , B 1 ( 0 ; 7 ) , B 2 ( 0 ; — 7 )
Определение центра окружности или эллипса по его точкам
Имеется несколько точек на плоскости, как правило от 6 до 8. Я точно знаю, что они лежат на некотором эллипсе или окружности (с некоторой погрешностью). Мне нужны координаты центра окружности/эллипса. Эта задача уже 100500 раз решена и мне совсем не хочется лепить очередной велосипед. Гугление выдало массу обсуждений задачи и к сожалению ни одной строчки кода.
Тыкните плиз пальцем, где я могу скачать код, который решает эту задачу, например методом наименьших квадратов.
Заранее премного благодарен.
- Вопрос задан более трёх лет назад
- 15685 просмотров
Оценить 4 комментария
- Вконтакте
мне точность в 1 пиксель хватит выше крыши. К сожалению больше чем примерно 25 точек я достать в любом случае не смогу. В идеале хотелось бы работать с 8 точками. Можно сслыку на статью и код?
P.S. точки довольно таки неплохо распределены по эллипсу/окружности, это должно по идее сильно упростить задачу.
Так в чем же проблема?
Уравнение эллипса известно — Ax 2 + Bxy + Cy 2 + Dx + Ey = 1.
Если выписать его для каждой точки, рассматривая x и y как известные величины, а A,B,C,D,E — как неизвестные, то получится обычная СЛАУ с пятью неизвестными и от 6 до 8 уравнениями.
Если бы координаты точек были заданы точно, это этого было бы достаточно для точного решения. Поскольку точность ограничена — надо найти больше точек и использовать МНК.
Если вы не знаете, как применять МНК к СЛАУ, то проще всего его запомнить в матричной форме:
есть уравнение вида M t = r
его решение методом МНК — это (t = M T M) -1 M T r
осталось реализовать умножение и обращение матриц.
Осталось определить центр эллипса. Для этого запишем уравнение в виде
A(x-x0) 2 + B(x-x0)(y-y0) + C(y-y0) 2 = F
и заметим, что
D = -(2Ax0 + By0),
E = -(2Cy0 + Bx0),
F — 1 = (Ax0 2 + Bx0y0 + Cy0 2 )
Из первых двух уравнений получаем центр, про третье — забываем.
Сложнее обстоит дело с погрешностью — точных формул я не помню, да и что считать несколько непонятно. Возьмите 25 точек, сделайте из них от 10 до 1000 случайных выборок по 12 точек, и решите задачу для этих выборок, после чего можно найти дисперсию распределения центров.
- Вконтакте
- Вконтакте
как вам сказать… Знания лишними не бывают, поэтому если можно, то расскажите.
Но вообще мне надо на java эту проблему решить, а потому мне надо или портировать какой нить код на яву или использовать какую нить библиотеку, которая имеет порт к яве.
Отстойные, но довольно быстрые, способы — через решение систем уравнений влоб. Типа, окружность по трем точкам, эллипс по восьми (?) точкам, перебираем комбинации все/случайным образом и усредняем результат. То, что предлагает mayorovp вторым пунктом. Почему отстойные — устойчивость плохая. Именно так мы делаем у себя — способы действительно отстойные и требуют костылей, но действительно быстрые. Разница между реальным центром и найденным таким способом намного меньше пикселя, но костылей действительно много. Например, отбирая треугольник при поиске окружности по 3-м точкам, нужно, чтобы все три точки были из разных четвертей окружности.
Я не рекомендую — кода много, а экономия оправдывает себя только на железе 20 летней давности, когда нужен околорилтайм. Для эллипса по-моему малореально вообще что-либо нормальное получить.
Универсальный способ — метод наименьших квадратов. То есть заставить компьютер подобрать такие параметры эллипса чтобы разница между эллипсом и нашими точками была минимальной. Лучше критерий сложно придумать — хотя иногда получается не то, что ожидаешь, но это скорее говорит о том, что исходные данные неправильные.
Алгоритм такой:
1. Выбираем подходящее уравнение эллипса.
2. Пишeм целевую функцию (сумма квадратов уравнения для каждой точки исходных данных). По необходимости добавляем к целевой функции дополнительные условия, типа невырождаемости эллипса в гиперболу. Типа, если условие нарушается, устремляем ее в бесконечность.
3. Выбираем минимизатор (градиентный спуск, нормальное уравнение т. д.)
4. Если результаты не устраивают по скорости или качеству, возвращаемся к п. 3 или к п. 1.
По поводу третьего пункта. В России почему-то считается, что МНК — это когда решение идет с помощью нормального уравнения (составляем матрицы и решаем (AtA)^-1*At*x=b без итераций в один присест). Это не так. Минимизировать можно каким угодно способом. Хоть генетическими алгоритмами. Нормальное уравнение хорошо тогда, когда член (AtA)^-1 получается маленькой квадратной матрицей. То есть когда параметров мало, а точек очень много. Систему уравнений для эллипса вообще к виду A*x-b=0 привести служно. Искать соответствующие статьи как это делается мне влом, поэтому я пойду влоб, в качестве минимизатора взяв стандартный матлабовский.
Используя формулы mayorovp.
- Вконтакте
Коллега, попрошу читать мои комментарии более внимательно, не забыв выспаться.
Между прочим, оправдано считается. Если исходное уравнение — вида A*x-b=0, то нормальное уравнение дает оптимальный результат.
Я его к этому виду привел.
Кстати, ваша программа вернет вам случайный результат, поскольку вы взяли ужасную целевую функцию. Она обращается в нуль при A=B=C=F=0 независимо от x0 и y0. Я-то написал такое уравнение, поскольку у меня первые три переменных были уже найденными (константами). А вам надо было, как и мне в первом уравнении, положить F=1.

 называется фокальным расстоянием.
называется фокальным расстоянием. . Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
. Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут. называется половина длины хорды , проходящей через фокус и перпендикулярной большой оси эллипса.
называется половина длины хорды , проходящей через фокус и перпендикулярной большой оси эллипса. . Величина, равная
. Величина, равная  называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением
называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением 














































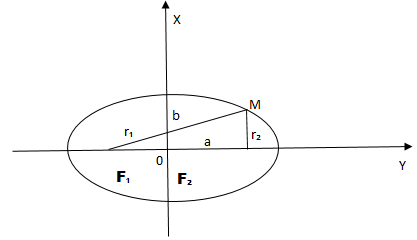
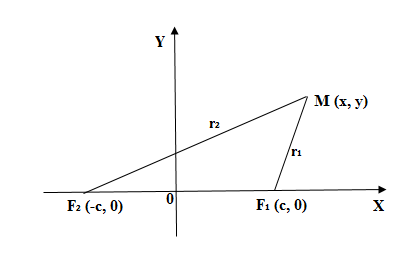
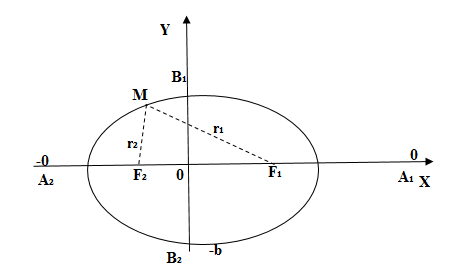


 .
. Эллипс это коническое сечение. Он может быть получен как пересечение плоскости с конусом.
Эллипс это коническое сечение. Он может быть получен как пересечение плоскости с конусом. 



