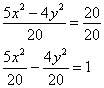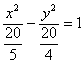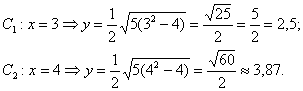Как найти центр гиперболы по каноническому уравнению - Исправление недочетов и поиск решений вместе с Examum.ru

Определение.
Пусть на плоскости заданы две точки F₁
и F₂,
расстояние между которыми равно 2c.
Пусть, кроме того, задано положительное
число a,
меньшее c.
Гиперболой
называется множество точек той же
плоскости, для каждой из которых модуль
разности расстояний до точек F₁
и F₂,
называемых фокусами
гиперболы, есть число постоянное, равное
2а.

Вывод канонического уравнения

Для вывода уравнения
гиперболы, которое мы впоследствии
назовём каноническим, выберем на
плоскости прямоугольную декартову
систему координат следующим образом:
ось

проведем через фокусы гиперболы, а ось

–
перпендикулярно ей через середину
отрезка F₁F₂
(рис. 3.1). По определению гиперболе
удовлетворяют те, и только те точки М
плоскости, для которых

Рис. 3.1.

.
(1)

Чтобы получить
уравнение гиперболы остаётся только
записать равенство (1) в координатах. В
выбранной системе координат фокусы
гиперболы имеют следующие координаты:
F₁
(–c;
0); F₂
(c;
0). Координаты произвольной (или текущей)
точки множества всегда обозначаются x
и y.
Таким образом, M(x;
y).
Так как

то уравнение (1)
равносильно следующему:

,
(2)

которое, в свою
очередь, равносильно уравнению:

.
(3)

Оба эти уравнения
являются уравнениями гиперболы, но они
имеют громоздкий вид, неудобны для
использования и для запоминания, поэтому
мы преобразуем их к более простому виду.
Проведем следующую цепочку преобразований:

(3)

Учитывая, что
,
разделив последнее уравнение на
,
получаем:

.
(4′)

Так как
,
то
,
поэтому найдется такое положительное
число
,
что
.
Теперь уравнение (4′) примет вид:

.
(4)

Мы доказали: если
точка принадлежит гиперболе, то её
координаты удовлетворяют уравнению
(3) или (4).

Докажем обратное:
если координаты точки удовлетворяют
уравнению (4) или (3), то она принадлежит
гиперболе. Итак,

{M
(x;
y)
удовлетворяет (4)}

.
(5)

Аналогично получаем:

.
(6)

Находим разность
расстояний:

[(4)

]=

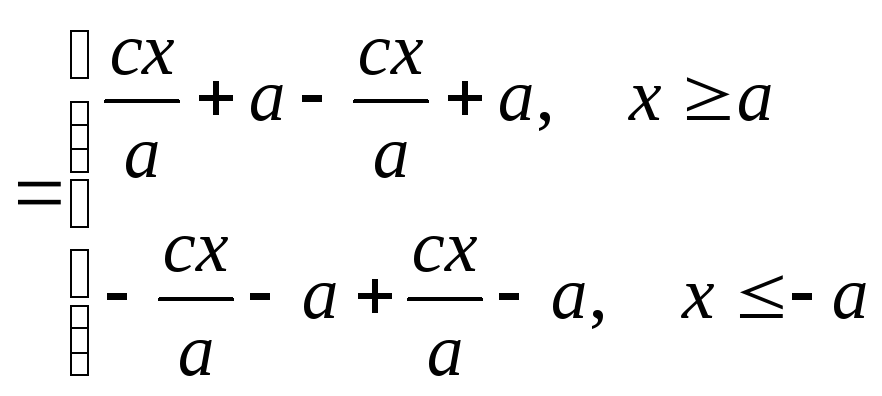
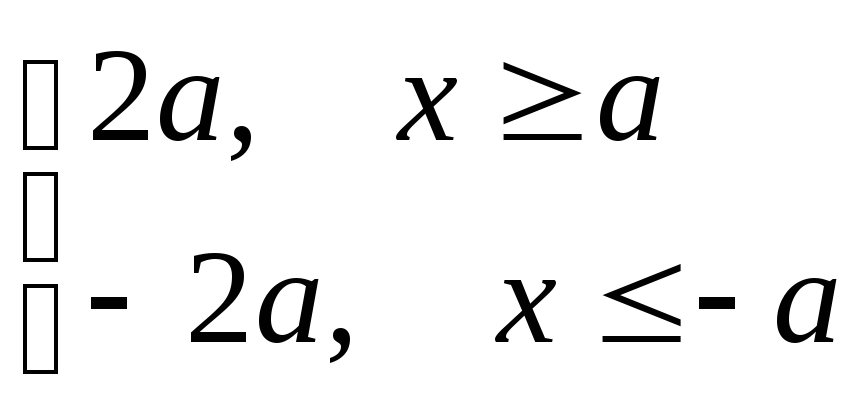
Таким образом, (4)
– уравнение гиперболы, которое и
называется её каноническим
уравнением.

Исследование формы гиперболы по ее каноническому уравнению

1. Симметрия.
Так как координаты x
и y
в уравнение
(4) входят только в чётных степенях, то

{M₁(x₀;
y₀)
Г}

{M₂(–x₀;
y₀)
Г, M₃(–x₀;
–y₀)
Г; M₄(x₀;
–y₀)Г}.

Это означает, что
гипербола (4) симметрична относительно
координатных осей и начала координат.
Оси симметрии гиперболы называются
осями
гиперболы,
центр симметрии – ее центром.

2. Пересечение
с осями. Если
y
= 0, то (4)

{x
= a}.
Значит, гипербола пересекает ось

в точках A₁
(–a;
0) и A₂
= (a;
0), которые называются вершинами
гиперболы. Если же x
= 0, то (4) решений не имеет, т.е. ось

гипербола не пересекает. Та ось гиперболы,
которую она пересекает, называется её
действительной
осью, а та, которую не пересекает –
мнимой.
Числа a
и b
называются полуосями
гиперболы, действительной и мнимой
соответственно.

3. В силу симметрии
гиперболы ее достаточно нарисовать в
первой координатной четверти, а затем
продолжить рисунок по симметрии. Если
,
,
то из (4) можно выразить y:

.
(7)

Если x
= a,
то y
= 0, если же
,
то и
.
Вычислим производную:

Если
,
то
,
поэтому гипербола в вершине имеет
вертикальную касательную.

. Асимптотами
гиперболы (4) называются прямые
.
Рассмотрим ту из них, которая проходит
в первой четверти:

.
(8)

равнивая (7) и (8), видим, что
:

,
значит, гипербола расположена ниже
своей асимптоты. Кроме того, ели М
– точка гиперболы, Р
– точка её асимптоты Рис.
3.2. с такой же
первой координатой,

–расстояние
от М до
гиперболы (рис.3.2), то

С
ледовательно,
при неограниченном удалении от начала
координат гипербола бесконечно близко
приближается к своей асимптоте, не
пересекая ее.

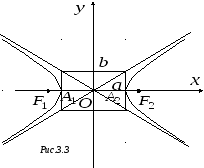
Теперь можно
приступить к рисованию. По обе стороны
от начала координат откладываем на
действительной оси действительные
полуоси, а на мнимой – мнимые. Рисуем
прямоугольник, стороны которого проходят
через полученные точки параллельно
осям координат. Точки пересечения
прямоугольника с действительной осью
– это вершины гиперболы

и
.
Затем проводим диагонали прямоугольника
и продляем их – это асимптоты гиперболы.
Рисуем гиперболу сначала в первой
четверти, начиная от вершины и неограниченно
приближая её к асимптоте, а затем
продолжаем по симметрии в остальные
координатные четверти (рис. 3.3).

В заключение
параграфа отметим, что уравнение

задаёт гиперболу, действительной осью
которой является ось
,
а школьное уравнение

при

–
это уравнение гиперболы с перпендикулярными
асимптотами, составленное относительно
её асимптот.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Способы построения гиперболы самостоятельно

Содержание:

Гипербола в математике — что это такое
Как построить гиперболу самостоятельно
Построение гиперболы по фокусам
Как построить гиперболу по точкам
Как построить график гиперболы по уравнению

Гипербола в математике — что это такое

определение 1

Гипербола представляет собой линию, определяемую в некой декартовой прямоугольной системе координат каноническим уравнением:

(frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref9})

Согласно записанному правилу, все точки гиперболы (|x| geq a). Таким образом, данные точки расположены за пределами вертикальной полосы ширины (2a), как показано на рисунке. Ось абсцисс канонической системы координат имеет точки пересечения с гиперболой. Координаты этих точек соответствуют: ((a, 0)) и ((-a, 0)). Такие точки называют вершинами гиперболы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Ось ординат не имеет общих точек с гиперболой. В состав гиперболы входят две части, которые не связаны между собой. Они носят название ветвей гиперболы. Числа «a» и «b» являются соответственно вещественной и мнимой полуосями гиперболы.

Ось ординат не имеет общих точек с гиперболой

Источник: univerlib.com

Определение 2

Ветви гиперболы — это две отдельные кривые, из которых состоит гипербола.

Определение 3

Ближайшие друг к другу точки двух ветвей гиперболы являются вершинами гиперболы.

Определение 4

Большая ось гиперболы — наименьшее расстояние между двумя ее ветвями.

Определение 5

Центр гиперболы — это середина ее большой оси.

Определение 6

Большая полуось гиперболы — расстояние, на которое удалены центр и одна из вершин, обозначается «а».

Определение 7

Фокальное расстояние гиперболы — расстояние, на которое удалены друг от друга центр и один из фокусов, обозначается «с».

Оба фокуса гиперболы расположены на продолжении большой оси и равноудалены от центра гиперболы.

Определение 8

Прямая, включающая в себя большую ось гиперболы, носит название действительной, или поперечной, оси гиперболы.

Определение 9

Прямая в виде перпендикуляра к действительной оси, которая пересекает центр гиперболы — мнимая, или сопряженная ось гиперболы.

Определение 10

Отрезок между фокусом гиперболы и гиперболой, который перпендикулярен к действительной оси, — это фокальный параметр.

Определение 11

Прицельный параметр — расстояние от фокуса до асимптоты гиперболы, обозначается «b».

Определение 12

Перицентрическое расстояние — расстояние, на которое фокус удален от ближайшей вершины гиперболы, обозначается ({displaystyle r_{p}}r_{p}).

Перечисленные характеристики гиперболы взаимосвязаны. Справедливы следующие соотношения:

({displaystyle c^{2}=a^{2}+b^{2}}{displaystyle c^{2}=a^{2}+b^{2}})
({displaystyle varepsilon =c/a}{displaystyle varepsilon =c/a})
({displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)}{displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)})
({displaystyle r_{p}=aleft(varepsilon -1right)}{displaystyle r_{p}=aleft(varepsilon -1right)})
({displaystyle a={frac {p}{varepsilon ^{2}-1}}}{displaystyle a={frac {p}{varepsilon ^{2}-1}}})
({displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}}{displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}})
({displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}}{displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}})
({displaystyle p={frac {b^{2}}{a}}}p={frac {b^{2}}{a}})

Определение 13

Оси симметрии гиперболы представляют собой оси канонической системы координат, а начало канонической системы является центром симметрии.

Когда требуется исследовать форму гиперболы, следует начать с поиска ее пересечения с произвольной прямой, пересекающей начало координат. Уравнение прямой можно задать в виде:

(y=kx)

Такой выбор связан с тем, что прямая (x=0 ) не пересекает гиперболу. Абсциссы точек пересечения можно вычислить с помощью уравнения:

(frac{x^{2}}{a^{2}}-frac{k^{2}x^{2}}{b^{2}}=1)

Таким образом, при (b^{2}-a^{2}k^{2} > 0) получим:

(x=pm frac{ab}{sqrt{b^{2}-a^{2}k^{2}}})

Полученное равенство позволит рассчитать координаты точек пересечения:

((ab/v, abk/v))

((-ab/v, -abk/v))

В данном случае:

(v=(b^{2}-a^{2}k^{2})^{1/2})

Руководствуясь свойством симметрии, можно проанализировать смещение первой из точек при изменении k, как показано на рисунке.

смещение первой из точек при изменении k

Источник: univerlib.com

Числитель дроби (ab/v) является постоянной величиной, а знаменатель характеризуется максимальным значением, если (k=0). Таким образом, самую маленькую абсциссу имеет вершина ((a, 0)). При увеличении (k ) знаменатель убывает, и x растет, стремясь к бесконечности, когда k приближается к числу (b/a).

Прямая (y=bx/a) с угловым коэффициентом (b/a) не имеет точек пересечения с гиперболой, как и прямые с большими угловыми коэффициентами. Какая-либо прямая, обладающая меньшим положительным угловым коэффициентом, пересекает гиперболу.

При сдвиге прямой от горизонтального положения по часовой стрелке, k будет уменьшаться, (k^{2}) — увеличиваться, и прямая будет иметь удаляющиеся точки пересечения с гиперболой до тех пор, пока не займет положения с угловым коэффициентом (-b/a).

К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из вышесказанного следует вывод, что гипербола имеет вид, изображенный на рисунке.

гипербола имеет вид

Источник: univerlib.com

Определение 14

Асимптоты гиперболы являются прямыми, описываемыми уравнениями (y=bx/a) и (y=-bx/a ) в канонической системе координат.

Предположим, что уравнения асимптот имеют вид:

(bx-ay=0)

(bx+ay=0)

Расстояния от точки (M(x, y)) до асимптот составят

(h_{1}=frac{|bx-ay|}{sqrt{a^{2}+b^{2}}},)( h_{2}=frac{|bx+ay|}{sqrt{a^{2}+b^{2}}})

В том случае, когда точка M расположена на гиперболе:

(b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2})

(h_{1}h_{2}=frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=frac{a^{2}b^{2}}{a^{2}+b^{2}})

Определение 15

Произведение расстояний от точки гиперболы до асимптот является постоянным и соответствует (a^{2}b^{2}/(a^{2}+b^{2})).

Из данного определения можно вывести ключевое свойство, которым обладают асимптоты гиперболы.

Определение 16

В том случае, когда точка совершает движение по гиперболе таким образом, что ее абсцисса по абсолютной величине неограниченно возрастает, расстояние от точки до одной из асимптот стремится к нулю.

В действительности получим, что хотя бы одно из расстояний (h_{1}) или (h_{2}) при этих условиях должно неограниченно увеличиваться. Если предположить, что утверждение не справедливо, то произведение не было бы постоянной величиной.

Введем такое число с, что:

(c^{2}=a^{2}+b^{2})

и (c > 0)

Определение 17

Фокусы гиперболы — точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат.

Фокусы гиперболы

Источник: univerlib.com

Отношение (varepsilon=c/a), как и для эллипса, называется эксцентриситетом. У гиперболы (varepsilon > 1).

Расстояния от произвольной точки (M(x, y)) на гиперболе до каждого из фокусов определяются абсциссой (x):

(r_{1}=|F_{1}M|=|a-varepsilon x|, r_{2}=|F_{2}M|=|a+varepsilon x|)

Расстояния от произвольной точки

Источник: univerlib.com

Следует отметить, что равенства eqref{ref11} можно представить в более подробной форме:

для правой ветви гиперболы ((x geq a): r_{1}=varepsilon x-a), ( r_{2}=varepsilon x+a);
для левой ветви гиперболы ((x leq -a): r_{1}= a-varepsilon x), ( r_{2}=-varepsilon x-a).

Таким образом, для правой ветви (r_{2}-r_{1}=2a), а для левой ветви (r_{1}-r_{2}=2a). В обоих случаях:

(|r_{2}-r_{1}|=2a)

Определение 18

Директрисы гиперболы — прямые, заданные в канонической системе координат уравнениями: (x=frac{a}{varepsilon}), ( x=-frac{a}{varepsilon}).

Директрисы расположены поблизости от центра в отличие от вершин. Из этого можно сделать вывод, что директрисы не имеют точек пересечения с гиперболой. Директриса и фокус, которые расположены по одну сторону от центра, считаются соответствующими друг другу.

Определение 19

Для того чтобы точка (M) была расположена на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы 2a.

С целью доказательства достаточности данного условия его следует записать в виде:

(sqrt{(x-c)^{2}+y^{2}}=pm 2a+sqrt{(x+c)^{2}+y^{2}})

Следующие действия отличаются от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством:

(c^{2}=a^{2}+b^{2}), а не (c^{2}=a^{2}-b^{2})

Определение 20

Для того чтобы точка была расположена на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету (varepsilon).

равнялось эксцентриситету

Источник: univerlib.com

Можно доказать, к примеру, необходимость условия для фокуса (F_{2}(-c, 0).) Предположим, что (M'(x, y)) является точкой гиперболы. Расстояние от (M’) до директрисы с уравнением (x=-a/varepsilon) равно:

(d’=left|x+frac{a}{varepsilon}right|=frac{1}{varepsilon}|varepsilon x+a|)

Таким образом:

(r’/d’=varepsilon).

Уравнение касательной к гиперболе в точке (M_{0}(x_{0}, y_{0})), которая принадлежит данной гиперболе, можно записать так же, как подобное уравнение в случае эллипса. Уравнение касательной к гиперболе:

(frac{xx_{0}}{a^{2}}-frac{yy_{0}}{b^{2}}=1)

Определение 21

Касательная к гиперболе в точке (M_{0}(x_{0}, y_{0})) представляет собой биссектрису угла между отрезками, которые соединяют рассматриваемую точку с фокусами.

Как построить гиперболу самостоятельно

Построение графика гиперболы следует начать с изображения прямоугольной системы координат Декарта. Алгоритм действий:

На листе бумаги нарисовать горизонтальную прямую. Выполнить действие следует таким образом, чтобы конец прямой с правой стороны был обозначен с помощью стрелки. Данная прямая является осью (X) и носит название абсциссы.
На середине оси ( Х) необходимо опустить перпендикуляр. Конец полученной прямой в верхней части нужно обозначить стрелкой. В результате получена ось (Y), которую называют ординатой.
На следующем шаге необходимо пронумеровать шкалу. С правой стороны на оси (Х) расположены положительные значения (Х) в порядке возрастания — от 1 и выше. С левой стороны — отрицательные. В верхней части на оси (Y) расположены положительные значения (Y) в порядке возрастания. В нижней части — отрицательные.

Примечание

Точка, в которой пересекаются абсцисса и ордината является началом координат, то есть числом 0. От данной точки следует откладывать все значения (Х) и (Y).

С помощью прямоугольной системы координат плоскость поделена на четыре части, которые называют четвертями и нумеруют против часовой стрелки. Для того чтобы построить график, требуется определить точки. Каждая точка координатной плоскости определяется парой чисел ((x;y)). Данные числа представляют собой координаты точки, где:

(х) — абсцисса точки;
(y) — ордината.

Гипербола представляет собой график функции, которая задана формулой:

(y=k/x)

где (k) — является каким-то коэффициентом, не равным нулю;

(x) — представляет собой независимую переменную.

Гипербола включает в себя две части, расположенные симметрично в разных четвертях. Данные части носят название ветвей гиперболы. При (k>0), ветви расположены в 1 и 3 четвертях. При (k<0), ветви гиперболы размещены во 2 и 4 четвертях.

Принцип построения гиперболы можно рассмотреть на примере, когда функция задана следующей формулой:

(y=3/х)

Так как коэффициент 3 обладает положительным значением, гипербола, соответственно, будет находиться в 1 и 3 четвертях. Можно взять произвольно значения (Х) и найти значения (Y). Таким образом, получатся координаты точек, с помощью которых можно изобразить гиперболу. Важно отметить, что (Х) не должно иметь нулевое значение, так как на 0 делить нельзя.

Поскольку мы знаем, что гипербола располагается в двух четвертях, то берем как положительные значения, так и отрицательные. Предположим, что (Х) равен: -6, -3, -1, 1, 3, 6. Далее можно рассчитать ординаты путем подстановки каждого значение (Х) в начальную формулу:

(y=3/-6)

(у=3/-3)

(у=3/-1)

(у=3/1)

(у=3/3)

(у=3/6)

В результате, значения ( Y) равны: -0.5, -1, -3, 3, 1, 0.5.

Полученные 6 точек с координатами необходимо отложить на системе координат. Далее точки соединяют с помощью кривых линий, как изображено на рисунке. В итоге получилась гипербола.

получилась гипербола

Источник: sovetclub.ru

Построение гиперболы по фокусам

Гиперболу можно построить, зная заданные вершины (А) и (В) и фокусное расстояние (FF1). Алгоритм построения следующий:

В первую очередь фокусное расстояние следует разделить пополам, чтобы получить точку 0.
Далее с левой стороны от фокуса (F) можно отметить ряд произвольных точек 1, 2, 3, 4 и так далее, расстояние между которыми постепенно увеличивается.
Затем нужно начертить вспомогательные окружности с центром в фокусе (F), имеющие радиусы (R1=1B), (R2=2B), (R3=3B), (R4=4B) и так далее.
На следующем этапе можно изобразить вспомогательные окружности с центром в фокусе (F1) и радиусами (r1=1A), (r2=2A), (r3=3A), (r4=4A) и так далее.
При пересечении вспомогательных окружностей определяется положение точек гиперболы. (С), (С1 )представляют собой точки, которые образованы в результате пересечения окружностей радиусов (R1) и (r1). Точки (D,D1) являются точками, в которых пересекаются окружности (R2) и (r2).
Полученные точки остается соединить с помощью плавной кривой линии, чтобы получить правую ветвь гиперболы.
Аналогичным способом следует выполнить построение левой ветви гиперболы.

FA1

FA2

FA3

FA4

FA5

FA6

FA7

FA8

FA9

FA10

Источник: graph.power.nstu.ru

Как построить гиперболу по точкам

Исходя из определения гиперболы, разница между расстояниями (r1) и (r2) для всех ее точек является постоянной величиной. Таким образом, переход от одной точки гиперболы к другой осуществляется путем увеличения или уменьшения данных характеристик. Алгоритм действий:

В первую очередь следует отложить точки (А1) и (А2). Точка ( А2) является точкой касания двух окружностей, центр одной из которых расположен в фокусе ( F1), а радиус составляет F1A2. Другая окружность обладает центром в фокусе (F2) и радиусом (F2A2).
Следующие точки гиперболы можно определить при пересечении пар окружностей с радиусами, которые равны:

пересечении пар окружностей

Источник: natalibrilenova.ru.

Пересечении пар окружностей с

Источник: natalibrilenova.ru.

Таким образом, новые значения радиусов превышают предыдущие на одинаковую величину. Чем ближе расположены точки, тем точнее будет построен график гиперболы.

Как построить график гиперболы по уравнению

Каноническое уравнение гиперболы записывают таким образом:

Каноническое уравнение гиперболы

Источник: mathter.pro

где («a») и («b») являются положительными действительными числами, причем, («а») может быть больше или меньше, чем («b»).

Важно отметить, что гипербола обладает двумя симметричными ветвями и двумя асимптотами.

Построение гиперболы можно рассмотреть на примере. Предположим, что она задана следующим уравнением:

построение гиперболы

Источник: mathter.pro

Рассматриваемое уравнение необходимо привести к каноническому виду:

Рассматриваемое уравнение

Источник: mathter.pro

Так как в правой части требуется получить единицу, необходимо обе части начального уравнения поделить на 20:

правой части требуется получить единицу

Источник: mathter.pro

Правая

Источник: mathter.pro

Далее следует сократить обе дроби:

Далее следует сократить обе дроби

Источник: mathter.pro

следует сократить обе дроби

Источник: mathter.pro

Затем нужно выделить квадраты в знаменателях:

Затем нужно выделить квадраты в знаменателях

Источник: mathter.pro

В результате получено каноническое уравнение:

В результате получено каноническое уравнение

Источник: mathter.pro

Существует два подхода к построению гиперболы:

геометрический;
алгебраический.

С практической точки зрения, эффективнее воспользоваться расчетами. В первую очередь следует определить асимптоты:

Источник: mathter.pro

Асимптоты равны:

Источник: mathter.pro

На втором этапе можно определить вершины гиперболы, которые соответствуют точкам на оси абсцисс с координатами:

Источник: mathter.pro

При у=0, каноническое уравнение гиперболы примет вид:

Источник: mathter.pro

Таким образом:

Источник: mathter.pro

Вершины гиперболы:

Источник: mathter.pro

Затем необходимо определить дополнительные точки. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Согласно каноническому уравнению, можно выразить:

Источник: mathter.pro

В результате получим две функции. Первая функция определяет верхние дуги гиперболы:

Источник: mathter.pro

Вторая функция выражает нижние дуги гиперболы:

Источник: mathter.pro

Напрашивается нахождение точек с абсциссами:

Источник: mathter.pro

На последнем этапе следует изобразить асимптоты, вершины, дополнительные точки, симметричные точки в других координатных четвертях:

Источник: mathter.pro

После того, как все точки соединены, будет изображена гипербола.

После того, как все точки соединены, будет изображена гипербола

Источник: mathter.pro

Источник

Гипербола: определение, свойства, построение

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек F_1 и F_2 есть величина постоянная (2a) , меньшая расстояния (2c) между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.

Фокальное свойство гиперболы

Точки F_1 и F_2 называются фокусами гиперболы, расстояние 2c=F_1F_2 между ними — фокусным расстоянием, середина отрезка F_1F_2 — центром гиперболы, число — длиной действительной оси гиперболы (соответственно, — действительной полуосью гиперболы). Отрезки F_1M и F_2M , соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение $e=frac{c}{a}$ , где $c=sqrt{a^2+b^2}$ , называется эксцентриситетом гиперболы. Из определения (2a<2c) следует, что e>1 .

Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1.$

(3.50)

Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F_1 к точке F_2 ); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Гипербола и фокальное свойство гипербол

Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов F_1(-c,0) и F_2(c,0) . Для произвольной точки M(x,y) , принадлежащей гиперболе, имеем:

$left||overrightarrow{F_1M}|-|overrightarrow{F_2M}|right|=2a.$

Записывая это уравнение в координатной форме, получаем:

$sqrt{(x+c)^2+y^2}-sqrt{(x-c)^2+y^2}=pm2a.$

Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1,,$

где $b=sqrt{c^2-a^2}$ , т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии $a^2!!not{phantom{|}},c$ от нее (рис.3.41,а). При a=0 , когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.

Гиперболу с эксцентриситетом e=1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство гиперболы). Здесь и — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

Директрисы гиперболы и директориальное свойство

В самом деле, например, для фокуса F_2 и директрисы d_2 (рис.3.41,а) условие $frac{r_2}{rho_2}=e$ можно записать в координатной форме:

$sqrt{(x-c)^2+y^2}=eleft(x-frac{a^2}{c}right)$

Избавляясь от иррациональности и заменяя $e=frac{c}{a},~c^2-a^2=b^2$ , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса F_1 и директрисы d_1 :

$frac{r_1}{rho_1}=e quad Leftrightarrow quad sqrt{(x+c)^2+y^2}= eleft(x+frac{a^2}{c} right).$

Уравнение гиперболы в полярной системе координат

Уравнение правой ветви гиперболы в полярной системе координат F_2rvarphi (рис.3.41,б) имеет вид

$r=frac{p}{1-ecdotcosvarphi}$ , где $p=frac{p^2}{a}$ — фокальный параметр гиперболы.

В самом деле, выберем в качестве полюса полярной системы координат правый фокус F_2 гиперболы, а в качестве полярной оси — луч с началом в точке F_2 , принадлежащий прямой F_1F_2 , но не содержащий точки F_1 (рис.3.41,б). Тогда для произвольной точки M(r,varphi) , принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем F_1M-r=2a . Выражаем расстояние между точками M(r,varphi) и F_1(2c,pi) (см. пункт 2 замечаний 2.8):

$F_1M=sqrt{(2c)^2+r^2-2cdot(2c)^2cdot rcdotcos(varphi-pi)}=sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}.$

Следовательно, в координатной форме уравнение гиперболы имеет вид

$sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}-r=2a.$

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

$r^2+4crcdotcosvarphi+4c^2=4a^2+4ar+r^2 quad Leftrightarrow quad aleft(1-frac{c}{a}cosvarphiright)r=c^2-a^2.$

Выражаем полярный радиус и делаем замены $e=frac{c}{a},~b^2=c^2-a^2,~p=frac{b^2}{a}$ :

$r=frac{c^2-a^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{b^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{p}{1-ecosvarphi},$

что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( e>1 для гиперболы, 0leqslant e<1 для эллипса).

Геометрический смысл коэффициентов в уравнении гиперболы

Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение y=0 , находим абсциссы точек пересечения: x=pm a . Следовательно, вершины имеют координаты (-a,0),,(a,0) . Длина отрезка, соединяющего вершины, равна . Этот отрезок называется действительной осью гиперболы, а число — действительной полуосью гиперболы. Подставляя x=0 , получаем y=pm ib . Длина отрезка оси ординат, соединяющего точки (0,-b),,(0,b) , равна . Этот отрезок называется мнимой осью гиперболы, а число — мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.

Замечания 3.10.

1. Прямые x=pm a,~y=pm b ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).

2. Прямые $y=pmfrac{b}{a},x$ , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).

Для равносторонней гиперболы, описываемой уравнением $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ (т.е. при a=b ), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат Ox'y' (рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид $y'=frac{a^2}{2x'}$ (гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).

Асимптоты гиперболы и равносторонняя гипербола

В самом деле, повернем каноническую систему координат на угол $varphi=-frac{pi}{4}$ (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами

$left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y',\ y&=-frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y'end{aligned}right. quad Leftrightarrow quad left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot(x'+y'),\ y&=frac{sqrt{2}}{2}cdot(y'-x')end{aligned}right.$

Подставляя эти выражения в уравнение $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ равносторонней гиперболы и приводя подобные члены, получаем

$frac{frac{1}{2}(x'+y')^2}{a^2}-frac{frac{1}{2}(y'-x')^2}{a^2}=1 quad Leftrightarrow quad 2cdot x'cdot y'=a^2 quad Leftrightarrow quad y'=frac{a^2}{2cdot x'}.$

3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.

Действительно, если точка M(x,y) принадлежит гиперболе $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ . то и точки M'(x,y) и M''(-x,y) , симметричные точке относительно координатных осей, также принадлежат той же гиперболе.

Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.

4. Из уравнения гиперболы в полярных координатах $r=frac{p}{1-ecosvarphi}$ (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси ( r=p при $varphi=frac{pi}{2}$ ).

5. Эксцентриситет характеризует форму гиперболы. Чем больше , тем шире ветви гиперболы, а чем ближе к единице, тем ветви гиперболы уже (рис.3.43,а).

Действительно, величина gamma угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника: $operatorname{tg}frac{gamma}{2}=frac{b}{2}$ . Учитывая, что $e=frac{c}{a}$ и c^2=a^2+b^2 , получаем

$e^2=frac{c^2}{a^2}=frac{a^2+b^2}{a^2}=1+{left(frac{b}{a}right)!}^2=1+operatorname{tg}^2frac{gamma}{2}.$

Чем больше , тем больше угол gamma . Для равносторонней гиперболы (a=b) имеем e=sqrt{2} и $gamma=frac{pi}{2}$ . Для e>sqrt{2} угол gamma тупой, а для 1<e<sqrt{2} угол gamma острый (рис.3.43,а).

Эксцентриситет гиперболы и сопряжённая гипербола

6. Две гиперболы, определяемые в одной и той же системе координат уравнениями $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ и $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ приводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение $frac{(x-x_0)^2}{a^2}-frac{(y-y_0)^2}{b^2}=1$ определяет гиперболу с центром в точке O'(x_0,y_0) , оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение $-frac{(x-x_0)^2}{a^2}+frac{(y-y_0)^2}{b^2}=1$ определяет сопряженную гиперболу с центром в точке O'(x_0,y_0) .

Параметрическое уравнение гиперболы

Параметрическое уравнение гиперболы в канонической системе координат имеет вид

$begin{cases}x=acdotoperatorname{ch}t,\y=bcdotoperatorname{sh}t,end{cases}tinmathbb{R},$

где $operatorname{ch}t=frac{e^t+e^{-t}}{2}$ — гиперболический косинус, a $operatorname{sh}t=frac{e^t-e^{-t}}{2}$ гиперболический синус.

Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству $operatorname{ch}^2t-operatorname{sh}^2t=1$ .

Построение гиперболы в канонической системе координат

Пример 3.21. Изобразить гиперболу $frac{x^2}{2^2}-frac{y^2}{3^2}=1$ в канонической системе координат Oxy . Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: a=2 — действительная полуось, b=3 — мнимая полуось гиперболы. Строим основной прямоугольник со сторонами 2a=4,~2b=6 с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя x=4 в уравнение гиперболы, получаем

$frac{4^2}{2^2}-frac{y^2}{3^2}=1 quad Leftrightarrow quad y^2=27 quad Leftrightarrow quad y=pm3sqrt{3}.$

Следовательно, точки с координатами (4;3sqrt{3}) и (4;-3sqrt{3}) принадлежат гиперболе. Вычисляем фокусное расстояние

$2cdot c=2cdotsqrt{a^2+b^2}=2cdotsqrt{2^2+3^2}=2sqrt{13}$

эксцентриситет $e=frac{c}{a}=frac{sqrt{13}}{2}$ ; фокальныи параметр $p=frac{b^2}{a}=frac{3^2}{2}=4,!5$ . Составляем уравнения асимптот $y=pmfrac{b}{a},x$ , то есть $y=pmfrac{3}{2},x$ , и уравнения директрис: $x=pmfrac{a^2}{c}=frac{4}{sqrt{13}}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

3.4.1. Каноническое уравнение и построение гиперболы

Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение.

Каноническое уравнение гиперболы имеет вид , где – положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие , то

есть, значение «а» может быть и меньше, чем «бэ».
Надо сказать, довольно неожиданно… – уравнение «школьной» гиперболы и

близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока раскинем на экране своего воображения график функции …. Какие мысли?

У гиперболы две симметричные ветви.

У гиперболы две асимптоты.

Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас вы с неподдельным восхищением заглянем в декольте этой линии:

Задача 99

Построить гиперболу, заданную уравнением

Решение: на первом шаге приведём данное уравнение к каноническому виду . Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому

обе части исходного уравнения делим на 20:

Здесь можно сократить обе дроби, но технически грамотнее сделать каждую из них трёхэтажной (см. Приложение Школьные

материалы):

и только после этого провести сокращение:

Выделяем квадраты в знаменателях:

Готово.

Почему преобразования лучше проводить именно так? Ведь дроби левой части можно сразу сократить и получить .

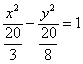
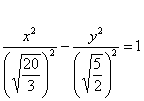
Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае получится что-нибудь вроде и без 3-го этажа не обойтись: .

Воспользуемся плодом наших трудов – каноническим уравнением :

Как построить гиперболу?

Существует два подхода к построению гиперболы – геометрический и алгебраический. С практической точки зрения вычерчивание с помощью циркуля я бы

даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты.

Целесообразно придерживаться следующего алгоритма (читайте и смотрите на чертёж ниже):

1) Сначала находим асимптоты. Если гипербола задана каноническим уравнением , то её асимптотами являются прямые . В нашем случае: . Данный пункт

обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.

2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках . Выводится элементарно: если , то каноническое уравнение превращается в , откуда и следует,

что . Наша гипербола имеет вершины

3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала

координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения на черновике выражаем:

и уравнение распадается на две функции:
– определяет верхние дуги гиперболы (то, что нам надо);
– определяет нижние дуги гиперболы.

Напрашивается нахождение точек с абсциссами :

4) Изобразим асимптоты , вершины , дополнительные и

симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:
Техническая трудность может возникнуть с иррациональным угловым коэффициентом , но это вполне преодолимая проблема.

Отрезок называют действительной осью гиперболы;

Число называют действительной полуосью гиперболы;

число – мнимой полуосью.

В нашем случае: , , и, очевидно, если гиперболу повернуть вокруг центра симметрии и / или переместить, то эти значения не

изменятся.

3.4.2. Определение гиперболы

3.3.4. Поворот и параллельный перенос эллипса

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Елена Борисовна Калюжная

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Каноническое уравнение гиперболы имеет следующий вид:
$frac{x^2}{a^2} — frac{y^2}{b^2} = 1$, где $a, b$ — положительные действительные числа.

Для того чтобы составить каноническое уравнение гиперболы, нужно привести квадратное уравнение к каноническому виду.

Вывод канонического уравнения гиперболы

уравнения гиперболы» />

Рисунок 1. Рис. 1.Вывод канонического уравнения гиперболы

Рассмотрим гиперболу с фокусами $F_1$ и $F_2$, находящимися на оси $OX$, причём точка $O$ лежит в центе между фокусами.

Следовательно координаты $F_1(-c; 0)$, а $F_2(c; 0)$, где $c$ — расстояние до фокуса гиперболы.

Рассмотрим произвольную точку $M$, принадлежащую гиперболе.

Отрезки $r_1 =|F_1M|$ и $r_2 =|F_2M|$ называются фокальными радиусами точки $M$ гиперболы.

Из определения гиперболы следует, что $|r_1 -r_2| =2a$, следовательно $r_1 – r_2=±2a$, причём $r_1 = sqrt{(x + c)^2 + y^2}$, а $r_2 = sqrt{(x — c)^2 + y^2}$.

Соответственно, уравнение $r_1 – r_2=±2a$ иначе можно записать как $sqrt{(x + c)^2 + y^2} — sqrt{(x — c)^2 + y^2} = ±2a$ (1).

Умножим выражение (1) на $frac{$sqrt{(x + c)^2 + y^2} + sqrt{(x — c)^2 + y^2}}{±2a}$, получается:, получается:

$frac{(x + c)^2 + y^2 — (x — c)^2 – y^2}{±2a} = sqrt{(x + c)^2 + y^2} + sqrt{(x — c)^2 + y^2}$

Упростим: $frac{2cx}{±a} = sqrt{(x + c)^2 + y^2} + sqrt{(x — c)^2 + y^2}$ (2)

Сложим уравнения (1) и (2), получим:

$±(frac{cx}{a}) + a = sqrt{(x + c)^2 + y^2}$ (3)

Возведём (3) в квадрат:

$frac{c^2 x^2}{a^2} + 2xc + a^2 = (x^2 +2x c + c^2 + y^2)$

$frac{c^2 – a^2}{a^2} cdot x^2 – y^2 = c^2 – a^2$

Пусть $b^2 = c^2 – a^2$, так как $c > 0$ и, следовательно $frac{b^2}{a^2}x^2 – y^2 = b^2$

«Каноническое уравнение гиперболы» 👇

Получаем уравнение:
$frac{x^2}{a^2} — frac{y^2}{b^2} = 1$ (4), являющееся каноническим уравнением гиперболы с центром в начале координат.

Каноническое уравнение параболы и гиперболы немного похожи между собой.

Уравнение параболы выглядит следующим образом:

$y^2 = px$, где число $p$ должно быть больше нуля; это число называется фокальным параметром.

Каноническое уравнение гиперболы примеры решения

Пример 1

Ниже небольшая инструкция о том, как найти каноническое уравнение гиперболы.

Приведём уравнение $5x^2 — 4y^2 = 20$ к каноническому виду гиперболического уравнения, для этого разделим всё уравнение на $20$:

$frac{5x^2}{4} — frac{y^2}{5} = 1$

Запишем знаменатели в виде степеней:

$frac{x^2}{2^2} — frac{y^2}{sqrt{5}^2} = 1$

Теперь вы знаете, как написать каноническое уравнение гиперболы. Дальше мы расскажем о том, как строить гиперболу по каноническому уравнению.

Построение гиперболы по каноническому уравнению

Теперь давайте рассмотрим, как построить гиперболу по каноническому уравнению.

Рисунок 2. Рис. 2. Построение гиперболы по каноническому уравнению

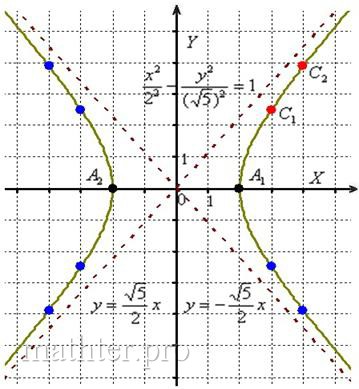
Для начала необходимо построить асимптоты для данной гиперболы, их формулы определяются из уравнения $y = ±frac{bcdot x}{a}$.
Для нашего канонического уравнения гиперболы они будут выглядеть так: $y = ±frac{sqrt{5}} {2}cdot x$
Теперь найдём вершины гиперболы, они расположены на оси абсисс в точках $(0; a)$ и $(0; -a)$, назовём их точками $A_1, A_2$.
Вершины нашей гиперболы находятся в точках $(2; 0)$ и $(-2; 0)$.

Далее необходимо найти две-три точки, принадлежащие любой из двух ветвей гиперболы, если гипербола без смещения – точки на второй ветви будут симметричны им относительно осей гиперболы.
Выразим $y$ из канонического уравнения нашей гиперболы:

$y = ±frac{1}{2} sqrt{5 x^2 — 4}$

Найдём точки для положительной части гиперболы:

при $x = 3, y =2.5$,
а при $x = 3, y ≈3,87$.

Теперь можно отложить все эти точки и построить график гиперболы.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник