Как найти центр масс четырехугольника

Четырехугольник

Мнемоника

Окружность вписанная в четырехугольник

Почему нельзя вписать окружность?

Задача

Окружность, описанная около четырехугольника

Задача 1

Задача 2

Задача 3

Центр тяжести

Распределительное свойство центров тяжести

Если разделить систему материальных точек S на дне части S’ и S«, то ее центр тяжести есть в то же время центр тяжести двух масс М’ и М» систем S’ и S«, помещенных соответственно в центрах тяжести этих двух систем.

Центр тяжести четырехугольника

(1)

(2)

Метод отвеса

Метод балансировки

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

С помощью геометрического разложения

Центр тяжести объекта в форме буквы L

Барицентр

Барицентрическая система отсчета

Барицентрические координаты

Случай двух тел

Центр тяжести четырехугольника. Выпуклого

Недавно внук,- он в восьмом классе,- выполнял задание по приблизительному определению центра тяжести четырехугольника, вырезанного из картона. Делать это очень просто: снизу картонки водится гвоздь и когда достигается равновесие (на острие гвоздя), то это и будет нужная точка.

Все это верно, конечно, но мне захотелось вместе с Андрюшей математически точно определить данный центр. И сопоставить с физическим опытом.

Вообще-то задача эта хорошо известна. Нужно начертить два диаметра фигуры, найти для четырех треугольников точки пересечения медиан и пары этих точек соединить. Точка пересечения двух прямых будет центром тяжести.

Но геометрическое решение тут довольно громоздкое. Придется столько дуг окружностей чертить, столько линий, что в результате будем иметь рыболовную сетку. Хотелось бы найти самое простое построение. И аналитику, конечно. Чтобы на компе быстро вычислять центр для самых разных вариантов выпуклых четырехугольников.

Эту математическую задачу мы запустили на лучшем форуме для студентов и школьников. Ответы были самые неожиданные. Одно решение предлагалось даже векторное! Между прочим, очень уж красивое. Может, когда-нибудь им и займемся, но в данный момент цель наша была — найти чисто школьный вариант. То есть цепочку формул, дающую в конце координаты центра.

Да, забыл сказать, что решили математическую модель строить через координаты вершин фигуры. Например, такие:

На форуме очень нам помог лучший в области геометрии специалист с ником Li6-D. Мы с Андрюшей чуточку его решение изменили и получили такую простоту, что сами удивились!
Глядим на рисунок. Имеем четырехугольник ABCD. Чертим две диагонали AC и BD. Точки K и P (с чертой наверху) — это середины диагоналей. Циркулем отмеряем отрезок BM и откладываем его на другом конце той же диагонали (отрезок DL). Точно так же отрезок AM дает на другом конце CT. Определенным образом соединяем пары точек TK и PL, как показано на рисунке и находим пересечением прямых точку S. Она и есть центр тяжести данного четырехугольника! Строить такое циркулем и линейкой — сплошное удовольствие!

Мы сопоставили аналитику с физикой и расхождение оказалось четыре миллиметра. Причина ясна: абсолютно ровно картон не разрезать. Особенно школьнику. Да и нужно понимать, что любая картонка не идеальна по толщине и плотности. Так что верить нужно формулам, а не гвоздику.

На скорую руку мы составили программу расчета на Yabasic. Двумя методами воспользовались. Первый нашли в инете — он самый легкий в плане аналитики. Второй — как раз о котором мы рассказ ведем. Вот текст:

xA=0:yA=0
xB=4:yB=5
xC=7:yC=7
xD=8:yD=0
S1=1/2*abs((xB-xA)*(yC-yA)-(xC-yA)*(yB-yA))
S2=1/2*abs((xC-xA)*(yD-yA)-(xD-yA)*(yC-yA))
xm1=(xA+xB+xC)/3:ym1=(yA+yB+yC)/3
xm2=(xA+xC+xD)/3:ym2=(yA+yC+yD)/3
x1=(S1*xm1+S2*xm2)/(S1+S2):y1=(S1*ym1+S2*ym2)/(S1+S2)
print «1) «;
print x1,y1
y0=(yA-yC)/(xA-xC)*(x0-xA)+yA
A0=sqrt((xA-x0)^2+(yA-y0)^2)
B0=sqrt((xB-x0)^2+(yB-y0)^2)
xL=xD-(x0-xB):yL=yD-(y0-yB)
xT=xC-(x0-xA):yT=yC-(y0-yA)
xK=(xB+xD)/2:yK=(yB+yD)/2
xP=(xA+xC)/2:yP=(yA+yC)/2
y2=(yK-yT)/(xK-xT)*(x1-xK)+yK
print «2) «;
print x2,y2

Оба метода дали точку (4.85185, 2.51852).

24 ноября 2020 г.

PS. Вчера исполнилось три года со дня рождения двух моих маленьких внучат: Никите и Илье.

Как можно найти центроид четырёх точек ( Quadrilateral ), зная координаты этих вершин?

Вот тут хорошо расписано.

Сначала надо триангулировать четырехугольник. Потом, центр масс каждого треугольника — среднее арифметическое координат. Далее, остается найти центр масс двух точек — центров масс треугольников, где в каждой точке лежит масса равная площади треугольника.

Чтобы это работало и с невыпуклыми многоугольниками надо считать площадь треугольников через векторное произведение сторон, разрешая таким образом отрицательные площади у треугольников снаружи вашей фигуры.

Итоговая фромула (в векторах):

Тут pi — i-ая вершина четырехугольника, pipj — вектор между точками i и j. pipj*pkpl — векторное произведение двух векторов.

Love Soft

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

Четырехугольник

Мнемоника

для запоминания условий, для того чтобы можно было вписать или описать окружность в четырехугольнике, у меня в опорном конспекте (и отложилось, фактически само по себе, в голове): две картинки: дорожный знак «кирпич», на котором написано 180. И вторая картинка, это инопланетянин в квадратном шлеме с плюсами вместо ушей. Ну и чем более абсурдный образ, тем лучше. Я никогда не перепутаю эти условия потому что, например, знак «кирпич» — окружность снаружи, а надпись 180 – означает суму противоположных углов.

Окружность вписанная в четырехугольник

Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.

Наоборот: если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.

Центр вписанной окружности лежит на пересечении биссектрис углов четырехугольника.

Почему нельзя вписать окружность?

в отличие от треугольника, далеко не во всякий четырехугольник можно поместить окружность так, чтобы она касалась всех его сторон.

Треугольник всегда является описанным – потому что во всякий треугольник можно вписать окружность. Чем же четырехугольник-то хуже? И вот оказывается, что чем-то, да хуже.

Представь себе, например, длинный прямоугольник. Как вот в него, спрашивается, можно вписать окружность? Конечно, никак. И это лишь один из примеров четырехугольника, в которой НЕЛЬЗЯ вписать окружность.

Задача

Окружность, описанная около четырехугольника

Если около выпуклого четырехугольника описана окружность, то сумма его противоположных углов равна ∠ϕ+∠γ=180∘.

И наоборот: Если сумма двух противоположных углов выпуклого четырехугольника равна ∠ϕ+∠γ=180∘, то около него можно описать окружность.

Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам.

Около выпуклого четырехугольника описана окружность ⇔ ∠α=∠β.

Площадь вписанного четырехугольника вычисляется по формуле

где a, b, c, d – его стороны, p — полупериметр

Задача 1

Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Задача 2

Стороны AB, BC, CD, AD четырехугольника ABCD стягивают дуги описанной окружности, градусные меры которых равны соответственно 95 ∘ ,49 ∘ ,71 ∘ ,145 ∘ . Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Угол B четырехугольника равен вписанному углу ABC. Этот угол опирается на дугу ADC, равную 145 ∘ +71 ∘ =216 ∘ . Так как вписанный угол равен половине дуги, на которую он опирается, то ∠B=∠ABC=108 ∘ .

Задача 3

Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB,BC,CD,DA, градусные величины которых относятся соответственно как 4:2:3:6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.

Так как дуги AB,BC,CD,DA относятся как 4:2:3:6, то можно принять дугу AB за 4x, дугу BC за 2x, дугу CD за 3x и дугу DA за 6x. Так как все эти дуги в совокупности дают целую окружность, градусная мера которой равна 360∘, то 4x+2x+3x+6x=360∘, откуда x=24∘. Угол A равен вписанному углу BAD, опирающемуся на дугу BCD, равную 2x+3x=5x=120∘. Так как вписанный угол равен половине этой дуги, то ∠A=60∘.

Центр тяжести

Центр тяжести системы материальных точек — обозначим через $m_k$ — массы точек, $x_k, y_k, z_k$ — координаты точек.

К каждой из точек приложен вектор величины $m_k$, все векторы параллельны и направлены в одну сторону.

Центр этих векторов есть точка с координатами $$M_x = sum m_k x_k, M_y = sum m_k y_k, M_z = sum m_k z_k$$

Если все точки имеют одинаковую массу, то $M = sum m_k$ — масса всей системы, тогда

$$M_x = M sum x_k, M_y = M sum y_k, M_z = M sum z_k$$

В математике и физике барицентр или геометрический центр области — это среднее арифметическое положений всех точек фигуры.

Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.

Центр масс (и центр тяжести в постоянном гравитационном поле) является средним арифметическим всех точек с учётом локальной плотности или удельного веса. Если физический объект имеет постоянную плотность, то его центр масс совпадает с барицентром фигуры той же формы.

Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.

Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильный многоугольник, правильный многогранник, цилиндр, прямоугольник, ромб, окружность, сфера, эллипс, эллипсоид, суперэллипс, суперэллипсоид, и т.д.) можно найти исходя исключительно из этого принципа.

В частности, барицентром параллелограмма является пересечение диагоналей. Вообще говоря, это неверно для других четырёхугольников.

Распределительное свойство центров тяжести

Если разделить систему материальных точек S на дне части S’ и S«, то ее центр тяжести есть в то же время центр тяжести двух масс М’ и М» систем S’ и S«, помещенных соответственно в центрах тяжести этих двух систем.

Центр тяжести четырехугольника

Центр тяжести площади четырехугольника определяется пересечением двух прямых, которые мы получаем, используя распределительное свойство центров тяжести.

Сначала делим четырехугольник диагональю на два треугольника. Центр тяжести четырехугольника лежит на прямой, соединяющей центры тяжести этих треугольников. Это первая искомая прямая.

Вторая искомая прямая получается аналогичным образом — разбивая четырехугольник на треугольники второй диагональю.

Центроид (барицентр или центр масс) произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника и отрезка, соединяющего середины диагоналей, и делит все три отрезка пополам.

Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершины.

Метод отвеса

Барицентр однородной плоской фигуры, такой как на рисунке ниже, можно найти экспериментально с использованием отвеса и булавки. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке. Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр.

Метод балансировки

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

С помощью геометрического разложения

Барицентр плоской фигуры можно вычислить, разделив её на конечное число более простых фигур.

Рассмотрим пример. Фигуру на рисунке легко разделить на квадрат и треугольник с положительным знаком площади и круглое отверстие с отрицательным знаком площади.

Квадрат — пересечение диагоналей $(5, 5)$. Площадь 100.

Прямоугольный треугольник — отложить по трети катета от вершины прямого угла $(10+10/3,10/3) = (13.33; 3.33)$. Площадь 50.

Окружность — центр $(2.5; 12.5)$. Площадь $6.25pi = 19.63$

Та же формула применима для любого трёхмерного объекта, только вместо площадей берут объёмы частей тела.

Центр тяжести объекта в форме буквы L

Делим на два прямоугольника, находим центры каждого из них как пересечение диагоналей, соединяем. Барицентр фигуры должен лежать на этом отрезке AB.

Делим фигуру на два прямоугольника другим способом. Находим барицентры этих двух прямоугольников. Проводим отрезок, соединяющий центры. Барицентр фигуры должен лежать на этом отрезке CD.

Барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.

Барицентр

это цетр масс двух и более тел, которые вращаются друг около друга.

Чем массивнее одно из двух тел, тем ближе к нему барицентр. Для системы Луна-Земля барицентр расположен примерно на расстоянии 4 671 км от центра Земли, радиус планеты 6 378 км.

Барицентрическая система отсчета

International Celestial Reference System (ICRS, Международная небесная система координат или Международная система астрономических координат) — с 1998 года стандартная небесная система координат.

Началом отсчёта является барицентр Солнечной системы. Координаты в этой системе максимально приближены к экваториальным эпохи J2000.0 (расхождение составляет доли секунды дуги)

Оси системы зафиксированы в пространстве относительно квазаров, которые считаются наиболее удалёнными объектами наблюдаемой Вселенной. Их предполагаемое собственное движение настолько мало, что им можно пренебречь. Внедрение системы обусловлено необходимостью повышения точности астрономических измерений до 0,05″.

Полученная система координат независима от вращения Земли.

Барицентрические координаты

Пусть дан треугольник ABC. Тогда любую точку P в плоскости треугольника можно представить как центр некоторых масс α, β, γ, помещенных в его вершины A, B, C.

Тройка чисел (α, β, γ) называется барицентрическими координатами точки P относительно треугольника.

Барицентрические координаты точки определены с точностью до ненулевого множителя: все тройки (kα, kβ, kγ) при любом k ≠ 0 задают одну и ту же точку P. Любые три числа с ненулевой суммой являются барицентрическими координатами некоторой точки. Иногда барицентрическими координатами называют ту из пропорциональных троек, у которой сумма чисел равна единице. Соответствие между такими тройками и точками плоскости взаимно-однозначно.

Если точка P лежит внутри треугольника ABC, то ее барицентрические координаты пропорциональны площадям треугольников PAB, PBC и PCA. Для точек вне треугольника это тоже верно, только нужно брать ориентированные площади.

Случай двух тел

Два тела взаимодействуют только друг с другом. Тела вращаются поэллиптической орбите пример двойные звезды.

Вот тут хорошо расписано.

Сначала надо триангулировать четырехугольник. Потом, центр масс каждого треугольника — среднее арифметическое координат. Далее, остается найти центр масс двух точек — центров масс треугольников, где в каждой точке лежит масса равная площади треугольника.

Чтобы это работало и с невыпуклыми многоугольниками надо считать площадь треугольников через векторное произведение сторон, разрешая таким образом отрицательные площади у треугольников снаружи вашей фигуры.

Итоговая фромула (в векторах):

C = ((p1+p2+p3)/3*(p1p2*p1p3)+(p3+p4+p1)/3*(p1p3*p1p4))/((p1p2*p1p3)+(p1p3*p1p4))

Тут pi — i-ая вершина четырехугольника, pipj — вектор между точками i и j. pipj*pkpl — векторное произведение двух векторов.

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как

[math]displaystyle{ vec{r}_b = V^{-1}int_Vvec{r}dV }[/math],

где интегрирование выполняется по объёму тела. Другое название барицентра в этом значении — центроид.

Неформально, геометрический барицентр есть точка равновесия фигуры, вырезанной из картона, в предположении, что картон имеет постоянную плотность, а внешнее гравитационное поле однородно.

В физике термин «барицентр» — синоним понятия «центр масс», используемый, в основном, в задачах космической механики. Центр масс объекта является средним арифметическим всех его точек с учётом локальной плотности массы. Для физических объектов с постоянной плотностью центр масс совпадает с барицентром фигуры той же формы.

Ниже барицентр рассматривается в математическом (геометрическом) смысле, о барицентре в физике см. статью Центр масс.

Свойства

Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.

Если барицентр известен, он является фиксированной точкой группы изометрии симметрий фигуры. Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильного многоугольника, правильного многогранника, цилиндра, прямоугольника, ромба, окружности, сферы, эллипса, эллипсоида, суперэллипса, суперэллипсоида и т. д.) можно найти исходя исключительно из этого принципа.

В частности, барицентром треугольника является точка пересечения его медиан (см. рисунок). Барицентром параллелограмма является точка пересечения его диагоналей, но это неверно для других четырёхугольников.

Барицентр объекта с трансляционной симметрией не определён (или лежит вне пространства фигуры), поскольку сдвиг не имеет фиксированной точки.

Центроид треугольника

• Барицентр треугольника называется центроидом и лежит на пересечении трёх медиан, также лежит на прямой Эйлера (проходящей и через другие ключевые точки, включая ортоцентр и центр описанной окружности)^[1][2].

• Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.
  • В частности, если [math]displaystyle{ M }[/math] — центроид треугольника [math]displaystyle{ ABC }[/math] то для любой точки [math]displaystyle{ O }[/math] верно, что

    [math]displaystyle{ overrightarrow{OM}=frac13(overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}) }[/math].

• Пусть [math]displaystyle{ M }[/math] — любая точка на плоскости, на которой лежит треугольник с вершинами [math]displaystyle{ A }[/math], [math]displaystyle{ B }[/math] и [math]displaystyle{ C }[/math]; и пусть [math]displaystyle{ G }[/math] — центроид этого треугольника, тогда сумма квадратов расстояний от [math]displaystyle{ M }[/math] до трёх вершин треугольника равна сумме квадратов расстояний от центроида [math]displaystyle{ G }[/math] до вершин треугольника плюс утроенный квадрат расстояния между [math]displaystyle{ M }[/math] и [math]displaystyle{ G }[/math]:

[math]displaystyle{ MA^2+MB^2+MC^2=GA^2+GB^2+GC^2+3MG^2 }[/math]^[3].

• Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин треугольника:

[math]displaystyle{ AB^2+BC^2+CA^2=3(GA^2+GB^2+GC^2) }[/math]^[3].

• Центр масс сторон треугольника совпадает с центром вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с инцентром дополнительного треугольника, или с центром Шпикера.
• О других свойствах центроида треугольника смотрите ниже.

Минимаксные свойства центроида треугольника

• Центроид или точка пресечения медиан треугольника является единственной точкой треугольника такой, что проведенные через неё три чевианы разделяют своими концами стороны треугольника на шесть отрезков. При этом произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально^[4].
• Центроид или точка пересечения трёх медиан является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).

Центроид четырёх точек (вершин четырёхугольника)

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противополежащих сторон. Точка пересечения делит все три отрезка пополам.

Центр масс вершин четырёхугольника не обязан совпадать с центром масс самого четырёхугольника как плоской фигуры.

Определение местоположения барицентра

Определение местоположения барицентра однородной плоской фигуры методом отвеса

Барицентр однородной плоской фигуры, такой как фигура (a) на рисунке, можно найти экспериментально с использованием отвеса и булавки путём нахождения центра масс тонкой пластины однородной плотности, имеющей ту же форму. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке (b). Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр (c).

Этот метод можно распространить (в теории) на вогнутые фигуры, когда барицентр лежит вне их, а также тела (постоянной плотности), но положение линии отвеса придётся отмечать каким-то иным способом.

Определение местоположения барицентра выпуклой двумерной фигуры методом балансировки

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например, на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

Определение местоположения барицентра для конечного множества точек

Барицентр конечного множества из [math]displaystyle{ {k} }[/math] точек [math]displaystyle{ mathbf{x}_1, mathbf{x}_2, ldots, mathbf{x}_k }[/math] в [math]displaystyle{ mathbb{R}^n }[/math] находится по формуле

[math]displaystyle{ mathbf{G} = frac{ mathbf{x}_1 + mathbf{x}_2 + cdots + mathbf{x}_k }{k} }[/math]^[5].

Полученная точка [math]displaystyle{ mathbf{G} }[/math] такая, что сумма квадратов расстояний между ней и точками множества является минимальной.

Определение местоположения барицентра с помощью геометрического разложения

Барицентр плоской фигуры [math]displaystyle{ X }[/math] можно вычислить, разделив её на конечное число более простых фигур [math]displaystyle{ X_1, X_2, dots, X_n }[/math], найдя положение барицентров [math]displaystyle{ G_i }[/math] и площадей [math]displaystyle{ A_i }[/math] каждой части, а затем вычислив

[math]displaystyle{ G_x = frac{ sum G_{i_x} A_i }{ sum A_i } , G_y = frac{ sum G_{i_y} A_i }{ sum A_i } . }[/math]

Дыры в фигуре [math]displaystyle{ X }[/math], наложения частей, или части, выступающие за фигуру, можно рассматривать как фигуры с отрицательной площадью [math]displaystyle{ A_i }[/math]. А именно, знак площади [math]displaystyle{ A_i }[/math] нужно выбирать так, чтобы сумма знаков [math]displaystyle{ A_i }[/math] для всех частей, включающих точку [math]displaystyle{ p }[/math], была равна 1, если [math]displaystyle{ p }[/math] принадлежит [math]displaystyle{ X }[/math], и 0 в противном случае.

Например, фигуру (a) на рисунке легко разделить на квадрат и треугольник с положительным знаком, круглое отверстие с отрицательным (b).

Барицентр каждой части легко найти в любом списке барицентров простых фигур (c). Затем вычисляется барицентр фигуры, как средневзвешенное трёх точек. Горизонтальное положение барицентра, считая от левого края фигуры, равно

[math]displaystyle{ x = frac{ 5 times 10^2 + 13.33 times frac{1}{2} 10^2 — 3 times pi 2.5^2 }{ 10^2 + frac{1}{2} 10^2 -pi 2.5^2 } approx 8.5 . }[/math]

Вертикальное положение вычисляется аналогично.

Та же формула применима для любого трёхмерного объекта, только [math]displaystyle{ A_i }[/math] обозначают уже объёмы частей тела [math]displaystyle{ X_i }[/math], а не площади. Формула верна также для пространства [math]displaystyle{ R^d }[/math] любой размерности [math]displaystyle{ d }[/math] при замене площади [math]displaystyle{ d }[/math]-мерными мерами частей.

Определение местоположения барицентра интегрированием

Барицентр подмножества X пространства [math]displaystyle{ R^n }[/math] можно вычислить с помощью интеграла

[math]displaystyle{ G = frac{ int x g(x) ; dx }{ int g(x) ; dx } , }[/math]

где интегрирование ведётся по всему пространству [math]displaystyle{ R^n }[/math], а g является характеристической функцией подмножества, принимающей 1 внутри X и 0 вне его^[6]. Заметим, что знаменатель равен мере множества X. Формула неприменима к множеству нулевой меры, а также к множествам, для которых интеграл расходится.

Другая формула для вычисления координат барицентра:

[math]displaystyle{ G_k = frac{ int z S_k(z) ; dz }{ int S_k(z) ; dz } , }[/math]

где G_k является k-й координатой G, а S_k(z) — мера пересечения X с гиперплоскостью, определяемой уравнением x_k = z. Снова знаменатель — это мера множества X.

Для плоской фигуры координатами барицентра будут

[math]displaystyle{ G_{ mathrm x } = frac{ int x S_{ mathrm y }(x) ; dx }{A} ; }[/math]

[math]displaystyle{ G_{ mathrm y } = frac{ int y S_{ mathrm x }(y) ; dy }{A} , }[/math]

где A — площадь фигуры X, S_y(x) — длина пересечения^{[неизвестный термин]} X с вертикальной прямой с абциссой x, S_x(y) — аналогичная величина при обмене осей.

Определение местоположения барицентра для области, ограниченной графиками непрерывных функций

Координаты барицентра [math]displaystyle{ ( bar{x}, ; bar{y} ) }[/math] области, ограниченной графиками непрерывных функций [math]displaystyle{ f }[/math] и [math]displaystyle{ g }[/math], таких что [math]displaystyle{ f(x) geq g(x) }[/math] на интервале [math]displaystyle{ [a, b] }[/math], [math]displaystyle{ a leq x leq b }[/math], задаются выражениями

[math]displaystyle{ bar{x} = frac{1}{A} int_a^b x left[ f(x) — g(x) right] ; dx }[/math]^[6].

[math]displaystyle{ bar{y} = frac{1}{A} int_a^b left[ frac{ f(x) + g(x) }{2} right] left[ f(x) — g(x) right] ; dx , }[/math]^[7]

где [math]displaystyle{ A }[/math] — площадь области (вычисляемая по формуле [math]displaystyle{ int_a^b left[ f(x) — g(x) right] ; dx }[/math])^[8][9].

Определение местоположения барицентра объекта, имеющего форму буквы L

Метод нахождения барицентра фигуры, имеющей форму буквы L.

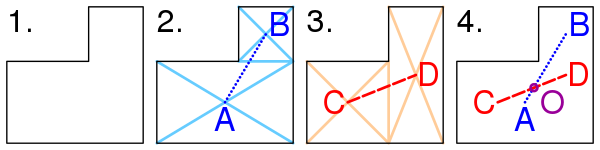
1. Фигуру делят на два прямоугольника (см. фигуру (2) на рисунке). Находят барицентры A и B этих двух прямоугольников как пересечение диагоналей. Рисуют отрезок AB, соединяющий барицентры. Барицентр фигуры должен лежать на этом отрезке AB.
2. Делят фигуру на два прямоугольника другим способом (см. фигуру (3) на рисунке). Находят барицентры C и D этих двух прямоугольников. Проводят отрезок CD, соединяющий барицентры. Барицентр фигуры должен лежать на отрезке CD.
3. Поскольку барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.

Барицентры треугольника и тетраэдра

Барицентр треугольника совпадает с пересечением медиан. Барицентр разбивает каждую медиану в отношении 2:1, то есть барицентр находится на расстоянии ⅓ от стороны до противоположной вершины (см. рисунок). Его декартовыми координатами является среднее координат трёх вершин. То есть, если вершинами треугольника являются [math]displaystyle{ a=(x_a,y_a) }[/math], [math]displaystyle{ b=(x_b,y_b) }[/math] и [math]displaystyle{ c=(x_c,y_c) }[/math], то координаты барицентра вычисляются по формуле

[math]displaystyle{ G=frac13(a+b+c)=left(frac13(x_a+x_b+x_c),frac13(y_a+y_b+y_c)right) }[/math].

Таким образом, барицентр имеет барицентрические координаты [math]displaystyle{ tfrac13:tfrac13:tfrac13 }[/math].

В трилинейных координатах барицентр можно получить одним из эквивалентных способов^[10]:

[math]displaystyle{ G = frac{1}{a} : frac{1}{b} : frac{1}{c} = bc : ca : ab = csc A : csc B : csc C }[/math]

[math]displaystyle{ = cos A + cos B cdot cos C : cos B + cos C cdot cos A : cos C + cos A cdot cos B }[/math]

[math]displaystyle{ = sec A + sec B cdot sec C : sec B + sec C cdot sec A : sec C + sec A cdot sec B . }[/math]

Барицентр является также физически центром масс треугольника, сделанного из однородного листового материала, а также, если вся масса сконцентрирована в вершинах и одинаково разделена между ними. Если же масса распределена равномерно вдоль периметра, то центр масс лежит в точке Шпикера (инцентре серединного треугольника), который (в общем случае) не совпадает с центроидом всего треугольника.

Площадь треугольника равна 3/2 длины любой стороны, умноженной на расстояние от центроида до стороны^[11].

Центроид треугольника лежит на прямой Эйлера между его ортоцентром [math]displaystyle{ H }[/math] и центром его описанной окружности [math]displaystyle{ O }[/math], ровно вдвое ближе ко второму, чем к первому:

[math]displaystyle{ GH=2GO }[/math].

Кроме того, для инцентра [math]displaystyle{ I }[/math] и центра девяти точек [math]displaystyle{ N }[/math], мы имеем

[math]displaystyle{ GH = 4 GN }[/math],

[math]displaystyle{ GO = 2 GN }[/math],

[math]displaystyle{ IG lt HG }[/math],

[math]displaystyle{ IH lt HG }[/math],

[math]displaystyle{ IG lt IO }[/math].

Аналогичными свойствами обладает тетраэдр — его барицентр является пересечением отрезков, соединяющих вершины с барицентрами противоположных граней. Эти отрезки делятся барицентром в отношении 3:1. Результат может быть обобщён на любой [math]displaystyle{ n }[/math]-мерный симплекс. Если вершины симплекса обозначить [math]displaystyle{ v_0,ldots,v_n }[/math] и рассматривать вершины как вектора, центроид равен

[math]displaystyle{ G=frac1{n+1}sum_{i=0}^nv_i }[/math].

Геометрический барицентр совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как [math]displaystyle{ n }[/math] равных масс.

Изогональным сопряжением центроида треугольника является точка пересечения его симедиан.

Барицентр тетраэдра

Тетраэдр является телом в трёхмерном пространстве, имеющим четыре треугольника в качестве граней. Отрезок, соединяющий вершину тетраэдра с барицентром противоположной грани, называется медианой, а отрезок, соединяющий середины двух противоположных сторон, называется бимедианой. Таким образом, имеется четыре медианы и две бимедианы. Эти шесть отрезков пересекаются в барицентре тетраэдра^[12]. Барицентр тетраэдра лежит посередине между точкой Монжа и центром описанной сферы. Эти точки задают прямую Эйлера тетраэдра, являющуюся аналогом прямой Эйлера треугольника.

Барицентр многоугольника

Барицентром самонепересекающегося замкнутого многоугольника, заданного [math]displaystyle{ n }[/math] вершинами [math]displaystyle{ (x_0,y_0) }[/math], [math]displaystyle{ (x_1,y_1) }[/math], [math]displaystyle{ ldots }[/math], [math]displaystyle{ (x_{n-1},y_{n-1}) }[/math], является точка [math]displaystyle{ (G_x,G_y) }[/math], где

[math]displaystyle{ G_x=frac1{6A}sum_{i=0}^{n-1}(x_i+x_{i+1})(x_iy_{i+1}-x_{i+1}y_i) }[/math];

[math]displaystyle{ G_y=frac1{6A}sum_{i=0}^{n-1}(y_i+y_{i+1})(x_iy_{i+1}-x_{i+1}y_i) }[/math]

и где [math]displaystyle{ A }[/math] является площадью многоугольника (со знаком):

[math]displaystyle{ A=frac12sum_{i=0}^{n-1}(x_iy_{i+1}-x_{i+1}y_i) }[/math]^[13].

В этой формуле предполагается, что вершины пронумерованы вдоль периметра многоугольника. Кроме того, вершина [math]displaystyle{ (x_n,y_n) }[/math] считается той же самой, что и [math]displaystyle{ (x_0,y_0) }[/math].
Заметим, что если точки пронумерованы по часовой стрелке, площадь [math]displaystyle{ A }[/math], вычисленная выше, будет отрицательной, но координаты барицентра подкорректируют этот случай.

Барицентры конуса и пирамиды

Барицентр конуса или пирамиды расположен на отрезке, соединяющем вершину тела с барицентром основания. Для целого конуса или пирамиды барицентр находится на расстоянии 1/4 от основания к вершине. Для поверхности конуса или пирамиды (боковая поверхность без внутренности и без основания) центроид находится на 1/3 расстояния от основания до вершины.

См. также

• Центр масс
• Центроид треугольника
• Центр тяжести
• Центр Чебышева^[en]
• Среднее Фреше^[en]
• k-means
• Список барицентров
• Теоремы Паппа — Гульдина
• Замечательные точки треугольника

Примечания

Литература

• Зетель, С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд/. — М. : Учпедгиз, 1962. — С. 12.
• Leung Kam-tim, Suen Suk-nam. Vectors, matrices and geometry. — Hong Kong University Press, 1994.

• Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — New York: Barnes & Noble, 1925.
• Paul Bourke. Calculating the area and centroid of a polygon. — 1997.
• Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007.
• David C. Kay. College Geometry. — New York: Holt, Rinehart and Winston, 1969.
• Roland E. Larson, Robert P. Hostetler, Bruce H. Edwards. Calculus of a Single Variable. — 6th. — Houghton Mifflin Company, 1998.
• Murray H. Protter, Charles B. Morrey Jr. College Calculus with Analytic Geometry. — 2nd. — Reading: Addison-Wesley, 1970.

Ссылки

• Characteristic Property of Centroid at cut-the-knot
• Barycentric Coordinates at cut-the-knot
• Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
• Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.