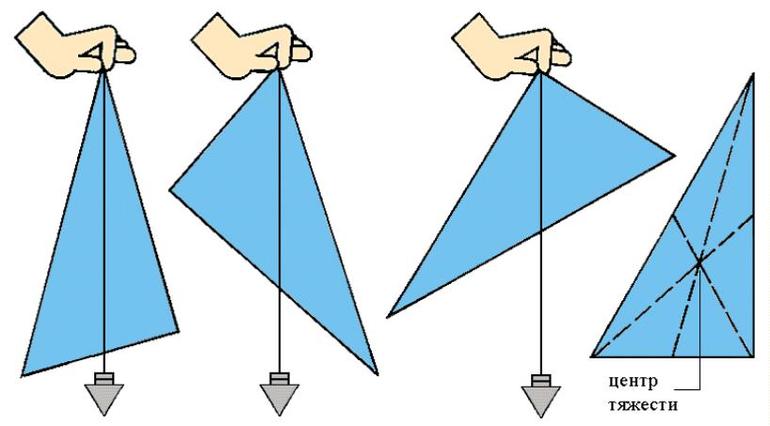
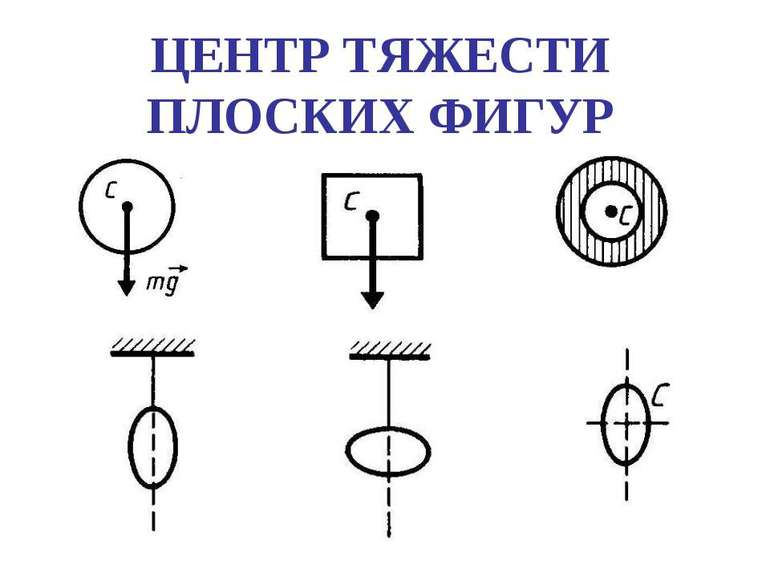
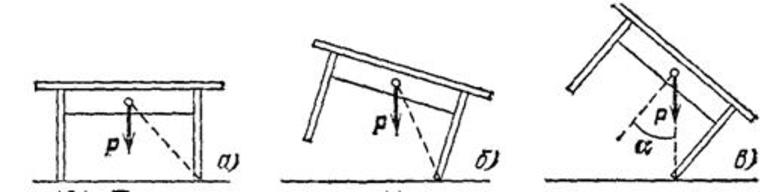
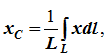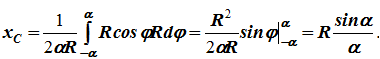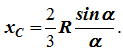2018-01-21
Определите положение центра масс однородного полушара радиусом $R$.
Решение:
Полушар симметричен относительно оси $x$ (рис.), поэтому его центр масс будет находиться на этой оси:
$r_{c} = x_{c} = frac{ sum_{i} Delta m_{i} x_{i}}{m}$, где $Delta m_{i}$ — элемент массы в виде диска радиусом $y$ и толщиной $Delta x$. Так как полушар сплошной, то от суммировании необходимо перейти к интегрированию, тогда $x_{c} = frac{ int_{0}^{R} xdm}{m}$.
$dm = rho dV = rho pi y^{2} dx; y^{2} = R^{2} — x^{2}; dm = rho pi (R^{2} — x^{2})dx$;
$rho$ — плотность материала полушара, $dV$ — элемент объема (диск). Масса полушара $m = frac{4}{6} pi R^{3} rho$, отсюда
$x_{c} = frac{6}{4 pi R^{3} rho } int_{0}^{R} rho pi (R^{2} — x^{2}) xdx = frac{3}{8}R$.
Новый коммент
24-07-2017 17:41:17
Судя по таблице удельной теплоёмкости, это может быть цинк.
22-11-2016 12:57:23
Дмитрий Да, перевод обязателен.
21-11-2016 19:00:39
1) –Обязательно ли переводить массу мяча в СИ?
21-11-2016 18:51:12
Условие смущает. Ладно, пусть время будет отрицательным, наблюдать можно с любого момента, но не ясно, каким моментам времени соответствуют моменты изменения скорости. Можно предположить, что первый пик где-то в районе -1,5 с, но так ли это?.. Третий пик вообще без координатной сетки не определишь. И еще: график чего именно надо построить? МОДУЛЯ скорости или ПРОЕКЦИИ скорости?
3-11-2016 00:11:19
Почему картика в блоке так размыта? А при просмотре в правой части (крупно) все выглядит гораздо лучше. Как то плохо пережимается картинка.
2-11-2016 15:29:02
t = 20ºC или 200 С ?
31-10-2016 20:21:46
Интересное задание. Пригодится.
27-10-2016 14:34:02
-
-
October 29 2005, 08:11
Привет!
Задача:
Определите положение центра масс половины круглого диска радиусом R, считая его однородным.
Метод определения центра масс
Изложены способы нахождения центра масс, в том числе теорема Вариньона; показано различие между центром тяжести и центром масс.
Центром масс системы называется воображаемая точка, радиус вектор которой
$vec{R} = frac{m_1vec{r_1} + m_2vec{r_2} + cdots + m_nvec{r_n}}{m_1 + m_2 + cdots + m_n} = frac{displaystylesum_{i=1}^{n} m_ivec{r_i}}{displaystylesum_{i=1}^{n} m_i}$.
Обозначим массу системы
$M = displaystylesum_{i=1}^{n} m_i$,
$Mvec{R} = m_1vec{r_1} + m_2vec{r_2} + cdots + m_nvec{r_n}$.
Найдем производную по времени:
$Mvec{v_ц} = m_1vec{v_1} + m_2vec{v_2} + cdots + m_nvec{v_n}$.
В правой части стоит суммарный импульс системы, а $vec{v_ц}$ – скорость центра масс.
Таким образом, центр масс системы движется как материальная точка массы $M$. Это теорема о движении центра масс.
Найдя еще одну производную, получим
$Mvec{a_ц} = displaystylesum_{i=1}^{n} vec{F_i^{вн}} = vec{F}$.
Здесь $vec{a_ц}$ – ускорение центра масс, $vec{F_i^{вн}}$ – внешняя сила, действующая на $i$-тое тело системы, а $F$ – равнодействующая всех сил, действующих на систему. Напомним. Что на основании третьего закона Ньютона сумма внутренних сил равна нулю.
$displaystylesum_{i=1}^{n} vec{F_i^{вн}} = 0$.
Этот результат дает возможность сформулировать следующее определение центра масс системы, подверженной внешним воздействиям вне зависимости от их природы. Центр масс такой системы – точка приложения равнодействующей всех сил. В случае действия одних лишь сил тяжести центр масс системы заменяют совпадающим с ним, но более узким по содержанию понятием центра тяжести.
В следующих задачах рассмотрим способы нахождения центра масс, а в следующей главе продемонстрируем применение теоремы о его движении.
Задача 1. К концам невесомого стержня длиной $l$ приложены силы $F_1$ и $F_2$ (рис.). Найти точку приложения равнодействующей силы.
Пусть $O$ – искомая точка. По правилу моментов
$F_1x = F_2(l — x)$,
откуда
$x = frac{F_2l}{F_1 + F_2}$.
Задача 2. Найти центр масс системы изображенной на рисунке.
Для сил $F_1$ и $F_2$ воспользуемся результатом задачи 1.
$ x = frac{F_2l}{F_1 + F_2}$.
Вторично воспользуемся им для сил
$vec{F_1} + vec{F_2}$ и $vec{F_3}$:
$y = frac{(F_1 + F_2)(l_1 + l_2 — x)}{F_1 + F_2 + F_3}$.
Подставив значение $x$, получим
$y = frac{(F_2l_2 + F_1(l_1 + l_2)}{F_1 + F_2 + F_3}$.
Решив эти две задачи, мы фактически методом математической индукции доказали теорему Вариньона: момент равнодействующей относительно произвольно выбранной оси равен сумме моментов всех сил относительно этой же оси. Эта ось проходит через точку $A$. Теорема дает возможность находить центр масс, причем ось удобно выбирать в точке приложения нескольких сил (моменты этих сил будут равны нулю).
Задача 3. Из тонкого однородного диска радиуса $R$ вырезан диск радиуса $r$ ($r < frac{R}{2}$). Расстояние между центрами диска $O$ и полости равно $a$ ($a > r$). Найти расположение центра масс.
1-й способ. Вырежем диск $C$ радиуса $r$ симметрично относительно центра $O$ (рис.).
$pi r^2(a — x) = pi (R^2 – 2r^2)x$,
отсюда
$x = frac{a}{frac{R^2}{r^2}} — 1$.
2-й способ (рис.). Задачу решаем методом отрицательных масс.
Мысленно заполним полость однородным веществом той же плотности, что и диск. Чтобы такая операция была правомерной, введенную массу удобно считать «отрицательной».
$pi R^2x + (-pi r^2)(x + a) = 0$ и $x = frac{a}{frac{R^2}{r^2}} — 1$.
Задача 4. На рисунке изображены цепочка длиной $L$ и два стержня длиной $L/2$ каждый. Чей центр масс выше?
Оттянув цепочку вниз, мы придадим ей форму стержней. Следовательно, центр масс стержней выше центра масс цепочки.
Задача 5. На поверхности воды плавает деревянный кубик квадратного сечения, плотность кубика в два раза меньше плотности воды. Какое из двух положений равновесия будет устойчивым?
В воде находится половина кубика, поэтому его центр тяжести в обоих случаях расположен на одной высоте.
Центр тяжести вытесненной воды в первом случае находится на расстоянии $frac{a}{4}$ от ее поверхности, во втором –
$frac{1}{3}afrac{sqrt{2}}{2} < frac{a}{4}$.
Это означает, что положение 2 устойчиво.
Задача 6. Найти центр масс тонкой проволоки согнутой в виде полуокружности радиуса $r$.
Впишем в окружность правильный многоугольник (рис.).
Пусть сила тяжести действует перпендикулярно чертежу. Момент сил тяжести, приложенных к серединам сторон многоугольника, относительно оси $AK^/$:
$M = rho g(ABcdot x_1 + BCcdot x_2 + CDcdot x_3 + cdots)$,
где $rho$ – масса единицы длины.
Поскольку
$ABcdot x_1 = AB^/ cdot h, BCcdot x_2 = B^/C^/ cdot h, CDcdot x_3 = C^/D^/ cdot h$ $cdots$,
то
$M = rho gh(AB^/ + C^/B^/ + cdots) = rho ghcdot 2r = 2rho ghr$.
Будем увеличивать число сторон многоугольника. Тогда $h to r$ и, следовательно, $M = 2rho gr^2$.
С другой стороны, $M = pi rrho gx$, отсюда
$x = frac{2r}{pi}$.
Задача 7. Определить положение центра тяжести однородного тонкого полукруга радиуса $r$.
Разбиваем полукруг на треугольники и сегменты (рис.).
Центры тяжести треугольника лежат на расстоянии $frac{r}{3}h$ от точки $O$.
При большом числе треугольников $h to r$.
Далее необходимо определить центр тяжести полуокружности
$ccdot r_0 = frac{2}{3}; OM = frac{2r_0}{pi} = frac{4r}{3pi}$.
Центр масс дает возможность решать не только статические задачи.
Задача 8. Брусок $2$ отпускают (рис.). Что произойдет раньше: брусок $2$ ударится о стенку, или $1$ упрется в блок?
На центр масс системы, первоначально находившейся на уровне стены, действует неотрицательная сила $Tcdot (1 — cosvarphi)$, направленная вправо от оси $x$, поэтому случай, когда $2$ раньше удариться о стену, исключается, поскольку тогда центр масс будет левее плоскости стены.
Задача 9. На гладкой горизонтальной поверхности на расстоянии $2l$ друг от друга неподвижно лежат два шарика, массой $m$ каждый, связанные невесомой нерастяжимой нитью длиной $2l$. Среднюю точку нити $A$ начинают двигать с постоянной скоростью $v$ в горизонтальном направлении, перпендикулярном нити. Какой путь пройдет точка $A$ до момента столкновения шаров?
Перейдем в систему отсчета связанную с центром масс. Тогда шарики будут двигаться со скоростью центра масс навстречу друг другу со скоростью $v$. И четверть окружности длиной $frac{2pi i}{4} = frac{pi l}{2}$ пройдут за время $t = frac{pi l}{2v}$. Теперь вернемся обратно и найдем расстояние, пройденное средней точки за это время
$S = frac{pi l}{2v} = frac{pi l}{2}$.
Задачи для самостоятельной работы.
Задача 10. Определить положение центра тяжести тонкой однородной проволоки, прогнутой по дуге радиуса $r$r (рис.).
$h = 2r frac{sin(alpha /2)}{alpha}$
Задача 11. Определить положение центра тяжести тонкой однородной пластинки, представляющей собой сектор радиуса $r$, имеющей центральный угол $alpha$ (рис.).
$OM = frac{4}{3}rfrac{sin(alpha /2)}{alpha}$
Задача 12. Найти центр масс фигуры (рис.).
$OC = frac{2}{3}frac{r}{4pi}$
Как найти центр масс окружности с вырезом
2016-11-20
Определить центр масс плоского однородного диска с вырезанным отверстием (см. рис.). Величины $R, r$ и $d$ известны.
При решении задач данного типа удобно применять следующий прием. Мысленно вырежем еще одно отверстие в диске, симметричное имеющемуся относительно точки О. Получившаяся фигура (диск без двух отверстий) обладает центром симметрии О и, следовательно, ее центр масс также расположен в точке О.
Центр масс мысленно вырезанного круга находится в его центре.
Будем отыскивать центр масс искомой фигуры, полагая, что она состоит из двух тел: круга и диска с двумя отверстиями. Согласно полученным во введении к разделу результатам, эта задача эквивалентна нахождению центра масс двух точечных масс, сосредоточенных в точках О и $O^< prime>$.
Выберем систему координат с началом в точке О.
Согласно определению центра масс:
Обозначим через $rho$ массу диска, приходящуюся на единицу его площади. Тогда масса круга равна:
а масса диска с двумя отверстиями:
Подставляя (2, 3) в (1) и сокращая на $rho pi$, окончательно получаем:
Таким образом, центр масс искомой фигуры расположен на отрезке $OO^< prime>$ на расстоянии $x_<цм>$ от точки О.
Тема 1.5. Центр тяжести тела
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.
Найти центр масс окружности
iSopromat.ru
Формулы для расчета координат положения центра тяжести треугольника, дуги окружности и кругового сегмента.
Центр тяжести треугольника
Центр тяжести площади треугольника совпадает с точкой пересечения его медиан (рисунок 1.10, а).
Центр тяжести дуги окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. yC = 0.
dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,
Центр тяжести кругового сектора
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.
Центр тяжести сектора совпадает с центром тяжести дуги AB:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Тема 1.5. Центр тяжести тела
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.
Центр тяжести тела — формулы и примеры нахождения
Общие сведения
Пусть имеется физическое тело, на которое не оказывается влияние, то есть другие объекты не действуют или их силы воздействия скомпенсированы. Рассматриваемое тело будет находиться в состоянии прямолинейного движения или покоя. Для удобства можно принять, что объект неподвижен, например, пусть это будет лодка на поверхности воды.
Если к плавательному средству приложить силу, смещённую к началу лодки F1, судно начнёт поворачиваться в сторону направления воздействия. Если ее переместить в горизонтальной плоскости в другой конец судна, лодка начнёт также поворачиваться, но направление вращения изменится. Отсюда можно сделать вывод, что существует такая точка приложения силы, точнее, линия, при воздействии на которую лодка не изменит своего положения, то есть плавательное средство начнёт двигаться ускоренно поступательно. Допустим, это будет сила F3.
Логично, что можно подобрать и другую силу, вызывающую поступательное прямолинейное перемещение, например, F4.
При этом точку воздействия можно перемещать по линии её направления, так как, согласно правилу, величина действия при этом не изменяется. В итоге получится точка, где пересекутся приложенные силы F3 и F4. Таких моментов можно приложить сколько угодно, при этом они все соединятся в одном месте. Точку пересечения линий действия сил, которые вызывают ускоренное поступательное движение тела, называют центром масс.
На лодку действует ещё одна сила — притяжения. На самом деле она воздействует на каждую частичку объекта, поэтому на тело одновременно оказывает влияние огромное количество моментов. Это множество и принято заменять их равнодействующей — то есть силой, приложенной к центру тяжести. В физике параметр обозначают как mg. Другими словами, это точка приложения равнодействующих сил тяжести.
Существует взаимосвязь между массой и тяжестью. Если тело разбить на кусочки и бросить их, скорость падения будет для всех тел одинаковой, так как ускорение не зависит от массы. При этом падающий объект движется поступательно.
А значит, приложенная сила проходит через центр масс, то есть через центр тяжести, поэтому несмотря на разный принцип определения этих точек, их положение совпадает.
Поиск центра тяжести
Чтобы определить центр тяжести для тела сложной формы, его нужно разделить на простые фигуры и определить точки равновесия для каждой из них. Для простых геометрических объектов используют симметрию. Например, в шаре параметр располагается в центре, в однородном цилиндре — в точке на середине оси. Частным случаем разбиения фигуры при определении является метод отрицательных площадей. Его применяют к телам, которые имеют вырезы, и при этом площадь удалённой части известна.
Вот формулы для вычисления центра в некоторых фигурах:
- В треугольнике: x = (1/3) * (x1 + x2 + x3); y = (1/3) * (y1 + y2 + y3). Физически центр находится в точке пересечения медиан и представляет собой среднее арифметическое из координат вершин.
- В прямоугольнике: x = b/2; y = h/2. Центр равновесия располагается в точке пересечения диагональных прямых.
- В полукруге: x =D/2; y = 4R/3π. Искомая точка лежит на оси симметрии.
- В круге: x = R; y = R. Точка тяжести находится в центре фигуры.
Стоит отметить, что центр тяжести объёмных тел может находиться и вне фигуры, например, как у кольца. Вообще же для трёхмерного пространства, как учат на уроках физики в 7 классе, центр тяжести тела вычисляют по формулам: x = (ΣΔ m * x) / m; y = (ΣΔ m * y) / m; z = (ΣΔ m * z) / m, где: m — масса тела, x, y, z — координаты искомой точки в пространстве. Уравнение можно переписать и в векторной форме: r = (1 / m) Σm * r, где r — радиус вектор.
Существует и ряд теорем, благодаря которым можно определить точку массы в теле:
- При рассмотрении однородного тела, имеющего плоскость симметрии, центр массы будет находиться в этой плоскости.
- Если однородное тело обладает осью симметрии, центр располагается на ней.
- Центр симметрии однородной фигуры совпадает с центром массы.
- Центр масс симметричных фигур находится в их геометрическом центре.
Точку равновесия фигуры можно находить и через объём: R = (1 / V) * ∫ ∫ ∫rdV. Для плоских объектов используется формула R = (1 / S) * ∫ ∫ ∫rdS, а однородной линии R = (1 / L) * ∫ ∫ ∫rdL. Стоит отметить, что понятие точки тяжести применимо только к твёрдым объектам. Если это не так, использование понятия не имеет смысла.
Пример задания
Теоретический материал лучше всего усваивается на практических заданиях. Не исключение и понятие о центре тяжести. Тема несложная, но при нахождении параметра желательно фигуру изобразить на рисунке.
Наиболее часто ученикам преподаватель предлагает решить задачу о нахождении центра масс сложного тела, но при этом достаточно симметричного. Например, пусть имеется диск из однородной пластины, в котором вырезан кусок треугольной формы. Необходимо найти центр равновесия оставшегося объекта.
Если нарисовать условие задачи, станет понятно, что треугольник прямоугольный, а центр масс находится на горизонтальной прямой, проходящей через середину диска. Пусть это будет ось x. Чтобы решить задачу, нужно разбить сложную фигуру на несколько частей, в каждой из которых можно найти искомую точку.
Симметрично удалённому треугольнику можно выделить аналогичную часть. В итоге останется круг с вырезанным внутри квадратом. Точка масс диска находится в центре. Для удобства её можно обозначить как x1. Вторая фигура — это треугольник. Точка равновесия у него находится на пересечении медиан. То есть на 1/3 высоты. Обозначить точку можно как x2.
Если масса треугольника равна М2, а круга М1, искомую координату можно определить по формуле: x = (m1x1 + m2x2) / m1 + m2. Далее, нужно найти, чему равняется сторона вырезанного треугольника. Из рисунка можно понять, что это расстояние будет r * √2, где r — радиус диска.
Теперь можно найти, чему будут равны x1 и x2. x1 будет равняться нулю, так как эту точку можно принять за начало координат. x2 же будет равняться 1/3 длины медианы. Высота фигуры совпадает с радиусом диска, значит: x2 = R/3.
В таких задачах самое сложное — это найти массы. Первую можно определить исходя из того, что она будет равняться массе диска минус значение квадрата. Так как фигура однородная, масса прямо пропорциональна площади. Тогда для первого участка m1 = σ * S = σ * (Sкруга — Sквадрата) = σ * (pR2 — 2R2) = σR2 * (p — 2), где: σ — поверхностная площадь. Соответственно, m2 = σ * Sтреугольника = σ * R2. Все найденные величины нужно подставить в формулу и найти ответ: x = ((r * σ * R 2 /3)) / (σ * R2 * (p — 2) + σ * R2) = (r / 3 (p — 1)). Это и будет искомая координата.
Простая задачка
Пусть имеются 2 шара. Они расположены так, что соприкасаются друг с другом. Сделаны тела из одного материала, но при этом радиусы у них отличаются вдвое. Значение первого равняется r = 20 см, а второго 40, то есть 2r. Найти, где находится точка равновесия такого объекта. Такого рода задачи обычно любят демонстрировать на презентациях, касающихся темы. Задача простая, но между тем помогает понять принцип нахождения центра равновесия.
Итак, при решении нужно будет воспользоваться формулой: x = (m1x1 + m2x2) / m1 + m2. Так как по условию радиусы шаров отличаются вдвое, их массы будут отличаться в 8 раз. Объём всегда пропорционален кубу линейных размеров.
Массу первого шара можно обозначить как m, а второго — 8m. Начало координат для удобства лучше поместить в центр меньшей фигуры. В результате середина большого шара будет иметь координату 3r. Значит, искомая координата равняется: x = ((m* 0 + 8m * 3r)) / (m + 8m) = (8 * 3r) / 9 = 8r/3.
То есть нужная точка находится на расстоянии 1/3 радиуса ближе к маленькому шару (если отсчитывать от середины большого).
http://www.sites.google.com/site/tehmehprimizt/lekcii/teoreticeskaa-mehanika/statika/centr-tazesti
http://b4.cooksy.ru/articles/nayti-tsentr-mass-okruzhnosti