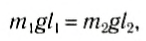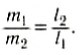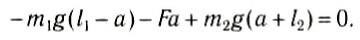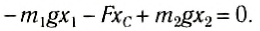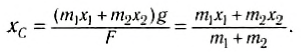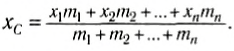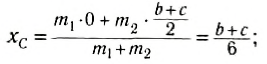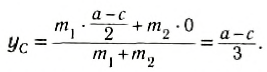Центр тяжести (центр масс):
Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.
Центр тяжести — геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.
На каждую точку тела в поле сил тяжести действует сила, а на все тело — равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.
Центр масс (центр инерции) — точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.
При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.
Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.
При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, — параллельными.
Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.
Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.
Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.
Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.
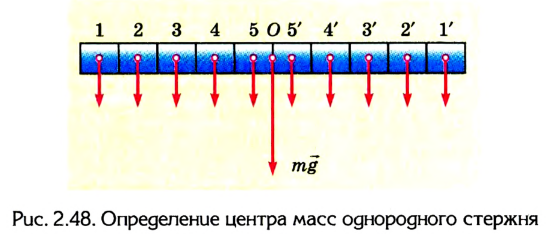
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О — середине стержня.
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.
Центр тяжести однородного стержня расположен в середине стержня.
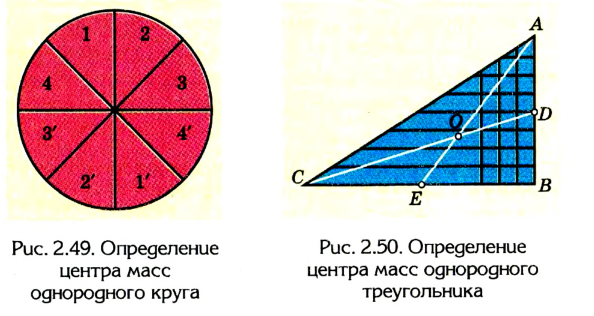
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.
Центр тяжести однородного круга совпадает с его центром.
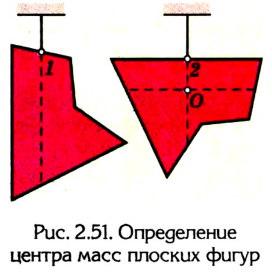
Центр тяжести однородного треугольника находится в точке пересечения его медиан.
3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.
Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.
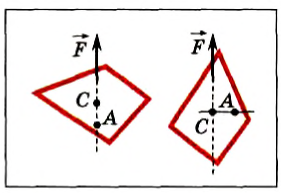
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.
Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.
Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.
- Заказать решение задач по физике
Центр тяжести тела и центр масс тела
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.
Рис. 151
Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.
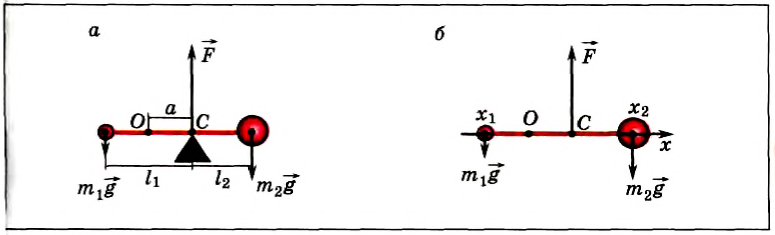
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:
или
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:
Рис. 152
Поскольку F=(m1 + m2)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х1, хс и х2. Запишем условие моментов относительно точки О:
Отсюда
При выводе этой формулы было использовано значение силы F = (m1 + m2) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии хс, определенном формулой (2).
Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.
Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.
Если произвольное тело можно разбить на n элементов, массы которых m1, m2…, mn, и если известны координаты центров масс этих элементов x1, x2…, xn относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:
Естественно, что такие же соотношения можно записать и для ус и zc. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m1 = 2m2). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C1) и линейки (C2).
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х1 = 0, y1 =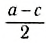
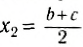
По формуле (3): .
Таким образом, центр масс угольника находится вне тела.
Главные выводы:
- Центр тяжести — точка, в которой приложена сила тяжести.
- Центр масс симметричных однородных тел находится в их геометрическом центре.
- Координаты центра масс тела можно вычислить по формуле (3).
- Импульс тела в физике
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
Загрузка…
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Рассмотрим твердое
тело произвольной геометрии и распределения
масс. Разобьем мысленно тело на малые
(не обязательно одинаковые) элементы и
пронумеруем их. Допустим, что к некоторому
элементу тела с номером i
и массой mi
приложена внешняя сила
и кроме этого действуют внутренние силы
со стороны остальных элементов тела
.
Под воздействием результирующей всех
сил, приложенных к рассматриваемому
элементу тела, будет происходить движение
в соответствии со II законом
Ньютона:
,
где
– сумма всех внутренних сил, действующих
на элемент c номером i
со стороны всех остальных элементов
тела;
– масса и ускорение элемента тела с
номером i.
Проведем суммирование по всем элементам
тела. При суммировании внутренние силы
взаимно сокращаются, так как всякой
силе, действующей на элемент тела i
со стороны элемента j,
согласно III закону Ньютона, имеется
равная и противоположно направленная
сила, действующая на элемент j
со стороны элемента i.
Сумма всех внешних сил (результирующая
сила) будет равна:
.
(13)
Рассмотрим теперь точку, радиус-вектор
которой
,
где M
– масса всего тела. Назовем эту точку
центром масс тела. Смысл этого
термина выясняется ниже.
Дважды продифференцируем последнее
выражение по времени:
.
(14)
Из сравнения (13) и (14) следует, что
.
Так как
,
является ускорением центра масс тела,
то последнее соотношение означает, что
центр масс движется в соответствии со
II законом Ньютона, причем движение
происходит так, как если бы вся масса
тела была сосредоточена в точке центра
масс.
Рассмотрим теперь замкнутую (изолированную)
систему тел. В замкнутой системе
(сумма всех внешних сил равна нулю),
поэтому центр масс будет либо двигаться
прямолинейно и равномерно либо оставаться
в покое. Внутренние силы, при этом, между
отдельными частями системы могут и не
равняться нулю, но как только что было
показано, они не могут повлиять на
движение центра масс, но влияют на
движение отдельных тел, составляющих
систему.
Заметим также, что вместо термина «центр
масс» иногда используется термин «центр
инерции».
В ряде случаев задача отыскания положения
центра масс может быть упрощена. Так,
например, если рассматривается движение
твердого тела, обладающего тем или иным
типом симметрии, то можно указать на
пространственное положение центра масс
и без детальных расчетов. Приведем
некоторые примеры:- центр масс однородного
по плотности шара совпадает с его
центром; центр масс тонкого однородного
по плотности стержня расположен на его
середине; три материальные точки
одинаковой массы, расположенные в
вершинах жесткого равностороннего
треугольника имеют центр масс в точке
пересечения биссектрис внутренних
углов треугольника и т.д.
Решение задач по определению положения
центра масс некоторого тела может быть
упрощена, если находить отдельно все
три проекции радиус-вектора
центра масс.
В качестве примера, рассмотрим два шара
массами m1 и m2
находящимися на фиксированном расстоянии
l друг от друга и
найдем центр масс этой системы (рис.9).
Каждый шар можно рассматривать как
материальную точку с массой, расположенной
в его центре.
Рис.9
Направим ось X
вдоль прямой проходящей через центры
шаров, а начало координат поместим на
расстоянии а от левого шара. Тогда
координату Xc
центра масс можно записать в виде:
.
Если поместить начало координат в центр
первого шара (т.е. положить а = 0),
то выражение для Xc
будет иметь более простой вид
.
В
частном случае, когда m1 = m2,
Хс = l/2,
т.е. для одинаковых шаров центр масс
будет находиться в точке, расположенной
посередине между шарами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Центр масс, теория и онлайн калькуляторы
Центр масс
Определение центра масс
Определение
При рассмотрении системы частиц, часто удобно найти такую точку, которая характеризует положение и движение
рассматриваемой системы как единого целого. Такой точкой является центр масс.
Если у нас две частицы одинаковой массы, то такая точка находится посередине между ними.
Координаты центра масс
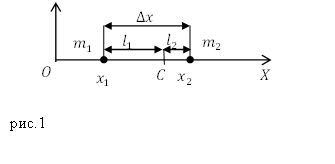
Допустим, что две материальные точки, имеющие массы $m_1$ и $m_2$ находятся на оси абсцисс и имеют координаты $x_1$ и $x_2$. Расстояние ($Delta x$) между этими частицами равно:
[Delta x=x_2-x_1left(1right).]
Определение
Точку С (рис.1), делящую расстояние между этими частицами на отрезки, обратно
пропорциональные массам частиц называют центром масс этой системы частиц.
В соответствии с определением для рис.1 имеем:
[frac{l_1}{l_2}=frac{m_2}{m_1}left(2right).]
Так как:
[l_1{=x}_c-x_1;; l_1{=x}_2-x_cleft(3right),]
где $x_c$ — координата центра масс, то получаем:
[m_1left(x_c-x_1right)=m_2{(x}_2-x_c)(4).]
Из формулы (4) получим:
[x_c=frac{m_1x_1+m_2x_2}{m_1+m_2}left(5right).]
Выражение (5) легко обобщается для множества материальных точек, которые расположены произвольным образом. При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
Аналогично получают выражения для ординаты ($y_c$) центра масс и его аппликаты ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(8right).]
Формулы (6-8) совпадают с выражениями, определяющими центр тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Если положение N материальных точек системы задано в векторной форме, то радиус — вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(9right).]
Движение центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) имеет вид:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(10right),]
где $overline{P}$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (10) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач с решением
Пример 1
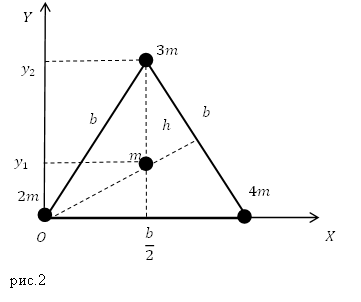
Задание. Запишите координаты центра масс системы из трех шариков, которые находятся в вершинах и центра равностороннего треугольника, сторона которого равна $b (м)$ (рис.2).
Решение. Для решения задачи используем выражения, определяющие координаты центра масс:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}(2.1);;]
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}(2.2).]
Из рис.2 мы видим, что абсциссы точек:
[left{ begin{array}{c}
m_1=2m, x_1=0;; \
{rm }m_2=3m, x_2=frac{b}{2};; \
m_3=m, x_3=frac{b}{2};; \
m_4=4m, x_4=b. end{array}
right.left(2.3right).]
Тогда абсцисса центра масса равна:
[x_c=frac{2mcdot 0+3mcdot frac{b}{2}+mcdot frac{b}{2}+4mcdot b}{2m+3m+m+4m}=frac{6mb}{10m}=0,6b (м);;]
Найдем ординаты точек.
[ begin{array}{c}
m_1=2m, y_1=0;; \
{rm }m_2=3m, y_2=frac{bsqrt{3}}{2};; \
m_3=m, y_3=frac{bsqrt{3}}{6};; \
m_4=4m, y_4=0. end{array}
left(2.4right).]
Для нахождения ординаты $y_2$ вычислим, чему равна высота в равностороннем треугольнике:
[h=sqrt{b^2-frac{b^2}{4}}=frac{bsqrt{3}}{2}=y_2left(2.5right).]
Ординату $y_3$ найдем, помня, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, получаем:
[y_3=hcdot frac{1}{3}=frac{bsqrt{3}}{6} left(2.6right).]
Вычислим ординату центра масс:
[y_c=frac{2mcdot 0+3mcdot frac{bsqrt{3}}{2}+mcdot frac{bsqrt{3}}{6}+4mcdot 0}{2m+3m+m+4m}=frac{10mfrac{bsqrt{3}}{6}}{10m}=frac{bsqrt{3} }{6}(м).]
Ответ. $x_c=0,6b {rm }{rm м}$; $y_c=frac{bsqrt{3} }{6}$ м
Пример 2
Задание. Запишите закон движения центра масс.
Решение. Закон изменения импульса системы частиц является законом движения центра масс. Из формулы:
[{overline{v}}_c=frac{overline{P}}{M}to overline{P}=M{overline{v}}_cleft(2.1right)]
при постоянной массе $M$ продифференцировав обе части выражения (2.1), получим:
[frac{doverline{P}}{dt}=Mfrac{d{overline{v}}_c}{dt}left(2.2right).]
Выражение (2.2) означает, что скорость изменения импульса системы равняется произведению массы системы на ускорение ее центра масс. Так как
[frac{doverline{P}}{dt}=sumlimits^N_{i=1}{{overline{F}}_ileft(2.3right),}]
имеем:
[Mfrac{d{overline{v}}_c}{dt}=sumlimits^N_{i=1}{{overline{F}}_ileft(2.4right).}]
В соответствии с выражением (2.4) получаем, что центр масс системы движется так, как двигалась бы одна материальная точка массы M, если на нее действует сила, равная сумме всех внешних сил, действующих на частицы, которые входят в рассматриваемую систему. Если $sumlimits^N_{i=1}{{overline{F}}_i=0,}$ то центр масс движется равномерно и прямолинейно.
Читать дальше: центр тяжести.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!