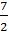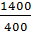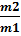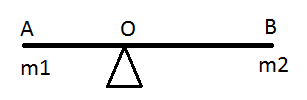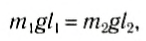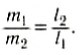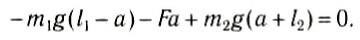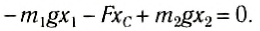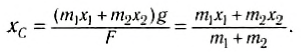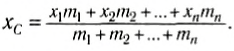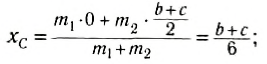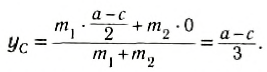Центр тяжести треугольника
Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин
Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.
Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.
Как рассчитать центр масс треугольника
Любите ли вы геометрию? Многие на этот вопрос отвечают «нет», потому что в школе она даётся труднее всего. Причём особенную нелюбовь вызывают у учеников задачи о пересекающихся отрезках в треугольнике, к которым трудно даже подступиться. В этой статье мы расскажем о замечательном методе решения подобных задач — методе масс.
Эта статья была опубликована в журнале OYLA №10(38). Оформить подписку на печатную и онлайн-версию можно здесь.
Наверняка в детстве вы качались на качелях-весах. И наверняка один из двоих чаще всего оказывался тяжелее и его сторона постоянно перевешивала. А что можно сделать в этой ситуации, чтобы уравновесить качели?
Вспоминаем правило рычага: чтобы система была в равновесии, моменты сил, действующих на качели, должны быть одинаковыми.
Так как силы в нашем случае — это силы тяжести, верно следующее равенство:
Сокращаем константу g и получаем, что отношение масс обратно пропорционально отношению расстояний от края качелей до опоры.
Обратите внимание: вес самих качелей мы не учитываем. То есть система состоит из двух точек — концов отрезка с «гирьками», а также третьей точки, которая делит этот отрезок в отношении, обратно пропорциональном отношению масс «гирек». Последняя точка имеет своё название — она является центром масс системы из двух точек-«гирек».
Что же такое центр масс, или, как его ещё называют, центр тяжести? Формальное определение звучит так:
Точка О называется центром масс системы из n точек А1, А2, …, Аn, где каждой точке соответствует масса m1, m2, …, mn, если верно следующее равенство:
Не пугайтесь этой формулы! На деле решать задачи данным методом можно не думая про векторы. Сделаем допущение, что груз на концах отрезков не имеет размера — только массу.
Чтобы найти центр масс системы из двух точек, надо всего лишь разбить отрезок в отношении, обратно пропорциональном массам точек. Это условие делает верным наше векторное равенство.
Теперь рассмотрим систему из трёх точек, образующих некий треугольник. Как найти его центр масс? Для большей наглядности представим большой поднос, на котором произвольно расставлены гири. И официанта, который ловко удерживает поднос на одном пальце. Точка, в которой палец соприкасается с подносом, и есть центр масс. Только условимся, что поднос обладает бесконечно малой массой.
Как же найти эту точку? Оказывается, у центра масс есть следующее полезное свойство.
Если есть система точек с массами в них и какую-то пару точек А(mA) и B(mB) мы заменим их центром масс Р(mA+mB), то центр масс исходной системы не изменится.
Доказать это свойство попробуйте самостоятельно: это несложное упражнение на векторы.
Давайте применим указанное свойство к треугольнику. Если есть треугольник с вершинами А, В, С с массами в них, то, чтобы найти центр масс данной системы, можно сперва найти центр масс точек А и В (точку Р), а затем найти центр масс точек Р и С. В каждом из двух случаев центр масс мы находим с помощью обычного правила рычага.
Всё это здорово, но возникает резонный вопрос: а зачем? Какое отношение имеют эти рассуждения к геометрическим задачам? Терпение, друзья!
Дан треугольник АВС. М — середина АВ, точка К лежит на отрезке АС и делит его в отношении 1:2 от вершины А. В каком отношении отрезок СМ делит отрезок ВК?
Решение Суть нашего метода в следующем. Расставим в точки А, В и С массы 2, 2 и 1 соответственно. Как вы видите, центр масс точек А(2) и В(2) — это точка М(4). Значит, центр масс всей системы из трёх точек находится на отрезке СМ и делит его в отношении 1:4 от С.
Теперь вернёмся к началу и найдём центр масс точек А и С. Это будет точка К(3). Значит, центр масс исходной системы лежит на отрезке ВК и делит его в отношении 3:2 от В.
Но речь идёт об одной и той же системе точек А, В и С, а значит, у них один и тот же центр масс, который лежит и на СМ, и на ВК. Таким образом, центр масс не что иное, как точка О. Отсюда следует, что искомое отношение ВО к ОК равно 3:2.
Ответ. 3:2.
Постойте-ка! А как это мы догадались расставить массы именно так: 2, 2 и 1? На самом деле никакой магии тут нет. Наша цель — расставить массы в вершинах треугольника так, чтобы их центром оказалась точка О. Но почему именно 2, 2 и 1? Всё дело в том, что О будет центром масс, если мы покажем, что центр масс одновременно лежит и на отрезке СМ, и на отрезке ВК. Следовательно, в первом случае массы из точек А и В должны сместиться в точку М. Вспоминаем правило качелей: так как АМ = ВМ, то массы в точки А и В надо ставить одинаковые. Запомним это.
Во втором случае мы должны поставить массы в А и С так, чтобы их центром была точка К. Но АК:СК = 1:2, значит, в точке А масса должна быть вдвое больше, чем в С. Следовательно, ставим в С массу 1, тогда в А будет 2 (вдвое больше) и в В — тоже 2 (как в А).
Методом масс можно не только решать задачи, но и доказывать теоремы.
Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин.
Решение Рассмотрим медианы ВК и СМ. В данном случае и К, и М — середины, поэтому поставим во все три вершины А, В и С массу 1. Далее рассмотрим точки А и В. Их центр масс — точка М(2). Значит, центр масс системы точек А, В и С лежит на отрезке СМ и делит его в отношении 2:1 от вершины С.
Теперь рассмотрим точки А и С, их центр масс — точка К(2). Значит, центр масс всё той же системы точек А, В и С лежит на отрезке ВК и делит его в отношении 2:1 от вершины В. Но тогда искомый центр масс — это точка О на пересечении отрезков ВК и СМ, причём каждый из отрезков эта точка делит в отношении 2:1 от вершин.
Осталось заметить, что если мы рассмотрим медианы ВК и АР, то их точка пересечения также будет центром масс и разделит ВК и АР в отношении 2:1 от вершин. Но точка, которая делит ВК в отношении 2:1 от В, единственная, значит, в обоих случаях речь идёт об одной и той же точке О. Итак, все три медианы проходят через точку О и делятся ею в отношении 2:1 от вершин, что и требовалось доказать.
Центр масс
Определение центра масс
При рассмотрении системы частиц, часто удобно найти такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой является центр масс.
Если у нас две частицы одинаковой массы, то такая точка находится посередине между ними.
Координаты центра масс
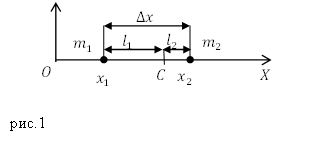
Допустим, что две материальные точки, имеющие массы $m_1$ и $m_2$ находятся на оси абсцисс и имеют координаты $x_1$ и $x_2$. Расстояние ($Delta x$) между этими частицами равно:
Точку С (рис.1), делящую расстояние между этими частицами на отрезки, обратно пропорциональные массам частиц называют центром масс этой системы частиц.
В соответствии с определением для рис.1 имеем:
где $x_c$ — координата центра масс, то получаем:
Из формулы (4) получим:
Выражение (5) легко обобщается для множества материальных точек, которые расположены произвольным образом. При этом абсцисса центра масс равна:
Аналогично получают выражения для ординаты ($y_c$) центра масс и его аппликаты ($z_c$):
Формулы (6-8) совпадают с выражениями, определяющими центр тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Если положение N материальных точек системы задано в векторной форме, то радиус — вектор, определяющий положение центра масс находим как:
Движение центра масс
Выражение для скорости центра масс ($<overline>_c=frac>_c>
где $overline
$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (10) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач с решением
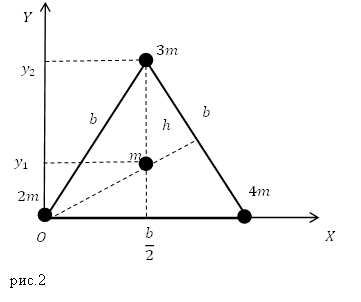
Задание. Запишите координаты центра масс системы из трех шариков, которые находятся в вершинах и центра равностороннего треугольника, сторона которого равна $b (м)$ (рис.2).
Решение. Для решения задачи используем выражения, определяющие координаты центра масс:
Из рис.2 мы видим, что абсциссы точек:
[left< begin m_1=2m, x_1=0;; \ <rm >m_2=3m, x_2=frac<2>;; \ m_3=m, x_3=frac<2>;; \ m_4=4m, x_4=b. end right.left(2.3right).]
Тогда абсцисса центра масса равна:
Найдем ординаты точек.
Для нахождения ординаты $y_2$ вычислим, чему равна высота в равностороннем треугольнике:
Ординату $y_3$ найдем, помня, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, получаем:
Вычислим ординату центра масс:
Задание. Запишите закон движения центра масс.
Решение. Закон изменения импульса системы частиц является законом движения центра масс. Из формулы:
при постоянной массе $M$ продифференцировав обе части выражения (2.1), получим:
Выражение (2.2) означает, что скорость изменения импульса системы равняется произведению массы системы на ускорение ее центра масс. Так как
В соответствии с выражением (2.4) получаем, что центр масс системы движется так, как двигалась бы одна материальная точка массы M, если на нее действует сила, равная сумме всех внешних сил, действующих на частицы, которые входят в рассматриваемую систему. Если $sumlimits^N_<<overline>_i=0,>$ то центр масс движется равномерно и прямолинейно.
http://oyla.xyz/article/kak-resat-zadacki-po-geometrii-metod-mass
http://www.webmath.ru/poleznoe/fizika/fizika_67_centr_mass.php
Download Article
Download Article
The center of gravity, or centroid, is the point at which a triangle’s mass will balance. To help visualize this, imagine you have a triangular tile suspended over the tip of a pencil. The tile will balance if the pencil tip is placed at its center of gravity. Finding the centroid might be necessary in various design and engineering applications, and can be found by using simple geometry.
-
1
Find the midpoint of one side of the triangle. To find the midpoint, measure the side, and divide the length in half. Label the midpoint A.
- For example, if one side of the triangle is 10 cm long, the midpoint will be at 5 cm, since
.
- For example, if one side of the triangle is 10 cm long, the midpoint will be at 5 cm, since
-
2
Find the midpoint of a second side of the triangle. Measure the length of the side, and divide the length in half. Label the midpoint B.[1]
- For example, if the side of the triangle is 12 cm long, the midpoint will be at 6 cm, since
.
Advertisement
- For example, if the side of the triangle is 12 cm long, the midpoint will be at 6 cm, since
-
3
Draw a line from the midpoint of each side to its opposite vertex. These two lines are the median of each side.[2]
- A vertex is the point at which two sides of a triangle meet.
-
4
Draw a point where the two medians intersect. This point is the triangle’s center of gravity, also called the centroid, or center of mass.[3]
- The center of gravity is where the three medians intersect, but since the medians only intersect in one point, you can use a shortcut and find the center of gravity by only finding the intersection of two medians.
Advertisement
-
1
Draw a median of your triangle. Remember, the median is a line drawn from the midpoint of a side to the opposite vertex. You can use any median in the triangle.
-
2
Measure the length of the median. Make sure the measurement is exact.
- For example, you might have a median that is 3.6 cm long.
-
3
Divide the length of the median into thirds. To do this, divide the length by three. Again, make an exact calculation. If you round, you will not find the center of gravity.
- For example, if your median is 3.6 cm long, you would divide 3.6 by 3:
, so ⅓ of the median is 1.2 cm.
- For example, if your median is 3.6 cm long, you would divide 3.6 by 3:
-
4
Mark a point on the median ⅓ from the midpoint. This point is the triangle’s centroid, which will always divide a median into a 2:1 ratio; that is, the centroid is ⅓ the median’s distance from the midpoint, and ⅔ the median’s distance from the vertex.[4]
- For example, on a median that is 3.6 cm long, the centroid will be 1.2 cm up from the midpoint.
Advertisement
-
1
Determine the coordinates of the three vertices of the triangle. This method only works if you are working with a coordinate plane. The coordinates may already be given, or you may have a triangle drawn on a graph without the coordinates labeled. Remember that coordinates should be listed
.[5]
- For example, you might be given triangle PQR, and you need to find and label point P (3, 5), point Q (4, 1), and R (1, 0).
-
2
Add the value of the x-coordinates. Remember to add all three coordinates. You will not calculate the correct center of gravity if you only use two coordinates.[6]
- For example, if your three x-coordinates are 3, 4, and 1, add these three values together:
.
- For example, if your three x-coordinates are 3, 4, and 1, add these three values together:
-
3
Add the value of the y-coordinates. Remember to add all three coordinates.[7]
- For example, if your three y-coordinates are 5, 1, and 0, add these three values together:
.
- For example, if your three y-coordinates are 5, 1, and 0, add these three values together:
-
4
Find the average of the x- and y-coordinates. These coordinates will correspond to the triangle’s center of gravity, also known as the centroid or center of mass.[8]
To find the average, divide the sum of the coordinates by 3. -
5
Plot the center of gravity on the triangle. The center of gravity, or centroid, is the average of the x- and y-coordinates.[9]
- In the example problem, the center of gravity is the point
.
- In the example problem, the center of gravity is the point
Advertisement
Add New Question
-
Question
The length of a rectangle is x units and the width is x-5. How do I find an equation for the perimeter and area of the rectangle?
For the perimeter, add the four sides together and simplify. For the area, multiply the length by the width.
-
Question
Is the center of gravity of triangular cardboard outside or on the body?
The center of gravity is always inside the triangle.
-
Question
How can I determine the center of gravity of an Isoceles triangle without knowing the mass?
The horizontal coordinate will be half of the base, and the vertical will be one third of the height.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
It does not matter which side you select, the center of gravity will be at the same point. If you perform this process on all three sides, the lines will cross at a single point.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate the center of gravity of a triangle, start by drawing a line from the midpoint of any 1 of the sides to the opposite vertex to create a median. Next, measure the median and divide it into thirds. For example, if the median is 3.6 cm long, mark the spots that are 1.2 cm and 2.4 cm along the median, starting from the midpoint. The spot that’s 1.2 inches from the midpoint is the centroid, or the center of gravity of the triangle. To learn more, like how to find the center of gravity of a triangle using intersecting medians, scroll down.
Did this summary help you?
Thanks to all authors for creating a page that has been read 274,504 times.
Did this article help you?
Загрузить PDF
Загрузить PDF
Центр тяжести треугольника (центроид) – это точка центра масс. Представьте себе треугольную линейку, положенную на кончик карандаша. Линейка будет балансировать, если кончик карандаша будет находиться в ее центре тяжести. Расположение центроида, которое легко находится с помощью геометрии, необходимо знать при работе над дизайнерским или инженерным проектом.
-
1
Найдите середину одной стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой A.
- Например, если сторона треугольника равна 10 см, то середина находится на расстоянии 5 см (
) от вершины треугольника.
- Например, если сторона треугольника равна 10 см, то середина находится на расстоянии 5 см (
-
2
Найдите середину второй стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой В.
- Например, если вторая сторона треугольника равна 12 см, то середина находится на расстоянии 6 см (
) от вершины треугольника.
- Например, если вторая сторона треугольника равна 12 см, то середина находится на расстоянии 6 см (
-
3
Соедините середины сторон с противолежащими вершинами. Вы получите две медианы.[1]
- Вершина – это точка, в которой сходятся две стороны треугольника.
-
4
Отметьте точку пересечения двух медиан. Эта точка является центром тяжести треугольника.[2]
[3]
- Центр тяжести находится на пересечении трех медиан, но так как медианы всегда пересекаются в одной точке, можно работать только с двумя медианами.
Реклама
-
1
Проведите медиану. Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. Можно работать с любой медианой.
-
2
Измерьте длину медианы. Сделайте это аккуратно и точно.
- Например, медиана равна 3,6 см.
-
3
Найдите третью часть (треть) медианы. Для этого разделите длину медианы на три. Сделайте это аккуратно и точно. Округлив полученное значение, вы не найдете центроид.
- В нашем примере медиана равна 3,6 см. Поэтому разделите 3,6 на 3:
. Таким образом, треть медианы равна 1,2 см.
- В нашем примере медиана равна 3,6 см. Поэтому разделите 3,6 на 3:
-
4
Треть медианы отметьте точкой. Эта точка является центроидом, потому что он всегда делит медиану треугольника в отношении 2:1. То есть центр тяжести находится на расстоянии, которое равно ⅓ длины медианы, от середины стороны, или на расстоянии, которое равно ⅔ длины медианы, от вершины треугольника.[4]
- Например, если медиана равна 3,6 см, то центроид находится на расстоянии 1,2 см от середины стороны.
Реклама
-
1
Определите координаты трех вершин треугольника. Координаты могут быть даны; в противном случае будет дан треугольник, построенный на координатной плоскости. Координаты представляются в виде
.
- Например, дан треугольник PQR, вершины которого имеют следующие координаты: P (3,5), Q (4,1), R (1,0).
-
2
Сложите значения координат «х». Не забудьте сложить все три значения. Вы не найдете центр тяжести, если будете работать только с двумя значениями.
- Например, если координаты «х» равны 3, 4 и 1, сложите эти значения:
.
- Например, если координаты «х» равны 3, 4 и 1, сложите эти значения:
-
3
Сложите значения координат «у». Не забудьте сложить все три значения.
- Например, если координаты «у» равны 5, 1 и 0, сложите эти значения:
.
- Например, если координаты «у» равны 5, 1 и 0, сложите эти значения:
-
4
Найдите средние значения сумм координат «х» и «у». Полученные значения будут соответствовать центру тяжести треугольника.[5]
Чтобы найти среднее значение, разделите каждую сумму на 3. -
5
Нанесите точку центра тяжести на треугольник. Центр тяжести находится в точке, координаты которой равны средним значениям сумм координат «х» и «у».
- В нашем примере центр тяжести – это точка с координатами
.
Реклама
- В нашем примере центр тяжести – это точка с координатами
Советы
- Не имеет значения, с какой стороной треугольника вы работаете – центр тяжести будет находится в одной и той же точке. Если построить медианы для всех трех сторон, они пересекутся в одной точке.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 145 472 раза.
Была ли эта статья полезной?
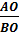
кружка для учащихся 9 классов
«Метод
масс при решении геометрических задач»
Солдатова
Светлана Анатольевна
учитель
математики высшей категории
МОУ
Угличский физико-математический лицей
Цели и задачи:
-
Образовательная:
познакомиться
с теорией способа решения задач методом
геометрии масс, повысить уровень
культуры решения геометрических задач. -
Воспитательная:
формировать личностные качества:
сосредоточенность и внимание;
настойчивость в достижение цели. -
Развивающая:
развивать познавательные интересы в
процессе решения геометрических задач
и поиска рационального решения, умения
владеть математической терминологией,
умения применять знания, полученные
на других предметах, правильно и четко
выражать мысль.
В школьном курсе
математики тема «Геометрия масс» не
рассматривается. Решения задач на
отношение длин при решении обычными
методами получаются достаточно объёмными.
Данный метод необходим для рационального
решения задач.
Родоначальником
метода был великий древнегреческий
мыслитель Архимед. Еще в III в. до н. э. он
обнаружил возможность доказывать новые
математические факты с помощью свойств
центра масс.
В частности, этим
способом им была установлена теорема
о том, что три медианы треугольника
пересекаются в одной точке. Соображения
Архимеда были позднее использованы и
развиты многими геометрами (Папп, Чева,
Гюльден, Люилье и др.).
-
Понятие центра масс
Чтобы понять, что
такое центр масс, рассмотрим детские
качели (рис.1).
рис.1
Многие замечали,
что более тяжелый ребёнок перевешивает.
Но стоит ему
начать приближаться ближе к центру, как
качели постепенно приходят в равновесие.
Насколько ближе он должен подвинуться
ответит метод масс. Переведём задачу
на язык математики
Пусть качели –
отрезок AB,
где m1,
m2
– массы, расположенные на концах качелей
(m1
>m2).
Центром масс
данной системы двух точек будет такая
точка О данного отрезка АВ, что АО·m1
= BO·m2,
или
= .
Чтобы найти
центр масс системы из двух точек, надо
всего лишь разбить отрезок в отношении,
обратно пропорциональном массам точек.
Пример:
Пусть масса, расположенная в точке A
равна 400г, а масса в точке B
равна 1400г (см. рис). Найти центр масс
данного отрезка.
Решение: из
определения центра масс получаем, что
точка O
делит отрезок AB
в отношении = . Значит центр масс O
делит отрезок так, что 7*АO
= 2*BO.
Принцип центра
масс является ничем иным, как законом
рычага, с помощью которого Архимед
собирался перевернуть Землю.
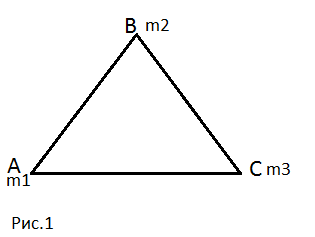
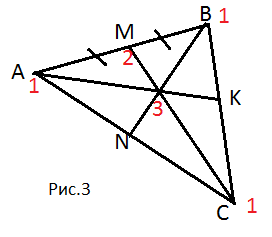
2 Центр масс системы
точек
Теперь найдём
центр масс треугольника. В точках A,
B,
C
расположены массы m1,
m2,
m3
(см. рис 1).
Если нам дана
система из нескольких точек с массой в
каждой из них, то если любую пару точек
заменить их центром масс, центр масс
исходной системы не изменится.
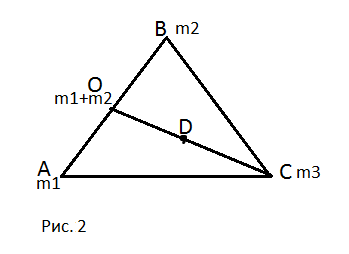
Таким образом
центр масс нашего треугольника (точка
D)
будет совпадать с центром масс точек O
(центр масс для точек A
и B)
и C
(рис.2).
Пример:
Дан треугольник ABC
с массами mA
= mB
= mC
= 1 в вершинах. Найти центр масс треугольника.
Решение: Для
начала найдём центр масс точек A
и B.
Это точка М, которая расположена в
середине отрезка AB,
т.к. на его концах одинаковые массы. В
точке М сосредоточена масса 1+1=2.
Значит центр масс
треугольника ABC
совпадает с центром масс отрезка MC
и делит отрезок в отношении 2:1 . Мы
доказали, что в треугольнике с одинаковыми
массами в вершинах его центр масс
расположен на медиане и делит её в
отношении 2:1. Аналогично можно найти
центр масс на медианах BN
и AK.
Однако у треугольника только один центр
масс, а значит мы все три раза попадали
в одну точку. Так мы доказали, что медианы
в треугольнике пересекаются в одной
точке и делятся ею в отношении 2:1 .
3 Задачи на применение
центра масс
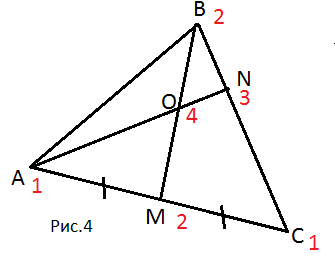
Задача 1:
Дан треугольник ABC
(рис.4). BM
– медиана, а AN
делит сторону BC
в отношении 1:2 от вершины B
и пересекается с BM
в точке O.
Найти отношение BO:OM.
Решение: Расположим
в вершинах A
и C
массы, равные 1, а в вершину B
– массу, равную 2. Тогда точка M
– центр масс для точек A
и C,
и концентрирует массу, равную 2. Точка
N
– центр масс отрезка BC,
т.к. BN:NC=1:2
(из условия), а mB:mC=2:1.
Предположим, что
точка O
– центр масс для отрезка BM.
Тогда она является и центром масс для
всего треугольника ABC
и концентрирует в себе массу 2+2=4. Если
O
– центр масс треугольника, то здесь же
и центр масс отрезка AN.
Проверим это. В точке A
сконцентрирована масса 1, в точке N
– 3, а в точке O
– 4.
1+3=4 , следовательно,
O
– центр масс отрезка AN
и всего треугольника. Тогда отношение
BO:OM
= 2:2 = 1.
Ответ: BO
= OM.
-
Дан
треугольник АВС, на стороне АС взята
точка Е так, что АЕ : ЕС = 2: 3, а на стороне
АВ взята точка D так, что АD : DB = 1: 4 .
Проведены отрезки СD и ВЕ. Найдите
отношение площади получившегося
четырехугольника к площади данного
треугольника. -
В
треугольнике ABC на
его медиане BM отмечена
точка K так,
что BK : KM =
7 : 3 . Прямая AK пересекает
сторону BC в
точке P.
Найдите отношение площади
треугольника BKP к
площади четырёхугольника KPCM. -
В
треугольнике АВС проведены чевианы ВМ
и АN
так, что ВN:
NC=2:3,
а АМ: МС=2:1. Найти ВО:ОМ и АО:ON,
где О – точка пересечения чевиан. -
В
треугольнике АВС на стороне ВС выбрана
точка D
так, что BD
: DC=1:2.
Медиана СЕ пересекает отрезок АD
в точке F.
Какую часть площади треугольника АВС
составляет площадь треугольника АЕF? -
Медиана BM и
биссектриса AP треугольника ABC пересекаются
в точке K,
длина стороны AC втрое
больше длины стороны AB.
Найдите отношение площади
треугольника ABK к
площади четырёхугольника KPCM. -
В треугольнике
АВС проведены чевианы ВМ и АN
так, что ВN:
NC=4:3,
а АМ: МС=2:3. Найти какую часть площади
АВС составляет площадь СМОN.
Использованная
литература:
-
М.Б.
Балк, В.Г.Болтянский. Геометрия масс.
Москва: Наука, 1987. -
Математика
в школе , №8, 2014 -
Материалы
сайта https://sdamgia.ru/
Центр тяжести (центр масс):
Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.
Центр тяжести — геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.
На каждую точку тела в поле сил тяжести действует сила, а на все тело — равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.
Центр масс (центр инерции) — точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.
При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.
Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.
При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, — параллельными.
Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.
Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.
Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.
Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.
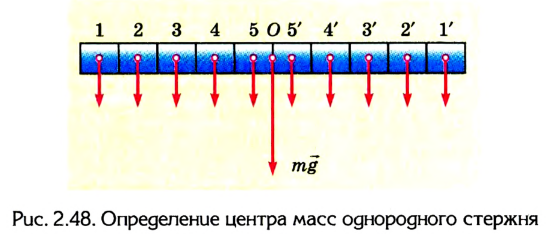
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О — середине стержня.
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.
Центр тяжести однородного стержня расположен в середине стержня.
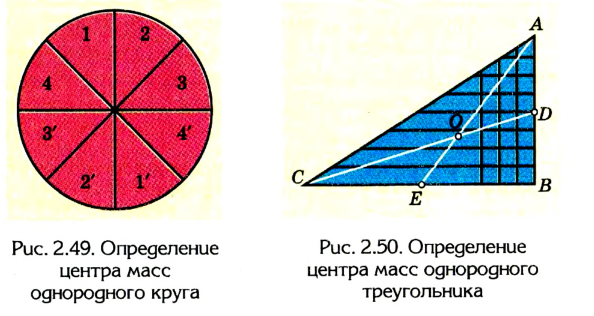
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.
Центр тяжести однородного круга совпадает с его центром.
Центр тяжести однородного треугольника находится в точке пересечения его медиан.
3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.
Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.
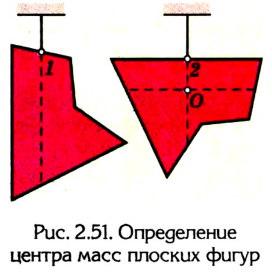
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.
Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.
Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.
- Заказать решение задач по физике
Центр тяжести тела и центр масс тела
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.
Рис. 151
Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:
или
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:
Рис. 152
Поскольку F=(m1 + m2)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.
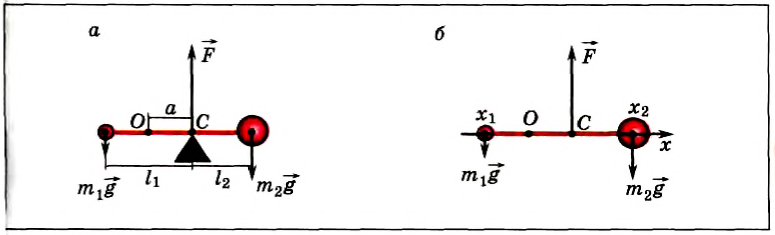
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х1, хс и х2. Запишем условие моментов относительно точки О:
Отсюда
При выводе этой формулы было использовано значение силы F = (m1 + m2) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии хс, определенном формулой (2).
Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.
Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.
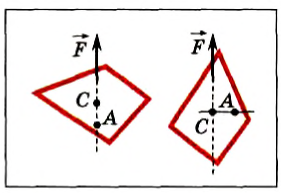
Если произвольное тело можно разбить на n элементов, массы которых m1, m2…, mn, и если известны координаты центров масс этих элементов x1, x2…, xn относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:
Естественно, что такие же соотношения можно записать и для ус и zc. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m1 = 2m2). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C1) и линейки (C2).
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х1 = 0, y1 =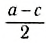
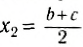
По формуле (3): .
Таким образом, центр масс угольника находится вне тела.
Главные выводы:
- Центр тяжести — точка, в которой приложена сила тяжести.
- Центр масс симметричных однородных тел находится в их геометрическом центре.
- Координаты центра масс тела можно вычислить по формуле (3).
- Импульс тела в физике
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике