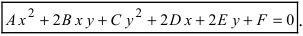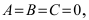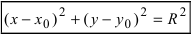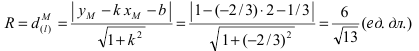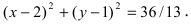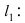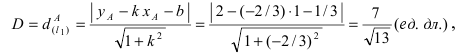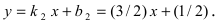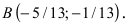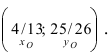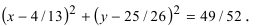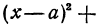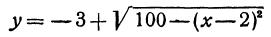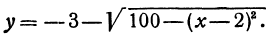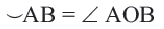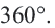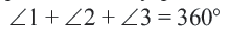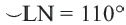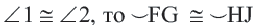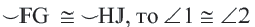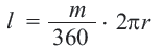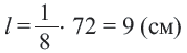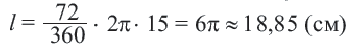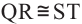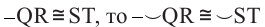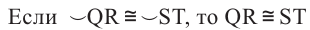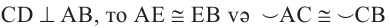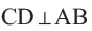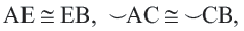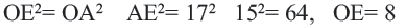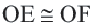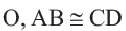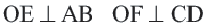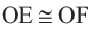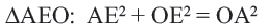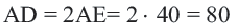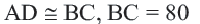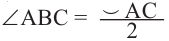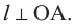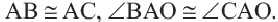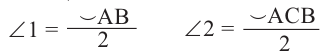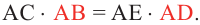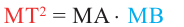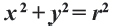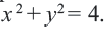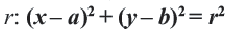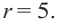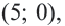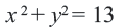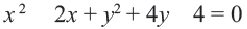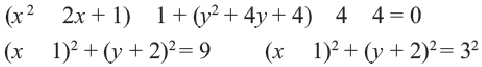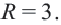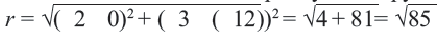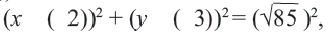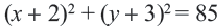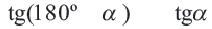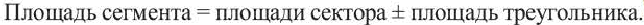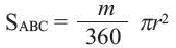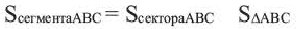Как найти центр окружности через координаты диаметра - Исправление недочетов и поиск решений вместе с Examum.ru

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Для каждой скобки применим метод выделения полного квадрата (подробнее смотри тут — Метод выделения полного квадрата), то есть заменим выражение вида на выражение вида . С учетом того, что коэффициенты при квадратах равны единице, а свободный член можно принять за ноль, формула для вычисления h и k упрощаются.

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

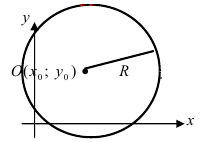
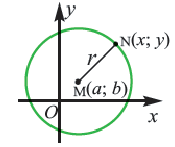
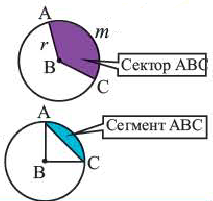
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

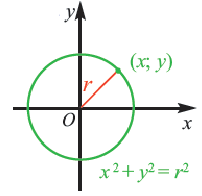
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

источники:

http://planetcalc.ru/9507/

http://www.calc.ru/Uravneniye-Okruzhnosti.html

Источник

Если окружность задана уравнением вида

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

найти центр (a;b) и радиус R такой окружности несложно.

Примеры.

Определить по уравнению окружности координаты её центра и радиуса:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

$[3){x^2} + {(y + 3)^2} = 9;]$

$[4){(x - 6)^2} + {y^2} = 5;]$

$[5){x^2} + {y^2} = 11.]$

Решение:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

a=3, b=7, R²=4.

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

$[3){x^2} + {(y + 3)^2} = 9;]$

a=0, b=-3, R²=9.

Центр окружности — (0;-3), радиус R=3.

$[4){(x - 6)^2} + {y^2} = 5;]$

a=6, b=0, R²=5.

Центр — в точке (6;0), радиус R=√5.

$[5){x^2} + {y^2} = 11.]$

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

$[{x^2} + {y^2} - 2ax - 2by + c = 0,]$

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

$[({x^2} - 2ax) + ({y^2} - 2by) + c = 0,]$

$[({x^2} - 2ax + {a^2}) - {a^2} + ({y^2} - 2by + {b^2}) - {b^2} + c = 0.]$

Отсюда

$[{(x - a)^2} + {(y - b)^2} + c - {a^2} - {b^2} = 0,]$

$[{(x - a)^2} + {(y - b)^2} = {a^2} + {b^2} - c.]$

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

$[R = sqrt {{a^2} + {b^2} - c} .]$

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.

Примеры.

Найти координаты центра и радиус окружности:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0;]$

$[2){x^2} + {y^2} - 5x + 4 = 0;]$

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0.]$

Решение:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0]$

Группируем слагаемые

$[({x^2} + 10x) + ({y^2} - 6y) - 15 = 0]$

$[{x^2} + 10x = ({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2}.]$

Аналогично

$[{y^2} - 6y = ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2}.]$

Таким образом,

$[({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2} + ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2} - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} - 25 - 9 - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} = 49]$

Центром этой окружности является точка (-5;3), радиус R=7.

$[2){x^2} + {y^2} - 5x + 4 = 0]$

$[({x^2} - 5x) + {y^2} + 4 = 0]$

$[({x^2} - 2 cdot x cdot 2,5 + {2,5^2}) - {2,5^2} + {y^2} + 4 = 0]$

$[{(x - 2,5)^2} + {y^2} + 4 - 6,25 = 0]$

$[{(x - 2,5)^2} + {y^2} = 2,25]$

Центр окружности — точка (2,5;0), радиус R=1,5.

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0]$

Разделим обе части уравнения на 3:

$[{x^2} + {y^2} - frac{4}{3}x - 3y + frac{4}{3} = 0]$

Далее — аналогично

$[({x^2} - frac{4}{3}x) + ({y^2} - 3y) + frac{4}{3} = 0]$

$[({x^2} - 2 cdot x cdot frac{2}{3} + {(frac{2}{3})^2}) - {(frac{2}{3})^2} + ({y^2} - 2 cdot y cdot frac{3}{2} + {(frac{3}{2})^2}) - ]$

$[ - {(frac{3}{2})^2} + frac{4}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} - frac{{{4^{backslash 4}}}}{9} - frac{{{9^{backslash 9}}}}{4} + frac{{{4^{backslash 12}}}}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} = frac{{49}}{{36}}]$

Центр этой окружности лежит в точке

$[(frac{2}{3};frac{3}{2}),R = frac{7}{6}.]$

Источник

Как найти координаты центра окружности

Окружность − геометрическое место точек плоскости, равноудаленных от центра на некоторое расстояние, называемое радиусом. Если задана нулевая точка отсчета, единичный отрезок и направление координатных осей, центр окружности будет характеризоваться определенными координатами. Как правило, окружность рассматривают в декартовой прямоугольной системе координат.

Инструкция

Аналитически окружность задается уравнением вида (x-x0)²+(y-y0)²=R², где x0 и y0 − координаты центра окружности, R − ее радиус. Итак, центр окружности (x0;y0) здесь задан в явном виде.

Пример. Установите центр фигуры, заданной в декартовой системе координат уравнением (x-2)²+(y-5)²=25.Решение. Данное уравнение является уравнением окружности. Ее центр имеет координаты (2;5). Радиус такой окружности равен 5.

Уравнение x²+y²=R² соответствует окружности с центром в начале координат, то есть, в точке (0;0). Уравнение (x-x0)²+y²=R² означает, что центр окружности имеет координаты (x0;0) и лежит на оси абсцисс. Вид уравнения x²+(y-y0)²=R² говорит о расположении центра с координатами (0;y0) на оси ординат.

Общее уравнение окружности в аналитической геометрии запишется как: x²+y²+Ax+By+C=0. Чтобы привести такое уравнение к выше обозначенному виду, надо сгруппировать члены и выделить полные квадраты: [x²+2(A/2)x+(A/2)²]+[y²+2(B/2)y+(B/2)²]+C-(A/2)²-(B/2)²=0. Для выделения полных квадратов, как можно заметить, требуется добавлять дополнительные величины: (A/2)² и (B/2)². Чтобы знак равенства сохранялся, эти же величины надо вычесть. Прибавление и вычитание одного и того же числа не меняет уравнения.

Таким образом, получается: [x+(A/2)]²+[y+(B/2)]²=(A/2)²+(B/2)²-C. Из этого уравнения уже видно, что x0=-A/2, y0=-B/2, R=√[(A/2)²+(B/2)²-C]. Кстати, выражение для радиуса можно упростить. Домножьте обе части равенства R=√[(A/2)²+(B/2)²-C] на 2. Тогда: 2R=√[A²+B²-4C]. Отсюда R=1/2·√[A²+B²-4C].

Окружность не может быть графиком функции в декартовой системе координат, так как, по определению, в функции каждому x соответствует единственное значение y, а для окружности таких «игреков» будет два. Чтобы убедиться в этом, проведите перпендикуляр к оси Ox, пересекающий окружность. Вы увидите, что точек пересечения две.

Но окружность можно представить как объединение двух функций: y=y0±√[R²-(x-x0)²]. Здесь x0 и y0, соответственно, представляют собой искомые координаты центра окружности. При совпадении центра окружности с началом координат объединение функций принимает вид: y=√[R²-x²].

Обратите внимание

Две окружности, имеющие центром точку с одними и теми же координатами, называются концентрическими. Если они заданы уравнениями (x-x0)²+(y-y0)²=R² и (x-x0′)²+(y-y0′)²=R’², тогда x0=x0′, y0=y0′. В общем уравнении для концентрических окружностей A1=A2 и B1=B2.

Полезный совет

Кстати, в физике окружность может рассматриваться как тонкое однородное кольцо. Центр этого кольца будет являться центром масс (или центром инерции) такого тела. Если кольцо имеет массу m и радиус r, а через центр перпендикулярно плоскости кольца провести ось, то момент инерции кольца относительно оси будет равен mr². Момент инерции принципиально важен при рассмотрении вращательного движения тела.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

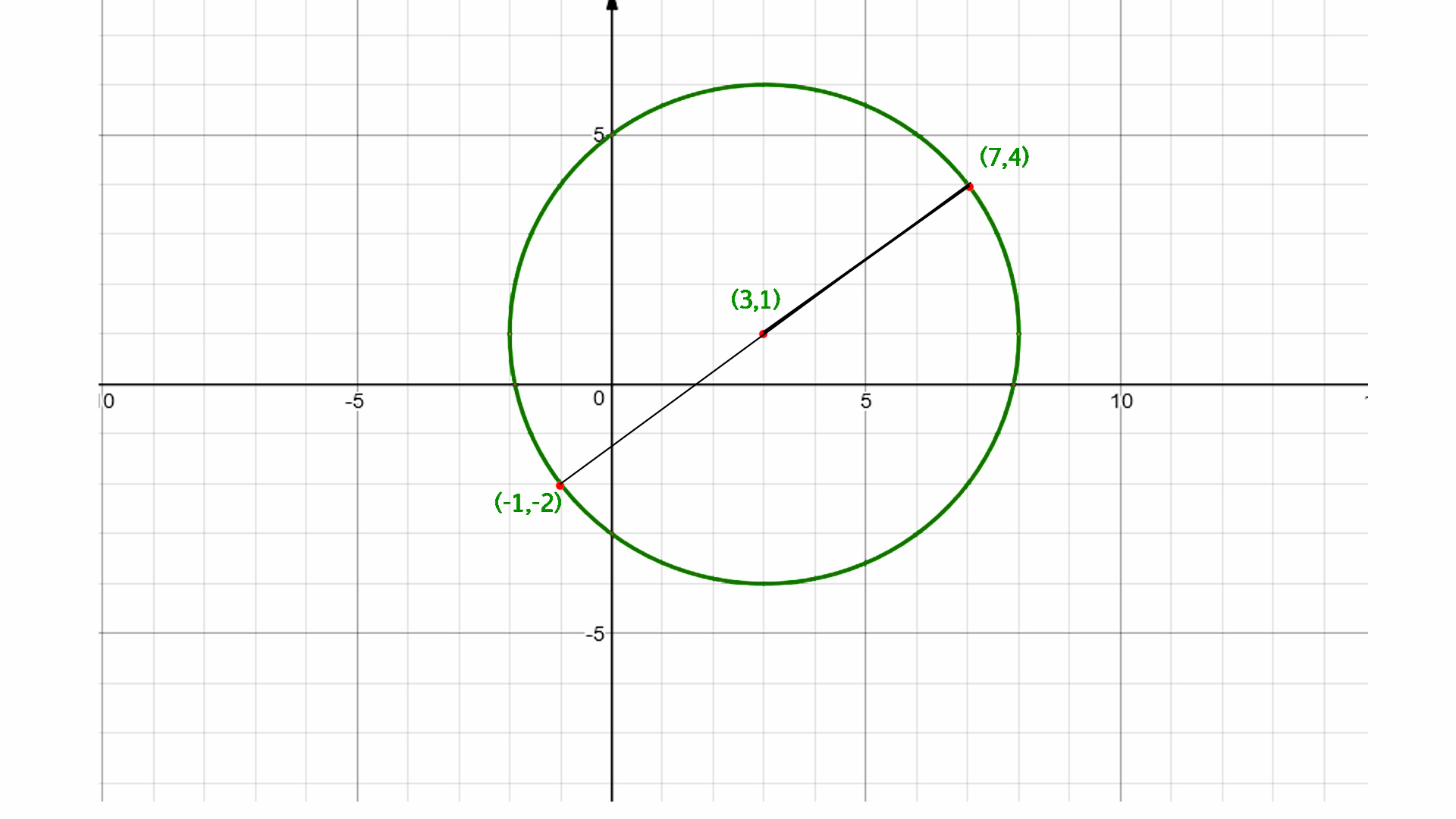
Given two endpoint of diameter of a circle (x1, y1) and (x2, y2) find out the center of a circle.
Examples :

Input  : x1 = -9, y1 = 3, and 
         x2 = 5, y2 = –7
Output : -2, –2

Input  :  x1 = 5, y1 = 3 and 
          x2 = –10 y2 = 4
Output : –2.5, 3.5

Midpoint Formula:
The midpoint of two points, (x1, y2) and (x2, y2) is : M = ((x ₁ + x ₂) / 2, (y ₁ + y ₂) / 2)
The center of the circle is the mid point of its diameter so we calculate the mid point of its diameter by using midpoint formula.

C++

#include <iostream>

using namespace std;

void center(int x1, int x2,

int y1, int y2)

{

cout << (float)(x1 + x2) / 2 <<

", " << (float)(y1 + y2) / 2;

}

int main()

{

int x1 = -9, y1 = 3, x2 = 5, y2 = -7;

center(x1, x2, y1, y2);

return 0;

}

Java

class GFG {

static void center(int x1, int x2,

int y1, int y2)

{

System.out.print((float)(x1 + x2) / 2

+ ", " + (float)(y1 + y2) / 2);

}

public static void main(String arg[]) {

int x1 = -9, y1 = 3, x2 = 5, y2 = -7;

center(x1, x2, y1, y2);

}

Python3

def center(x1, x2, y1, y2) :

print(int((x1 + x2) / 2), end= "")

print(",", int((y1 + y2) / 2) )

x1 = -9; y1 = 3; x2 = 5; y2 = -7

center(x1, x2, y1, y2)

C#

using System;

class GFG {

static void center(int x1, int x2,

int y1, int y2)

{

Console.WriteLine((float)(x1 + x2) / 2

+ ", " + (float)(y1 + y2) / 2);

}

public static void Main() {

int x1 = -9, y1 = 3, x2 = 5, y2 = -7;

center(x1, x2, y1, y2);

}

PHP

<?php

function center($x1, $x2, $y1, $y2)

{

echo((float)($x1 + $x2) / 2 . ", " .

(float)($y1 + $y2) / 2);

}

$x1 = -9; $y1 = 3; $x2 = 5; $y2 = -7;

center($x1, $x2, $y1, $y2);

?>

Javascript

<script>

function center(x1, x2,

y1, y2)

{

document.write((x1 + x2) / 2

+ ", " + (y1 + y2) / 2);

}

let x1 = -9, y1 = 3, x2 = 5, y2 = -7;

center(x1, x2, y1, y2);

</script>

Output :

-2, -2

Time complexity: O(1)
Auxiliary Space: O(1)

Last Updated :
20 Feb, 2023

Like Article

Save Article

Источник

Содержание:

Окружность:

Определение: Кривой второго порядка называется линия, описываемая уравнением

Замечание: Если коэффициенты

При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.

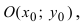
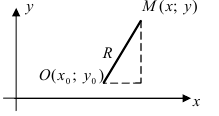
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки называемой центром окружности, на расстояние R, которое называется радиусом окружности.

Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:

Рис. 27. Вывод уравнения окружности.

Из рисунка видно, что по теореме Пифагора 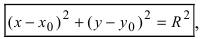которое определяет уравнение окружности (Рис. 28):

Рис. 28. Окружность.

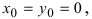
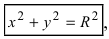
Если то уравнение принимает вид который называется каноническим уравнением окружности.

Пример:

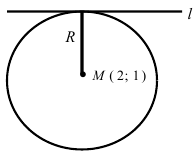
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 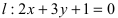является касательной к окружности.

Решение:

Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.

В уравнении окружности 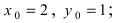таким образом оно имеет вид:

Пример:

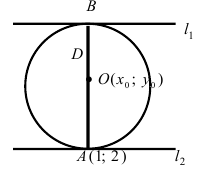
Составить уравнение окружности, касающейся двух параллельных прямых 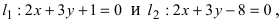причем одной из них в т. А (1; 2).

Решение:

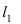
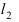
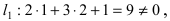
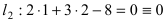
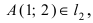
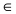
Прежде всего определим, на какой из прямых или лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых

следовательно, точка A(1; 2) принадлежит линии (в сокращенной форме это предложение пишут так: где значок означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой

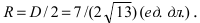
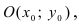
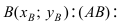
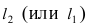
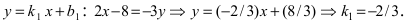
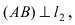
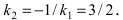
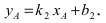
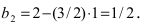
а радиус окружности Найдём координаты центра окружности точки которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом Так как прямаято её угловой коэффициент Прямая (АВ) проходит через известную точку A(1;2), следовательно, Отсюда находим Таким образом,уравнение прямой (АВ):

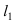
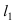
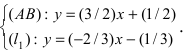
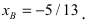
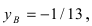
Найдем координаты точки B, которая является пересечением прямых и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых и (АВ): (В): Подставим выражение для переменной у из второго у равнения в первое, получим Подставив это значение во второе уравнение системы, найдем т.е.

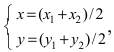
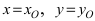
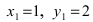
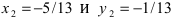
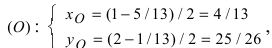
Для вычисления координат точки О применим формулы деления отрезка пополам (О): в этой формуле (координаты точки О), (координаты точки А), (координаты точки В), следовательно, т.е. координаты точки О

Таким образом, уравнение искомой окружности имеет вид:

Окружность в высшей математике

Рассмотрим уравнение

которое получается из уравнения (I), если положить , .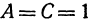

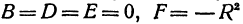
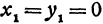
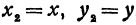
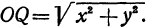
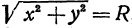
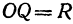
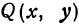
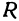
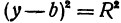
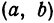
Если в формулу, выражающую расстояние между двумя точками, подставить , , то получим Из уравнения (1) находим, что , т. е. . Это значит, что все точки , координаты которых удовлетворяют уравнению (1), находятся на расстоянии от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса с центром в начале координат. Аналогично получаем, что уравнение определяет окружность радиуса с центром в точке .

Пример:

Найдем уравнение окружности с центром в точке и радиусом, равным 10.

Решение:

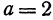
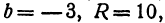
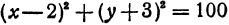
Полагая, получим .

Разрешим это уравнение относительно 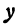, будем иметь

Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.

Центральный угол. Градусная мера дуги

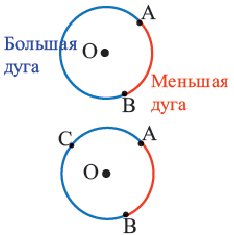
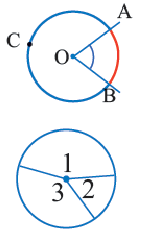
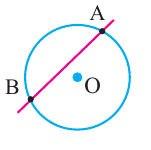
Дуга окружности. Если отметить на окружности точки и , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка является какой-либо точкой дуги , то . Если точки и являются концами диаметра, го каждая дуга является полуокружностью.

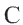
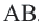
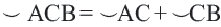
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла:

Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна

Дуги окружности и их величины

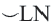
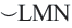
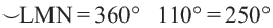
Пример: минорная дуга:

мажорная дуга:

Конгруэнтные дуги

В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.

Если

Длина дуги

Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.

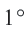
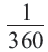
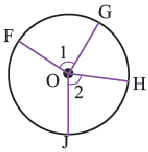
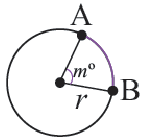
Длина дуги в равна части длины окружности.

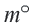
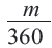
Длина дуги, соответствующей центральному углу с градусной мерой , составляет части длины окружности:

Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)

Пример №1

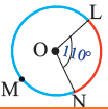
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу .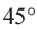

Решение:

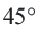
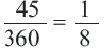
Так как центральный угол составляет часть полного угла, то длина искомой дуги:

Пример №2

Найдите длину дуги, соответствующей центральному углу 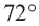в окружности радиусом 15 см.

Решение: подставляя значения 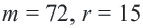в формулу длины дуги находим:

Окружность и хорда

Теорема о конгруэнтных хордах

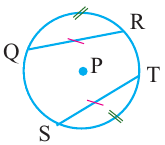
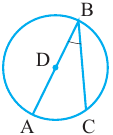
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.

Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.

1)Если 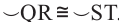, то

2)Если

Доказательство теоремы 1:

Теорема о серединном перпендикуляре хорд

Теорема 2.

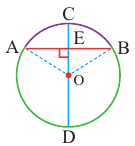
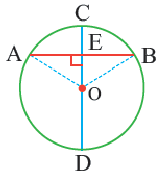
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.

Если

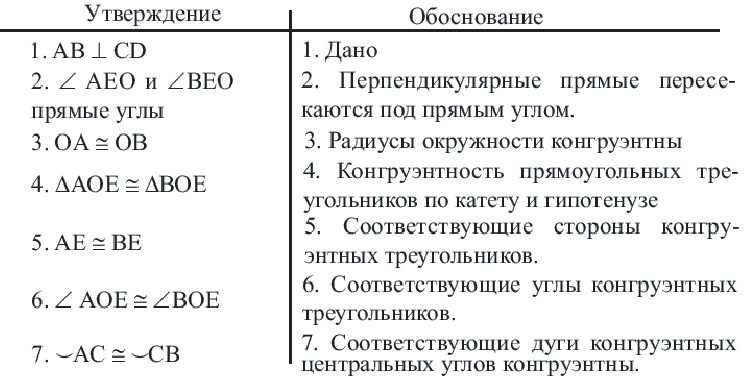
Доказательство теоремы 2.

Дано: — центральный угол,

Докажите:

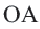
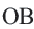
Начертите радиусы и окружности.

Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.

Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.

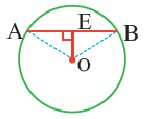
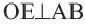
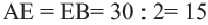
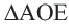
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если , то . Из по теореме Пифагора имеем:

Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности

Теорема 3.

Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.

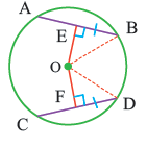
Если 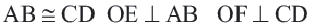, то

Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.

Доказательство теоремы 3

Дано: Окружность с центром

Докажите:

Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. и — серединные перпендикуляры конгруэнтных хорд и . , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности и : . Прямоугольные треугольники, и конгруэнтны (по катету и гипотенузе). Так как и являются соответствующими сторонами данных треугольников, то они конгруэнтны: . Теорема доказана.

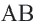
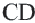
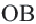
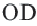
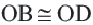
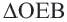
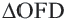
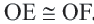
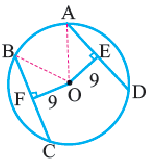
Задача. Хорды и находятся на одинаковом расстоянии от центра окружности. . Если радиус окружности равен 41 единице, то найдите .

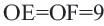
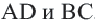
Решение: Так как хорды и находятся на одинаковом расстоянии от центра, то они конгруэнтны: Соединим точки и с точкой В прямоугольном треугольнике ; ; ;

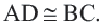
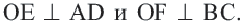
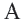
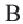
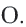
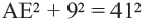
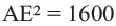
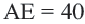
Так как

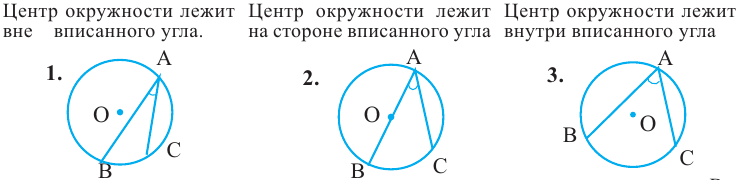
Угол, вписанный в окружность

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.

является углом вписанным в окружность с центром , а дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.

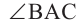
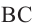
Угол, вписанный в окружность:

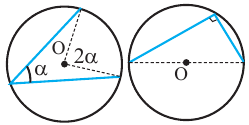
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается.

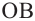
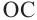
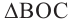
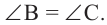
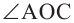
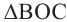
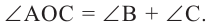
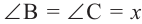
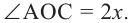
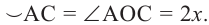
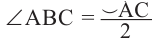
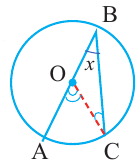
Доказательство (текстовое): и радиусы окружности и равнобедренный треугольник. Значит, Так как является внешним углом , Если примем, что , то Так как градусные меры центрального угла и опирающейся на него дуги равны, то Следовательно, .

Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.

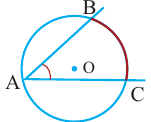
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.

Конгруэнтные углы, вписанные в окружность

Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. , .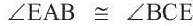

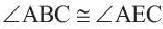
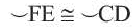
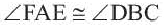
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если , то .

Касательная к окружности

Касательная. Признак касательной

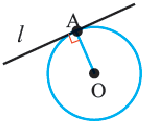
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

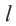
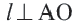
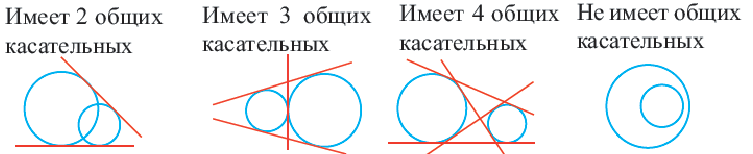
Прямая является касательной к окружности. Значит, Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.

Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.

Доказательство теоремы 1. Если прямая — касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая не перпендикулярна радиусу Проведем и на прямой выделим отрезок Тогда так как Значит, точка также находится на окружности. То есть прямая имеет с окружностью две общие точки, что противоречит условию. Значит,

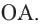
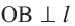
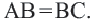
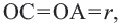
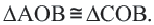
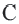
Свойства касательных, проведенных к окружности из одной точки

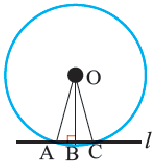
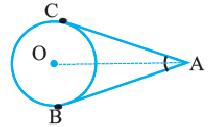
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.

и касательные, проведенные из точки к окружности с центром

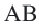
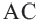
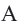
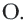
Углы, образованные секущими и касательными

Прямая, имеющая две общие точки с окружностью, называется секущей окружности.

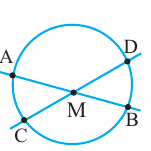
Углы между двумя секущими

Вершина угла находится внутри окружности

Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному.

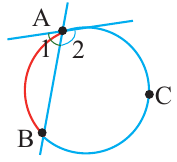
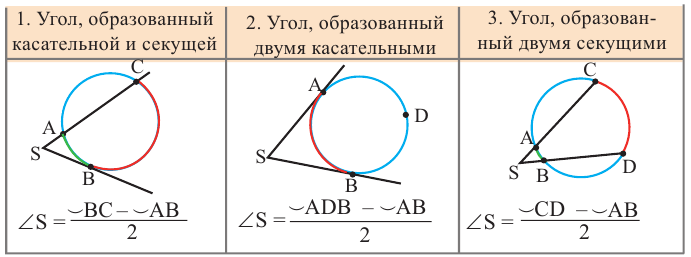
Углы между касательной и секущей

Вершина угла находится на окружности

Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.

Углы, образованные касательной и секущей

Вершина угла находится вне окружности

Теорема 1.

Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.

Отрезки секущих и касательных

Длина отрезков, секущих окружность

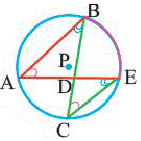
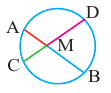
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.

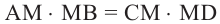
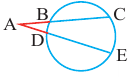
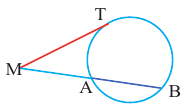
Теорема 2. Если из точки провести две прямые, пересекающие окружность соответственно в точках и , и то верно равенство

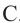
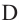
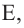
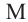
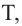
Теорема 3. Если из точки проведены прямая, которая пересекает окружность в точках и и касательная к окружности в точке то верно равенство:

Уравнение окружности

Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом и с центром в начале координат. Расстояние между центром окружности и ее любой точкой равно радиусу окружности.

Расстояние между двумя точками

Упрощение

Возведение обеих частей в квадрат

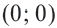
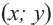
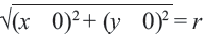
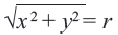
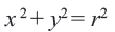
Уравнение окружности с центром в начале координат и радиусом :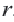

Например, уравнение окружности с центром в начале координат 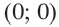и радиусом 2 имеет вид:

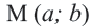
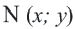
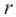
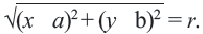
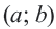
По формуле расстояния между центром окружности и точки на окружности радиуса имеем Возведя в квадрат обе части, получаем уравнение окружности с центром в точке и радиусом

Например, уравнение окружности с центром в точке 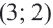и радиусом 4 имеет вид:

Пример №3

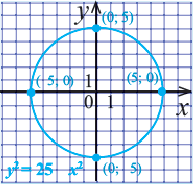
Постройте на координатной плоскости окружность, заданную уравнением

Решение: Напишем уравнение в виде 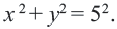Как видно,

Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 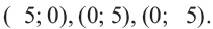Проведем окружность через эти точки.

Пример №4

Точка 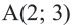находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.

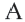
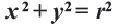
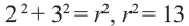
Решение: Записав координаты точки в уравнении , получим: Уравнение этой окружности:

Пример №5

Найдем центр и радиус окружности, заданной уравнением

Решение:

Центр окружности точка 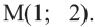Радиус

Пример №6

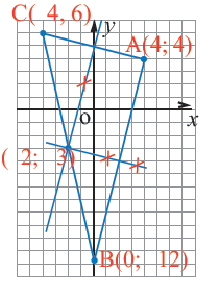
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 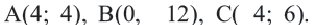На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.

Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 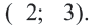Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,

Уравнение окружности:

Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.

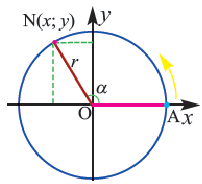
Координаты точек, находящихся на окружности, и тригонометрические отношения

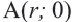
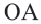
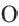
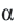
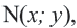
Если точка при повороте радиуса вокруг точки против движения часовой стрелки на угол преобразуется в точку то

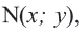
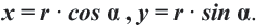
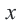
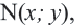
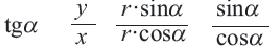
Для координат точки соответствующей углу поворота на окружности, верны формулы В этих формулах — угол, отсчитываемый от положительной оси против движения часовой стрелки. Если точка не находится на оси ординат, то .

Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 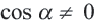почленным делением получаем:

С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.

Сектор и сегмент

Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.

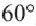
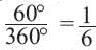
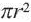
Например, часть круга, соответствующая центральному углу , составляет часть всего круга. Так как площадь круга , то площадь этого сектора будет Сегмент часть круга, ограниченная хордой и соответствующей дугой.

Площадь сектора

Площадь сектора:

Площадь сегмента:

Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь

Эллипс
Гипербола
Парабола
Многогранник
Сфера в геометрии
Шар в геометрии
Правильные многогранники в геометрии
Многогранники

Источник