Как найти центр окружности на графике - Исправление недочетов и поиск решений вместе с Examum.ru

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
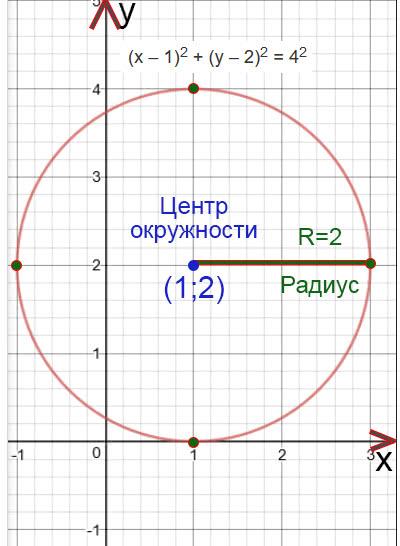
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Уравнение с двумя переменными и его график. Уравнение окружности

п.1. Понятие уравнения с двумя переменными

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.

Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm<frac1x>) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

Симметричное отображение относительно оси OY

Симметричное отображение относительно оси OX

Центральная симметрия относительно начала координат

Параллельный перенос графика на a единиц вправо

Параллельный перенос графика на a единиц влево

Параллельный перенос графика на b единиц вниз

Параллельный перенос графика на b единиц вверх

Сжатие графика к оси OY в a раз

Сжатие графика к оси OX в b раз

F(x; by) = 0
0 Например:

Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm <(x-2)^2+(y-1)^2=9>$$

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<7>=-frac<2> + 2 > ) – это прямая

б) xy + 4 = 0
Выразим y из уравнения: ( mathrm> ) – это гипербола

в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm=2> )

г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<5>> ) – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<5>=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) (mathrm<frac<|x-1|><2>+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

источники:

http://reshator.com/sprav/algebra/9-klass/uravnenie-s-dvumya-peremennymi-i-ego-grafik-uravnenie-okruzhnosti/

Найти центр и радиус окружности

Источник

Каждое уравнение с
двумя переменными х и у определяет некоторое множество пар (х; у) значений
переменных, которые являются решениями этого уравнения, т. е. задаёт некоторое
отношение между значениями переменной х и значениями
переменной у. График отношения, заданного уравнением с двумя
переменными, или, короче, график уравнения с двумя переменными, есть, как
известно, множество точек плоскости, координаты которых служат решениями
уравнения. Мы знаем, что графиком уравнения вида ax + by = c,
где a ≠ 0 или b ≠ 0,
служит прямая линия, график уравнения вида

y = ax² +
bx + c (a ≠ 0)

парабола, график
уравнения вида

xy = k

гипербола.

На рисунку
изображён график уравнения

х² + 9у²
= 81.

Кривая такого вида
называется эллипсом.

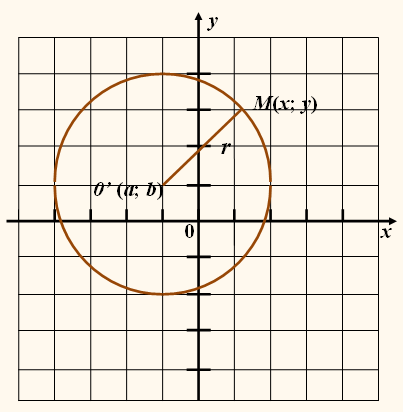
Графиком уравнения

(x – a)² +
(y – b)² =
r²

является окружность на координатной плоскости хОу с центром в точке О’(a; b) и радиусом
r (r
> 0).

Уравнением фигуры
на плоскости в декартовых координатах
называется уравнение с двумя переменными
х и у, которые будут координатами любой точки фигуры. И наоборот:
любые два числа, которые будут решением этого уравнения, будут координатами некоторой
точки фигуры.

Составим уравнение окружности
с центром в точке А₀(а; b) и радиусом R.

Возьмём произвольную
точку А(х; у) на окружности. Расстояние от неё до
центра А₀ равно R. Квадрат расстояния от точки А до А₀ равен:

(х – a)²
+ (у – b)².

Таким образом, координаты х, у каждой точки А окружности будут корнями уравнения:

(х – a)²
+ (у – b)² = R².

Наоборот: любая
точка А, координаты которой будут решениями уравнения, принадлежат окружности, так как расстояние
от неё до точки А₀ равно R. Отсюда вытекает, что это уравнение будет уравнением окружности
с центром А₀ и радиусом
R.

Обратите внимание, что
когда центром окружности будет начало координат, то уравнение окружности имеет
вид:

х² + у² = R².

ПРИМЕР:

Какая геометрическая фигура задано уравнением ?

х² + у²
+ ах + bу + с = 0.

РЕШЕНИЕ:

видим, что искомая фигура – окружность с центром

ПРИМЕР:

Построить график уравнения:

х² + у²
= 16.

Перепишем уравнение в виде

(х – 0)² + (у – 0)² = 4².

Графиком этого уравнения является окружность с центром в
точке О(0;
0) и
радиусом 4.

ПРИМЕР:

Построить график уравнения:

(х – 1)² + (у – 2)² = 9.

Перепишем уравнение в виде

(х – 1)² + (у – 2)² = 3².

Графиком этого уравнения является окружность с центром в
точке (1;
2) и
радиусом 3.

ПРИМЕР:

Построить график уравнения:

х² + у²
+ 4х = 0.

Перепишем уравнение в виде

х² +
4х + 4 + у² = 4,

(х+ 2)² + у²
= 4,

(х– (–2))² + (у – 0)² = 2²,

Графиком этого уравнения является окружность с центром в
точке (–2;
0) и
радиусом 2.

От графиков функций
необходимо отличать графики уравнений.

ПРИМЕР:

На координатной плоскости изображена окружность радиусом r = 5 с центром в начале координат. Уравнение этой окружности:

х² + у²
= 25.

Можно сказать и так: графиком уравнения

х² + у²
= 25

будет окружность, изображённая на рисунку.

А можно график уравнения

х² + у²
= 25

считать графиком некоторой функции ? Нет. Если переменные х и у связаны соотношением

х² + у²
= 25,

то одному значению
х = 3 соответствует два
разных значения переменной у: 4 и –4.
А соотношение между переменными х и у только тогда считается функцией, когда каждому
значению х из области определения соответствует одно
значение у.
График уравнения только тогда будет графиком некоторой функции, если каждая
прямая, параллельная оси у, пересекает
его не больше чем в одной точке.

ПРИМЕР:

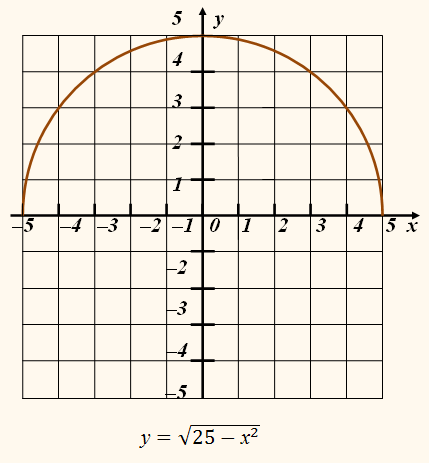
Изображённые на рисунке полуокружности – графики функций

Их объединение – вся окружность – график не функции, а уравнения

у²= 25 – х², или

у²+
х² = 25.

Задания к уроку 27

Источник

Как найти координаты центра окружности

Окружность − геометрическое место точек плоскости, равноудаленных от центра на некоторое расстояние, называемое радиусом. Если задана нулевая точка отсчета, единичный отрезок и направление координатных осей, центр окружности будет характеризоваться определенными координатами. Как правило, окружность рассматривают в декартовой прямоугольной системе координат.

Инструкция

Аналитически окружность задается уравнением вида (x-x0)²+(y-y0)²=R², где x0 и y0 − координаты центра окружности, R − ее радиус. Итак, центр окружности (x0;y0) здесь задан в явном виде.

Пример. Установите центр фигуры, заданной в декартовой системе координат уравнением (x-2)²+(y-5)²=25.Решение. Данное уравнение является уравнением окружности. Ее центр имеет координаты (2;5). Радиус такой окружности равен 5.

Уравнение x²+y²=R² соответствует окружности с центром в начале координат, то есть, в точке (0;0). Уравнение (x-x0)²+y²=R² означает, что центр окружности имеет координаты (x0;0) и лежит на оси абсцисс. Вид уравнения x²+(y-y0)²=R² говорит о расположении центра с координатами (0;y0) на оси ординат.

Общее уравнение окружности в аналитической геометрии запишется как: x²+y²+Ax+By+C=0. Чтобы привести такое уравнение к выше обозначенному виду, надо сгруппировать члены и выделить полные квадраты: [x²+2(A/2)x+(A/2)²]+[y²+2(B/2)y+(B/2)²]+C-(A/2)²-(B/2)²=0. Для выделения полных квадратов, как можно заметить, требуется добавлять дополнительные величины: (A/2)² и (B/2)². Чтобы знак равенства сохранялся, эти же величины надо вычесть. Прибавление и вычитание одного и того же числа не меняет уравнения.

Таким образом, получается: [x+(A/2)]²+[y+(B/2)]²=(A/2)²+(B/2)²-C. Из этого уравнения уже видно, что x0=-A/2, y0=-B/2, R=√[(A/2)²+(B/2)²-C]. Кстати, выражение для радиуса можно упростить. Домножьте обе части равенства R=√[(A/2)²+(B/2)²-C] на 2. Тогда: 2R=√[A²+B²-4C]. Отсюда R=1/2·√[A²+B²-4C].

Окружность не может быть графиком функции в декартовой системе координат, так как, по определению, в функции каждому x соответствует единственное значение y, а для окружности таких «игреков» будет два. Чтобы убедиться в этом, проведите перпендикуляр к оси Ox, пересекающий окружность. Вы увидите, что точек пересечения две.

Но окружность можно представить как объединение двух функций: y=y0±√[R²-(x-x0)²]. Здесь x0 и y0, соответственно, представляют собой искомые координаты центра окружности. При совпадении центра окружности с началом координат объединение функций принимает вид: y=√[R²-x²].

Обратите внимание

Две окружности, имеющие центром точку с одними и теми же координатами, называются концентрическими. Если они заданы уравнениями (x-x0)²+(y-y0)²=R² и (x-x0′)²+(y-y0′)²=R’², тогда x0=x0′, y0=y0′. В общем уравнении для концентрических окружностей A1=A2 и B1=B2.

Полезный совет

Кстати, в физике окружность может рассматриваться как тонкое однородное кольцо. Центр этого кольца будет являться центром масс (или центром инерции) такого тела. Если кольцо имеет массу m и радиус r, а через центр перпендикулярно плоскости кольца провести ось, то момент инерции кольца относительно оси будет равен mr². Момент инерции принципиально важен при рассмотрении вращательного движения тела.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Если окружность задана уравнением вида

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

найти центр (a;b) и радиус R такой окружности несложно.

Примеры.

Определить по уравнению окружности координаты её центра и радиуса:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

$[3){x^2} + {(y + 3)^2} = 9;]$

$[4){(x - 6)^2} + {y^2} = 5;]$

$[5){x^2} + {y^2} = 11.]$

Решение:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

a=3, b=7, R²=4.

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

$[3){x^2} + {(y + 3)^2} = 9;]$

a=0, b=-3, R²=9.

Центр окружности — (0;-3), радиус R=3.

$[4){(x - 6)^2} + {y^2} = 5;]$

a=6, b=0, R²=5.

Центр — в точке (6;0), радиус R=√5.

$[5){x^2} + {y^2} = 11.]$

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

$[{x^2} + {y^2} - 2ax - 2by + c = 0,]$

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

$[({x^2} - 2ax) + ({y^2} - 2by) + c = 0,]$

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

$[({x^2} - 2ax + {a^2}) - {a^2} + ({y^2} - 2by + {b^2}) - {b^2} + c = 0.]$

Отсюда

$[{(x - a)^2} + {(y - b)^2} + c - {a^2} - {b^2} = 0,]$

$[{(x - a)^2} + {(y - b)^2} = {a^2} + {b^2} - c.]$

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

$[R = sqrt {{a^2} + {b^2} - c} .]$

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.

Примеры.

Найти координаты центра и радиус окружности:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0;]$

$[2){x^2} + {y^2} - 5x + 4 = 0;]$

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0.]$

Решение:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0]$

Группируем слагаемые

$[({x^2} + 10x) + ({y^2} - 6y) - 15 = 0]$

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

$[{x^2} + 10x = ({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2}.]$

Аналогично

$[{y^2} - 6y = ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2}.]$

Таким образом,

$[({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2} + ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2} - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} - 25 - 9 - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} = 49]$

Центром этой окружности является точка (-5;3), радиус R=7.

$[2){x^2} + {y^2} - 5x + 4 = 0]$

$[({x^2} - 5x) + {y^2} + 4 = 0]$

$[({x^2} - 2 cdot x cdot 2,5 + {2,5^2}) - {2,5^2} + {y^2} + 4 = 0]$

$[{(x - 2,5)^2} + {y^2} + 4 - 6,25 = 0]$

$[{(x - 2,5)^2} + {y^2} = 2,25]$

Центр окружности — точка (2,5;0), радиус R=1,5.

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0]$

Разделим обе части уравнения на 3:

$[{x^2} + {y^2} - frac{4}{3}x - 3y + frac{4}{3} = 0]$

Далее — аналогично

$[({x^2} - frac{4}{3}x) + ({y^2} - 3y) + frac{4}{3} = 0]$

$[({x^2} - 2 cdot x cdot frac{2}{3} + {(frac{2}{3})^2}) - {(frac{2}{3})^2} + ({y^2} - 2 cdot y cdot frac{3}{2} + {(frac{3}{2})^2}) - ]$

$[ - {(frac{3}{2})^2} + frac{4}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} - frac{{{4^{backslash 4}}}}{9} - frac{{{9^{backslash 9}}}}{4} + frac{{{4^{backslash 12}}}}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} = frac{{49}}{{36}}]$

Центр этой окружности лежит в точке

$[(frac{2}{3};frac{3}{2}),R = frac{7}{6}.]$

Источник

Содержание:

1 Шаг 1
- - - 1.0.0.1 Этот видеоурок доступен по абонементу
2 1. Тема урока, введение
3 2. График линейного уравнения
4 3. График рационального уравнения
5 4. График уравнения – гипербола
6 5. График уравнения окружности
7 6. Вывод

Центр окружности имеет координаты О (a; b), радиус равен R.

Пусть дано следующее уравнение окружности:

Шаг 1

Найдем координаты центра окружности.

Для этого приравняем каждое из слагаемых к нулю:

Следовательно, центр окружности будет находиться в точке О(3, -1).

Как построить окружность?

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Тема: Системы уравнений

Урок: Графики уравнений

1. Тема урока, введение

Мы рассматриваем рациональное уравнение вида 2. График линейного уравнения

1. Линейное уравнение с двумя переменными

x, y – в первой степени; a,b,c – конкретные числа.

Пример:

Графиком этого уравнения является прямая линия.

Мы действовали равносильными преобразованиями – y оставили на месте, всё остальное перенесли в другую сторону с противоположными знаками. Исходное и полученное уравнения равносильны, т.е. имеют одно и то же множество решений. График этого уравнения мы умеем строить, и методика его построения такова: находим точки пересечения с координатными осями и по ним строим прямую.

В данном случае

Зная график уравнения, мы можем многое сказать о решениях исходного уравнения, а именно: если Если точка имеет абсциссу x, то ордината этой точки

Значит, решением исходного уравнения является множество пар чисел

У нас было уравнение, мы построили график, нашли решения. Множество всех пар – сколько их? Бесчисленное множество.

3. График рационального уравнения

Это рациональное уравнение,

Найдем y, равносильными преобразованиями получаем

Положим и получаем квадратичную функцию, ее график нам известен.

Пример: Построить график рационального уравнения.

Графиком является парабола, ветви направлены вверх.

Найдем корни уравнения:

Схематически изобразим график (Рис. 2).

С помощью графика мы получаем всевозможные сведения и о функции, и о решениях рационального уравнения. Мы определили промежутки знакопостоянства, теперь найдем координаты вершины параболы.

У уравнения Если мы зададим любое x, то получим точку

Решением исходного уравнения является множество пар

4. График уравнения – гипербола

3. Построить график уравнения

Необходимо выразить y. Рассмотрим два варианта.

Графиком функции является гипербола, функция не определена при

Функция убывающая.

Если

Если мы возьмем точку с абсциссой Решением исходного уравнения является множество пар

Построенную гиперболу можно сдвигать относительно осей координат.

Например, график функции – тоже гипербола – будет сдвинут на единицу вверх по оси ординат.

5. График уравнения окружности

4. Уравнение окружности

Это рациональное уравнение с двумя переменными. Множеством решений являются точки окружности. Центр в точке радиус равен R (Рис. 4).

Рассмотрим конкретные примеры.

Приведем уравнение к стандартному виду уравнения окружности, для этого выделим полный квадрат суммы:

Построим график уравнения (Рис. 5).

b. Построить график уравнения

Вспомним, что произведение равно нулю тогда и только тогда, когда один из сомножителей равен нулю, а второй существует.

График заданного уравнения состоит из совокупности графиков первого и второго уравнений, т.е. двух прямых.

Построим его (Рис. 6).

Построим график функции Прямая будет проходить через точку (0; -1). Но как она пройдет – будет возрастать или убывать? Определить это нам поможет угловой коэффициент, коэффициент при x, он отрицательный, значит функция убывает. Найдем точку пересечения с осью ox, это точка (-1; 0).

Аналогично строим график второго уравнения. Прямая проходит через точку (0; 1), но возрастает, т.к. угловой коэффициент положителен.

Координаты всех точек двух построенных прямых и являются решением уравнения.

6. Вывод

Итак, мы проанализировали графики важнейших рациональных уравнений, они будут использоваться и в графическом методе и в иллюстрации других методов решения систем уравнений.

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

Рекомендованные ссылки на интернет-ресурсы

1. Раздел College.ru по математике (Источник).

2. Интернет-проект «Задачи» (Источник).

3. Образовательный портал «РЕШУ ЕГЭ» (Источник).

Рекомендованное домашнее задание

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 95-102.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Источник