Центры тяжести многоугольников и многогранников
Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где — массы точек, — их радиус-векторы (задающие их положение относительно начала координат), и — искомый радиус-вектор центра масс.
В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке , в которой сумма моментов всех сил равна нулю. В данном случае это превращается в условие того, чтобы сумма радиус-векторов всех точек относительно точки , домноженных на массы соответствующих точек, равнялась нулю:
и, выражая отсюда , мы и получаем требуемую формулу.
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где — точка-середина -ой стороны многоугольника, — длина -ой стороны, — периметр, т.е. сумма длин сторон.
Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник на четыре, соединив середины сторон, как показано на рисунке:
Четыре получившихся треугольника подобны треугольнику с коэффициентом .
Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника :
Пусть теперь вектор — вектор, проведённый из вершины к центру масс треугольника №1, и пусть вектор — вектор, проведённый из к точке (которая, напомним, является серединой стороны, на которой она лежит):
Наша цель — показать, что вектора и коллинеарны.
Обозначим через и точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка , являющаяся серединой отрезка . Более того, вектор от точки к точке совпадает с вектором .
Искомый центр масс треугольника лежит посередине отрезка, соединяющего точки и (поскольку мы разбили треугольник на две части равных площадей: №1-№2 и №3-№4):
Таким образом, вектор от вершины к центроиду равен . С другой стороны, т.к. треугольник №1 подобен треугольнику с коэффициентом , то этот же вектор равен . Отсюда получаем уравнение:
Таким образом, мы доказали, что вектора и коллинеарны, что и означает, что искомый центроид лежит на медиане, исходящей из вершины .
Более того, попутно мы доказали, что центроид делит каждую медиану в отношении , считая от вершины.
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где — центроид -го треугольника в триангуляции заданного многоугольника, — площадь -го треугольника триангуляции, — площадь всего многоугольника.
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники , где .
Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка , а затем суммируются знаковые площади треугольников, образованных этой точкой и точками многоугольника: . Аналогичный приём можно применить и для поиска центра масс: только теперь мы будем суммировать центры масс треугольников , взятых с коэффициентами, пропорциональными их площадям, т.е. итоговая формула для центра масс такова:
где — произвольная точка, — точки многоугольника, — центроид треугольника , — знаковая площадь этого треугольника, — знаковая площадь всего многоугольника (т.е. ).
Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении )
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
Пирамида
Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное.
Виды пирамид
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Пирамида. Правильная пирамида
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный видеоурок поможет пользователям получить представление о теме Пирамида. Правильная пирамида. На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение. Рассмотрим, что такое правильная пирамида и какими свойствами она обладает. Затем докажем теорему о боковой поверхности правильной пирамиды.
http://interneturok.ru/lesson/geometry/10-klass/mnogogranniki/piramida-pravilnaya-piramida
Куб. Формулы, признаки и свойства куба
Определение.
Куб (гексаедр) — это трехмерная фигура, которая состоит из шести динаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов. Также кубом можно назвать прямоугольный параллелепипед, у которого все ребра равны.
Определение. Грань куба — это часть плоскости, ограниченная сторонами квадрата.
— куб имеет шесть граней;
— каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани;
— грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.
Определение. Ребро куба — это отрезок, образованный пересечением двух граней куба.
— куб имеет двенадцать ребер;
— каждый конец ребра соединен с двумя соседними ребрами под прямым углом;
— ребра куба имеют одинаковую длину.
Определение. Вершина куба — это самая отдаленная от центра куба точка, которая лежит на пересечения трех граней куба.
— куб имеет восемь вершин;
— каждая вершина образована только тремя гранями и тремя ребрами.
Определение. Центр грани куба (O1) — это равноудалена точка от всех ребер грани куба.
Определение. Центр куба (O) — это равноудалена точка от всех граней куба.
Определение. Ось куба (i) — это прямая, проходящая через центр куба и центры двух параллельных граней куба.
— куб имеет три оси;
— оси куба взаимно перпендикулярны.
Определение. Диагональ куба (d1) — отрезок, который соединяет противоположные вершины куба и проходит через центр куба.
— куб имеет четыре диагонали;
— диагонали куба пересекаются и делятся пополам в центре куба;
— диагонали куба имеют одинаковую длину.
Формула. Диагональ куба d1 через длину ребра a:
d1 = a√3
Определение. Диагональ грани куба (d2) -отрезок, который соединяет противоположные углы грани куба и проходит через центр грани куба.
Формула. Диагональ грани d2 через длину ребра a:
d2 = a√2
Определение. Объём куба — это совокупность всех точек в пространстве, ограниченные гранями куба.
Формула. Объём куба через длину ребра a:
V = a3
Формула. Объём куба через длину диагонали куба d1:
Определение. Площадь поверхности куба — это совокупность плоскостей всех граней.
Формула. Площадь поверхности куба через длину ребра a:
S = 6a2
Определение. Периметр куба — это совокупность длин всех ребер куба.
Формула. Периметр куба P через длину ребра a:
P = 12a
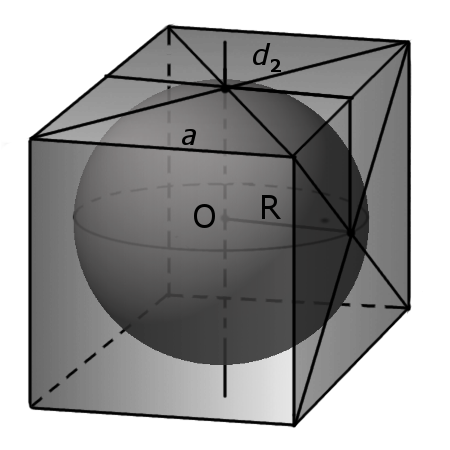
Определение. Сферой вписанной в куб называется сфера, центр которой совпадает с центром куба и которая касается центров граней куба.
— все шесть граней куба являются касательными плоскостями к вписанной сферы;
— радиус вписанной сферы равен половине длины ребра a.
Формула. Радиус вписанной сферы r через длину ребра a:
Формула. Объема вписанной сферы V через длину ребра a:
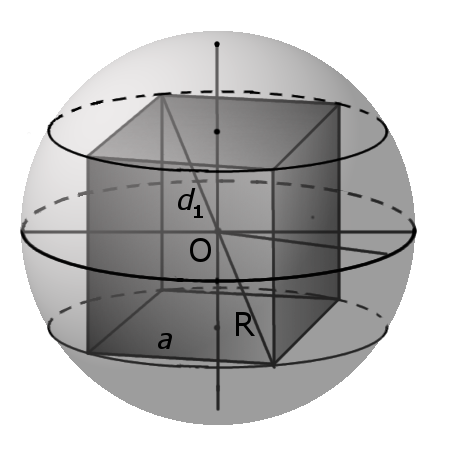
Определение. Сферой описанной вокруг куба называется сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами куба.
— радиус описанной сферы равен половине длины диагонали (d1) куба.
Формула. Радиус описанной сферы R через длину ребра a:
Формула. Объема сферы описанной вокруг куба V через длину ребра a:
Свойства куба
1. В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырех вершинах куба, а все шесть ребер тетраэдра будут лежать на шести гранях куба и ребра будут равны диагонали грани куба.
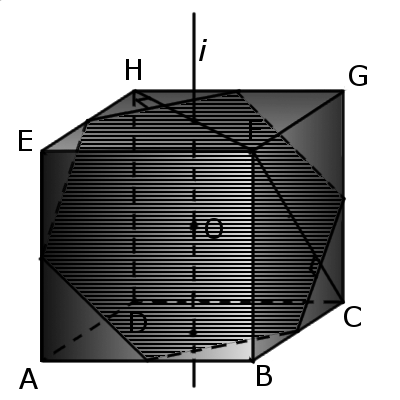
2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.
Координаты вершин куба
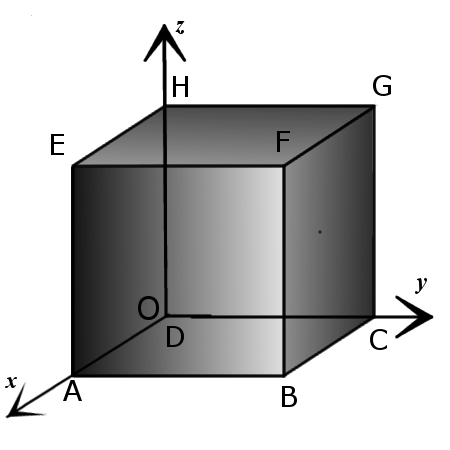
1. Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат:
A(a, 0, 0),
B(a, a, 0),
C(0, a, 0),
D(0, 0, 0),
E(a, 0, a),
F(a, a, a),
G(0, a, a),
H(0, 0, a).
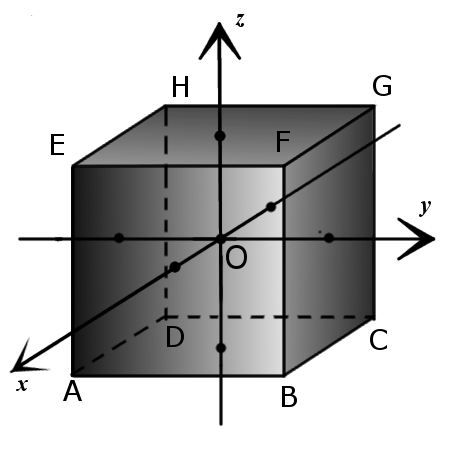
2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:
A(a, —a, —a),
B(a, a, —a),
C(-a, a, —a),
D(-a, —a, —a),
E(a, —a, a),
F(a, a, a),
G(-a, a, a),
H(-a, —a, a).
Определение. Единичный куб — это куб, у которого длина ребер равна единице.
Пересечение куба плоскостью
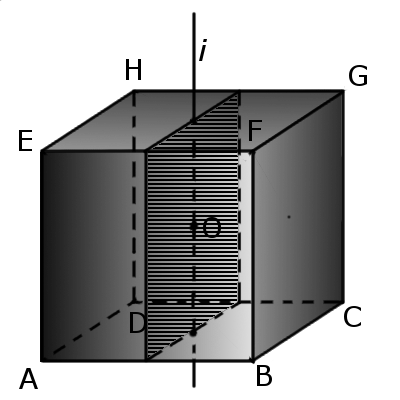
1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Эта плоскость делит куб два равных прямоугольных параллелепипеда.
2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами a и a√2, площадью сечения a2√2. Эта плоскость делит куб две равные призмы.
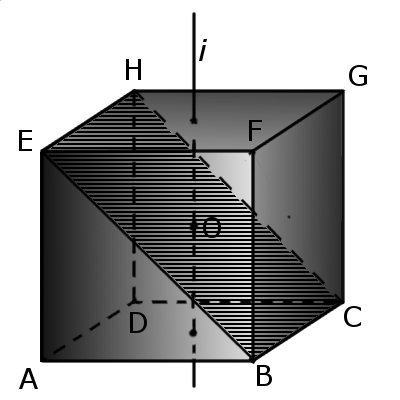
3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной a√2/2, площадью сечения a2(3√3)/4. У куба одна из диагоналей (FC) каждой грани, что пересекаются, перпендикулярна стороне шестиугольника.
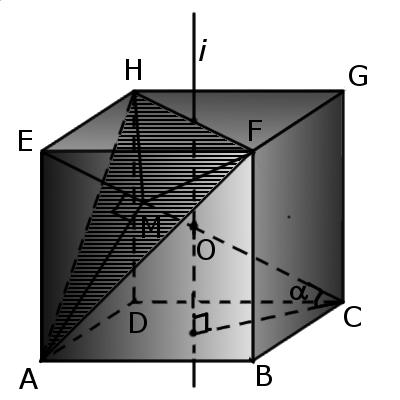
4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной a√2, площадью сечения a2√3/2 и объемом большей части — 5a3/6 и меньшей — a3/6. Одна из диагоналей куба (EC) перпендикулярна к плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении MC:EМ = 2:1.
План урока:
Понятие сферы и шара
Уравнение сферы
Пересечение сферы плоскостью
Касательная плоскость к сфере
Пересечение двух сфер
Площадь сферы
Вписанные и описанные сферы
Понятие сферы и шара
Люди постоянно сталкиваются с предметами, имеющими форму шара. В большинстве спортивных игр (баскетболе, большом и настольном теннисе, футболе) используются мячи, которые по форме как раз являются шарами. Такую же форму имеют многие фрукты – яблоки, апельсины, мандарины. Более того, известно, что Земля, другие планеты и звезды, большинство крупных спутников также представляют собой шары.
Важно отличать шар от сферы. Сферой называют только поверхность шара. Сам же шар является объемной фигурой, к нему относят всю часть пространства, ограниченную сферой.
Дадим строгие определения сферы и шара:
Отрезок, соединяющий точку на сфере с ее центром, именуется радиусом сферы. Он же называется и радиусом шара, заключенного внутри этой сферы.
Проходящий через центр сферы отрезок, чьи концы принадлежат сфере, именуется диаметром сферы. Сама сфера считается частью шара, также как и окружность считается частью круга.Показывают шар или сферу на рисунке так:
Из определения сферы явно вытекает тот факт, что все ее радиусы одинаковы. Это в свою очередь означает, что центр сферы – это середина диаметра, и диаметр вдвое длиннее радиуса.
Заметим, что сфера является телом вращения. Она получается при повороте полуокружности вокруг ее диаметра:
Уравнение сферы
В планиметрии мы уже изучали уравнения линии. Так назывались ур-ния с двумя переменными, каждое решение которых соответствовало точке на координатной плос-ти, принадлежавшей заданной линии. Если же точка не принадлежала линии, то ее координаты решением соответствующего ур-ния не являлись. В частности, нам удалось получить уравнения прямой и окружности.
Аналогично в стереометрии вводится понятие уравнения поверхности. Так как в пространстве используются уже три координаты (х, у и z), то ур-ния поверхности содержат три переменных. Координаты всякой точки, принадлежащей поверхности, будут являться решениями ур-ния этой поверхности. И наоборот, координаты точки, не принадлежащей поверхности, будут обращать ур-ние поверхности в неверное равенство.
Выведем ур-ние сферы. Пусть ее центр располагается в точке С с координатами (х0, у0, z0), а радиус обозначен как R. Возьмем произвольную точку А на сфере. По определению сферы расстояние между А и С должно составлять R:
Мы уже знаем формулу для расчета расстояния между А и С:
Точки, координаты которых удовлетворяют этому неравенству, находятся от центра сферы на расстоянии меньше ее радиуса. Это значит, что они находятся внутри сферы, то есть принадлежат шару, чьей поверхностью является рассматриваемая сфера. Если же координаты точки удовлетворяют неравенству
то можно утверждать, что точка находится вне пределов сферы, то есть она не принадлежит ни сфере, ни шару.
Задание. Напишите уравнение сферы, центр которой располагается в точке (2; – 4; 7) и чей радиус равен 3.
Решение. Здесь мы просто подставляем координаты центра сферы и ее радиус в ур-ние сферы:
Задание. Есть сфера с радиусом 9, чей центр располагается в точке О(2; 3; 4). Определите, какие из следующих точек будут принадлежать этой сфере: А(1; 7; – 4), В(0; 6; 10), С(– 2; – 1; 11), D(5; 6; 8).
Решение. Сначала составляем уравнение сферы, описанной в условии:
Равенство неверное, значит, В не располагается на сфере (более того, раз 49 < 81, то можно утверждать, что точка располагается внутри сферы). Далее проверяем точку С(– 2; – 1; 11):
Задание. Докажите, что ур-ние
является ур-нием сферы, после чего определите радиус этой сферы.
Решение. Здесь необходимо выполнить некоторые преобразования ур-ния, чтобы оно стало похожим на ур-ние сферы. Для этого используем формулы квадратов суммы и разности:
Пересечение сферы плоскостью
Рассмотрим ситуацию, когда секущая плоскость α пересекает сферу. Нас в первую очередь интересует форма получающегося сечения. Опустим из точки О, центра сферы, перпендикуляр ОН на секущую плос-ть (пока мы рассматриваем случай, когда секущая плос-ть проходит не через О):
Буквами А и В обозначим любые две точки сечения, которые принадлежат одновременно и сфере, и плос-ти α. Теперь сравним ∆ОНА и ∆ОНВ. Они прямоугольные, ведь ОН – перпендикуляр к α. При этом у них есть общий катет ОН и одинаковые гипотенузы ОА и ОВ (это радиусы одной сферы).Тогда эти ∆ОНА и ∆ОНВ одинаковы, и поэтому
AH = BH
Мы выбрали точки А и В произвольно, и они оказались равноудаленными от Н. Значит, А и В находятся на одной окруж-ти с центром Н. Легко показать и обратное – любая точка этой окруж-ти будет лежать и на сфере (попробуйте сделать этот сами). Значит, сечение имеет форму окруж-ти, причем ее центр – это основание перпендикуляра, проведенного из О на α.
Обозначим длину перпендикуляра ОН буквой h, радиус сферы буквой R и радиус сечения буквой r. Тогда, используя теорему Пифагора, мы можем составить формулу для расчета радиуса r сечения:
Видно, что чем длиннее перпендикуляр h(он представляет собой расстояние от О до α), тем меньше радиус сечения. Тогда ясно, что наибольший радиус будет у того сечения, которое проходит через центр О. Действительно, если сечение проходит через О, то все его точки по определению сферы будут удалены на расстояние R от О. Но уже по другому определению такое множество точек – окруж-ть с центром в О и радиусом R. Плос-ть, проходящая через центр сферы, именуется диаметральной плоскостью, а само сечение именуют большой окружностью сферы. Радиус большой окруж-ти совпадает с радиусом самой сферы.
Задание. Сфера с радиусом 41 пересечена плос-тью, которая находится на расстоянии 9 от центра этой сферы. Найдите площадь сечения.
Решение. Опустим из центра сферы О перпендикуляр ОН на секущую плос-ть, тогда по условию ОН = 9. Пусть А – точка на сечении, тогда ОА = 41. ∆ОНА – прямоугольный, поэтому мы можем найти радиус АН:
Теперь площадь сечения можно рассчитать по известной формуле площади круга:
Ответ: 1600π.
Задание. Докажите, что если через три точки сферы провести окруж-ть, то все точки этой окруж-ти будут также принадлежать сфере.
Решение. Пусть на сфере есть точки А, В, С. Проведем через них окруж-ть L. Надо доказать, что произвольная точка D, принадлежащая этой окруж-ти, также будет находиться на сфере.
Через точки А, В и С можно провести единственную плос-ть АВС. Она будет секущей для сферы, ведь она имеет с ней как минимум три общих точки – А, В и С. Формой этого сечения будет некоторая окруж-ть L1. L1 обязательно будет проходить через А, В и С. Но через любые три точки можно провести не более одной окружности, поэтому L и L1 совпадают. Значит, D, принадлежащая по условию L, будет также принадлежать и L1. Но L1– это сечение, все его точки, в том числе и D, принадлежат сфере, ч. т. д.
Есть смысл запомнить доказанное утверждение:
Задание. На сфере радиусом 13 отмечены точки А, В и С так, что АВ = 6, ВС = 8 и АС = 10. Каково расстояние между центром сферы и плос-тью АВС?
Решение. Сначала заметим, что ∆АВС является прямоугольным, ведь его стороны удовлетворяют теореме Пифагора:
Напомним одного из свойств прямоугольного треугольника – центр окруж-ти, описанной около него, совпадает с серединой его гипотенузы. То есть если через точки А, В и С провести окруж-ть, то ее центр Н будет серединой АВ, и поэтому
Теперь заметим, что эта описанная окруж-ть должна быть сечением сферы. Это значит, что ОН – перпендикуляр к плос-ти АВС, ведь центр сечения должен лежать на перпендикуляре к плос-ти, проведенном из О. Тогда ∆ОНС – прямоугольный, и ОН – искомое нами расстояние. ОС – радиус сферы. Рассчитаем по теореме Пифагора ОН:
Касательная плоскость к сфере
Плос-ть, имеющая со сферой строго одну общую точку, именуется касательной плоскостью к сфере.
Действительно, если плос-ть касается окруж-ти, то точка касания А должна располагаться на расстоянии R от центра сферы О, где R– радиус сферы. Все остальные точки касательной плос-ти находятся вне пределов сферы, то есть должны находиться от О на расстоянии, превышающем R. Это значит, что отрезок ОА должен быть кратчайшим отрезком, соединяющим О и касательную плос-ть. Но мы знаем, что кратчайший отрезок между плос-тью и точкой – это как раз перпендикуляр, опущенный из точки на плос-ть.
Справедливо и обратное утверждение:
Доказательство. Если радиус ОА – перпендикуляр к плос-ти α, то он является кратчайшим расстоянием между плос-тью и центром О. Тогда все остальные точки плос-ти располагаются на большем расстоянии от О, чем точка А. Это значит, что они не располагаются на сфере. Значит, у сферы и плос-ти α одна общая точка А, а потому α по определению – касательная плос-ть.
По аналогии с касательной плос-тью существует понятие касательной прямой к сфере.
Касательная к сфере обладает почти теми же свойствами, что и касательная к окруж-ти.
Доказательство. Пусть m– касательная прямая к сфере с центром О. обозначим точку касания как А. Далее через прямую m и центр О проведем плос-ть α. Нам надо показать, что ОА⊥m:
Плос-ть α будет диаметральной плос-тью. Сечение будет иметь форму окруж-ти с центром О и радиусом ОА. Прямая m будет касательной к этой окруж-ти, ведь она имеет с ней общую точку А, а второй общей точки m и окруж-ть иметь не могут, ведь такая бы точка была бы также общей для m и сферы, а m по определению имеет лишь одну общую точку со сферой. Напомним, что касательная к окруж-ти перпендикулярна радиусу, то есть m⊥ОА, ч. т. д.
Будет верным и обратное утверждение:
Для доказательства используем ту же картинку. Известно, что m⊥ОА, надо показать, что m– касательная к сфере. Проведем через пересекающиеся прямые m и ОА плос-ть α. Она снова окажется диаметральной плоскостью, и снова сечением будут окруж-ть с радиусом ОА. По признаку касательной, который мы изучали в планиметрии, m– касательная к этой окруж-ти, ведь m⊥ОА. То есть в плос-ти α есть лишь одна общая точка m и сферы. В других плос-тях у них не может быть общих точек, так как m полностью принадлежит α. В итоге у m и сферы только одна общая точка, а потому m– касательная к сфере, ч. т. д.
Рассмотрим ещё одно утверждение:
Сначала разберемся с понятием отрезков касательных. Пусть из точки А, лежащей вне сферы, к ней проведены две касательные, а точки касания обозначены буквами В и С. Тогда АВ и АС как раз и будут отрезками касательных:
Докажем, что эти отрезки одинаковы. Для этого к точкам касания проведем радиусы ОВ и ОС. Теперь сравним ∆АВО и ∆АСО. Они прямоугольные, ведь ОВ⊥АВ по свойству касательной, и ОС⊥АС. Гипотенуза АО у этих треугольников общая, а катеты ОВ и ОС – это одинаковые радиусы. Получается, что ∆АВО и ∆АСО равны, а потому отрезки АВ и АС одинаковы.
Задание. Дан шар радиусом 10 см, к которому проведена касательная плос-ть α. Через точку касания проведена секущая плос-ть β, образующая с α угол в 30°. Вычислите площадь сечения шара плос-тью β.
Решение. Обозначим точку касания как А. Опустим из центра сферы о перпендикуляр ОН на плос-ть β. Тогда отрезок АН будет радиусом сечения. Так как угол между плос-тями α и β составляет 30° (на рисунке он показан как ∠НАС), то
Ответ: 25π см2.
Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.
Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:
Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?
Решение. Обозначим вершины треугольника точками А, В и С. Пусть
AB = 13
AC = 14
BC = 15
Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?
Напомним одну из формул для расчета площади треугольника:
Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:
Пересечение двух сфер
Пусть есть две пересекающиеся сферы с центрами в точках О1 и О2 с радиусами R1 и R2 соответственно. Какую форму будет иметь линия L, по которой они пересекаются?
Эта линия является множеством точек, которые принадлежат как первой, так и второй сфере. Обозначим две произвольные точки этой линии буквами А и В:
Проведем радиусы О1А, О1В, О2А и О2В. Теперь сравним ∆АО1О2 и ∆ВО1О2. Сторона О1О2 у них общая, а другие стороны попарно равны как радиусы сфер:
Получается, что ∆АО1О2 и ∆ВО1О2 равны. Теперь из точек А и В опустим высоты на прямую О1О2. Из равенства ∆АО1О2 и ∆ВО1О2 вытекает два факта:
- эти высоты упадут в одну точку Н;
- эти высоты будут одинаковы, то есть АН = НВ.
Другими словами, А и В равноудалены от Н. Получается, что точки А и В находятся на окруж-ти, центр которой – точка Н. Заметим, что О1О2 – перпендикуляр к плоскости окружности, ведь О1О2⊥АН и О1О2⊥ВН.
Точки А и В были выбраны произвольно, поэтому можно утверждать, что любые точки линии L будут находиться на одной окруж-ти. Докажем и обратное утверждение – любая точка, лежащая на этой окруж-ти, будет принадлежать линии L. Возьмем на окруж-ти какую-нибудь точку С и построим радиус НС:
Теперь сравним ∆О1НС и ∆О1НА. Они прямоугольные, ведь О1Н – перпендикуляр к плос-ти окружности. Катет О1Н у них общий, а катеты АН и НС одинаковы как радиусы окруж-ти. Значит, ∆О1НС и ∆О1НА равны, и потому
Это равенство означает, что С принадлежит сфере с центром в О1. Аналогично рассмотрев ∆О2НС и ∆О2НА, можно показать, что С также принадлежит и второй сфере. Тогда С принадлежит пересечению этих сфер.
Итак, всякая точка линии L лежит на окруж-ти с центром Н, и наоборот, каждая точка этой окруж-ти лежит на линии L. Это означает, что L как раз и является этой окружностью.
Отметим ещё один факт: по неравенству треугольника отрезок О1О2 должен быть меньше суммы отрезков О1А и О2А, то есть суммы радиусов сфер.
Задание. Сферы имеют радиусы 25 см и 29 см, а расстояние между их центрами составляет 36 см. Вычислите радиус окруж-ти, по которой они пересекаются.
Решение. Пусть А – одна их точек сечения. Искомый радиус обозначим как АН. В итоге получим такую картинку:
Площадь сферы
Сферическая поверхность, как и всякая другая ограниченная поверхность, имеет какую-то площадь. Напомним, что для вычисления площадей цилиндрической и конической поверхности мы строили их плоские развертки и находили площади уже этих разверток, используя формулы из планиметрии. Оказывается, что для сферы построить такую развертку невозможно. Мы не будем доказывать строго этот факт, но он известен из географии – любая карта Земли, которая как раз и должна быть разверткой сферической поверхности нашей планеты, является неточной и сильно искажает форму и размеры континентов. Если бы существовал способ построить точную развертку, то и географические карты не имели бы таких искажений.
Однако вычислить площадь сферы всё же можно по известной формуле:
Сейчас мы не будем доказывать эту формулу. Отметим лишь, что для ее получения необходимо использовать интегралы.
Задание. Какова площадь сферы с радиусом 5 см?
Решение. Просто используем формулу:
Ответ: 100π см2.
Вписанные и описанные сферы
Если каждая точка многогранника лежит на поверхности сферы, то говорят, что многогранник вписан в сферу. Тогда сферу именуют описанной, а многогранник – вписанным.
Если же сфера касается каждой грани многогранника, то уже наоборот, сфера вписана в многогранник. Тогда уже сфера будет вписанной фигурой, а многогранник – описанной.
Заметим, что не в каждый многогранник может быть вписанным или описанным. Например, в куб вписать сферу можно, а в прямоугольный параллелепипед, измерения которого отличаются, уже вписать сферу не получится.
Надо отметить, что в сферу можно вписать не только в многогранник, но и другие геометрические фигуры, в частности конус и цилиндр. Здесь нужно уточнить (без доказательства), что если касание плос-ти и сферы происходит только в одной точке, то цилиндрическая и коническая поверхности касаются сферы уже по окруж-ти.
Задание. Правильная пирамида вписана в сферу. Докажите, высота этой пирамиды проходит через центр сферы.
Решение. Опустим из центра сферы О перпендикуляр ОН на основание пирамиды. Далее возьмем произвольную вершину Х основания пирамиды, и соединим ее с Н отрезком ХН. По теореме Пифагора можно вычислить длину ХН (радиус сферы ОХ обозначим, буквой R):
Получилось, что расстояние ХН не зависит от самой точки Х. То есть все вершины основания равноудалены от точки, то есть Н – центр описанной около основания окруж-ти. Это означает, что перпендикуляр ОН одновременно является высотой правильной пирамиды, ч. т. д.
Задание. Вычислите радиус описанной сферы, в которую вписан правильный тетраэдр со стороной а.
Решение. Правильный тетраэдр можно считать правильной треугольной пирамидой, поэтому (согласно предыдущей задаче) из центра сферы О можно опустить перпендикуляр на основание АВС, который упадет в точку Н – центр основания. Так как тетраэдр правильный, то ∆АВС – равносторонний, то есть Н – эта точка пересечения и медиан, и высот. Опустим из А высоту АК, она пройдет через Н. Так как АК – ещё и медиана, то
Далее найдем длину АН. Вспомним, что АН – медиана, а точка пересечения медиан Н делит их в отношении 2:1. Это значит, что
Буквой R здесь обозначен радиус описанной сферы. Осталось применить теорему Пифагора к ∆АНD:
Задание. Докажите что вокруг любого тетраэдра можно описать сферу.
Решение. Обозначим вершины произвольного тетраэдра буквами А, В, С и D. Далее на грани АВС отметим точку К – центр окруж-ти, описанной около ∆АВС. Аналогично на грани АВD отметим Н – центр окруж-ти, описанной около ∆АВD:
Напомним, что центры описанных окружностей располагаются в той точке, где пересекаются серединные перпендикуляры. Это значит, что если мы из К и Н опустим перпендикуляры на ребро АВ, то эти перпендикуляры будут серединными, то есть они попадут в одну точку М, являющуюся серединой ребра АВ.
Мы получили плос-ть НМК. Заметим, что НМК⊥АВ по признаку перпендикулярности прямой и плоскости, так как АВ⊥МН и АВ⊥МК. Но тогда АВС⊥МНК уже по признаку перпендикулярности плоскостей, ведь АВС проходит через АВ, являющийся перпендикуляром к НМК. По той же причине и АВD⊥НМК.
Далее проведем через К перпендикуляр m к АВС. Он должен будет принадлежать НМК, ведь НМК⊥АВD. Аналогично и через Н проведем перпендикуляр n к АВD, который также будет принадлежать НМК.
В плос-ти НМК есть две прямые, mи n. Они либо параллельны, либо пересекаются. Но перпендикуляры к двум плос-тям могут быть параллельны только в случае, если сами эти плос-ти параллельны (или совпадают). Но АВС и АВD непараллельны и не совпадают, поэтому m и n непаралелльны, то есть они пересекаются в какой-то точке О.
Покажем, что точка О равноудалена от всех вершин тетраэдра. Сравним ∆АОК и ∆СОК. Они прямоугольные, ведь ОК – перпендикуляр к АВС. ОК – общий катет, а катеты АК и СК одинаковы как радиусы описанной окруж-ти. Значит, ∆АОК и ∆СОК равны, ОА = ОС. Аналогично рассмотрев ∆АОК и ∆ВОК, приходим к выводу, что ОА = ОВ. Далее рассматриваем ∆ОНD и ∆ОНА и получаем, что ОА = ОD. Эти три равенства все вместе означают, что О равноудалена от точек А, В, С и D. А это значит, что на сфере с центром О и радиусом ОА будут лежать все вершины тетраэдра, то есть такая сфера окажется описанной, ч. т. д.
Примечание. Несложно доказать, что описанная сфера будет единственной. Действительно, если бы около тетраэдра можно было описать две различных сферы, то они пересекались бы в точках А, В, С и D. Сферы пересекаются по окруж-ти, то есть А, В, С и D должны лежать на одной окруж-ти, но это невозможно, ведь они не располагаются в одной плос-ти. Значит, двух описанных сфер существовать не может.
Доказанное в задаче утверждение можно сформулировать несколько иначе:
Сегодня мы изучили сферу – одну из важнейших геометрических фигур. Именно сферическую форму имеют звезды и планеты. Жидкость, оказавшаяся в невесомости, также принимает форму шара. Важно запомнить, что сечение сферы имеет форму окруж-ти, и касательные к сфере обладают почти такими ми же свойствами, как и касательные к окруж-ти в планиметрии.
Проверяемые элементы содержания и виды деятельности: владение понятиями о стереометрических фигурах; знание их свойств; знание формул для вычисления площадей поверхностей и объемов тел; умение применять эти знания при решении задач.
Ориентировочное время выполнения учащимися: 10—15 минут.
Типы заданий:
• Элементы, площадь поверхности, объем стереометрических фигур.
Особенности экзаменационных заданий по стереометрии
Задания этого вида представляют собой стереометрические задания на установление взаимосвязи между основными элементами многогранников и круглых тел, а также на использование формул для вычисления их площадей поверхностей и объемов. Вычислительной трудности задания не представляют; решение, как правило, сводится к использованию одной-двух формул. Соответствующие формулы нужно знать наизусть.
Куб
Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Куб является частный случаем параллелепипеда и призмы, поэтому для него выполнены все их свойства. Кроме того, если а — длина ребра куба, — диагональ основания,
— диагональ куба,
— площадь полной поверхности, а V — объем куба, то справедливы формулы:
Призма. Прямоугольный параллелепипед
Призмой (n-угольной призмой) называется многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы.
Правильной призмой называется прямая призма, основание которой — правильный многоугольник.
Прямая призма
Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна ее боковому ребру, а все боковые грани прямой призмы — прямоугольники.
Соотношения для прямой призмы
Пусть H — высота прямой призмы, AA1 — боковое ребро, — периметр основания,
— площадь основания,
— площадь боковой поверхности,
— площадь полной поверхности, V — объем прямой призмы. Тогда имеют место следующие соотношения:
Особенности правильной шестиугольной призмы
В основании правильной шестиугольной призмы лежит правильный шестиугольник. Напомним его свойства.
— Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
— Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
— Меньшая диагональ правильного шестиугольника в раз больше его стороны.
— Угол между сторонами правильного шестиугольника равен 120°.
— Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
— Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Пирамида
Пусть вне плоскости многоугольника задана точка P. Тогда фигура, образованная треугольниками
,
и многоугольником
вместе с их внутренними областями называется пирамидой (n-угольной пирамидой).
Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.
Соотношения для правильной пирамиды
Пусть H — высота правильной пирамиды, h — ее апофема, — периметр основания пирамиды,
— площадь основания,
— площадь боковой поверхности,
— площадь полной поверхности, V — объем правильной пирамиды. Тогда имеют место следующие соотношения:
Сечения
Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).
Теоремы, используемые при построении сечений
Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.
Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости то она параллельна и самой плоскости
Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.
Алгоритм построения сечений
Для построения сечений рекомендуем пользоваться следующим алгоритмом.
1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.
2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.
3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.
Для контроля правильности построенного сечения, проверяйте, что:
— все вершины сечения лежат на рёбрах многогранника;
— все стороны сечения лежат в гранях многогранника;
— в каждой грани многогранника лежит не более одной стороны сечения.
Цилиндр
Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.
Соотношения для цилиндра
Пусть h — высота цилиндра, r — радиус основания, Sбок — площадь боковой поверхности, Sполн — площадь полной поверхности, V — объем цилиндра. Тогда имеют место следующие соотношения:
Конус
Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет.
Соотношения для конуса
Пусть h — высота конуса, r — радиус основания, l — образующая, Sбок — площадь боковой поверхности, Sполн — площадь полной поверхности, V — объем конуса. Тогда имеют место следующие соотношения:
Сфера и шар
Шаром называется фигура, полученная при вращении полукруга вокруг оси, содержащей его диаметр. Сферой называется поверхность шара. Пусть R — радиус шара, S — площадь сферы, V — объем шара. Тогда имеют место следующие соотношения:
Комбинации круглых тел. Вписанные сферы
Сфера называется вписанной в цилиндр, если она касается обоих оснований цилиндра и каждой его образующей.
Сфера называется вписанной в конус, если она касается основания конуса и каждой его образующей.
Сфера называется вписанной в усечённый конус, если она касается обоих оснований конуса и всех его образующих.
Теорема 1: В прямой круговой цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания. Причём центр сферы есть середина оси цилиндра.
Теорема 2: В любой прямой круговой конус можно вписать сферу. Причём центр сферы есть точка пересечения оси конуса с биссектрисой угла наклона образующей конуса к плоскости его основания.
Теорема 3. В усечённый конус можно вписать сферу тогда и только тогда, когда он прямой круговой, и длина его образующей равна сумме длин радиусов оснований. Причём центр сферы есть середина оси усечённого конуса.
Комбинации круглых тел. Описанные сферы
Сфера называется описанной около цилиндра, если окружности его оснований лежат на сфере.
Сфера называется описанной около конуса, если вершина конуса и его основание лежат на сфере.
Теорема 1: около цилиндра можно описать сферу тогда и только тогда, когда он прямой круговой. Причём центр сферы есть середина оси цилиндра.
Теорема 2: около конуса можно описать сферу тогда и только тогда, когда он круговой. Причём центр сферы есть точка пересечения прямой, перпендикулярной к плоскости основания и проходящей через центр его, и плоскости, перпендикулярной какой-либо его образующей конуса и проходящей середину этой образующей.
Следствие: сферу можно описать около любого прямого кругового конуса. В этом случае, центр сферы — точка пересечения прямой, содержащей высоту конуса с плоскостью, перпендикулярной какой-либо из его образующих и проходящей через ее середину.
Комбинации конуса и цилиндра
Цилиндр называется вписанным в конус, если одно его основание лежит на основании конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию. Конус в этом случае называется описанным вокруг цилиндра.
Цилиндр называется описанным вокруг конуса, если центр одного из оснований цилиндра является вершиной вершина конуса, а противоположное основание цилиндра совпадает с основанием конуса. Конус в этом случае называется вписанным в цилиндр.
Комбинации многогранников и круглых тел. Описанные сферы
Сфера называется описанной около многогранника, если все его вершины лежат на этой сфере. Многогранник называется в этом случае вписанным в сферу.
Возможность описать сферу около многогранника означает существование точки (центра сферы), равноудалённой ото всех вершин многогранника.
Теорема 1: если из центра описанной около многогранника сферы опустить перпендикуляр на какое-либо из его рёбер, то основание этого перпендикуляра разделит ребро на две равные части.
Теорема 2: если из центра описанной около многогранника сферы опустить перпендикуляр на какую-либо из его граней, то основание этого перпендикуляра попадёт в центр круга, описанного около соответствующей грани.
Теорема 3: если около многогранника описана сфера, то её центр лежит на пересечении перпендикуляров к каждой грани пирамиды, проведённых через центр окружности, описанной около соответствующей грани.
Теорема 4: если около многогранника описана сфера, то её центр является точкой пересечений всех плоскостей, проведённых через середины рёбер пирамиды перпендикулярно к этим рёбрам.
Комбинации многогранников и круглых тел. Вписанные сферы
Сфера называется вписанной в многогранник, если все его грани касаются этой сферы. Многогранник называется в этом случае описанным около сферы.
Теорема: если в многогранник с площадью поверхности S и объёмом V вписан шар радиуса r, то справедливо соотношение:
Комбинации конуса, цилиндра и многогранников
В условиях задач встречаются также следующие понятия, не входящие в школьные учебники, которые уточняются непосредственно в условиях задач. Приведем наиболее употребительные из них.
Цилиндр вписан в призму: основания цилиндра вписаны в основания призмы.
Цилиндр описан вокруг призмы: основания цилиндра описаны вокруг оснований призмы.
Цилиндр вписан в пирамиду: одно из основание цилиндра вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание цилиндра принадлежит основанию пирамиды.
Цилиндр описан вокруг пирамиды: вершина пирамиды принадлежит одному из оснований цилиндра, а другое его основание описано вокруг основания пирамиды.
Конус вписан в призму: основание конуса вписано в основание призмы, а вершина конуса принадлежит противоположному основанию призмы.
Конус описан вокруг призмы: одно из оснований призмы вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание призмы вписано в основание конуса.
Конус вписан в пирамиду: их вершины совпадают, а основание конуса вписано в основание пирамиды. Вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой.
Конус описан вокруг пирамиды: их вершины совпадают, а основание конуса описано вокруг основания пирамиды.
Тема “Разные задачи на многогранники, цилиндр,
конус и шар” является одной из самых сложных в
курсе геометрии 11 класса. Перед тем, как решать
геометрические задачи, обычно изучают
соответствующие разделы теории, на которые
ссылаются при решении задач. В учебнике
С.Атанасяна и др. по данной теме (стр. 138) можно
найти только определения многогранника,
описанного около сферы, многогранника,
вписанного в сферу, сферы, вписанной в
многогранник, и сферы, описанной около
многогранника. В методических рекомендациях к
этому учебнику (см. книгу “Изучение геометрии в
10–11-х классах” С.М.Саакяна и В.Ф.Бутузова, стр.159)
сказано, какие комбинации тел рассматриваются
при решении задач № 629–646, и обращается внимание
на то, что “при решении той или иной задачи
прежде всего нужно добиться того, чтобы учащиеся
хорошо представляли взаимное расположение
указанных в условии тел”. Далее приводится
решение задач №638(а) и №640.
Учитывая все выше сказанное, и то, что наиболее
трудными для учащихся являются задачи на
комбинацию шара с другими телами, необходимо
систематизировать соответствующие
теоретические положения и сообщить их учащимся.
Определения.
1. Шар называется вписанным в многогранник, а
многогранник описанным около шара, если
поверхность шара касается всех граней
многогранника.
2. Шар называется описанным около
многогранника, а многогранник вписанным в шар,
если поверхность шара проходит через все вершины
многогранника.
3. Шар называется вписанным в цилиндр, усеченный
конус (конус), а цилиндр, усеченный конус (конус) –
описанным около шара, если поверхность шара
касается оснований (основания) и всех образующих
цилиндра, усеченного конуса (конуса).
(Из этого определения следует, что в любое
осевое сечение этих тел может быть вписана
окружность большого круга шара).
4. Шар называется описанным около цилиндра,
усеченного конуса (конуса), если окружности
оснований (окружность основания и вершина)
принадлежат поверхности шара.
(Из этого определения следует, что около
любого осевого сечения этих тел может быть
описана окружность большего круга шара).
Общие замечания о положении центра
шара.
1. Центр шара, вписанного в многогранник, лежит в
точке пересечения биссекторных плоскостей всех
двугранных углов многогранника. Он расположен
только внутри многогранника.
2. Центр шара, описанного около многогранника,
лежит в точке пересечения плоскостей,
перпендикулярных ко всем ребрам многогранника и
проходящих через их середины. Он может быть
расположен внутри, на поверхности и вне
многогранника.
Комбинация шара с призмой.
1. Шар, вписанный в прямую призму.
Теорема 1. Шар можно вписать в прямую
призму в том и только в том случае, если в
основание призмы можно вписать окружность, а
высота призмы равна диаметру этой окружности.
Следствие 1. Центр шара, вписанного в прямую
призму, лежит в середине высоты призмы,
проходящей через центр окружности, вписанной в
основание.
Следствие 2. Шар, в частности, можно вписать
в прямые: треугольную, правильную,
четырехугольную (у которой суммы
противоположных сторон основания равны между
собой) при условии Н = 2r, где Н – высота призмы, r –
радиус круга, вписанного в основание.
2. Шар, описанный около призмы.
Теорема 2. Шар можно описать около
призмы в том и только в том случае, если призма
прямая и около ее основания можно описать
окружность.
Следствие 1. Центр шара, описанного около
прямой призмы, лежит на середине высоты призмы,
проведенной через центр круга, описанного около
основания.
Следствие 2. Шар, в частности, можно описать:
около прямой треугольной призмы, около
правильной призмы, около прямоугольного
параллелепипеда, около прямой четырехугольной
призмы, у которой сумма противоположных углов
основания равна 180 градусов.
Из учебника Л.С.Атанасяна на комбинацию шара с
призмой можно предложить задачи № 632, 633, 634, 637(а),
639(а,б).
Комбинация шара с пирамидой.
1. Шар, описанный около пирамиды.
Теорема 3. Около пирамиды можно описать
шар в том и только в том случае, если около ее
основания можно описать окружность.
Следствие 1. Центр шара, описанного около
пирамиды лежит в точке пересечения прямой,
перпендикулярной основанию пирамиды, проходящей
через центр окружности, описанной около этого
основания, и плоскости, перпендикулярной любому
боковому ребру, проведенной через сере дину
этого ребра.
Следствие 2. Если боковые ребра пирамиды
равны между собой (или равно наклонены к
плоскости основания), то около такой пирамиды
можно описать шар.Центр этого шара в этом случае
лежит в точке пересечения высоты пирамиды (или ее
продолжения) с осью симметрии бокового ребра,
лежащей в плоскости бокового ребра и высоты.
Следствие 3. Шар, в частности, можно описать:
около треугольной пирамиды, около правильной
пирамиды, около четырехугольной пирамиды, у
которой сумма противоположных углов равна 180
градусов.
2. Шар, вписанный в пирамиду.
Теорема 4. Если боковые грани пирамиды
одинаково наклонены к основанию, то в такую
пирамиду можно вписать шар.
Следствие 1. Центр шара, вписанного в
пирамиду, у которой боковые грани одинаково
наклонены к основанию, лежит в точке пересечения
высоты пирамиды с биссектрисой линейного угла
любого двугранного угла при основании пирамиды,
стороной которого служит высота боковой грани,
проведенная из вершины пирамиды.
Следствие 2. В правильную пирамиду можно
вписать шар.
Из учебника Л.С.Атанасяна на комбинацию шара с
пирамидой можно предложить задачи № 635, 637(б), 638,
639(в),640, 641.
Комбинация шара с усеченной
пирамидой.
1. Шар, описанный около правильной усеченной
пирамиды.
Теорема 5. Около любой правильной
усеченной пирамиды можно описать шар. (Это
условие является достаточным, но не является
необходимым)
2. Шар, вписанный в правильную усеченную
пирамиду.
Теорема 6. В правильную усеченную
пирамиду можно вписать шар в том и только в том
случае, если апофема пирамиды равна сумме апофем
оснований.
На комбинацию шара с усеченной пирамидой в
учебнике Л.С.Атанасяна есть всего лишь одна
задача (№ 636).
Комбинация шара с круглыми телами.
Теорема 7. Около цилиндра, усеченного
конуса (прямых круговых), конуса можно описать
шар.
Теорема 8. В цилиндр (прямой круговой)
можно вписать шар в том и только в том случае,
если цилиндр равносторонний.
Теорема 9. В любой конус (прямой
круговой) можно вписать шар.
Теорема 10. В усеченный конус (прямой
круговой) можно вписать шар в том и только в том
случае, если его образующая равна сумме радиусов
оснований.
Из учебника Л.С.Атанасяна на комбинацию шара с
круглыми телами можно предложить задачи № 642, 643,
644, 645, 646.
Для более успешного изучения материала данной
темы необходимо включать в ход уроков устные
задачи:
1. Ребро куба равно а. Найти радиусы шаров:
вписанного в куб и описанного около него. (r = a/2, R =
a3).
2. Можно ли описать сферу (шар) около: а) куба; б)
прямоугольного параллелепипеда; в) наклонного
параллелепипеда, в основании которого лежит
прямоугольник; г) прямого параллелепипеда; д)
наклонного параллелепипеда? (а) да; б) да; в) нет;
г) нет; д) нет)
3. Справедливо ли утверждение, что около любой
треугольной пирамиды можно описать сферу? (Да)
4. Можно ли описать сферу около любой
четырехугольной пирамиды? (Нет, не около любой
четырёхугольной пирамиды)
5. Какими свойствами должна обладать пирамида,
чтобы около нее можно было описать сферу? (В её
основании должен лежать многоугольник, около
которого можно описать окружность)
6. В сферу вписана пирамида, боковое ребро
которой перпендикулярно основанию. Как найти
центр сферы? (Центр сферы – точка пересечения
двух геометрических мест точек в пространстве.
Первое – перпендикуляр, проведённый к плоскости
основания пирамиды, через центр окружности,
описанной около него. Второе – плоскость
перпендикулярная данному боковому ребру и
проведённая через его середину)
7. При каких условиях можно описать сферу около
призмы, в основании которой – трапеция? (Во-первых,
призма должна быть прямой, и, во-вторых, трапеция
должна быть равнобедренной, чтобы около неё
можно было описать окружность)
8. Каким условиям должна удовлетворять призма,
чтобы около нее можно было описать сферу?
(Призма должна быть прямой, и её основанием
должен являться многоугольник, около которого
можно описать окружность)
9. Около треугольной призмы описана сфера, центр
которой лежит вне призмы. Какой треугольник
является основанием призмы? (Тупоугольный
треугольник)
10. Можно ли описать сферу около наклонной
призмы? (Нет, нельзя)
11. При каком условии центр сферы, описанной
около прямой треугольной призмы, будет находится
на одной из боковых граней призмы? (В основании
лежит прямоугольный треугольник)
12. Основание пирамиды – равнобедренная
трапеция .Ортогональная проекция вершины
пирамиды на плоскость основания – точка,
расположенная вне трапеции. Можно ли около такой
трапеции описать сферу? (Да, можно. То что
ортогональная проекция вершины пирамиды
расположена вне её основания, не имеет значения.
Важно, что в основании пирамиды лежит
равнобедренная трапеция – многоугольник, около
которого можно описать окружность)
13. Около правильной пирамиды описана сфера. Как
расположен ее центр относительно элементов
пирамиды? (Центр сферы находится на
перпендикуляре, проведенном к плоскости
основания через его центр)
14. При каком условии центр сферы, описанной
около прямой треугольной призмы, лежит: а) внутри
призмы; б) вне призмы? (В основании призмы: а)
остроугольный треугольник; б) тупоугольный
треугольник)
15. Около прямоугольного параллелепипеда, ребра
которого равны 1 дм, 2 дм и 2 дм, описана сфера.
Вычислите радиус сферы. (1,5 дм)
16. В какой усеченный конус можно вписать сферу? (В
усечённый конус, в осевое сечение которого можно
вписать окружность. Осевым сечением конуса
является равнобедренная трапеция, сумма её
оснований должна равняться сумме её боковых
сторон. Другими словами, у конуса сумма радиусов
оснований должна равняться образующей)
17. В усеченный конус вписана сфера. Под каким
углом образующая конуса видна из центра сферы? (90
градусов)
18. Каким свойством должна обладать прямая
призма, чтобы в нее можно было вписать сферу? (Во-первых,
в основании прямой призмы должен лежать
многоугольник, в который можно вписать
окружность, и, во-вторых, высота призмы должна
равняться диаметру вписанной в основание
окружности)
19. Приведите пример пирамиды, в которую нельзя
вписать сферу? (Например, четырёхугольная
пирамида, в основании которой лежит
прямоугольник или параллелограмм)
20. В основании прямой призмы лежит ромб. Можно
ли в эту призму вписать сферу? (Нет, нельзя, так
как около ромба в общем случае нельзя описать
окружность)
21. При каком условии в прямую треугольную
призму можно вписать сферу? (Если высота призмы
в два раза больше радиуса окружности, вписанной в
основание)
22. При каком условии в правильную
четырехугольную усеченную пирамиду можно
вписать сферу? (Если сечением данной пирамиды
плоскостью, проходящей через середину стороны
основания перпендикулярно ей, является
равнобедренная трапеция, в которую можно вписать
окружность)
23. В треугольную усеченную пирамиду вписана
сфера. Какая точка пирамиды является центром
сферы? (Центр вписанной в данную пирамиду сферы
находится на пересечении трёх биссектральных
плоскостей углов, образованных боковыми гранями
пирамиды с основанием)
24. Можно ли описать сферу около цилиндра
(прямого кругового)? (Да, можно)
25. Можно ли описать сферу около конуса,
усеченного конуса (прямых круговых)? (Да, можно,
в обоих случаях)
26. Во всякий ли цилиндр можно вписать сферу?
Какими свойствами должен обладать цилиндр, чтобы
в него можно было вписать сферу? (Нет, не во
всякий: осевое сечение цилиндра должно быть
квадратом)
27. Во всякий ли конус можно вписать сферу? Как
определить положение центра сферы, вписанной в
конус? (Да, во всякий. Центр вписанной сферы
находится на пересечении высоты конуса и
биссектрисы угла наклона образующей к плоскости
основания)
Автор считает, что из трех уроков, которые
отводятся по планированию на тему “Разные
задачи на многогранники, цилиндр, конус и шар”,
два урока целесообразно отвести на решение задач
на комбинацию шара с другими телами. Теоремы,
приведенные выше, из-за недостаточного
количества времени на уроках доказывать не
рекомендуется. Можно предложить учащимся,
которые владеют достаточными для этого навыками,
доказать их, указав (по усморению учителя) ход или
план доказательства.
Автор надеется, что материал этой статьи
поможет молодым коллегам при подготовке к урокам
по данной теме.