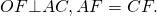Как найти центр описанной окр - Исправление недочетов и поиск решений вместе с Examum.ru

Описанная окружность — подробнее

Определение

Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.

Свойства и центр описанной кружности

И вот, представь себе, имеет место удивительный факт:

Вокруг всякого треугольника можно описать окружность.

Почему этот факт удивительный?

Потому что треугольники ведь бывают разные!

И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.

Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.

Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!

А есть только для прямоугольника:

Подробнее об этом смотри в статье о вписанных четырехугольниках!

Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.

Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.

Знаешь ли ты, что такое серединный перпендикуляр?

Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.

Прямая ( displaystyle a) – это серединный перпендикуляр к отрезку ( displaystyle AB).

А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.

Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке ( displaystyle O).

Это и есть центр описанной около (вокруг) треугольника ( displaystyle ABC) окружности.

Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!

Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!

Вот так:

А вот если остроугольный, то внутри:

Что же делать с прямоугольным треугольником?

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.

Здорово, правда?

Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!

Да ещё с дополнительным бонусом:

В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.

Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.

А именно:

В произвольном треугольнике:
( Large displaystyle frac{a}{sin angle A}=2R)

Ну и, конечно,

( displaystyle begin{array}{l}frac{b}{sin angle B}=2R\frac{c}{sin angle C}=2Rend{array})

Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.

То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.

Хорошая формула? По-моему, просто отличная!

Доказательство теоремы

Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.

Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

Смотри, вот так:

opisannaya okruzhnost vokrug okolo treugolnika

Давай наберёмся мужества и докажем эту теорему.

Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.

Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).

Геометрическое место точек, обладающих свойством «( displaystyle X)» — такое множество точек, что все они обладают свойством «( displaystyle X)» и никакие другие точки этим свойством не обладают.

Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.

А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.

В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:

Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.

Тут множество – это серединный перпендикуляр, а свойство «( displaystyle X)» — это «быть равноудаленной (точкой) от концов отрезка».

Проверим? Итак, нужно удостовериться в двух вещах:

Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему

Приступим:

Проверим 1. Пусть точка ( displaystyle M) лежит на серединном перпендикуляре к отрезку ( displaystyle AB).

Соединим ( displaystyle M) с ( displaystyle A) и с ( displaystyle B).Тогда линия ( displaystyle MK) является медианой и высотой в ( displaystyle Delta AMB).

Значит, ( displaystyle Delta AMB) – равнобедренный, ( displaystyle MA=MB) – убедились, что любая точка ( displaystyle M), лежащая на серединном перпендикуляре, одинаково удалена от точек ( displaystyle A) и ( displaystyle B).

Теперь 2. Почти точно так же, но в другую сторону. Пусть точка ( displaystyle M) равноудалена от точек ( displaystyle A) и ( displaystyle B), то есть ( displaystyle MA=MB).

Возьмём ( displaystyle K) – середину ( displaystyle AB) и соединим ( displaystyle M) и ( displaystyle K). Получилась медиана ( displaystyle MK). Но ( displaystyle Delta AMB) – равнобедренный по условию ( displaystyle (MA=MB)Rightarrow MK) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка ( displaystyle M) — точно лежит на серединном перпендикуляре.

Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.

Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».

Рассмотрим треугольник ( displaystyle ABC). Проведём два серединных перпендикуляра ( displaystyle {{a}_{1}}) и ( displaystyle {{a}_{2}}), скажем, к отрезкам ( displaystyle AB) и ( displaystyle BC). Они пересекутся в какой-то точке, которую мы назовем ( displaystyle O).

А теперь, внимание!

Точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{1}}Rightarrow OA=OB);
точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{2}}Rightarrow OB=OC).
И значит, ( displaystyle OA=OB=OC) и ( displaystyle OA=OC).

Отсюда следует сразу несколько вещей:

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 6. Описанная окружность. Многоугольники

Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.

Около каких фигур можно, а вокруг каких нельзя описать окружность.

Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.

Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.

ЕГЭ 6. Вписанная окружность

В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие свойства.

В какие фигуры можно, а в какие нельзя вписать окружность. Научимся решать задачи на вписанную окружность.

Источник

Где находится центр описанной около треугольника окружности? Что можно сказать о центре окружности, описанной около многоугольника?

Теорема.

Центр описанной около треугольника окружности является точкой пересечения серединных перпендикуляров к сторонам треугольника.

Дано: ∆ ABC,

окружность (O;R) — описанная около ∆ ABC.

Доказать:

O — точка пересечения серединных перпендикуляров к сторонам ∆ ABC.

Доказательство:

Соединим отрезками точки O и A, O и C.

OA=OC (как радиусы), следовательно, треугольник AOC — равнобедренный с основанием AC (по определению).

По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):

Следовательно, центр описанной окружности — точка O — лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину, то есть на серединном перпендикуляре к AC.

Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.

Так как серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, то точка O — центр описанной около треугольника ABC окружности.

Что и требовалось доказать.

Замечание.

Аналогичные рассуждения можно применить и для многоугольника, около которого можно описать окружность.

Центр описанной около многоугольника окружности является точкой пересечения серединных перпендикуляров к сторонам этого многоугольника.

Источник

Центр описанной окружности

окружность (O;R) — описанная около ∆ ABC.

O — точка пересечения серединных перпендикуляров к сторонам ∆ ABC.

Соединим отрезками точки O и A, O и C.

OA=OC (как радиусы), следовательно, треугольник AOC — равнобедренный с основанием AC (по определению).

По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):

Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.

Что и требовалось доказать.

Аналогичные рассуждения можно применить и для многоугольника, около которого можно описать окружность.

2 Comments

на мой взгляд у вас опечатка — «Соединим отрезками точки O и A, O и C.

OA=OB( написано ОВ вместо ОС) (как радиусы), следовательно, треугольник AOB — равнобедренный с основанием AC (по определению).»

Как определить центр описанной окружности треугольника

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Первый вопрос, который может возникнуть: описанная – вокруг чего?

Ну, вообще-то иногда бывает и вокруг чего угодно, а мы будем рассуждать об окружности, описанной вокруг (иногда ещё говорят «около») треугольника. Что же это такое?

Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.

И вот, представь себе, имеет место удивительный факт:

Вокруг всякого треугольника можно описать окружность.

Почему этот факт удивительный?

Но ведь треугольники – то бывают разные!

И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.

Доказательство этого удивительного факта можешь найти в следующих уровнях теории, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины. Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!

А есть только для прямоугольника:

Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.

Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.

Знаешь ли ты, что такое серединный перпендикуляр?

Это прямая, проходящая через середину отрезка и перпендикулярная ему.Прямая – это серединный перпендикуляр к отрезку .

Это и есть центр описанной около (вокруг) треугольника окружности.

Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!

А вот если остроугольный, то – внутри:

Что же делать с прямоугольным треугольником?

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.

Правда, здорово?Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!

Да ещё с дополнительным бонусом:

в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы

В произвольном треугольнике:

Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол. Хорошая формула? По-моему, просто отличная!

ОПИСАННАЯ ОКРУЖНОСТЬ. СРЕДНИЙ УРОВЕНЬ

В этой части мы обсудим окружность, описанную вокруг (часто говорят «около») треугольника. Прежде всего дадим определение.

Окружность , описанная около треугольника – такая окружность, что происходит через все три вершины этого треугольника.

1. Существование и центр описанной окружности

Тут возникает вопрос: а для всякого ли треугольника существует такая окружность? Вот оказывается, что да, для всякого. И более того, мы сейчас сформулируем теорему, которая ещё и отвечает на вопрос, где же находится центр описанной окружности.

Теорема. Вокруг всякого треугольника можно описать окружность , при том единственным образом .

Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

Давай наберёмся мужества и докажем эту теорему. Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.

Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).

Геометрическое место точек , обладающих свойством « » — такое множество точек, что все они обладают свойством « » и никакие другие точки этим свойством не обладают.

Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы. А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют. В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:

Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.

Тут множество – это серединный перпендикуляр, а свойство « » — это «быть равноудаленной (точкой) от концов отрезка».

Проверим? Итак, нужно удостовериться в двух вещах:

Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему.

Проверим 1. Пусть точка лежит на серединном перпендикуляре к отрезку .

Соединим с и с .Тогда линия является медианой и высотой в . Значит, – равнобедренный, – убедились, что любая точка , лежащая на серединном перпендикуляре, одинаково удалена от точек и .

Теперь 2. Почти точно так же, но в другую сторону. Пусть точка равноудалена от точек и , то есть .

Возьмём – середину и соединим и . Получилась медиана . Но – равнобедренный по условию не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка — точно лежит на серединном перпендикуляре.

Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.

Рассмотрим треугольник . Проведём два серединных перпендикуляра и , скажем, к отрезкам и . Они пересекутся в какой-то точке, которую мы назовем .

А теперь, внимание!

Точка лежит на серединном перпендикуляре ;
точка лежит на серединном перпендикуляре .
И значит, и .

Отсюда следует сразу несколько вещей:

Во – первых , точка обязана лежать на третьем серединном перпендикуляре, к отрезку .

То есть серединный перпендикуляр тоже обязан пройти через точку , и все три серединных перпендикуляра пересеклись в одной точке.

Во – вторых : если мы проведём окружность с центром в точке и радиусом , то эта окружность также пройдёт и через точку , и через точку , то есть будет описанной окружностью . Значит, уже есть, что пересечение трёх серединных перпендикуляров – центр описанной окружности для любого треугольника.

И последнее: о единственности. Ясно (почти), что точку можно получить единственным образом, поэтому и окружность – единственная. Ну, а «почти» — оставим на твоё размышление. Вот и доказали теорему. Можно кричать «Ура!».

2. Радиус описанной окружности.

А если в задаче стоит вопрос «найдите радиус описанной окружности»? Или наоборот, радиус дан, а требуется найти что – то другое? Есть ли формула, связывающая радиус описанной окружность с другими элементами треугольника?

Есть, конечно! И эта формула называется «Теорема синусов» (доказательство смотри именно в этой теме).

Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, тебе нужна одна сторона (любая!) и противолежащий ей угол . И всё!

3. Центр окружности – внутри или снаружи

А теперь вопрос: может ли центр описанной окружности лежать снаружи треугольника.
Ответ: ещё как может. Более того, так всегда бывает в тупоугольном треугольнике.

В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника.

В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы , а радиус равен половине гипотенузы.

ОПИСАННАЯ ОКРУЖНОСТЬ. КОРОТКО О ГЛАВНОМ

1. Окружность, описанная около треугольника

– это окружность, которая проходит через все три вершины этого треугольника.

Вокруг всякого треугольника можно описать окружность.

2. Существование и центр описанной окружности

Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

3. Радиус описанной окружности

Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, нужна одна сторона (любая!) и противолежащий ей угол.

4. Центр окружности – внутри или снаружи

В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника

В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы , а радиус равен половине гипотенузы.

P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это — не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время.

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте — нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Я рекомендую использовать для этих целей наш учебник «YouClever» (который ты сейчас читаешь) и решебник и программу подготовки «100gia».

Условия их приобретения изложены здесь. Кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!

И в заключение.

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” — это совершенно разные навыки. Тебе нужны оба.

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности	Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

окружность (O;R) — описанная около ∆ ABC.

O — точка пересечения серединных перпендикуляров к сторонам ∆ ABC.

Соединим отрезками точки O и A, O и C.

OA=OC (как радиусы), следовательно, треугольник AOC — равнобедренный с основанием AC (по определению).

По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):

Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.

Что и требовалось доказать.

Аналогичные рассуждения можно применить и для многоугольника, около которого можно описать окружность.

2 Comments

на мой взгляд у вас опечатка — «Соединим отрезками точки O и A, O и C.

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Описанная окружность

Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Вписанная окружность

Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

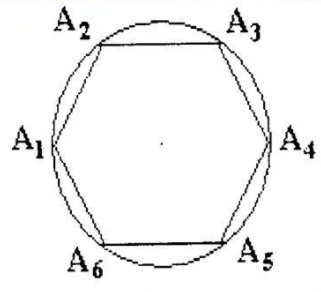
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 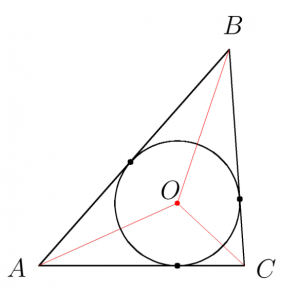Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

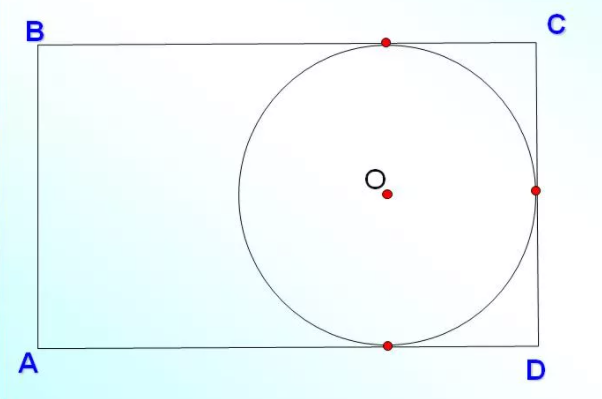
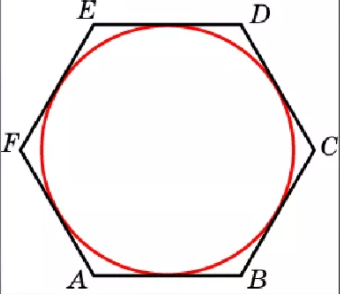
Условие вписанной в 4-х угольник окружности

Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

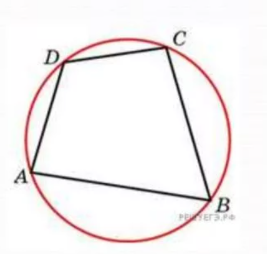
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

источники:

http://hd01.ru/info/kak-opredelit-centr-opisannoj-okruzhnosti/

Описанная и вписанная окружность

Источник

Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).

Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).

Свойства вписанной окружности

1. Окружность можно вписать в любой треугольник.

2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.

Например, на рисунке 8.106 .

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.

Свойства описанной окружности

1. Окружность можно описать около любого треугольника.

2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.

Например, на рисунке 8.107 $LaTeX formula: angle A+angle C=angle B+angle D=180^{circ}$ .

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

Расположение центров окружностей, описанных около треугольника:

1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;

2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:

а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);

4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).

Расположение центров окружностей, вписанных в треугольник:

1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);

2) центром окружности является точка пересечения биссектрис треугольника;

3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Формулы для вычисления радиусов вписанной и описанной окружностей

Радиус окружности, описанной около многоугольника, как правило, обозначают , а радиус окружности, вписанной в многоугольник, обозначают :

1) для равностороннего треугольника со стороной :

$LaTeX formula: R=frac{a}{sqrt{3}}$ , (8.34)

$LaTeX formula: r=frac{a}{2sqrt{3}}$ ; (8.35)

2) для произвольного треугольника со сторонами и площадью :

$LaTeX formula: R=frac{abc}{4S}$ , (8.36)

$LaTeX formula: r=frac{2S}{a+b+c}$ ; (8.37)

3) для прямоугольного треугольника с катетами и гипотенузой :

$LaTeX formula: R=frac{c}{2}$ , (8.38)

$LaTeX formula: r=frac{a+b-c}{2}$ ; (8.39)

4) для квадрата со стороной и диагональю :

$LaTeX formula: R=frac{d}{2}$ , (8.40)

$LaTeX formula: r=frac{a}{2}$ ; (8.41)

5) для прямоугольника с диагональю :

$LaTeX formula: R=frac{d}{2}$ ; (8.42)

6) для ромба с высотой :

$LaTeX formula: r=frac{h}{2}$ ; (8.43)

7) для трапеции с высотой , при условии, что в трапецию можно вписать окружность:

$LaTeX formula: r=frac{h}{2}$ . (8.44)

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами и площадью , по формуле $LaTeX formula: R=frac{abc}{4S}$ найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);

для правильного шестиугольника со стороной :

, (8.45)

$LaTeX formula: r=frac{asqrt{3}}{2}$ . (8.46)

Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка является центром вписанной в него и описанной около него окружностей.

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна .

Решение. Так как площадь круга радиуса находят по формуле 8.32, а площадь квадрата со стороной находят по формуле $LaTeX formula: S=a^{2}$ , то согласно условию задачи запишем: $LaTeX formula: S_{square }-S_{bigcirc }=12$ , $LaTeX formula: pi r^{2}-a^{2}=2pi -8$ .

А так как $LaTeX formula: r=frac{a}{2}$ , то $LaTeX formula: frac{pi a^{2}}{4}-a^{2}=2pi -8$ , $LaTeX formula: pi a^{2}-4a^{2}=4(2pi -8)$ , $LaTeX formula: a^{2}(pi -4)=8(pi -4)$ , $LaTeX formula: a^{2}=8$ , .

Ответ: .

Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами и находят по формуле .

Пусть , тогда (рис. 8.118).

Получим: , $LaTeX formula: x^{2}+3x-4=0$ , откуда , следовательно, , .

По теореме Пифагора найдем диагональ прямоугольника: $LaTeX formula: d^{2}=1+16=17$ , . Согласно формуле 8.42 .

Ответ: .

Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.

Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):

$LaTeX formula: a^{2}=left (frac{d_{1}}{2} right )^{2}+left ( frac{d_{2}}{2} right )^{2}$ , $LaTeX formula: a^{2}=3^{2}+4^{2}$ , .

По формуле 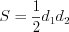$LaTeX formula: S=frac{1}{2}d_{1}d_{2}$ найдем площадь ромба: $LaTeX formula: S=frac{1}{2}cdot 6cdot 8=24$ .

Но площадь ромба можно найти и по формуле , а так как , то . Тогда , а .

Ответ: 2,4.

Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна .

Решение. Площадь правильного треугольника со стороной находят по формуле: $LaTeX formula: S=frac{sqrt{3}a^{2}}{4}$ .

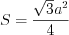
Зная площадь треугольника, найдем его сторону: $LaTeX formula: frac{sqrt{3}a^{2}}{4}=4sqrt{3}$ , $LaTeX formula: a^{2}=16$ , .

По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: $LaTeX formula: r=frac{4}{2sqrt{3}}=frac{2}{sqrt{3}}$ .

По формуле 8.30 найдем длину окружности: $LaTeX formula: C=frac{4pi }{sqrt{3}}$ .

Ответ: $LaTeX formula: frac{4sqrt{3}pi }{3}$ .

Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.

Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой находят по формуле 8.38. Тогда .

Так как треугольник равнобедренный, то его катеты и раны и по теореме Пифагора $LaTeX formula: c^{2}=2a^{2}$ , откуда $LaTeX formula: a=frac{C}{sqrt{2}}$ , $LaTeX formula: a=frac{4}{sqrt{2}}=2sqrt{2}$ .

Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае $LaTeX formula: r=frac{2a-c}{2}$ , $LaTeX formula: r=frac{4sqrt{2}-4}{2}=2sqrt{2}-2$ .

Ответ: .

Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник . Точка является центром вписанной в треугольник окружности (рис. 8.120).

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат со стороной 3. Если катет , а сторона квадрата , то .

Пусть отрезок . По свойству касательных и .

Тогда по теореме Пифагора $LaTeX formula: BC^{2}=AC^{2}+AB^{2}$ или $LaTeX formula: 25+10x+x^{2}=64+9+6x+x^{2}$ , откуда , .

Найдем катет : .

Найдем площадь треугольника: $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot ACcdot AB$ , $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot 8cdot 15=60$ .

Ответ: 60.

Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).

Решение. Согласно свойству биссектрисы треугольника запишем: $LaTeX formula: frac{6}{4}=frac{x}{8}$ , откуда .

Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.

В свою очередь по формуле Герона найдем площадь треугольника. Так как , то .

Тогда $LaTeX formula: r=frac{18sqrt{15}}{30}=frac{3sqrt{15}}{5}=0,6sqrt{15}$ .

Ответ: .

Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.

Решение. Согласно условию задачи и рисунку 8.122, запишем: , .

По свойству четырехугольника, описанного около окружности, получим: , , .

Согласно формуле 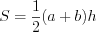$LaTeX formula: S=frac{1}{2}(a+b)h$ найдем площадь трапеции: $LaTeX formula: S=frac{1}{2}cdot 15cdot 6=45$ .

Ответ: 45.

Пример 9. Длины оснований равнобедренной трапеции относятся как , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.

Решение. Рассмотрим равнобедренную трапецию (рис. 8.123) и проведем диагональ трапеции .

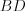
Радиус окружности, описанной около треугольника , найдем по формуле 8.36:

$LaTeX formula: R=frac{ABcdot BDcdot AD}{4cdot S_{triangle ABD}}=frac{ABcdot BDcdot AD}{4cdot frac{1}{2}cdot ADcdot BN}$ , $LaTeX formula: R=frac{ABcdot BD}{2cdot BN}$ .

Зная, что и вводя коэффициент пропорциональности , получим , .

Так как длина средней линии трапеции равна высоте трапеции, то $LaTeX formula: frac{1}{2}(5k +12k)=17$ , откуда . Тогда , .

Поскольку четырехугольник является прямоугольником, то , тогда $LaTeX formula: AN=KD=frac{1}{2}(24-10)=7$ .

Согласно теореме Пифагора запишем:

$LaTeX formula: AB=sqrt{AN^{2}+BN^{2}}$ , $LaTeX formula: AB=sqrt{17^{2}+7^{2}}=sqrt{338}$ ;

$LaTeX formula: BD=sqrt{BN^{2}+ND^{2}}$ , $LaTeX formula: BD=sqrt{17^{2}+17^{2}}=17sqrt{2}$ .

По формуле 8.36 найдем радиус окружности, описанной около треугольника , а, следовательно, и около трапеции :

$LaTeX formula: R=frac{sqrt{338}cdot 17sqrt{2}}{2cdot 17}=frac{2cdot 13}{2}=13$ .

Согласно формуле 8.32 найдем площадь круга: .

Ответ: .

Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна .

Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника: .

По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как , то $LaTeX formula: r=frac{3}{2}$ .

Площадь круга находят по формуле 8.32. Тогда $LaTeX formula: S_{1}=3pi$ , а $LaTeX formula: S_{2}=frac{9pi}{4}$ .

Найдем площадь кольца: $LaTeX formula: S_{K}=S_{1}-S_{2}$ , $LaTeX formula: S_{K}=3pi -frac{9pi }{4}=frac{3pi }{4}$ .

Ответ: .

1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.

3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.

5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.

Длину окружности радиуса находят по формуле:

. (8.30)

Площадь круга радиуса находят по формуле:

$LaTeX formula: S=pi R^{2}$ . (8.32)

Источник

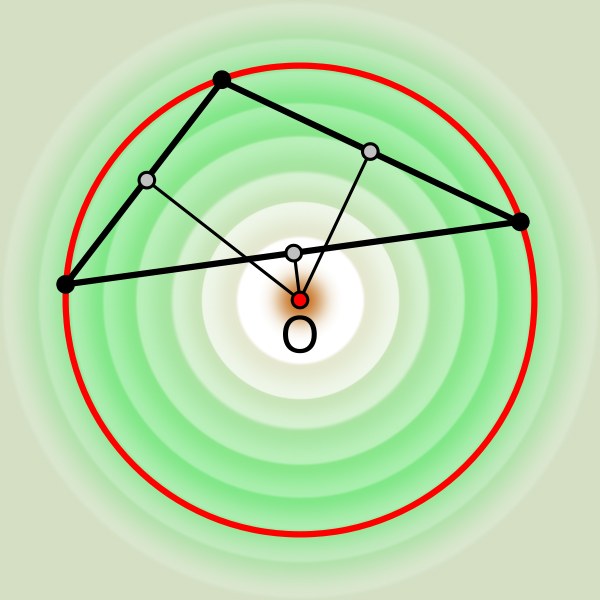
Как найти центр описанной окружности

Иногда около выпуклого многоугольника можно начертить окружность таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной. Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности, найти эту точку, как правило, не очень трудно.

Вам понадобится

Линейка, карандаш, транспортир или угольник, циркуль.

Инструкция

Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центра круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.

Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым числом сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим сторонам.

Для правильных многоугольников определение центра вписанной окружности может быть намного проще. Например, если это квадрат, то начертите две диагонали — их пересечение и будет центром вписанной окружности. В правильном многоугольнике с любым четным числом сторон достаточно соединить вспомогательными отрезками две пары лежащих друг напротив друга углов — центр описанной окружности должен совпадать с точкой их пересечения. В прямоугольном треугольнике для решения задачи просто определите середину самой длинной стороны фигуры — гипотенузы.

Если из условий неизвестно, можно ли в принципе начертить описанную окружность для данного многоугольника, после определения предполагаемой точки центра любым из описанных способов вы можете это выяснить. Отложите на циркуле расстояние между найденной точкой и любой из вершин, установите циркуль в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности. Если это не так, значит, не выполняется одно из основных свойств и описать окружность около данного многоугольника нельзя.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник