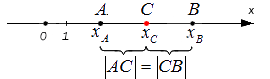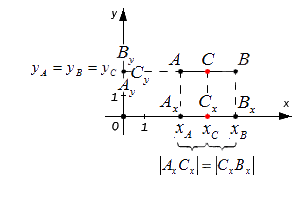- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Построения циркулем и линейкой
- Построение середины отрезка
Пример:
Построить середину данного отрезка.
Дано: отрезок АВ.
Построить: середину АВ.
Решение:
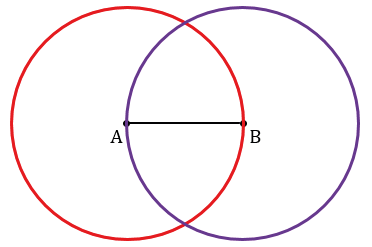
Строим с помощью линейки произвольный отрезок АВ.
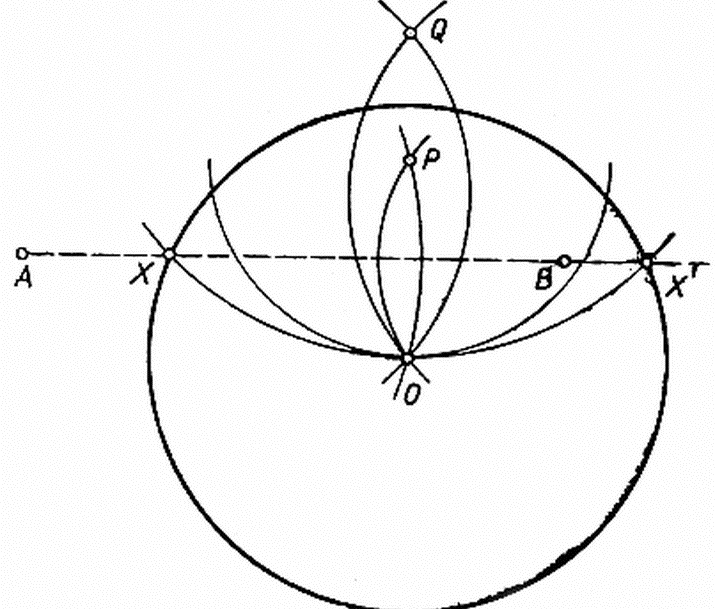
Далее с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В.
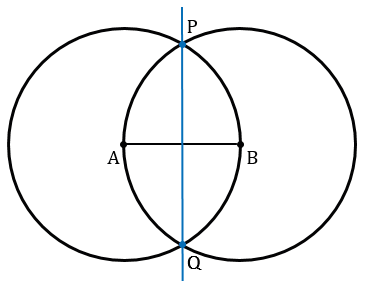
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q. Проведем с помощью линейки через точки Р и Q прямую РQ.
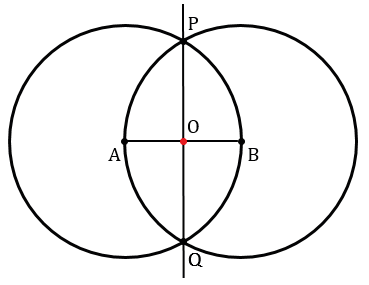
Точку пересечения прямой РQ и отрезка АВ обозначим О.
Докажем, что точка О — искомая точка, т.е. точка О — середина отрезка АВ.
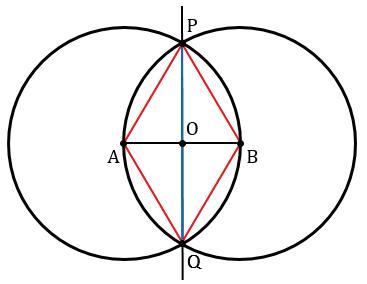
Рассмотрим треугольники РАQ и РВQ.
По построению АР = ВР, АQ = BQ (как радиусы одинаковых окружностей), PQ — общая, следовательно, 

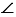
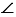

В 


Советуем посмотреть:
Построение угла, равного данному
Построение биссектрисы угла
Построение перпендикулярных прямых
Среднее пропорциональное
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 292,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 320*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 352,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 393,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 588,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 669,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 876,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 900,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1282,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1283,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
В этой статье вы узнаете, как разделить тот или иной отрезок с помощью такого инструмента, как циркуль. Ведь не всегда есть линейка под рукой. Такие знания пригодятся на практике.
Содержание
- Как определить середину отрезка с помощью одного циркуля?
- Как построить середину отрезка с помощью циркуля и линейки?
- Видео: Как середину отрезка только циркулем?
Геометрия – это предмет, который изучается в школе и имеет применение на практике. Благодаря знаниям этого предмета можно узнать площадь, объем той или иной фигуры, или емкости, а также с легкостью разделить отрезок пополам с помощью сподручных инструментов. Узнаем дальше, как определить середину отрезка с помощью циркуля.
Как определить середину отрезка с помощью одного циркуля?
Интересно то, что определить середину отрезка с помощью циркуля можно и без линейки – это доказал еще в восемнадцатом веке итальянец Маскерони. Процесс построения сложнее, чем с помощью двух этих инструментов, но знания по этому поводу не помешают. Вначале определимся, что такое отрезок. Отрезком называют прямую, ограниченную двумя точками. И, чтобы найти середину отрезка, придется построить множество окружностей и найти множество точек их пересечения на них, пока не найдется середина отрезка.
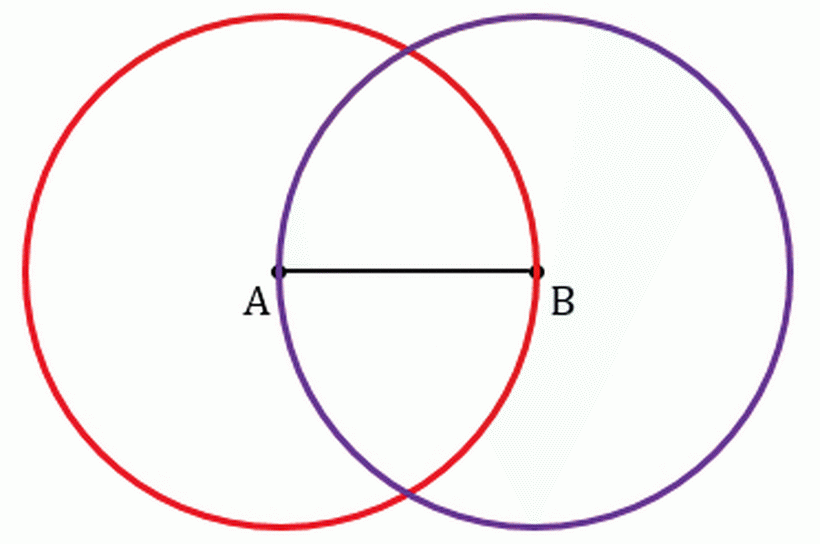
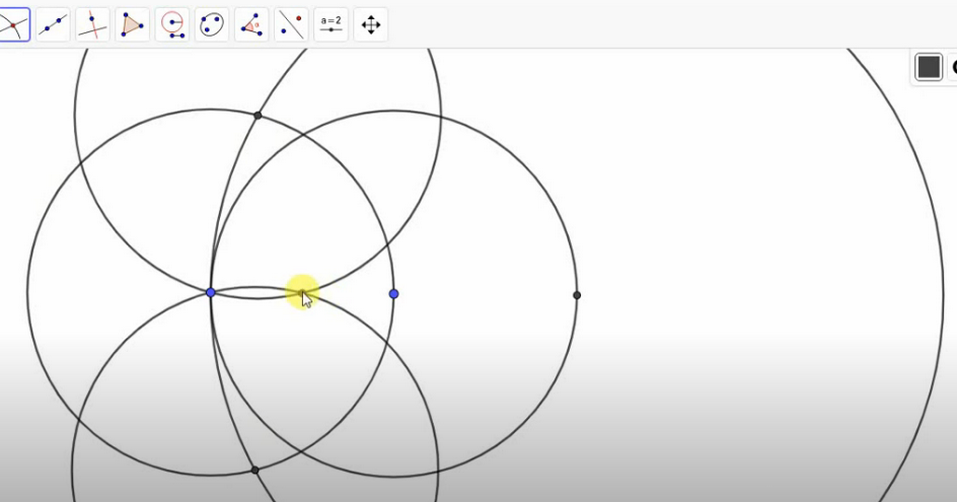
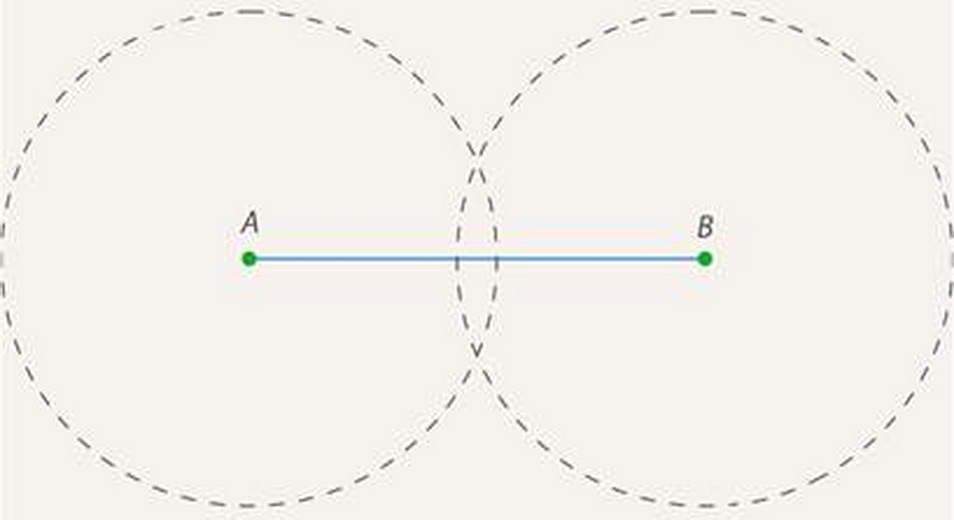
- Если запомнить последовательность, построения окружностей, то процесс определения середины несложный. Вначале удваивают отрезок путем построения двух окружностей радиусом равным длине заданного отрезка, фото ниже:
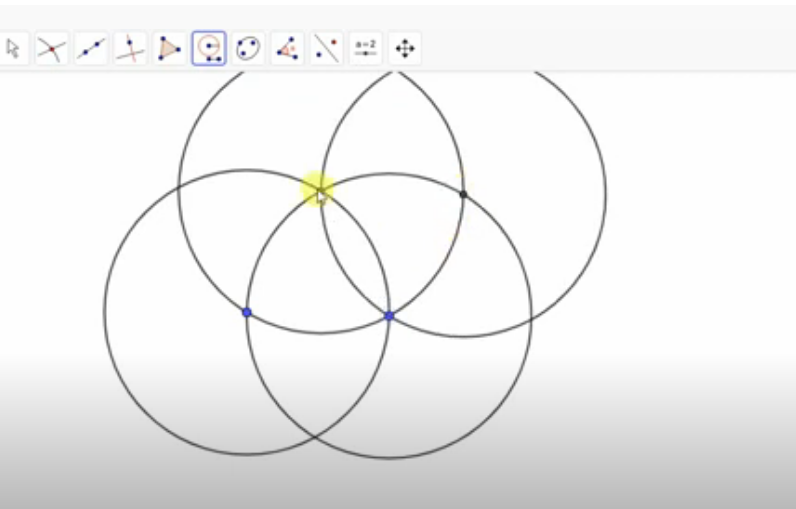
- Следующий шаг — постройте окружность тем же радиусом вверху на точке пересечения двух окружностей, наглядно это будет смотреться так:
- Из точки пересечения второй и третьей окружности, нарисуйте еще четвертую окружность такого же радиуса, должен получиться вот такой рисунок:
- Эти окружности строились, чтобы получить точку (третью точку, как продолжение отрезка), она находится на пересечении четвертой и второй окружности. Теперь эту точку оставьте, а две окружности сверху сотрите, они не понадобятся вам.
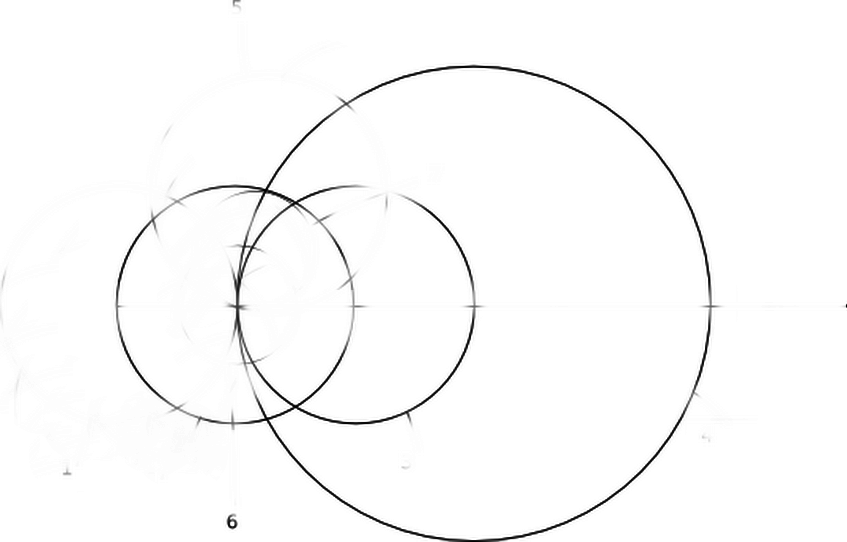
- Постройте окружность с радиусом в два раза больше, чем предыдущие:
- Отметьте две точки пересечения на первой окружности и большой. Через эти две точки проведите окружности с радиусом отрезка, а точка их пересечения и будет серединой отрезка.
ВАЖНО: Поиск середины отрезка сводится к нескольким шагам. Вначале отрезок следует удлинить ровно в два раза благодаря окружности большего диаметра, а потом рядом построений уже и найти саму точку отрезка, что делит его пополам.
Как построить середину отрезка с помощью циркуля и линейки?
Еще можно построить середину отрезка с помощью циркуля, линейки. Сделать это намного проще, чем в предыдущем варианте. Вам не понадобится рисовать множество окружностей разного диаметра, а достаточно построить лишь две одинаковые, а после провести перпендикуляр через точки пересечения с линиями окружности. Еще этот перпендикуляр называют серединным, что означает прямую, которую проводят под углом 90 градусов к отрезку.
Далее будет представлен мастер-класс на эту тему в подробностях и наглядно:
- Нарисуйте нужный отрезок на листке в клеточку, так вам удобнее будет разобраться в данной теме.
- Возьмите циркуль и нарисуйте две окружности с радиусом большим, чем середина отрезка или радиусом с длину отрезка – нет особой надобности рисовать слишком большие окружности, особенно, если отрезок большой длины.
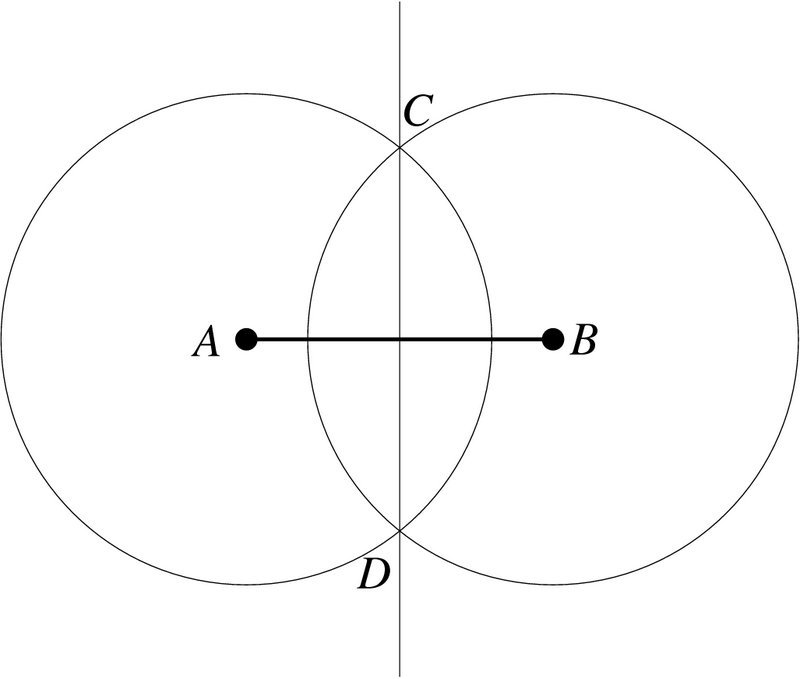
- На рисунке выше видно, что окружности образуют две точки пересечения (вверху и внизу). Теперь понадобится линейка. Соедините эти две точки серединным перпендикуляром. Точка пересечения линии и отрезка и будет серединой.
Итак, среднюю точку отрезка нашли, теперь еще и не помешает доказать, что именно CD – срединный перпендикуляр, и он делит отрезок пополам. Это сделать просто. Ведь две окружности, что образуют линию, имеют одинаковый радиус, диаметр. А у окружностей все точки на линии одинаково удалены от ее центра. Значит точки C и D также находятся на одинаковых расстояниях от точек A и B. Прямая которая соединяет точки D и C может быть лишь одна в плоскости. И точка пересечения на отрезке находится на одном и том же расстоянии. Все это и требовалось прояснить.
Видео: Как середину отрезка только циркулем?
Построение середины отрезка
Пример:
Дано: отрезок АВ.
Построить: середину АВ.
Решение:
Строим с помощью линейки произвольный отрезок АВ.
Далее с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В.
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q. Проведем с помощью линейки через точки Р и Q прямую РQ.
Точку пересечения прямой РQ и отрезка АВ обозначим О.
Докажем, что точка О — искомая точка, т.е. точка О — середина отрезка АВ.
Рассмотрим треугольники РАQ и РВQ.
По построению АР = ВР, АQ = BQ (как радиусы одинаковых окружностей), PQ — общая, следовательно, 

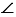

В 


Поделись с друзьями в социальных сетях:
Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B : необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В , верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — ( x B — x C )
Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A ( x A ) и B ( x B ):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
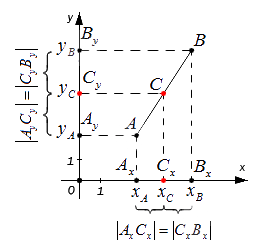
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y ).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
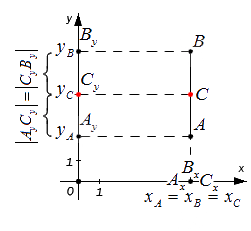
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A ( x A , y A ) и B ( x B , y B ) определяются как:
( x A + x B 2 , y A + y B 2 )
Середина отрезка в пространстве
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
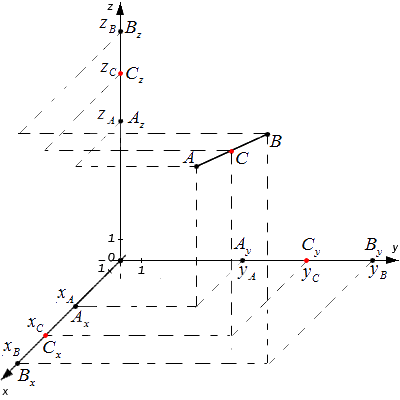
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A ( x A , y A ) и B ( x B , x B ) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) , O B → = ( x B , y B ) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C ( x A + x B 2 , y A + y B 2 , z A + z B 2 )
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Исходные данные: на плоскости – точки с заданными координатами А ( — 7 , 3 ) и В ( 2 , 4 ) . Необходимо найти координаты середины отрезка А В .
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ: координаты середины отрезка А В — 5 2 , 7 2 .
Исходные данные: известны координаты треугольника А В С : А ( — 1 , 0 ) , В ( 3 , 2 ) , С ( 9 , — 8 ) . Необходимо найти длину медианы А М .
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M :
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + ( — 8 ) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М ), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М :
A M = ( 6 — ( — 1 ) ) 2 + ( — 3 — 0 ) 2 = 58
Ответ: 58
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 ( 1 , 1 , 0 ) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M ( 4 , 2 , — 4 ) . Необходимо рассчитать координаты точки А .
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А : x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · ( — 4 ) — 0 = — 8
Ответ: координаты точки А ( 7 , 3 , — 8 ) .
Середина отрезка. Координаты середины отрезка
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, .
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления координат середины отрезка с концами A( xa , ya ) и B( xb , yb ) на плоскости:
| xc = | xa + xb | yc = | ya + yb |
| 2 | 2 |
Формула вычисления координат середины отрезка с концами A( xa , ya , za ) и B( xb , yb , zb ) в пространстве:
| xc = | xa + xb | yc = | ya + yb | zc = | za + zb |
| 2 | 2 | 2 |
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Примеры вычисления координат середины отрезка в пространстве
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-serediny-otrezka/
http://ru.onlinemschool.com/math/library/analytic_geometry/points_center/
|
Как найти середину отрезка АВ с помощью циркуля и линейки без шкалы? Как построить точку М середину отрезка АВ? Нужно начертить две дуги (из центра А и из центра В) радиусом произвольным, но чисто визуально явно большим, чем расстояние до середины.Через точки пересечения дуг провести прямую.Эта прямая разделит отрезок АВ точно посередине И никакой шкальной линейки не нужно — можете вообще приложить к точкам зеркальце или пилочку для ногтей :))) автор вопроса выбрал этот ответ лучшим Знаете ответ? |