Как найти центр поворота отрезка

А чем строить не важно?

Проводим прямую через начальные точки двух отрезков $%AA’$%, из точки $%B$% проводим прямую параллельную полученной, из точки $%A’$% циркулем проводим дугу с радиусом $%A’B’$% до пересечения с прямой из точки $%B$%, получаем точку $%B’_1$%. Строим к прямой $%B’B’_1$% перпендикуляр через точку $%A’$%. Он по идее пройдёт через середину отрезка $%B’B’_1$%. Так же из середины отрезка $%AA’$% строим перпендикуляр. Точка пересечения перпендикуляров будет центром поворота, что можно легко проверить тем же циркулем.

Цели урока:

Образовательные

• ввести понятие поворота и доказать, что поворот
  есть движение;
• рассмотреть поворот отрезка, в зависимости от
  центра поворота (центр поворота лежит вне
  отрезка, на отрезке и является одним из концов
  отрезка);
• научить построению отрезка при повороте его на
  данный угол;
• проверить усвоение материала, изученного на
  предыдущих уроках и материала, пройденного на
  этом уроке.

Развивающие

• развивать умение анализировать условие задачи,
  строить логическую цепочку при решении задач,
  обоснованно делать выводы;
• развивать мыслительный процесс, познавательный
  интерес, математическую речь учащихся;

Воспитательные

• воспитывать внимательность, наблюдательность,
  положительное отношение к обучению.

Содержание темы: урок по геометрии
разработан для учащихся 9 класса.

Тип урока: урок изучения нового
материала и промежуточного контроля усвоения
учащимися пройденного на этом уроке и изученного
ранее материала.

Организационные формы общения: коллективная,
индивидуальная, фронтальная, в парах.

Структура занятия:

1. Мотивационная беседа с учащимися с последующей
   постановкой целей;
2. Проверка домашнего задания;
3. Актуализация опорных знаний;
4. Обогащение знаний;
5. Закрепление изученного материала;
6. Проверка усвоения изученного материала
   (тестирование с последующей взаимопроверкой);
7. Подведение итога занятия (рефлексия);
8. Домашнее задание.

 Оформление: мультимедийный
проектор, экран, ноутбук, компьютерная
презентация, сигнальные карточки.

Мотивационная беседа.

Без движения — жизнь только
летаргический сон.
Жан Жак Руссо

I. Сообщение темы, целей и хода урока.
(СЛАЙД 2)

— Ребята, Вы знаете какую важную роль имеет
движение в жизни человека, общества, науки.
Большую роль играет движение и в математике:
преобразование графиков, отображение точек,
фигур, плоскостей – всё это движение. На
предыдущих уроках мы с Вами рассмотрели
несколько видов движения. Сегодня мы
познакомимся ещё с одним видом движения:
поворотом. Тема урока: поворот.

И наш урок тоже является примером движения,
только движения не с физической точки зрения, а
движением в умственном развитии, познании нового
и приобретения новых знаний. В течение всего
урока Вы будете выполнять различные задачи,
тесты. Поэтому будьте активны, продвигайтесь в
своих знаниях вперёд на протяжении всего урока и
улучшайте свои результаты от одного этапа к
другому!

В течение всего урока, как мою речь, так и вашу
будет сопровождать презентация, которая поможет
проверить правильность выполнения Вами домашней
работы, предложенных тестов и самостоятельно
решённых задач.

II. Проверка домашнего задания.

С помощью СЛАЙДОВ 3-5 проверить решение № 1165.

III. Актуализация опорных знаний.

Тест №1. (СЛАЙДЫ 6-13)

Приложение 1

После выполнения теста ребята обмениваются
тетрадями и выполняют взаимопроверку.

IV. Изучение нового материала.
(обогащение знаний)

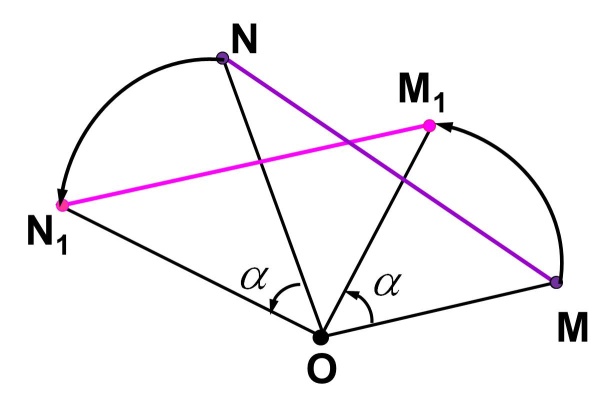
(СЛАЙД 14) Отметим на плоскости точку О
(неподвижная точка), и зададим угол a – угол
поворота. Поворотом плоскости вокруг точки О на
угол a называется отображение плоскости на
себя, при котором каждая точка M отображается в
такую точку M₁, что OM =OM₁ и угол MOM₁
= a.

(СЛАЙД 15) При этом точка O остаётся на месте, т.е.
отображается сама в себя, а все остальные точки
поворачиваются вокруг точки O в одном и том же
направлении на угол a по часовой стрелки или
против часовой стрелки.

(СЛАЙД 16) Точка О называется центром поворота, a
– угол поворота. Обозначается Р_о^a.

(СЛАЙД 17) Если поворот выполняется по часовой
стрелке, то угол поворота a считается
отрицательным. Если поворот выполняется против
часовой стрелки, то угол поворота –
положительный.

— Ребята, давайте вспомним понятие движения. Как
Вы думаете, является ли поворот движением?
(высказывают предположения)

— Поворот – является движением, т.е.
отображением плоскости на себя. Докажем это.

Рис.1

(СЛАЙД 18 или СЛАЙД 19)

(Доказательство может выполнить сильный ученик
по СЛАЙДУ 18. В этом случае можно сразу после
доказательства перейти к СЛАЙДУ 20.
Доказательство может выполнить учитель вместе с
классом по СЛАЙДУ 19, на котором отображаются
этапы доказательства.)

V. Закрепление изученного материала.

Задание. Построить точку M₁,
которая получается из точки M поворотом на угол 60^o.
Поэтапно с помощью слайда 20 прорабатывается
построение точки M₁.

(СЛАЙД 20)

— Какие инструменты нам понадобятся для того,
чтобы выполнить поворот? (линейка, циркуль,
транспортир)

— Ребята, что сначала нужно отметить? (точку M и
центр поворота – точку O)

— Как задаём центр поворота? Отмечаем в
определённом месте? (нет, произвольно)

— Как будем выполнять поворот по часовой или
против часовой стрелки? Почему? (против, т.к. угол
положительный)

— Что нужно построить, чтобы отложить угол 60^o?
(луч OM)

— Как найти на второй стороне угла точку M₁?
(с помощью циркуля отложить отрезок OM₁=OM)

— Рассмотрим, как выполняется поворот отрезка в
зависимости от расположения центра поворота.

— Рассмотрим случай, когда центр поворота лежит
вне отрезка. Решим № 1166 (а). (Если класс сильный, то
можно вместе с детьми составить план решения
задачи, дать задание решить № 1166 (а)
самостоятельно. Решение проверить с помощью
СЛАЙДА 21. Если ребята затрудняются с выполнением
задания, то решать коллективно, опираясь на СЛАЙД
21)

Работа в парах.

Задание. Построить фигуру, которая
получится при повороте отрезка AB на угол — 100^o
вокруг точки А.

(наводящие вопросы)

— Какая точка является центром поворота? Что
можно о ней сказать? (это один из концов отрезка –
точка А, она будет неподвижной, оставаться на
месте)

— Как будем выполнять поворот по часовой
стрелки или против часовой? (по часовой, т.к. угол
отрицательный)

— Составьте план решения задачи.

Задание выполняют по парам. Проверяют решение с
помощью СЛАЙДА 22.

Индивидуальная работа.

Задание. Построить фигуру, в которую
переходит отрезок AB при повороте на угол – 100^o
вокруг точки О – середины отрезка AB.

— Составьте план решения задачи. Задание
выполняют самостоятельно, решение проверяем с
помощью СЛАЙДА 23.

— Сегодня на уроке мы рассмотрели поворот
отрезка в зависимости от расположения центра
поворота. На следующих уроках мы рассмотрим
повороты других фигур. (продемонстрировать
СЛАЙДЫ 24-25)

VI. Проверка усвоения изученного материала.

Тест №2. (СЛАЙДЫ 26-30)

Приложение 2

Самопроверка.

VII. Подведение итога урока. (рефлексия)

— Ребята, давайте выделим тех, кто был лучшим на
каждом этапе. (подводится итог, выставляются
оценки)

— Поднимите руки, кому понравился урок.
Отметьте, что интересного было на уроке?

VII. Домашнее задание.

• № 1166 (б), № 1167 – для тех, кто получил оценку “3”.
• № 1167 (рассмотреть три случая расположения
  центра поворота: центр — вершина А, центр
  расположен вне треугольника, центр лежит на
  стороне АВ треугольника) – для тех, кто получил
  оценку “4” и “5”.

Вращение вокруг заданной оси.

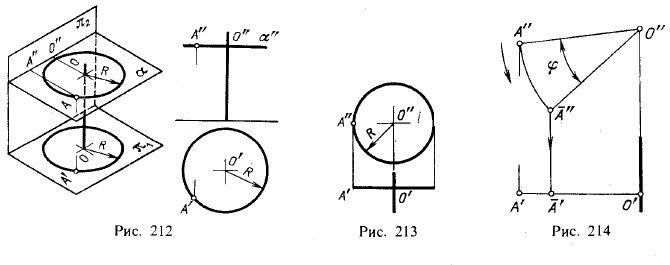
1. Пусть точка А вращается вокруг оси, перпендикулярной к пл. π₁ (рис. 212). Через точку А проведена пл. α, перпендикулярная к оси вращения и, следовательно, параллельная пл. π₁. При вращении точка А описывает в пл. α окружность радиуса R; величина радиуса выражается длиной перпендикуляра, проведенного из точки А на ось. Окружность, описанная в пространстве точкой А, проецируется на пл. π₁ без искажения. Так как пл. α перпендикулярна к пл. π₂, то проекции точек окружности на пл. π₂ расположатся на α», т. е. на прямой, перпендикулярной к фронтальной проекции оси вращения. Чертеж дан на рис. 212 справа: окружность, описанная точкой А при вращении ее вокруг оси, спроецирована без искажения на пл. π₁. Из точки О’, как из центра, проведена окружность радиуса R=О’А’; на пл. π₂ эта окружность изображена отрезком прямой, равным 2R.

На рис. 213 изображено вращение точки А вокруг оси, перпендикулярной к пл. π₂. Окружность, описанная точкой А, спроецирована без искажения на пл. π₂. Из точки О», как из центра, проведена окружность радиуса R=О’А’; на пл. π₁ эта окружность изображена отрезком прямой, равным 2R.

Из рассмотрения рис. 212 и рис. 213 отчетливо видно, что при вращении точки вокруг оси, перпендикулярной к какой-нибудь из плоскостей проекций, одна из проекций вращаемой точки перемещается по прямой, перпендикулярной к проекции оси вращения.

На рис. 214 показан поворот точки А против движения часовой стрелки на угол φ вокруг оси, проходящей через точку О перпендикулярно к пл. π₂. Из точки О», как из центра, проведена дуга радиуса О»А», соответствующая углу φ и направлению вращения. Новое положение фронтальной проекции точки А — точка А«

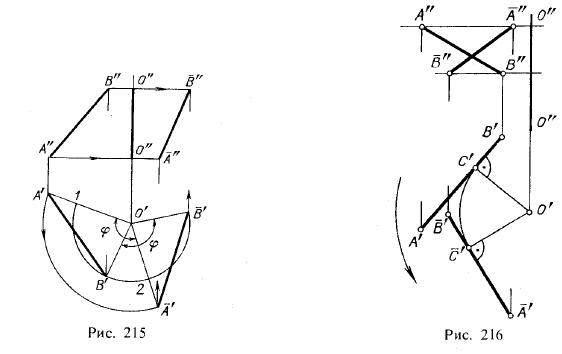
2.Теперь рассмотрим поворот отрезка прямой линии вокруг заданной оси. Отрезок АВ (рис. 215) повернут в положение АВ. Очевидно, дело свелось к повороту точек A и В на заданный угол φ по заданному направлению. Пути перемещения фронтальных проекций этих точек указаны прямыми, проведенными через А» и В» перпендикулярно к фронтальной проекции оси вращения.

Новое положение горизонтальной проекции точки А (точка А‘) получено при повороте радиуса О’А’ на заданный угол φ. Для нахождения точки B‘ (положение горизонтальной проекции точки В после поворота) проведена дуга радиусом О’В’

и в этой дуге отложена хорда В’B‘, равная хорде 1—2; это соответствует повороту точки В на тот же угол φ.

Далее, из точек A‘ и B‘ проведены линии связи до пересечения с направлениями перемещения фронтальных проекций; получены проекции A» и B«.

Отрезки прямых между точками A» и B» и между точками A‘ и B‘ определяют новые положения фронтальной и горизонтальной проекций отрезка АВ после его поворота в положение AB.

Так как в треугольниках А’В’О’ и A‘B‘О’ (рис. 215) стороны В’О’ и А’О’ треугольника А’В’О’ равны (как радиусы) соответственно сторонам B‘О’ и A‘О’ треугольника A‘B‘О’ и углы, заключенные между указаннымирторонами, также равны, то эти треугольники равны между собой. Значит, А’В’ = A‘B‘, т. е. величина горизонтальной проекции отрезка, повернутого вокруг оси, перпендикулярной к пл. π₁, не изменяется. Очевидно, такое же заключение справедливо в отношении фронтальной проекции отрезка при его повороте вокруг оси, перпендикулярной к пл. π₂.

В равных между собой треугольниках А’В’О’ и A‘B‘О’ (рис. 215) будут равны и их высоты, проведенные, например, из точки О’ на А’В’ и A‘B‘.

Сделанные выводы позволяют установить следующий способ построения новых проекций отрезка, вращаемого около оси на заданный угол (рис. 216). Через точку О’ проводим прямую, перпендикулярную к А’В’; точку С’ (пересечение перпендикуляра с А’В’) повертываем на заданный угол. Проведя через точку С’ (новое положение точки С’) прямую, перпендикулярную к радиусу O’C‘, получаем направление нового положения горизонтальной проекции отрезка. Так ткак отрезки С’А’ и С’В’ не изменяют своей величины, то, откладывая от точки C‘ отрезки C‘A‘=С’А’ и C‘B‘=С’В’ , находим новое положение A‘B‘ проекции всего отрезка. Нахождение нового положения фронтальной проекции A«B» остается прежним.

Указанным способом можно не только повернуть отрезок на заданный угол, но и определить угол, на который надо повернуть заданный отрезок, чтобы придать ему некоторое требуемое положение (например, расположить параллельно плоскости π₂).

3.Поворот плоскости вокруг заданной оси сводится к повороту принадлежащих ей точек и прямых линий.

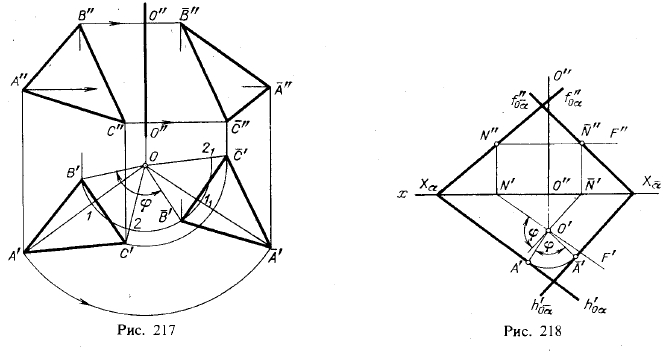
Пример дан на рис. 217: треугольник АВС, определяющий плоскость, повернут в положение ABC согласно заданным углу φ и направлению, указанному стрелкой. Построение подобно показанному на рис. 215: там были повернуты две точки А и В, здесь же три точки — вершины А, В и С, а следовательно, и вся фигура. Треугольники А’В’С и A‘B‘C‘ равны между собой по построению: при оси, перпендикулярной к пл. π₁ горизонтальная проекция величины своей не изменяет. Это

соответствует тому, что угол наклона пл. АВС по отношению к пл.π₁ не изменяетя, если ось вращения перпендикулярна к пл.π₁ Очевидно, при повороте вокруг оси, перпендикулярной к пл. π₂, не изменяется угол наклона вращаемой плоскости к пл. π₂ и сохраняется величина фронтальных проекций.

При вращении плоскости, выраженной ее следами, обычно поворачивают один из следов и горизонталь (или фронталь) плоскости. Пример дан на рис. 218; плоскость общего положения α повернута на угол φ вокруг оси, перпендикулярной к пл. π₁. На следе h’_0α взята точка, ближайшая к оси вращения, — точка A’ (O’A’⊥h’_0α), подобно тому, как была на рис. 216 взята точка С’. Затем точка А’ повернута на угол φ. Через полученную точку A‘ проведена прямая линия, перпендикулярная к О’A‘; это горизонтальный след плоскости в ее новом положении.

Для нахождения фронтального следа плоскости после ее поворота достаточно найти, помимо найденной точки Х_α на оси x, еще одну точку, принадлежащую следу. В пл. α взята горизонталь N’F’, N»F», пересекающая ось вращения (N’F’ проходит через горизонтальную проекцию оси вращения). Конечно, можно взять горизонталь и не пересекающую ось вращения. Так как горизонталь и при новом положении плоскости останется параллельной ее горизонтальному следу, то надо провести через О’ прямую, параллельную h’_0α получится новое положение горизонтальной проекции горизонтали. Фронтальная ее проекция не изменит своего направления, а поэтому легко найти новый фронтальный след горизонтали — точку N«. Теперь можно построить фронтальный след (f»_0α)

Вращение вокруг выбранной оси. В ряде случаев ось вращения может быть выбрана. При этом, если ось вращения выбрать проходящей через один из концов отрезка, то построение упростится, так как точка, через которую проходит ось, будет «неподвижной» и для поворота отрезка надо построить новое положение проекций только одной точки — другого конца.

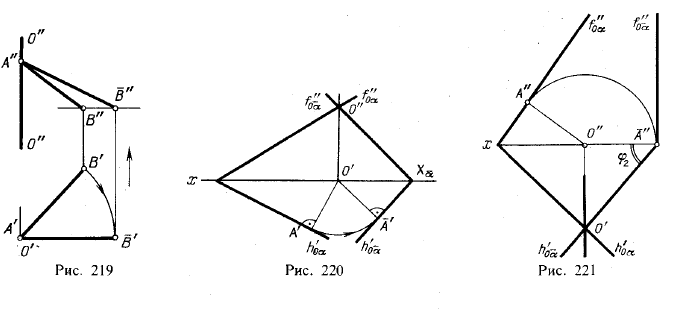
На рис. 219 показан случай, когда для поворота отрезка АВ выбрана ось вращения, перпендикулярная к пл. π₁ и проходящая через точку А. При повороте вокруг такой оси можно, например, расположить отрезок параллельно пл. π₂.

Именно такое положение показано на рис. 219. Горизонтальная проекция отрезка в своем новом положении перпендикулярна к линии связи А’А». Найдя точку В» и построив отрезок А»В«, получаем фронтальную проекцию отрезка АВ в его новом положении. Проекция А»В» выражает длину отрезка АВ. Угол А»В«В» равен углу между прямой АВ и пл. π₁

Если поставить перед собой цель — определить угол наклона прямой общего положения к пл. π₂, то надо провести ось вращения перпендикулярно к пл. π₂ и повернуть прямую так, чтобы она стала параллельной пл. π₁. Предоставляем читателю выполнить такое построение.

Если при повороте плоскости, выраженной следами, можно выбрать ось вращения, то ее целесообразно расположить в плоскости проекций; построения в этом случае упрощаются. Пример дан на рис. 220. Положим, что ось вращения должна быть перпендикулярна к пл. π₁. Если ее взять в пл. π₂, то на следе f»_0α, оказывается «неподвижная» точка О (в пересечении с осью вращения). После поворота плоскости фронтальный след должен пройти через эту точку. Следовательно, найдя положение горизонтального следа (h’_0α) после поворота, надо провести след f’_0α через точку Х_α и через точку О». По сравнению с рис. 218 упрощение состоит в том, что отпала горизонталь. Она понадобилась бы в случае «ухода» точки X_α за пределы чертежа; но в аналогичном случае на рис. 218 пришлось бы взять две вспомогательные линии.

На рис. 221 плоскость общего положения повернута в положение горизонтально-проецирующей; при этом определился угол наклона пл. α к пл. π₂. Если взять ось вращения, перпендикулярную к пл. π₁ то можно пл. α поставить в положение фронтально-проецирующей, определив при этом угол наклона плоскости к пл. π₁.

Сравнивая между собой плоскости до и после поворота, замечаем, что угол, образуемый следами f»_0α и h’_0α на чертеже, вообще изменяется.

Если представить себе круговой конус с вершиной в точке О и с основанием на рис. 220 в пл. π₁ а на рис. 221 в пл. π₂, и касательную к конусу пл. α, то поворот пл. α вокруг оси вращения совпадающей с осью конуса, представляет собой как бы «обкатку» конуса касательной к нему плоскостью.

Вопросы к §§ 34-35

1. В чем заключается способ вращения?
2. Что такое плоскость вращения точки и как она располагается по отношению к оси вращения?
3. Что такое центр вращения точки при повороте ее вокруг некоторой оси?
4. Что такое радиус вращения точки?

Последующие вопросы относятся к вращению вокруг оси, перпендикулярной к плоскости проекций.

5. Как перемещаются проекции точки?
6. Какая из проекций отрезка прямой линии не изменяет своей величины?
7. Как осуществляется поворот плоскости: а) не выраженной следами, б) выраженной следами?
8. В каком случае не изменяется при вращении наклон прямой линии по отношению: а) к пл. π₁, б) к пл. π₂?
9. Такой же вопрос относительно плоскости π₃.
10. Можно ли путем поворота определить длину отрезка прямой линии и угол ее наклона к пл.π₁ и к пл. π₂?
11. Можно ли путем поворота плоскости определить угол ее наклона к пл. π₁ и к пл. π₂?
12. Какое выгодное положение можно придать оси вращения при повороте: 1) отрезка прямой, 2) плоскости, выраженной следами?

Прежде чем
приступить к изучению нового материала давайте повторим, что если каждой точке
плоскости ставится в соответствие какая-то точка этой же плоскости, причем
любая точка плоскости оказывается сопоставленной некоторой точке, тогда говорят,
что дано отображение плоскости на себя.

Вспомним, что
движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.

Мы уже
познакомились и повторили некоторые виды движения: такие как осевая симметрия,
центральная симметрия, параллельный перенос.

Сегодня на уроке мы
познакомимся с еще одним видом отображения плоскости на себя – поворотом.

Давайте отметим на
плоскости произвольную точку О, назовем ее центром поворота, и зададим угол
α (назовем его углом поворота).

Поворотом плоскости
вокруг точки О на угол α называется отображение плоскости на себя, при
котором каждая точка М отображается в такую точку М₁, что  и угол MOM₁=α. Заметим, что
точка О остается на месте, то есть другими словами, отображается сама в себя, а
все остальные точки поворачиваются вокруг точки О, причем, если , то против часовой стрелки, если , то по часовой стрелке 

Иногда в литературе
можно встретить следующее обозначение для поворота вокруг центра О и на угол
α: .

Теперь давайте
попробуем определить, будет ли поворот движением? Для этого достаточно
показать, что при повороте сохраняется расстояние между точками.

Пусть точка О –
центр поворота, а угол α– угол поворота.

Рассмотрим случай,
когда α>0, то есть поворачивать относительно точки О будем против
часовой стрелки. Случай, когда α<0, то есть случай, когда поворачивать
будем по часовой стрелке рассматривается аналогично, это вы можете сделать
самостоятельно.

Пусть при этом
повороте точки М и N отображаются в точки M₁ и  N₁
соответственно. Рассмотрим треугольники ОМN и OM₁N₁.

 

 

,  

 

, другими словами, при повороте расстояние
между точками сохраняется. Значит, поворот – это еще один вид движения. Его
можно представить себе как поворот всей плоскости вокруг данной точки О на
данный угол α.

Задача. Построить
отрезок , который получается из отрезка  поворотом вокруг данного центра  на:

а) , б) , в) .

Решение.

Для поворота
отрезка, повернем концы этого отрезка. Для того, чтобы повернуть точку А,
построим прямую ОА. От точки О с помощью транспортира отметим 150° (мы помним,
что если угол меньше 0, то поворачиваем по часовой стрелки, то есть угол будем
откладывать в эту сторону). С помощью циркуля измеряем расстояние АО и отложим
это расстояние на получившейся прямой.

Поставим точку А₁.
Аналогично, построим точку B₁. Тогда
получившийся отрезок A₁B₁
– искомый. Для того, чтобы выполнить поворот на 100°, надо 100° отложить против
часовой стрелки.

Все остальные
построения проводятся аналогично тому, как мы делали в первом пункте. При
повороте на 180° точка A₁ будет лежать на
продолжении прямой ОА. Точка B₁ будет лежать
на продолжении прямой OB.

Задача. Постройте
треугольник, который получается из данного треугольника  поворотом вокруг:

а) точки  на ,

б) вокруг точки , не лежащей внутри треугольника на ,

в) вокруг точки , лежащей внутри треугольника на .

Решение.

Строить треугольник
будем по точкам. Поскольку центром поворота является точка А, то она
отображается сама на себя. Отобразим точку B. От точки
А отложим против часовой стрелки угол равный 80°. Отложим на этой прямой
отрезок равный стороне AB и
получим точку B₁. Аналогично построим точку C₁. Тогда треугольник AB₁C₁
– искомый.

Проведя аналогичные
построения, построим треугольники A₁B₁C₁ для
остальных двух случаев.

                                                     

Сегодня мы
заканчиваем с вами изучение темы Движение. Давайте еще раз вспомним, что такое
движение и с какими видами движения мы успели познакомиться.

Движение плоскости
– это отображение плоскости на себя, сохраняющее расстояния.

Мы доказали, что
движением являются: осевая симметрия, центральная симметрия, параллельный
перенос и поворот.