Правильный шестиугольник
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
Правильный шестиугольник
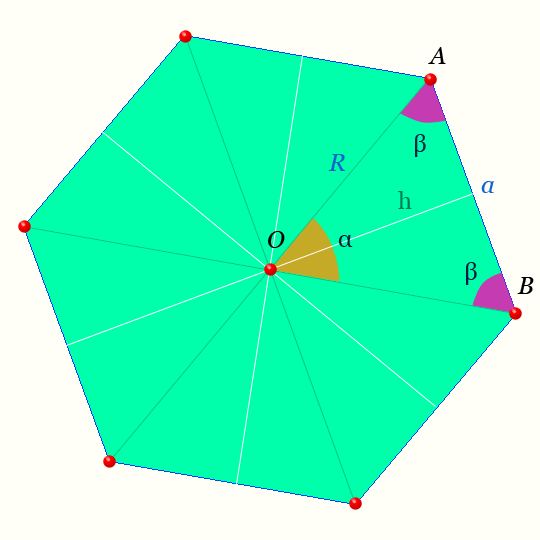
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
| n=6 | число сторон и вершин правильного шестиугольника, | шт |
|---|---|---|
| α | центральный угол правильного шестиугольника, | радианы, ° |
| β | половина внутреннего угла правильного шестиугольника, | радианы, ° |
| γ | внутренний угол правильного шестиугольника, | радианы, ° |
| a | сторона правильного шестиугольника, | м |
| R | радиусы правильного шестиугольника, | м |
| p | полупериметр правильного шестиугольника, | м |
| L | периметр правильного шестиугольника, | м |
| h | апофемы правильного шестиугольника, | м |
Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
[ L = 6a ]
Полупериметр правильного шестиугольника
[ p = 3a ]
Центральный угол правильного шестиугольника в радианах
[ α = frac{π}{3} ]
Центральный угол правильного шестиугольника в градусах
[ α = frac{180°}{3} = 60° ]
Половина внутреннего угла правильного шестиугольника в радианах
[ β = frac{π}{3} ]
Половина внутреннего угла правильного шестиугольника в градусах
[ β = frac{180°}{3} = 60° ]
Внутренний угол правильного шестиугольника в радианах
[ γ = 2β = frac{2}{3}π ]
Внутренний угол правильного шестиугольника в градусах
[ γ = frac{2}{3}180° = 120° ]
Площадь правильного шестиугольника
[ S = ph = 3ha ]
Или учитывая формулу Площади правильного шестиугольника получим
[ S = frac{3sqrt{3}}{2}a^2 ]
Отсюда получим апофему правильного шестиугольника
[ h = frac{sqrt{3}}{2}a ]
Правильный шестиугольник |
стр. 270 |
|---|
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n)–угольника равна (180^circ(n-2)), то каждый угол правильного (n)–угольника равен [alpha_n=dfrac{n-2}n cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac {4-2}4cdot 180^circ=90^circ);
каждый угол правильного шестиугольника равен (dfrac{6-2}6cdot
180^circ=120^circ).
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
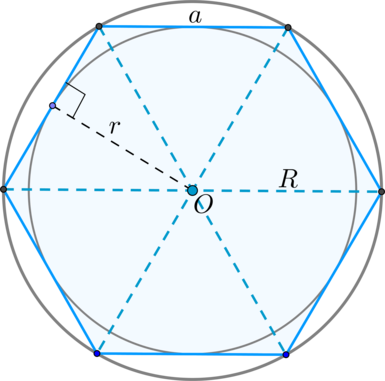
Если (a) – сторона правильного (n)–угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin{aligned}
S&=dfrac n2ar\
a&=2Rcdot sindfrac{180^circ}n\
r&=Rcdot cosdfrac{180^circ}n end{aligned}]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R).
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ).
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac{3sqrt{3}}{2}a^2).
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n)-угольник инвариантен относительно поворота на угол (dfrac{360^circ}{n}).
Задача 26595 4.1.38) Найти координаты центра…
Условие
4.1.38) Найти координаты центра правильного шестиугольника, зная две его смежные вершины: А (2;0) и В(5; 3sqrt(3)).
математика ВУЗ
5182
Решение
★
Пусть центр правильного шестиугольника имеет координаты O(x;y) ,
Так как OA=OB,то
sqrt((x-2)^2+(y-0)^2)=sqrt((x-5)^2+(y-3sqrt(3))^2)
Возводим в квадрат
(x-2)^2+y^2=(x-5)^2+(y-3sqrt(3))^2
(x-2)^2-(x-5)^2=(y-3sqrt(3))^2-y^2
(x-2-x+5)*(x-2+x-5)=(y-3sqrt(3)-y)*(y-3sqrt(3)+y)
3*(2x-7)=-3sqrt(3)*(2y-3sqrt(3))
(2x-7)=-sqrt(3)*(2y-3sqrt(3))
2x+2sqrt(3)y-16=0
x+sqrt(3)y-8=0
( это уравнение серединного перпендикуляра к прямой АВ)
AB=sqrt((5-2)^2+(3sqrt(3)-0)^2)=sqrt(9+27)=sqrt(36)=6
Составляем уравнение окружности с центром в точке А и радиусом АВ=6
(x-2)^2+y^2=36
Решаем систему двух уравнений
{x+sqrt(3)y-8=0 ⇒ x =8-sqrt(3)y
{(x-2)^2+y^2=36
(8-sqrt(3)y-2)+y^2=36
(6-sqrt(3)y)^2+y^2=36
36 — 12sqrt(y)+3y^2+y^2=36
4y^2-12sqrt(3)y=0
4y*(y-3sqrt(3))=0
y_(1)=0 или y_(2)=3sqrt(3)
x_(1)=8-sqrt(3)*0=8 или х=8-sqrt(3)3*sqrt(3)=8-9=-1
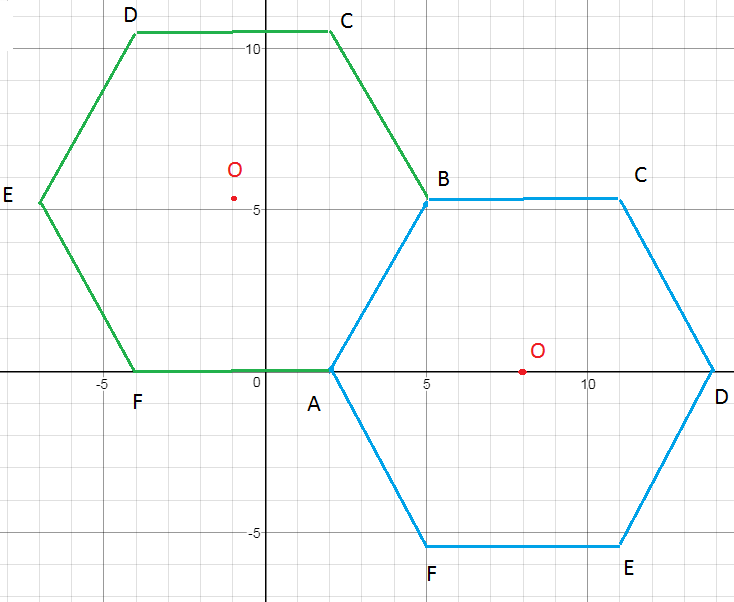
О т в е т. (8;0) или (-1; 3sqrt(3))
Cм рисунок. Графическое решение
Все решения

Написать комментарий
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где
— сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольника.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
.
Радиус такой окружности равен .
Ответ: .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Ответ: .
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Правильный шестиугольник: свойства, формулы, площадь» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Задание фигур в пространстве
Пусть
в пространстве введена система координат
Охуz.
Как мы показали, положение любой точки
однозначно определяется ее координатами.
Если Ф – некоторое множество точек (
фигура ), то всем ее точкам характерно
некоторое свойство, присущее только
точкам этой фигуры, а значит и для
координат точек этой фигуры выполняется
соотношение, присущее только точкам
этой фигуры.
Определение.
Пусть в
данной системе координат имеем некоторое
уравнение
F
(x,
y,
z)
= 0.
(1)
Уравнение
(1) называется уравнением фигуры Ф,
если координаты любой точки этой фигуры,
и только они, удовлетворяют этому
уравнению.
Следует
добавить, что уравнение (1) будет уравнением
фигуры Ф,
если выполняются два условия: 1) Если
М(
)
Ф, то координаты
(
)
удовлетворяют (1); 2) Если координаты (
)
удовлетворяют уравнению (1), то М(
)
Ф.
Под
уравнением фигуры мы понимаем не только
алгебраические уравнения, но и неравенства,
системы уравнений и неравенств, а также
их любые комбинации. Например, неравенство
(х
–- )2
+(у – )2
+ (z
– )2
R2
является
уравнением шара с центром в точке Q(;
;
)
и радиусом R.
Аналогично
определяется уравнение фигуры на
плоскости, только в системе координат
Оху.
Уравнение
является уравнением точек первой
четверти, причем точки, лежащие на осях
координат, не принадлежат данному
множеству.
Пример
1. Центр
О и вершина
А
правильного шестиугольника ABCDEF
имеют координаты О(–1;
2), А(1;
4). Найти
координаты остальных вершин.
Решение.
Так как точка
О является
серединой отрезка АD,
то находим координаты точки D.
Обозначим
D(х;
у), тогда
согласно (3) имеем:
,
.
Отсюда
получим: х
= – 3, у = 0. D(-3;
0).
Так
как данный шестиугольник правильный,
то АВО и
AFO
– правильные треугольники. Значит,
точки В
и F
являются точками, равноудаленные от
точек А
и О.
Пусть В(х;
у). Из условия
|AB|
= |OB|
= |OA|
получим |AВ|2
= |ОB|2
= |ОА|2.
В координатной форме это выглядит так:
Û
Следовательно,
B(
;3-
)
и
F
(–
;
3 +
).
Так
как точки Е
и С
симметричны точкам В
и F
относительно точки О,
то находим их координаты аналогично
тому, как мы находили координаты точки
D.
Обозначим Е(х;
у), тогда
согласно (3) имеем:
,
.
Отсюда
получим: х
= – (
+2),
у = 1+
.
Е(-(
+2);1+
).
Обозначим
С(х; у),
тогда согласно (3) имеем:
,
.
Отсюда
получим: х
=
-2,
у = 1-
.
С(
-2;
1-
).
Ответ:
С(
-2;
1-
),
Е(-(
+2);1+
),
B(
;3-
),
F
(–
;
3 +
),
D(–
3;0).
Пример
2. Найти
уравнение множества всех точек плоскости,
для каждой из которых сумма квадратов
расстояний до осей координат равна 5.
Решение.
Рассматриваем систему координат О
.
Обозначим заданное множество точек
F,
а М (х; у)
– произвольную точку плоскости.
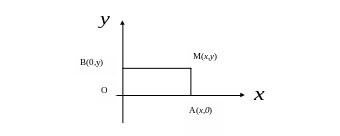
Тогда,
согласно условию задачи, получим
М
F
|MB|2
+ |MA|2
= 5.
В
координатах последнее уравнение имеет
вид
х2+
у2
= 5.
Получили
известное уравнение окружности с центром
в начале координат и радиусом равным
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #