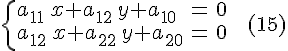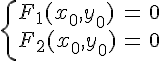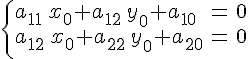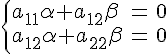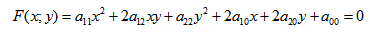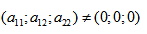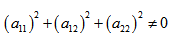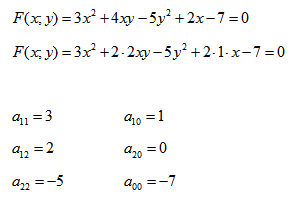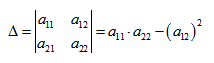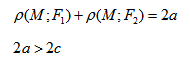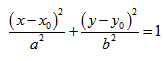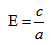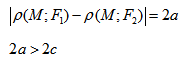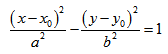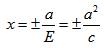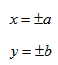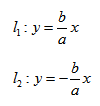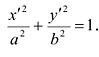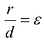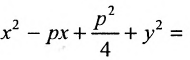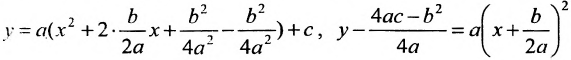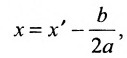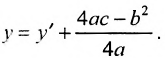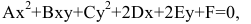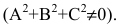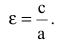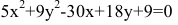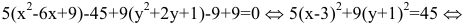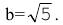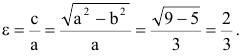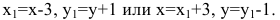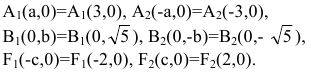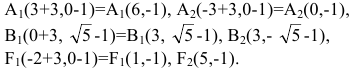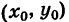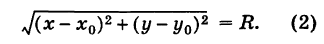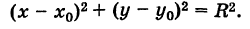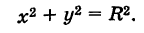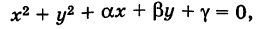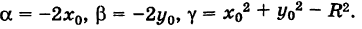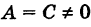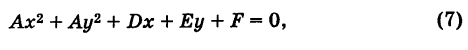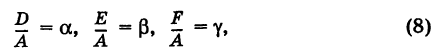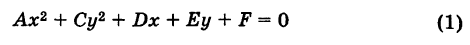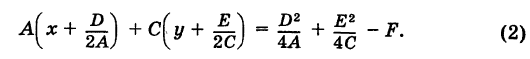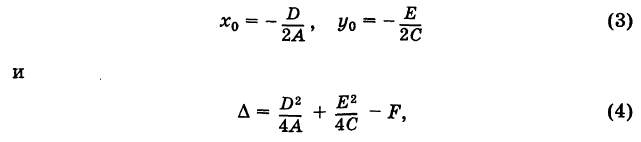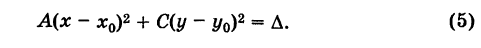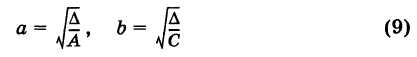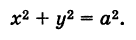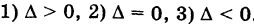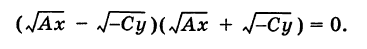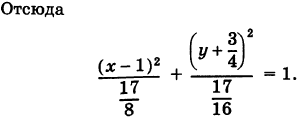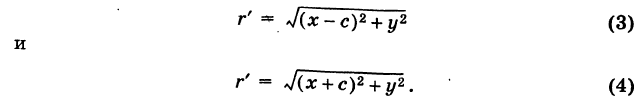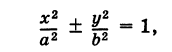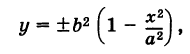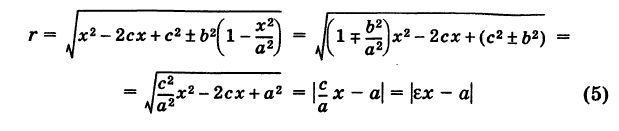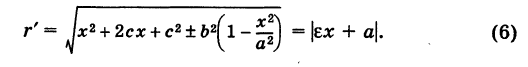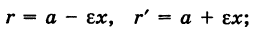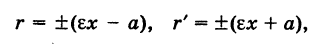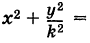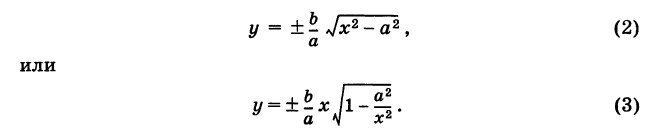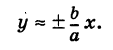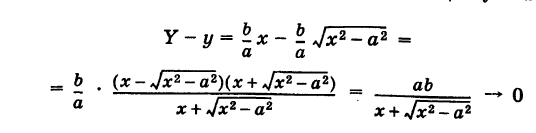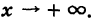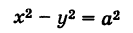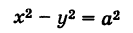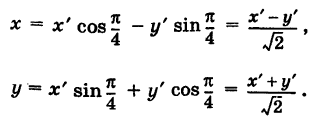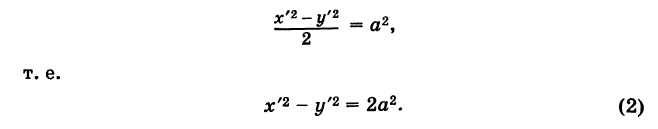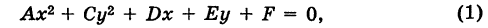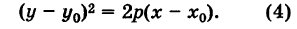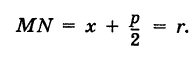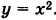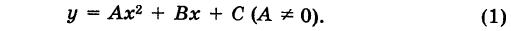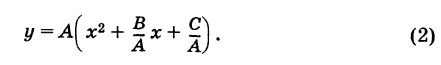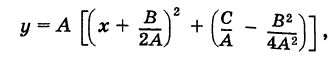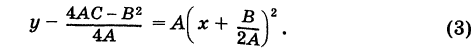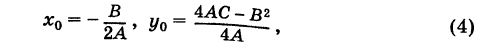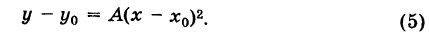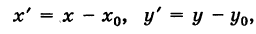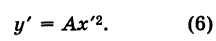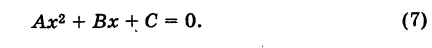Определение
9.1. Центром
линии второго порядка называется центр
симметрии этой линии.
ТЕОРЕМА
9.1. Пусть
относительно аффинной системы координат
задана линия второго порядка общим
уравнением
Для
того чтобы начало координат являлось
ее центром, необходимо и достаточно,
чтобы в уравнении
отсутствовали
члены с
и
в
первой степени, т.е. чтобы
,
иначе, чтобы уравнение линии имело
вид
Доказательство
достаточности. Если
,
то уравнение линии имеет вид
,
и если ему удовлетворяют
координаты
и
точки
,
то ему удовлетворяют и координаты
и
точки
,
симметричной точке
относительно
начала координат.
Доказательство
необходимости. Пусть
начало координат является центром
линии
.
Возьмем на линии произвольную точку
.
Ее координаты удовлетворяют уравнению
,
а так как начало координат
является
центром симметрии линии, то этому
уравнению удовлетворят и координаты
точки
,
симметричной точке
относительно
начала координат, т.е.
.
Вычитая
из
соотношение
,
находим, что координаты всех точек линии
удовлетворяют уравнению
.
Следовательно, уравнение линии приводится
к виду
,
то есть не
содержит членов с
и
в
первой степени.
ТЕОРЕМА
9.2. Если
относительно аффинной системы координат
задана линия второго порядка общим
уравнением
то
координаты
ее
центра определяются из системы
уравнений
причем
в случае несовместности этой системы
линия не имеет центра (т.е. является
параболой).
Доказательство. Произведем
перенос данной системы координат так,
чтобы новым началом стала точка
.
В новой системе координат уравнение
линии
будет
иметь вид (согласно формулам
).
По
предыдущей теореме точка
является
центром данной линии тогда и только
тогда, когда
или
подробнее
Определение
9.2. Любая
кривая второго порядка, имеющая
единственный центр называется
центральной.
Следовательно, кривая
является центральной, если
Замечание
9.1. При
приведении центральных кривых к
каноническому виду целесообразно
пользоваться следующим планом:
1. Найти
центр кривой.
2. Выполнить
параллельный перенос в центр и записать
уравнение кривой в перенесенной системе
координат
3. Повернуть
перенесенную систему координат на
угол
и
получить каноническую систему координат.
10 Пересечение кривой второго порядка с прямой. Асимптотические направления относительно кривой второго порядка
Пусть
задана кривая второго порядка общим
уравнением
и
прямая
параметрическими
уравнениями
.
Найдем
точки пересечения этой прямой с кривой
второго порядка.
Для этого подставим
значения переменных
и
из
уравнений
в
уравнение
.
Получаем уравнение с одним неизвестным
Преобразуем
его к виду
Введем
обозначения:
В
этих обозначениях, полученное уравнение,
запишется более просто, а именно
Находя
корни уравнения
,
и подставляя их в уравнения
,
мы получим координаты точек пересечения
кривой второго порядка и прямой
.
При этом возможны следующие случаи:
1.
.
Следовательно,
—
квадратное уравнение, а поэтому оно
имеет два корня (вещественных или
комплексных),значит, прямая пересекает
КВП в двух точках(вещественных или
комплексно-сопряженных).
2.
.
Тогда уравнение
примет
вид
.
a). Если
,
то прямая пересекает кривую в единственной
действительной точке.
b). Если
,
то прямая не имеет с кривой ни одной
общей точки(ни действительной, ни
мнимой).
c). Если
,
тогда любое значение
является
решением уравнения
,
а потому
лежит
на кривой второго порядка.
Определение
10.1. Множество
всех прямых, из которых любые две
параллельны, называется направлением.
Отметим,
что направление можно определить любым
направляющим вектором каждой из этих
прямых. Заметим, что коэффициент в
уравнении
зависит
только от направления прямой
и
не зависит от координат точки
,
лежащей на прямой.
Определение
10.2. Направление,
определяемое ненулевым вектором
,
называется асимптотическим направлением
относительно кривой второго порядка,
если любая прямая, параллельная
вектору
,
либо имеет с кривой не более одной общей
точки, либо содержится в кривой.
Из
предыдущего следует: направление,
определяемое ненулевым вектором
,
является асимптотическим направлением
относительно кривой второго порядка
,
тогда и только тогда, когда
Пользуясь
этой формулой, легко найти асимптотические
направления относительно кривой второго
порядка.
Если
,
то из
следует,
что
(
так как
—
ненулевой вектор), поэтому из
,
обозначая через
получаем
Отсюда
находим
Если
же
,
то уравнение
примет
вид
.
Этому уравнению удовлетворяют координаты
векторов
Выясним
теперь, сколько существует различных
асимптотических направлений относительно
кривой второго порядка.
Рассмотрим
три случая.
1.
и,
значит,
.
Из формулы
мы
заключаем, что относительно кривой
второго порядка не существует
асимптотических направлений.
2.
.
В этом случае существует два различных
асимптотических направления.
В самом
деле, если
,
то этот вывод следует из формулы
,
а если
,
то из
.
(Заметим, что в последнем случае
,
поэтому векторы из
не
коллинеарны.)
3.
.
Очевидно, что в этом случае имеем
единственное асимптотическое направление,
определяемое вектором
.
Действительно, если
,
то это вытекает из
,
а если
,
то из
.
(Заметим, что в последнем случае
,
поэтому векторы из
коллинеарны.)
Ранее
было показано, что
не
зависит от выбора системы координат. В
соответствии с таблицей значений
инвариантов и количеством асимптотических
направлений принято разделять кривые
второго порядка на три
класса:
эллиптические
, гиперболические
и параболические
.
Определение
10.3. Асимптотой
кривой второго порядка называется
прямая асимптотического направления,
которая либо лежит на кривой, либо не
имеет с ней общих точек.
ТЕОРЕМА
10.1. Асимптота
к кривой гиперболического типа задается
уравнением
где
удовлетворяют
.
Доказательство. Запишем
уравнение
в
виде
или
в эквивалентной форме
Отметим
сначала, что это уравнение является
уравнением первой степени. Действительно,
предположим, что
Откуда
следует, что
,
так как
.
А это противоречит тому, что вектор,
удовлетворяющий
,
ненулевой. Теперь необходимо проверить,
что прямая
имеет
асимптотическое направление, т.е. надо
убедится
в том, что вектор
имеет
асимптотическое направление. Действительно,
так как
—
вектор асимптотического направления,
то он удовлетворяют равенству
,
которое
равносильно
Таким
образом, вектор
коллинеарен
вектору асимптотического направления,
а значит, имеет асимптотическое
направление. Итак, прямая, заданная
уравнением
имеет
асимптотическое направление.
Кроме
того, если точка лежит на этой прямой,
то ее координаты
удовлетворяют
уравнению
:
.
Рассмотрим
выражение
Что
и требовалось доказать.
Замечание
10.1. Если
в общем уравнении кривой второго порядка
гиперболического типа
,
то уравнения
асимптот можно искать
в виде
где
определяются
по формуле
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Общее уравнение кривой второго порядка. Центр кривой
Определение. Кривой второго порядка называется геометрическое место точек, координаты которых удовлетворяют уравнению
в котором хотя бы один из коэффициентов а11, а12, а22 отличен от нуля. Выражение
Если мы перейдем к новой СК Ox¢y¢, то формулы замены координат будут иметь вид

Если мы подставим эти выражения в (8), то снова получим уравнение такого же вида, т.е. содержащее x¢ и y¢ во второй степени. Поэтому наше определение корректно, т.е не зависит от выбора СК. В дальнейшем, СК всегда предполагается декартовой.
Определение. Точка O¢ называется центром кривой второго порядка, если она является ее центром симметрии. Кривая, которая имеет центр, называется центральной.
Предположим, что СК выбрана так, что ее начало находится в центре кривой. Тогда одновременно с точкой M(x, y) кривой будет принадлежать и точка M¢(– x,– y). Подставим ее координаты в (7) и получим
Вычтем из равенства (8) равенство (8¢):
И это должно выполняться для любой точки M(x, y) на кривой. Поэтому а1 = а2 = 0, если начало координат находится в центре. Поэтому, если изначально начало координат не находится в центре O¢, то мы совершим параллельный перенос координатных осей в центр, и уравнение кривой в новой СК O¢х¢у¢ примет вид
т.е. линейная часть уравнения исчезнет. При этом, коэффициенты квадратичной части останутся прежними; это будет установлено в процессе доказательства следующей теоремы.
Теорема 5. Координаты (xo, yo) центра кривой, заданной уравнением (8), находятся из системы линейных уравнений


Доказательство. Введем новую декартову СК O¢х¢у¢, которая получается из Oху переносом начала в центр O¢(xo, yo) кривой. Тогда формулы замены координат имеют вид:


Подставим эти формулы в (7):
После преобразований получаем
где с¢ = j(xo, yo) – значение левой части уравнения (7) в точке O¢. Поскольку в новой СК коэффициенты при x¢ и y¢ должны быть равны нулю, то получаем (10).
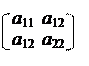



d = det A, dx = – , dy = – .
1 случай. d ¹ 0. Тогда по правилу Крамера система (10) имеет единственное решение
а кривая имеет единственный центр. Минусы были поставлены выше потому, что а1 и а2 находятся в (10) не в правой части, а в левой.
2 случай. d = 0, dx¹ 0 и dy¹ 0 (заметим, что в случае d = 0, определители dx и dy будут равны или неравны нулю только одновременно). Тогда ранг расширенной матрицы системы (10) будет равен 2, а rank A=1. Значит, согласно теореме Кронекера-Капелли система (10) не имеет решений, а кривая не имеет центра.
3 случай. d = 0, dx = dy = 0. Тогда оба уравнения в (10) пропорциональны, а значит, эта система имеет бесконечное количество решений, а кривая – бесконечное количество центров.
Упростим еще величину с¢:
В силу (9) выражения в скобках равны нулю, и мы имеем
Подставляя сюда (*) получаем


В скобках как раз стоит разложение D по последней строке или последнему столбцу. Равенство (13) позволяет выписать (9) не находя координат центра кривой. Но, если уже центр найден, то легче вычислить с¢ по формулам (12).
Кривые второго порядка
Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
или можно встретить следующую форму записи:
К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
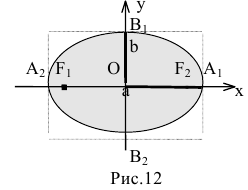
если Δ F1 и F2 — фокусы.
с — фокальное расстояние,
Каноническое уравнение эллипса с центром симметрии в начале координат:
2а — большая ось эллипса, 2b — малая ось эллипса.
а — большая полуось эллипса, b — малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
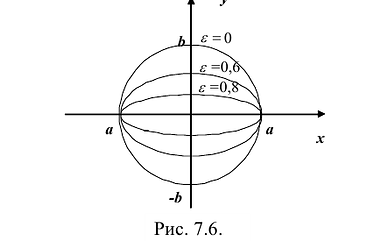
Эксцентриситет — число, равное отношению фокального расстояния к большей полуоси:
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
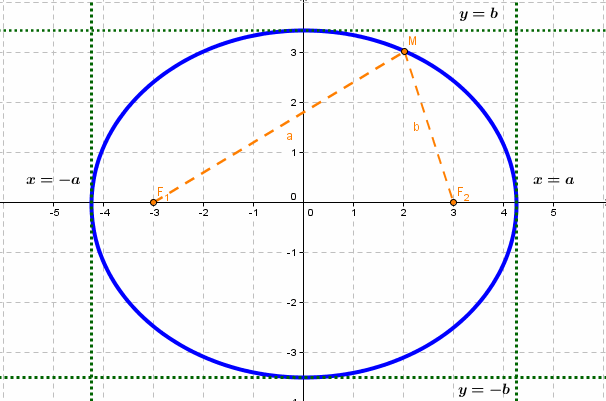
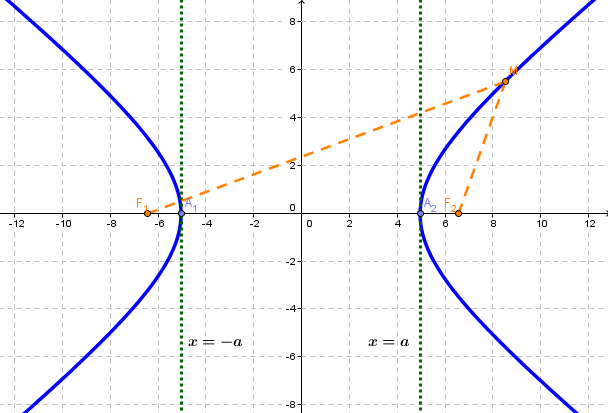
Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
с — фокальное расстояние,
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:
x — действительная ось, y — мнимая ось.
а — действительная полуось, b — мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 — правая директриса, f2 — левая директриса.
Порядок построения гиперболы :
1. Строим прямоугольник со сторонами 2a и 2b.
2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.
3. Строим гиперболу с вершинами в точках А 1 (-а;0), А 2 (а;0).
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 
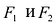
Точки 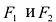
Если а =Ь, то уравнение (7.3) можно переписать в виде:
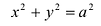
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 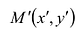
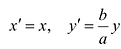
Число 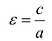
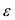
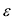
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 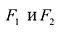
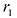
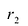
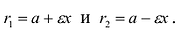
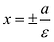
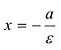
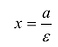
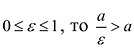
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 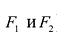
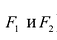
Точки 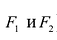
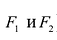
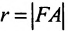
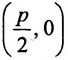
Тогда 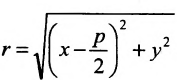
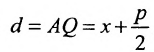
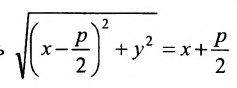
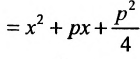
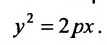
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 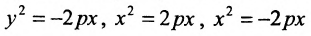
Легко показать, что уравнение 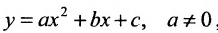
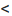
и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 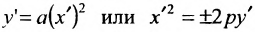
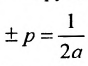
Пример:
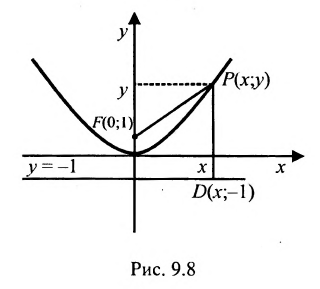
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию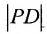
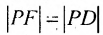
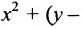
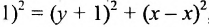
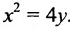
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
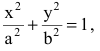
Число а называют большей полуосью эллипса, число 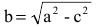
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 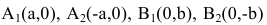
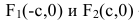
Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 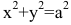
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 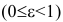
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
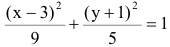
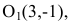
Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 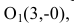
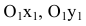
В новой системе координат координаты 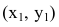
Переходя к старым координатам, получим:
Построим график эллипса.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://matecos.ru/mat/matematika/krivye-vtorogo-poryadka.html
http://www.evkova.org/krivyie-vtorogo-poryadka
Рассмотрим уравнение кривой второго порядка (1)
без члена с произведением координат
и
.
Дополним члены, содержащие и
До полных квадратов. Будем иметь

Полагая
(3)
И

Получаем
. (5)
Точка есть центр симметрии кривой (5). Параллельные осям координат
И
прямые
являются осями симметрии кривой (5).
Действительно, если точка лежит на кривой (5), то симметричная ей относительно прямой
точка
также лежит на этой кривой. Аналогичным свойством обладает прямая
.
В дальнейшем будем предполагать, что центр кривой находится в начале координат, т. е. . Тогда уравнение кривой примет вид
. (6)
Определение 1. Кривая второго порядка (6) называется эллипсом (т. е. принадлежит эллиптическому типу), если коэффициенты А и С имеют одинаковые знаки, т. е.
. (7)
Будем предполагать, что и
. Возможны три случая:1)
, 2)
и 3)
.
В первом случае, имеем действительный эллипс

Где числа


Уравнение (8) называется
Каноническим уравнением эллипса
с полуосями и
(рис.14). Точки
называются
Вершинами эллипса
и отрезки и
— его
Осями
.
Отметим, что из уравнения (8) имеем При
получаем Окружность
.
Во втором случае, , кривая (6) представляет собой точку
(вырожденный эллипс).
В третьем случае, , кривая (6) не имеет действительных точек; ее условно называют мнимым эллипсом.
Определение 2. Кривая второго порядка называется Гиперболой (т. е. кривой гиперболического типа), если коэффициенты и
имеют противоположные знаки, т. е.
. (10)
Пусть , а
. Рассмотрим три случая: 1)
, 2)
и
3) .
В первом случае, , имеем гиперболу с каноническим уравнением




— называются вершинами гиперболы, где
Во втором случае, , получаем пару пересекающихся прямых (вырожденная гипербола)
В третьем случае, , получим гиперболу

С полуосями 

и
, то гипербола (12) называется Сопряженной к гиперболе (11); ее вершины
(рис.15).
Отрезок называется действительной осью, а отрезок
— мнимой осью гиперболы (11).
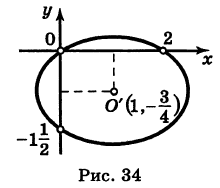
Пример. Определить вид и расположение кривой
Решение. Дополняя члены, содержащие и
, соответственно, до полных


Приведем к каноническому виду
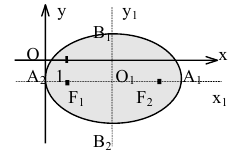
Следовательно, данная кривая есть эллипс с полуосями , центр которого находится в точке

| < Предыдущая | Следующая > |
|---|
Содержание:
Линии второго порядка
Окружность
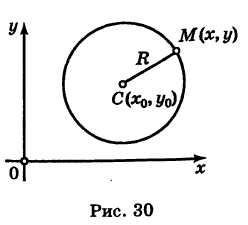
Выведем уравнение окружности (рис. 30) с центром С
MC=R.
Отсюда, вспоминая формулу расстояния между двумя точками, имеем
Так как обе части равенства (2) положительны, то, возводя в квадрат, получим равносильное уравнение
Итак, координаты любой точки М (х, у) данной окружности удовлетворяют уравнению (3). Справедливо также обратное утверждение.
Таким образом, уравнение (3) представляет собой уравнение окружности радиуса R с центром в точке С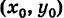
В частности, полагая х0 = 0 и у0 = 0, получим уравнение окружности с центром в начале координат
Уравнение окружности (3) после несложных преобразований можно привести к виду
где
Таким образом, окружность является кривой второго порядка.
Сравнивая уравнение (5) с общим уравнением кривой второго порядка
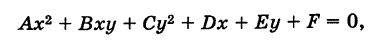
мы видим, что в (5) В = 0 и, кроме того, А — 1, С = 1, т. е. А = С. Обратно, положим в (6) В = 0 и
Деля уравнение (7) почленно на 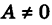
мы приходим к уравнению вида (5).
Уравнение (7) называется общим уравнением окружности. Заметим, однако, что не всякое уравнение (7) является уравнением действительной окружности. Легко показать, что (7) определяет действительную кривую (окружность) лишь при 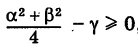
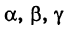
Таким образом, действительная кривая второго порядка является окружностью тогда и только тогда, когда: 1) коэффициенты при квадратных текущих координат равны между собой и 2) отсутствует член, содержащий произведение текущих координат.
Центральные кривые второго порядка
Рассмотрим уравнение второго порядка
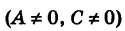
В нашем кратком курсе при рассмотрении общих уравнений кривых второго порядка мы ограничимся лишь этим случаем.
Отсюда, полагая
получаем
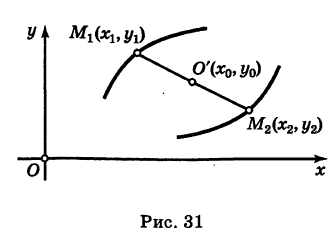
Точка О'(х0, у0) представляет собой центр симметрии кривой (5) (центр кривой). Действительно, если точка Мх(х19 У) лежит на кривой (5), то симметричная ей относительно О’ точка М2(х2, у2) где 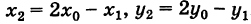
Параллельные осям координат Ох и Оу прямые у = у0 и х = х0 являются осями симметрии кривой (5) (оси кривой). Действительно, если точка 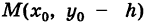
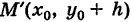
В дальнейшем, для простоты исследования, будем предполагать, что центр кривой находится в начале координат, т. е. х0 = О, 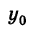
Определение: Кривая второго порядка (6) называется эллипсом (точнее, принадлежит эллиптическому шипу)у если коэффициенты А и С имеют одинаковые знаки, т. е.
Для определенности будем полагать, что А > 0 и С > 0 (так как в противном случае знаки членов уравнения (6) можно изменить на обратные).
Возможны три случая: 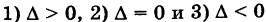
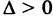

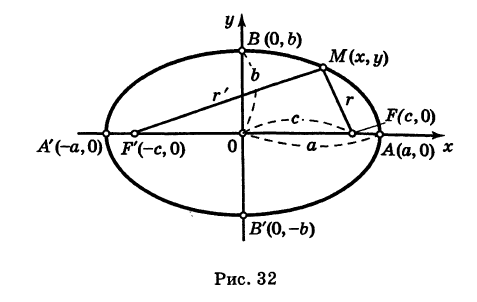
называются полуосями эллипса. Обычно полагают 0 < b < а (этого всегда можно добиться путем надлежащего выбора осей Ох и Оу). Уравнение (8) называется каноническим уравнением эллипса с полуосями аиЬ (рис. 32). Точки А (а, 0), В (О, Ь), А’ (-а, 0), В’ (0, -Ь) называются вершинами эллипса, а отрезки А’А = 2а и = -26 — его осями. Отметим, что из уравнения (8) имеем 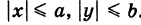
Заметим, что при а = b получаем окружность
Во втором случае, Д = О, кривая (6) представляет собой точку О (0, 0) (вырожденный эллипс).
Наконец, в третьем случае, Д < 0, кривая (6) не имеет действительных точек; ее условно называют мнимым эллипсом.
Определение: Кривая второго порядка (6) называется гиперболой (точнее, кривой гиперболического типа), если коэффициенты А и С имеют противоположные знаки, т. е.
Положим, для определенности, А > О, тогда С < 0. Возможны три случая:
В первом случае, 
где 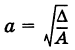
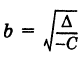
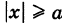
Во втором случае, А = 0, получаем пару пересекающихся прямых (вырожденная гипербола)
Наконец в третьем случае, 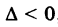
с полуосями 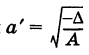
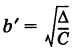
Отрезок А’А = 2а называется действительной осью, а отрезок В’В = 2Ь — мнимой осью гиперболы (11).
Пример:
Определить вид и расположение кривой
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, будем иметь
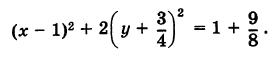
Следовательно, кривая (13) представляет собой эллипс с полуосями 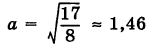
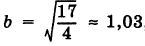
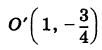
Фокальные свойства центральных кривых второго порядка
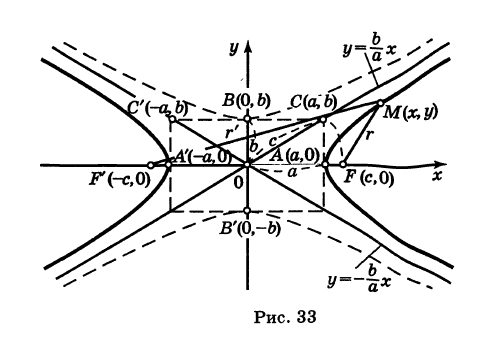
Точки F (с, 0) и F’ (-с, 0), где
называются фокусами, соответственно, эллипса, заданного каноническим уравнением (8), рис. 32 (знак -), и гиперболы, заданной каноническим уравнением (11), рис. 33 (знак +). Отношение
называется эксцентриситетом центральной кривой второго порядка.
Из формулы (1) имеем: для эллипса 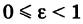
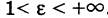
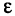
Пусть г = MF и г’ = MF’ — расстояния от точки М центральной кривой второго порядка до ее фокусов (так называемые фокальные радиусы точки М). Имеем
Так как
где знак плюс соответствует эллипсу, знак минус — гиперболе, то
и, следовательно, с учетом (1) получаем
и, аналогично,
Если кривая — эллипс, то 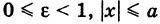
отсюда
причем для любых г и г’, удовлетворяющих равенству (7), существует точка данного эллипса.
Таким образом, для любой точки эллипса сумма ее фокальных радиусов есть величина постоянная (характеристическое свойство эллипса). Это свойство часто принимают за определение эллипса.
Для гиперболы имеем 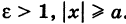
где знак плюс соответствует правой ветви гиперболы (х > 0), а знак минус — левой ветви (х < 0). Отсюда
Итак, для любой точки гиперболы модуль разности ее фокальных радиусов есть величина постоянная (характеристическое свойство гиперболы).
- Заказать решение задач по высшей математике
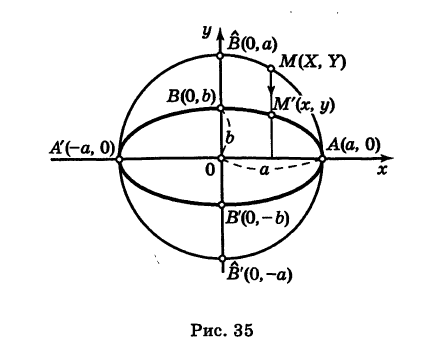
Эллипс как равномерная деформация окружности
Рассмотрим окружность радиуса а. Выберем некоторую прямоугольную систему координат Оху, начало которой, для простоты, поместим в центре окружности 0(0, 0). Текущие координаты точки окружности М, для удобства дальнейших рассуждений, обозначим через X и У. В таком случае уравнение окружности будет иметь вид
Произведем равномерную деформацию окружности (1) в направлении одного из ее диаметров, который, без нарушения общности рассуждения, можно считать вертикальным, т. е. направленным по оси Оу. Пусть k — коэффициент деформации окружности в выбранном направлении, т. е. k есть отношение длины преобразованного вертикального отрезка к его первоначальной длине. Заметим, что при 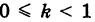
Предположим, что при нашей деформации точка окружности М(Х, У) переходит в некоторую точку М(х, у) преобразованной кривой (рис. 35). Так как точки М и М’ лежат на одной и той же вертикали, то имеем

Отсюда при 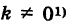
Подставляя эти выражения в уравнение (1), находим 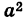
где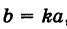
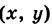
Обратно, если точка М’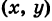
Таким образом, результат равномерной деформации окружности вдоль одного из ее диаметров представляет собой эллипс.
Асимптоты гиперболы
Рассмотрим гиперболу (см. рис. 33)
Решая уравнение (1) относительно у, получаем
Если х неограниченно возрастает, то 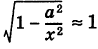
Покажем, что ветви гиперболы (1) сколь угодно близко подходят к прямым (см. рис. 33)
носящим название асимптот гиперболы. Действительно, например, при х > О возьмем в формулах (2) и (4) знаки плюс. Рассмотрим соответствующие точки М (х, у) гиперболы (2) и N (х, У) прямой (4), имеющие одну и ту же абсциссу х. Тогда
при
Аналогично рассматриваются еще три случая: знаки минус в (2) и в (4) при 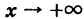
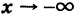
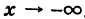
как нетрудно проверить, имеет общие асимптоты с гиперболой (1).
Для равнобочной гиперболы (а = Ь)
ее асимптоты у = ±х взаимно перпендикулярны.
График обратной пропорциональности
Рассмотрим кривую (рис. 36)
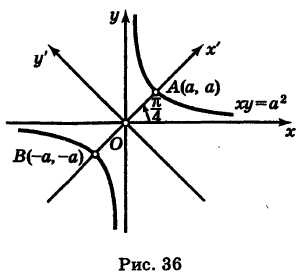
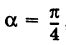
Отсюда на основании (1) получаем
Таким образом, графиком обратной пропорциональности (1) является равнобочная гипербола.
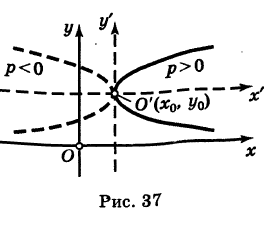
Нецентральные кривые второго порядка
Кривая второго порядка называется нецентральной, если она или не имеет центра симметрии, или же имеет бесконечно много центров симметрии (т. е. не имеет единственного центра). Рассмотрим кривую второго порядка
где 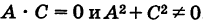
Кроме того, предположим, что 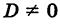
Дополняя в уравнении (1) члены с у до полного квадрата, будем иметь 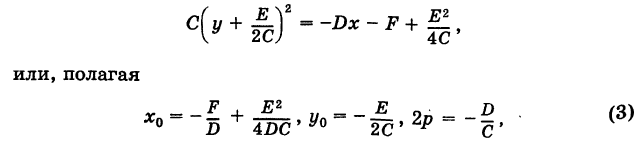
Кривая (4) называется параболой (рис. 37); точка О’ (х0, у0) носит название вершины параболы у а число р называется параметром параболы. Легко убедиться, что прямая у = Уо является осью симметрии параболы (ось параболы); центра симметрии парабола (4) не имеет.
Если вершина параболы находится в начале координат, а ее осью является ось Ох, то мы получаем так называемое каноническое уравнение параболы 
Заметим, что если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид
Это уравнение параболы с вертикальной осью (рис. 38, б).
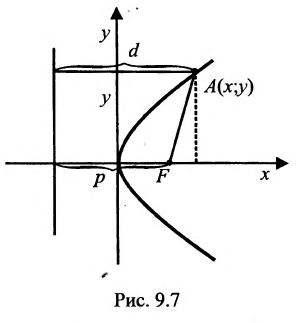
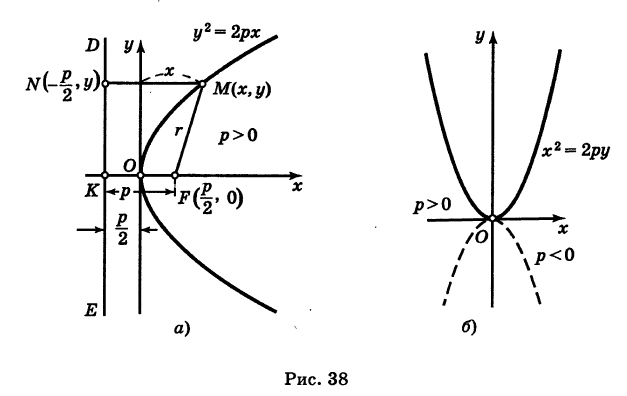
Фокальное свойство параболы
Рассмотрим параболу (рис. 38, а)
Точка 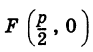
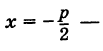
Для точки М(х, у) ее фокальный радиус г = MF равен
Далее, расстояние от этой точки до директрисы равно
Таким образом, парабола представляет собой множество всех точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы). Это характеристическое свойство параболы.
Пример:
Определить координаты фокуса и уравнение директрисы параболы
Решение:
Сравнивая это уравнение с уравнением (6), получим 2р = 1; отсюда р = 1/2. Следовательно, фокус параболы имеет координаты (0, 1/4), а уравнение директрисы есть у = -1/4.
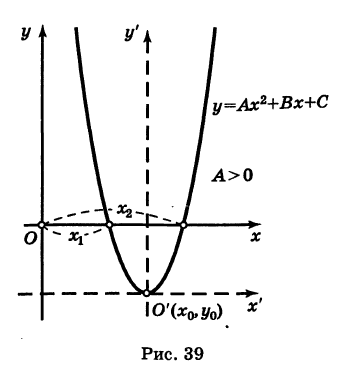
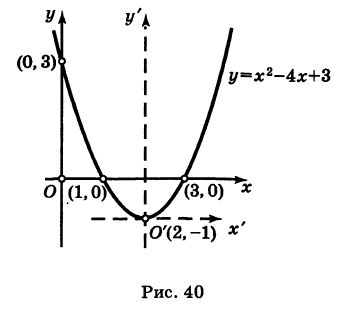
График квадратного трехчлена
Рассмотрим квадратный трехчлен
Отсюда
Дополняя выражение, стоящее в скобках, до полного квадрата, получим
или
Если положить
то из формулы (3) получим
Делая параллельный перенос системы координат
окончательно будем иметь
Уравнение (6) , формула (6) представляет собой каноническое уравнение параболы с вертикальной осью, вершина которой находится в точке 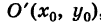
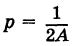
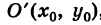
Заметим, что абсциссы 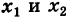
На этом свойстве основан графический способ решения квадратного уравнения (7).
Пример:
Привести уравнение 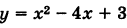
Решение:
Перенося свободный член в левую часть уравнения и дополняя правую часть до полного квадрата, будем иметь у — 3 + 4 = = х2- 4х + 4, или
Полагая х-2=х’,у + 1 = у’, получим
Таким образом, заданное уравнение есть уравнение параболы с вершиной в точке 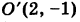
- Полярные координаты
- Непрерывность функции
- Уравнения поверхности и линии в пространстве
- Общее уравнение плоскости
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Прямоугольная система координат на плоскости и ее применение
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов 
Таким образом кривая второго порядка является частным случаем алгебраической кривой.
Содержание
- 1 История
- 2 Инварианты
- 3 Характеристическая квадратичная форма и характеристическое уравнение
- 4 Классификация кривых второго порядка
- 4.1 Невырожденные кривые
- 4.2 Вырожденные кривые
- 5 Диаметры и центр кривой второго порядка
- 6 Главные оси и вершины кривой второго порядка
- 7 Уравнения
- 7.1 Общее уравнение в матричном виде
- 7.2 Канонический вид
- 7.3 Через эксцентриситет
- 7.4 Полярные координаты
- 7.5 Кривая, заданная своими пятью точками
- 7.6 Касательные и нормали
- 7.7 Полюсы и поляры
- 8 Теоремы, связанные с кривыми второго порядка
- 9 См. также
- 10 Ссылки
- 11 Литература
- 12 Примечания
История
Впервые кривые второго порядка изучались Менехмом, учеником Евдокса.[1][2] Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы образованного ими угла, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур (см. ниже).
Однако эти научные знания нашли применение лишь в XVII веке, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, при достижении второй космической скорости — по параболе, а при скорости, большей второй космической — по гиперболе.
Инварианты
Вид кривой зависит от четырёх инвариантов:
- инварианты относительно поворота и сдвига системы координат:
- инвариант относительно поворота системы координат (полуинвариант):[источник не указан 1918 дней]
Иногда встречающееся выражение «инвариант кривой» является неточным. Если умножить уравнение на ненулевое число k, то получится уравнение, задающее ту же самую кривую. При этом значения инвариантов изменятся. 
Характеристическая квадратичная форма и характеристическое уравнение
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой
Так, например, невырожденная кривая 

или
Корни этого уравнения являются собственными значениями вещественной симметричной матрицы
и, как следствие этого, всегда вещественны.[3]
Классификация кривых второго порядка
Невырожденные кривые
Кривая второго порядка называется невырожденной, если 
Вырожденные кривые
Кривая второго порядка называется вырожденной, если 
Диаметры и центр кривой второго порядка
Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол 

Если выполняется условие 

Координаты центра 

Решая эту систему относительно 


Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду

где 
Главные оси и вершины кривой второго порядка
Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым к ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая 

Направляющие косинусы нормалей к главным осям удовлетворяют уравнениям

где 

Из всех видов кривых второго порядка только окружность имеет неопределённые главные направления.
Уравнения
Общее уравнение в матричном виде
Общее уравнение кривой можно записать в матричном виде
Канонический вид
Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты 

Замечание. При переходе к канонической форме уравнения может понадобиться умножить уравнение на число, не равное нулю. Поэтому численные значения инвариантов канонического уравнения могут отличаться от значений инвариантов для исходного уравнения. Неизменными остаются знаки величин 

| Вид кривой | Каноническое уравнение | Инварианты |
|---|---|---|
Невырожденные кривые ( ) )
|
||
| Эллипс | 
|

|
| Гипербола | 
|

|
| Парабола | 
|

|
Вырожденные кривые ( ) )
|
||
| Две мнимые пересекающиеся прямые | 
|

|
| Две пересекающиеся прямые | 
|

|
| Две параллельные прямые | 
|

|
| Две совпадающие прямые | 
|

|
Для центральной кривой в каноническом виде её центр 
Через эксцентриситет
Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду

В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых 




Уравнение директрисы кривой выражается уравнением 


Если кривая второго порядка центральная (эллипс или гипербола), то прямая

является осью симметрии и, следовательно, кривая имеет два фокуса и две директрисы.
Параметр 
Полярные координаты
Если взять в качестве полюса полярной системы координат 



Кривая, заданная своими пятью точками
Кривая второго порядка вполне определяется пятью своими точками, если никакие четыре из них не лежат на одной прямой. Уравнение кривой, проходящей через точки 





Кривая, заданная пятью точками вырождается в том и только в том случае, когда три из заданных точек лежат на одной прямой.
Касательные и нормали
Уравнение касательной к кривой второго порядка 


Уравнение нормали к кривой второго порядка в точке 

Полюсы и поляры
Уравнение
помимо касательной определяет прямую, называемую полярой точки 

Теоремы о полюсах и полярах:[источник не указан 1918 дней]
- Если прямая, проведённая через полюс
пересекает поляру в точке
а кривую второго порядка — в точках
и
то точки
и
гармонически разделяют отрезок
то есть выполняется условие
- Если точка лежит на некоторой прямой, то её поляра проходит через полюс этой прямой. Если прямая проходит через некоторую точку, то её полюс лежит на поляре этой точки.
- Диаметр кривой второго порядка есть поляра бесконечно удалённой точки, через которую проходят сопряжённые ему хорды, а центр кривой есть полюс бесконечно удалённой прямой.
- Фокус кривой есть центр пучка, обладающего тем свойством, что полюс любой его прямой принадлежит перпендикулярной к ней прямой этого пучка. Директрисса есть поляра фокуса.
Из этих утверждений, в частности, следует, что:
- если через точку можно провести две касательные к кривой, то поляра этой точки проходит через точки касания;
- касательные к кривой в концах диаметра параллельны сопряжённым ему хордам;
- точка пересечения касательных к кривой в концах любой её хорды, проходящей через фокус, лежит на директриссе;
- каждая хорда, проходящая через фокус, перпендикулярна к прямой, проведённой через её фокус и точку пересечения касательных в концах хорды.
Теоремы, связанные с кривыми второго порядка
- Теорема Паскаля: точки пересечения противоположных сторон шестиугольника, вписанного в кривую второго порядка, лежат на одной прямой.
- Теорема Брианшона: диагонали, проходящие через противоположные вершины шестиугольника, описанного около кривой второго порядка, пересекаются в одной точке.
См. также
- Коническое сечение
- Квадрика
- Поверхности второго порядка
Ссылки
- Общее уравнение кривой второго порядка
- Кривые второго порядка (недоступная ссылка) (недоступная ссылка с 18-05-2013 [1993 дня])
- Кривые второго порядка: гипербола, парабола
Литература
- Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64—69.
Примечания
- ↑ Б. А. Розенфельд, Аполлоний Пергский, М.: МЦНМО, 2004, c. 32.
- ↑ Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Menaechmus (англ.) — биография в архиве MacTutor.
- ↑ Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.