Как найти центр спирали

attempt at finding center of arithmetic spiral to be tangent to two lines

Given the two orange lines in the picture, how can I calculate the center for an arithmetic spiral that will join the two lines whilst simultaneously being tangent to the ends of those lines. There is a similar question that has already been solved that deals with finding the center of logarithmic spirals in How to find the center of a log spiral? but the properties of logarithmic spirals being a constant angle means that it is inapplicable in this case though it does seem close. I believed that it could be possible to constrain the angles to find the center but an arithmetic spiral has different angles at every point of the curve so I would need to somehow use the fact that the radius changes linearly with the change in angle. I don’t quite know how to do that though.

Any Ideas?

Update: I now have something that almost works, thanks to the image provided in the comments and with that I have this spiral that is tangent to one original line and needs a separate line shown in green that is parallel to the unused orange original line. I had just renamed aθ to be either r1 or r2 as that is more relevant in my use case than knowing what the θ is but it should not create the error that is shown in the image.

Suggestions?

Here is what the tool for creating the spiral is doing. It requires a circle to be drawn first for the starting diameter of the spiral and takes in the variables of start angle, swept angle and pitch in order to fully define the spiral. All those values are pulled directly from the earlier sketch or calculated for the pitch by multiplying dimension a times 2pi.

Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).

Что такое спираль Архимеда?

Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.

Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.

В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.

Уравнение спирали Архимеда в полярной системе координат записывается, как:

r=a+btheta

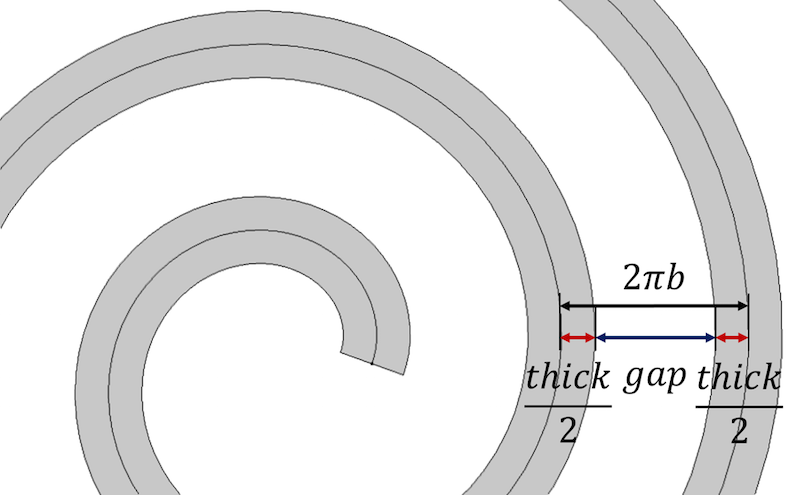
где a и b — параметры, определяющие начальный радиус спирали и расстояние между витками, которое равно 2 pi b. Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью. Это имя связывают с арифметической зависимостью расстояния от начала кривой до точек спирали, находящихся на одной радиальной линии.

Задание параметризированной геометрии спирали Архимеда

Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.

Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.

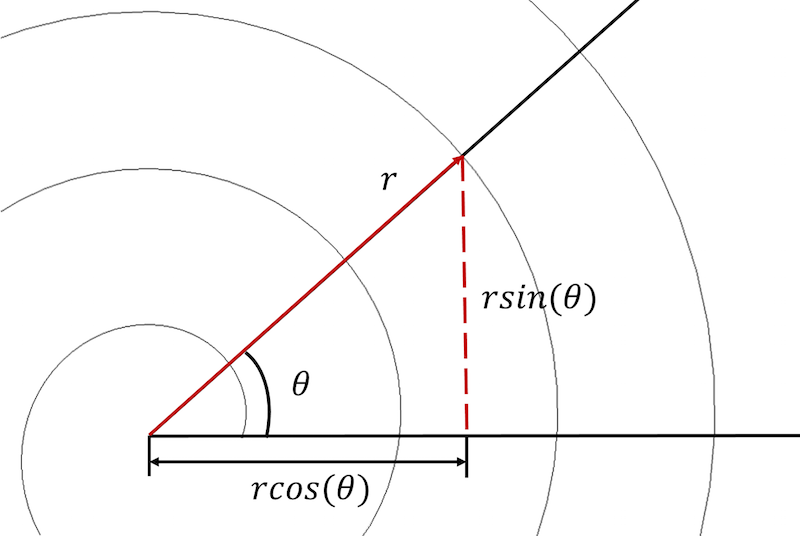
Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:

begin{align*} x_{component}=rcos(theta) \ y_{component}=rsin(theta) end{align*}

После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:

begin{align*} x_{component}=(a+btheta)cos(theta) \ y_{component}=(a+btheta)sin(theta) end{align*}

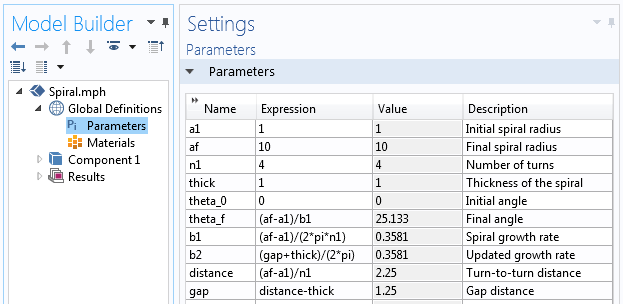
В COMSOL Multiphysics необходимо определить набор параметров, с помощью которых будем задавать геометрию спирали. В нашем случае — это начальный и конечный радиусы спирали a_{initial} и a_{final}, соответственно, и количество витков n. Показатель роста спирали b находится, как:

b=frac{a_{final}-a_{initial}}{2 pi n}

Также необходимо определить начальный и конечный углы спирали — theta_0 и theta_f, соответственно. Давайте с них и начнём — theta_0=0 и theta_f=2 pi n. Исходя из заданной информации, определяем параметры для построения геометрии спирали.

Параметры, которые используются для построения геометрии спирали.

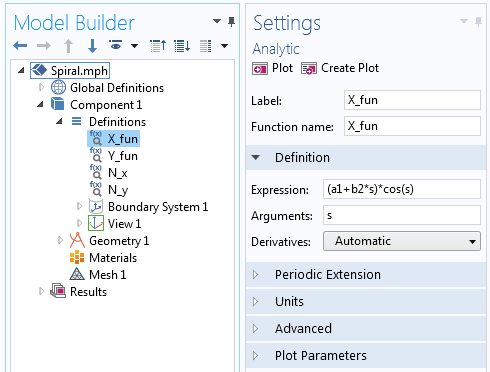
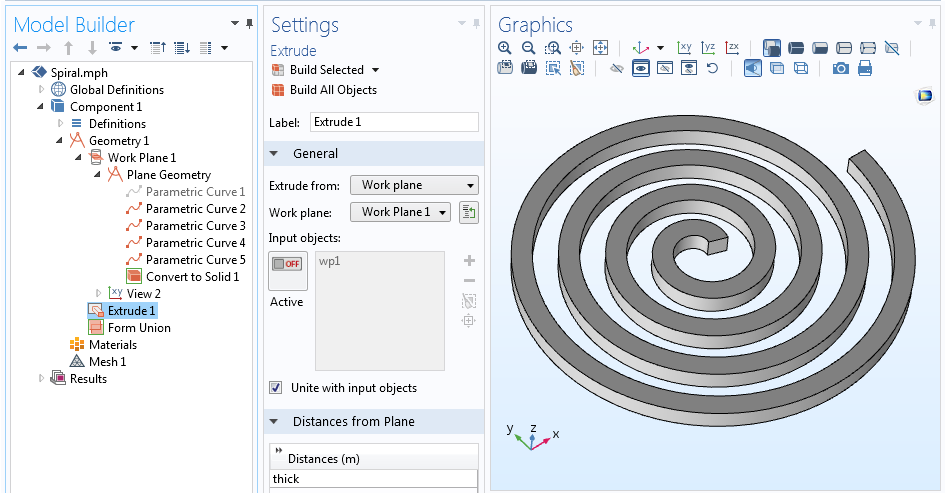
Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):

begin{align*} X_{fun}=(a+bs)cos(s) \ Y_{fun}=(a+bs)sin(s) \ end{align*}

Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.

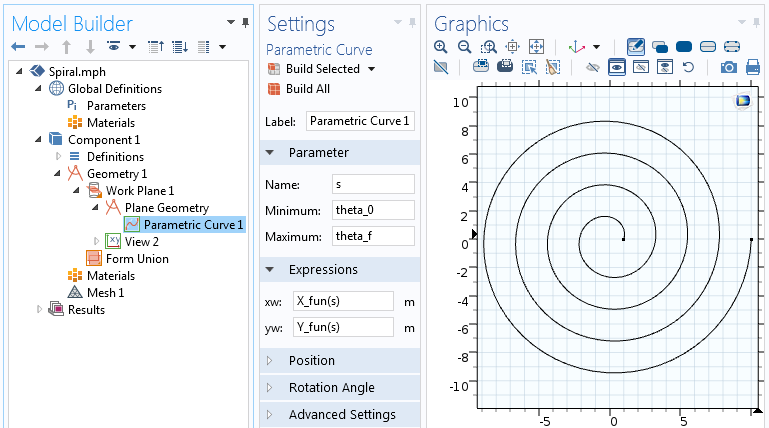
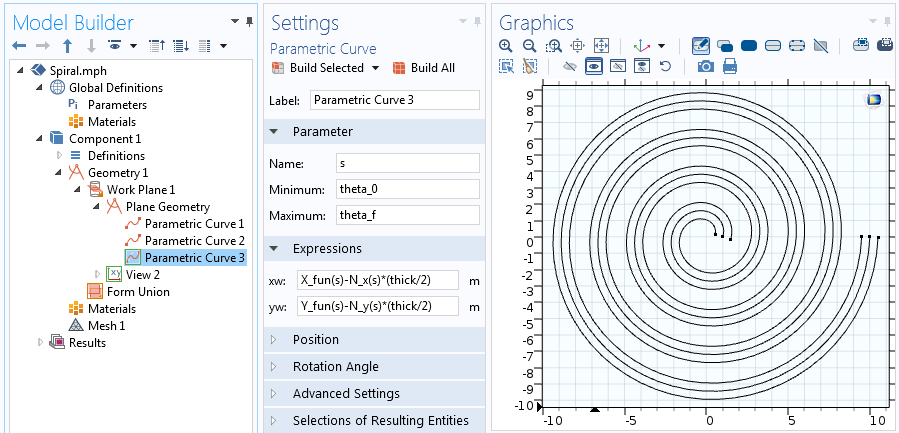
Аналитическая функция затем может использоваться в качестве выражения в узле Parametric Curve. Во вкладке Parameter задаём параметр s от начального угла, theta_0, до его конечного значения, theta_f=2 pi n.

Настройки для Parametric Curve (Параметрической кривой).

Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.

До этого момента параметрами нашей кривой были начальный (a_{initial}) и конечный (a_{final}) радиусы и количество витков n. Теперь мы хотим добавить ещё один – толщину спирали.

Ещё раз напомним главное свойство спирали — расстояние между витками постоянно и равно 2 pi b. Что эквивалентно frac{a_{final}-a_{initial}}{n}. Чтобы добавить толщину в наши уравнения, представляем расстояние между витками суммой толщины спирали и зазора thick+gap.

Расстояние между витками определяется толщиной спирали и величиной зазора.

Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:

begin{align*} distance=frac{a_{initial}-a_{final}}{n} \ gap=distance-thick end{align*}

После этого выражаем показатель роста спирали через толщину:

begin{align*} distance=2pi b \ b=frac{gap+thick}{2pi} end{align*}

Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:

begin{align*} theta_{final}=2 pi n \ a_{final}=text{total distance}+a_{initial} \ a_{final}=2 pi bn+a_{initial} \ n=frac{a_{final}-a_{initial}}{2 pi b} \ theta_{final}=frac{2 pi (a_{final}-a_{initial})}{2 pi b} \ theta_{final}=frac{a_{final}-a_{initial}}{b} end{align*}

Хотите задать отличный от нуля начальный угол спирали? Если так, то его надо будет добавить в выражение для определения конечного угла: theta_f=frac{a_{final}-a_{initial}}{b}+theta_0.

Дублирование кривой спирали дважды со смещением на -frac{thick}{2} и +frac{thick}{2} по отношению к начальной кривой позволяет построить спираль заданной толщины. Чтобы правильно расположить внутреннюю и внешнюю спирали, необходимо убедиться, что начала данных кривых перпендикулярны линии, на которой расположены их начальные точки. Это можно сделать, домножив расстояние смещения pmfrac{thick}{2} на единичный вектор, расположенный по нормали к начальной кривой спирали. Уравнения векторов нормали в параметрическом виде:

n_x=-frac{dy}{ds} quad text{and} quad n_y=frac{dx}{ds}

где s — это параметр, используемый в узле Parametric Curve. Чтобы получить нормированные единичные вектора, необходимо эти выражения разделить на длину нормали:

sqrt{(dx/ds)^2+(dy/ds)^2 }

Обновленные параметрические уравнения спирали Архимеда со смещением:

begin{align*} x_{component}=(a+bs)cos(s)-frac{dy/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}}frac{thick}{2} \ y_{component}=(a+bs)sin(s)+frac{dx/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}}frac{thick}{2} end{align*}

Записывать такие длинные выражения довольно неудобно, поэтому введём следующие обозначения:

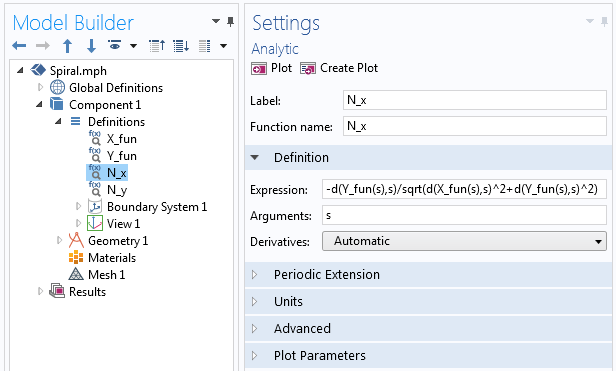
begin{align*} N_x=-frac{dy/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}} \ N_y=frac{dx/ds}{sqrt{(dx/ds)^2+(dy/ds)^2 }} end{align*}

где N_x и N_y определяются аналитическими функциями в COMSOL Multiphysics, аналогично X_{fun} и Y_{fun} в первом примере. Внутри функции используется оператор производной, d(f(x),x), как показано на скриншоте ниже.

Примеры оператора производной, который используется в аналитической функции

Функции X_{fun}, Y_{fun}, N_x, и N_y могут быть использованы в выражениях для задания параметрической кривой, как с одной стороны:

begin{align*} x_{lower}=X_{fun}(s)+N_x(s)frac{thick}{2} \ y_{lower}=Y_{fun}(s)+N_y(s)frac{thick}{2} end{align*}

Так и с другой:

begin{align*} x_{upper}=X_{fun}(s)-N_x(s)frac{thick}{2} \ y_{upper}=Y_{fun}(s)-N_y(s)frac{thick}{2} end{align*}

Выражения для второй смещённой параметрической кривой.

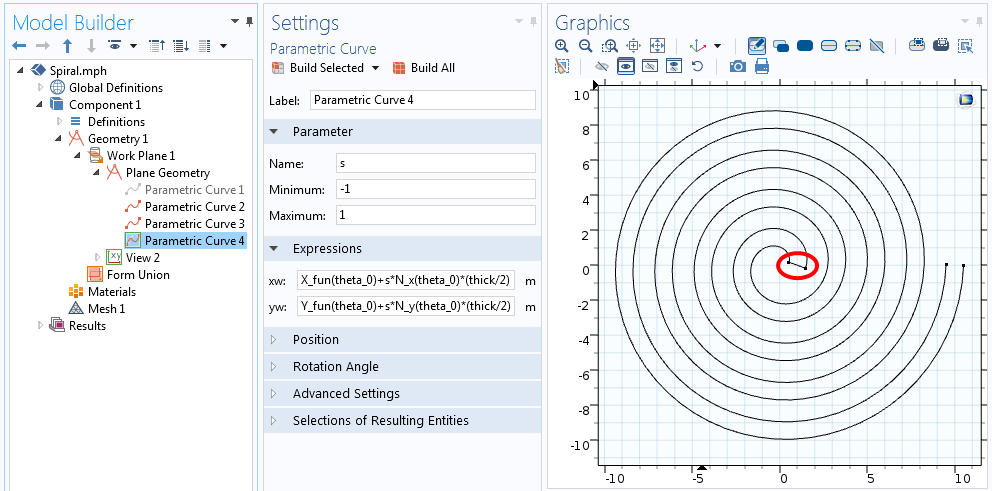
Чтобы соединить концы, добавим ещё две параметрические кривые, используя незначительные изменения уравнений выше. Для кривой, которая будет соединять спираль в центре, необходимо задать X_{fun}, Y_{fun}, N_x, и N_y для начального значения угла, theta. Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:

begin{align*} X_{fun}(theta_0)+scdot N_x(theta_0)cdotfrac{thick}{2} \ Y_{fun}(theta_0)+scdot N_y(theta_0)cdotfrac{thick}{2} end{align*}

Уравнения кривой на конце:

begin{align*} X_{fun}(theta_f)+scdot N_x(theta_f)cdotfrac{thick}{2} \ Y_{fun}(theta_f)+scdot N_y(theta_f)cdotfrac{thick}{2} end{align*}

В этих уравнениях параметр s изменяется от -1 до 1, как показано на скриншоте ниже.

Уравнения кривой, соединяющей спираль в центре.

В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid, создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.

Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.

Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics

В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.

Дополнительные ресурсы по проектированию и расчёту спиралей

• Для улучшения навыков моделирования спиралей, ознакомьтесь со следующими учебными моделями:
  • Спирально-щелевая антенна
• Познакомьтесь с опытом одного из наших пользователей: Анализ спиральных резонаторных фильтров

Наверх

Спиралью называется плоская кривая, описываемая точкой, удаляющейся от центра при совершении кругового движения в плоскости чертежа вокруг центра спирали. На практике различают спирали с постоянным и постепенно возрастающим расстоянием между завитками. Обычно спирали строят по точкам и вычерчивают с помощью лекала.

Для того чтобы расчертить спираль, необходимо наметить не менее двух ее центров. Если вычерчивают спираль из трех или более центров, то обычно центрами спирали являются вершины правильного треугольника или правильного многоугольника. Каждую дугу проводят из последующей вершины до пересечения с лучом из угла треугольника или многоугольника. Радиус при этом каждый раз увеличивается на длину, равную длине стороны треугольника или многоугольника.

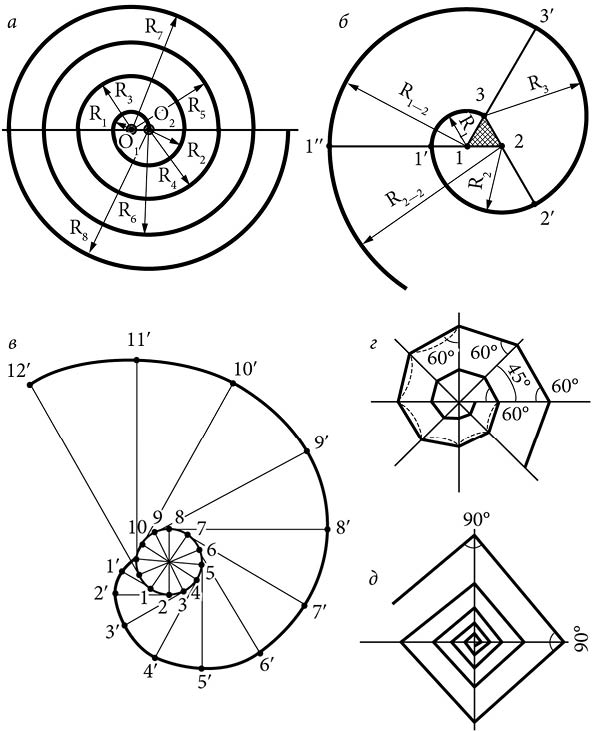
Рассмотрим, например, как начертить так называемую «архимедову спираль» (рис. 17, а ). Для этого нужно провести горизонтальную линию и отметить на ней две точки О 1 и О 2, отстоящие одна от другой примерно на 3 мм. Поставив ножку циркуля в одну из этих точек (О 1), проведите дугу радиусом 3 мм (R 1), равную половине окружности. Концы этой дуги должны опираться на горизонтальную ось (в данном примере – сверху).

Затем перенесите ножку циркуля во вторую из отмеченных точек и увеличьте его раствор так, чтобы карандаш попал в конец первой дуги. Снова проведите половину окружности радиусом R 2, опирающуюся на горизонтальную линию, но уже с противоположной стороны (снизу). Таким же образом, переставляя ножку циркуля то в первую, то во вторую точку и каждый раз увеличивая его раствор, продолжайте разворачивать спираль. На рис. 17, а , изображено четыре полных оборота.

Для построения спирали, имеющей три центра (рис. 17, б), находящихся на равных расстояниях один от другого, необходимо предварительно построить равносторонний треугольник 1–2–3 (заштрихован) и продолжить его стороны так, как это показано на рисунке (линии 1–1’, 2–2’ и 3–3’ ).

Из центра 1 проводим дугу 3–1’ радиусом R 1, равным длине стороны треугольника, до пересечения с продолжением стороны 1–1’ . Затем из центра 2 описываем дугу радиусом R 2 = 2R 1 до пересечения с продолжением стороны 2 (линия 2–2’ ). После этого из центра 3 проводим дугу радиусом R 3 = 3R 1 до пересечения с продолжением стороны 3 (линия 3–3’ ) в точке 3’ . После этого возвращаемся в центр 1 и продолжаем построение в такой же последовательности, каждый раз увеличивая радиус дуги на величину стороны треугольника.

Рис. 17. Построение спиралей: а – «архимедова спираль» с двумя центрами; б – трехцентровая спираль; в – эвольвента круга; г, д – ломаные (хордовые) спирали.

Аналогично выполняют спирали с четырьмя, пятью и т. д. центрами.

Эвольвента круга (рис. 17, в ) – это плоская кривая, образуемая точкой на прямой, которая перемещается без скольжения по неподвижной окружности заданного радиуса. Эта кривая иногда называется разверткой окружности. Построение эвольвенты начинается с деления заданной окружности на произвольное число равных частей, например 12. В каждой точке деления проводим касательные к окружности. На каждой из этих касательных последовательно откладываем длину окружности, равную πd /12: в точке 1 – πd /12, в точке 2 – 2πd /12, в точке 3 – 3πd /12 и т. д. На касательной к точке 12 откладываем длину окружности, равную πd . Соединяя последовательно плавной кривой по лекалу полученные на касательных точки 1’, 2’, 3’ и т. д., получим кривую, называемую эвольвентой.

Схема построения ломаных спиралей показана на рис. 17, г, д . Они строятся так же, как и циркульные, но дуги заменяются соответствующими хордами.

Золотая спираль или спираль Фибоначчи — логарифмическая спираль, коэффициент роста которой равен φ 4 , где φ — золотое сечение. Коэффициент роста логарифмической спирали показывает во сколько раз изменился полярный радиус спирали при повороте на угол 360°. [1] Свое название эта спираль получила из-за связи с последовательностью вложенных друг в друга прямоугольников с отношением сторон, равным φ , которые принято называть золотыми. Золотую спираль можно как вписать в систему таких прямоугольников, так и описать вокруг нее. Популярность золотая спираль приобрела из-за того, что известная с начала XVI века и применяющаяся в искусстве [2] спираль, построенная по методу Дюрера [3] [4] , оказалась хорошей аппроксимацией для золотой спирали (см. рисунок)

Содержание

Формула [ править | править код ]

Уравнение для золотой спирали в полярной системе координат то же самое, что и для других логарифмических спиралей, но со специальным значением коэффициента роста — φ 4 :

r = a φ ± 2 θ π <displaystyle r=avarphi ^<pm <frac <2 heta ><pi >>>> ,

где a — произвольная положительная вещественная константа, а φ = 5 + 1 2 <displaystyle varphi =<frac <<sqrt <5>>+1><2>>> — золотое сечение.

Основное свойство логарифмической спирали: угол между радиус-вектором, исходящим из полюса, и касательной к спирали — μ — постоянен, и для золотой спирали определяется формулой:

tg ⁡ μ = r r ′ = π 2 ln ⁡ φ <displaystyle operatorname mu =<dfrac , где r ′ =»» d r d θ >> .

Откуда μ ≈ 73 ∘ <displaystyle mu approx 73^<circ >> .

Приближения золотой спирали [ править | править код ]

Существует несколько похожих спиралей, которые близки, но не совпадают в точности с золотой спиралью [5] , с которой их часто путают.

Как уже было написано выше, при вписывании золотой спирали в последовательность вложенных друг в друга золотых прямоугольников, она аппроксимируется спиралью, построенной по методу Дюрера. Золотой прямоугольник можно разделить на квадрат и подобный ему прямоугольник, его, в свою очередь, разделить тем же образом, и продолжать этот процесс произвольное число раз. Если в эти квадраты вписать соединенные между собой четвертинки окружностей, то получается спираль, изображенная на первом рисунке.

Ещё одной аппроксимацией является спираль Фибоначчи, которая строится подобно вышеописанной спирали, за исключением того, что начинают с прямоугольника из двух квадратов и добавляют потом к большей стороне прямоугольника квадрат такой же длины. Поскольку отношение между соседними числами Фибоначчи стремится к золотой пропорции, спираль всё больше приближается к золотой спирали по мере добавления квадратов (см. второй рисунок).

Спирали в природе [ править | править код ]

В природе встречаются приближения к логарифмическим спиралям с коэффициентом роста равным φ k . Так раковины моллюсков Nautilus pompilius и окаменелых аммонитов хорошо описываются при k = 2, а раковины некоторых улиток при k = 1. [6] Отношение длин трех витков спирали уха у человека равно φ [7] , что соответствует спирали с k = 1. Рукава спиральных галактик, несмотря на существующие утверждения [8] , если и описываются логарифмической, то не золотой спиралью. В данном случае, описание ею является проявлением случайной близости. Недавний анализ спиралей, встречающихся в роговичном эпителии мышей, показал, что там встречаются как золотая, так и другие логарифмические спирали. [9]

Построение спирали Архимеда.

Спираль Архимеда — это траектория точки, движущейся с постоянной скоростью от центра окружности по

радиусу, вращающемуся также с постоянной угловой скоростью.

1. Делим радиус окружности на одинаковое число равных частей (в примере на 8).

2. Делим окружность на такое же число равных частей.

3. Проводим лучи из центра через точки деления окружности.

4. На первом луче откладываем одно деление радиуса.

5. На втором луче откладываем два деления радиуса и т. д.

6. Если строить спираль дальше, то на луче 1 откладываем 8+1 деление радиуса (получаем точку IX ).

7. На втором луче откладываем 8+2 деления радиуса (получаем точку X) .

8. На третьем луче откладываем 8+3 деления радиуса (получаем точку XI) и т. д.

Соединяем точки по лекалу.

Спираль. Спираль Архимеда. Построение спирали Архимеда.