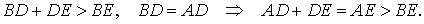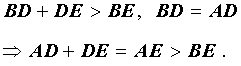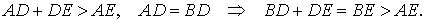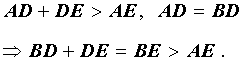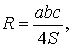Как найти центр треугольника в геометрии

Центр треугольника

Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.

Существует несколько понятий центра для треугольника.

Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.

Ортоцентр — точка пересечения его высот.

Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.

Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).

Как найти центр треугольника

Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.

Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.

Центр равностороннего треугольника является также центром вписанной и описанной окружности.

Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.

Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:

• ввести в поле калькулятора координаты вершин треугольника;
• нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

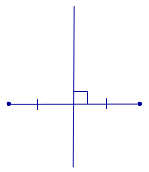
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

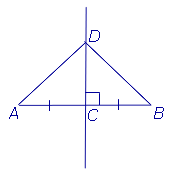
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

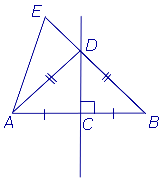
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

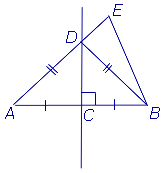
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

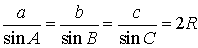
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		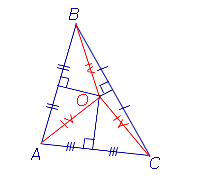Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		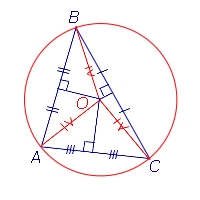Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности	Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		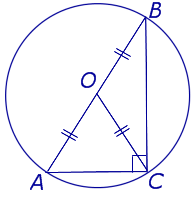Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		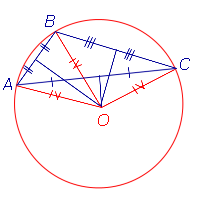Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов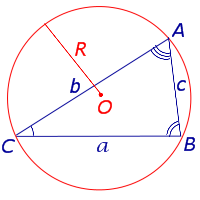
Площадь треугольника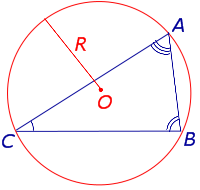
Радиус описанной окружности

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

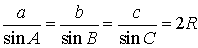
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

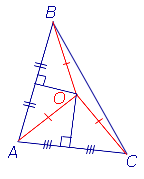
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

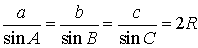
Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Как определить центр треугольника?

Как найти середину у треугольника?

Пересекающиеся медианы Найдите середину одной стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой A.

Как найти центр тяжести в треугольнике?

Центроид треугольника (также барицентр треугольника и центр тяжести треугольника) — точка пересечения медиан в треугольнике. . Центроид треугольника относится к замечательным точкам треугольника и он перечислен в энциклопедии центров треугольника Кларка Кимберлинга, как точка X(2).

Как найти центр тяжести в прямоугольном треугольнике?

Как найти координаты центра тяжести треугольника?

1. Рисуем треугольник ABC.
2. Ставим точку M — середина BC.
3. Ставим точку H — середина AC.
4. Пересечение BH и AM — и есть центр тяжести треугольника ABC.
5. Найдем его координаты (координаты точки O (xo, yo, zo) )

Как найти Инцентр?

Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник. Инцентр лежит ближе к вершине, расположенной напротив большей стороны треугольника.

Как найти центр тяжести тела неправильной формы?

Центр тяжести тела неправильной формы можно определить так: подвесить его за любую точку, и провести вертикальную линию по отвесу. Затем повернуть тело и повторить операцию. Точка пересечения двух прямых и есть центр тяжести тела.

Где находится центр тяжести призмы?

Так, центр тяжести призмы и цилиндра лежит на середине линии, соединяющей центры тяжести оснований. Центр тяжести шара совпадает с его геометрическим центром. Центр тяжести пирамиды (рис. 18, а) лежит на прямой, соединяющей центр тяжести площади основания с противоположной вершиной на расстоянии /4 высоты от основания.

Где находится центр тяжести у кольца?

Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.

Как найти Центроид фигуры?

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противополежащих сторон. Точка пересечения делит все три отрезка пополам.

Где находится центр тяжести однородного треугольника?

Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.

Где находится центр тяжести у трапеции?

Для произвольной трапеции (то есть она может быть прямоугольной, тупоугольной, равнобокой или любой другой) справедливо то, что центр ее тяжести лежит на прямой, которая соединяет середины оснований трапеции.

Как найти центр масс треугольника?

Как найти центр треугольника

Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.

Как найти длину медианы в прямоугольном треугольнике?

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Где находится центр круга?

Центр вписанной окружности треугольника (инцентр) — одна из замечательных точек треугольника, точка пересечения биссектрис треугольника. Центр вписанной в треугольник окружности также иногда называют инцентром.

Где лежит центр равнобедренного треугольника?

В равнобедренном треугольнике высота, проведенная к основанию, является серединным перпендикуляром. Следовательно, центр описанной около равнобедренного треугольника окружности будет лежать на серединном перпендикуляре, который является и высотой, и медианой, и биссектрисой угла при вершине.

Где лежит центр окружности?

Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью. Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.

Была ли эта статья полезной?

This article is about a geometry concept. For the place in Lexington, Kentucky, see Triangle Center.

In geometry, a triangle center or triangle centre is a point in the triangle’s plane that is in some sense in the middle of the triangle. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.

Each of these classical centers has the property that it is invariant (more precisely equivariant) under similarity transformations. In other words, for any triangle and any similarity transformation (such as a rotation, reflection, dilation, or translation), the center of the transformed triangle is the same point as the transformed center of the original triangle.
This invariance is the defining property of a triangle center. It rules out other well-known points such as the Brocard points which are not invariant under reflection and so fail to qualify as triangle centers.

For an equilateral triangle, all triangle centers coincide at its centroid. However the triangle centers generally take different positions from each other on all other triangles. The definitions and properties of thousands of triangle centers have been collected in the Encyclopedia of Triangle Centers.

History[edit]

Even though the ancient Greeks discovered the classic centers of a triangle they had not formulated any definition of a triangle center. After the ancient Greeks, several special points associated with a triangle like the Fermat point, nine-point center, Lemoine point, Gergonne point, and Feuerbach point were discovered.

During the revival of interest in triangle geometry in the 1980s it was noticed that these special points share some general properties that now form the basis for a formal definition of triangle center.^[1][2] As of 17 June 2022, Clark Kimberling’s Encyclopedia of Triangle Centers contains an annotated list of 50,730 triangle centers.^[3] Every entry in the Encyclopedia of Triangle Centers is denoted by or where is the positional index of the entry. For example, the centroid of a triangle is the second entry and is denoted by or .

Formal definition[edit]

A real-valued function f of three real variables a, b, c may have the following properties:

• Homogeneity: f(ta,tb,tc) = tⁿ f(a,b,c) for some constant n and for all t > 0.
• Bisymmetry in the second and third variables: f(a,b,c) = f(a,c,b).

If a non-zero f has both these properties it is called a triangle center function. If f is a triangle center function and a, b, c are the side-lengths of a reference triangle then the point whose trilinear coordinates are f(a,b,c) : f(b,c,a) : f(c,a,b) is called a triangle center.

This definition ensures that triangle centers of similar triangles meet the invariance criteria specified above. By convention only the first of the three trilinear coordinates of a triangle center is quoted since the other two are obtained by cyclic permutation of a, b, c. This process is known as cyclicity.^[4][5]

Every triangle center function corresponds to a unique triangle center. This correspondence is not bijective. Different functions may define the same triangle center. For example, the functions f₁(a,b,c) = 1/a and f₂(a,b,c) = bc both correspond to the centroid.
Two triangle center functions define the same triangle center if and only if their ratio is a function symmetric in a, b and c.

Even if a triangle center function is well-defined everywhere the same cannot always be said for its associated triangle center. For example, let f(a, b, c) be 0 if a/b and a/c are both rational and 1 otherwise. Then for any triangle with integer sides the associated triangle center evaluates to 0:0:0 which is undefined.

Default domain[edit]

In some cases these functions are not defined on the whole of ℝ³. For example, the trilinears of X₃₆₅ which is the 365th entry in the Encyclopedia of Triangle Centers, are a^1/2 : b^1/2 : c^1/2 so a, b, c cannot be negative. Furthermore, in order to represent the sides of a triangle they must satisfy the triangle inequality. So, in practice, every function’s domain is restricted to the region of ℝ³ where a ≤ b + c, b ≤ c + a, and c ≤ a + b. This region T is the domain of all triangles, and it is the default domain for all triangle-based functions.

Other useful domains[edit]

There are various instances where it may be desirable to restrict the analysis to a smaller domain than T. For example:

• The centers X₃, X₄, X₂₂, X₂₄, X₄₀ make specific reference to acute triangles, namely that region of T where a² ≤ b² + c², b² ≤ c² + a², c² ≤ a² + b².
• When differentiating between the Fermat point and X₁₃ the domain of triangles with an angle exceeding 2π/3 is important, in other words triangles for which a² > b² + bc + c² or b² > c² + ca + a² or c² > a² + ab + b².
• A domain of much practical value since it is dense in T yet excludes all trivial triangles (i.e. points) and degenerate triangles (i.e. lines) is the set of all scalene triangles. It is obtained by removing the planes b = c, c = a, a = b from T.

Domain symmetry[edit]

Not every subset D ⊆ T is a viable domain. In order to support the bisymmetry test D must be symmetric about the planes b = c, c = a, a = b. To support cyclicity it must also be invariant under 2π/3 rotations about the line a = b = c. The simplest domain of all is the line (t,t,t) which corresponds to the set of all equilateral triangles.

Examples[edit]

Circumcenter[edit]

The point of concurrence of the perpendicular bisectors of the sides of triangle ABC is the circumcenter. The trilinear coordinates of the circumcenter are

a(b² + c² − a²) : b(c² + a² − b²) : c(a² + b² − c²).

Let f(a,b,c) = a(b² + c² − a²). Then

f(ta,tb,tc) = (ta) ( (tb)² + (tc)² − (ta)² ) = t³ ( a( b² + c² − a²) ) = t³ f(a,b,c) (homogeneity)

f(a,c,b) = a(c² + b² − a²) = a(b² + c² − a²) = f(a,b,c) (bisymmetry)

so f is a triangle center function. Since the corresponding triangle center has the same trilinears as the circumcenter it follows that the circumcenter is a triangle center.

1st isogonic center[edit]

Let A’BC be the equilateral triangle having base BC and vertex A’ on the negative side of BC and let AB’C and ABC’ be similarly constructed equilateral triangles based on the other two sides of triangle ABC. Then the lines AA’, BB’ and CC’ are concurrent and the point of concurrence is the 1st isogonal center. Its trilinear coordinates are

csc(A + π/3) : csc(B + π/3) : csc(C + π/3).

Expressing these coordinates in terms of a, b and c, one can verify that they indeed satisfy the defining properties of the coordinates of a triangle center. Hence the 1st isogonic center is also a triangle center.

Fermat point[edit]

Let

Then f is bisymmetric and homogeneous so it is a triangle center function. Moreover, the corresponding triangle center coincides with the obtuse angled vertex whenever any vertex angle exceeds 2π/3, and with the 1st isogonic center otherwise. Therefore, this triangle center is none other than the Fermat point.

Non-examples[edit]

Brocard points[edit]

The trilinear coordinates of the first Brocard point are c/b : a/c : b/a. These coordinates satisfy the properties of homogeneity and cyclicity but not bisymmetry. So the first Brocard point is not (in general) a triangle center. The second Brocard point has trilinear coordinates b/c : c/a : a/b and similar remarks apply.

The first and second Brocard points are one of many bicentric pairs of points,^[6] pairs of points defined from a triangle with the property that the pair (but not each individual point) is preserved under similarities of the triangle. Several binary operations, such as midpoint and trilinear product, when applied to the two Brocard points, as well as other bicentric pairs, produce triangle centers.

Some well-known triangle centers[edit]

Classical triangle centers[edit]

(*) : actually the 1st isogonic center, but also the Fermat point whenever A,B,C ≤ 2π/3

Encyclopedia of Triangle Centers reference	Name	Standard symbol	Trilinear coordinates	Description
X1	Incenter	I	1 : 1 : 1	Intersection of the angle bisectors. Center of the triangle’s inscribed circle.
X2	Centroid	G	bc : ca : ab	Intersection of the medians. Center of mass of a uniform triangular lamina.
X3	Circumcenter	O	cos A : cos B : cos C	Intersection of the perpendicular bisectors of the sides. Center of the triangle’s circumscribed circle.
X4	Orthocenter	H	sec A : sec B : sec C	Intersection of the altitudes.
X5	Nine-point center	N	cos(B − C) : cos(C − A) : cos(A − B)	Center of the circle passing through the midpoint of each side, the foot of each altitude, and the midpoint between the orthocenter and each vertex.
X6	Symmedian point	K	a : b : c	Intersection of the symmedians – the reflection of each median about the corresponding angle bisector.
X7	Gergonne point	Ge	bc/(b + c − a) : ca/(c + a − b) : ab/(a + b − c)	Intersection of the lines connecting each vertex to the point where the incircle touches the opposite side.
X8	Nagel point	Na	(b + c − a)/a : (c + a − b)/b: (a + b − c)/c	Intersection of the lines connecting each vertex to the point where an excircle touches the opposite side.
X9	Mittenpunkt	M	(b + c − a) : (c + a − b) : (a + b − c)	Symmedian point of the excentral triangle (and various equivalent definitions).
X10	Spieker center	Sp	bc(b + c) : ca(c + a) : ab(a + b)	Incenter of the medial triangle. Center of mass of a uniform triangular wireframe.
X11	Feuerbach point	F	1 − cos(B − C) : 1 − cos(C − A) : 1 − cos(A − B)	Point at which the nine-point circle is tangent to the incircle.
X13	Fermat point	X	csc(A + π/3) : csc(B + π/3) : csc(C + π/3) (*)	Point that is the smallest possible sum of distances from the vertices.
X15 X16	Isodynamic points	S S′	sin(A + π/3) : sin(B + π/3) : sin(C + π/3) sin(A − π/3) : sin(B − π/3) : sin(C − π/3)	Centers of inversion that transform the triangle into an equilateral triangle.
X17 X18	Napoleon points	N N′	sec(A − π/3) : sec(B − π/3) : sec(C − π/3) sec(A + π/3) : sec(B + π/3) : sec(C + π/3)	Intersection of the lines connecting each vertex to the center of an equilateral triangle pointed outwards (first Napoleon point) or inwards (second Napoleon point), mounted on the opposite side.
X99	Steiner point	S	bc/(b2 − c2) : ca/(c2 − a2) : ab/(a2 − b2)	Various equivalent definitions.

Recent triangle centers[edit]

In the following table of more recent triangle centers, no specific notations are mentioned for the various points.
Also for each center only the first trilinear coordinate f(a,b,c) is specified. The other coordinates can be easily derived using the cyclicity property of trilinear coordinates.

Encyclopedia of Triangle Centers reference	Name	Center function f(a,b,c)	Year described
X21	Schiffler point	1/(cos B + cos C)	1985
X22	Exeter point	a(b4 + c4 − a4)	1986
X111	Parry point	a/(2a2 − b2 − c2)	early 1990s
X173	Congruent isoscelizers point	tan(A/2) + sec(A/2)	1989
X174	Yff center of congruence	sec(A/2)	1987
X175	Isoperimetric point	− 1 + sec(A/2) cos(B/2) cos(C/2)	1985
X179	First Ajima-Malfatti point	sec4(A/4)
X181	Apollonius point	a(b + c)2/(b + c − a)	1987
X192	Equal parallelians point	bc(ca + ab − bc)	1961
X356	Morley center	cos(A/3) + 2 cos(B/3) cos(C/3)	1978[7]
X360	Hofstadter zero point	A/a	1992

General classes of triangle centers[edit]

Kimberling center[edit]

In honor of Clark Kimberling who created the online encyclopedia of more than 32,000 triangle centers, the triangle centers listed in the encyclopedia are collectively called Kimberling centers.^[8]

Polynomial triangle center[edit]

A triangle center P is called a polynomial triangle center if the trilinear coordinates of P can be expressed as polynomials in a, b and c.

Regular triangle center[edit]

A triangle center P is called a regular triangle point if the trilinear coordinates of P can be expressed as polynomials in Δ, a, b and c, where Δ is the area of the triangle.

Major triangle center[edit]

A triangle center P is said to be a major triangle center if the trilinear coordinates of P can be expressed in the form f(A) : f(B) : f(C) where f(X) is a function of the angle X alone and does not depend on the other angles or on the side lengths.^[9]

Transcendental triangle center[edit]

A triangle center P is called a transcendental triangle center if P has no trilinear representation using only algebraic functions of a, b and c.

Miscellaneous[edit]

Isosceles and equilateral triangles[edit]

Let f be a triangle center function. If two sides of a triangle are equal  (say a = b)  then

so two components of the associated triangle center are always equal. Therefore, all triangle centers of an isosceles triangle must lie on its line of symmetry. For an equilateral triangle all three components are equal so all centers coincide with the centroid. So, like a circle, an equilateral triangle has a unique center.

Excenters[edit]

Let

This is readily seen to be a triangle center function and (provided the triangle is scalene) the corresponding triangle center is the excenter opposite to the largest vertex angle. The other two excenters can be picked out by similar functions. However, as indicated above only one of the excenters of an isosceles triangle and none of the excenters of an equilateral triangle can ever be a triangle center.

Biantisymmetric functions[edit]

A function f is biantisymmetric if f(a,b,c) = −f(a,c,b) for all a,b,c. If such a function is also non-zero and homogeneous it is easily seen that the mapping (a,b,c) → f(a,b,c)² f(b,c,a) f(c,a,b) is a triangle center function. The corresponding triangle center is f(a,b,c) : f(b,c,a) : f(c,a,b). On account of this the definition of triangle center function is sometimes taken to include non-zero homogeneous biantisymmetric functions.

New centers from old[edit]

Any triangle center function f can be normalized by multiplying it by a symmetric function of a,b,c so that n = 0. A normalized triangle center function has the same triangle center as the original, and also the stronger property that f(ta,tb,tc) = f(a,b,c) for all t > 0 and all (a,b,c). Together with the zero function, normalized triangle center functions form an algebra under addition, subtraction, and multiplication. This gives an easy way to create new triangle centers. However distinct normalized triangle center functions will often define the same triangle center, for example f and (abc)⁻¹(a+b+c)³f .

Uninteresting centers[edit]

Assume a,b,c are real variables and let α,β,γ be any three real constants. Let

Then f is a triangle center function and α : β : γ is the corresponding triangle center whenever the sides of the reference triangle are labelled so that a < b < c. Thus every point is potentially a triangle center. However the vast majority of triangle centers are of little interest, just as most continuous functions are of little interest.

Barycentric coordinates[edit]

If f is a triangle center function then so is af and the corresponding triangle center is af(a,b,c) : bf(b,c,a) : cf(c,a,b). Since these are precisely the barycentric coordinates of the triangle center corresponding to f it follows that triangle centers could equally well have been defined in terms of barycentrics instead of trilinears. In practice it isn’t difficult to switch from one coordinate system to the other.

Binary systems[edit]

There are other center pairs besides the Fermat point and the 1st isogonic center. Another system is formed by X₃ and the incenter of the tangential triangle. Consider the triangle center function given by:

For the corresponding triangle center there are four distinct possibilities:

•   cos(A) : cos(B) : cos(C)     if the reference triangle is acute (this is also the circumcenter).
•   [cos(A) + sec(B)sec(C)] : [cos(B) − sec(B)] : [cos(C) − sec(C)]     if the angle at A is obtuse.
•   [cos(A) − sec(A)] : [cos(B) + sec(C)sec(A)] : [cos(C) − sec(C)]     if the angle at B is obtuse.
•   [cos(A) − sec(A)] : [cos(B) − sec(B)] : [cos(C) + sec(A)sec(B)]     if the angle at C is obtuse.

Routine calculation shows that in every case these trilinears represent the incenter of the tangential triangle. So this point is a triangle center that is a close companion of the circumcenter.

Bisymmetry and invariance[edit]

Reflecting a triangle reverses the order of its sides. In the image the coordinates refer to the (c,b,a) triangle and (using «|» as the separator) the reflection of an arbitrary point α : β : γ is γ | β | α. If f is a triangle center function the reflection of its triangle center is f(c,a,b) | f(b,c,a) | f(a,b,c) which, by bisymmetry, is the same as f(c,b,a) | f(b,a,c) | f(a,c,b). As this is also the triangle center corresponding to f relative to the (c,b,a) triangle, bisymmetry ensures that all triangle centers are invariant under reflection. Since rotations and translations may be regarded as double reflections they too must preserve triangle centers. These invariance properties provide justification for the definition.

Alternative terminology[edit]

Some other names for dilation are uniform scaling, isotropic scaling, homothety, and homothecy.

Non-Euclidean and other geometries[edit]

The study of triangle centers traditionally is concerned with Euclidean geometry, but triangle centers can also be studied in non-Euclidean geometry.^[10] Spherical triangle centers can be defined using spherical trigonometry.^[11] Triangle centers that have the same form for both Euclidean and hyperbolic geometry can be expressed using gyrotrigonometry.^[12][13][14] In non-Euclidean geometry, the assumption that the interior angles of the triangle sum to 180 degrees must be discarded.

Centers of tetrahedra or higher-dimensional simplices can also be defined, by analogy with 2-dimensional triangles.^[14]

Some centers can be extended to polygons with more than three sides. The centroid, for instance, can be found for any polygon. Some research has been done on the centers of polygons with more than three sides.^[15][16]

See also[edit]

• Central line
• Encyclopedia of Triangle Centers
• Triangle conic
• Central triangle
• Modern triangle geometry

Notes[edit]

External links[edit]

• Manfred Evers, On Centers and Central Lines of Triangles in the Elliptic Plane
• Manfred Evers, On the geometry of a triangle in the elliptic and in the extended hyperbolic plane
• Clark Kimberling, Triangle Centers from University of Evansville
• Ed Pegg, Triangle Centers in the 2D, 3D, Spherical and Hyperbolic from Wolfram Research.
• Paul Yiu, A Tour of Triangle Geometry from Florida Atlantic University.

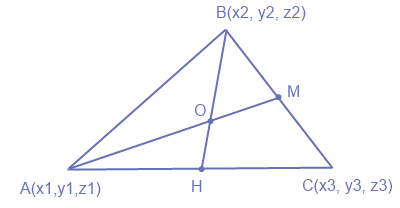
В этой статье и разберу как нарисовать центр тяжести треугольника и найти его координаты.

1) Рисуем треугольник ABC
2) Ставим точку M — середина BC
3) Ставим точку H — середина AC
4) Пересечение BH и AM — и есть центр тяжести треугольника ABC
5) Найдем его координаты (координаты точки O

(x_(o), y_(o), z_(o))

)

[x_{0}=frac{x_{1}+x_{2}+x_{3}}{3}, y_{0}=frac{y_{1}+y_{2}+y_{3}}{3}, z_{0}=frac{z_{1}+z_{2}+z_{3}}{3}]

Пример: Найти координаты центра тяжести треугольника с вершинами A(2;3;4), B(3;1;2) и C(4;-1;3). Решение.

Просмотры: 42905 |
Статью добавил: slava191 |
Категория: аналитическая_геометрия

Точка в треугольнике, которую можно рассматривать как его середину при некоторых критериях

В геометрии, центр треугольника (или центр треугольника ) — это точка на плоскости, которая в некотором смысле является центром треугольника, аналогичным центрам квадраты и кружки, то есть точка, которая по какой-то мере находится в середине рисунка. Например, центроид, центр окружности, центр окружности и ортоцентр были известны древним грекам и могут быть полученные простыми конструкциями.

Каждый из этих классических центров обладает тем свойством, что он инвариантен (точнее, эквивариантен ) относительно преобразований подобия. Другими словами, для любого треугольника и любого преобразования подобия (например, вращение, отражение, растяжение или перевод ) центр преобразованного треугольника совпадает с точкой преобразованного центра исходного треугольника. Эта инвариантность является определяющим свойством центра треугольника. Он исключает другие хорошо известные точки, такие как точки Брокара, которые не являются инвариантными при отражении и поэтому не могут считаться центрами треугольников.

Все центры равностороннего треугольника совпадают в его центроиде, но обычно они отличаются друг от друга в разносторонних треугольниках. Определения и свойства тысяч центров треугольников собраны в Энциклопедии центров треугольников.

Содержание

• 1 История
• 2 Формальное определение
  • 2.1 Домен по умолчанию
  • 2.2 Другие полезные домены
  • 2.3 Симметрия домена
• 3 Примеры
  • 3.1 Окружной центр
  • 3.2 1-й изогонический центр
  • 3.3 Точка Ферма
• 4 Не примеры
  • 4.1 Точки Брокара
• 5 Позиционные векторы
• 6 Некоторые хорошо известные центры треугольников
  • 6.1 Центры классических треугольников
  • 6.2 Последние центры треугольников
• 7 Общие классы центров треугольников
  • 7.1 Центр Кимберлинга
  • 7.2 Центр полиномиального треугольника
  • 7.3 Центр правильного треугольника
  • 7.4 Центр большого треугольника
  • 7.5 Центр трансцендентного треугольника
• 8 Разное
  • 8.1 Равнобедренные и равносторонние треугольники
  • 8.2 Excenters
  • 8.3 Биантосимметричные функции
  • 8.4 Новые центры из старого
  • 8.5 Неинтересные центры
  • 8.6 Барицентрические координаты
  • 8.7 Бинарные системы
  • 8.8 Бисимметрия и инвариантность
  • 8.9 Альтернатива t erminology
• 9 центров гиперболических треугольников
• 10 центров тетраэдров и n-симплексных центров
• 11 См. также
• 12 Примечания
• 13 Внешние ссылки

История

Хотя древние Греки открыли классические центры треугольника, они не сформулировали никакого определения центра треугольника. После древних греков, несколько особых точек, связанных с треугольником, таких как точка Ферма, центр из девяти точек, точка Лемуана, точка Жергонна и точка Фейербаха. Во время возрождения интереса к геометрии треугольника в 1980-х годах было замечено, что эти особые точки обладают некоторыми общими свойствами, которые теперь составляют основу для формального определения центра треугольника. По состоянию на 1 сентября 2020 года Кларк Кимберлинг Энциклопедия центров треугольников содержит аннотированный список из 39 474 центров треугольников.

Формальное определение

A вещественнозначная функция f трех вещественных переменных a, b, c может иметь следующие свойства:

• Однородность: f (ta, tb, tc) = tf (a, b, c) для некоторой константы n и для всех t>0.
• Бисимметрия во второй и третьей переменных: f (a, b, c) = f (a, c, b).

Если ненулевое f имеет оба этих свойства, оно называется функция центра треугольника . Если F представляет собой треугольник центр функции и, Ь, с боковыми длинами опорного треугольника, то точка, трилинейной координата являются F (а, б, в): F (B, C, a): f (c, a, b) называется центром треугольника .

. Это определение гарантирует, что центры треугольников подобных треугольников удовлетворяют критериям инвариантности, указанным выше. По соглашению цитируется только первая из трех трилинейных координат центра треугольника, поскольку две другие получаются путем циклической перестановки точек a, b, c. Этот процесс известен как цикличность .

Каждая функция центра треугольника соответствует уникальному центру треугольника. Это соответствие не является биективным. Различные функции могут определять один и тот же центр треугольника. Например, функции f 1 (a, b, c) = 1 / a и f 2 (a, b, c) = bc обе соответствуют центроиду. Две функции центра треугольника определяют один и тот же центр треугольника тогда и только тогда, когда их отношение является функцией, симметричной относительно a, b и c.

Даже если функция центра треугольника хорошо определена везде, то же самое нельзя всегда сказать о соответствующем центре треугольника. Например, пусть f (a, b, c) равно 0, если a / b и a / c оба рациональны, и 1 в противном случае. Тогда для любого треугольника с целыми сторонами центр связанного треугольника оценивается как 0: 0: 0, что не определено.

Домен по умолчанию

В некоторых случаях эти функции не определены для всего ℝ. Например, трилинейные линии X 365 — это a: b: c, поэтому a, b, c не могут быть отрицательными. Кроме того, чтобы изобразить стороны треугольника, они должны удовлетворять неравенству треугольника. Таким образом, на практике каждая функция домен ограничена областью ℝ, где a ≤ b + c, b ≤ c + a и c ≤ a + b. Эта область T является областью всех треугольников и областью по умолчанию для всех функций на основе треугольников.

Другие полезные области

Существуют различные случаи, когда может быть желательно ограничить анализ областью меньшего размера, чем T . Например:

• Центры X 3, X 4, X 22, X 24, X 40 сделайте конкретную ссылку на острые треугольники,., а именно на ту область T, где a ≤ b + c, b ≤ c + a, c ≤ a + b.
• При различении точки Ферма и X 13 важна область треугольников с углом, превышающим 2π / 3,. другими словами треугольников, для которых a>b + bc + c или b>c + ca + a или c>a + ab + b.
• Область, имеющая большую практическую ценность, поскольку она плотна в T, но исключает все тривиальные треугольники (т.е. точки) и вырожденные треугольники. (т.е. линии) — это набор всех разносторонних треугольников. Он получается удалением плоскостей b = c, c = a, a = b из T.

Симметрия домена

Не каждое подмножество D⊆ Tявляется жизнеспособным доменом. Для подтверждения теста на бисимметрию D должен быть симметричным относительно плоскостей b = c, c = a, a = b. Для поддержки цикличности он также должен быть инвариантным относительно 2π / 3 поворотов вокруг прямой a = b = c. Самой простой областью является прямая (t, t, t), которая соответствует набору всех равносторонних треугольников.

Примеры

Треугольник (ΔABC) с центроидом (G), центром (I), центром описанной окружности (O), ортоцентр (H) и центр из девяти точек (N)

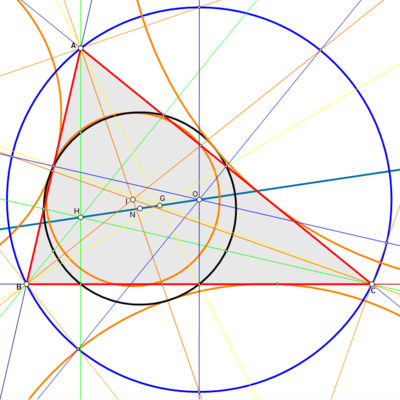
Центр окружности

Точка пересечения серединных перпендикуляров сторон треугольника ABC — это центр окружности. Трилинейные координаты центра описанной окружности следующие:

a (b + c — a): b (c + a — b): c (a + b — c).

Пусть f (a, b, c) = а (б + с — а). Тогда

f (ta, tb, tc) = (ta) ((tb) + (tc) — (ta)) = t (a (b + c — a)) = tf (a, b, c) (однородность)

f (a, c, b) = a (c + b — a) = a (b + c — a) = f (a, b, c) (бисимметрия)

так что f — функция центра треугольника. Поскольку соответствующий центр треугольника имеет те же трилинейи, что и центр описанной окружности, следует, что центр описанной окружности является центром треугольника.

1-й изогонический центр

Пусть A’BC будет равносторонним треугольником, имеющим основание BC и вершину A ‘на отрицательной стороне BC, и пусть AB’C и ABC’ построены аналогичным образом равносторонними треугольниками на основе на двух других сторонах треугольника ABC. Тогда прямые AA ‘, BB’ и CC ‘совпадают, и точка совпадения — это 1-й изогональный центр. Его трилинейные координаты:

csc (A + π / 3): csc (B + π / 3): csc (C + π / 3).

Выражая эти координаты через a, b и c, получаем единицу можно проверить, что они действительно удовлетворяют определяющим свойствам координат центра треугольника. Следовательно, 1-й изогонический центр также является центром треугольника.

Точка Ферма

Пусть

f (a, b, c) = {1, если a 2>b 2 + bc + c 2 (эквивалентно A>2 π / 3), 0, если b 2>c 2 + ca + a 2 или c 2>a 2 + ab + b 2 (эквивалентно B>2 π / 3 или C>2 π / 3), csc ⁡ (A + π / 3) в противном случае (эквивалентно, ни один угол при вершине не превышает 2 π / 3). { displaystyle f (a, b, c) = { begin {cases} 1 quad { text {if}} a ^ {2}>b ^ {2} + bc + c ^ {2} ({ text {эквивалентно}} A>2 pi / 3), \ 0 quad { text {if}} b ^ {2}>c ^ {2} + ca + a ^ {2} { text { или}} c ^ {2}>a ^ {2} + ab + b ^ {2} ({ text {эквивалентно}} B>2 pi / 3 { text {или}} C>2 pi / 3), \ csc (A + pi / 3) quad { text {иначе}} ({ text {эквивалентно, что ни один угол при вершине не превышает}} 2 pi /3).end{cases} }}

Тогда f является бисимметричным и однородным, поэтому это функция центра треугольника. Более того, центр соответствующего треугольника совпадает с вершиной с тупым углом, когда любой угол вершины ds 2π / 3, а с 1-м изогоническим центром в противном случае. Следовательно, центр этого треугольника — не что иное, как точка Ферма.

Непримеры

Точки Брокара

Трилинейные координаты первой точки Брокара — c / b: a / c : б / у. Эти координаты удовлетворяют свойствам однородности и цикличности, но не бисимметрии. Итак, первая точка Брокара не является (в общем) центром треугольника. Вторая точка Брокара имеет трилинейные координаты b / c: c / a: a / b; применимы аналогичные замечания.

Первая и вторая точки Брокара — это одна из многих бицентрических пар точек, пар точек, определенных из треугольника со свойством, что пара (но не каждая отдельная точка) сохраняется при сходстве с треугольником. Несколько бинарных операций, таких как средняя точка и трилинейное произведение, при применении к двум точкам Брокара, а также к другим бицентрическим парам, создают центры треугольников.

Векторы положения

Центры треугольников можно записать следующим образом:

P = w A A + w B B + w C C w A + w B + w C. { displaystyle P = { frac {w_ {A} A + w_ {B} B + w_ {C} C} {w_ {A} + w_ {B} + w_ {C}}}.}

Здесь, P, A, B, C { displaystyle P, A, B, C}— векторы положения, и координаты w A, w B, w C { displaystyle w_ {A}, w_ {B}, w_ {C}}— скаляры, определение которых соответствует каждому центральному экземпляру, можно увидеть в следующей таблице, где, a, b, c { displaystyle a, b, c}— длины сторон, и S { displaystyle S}— площадь треугольника, для получения которой можно использовать формулу Герона.

	вес A { displaystyle w_ {A}}	w B { displaystyle w_ {B}}	w C { displaystyle w_ {C}}	w A + w B + w C { displaystyle w_ {A} + w_ {B} + w_ {C}}
Incenter	a { displaystyle a}	b { displaystyle b}	c { displaystyle c}	a + b + c { displaystyle a + b + c}
Excenter	— a { displaystyle -a}	b { displaystyle b}	c { displaystyle c}	b + c — a { displaystyle b + ca}
a { displaystyle a}	— b { displaystyle -b}	c { displaystyle c}	c + a — b { displaystyle c + ab}
a { displaystyle a}	b { displaystyle b}	— c { displaystyle -c}	a + b — c { displaystyle a + bc}
Центроид	1 { displaystyle 1}	1 { displaystyle 1}	1 { displaystyle 1}	3 { displaystyle 3}
Circumcenter	a 2 (b 2 + c 2 — a 2) { displaystyle a ^ {2} (b ^ {2} + c ^ {2} -a ^ {2})}	b 2 (c 2 + a 2 — b 2) { displaystyle b ^ {2} (c ^ {2} + a ^ {2} -b ^ {2})}	c 2 (a 2 + b 2 — c 2) { displaystyle c ^ {2} (a ^ {2} + b ^ {2} -c ^ {2})}	16 S 2 { displaystyl e 16S ^ {2}}
Ортоцентр	a 4 — (b 2 — c 2) 2 { displaystyle a ^ {4} — (b ^ {2} -c ^ {2}) ^ {2 }}	b 4 — (c 2 — a 2) 2 { displaystyle b ^ {4} — (c ^ {2} -a ^ {2}) ^ {2}}	c 4 — ( a 2 — b 2) 2 { displaystyle c ^ {4} — (a ^ {2} -b ^ {2}) ^ {2}}	16 S 2 { displaystyle 16S ^ {2}}

a ≡ BC ¯ = (BC →, BC →), { displaystyle a эквив { overline {BC}} = { sqrt {({ vec {BC}}, { vec {BC}}) }},}

b ≡ CA ¯ = (CA →, CA →), { displaystyle b Equiv { overline {CA}} = { sqrt {({ vec {CA}}, { vec {CA}})}},}

c ≡ AB ¯ = (AB →, AB →), { displaystyle c Equiv { overline {AB}} = { sqrt {({ vec {AB} }, { vec {AB}})}},}

16 S 2 = (a 2 + b 2 + c 2) 2 — 2 (a 4 + b 4 + c 4). { displaystyle 16S ^ {2} = (a ^ {2} + b ^ {2} + c ^ {2}) ^ {2} -2 (a ^ {4} + b ^ {4} + c ^ { 4}).}

Некоторые хорошо известные центры треугольников

Классические центры треугольников

Энциклопедия. Центров треугольников. ссылка	Имя	Стандартный символ	Трилинейные координаты	Описание
X1	Incenter	I	1: 1: 1	Пересечение биссектрисы угла. Центр вписанной окружности треугольника.
X2	Центроид	G	bc: ca: ab	Пересечение медиан. Центр масс однородной треугольной пластинки.
X3	Круговой центр	O	cos A: cos B: cos C	Пересечение серединного перпендикуляра стороны. Центр описанной окружности треугольника.
X4	Ортоцентр	H	tan A: tan B: tan C	Пересечение высот.
X5	Девятиточечный центр	N	cos (B — C): cos (C — A): cos (A — B)	Центр круга, проходящего через среднюю точку каждой стороны, основание каждой высоты и среднюю точку между ортоцентром и каждой вершиной.
X6	Точка симмедианы	K	a: b: c	Пересечение симмедиан — отражение каждой медианы относительно соответствующей биссектрисы угла.
X7	Точка Жергонна	Ge	bc / (b + c — a): ca / ​​(c + a — b): ab / (a ​​+ b — c)	Пересечение линий, соединяющих каждую вершину до точки, где вписанная окружность касается противоположной стороны.
X8	Точка Нагеля	Na	(b + c — a) / a: (c + a — b) / b: (a + b — c) / c	Пересечение линий, соединяющих каждую вершину до точки соприкосновения вневписанной окружности с противоположной стороны.
X9	Mittenpunkt	M	b + c — a: c + a — b: a + b — c	Различные эквивалентные определения.
X10	Центр Шпикера	Sp	bc (b + c): ca (c + a): ab (a + b)	Центр среднего треугольника. Центр масс равномерного треугольного каркаса.
X11	Точка Фейербаха	F	1 — cos (B — C): 1 — cos (C — A): 1 — cos (A — B)	Точка, в которой окружность с девятью точками касается касательной к вписанному кругу.
X13	Точка Ферма	X	csc (A + π / 3): csc (B + π / 3): csc (C + π / 3) *	Точка, которая представляет собой наименьшую возможную сумму расстояний из вершин.
X15. X16	Изодинамические точки	S. S ′	sin (A + π / 3): sin (B + π / 3): sin (C + π / 3). sin (A — π / 3): sin (B — π / 3): sin (C — π / 3)	Центры инверсии, которые превращают треугольник в равносторонний треугольник.
X17. X18	Очки Наполеона	N. N ′	сек (A — π / 3): сек (B — π / 3): сек (C — π / 3). сек (A + π / 3): sec (B + π / 3): sec (C + π / 3)	Пересечение линий, соединяющих каждую вершину с центром равностороннего треугольника, направленного наружу (первая точка Наполеона) или внутрь (вторая точка Наполеона), установленная на противоположной стороне.
X99	Точка Штейнера	S	bc / (b — c): ca / ​​(c — a): ab / (a ​​- b)	Различные эквивалентные определения.

(*): фактически 1-й изогонический центр, но также и точка Ферма, когда A, B, C ≤ 2π / 3

Центры недавних треугольников

В следующей таблице более поздних центров треугольников, никаких специальных обозначений для различных точек не упоминается. Также для каждого центра указывается только первая трилинейная координата f (a, b, c). Остальные координаты можно легко получить, используя свойство цикличности трилинейных координат.

Энциклопедия. центров треугольников. ссылка	Имя	Функция центра. f (a, b, c)	Год описания
X21	Точка Шиффлера	1 / (cos B + cos C)	1985
X22	точка Эксетера	a (b + c — a)	1986
X111	Точка парирования	a / (2a — b — c)	начало 1990-х
X173	Точка конгруэнтных изоселизаторов	tan (A / 2) + sec (A / 2)	1989
X174	Yff центр конгруэнтности	сек (A / 2)	1987
X175	Изопериметрическая точка	— 1 + сек (A / 2) cos (B / 2) cos (C / 2)	1985
X179	Первая точка Аджима-Мальфатти	сек (A / 4)
X181	точка Аполлония	a (b + c) / (b + c — a)	1987
X192	точка равных параллелий	bc (ca + ab — bc)	1961
X356	Центр Морли	cos (A / 3) + 2 cos (B / 3) cos (C / 3)
X360	Нулевая точка Хофштадтера	A / a	1992

Общие классы треугольных центров

Кимберлинг-центр

В честь Кларка Кимберлинга, создавшего онлайн-энциклопедию более чем 32 000 центров треугольников, центры треугольников, перечисленные в энциклопедии, вместе называются центрами Кимберлинга.

Центр полиномиального треугольника

Центр треугольника P называется центром полиномиального треугольника, если трилинейные координаты P могут быть выражается в виде многочленов от a, b и c.

Центр правильного треугольника

Центр треугольника P называется точкой правильного треугольника, если трилинейные координаты P могут быть выражены как полиномы от Δ, a, b и c, где Δ — площадь треугольника.

Центр большого треугольника

Центр треугольника P называется центром большого треугольника, если трилинейные координаты P могут быть выражены в форме f (A): f (B): f (C) где f (A) является функцией только угла A и не зависит от других углов или длин сторон.

Центр трансцендентного треугольника

Центр треугольника P равен называется трансцендентным треугольным центром, если P не имеет трилинейного представления с использованием только алгебраических функций от a, b и c.

Разное

Равнобедренные и равносторонние треугольники

Пусть f — функция центра треугольника. Если две стороны треугольника равны (скажем, a = b), то

f (a, b, c) = f (b, a, c) { displaystyle f (a, b, c) = f (b, a, c)}(поскольку a = b)

= f (b, c, a) { displaystyle quad quad quad quad = f (b, c, a) }(по бисимметрии)

, поэтому два компонента центра соответствующего треугольника всегда равны. Следовательно, центры всех треугольников равнобедренного треугольника должны лежать на его линии симметрии. В равностороннем треугольнике все три компонента равны, поэтому все центры совпадают с центроидом. Итак, как и у круга, равносторонний треугольник имеет уникальный центр.

Excenters

Пусть

f (a, b, c) = {- 1, если a ≥ b и a ≥ c, 1 в противном случае. { displaystyle f (a, b, c) = { begin {case} -1 quad { text {if}} a geq b { text {and}} a geq c, \; ; ; 1 quad { text {else}}. End {ases}}}

Легко видеть, что это функция центра треугольника, и (при условии, что треугольник разносторонний) соответствующий центр треугольника является центром противоположного до наибольшего угла при вершине. Два других специалиста могут быть выбраны аналогичными функциями. Однако, как указано выше, только одна из сторон равнобедренного треугольника и ни одна из сторон равностороннего треугольника никогда не может быть центром треугольника.

Биантисимметричные функции

Функция f биантисимметрична, если f (a, b, c) = −f (a, c, b) для всех a, b, c. Если такая функция также не равна нулю и однородна, легко видеть, что отображение (a, b, c) → f (a, b, c) f (b, c, a) f (c, a, b) функция центра треугольника. Соответствующим центром треугольника является f (a, b, c): f (b, c, a): f (c, a, b). По этой причине определение функции центра треугольника иногда включает ненулевые однородные биантисимметричные функции.

Новые центры из старого

Любую функцию треугольного центра f можно нормализовать, умножив ее на симметричную функцию от a, b, c, так что n = 0. A нормализованная функция центра треугольника имеет тот же центр треугольника, что и исходная, а также более сильное свойство: f (ta, tb, tc) = f (a, b, c) для всех t>0 и всех (a, b, c). Вместе с нулевой функцией нормализованные функции центра треугольника образуют алгебру при сложении, вычитании и умножении. Это дает простой способ создавать новые центры треугольников. Однако различные нормализованные функции центра треугольника часто определяют один и тот же центр треугольника, например f и (abc) (a + b + c) f.

Неинтересные центры

Предположим, что a, b, c — действительные переменные, и пусть α, β, γ — любые три действительные константы. Пусть

f (a, b, c) = {α, если a < b and a < c (equivalently the first variable is the smallest), γ if a>b и a>c (эквивалентно первая переменная самая большая), β в противном случае (эквивалентно первая переменная находится посередине). { displaystyle f (a, b, c) = { begin {case} alpha quad { text {if}} a b { text {and}} a>c quad { text {(эквивалентно первая переменная самая большая)}}, \ beta quad ; { text {else}} quad ; quad quad , quad { text {(эквивалентно первая переменная находится посередине)}}. end {ases}}}

Тогда f равно a функция центра треугольника, а α: β: γ — соответствующий центр треугольника, если стороны контрольного треугольника помечены так, что < b < c. Thus every point is potentially a triangle center. However the vast majority of triangle centers are of little interest, just as most continuous functions are of little interest. The Энциклопедия центров треугольников представляет собой постоянно расширяющийся список интересных.

Барицентрические координаты

Если f — функция центра треугольника, то также af и соответствующий центр треугольника af (a, b, c): bf (b, c, a): cf (c, a, b). Поскольку это в точности барицентрические координаты центра треугольника, соответствующего f, следует, что центры треугольников с таким же успехом можно было бы определить в терминах барицентрических, а не трилинейных. На практике переключиться с одной системы координат на другую несложно.

Двоичные системы

Помимо точки Ферма и 1-го изогонического центра, существуют и другие пары центров. Другая система образована X 3 и центром тангенциального треугольника. Рассмотрим функцию центра треугольника, задаваемую формулой

f (a, b, c) = {cos ⁡ (A), если треугольник острый, cos ⁡ (A) + sec ⁡ (B) sec ⁡ (C), если угол при вершине в A тупой, cos ⁡ (A) — sec ⁡ (A), если любой из углов в B или C тупой. { Displaystyle е (a, b, c) = { begin {case} соз (A) quad ; quad ; quad ; quad ; quad ; quad ; , , { text {если треугольник острый}}, \ cos (A) + sec (B) sec (C) quad { text {если угол при вершине в}} A { text {равен obtuse}}, \ cos (A) — sec (A) quad ; quad ; quad ; , { text {если любой из углов в}} B { text {или} } C { text {тупой}}. End {ases}}}

Для соответствующего центра треугольника есть четыре различных возможности:

• cos (A): cos (B): cos (C), если справочный треугольник острый (это также центр описанной окружности).
• [cos (A) + sec (B) sec (C)]: [cos (B) — sec (B)]: [cos ( C) — sec (C)], если угол в A тупой.
• [cos (A) — sec (A)]: [cos (B) + sec (C) sec (A)]: [cos (C) — sec (C)], если угол в B тупой.
• [cos (A) — sec (A)]: [cos (B) — sec (B)]: [ cos (C) + sec (A) sec (B)], если угол в точке C тупой.

Обычный расчет показывает, что в каждом случае эти трилинейные линии представляют центр тангенциального треугольника. Таким образом, эта точка является центром треугольника, который является близким спутником центра описанной окружности.

Бисимметрия и инвариантность

Отражение треугольника меняет порядок его сторон на обратный. На изображении координаты относятся к треугольнику (c, b, a) и (используя «|» в качестве разделителя) отражение произвольной точки α: β: γ есть γ | β | α. Если f — функция центра треугольника, отражение его центра треугольника равно f (c, a, b) | f (b, c, a) | f (a, b, c), которая по бисимметрии совпадает с f (c, b, a) | f (b, a, c) | е (а, в, б). Поскольку это также центр треугольника, соответствующий f относительно треугольника (c, b, a), бисимметрия гарантирует, что все центры треугольника инвариантны относительно отражения. Поскольку повороты и сдвиги можно рассматривать как двойные отражения, они также должны сохранять центры треугольников. Эти свойства инвариантности служат обоснованием для определения.

Альтернативная терминология

Некоторые другие названия для расширения: равномерное масштабирование, изотропное масштабирование, гомотетия и гомотезия.

Центры гиперболических треугольников

Изучение центров треугольников традиционно связано с евклидовой геометрией, но центры треугольников также можно изучать в гиперболической геометрии. Используя гиротригонометрию, можно вычислить выражения для тригонометрических барицентрических координат, которые имеют одинаковую форму как для евклидовой, так и для гиперболической геометрии. Чтобы выражения совпадали, выражения не должны включать в себя спецификацию суммы углов, равной 180 градусов.

Центры тетраэдров и центры n-симплексов

Обобщение центров треугольников на более высокие измерения — центры тетраэдров или многомерных симплексов.

См. также

Примечания

1. ^Кимберлинг, Кларк. «Центры треугольников». Проверено 23 мая 2009. В отличие от квадратов и кругов, треугольники имеют множество центров. Древние греки нашли четыре: центр тяжести, центр тяжести, центр окружности и ортоцентр. Пятый центр, обнаруженный намного позже, — это точка Ферма. После этого в литературу были добавлены точки, которые теперь называются центром девяти точек, точкой симедианы, точкой Жергонна и точкой Фейербаха. В 1980-х годах было замечено, что эти особые точки обладают некоторыми общими свойствами, которые теперь составляют основу формального определения центра треугольника
2. ^Kimberling, Clark (11 апреля 2018 г.) [1994]. «Центральные точки и центральные линии на плоскости треугольника». Математический журнал. 67 (3): 163–187. doi : 10.2307 / 2690608. JSTOR 2690608.
3. ^Кимберлинг, Кларк. «Это ЧАСТЬ 20: Центры X (38001) — X (40000)». Энциклопедия треугольных центров.
4. ^Вайсштейн, Эрик В.. «Центр треугольника». MathWorld — Интернет-ресурс Wolfram. Проверено 25 мая 2009 г.
5. ^Вайсштейн, Эрик У. «Функция центра треугольника». MathWorld — Интернет-ресурс Wolfram. Проверено 1 июля 2009 г.
6. ^Бицентрические пары точек, Энциклопедия центров треугольников, дата обращения 2012-05-02
7. ^Вайсштейн, Эрик У. «Kimberling Center». MathWorld — Интернет-ресурс Wolfram. Проверено 25 мая 2009 г.
8. ^Вайсштейн, Эрик У. «Центр Большого Треугольника». MathWorld — Интернет-ресурс Wolfram. Проверено 25 мая 2009 г.
9. ^Гиперболические барицентрические координаты, Абрахам А. Унгар, Австралийский журнал математического анализа и приложений, AJMAA, том 6, выпуск 1, статья 18, стр. 1-35, 2009
10. ^Центры гиперболических треугольников: специальный релятивистский подход, Abraham Ungar, Springer, 2010
11. ^ Барицентрическое исчисление в евклидовой и гиперболической геометрии: сравнительное введение, Abraham Ungar, World Scientific, 2010

Внешние ссылки