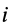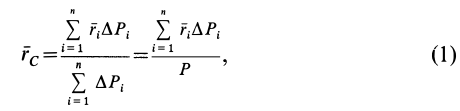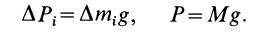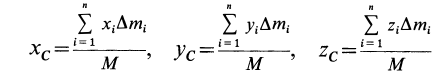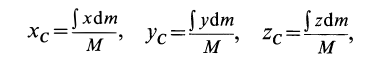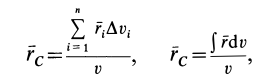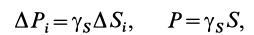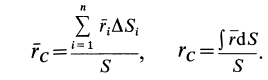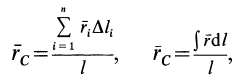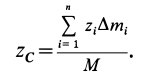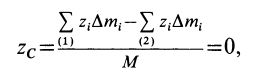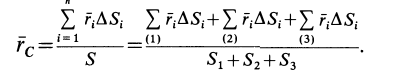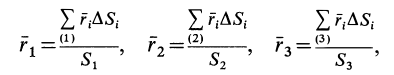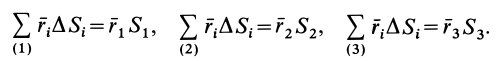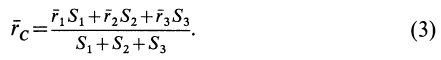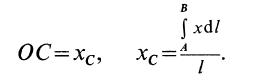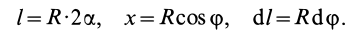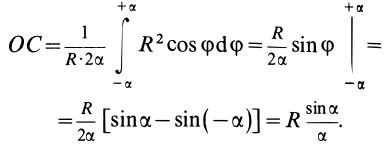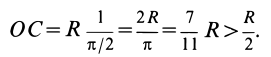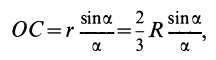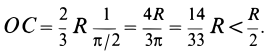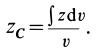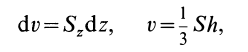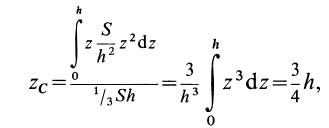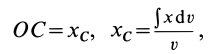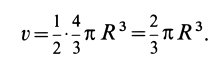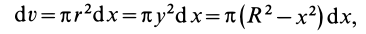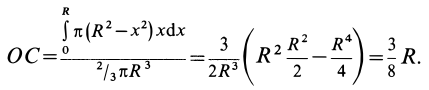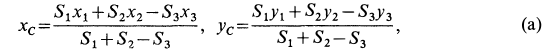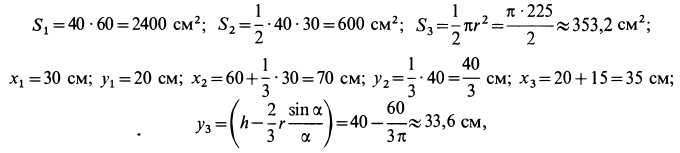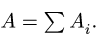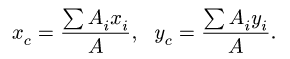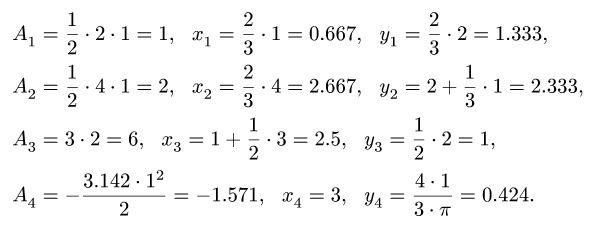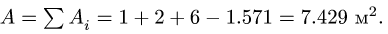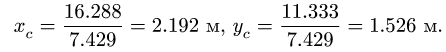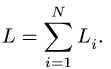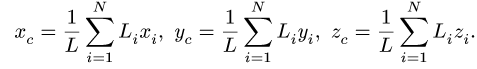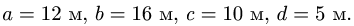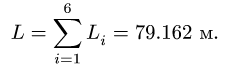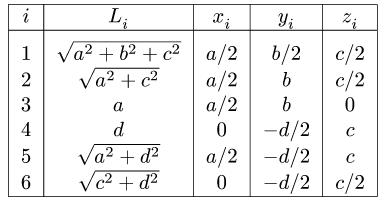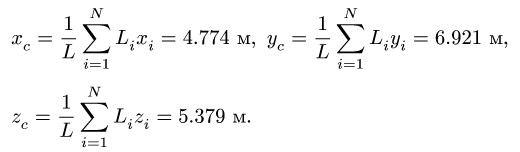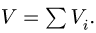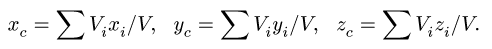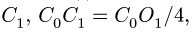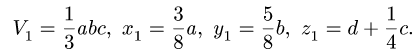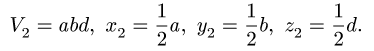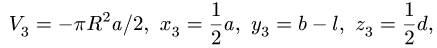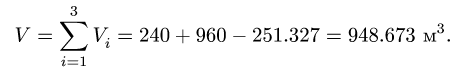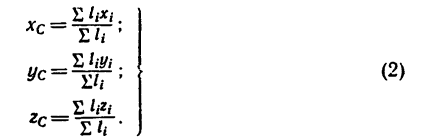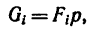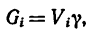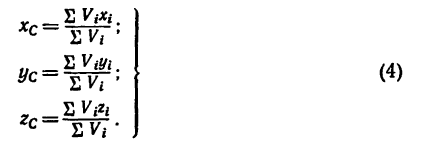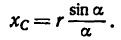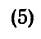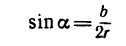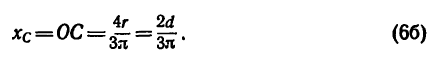Содержание:
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
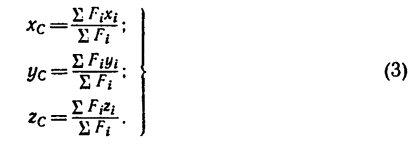
Определения и формулы для вычисления центров тяжести
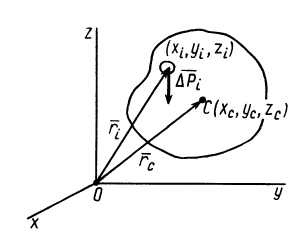
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом
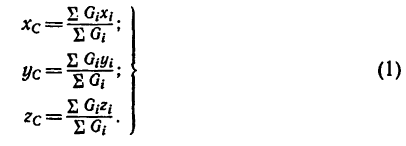
Радиус-вектор центра тяжести тела 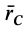
где 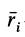

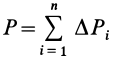

Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей 

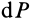
где 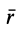
где 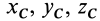
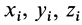
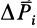
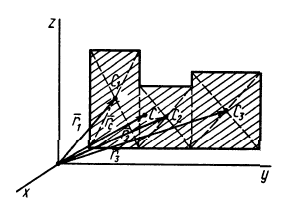
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 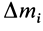
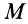

Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на 
и соответственно
По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
и
где 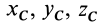
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
где 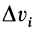


где 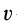


по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
где 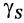
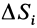
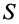
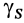
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
где 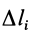
Методы определения центров тяжести (Центров масс)
Метод симметрии
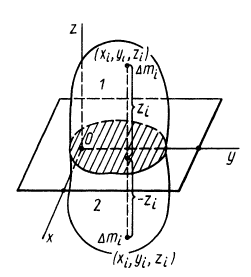
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 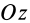
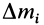
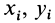
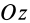
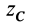
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 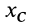
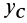
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
Рис. 89
Метод разбиения на части (метод группировки)
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 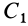
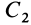
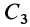
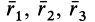
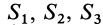
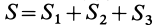
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
или
Используя эти формулы для радиуса-вектора всей фигуры, имеем
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
Рис. 90
Метод отрицательных масс
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 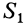
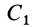
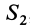
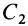
В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
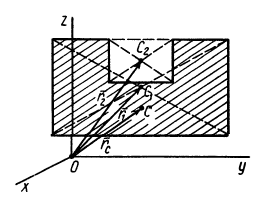
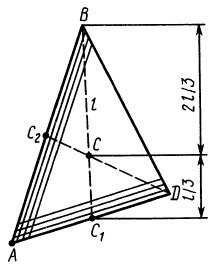
Площадь треугольника
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 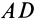

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне 
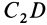

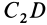
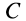

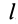
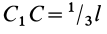
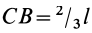
Рис. 92
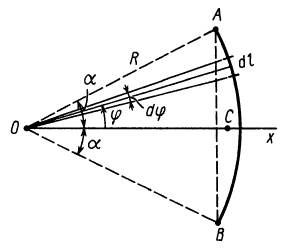
Дуга окружности
Дуга окружности 
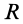
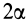
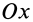

Рис. 93
В рассматриваемом случае
Подставляя эти значения в формулу для 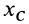
Таким образом,
Для полуокружности 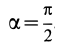
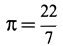
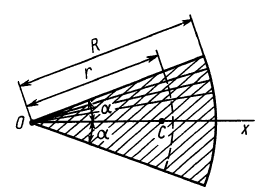
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 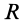
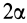
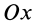
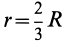
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
или
Для площади полукруга 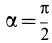
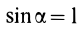
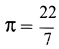
Объем пирамиды и конуса
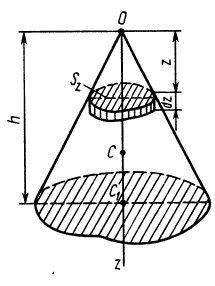
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 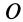
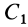
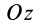
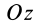
Разобьем конус плоскостями, перпендикулярными оси 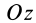
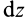
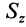
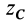
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 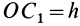
Учитывая, что
имеем
или
Таким образом, центр тяжести прямого конуса находится на расстоянии 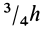
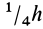
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 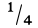
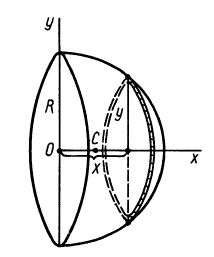
Объем полушара
Полушар имеет ось симметрии, которую примем за координатную ось 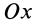
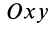
где 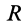
где 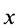
Объем элементарного диска
так как радиус диска 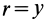
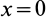
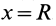
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии
Это расстояние меньше половины радиуса полушара.
Рис. 96
Задача №1
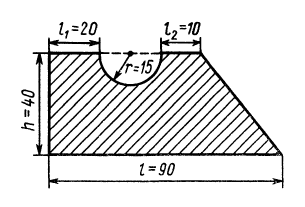
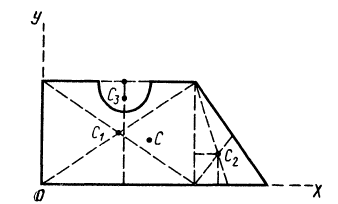
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
Рис.97
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
где 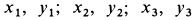
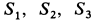
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
так как 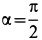
Подставляя полученные значения в (а), получим:
Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 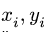
3. Находим общую площадь фигуры по формуле
4. Определяем координаты центра тяжести фигуры:
Задача №2
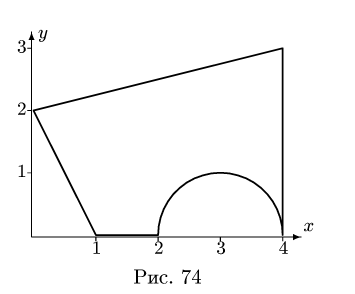
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
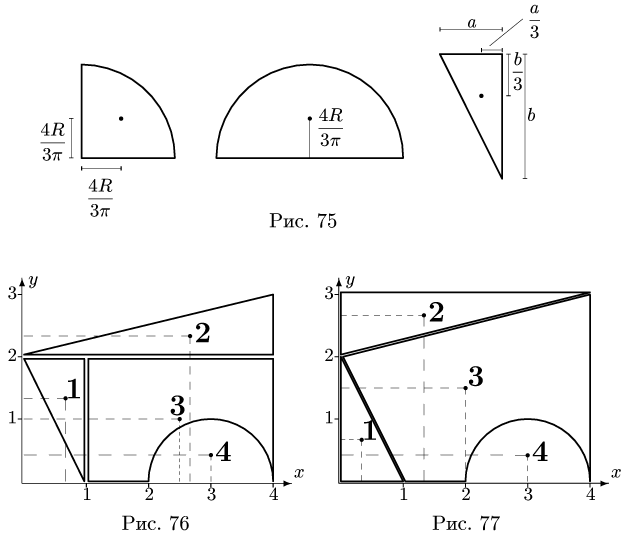
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 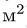
Площадь выреза берем со знаком минус.
3.Площадь фигуры
4. Находим координаты центра тяжести всей фигуры:
Вычисления удобно свести в таблицу:
Сначала заполняем столбцы 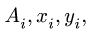
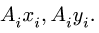
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 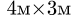
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 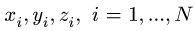
3. Находим суммарную длину стержней системы
4. Определяем координаты центра тяжести тела по формулам
Задача №3
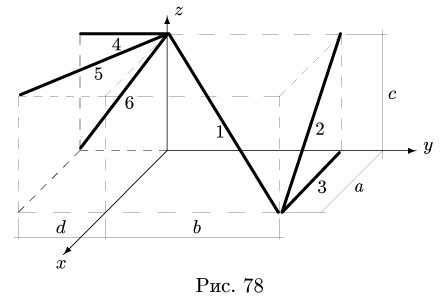
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры:
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 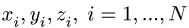
3. Находим суммарную длину стержней системы:
Промежуточные результаты удобно занести в таблицу:
4. Определяем координаты центра тяжести тела по формулам
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 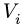
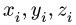
3. Находим общий объем тела по формуле
4. Определяем координаты центра тяжести тела:
Задача №4
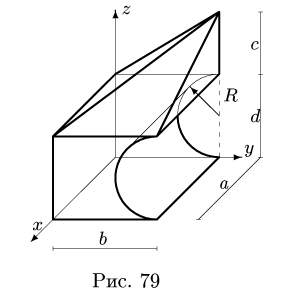
Найти координаты центра тяжести однородного объемного тела (рис.79);
Решение
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 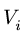
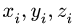
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
Объем половины цилиндра 3 берем со знаком минус:
где 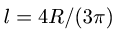
3. Находим общий объем тела:
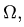
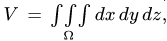
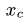
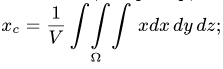
4. Определяем координаты центра тяжести тела:
Центр тяжести
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
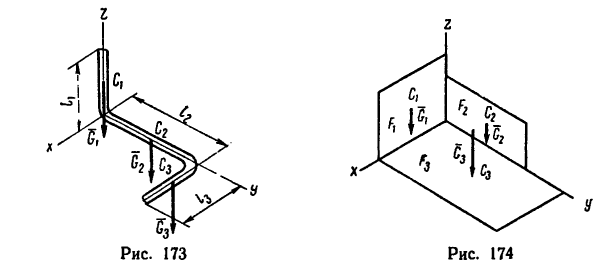
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 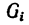
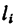
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 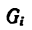
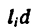
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
то вес каждой плоскости (поверхности) можно представить так:
где 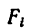
После подстановки этого значения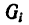
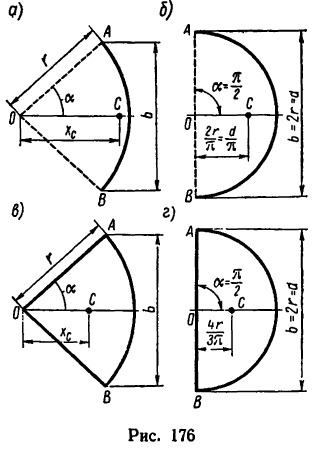
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
где 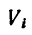
После подстановки значений 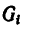
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
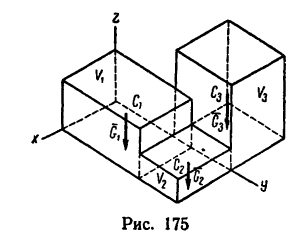
Если же задана хорда 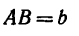
и тогда
В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы
Если же задана хорда сектора, то
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
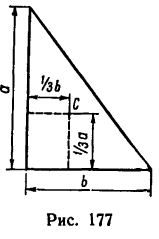
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил
Тема: Стержень цилиндрической формы (Прочитано 6070 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Стержень цилиндрической формы длиной l = 40 см состоит наполовину своей длины из свинца и на половину из меди. Найти центр тяжести стержня. Плотность свинца ρС = 11,3 г/см3, плотность меди – ρМ = 8,9 г/см3.
« Последнее редактирование: 24 Февраля 2015, 21:29 от Сергей »
Записан
Решение.
Покажем рисунок. Запишем условие равновесия рычага.
[ begin{align}
& {{M}_{1}}+{{M}_{2}}=0, {{F}_{C}}cdot {{l}_{1}}={{F}_{M}}cdot {{l}_{2}} (1), \
& {{F}_{C}}={{m}_{C}}cdot g={{rho }_{C}}cdot Scdot frac{1}{2}cdot lcdot g (2),{{F}_{M}}={{m}_{M}}cdot g={{rho }_{M}}cdot Scdot frac{1}{2}cdot lcdot g (3), \
& {{l}_{1}}=frac{1}{2}cdot l-x (4), {{l}_{2}}=frac{1}{2}cdot l+x (5), \
& {{rho }_{C}}cdot Scdot frac{1}{2}cdot lcdot gcdot (frac{1}{2}cdot l-x)={{rho }_{M}}cdot Scdot frac{1}{2}cdot l cdot gcdot (frac{1}{2}cdot l+x), \
end{align} ]
[ {{rho }_{C}}cdot (frac{1}{2}cdot l-x)={{rho }_{M}}cdot (frac{1}{2}cdot l+x), x=frac{lcdot ({{rho }_{C}}-{{rho }_{M}})}{2cdot ({{rho }_{C}}+{{rho }_{M}})}. ]
х = 0,0238 м, х = 2,38 см.
Центр тяжести стержня находится на расстоянии 37,62 см от левого конца стержня.
« Последнее редактирование: 11 Марта 2015, 15:50 от alsak »
Записан
Центр — тяжесть — стержень
Cтраница 1
Центр тяжести стержня лежит на его оси, так как это ось его симметрии.
[1]
Центр тяжести стержня расположен на расстоянии 52 см от левой опоры.
[2]
Центр тяжести стержня лежит на его оси, так как это ось его симметрии.
[3]
Центр тяжести стержня расположен на расстоянии 52 см от левой опоры.
[4]
Центр тяжести однородного криволинейного стержня называют центром тяжести линии.
[5]
Так как центр тяжести стержня С лежит на одной вертикали с центром цилиндра О, то линия действия силы тяжести проходит через точку О. На стержень наложены две связи: гладкая поверхность полуцилиндра и шероховатый пол. Применим закон освобождаемости от связей. Отбросим мысленно связи ( рис. б) и заменим их действие реакциями. Реакция гладкой стенки полуцилиндра направлена нормально к его поверхности, т.е. по радиусу А О. Но стержень находится в равновесии под действием трех сил: Т, Р и реакции пола в точке В. Согласно теореме о трех непараллельных силах пиния действия реакции пола R должна также пересекать точку О.
[6]
В положении равновесия центр тяжести стержня С находится на вертикальном диаметре полуцилиндра.
[7]
В положении равновесия системы центр тяжести стержня С находится на середине расстояния 0 02, а пружина не деформирована.
[8]
В начальный момент материальная точка находится в центре тяжести стержня.
[9]
На стержень действует сила тяжести mg, приложенная в центре тяжести стержня — точкз С. Разложим силу тяжести на две параллельные составляющие. Точки приложения этих составляющих находятся в точках В и О.
[10]
В первом случае определено перемещение той точки, в которой находился центр тяжести стержня до деформации. Во втором случае определено расстояние от точки нового положения центра тяжести до точки старого положения, а это не одно и то же.
[11]
Активная сила здесь одна — вес стержня Р, приложенный в центре тяжести стержня С.
[12]
Смысл этого условия очевиден: если длина стержня 2L превышает удвоенный диаметр чашки, то центр тяжести стержня выходит за край чашки и стержень вываливается из нее. Если L 2R, стержень расположен горизонтально ( а 0) и опирается на чашку в одной точке С.
[13]
Смысл этого условия очевиден: если длина стержня 2L превышает удвоенный диаметр чашки, то центр тяжести стержня выходит-за край чашки и стержень вываливается из нее. Если L — 2R, стержень расположен горизонтально ( а — 0) и опирается на чашку в одной точке С.
[14]
Масса стержня CD равна т, его момент инерции относительно оси вращения равен /, а расстояние от центра тяжести стержня до этой оси равно а.
[15]
Страницы:
1
2
3

Глава 5
ЦЕНТР ТЯЖЕСТИ
5.1 Центр тяжести плоской фигуры
ПОСТАНОВКА ЗАДАЧИ. Найти площадь и координаты центра тяжести плоской фигуры.
План решения
1.Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2.Выбираем систему координат. Вычисляем площади и координаты
xi, yi центров тяжести отдельных частей. Площади вырезанных частей берем со знаком минус.
3.Находим общую площадь фигуры по формуле A = P Ai.
4.Определяем координаты центра тяжести фигуры:
|
xc = |
P Ai i |
, yc = |
|
A x |
||
|
123 |
|
124 |
Глава 5. Центр тяжести |
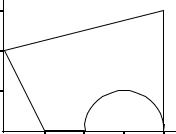
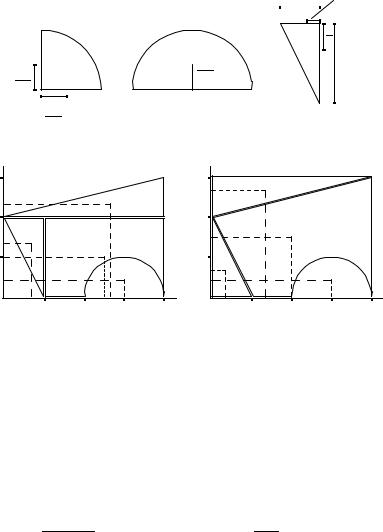
ПРИМЕР. Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ox (рис. 74). Размеры на рисунке даны в метрах.
|
y |
|||
|
3 6 |
|||
|
2 |
|||
|
1 |
|||
|
— x |
|||
|
1 |
2 |
3 |
4 |
|
Рис. 74 |
|
5.1. Центр тяжести плоской фигуры |
125 |
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в
|
задачах, изображено на рис. 75. |
a |
||
|
a |
|||
|
3 |
|||
|
q |
b |
|||||||||
|
q |
q |
3 |
||||||||
|
4R |
3π |
b |
||||||||
|
4R |
||||||||||
|
3π |
||||||||||
|
4R |
||||||||||
|
3π |
Рис. 75 |
|||||||||
|
y |
y |
q2 |
||||||||
|
3 6 |
q2 |
3 6 |
||||||||
|
2 |
q |
q |
2 |
1 |
||||||
|
3 |
||||||||||
|
1 |
1 |
3 |
q4 |
1 |
q |
q |
q4 |
|||
|
— x |
— x |
|||||||||
|
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
|||
|
Рис. 76 |
Рис. 77 |
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в м2) и координаты центра тяжести (в м)
|
каждого элемента: |
|||||||||||||||||||||
|
A1 |
= |
1 |
· 2 · 1 = 1, |
x1 = |
2 |
· 1 = 0.667, |
y1 = |
2 |
· 2 = 1.333, |
||||||||||||
|
2 |
3 |
3 |
|||||||||||||||||||
|
A2 |
= |
1 |
· 4 · 1 = 2, |
x2 = |
2 |
· 4 = 2.667, |
y2 = 2 + |
1 |
· 1 = 2.333, |
||||||||||||
|
2 |
3 |
3 |
|||||||||||||||||||
|
A3 = 3 · 2 = 6, x3 = 1 + |
1 |
· 3 = 2.5, y3 = |
1 |
· 2 = 1, |
|||||||||||||||||
|
2 |
2 |
||||||||||||||||||||
|
A |
= |
− |
3.142 · 12 |
= |
− |
1.571, x = 3, |
y |
4 |
= |
4 · 1 |
= 0.424. |
||||||||||
|
4 |
2 |
4 |
3 |
· |
π |
||||||||||||||||
Площадь выреза берем со знаком минус.
|
126 |
Глава 5. Центр тяжести |
3.Площадь фигуры A = P Ai = 1 + 2 + 6 − 1.571 = 7.429 м2.
4.Находим координаты центра тяжести всей фигуры:
|
xc = |
P Ai |
i |
= |
0.667 |
· |
1 + 2.667 |
7· .429 |
· |
6 |
− |
3 |
· |
1.571 |
= 2.192 м, |
||||||||||||||
|
A x |
2 + 2.5 |
|||||||||||||||||||||||||||
|
yc = |
P Ai |
i |
= |
1.333 |
· |
1 + 2.333 |
· |
7.429 |
· |
6 |
− |
0.424 |
· |
1.571 |
= 1.526 м. |
|||||||||||||
|
A y |
2 + 1 |
|||||||||||||||||||||||||||
|
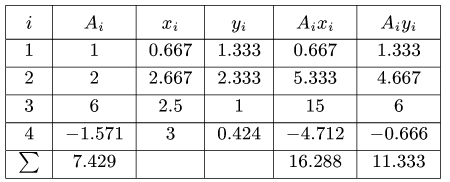
Вычисления удобно свести в таблицу: |
||||||||||||||||||||||||||||
|
i |
Ai |
xi |
yi |
Aixi |
Aiyi |
|||||||||||||||||||||||
|
1 |
1 |
0.667 |
1.333 |
0.667 |
1.333 |
|||||||||||||||||||||||
|
2 |
2 |
2.667 |
2.333 |
5.333 |
4.667 |
|||||||||||||||||||||||
|
3 |
6 |
2.5 |
1 |
15 |
6 |
|||||||||||||||||||||||
|
4 |
−1.571 |
3 |
0.424 |
−4.712 |
−0.666 |
|||||||||||||||||||||||
|
P |
7.429 |
16.288 |
11.333 |
Сначала заполняем столбцы Ai, xi, yi, затем вычисляем статические моменты Aixi, Aiyi. Внизу записываем суммы столбцов, необходимые для вычисления координат центра тяжести. Таким образом
|
xc = |
16.288 |
= 2.192 м, yc = |
11.333 |
= 1.526 м. |
|
7.429 |
7.429 |
|||
ЗАМЕЧАНИЕ 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 4м×3м и вырезанных из него полукруга 4 и двух треугольников 1 и 2 (рис. 77).
ЗАМЕЧАНИЕ 2. Решение задачи в системе Maple V методом контурного интегрирования приведено в § 6.2, c. 145.
Условия задач. Найти площадь (в м2) и координаты центра тяжести плоской фигуры (в м). Отметки на осях даны в метрах. Криволинейный участок контура является дугой половины или четверти окружности.

|
5.1. |
Центр тяжести плоской фигуры |
127 |
||||||||
|
1 |
y |
2 |
y |
|||||||
|
7 |
6 |
7 6 |
||||||||
|
6 |
‘ |
6 |
||||||||
|
4 |
4 |
& |
||||||||
|
2 |
2 |
|||||||||
|
1 |
—x |
1 |
—x |
|||||||
|
2 |
4 |
6 |
8 |
11 |
2 |
5 |
7 |
10 |
|
3 |
y |
|||||
|
5 |
6 |
|||||
|
4 |
||||||
|
3 |
||||||
|
2 |
||||||
|
1 |
x |
|||||
|
— |
||||||
|
1 |
3 |
4 |
6 |
9 |
||
|
5 |
y |
|||||
|
6 |
6 |
|||||
|
5 |
‘ |
|||||
|
4 |
& |
|||||
|
2 |
||||||
|
1 |
—x |
|||||
|
2 |
4 |
6 |
8 |
11 |
||
|
7 |
y |
|||||
|
5 |
6 |
|||||
|
4 |
||||||
|
3 |
%4 6 |
|||||
|
1 |
7 |
—x |
||||
|
9 |
y |
|||||
|
6 |
6 |
|||||
|
5 |
||||||
|
4 |
||||||
|
2 |
||||||
|
1 |
—x |
|||||
|
3 |
5 |
7 |
|
4 |
y |
|||||||
|
5 |
6 |
|||||||
|
34 |
||||||||
|
1 |
1 |
3 |
4 |
6 |
9 |
—x |
||
|
6 |
y |
$ |
||||||
|
6 |
6 |
|||||||
|
5 |
||||||||
|
4 |
||||||||
|
2 |
||||||||
|
1 |
x |
|||||||
|
— |
||||||||
|
3 |
5 |
|||||||
|
8 |
y |
|||||||
|
5 |
6 |
|||||||
|
4 |
||||||||
|
3 |
||||||||
|
1 |
x |
|||||||
|
— |
||||||||
|
2 |
3 |
5 |
7 |
|||||
|
10 |
y |
$ |
||||||
|
6 |
6 |
|||||||
|
5 |
||||||||
|
4 |
% |
|||||||
|
2 |
||||||||
|
1 |
—x |
|||||||
|
3 |
5 |
8 |
|
128 |
Глава 5. Центр тяжести |
ЗАМЕЧАНИЕ 3. Во всех вариантах фигуру можно разбить на пять частей.
Ответы
|
A |
xc |
yc |
A |
xc |
yc |
||
|
1 |
40.642 |
5.203 |
3.627 |
6 |
17.858 |
2.380 |
2.964 |
|
2 |
35.642 |
4.764 |
3.495 |
7 |
27.358 |
3.582 |
2.653 |
|
3 |
27.071 |
3.887 |
2.492 |
8 |
19.429 |
2.668 |
2.945 |
|
4 |
26.071 |
3.755 |
2.441 |
9 |
23.929 |
2.668 |
3.585 |
|
5 |
39.783 |
4.702 |
3.351 |
10 |
22.217 |
3.593 |
2.950 |
5.2 Пространственная стержневая система
ПОСТАНОВКА ЗАДАЧИ. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения
1.Разбиваем фигуру на отдельные стержни.
2.Выбираем систему координат. Вычисляем длины и координаты
xi, yi, zi, i = 1, …, N центров тяжести отдельных стержней. Координаты центра прямолинейного однородного стержня вычисляем как полусумму координат его концов.
N
X
3. Находим суммарную длину стержней системы L = Li.
i=1
4. Определяем координаты центра тяжести тела по формулам
|
1 |
N |
1 |
N |
1 |
N |
||||
|
X |
X |
X |
|||||||
|
xc = |
Lixi, yc = |
Liyi, zc = |
Lizi. |
||||||
|
L |
i=1 |
L |
i=1 |
L |
|||||
|
i=1 |
ПРИМЕР. Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры: a = 12 м, b = 16 м, c = 10 м, d = 5 м.
Решение
1.Разбиваем фигуру на шесть стержней.
2.Выбираем систему координат (рис. 78). Вычисляем длины и координаты xi, yi, zi, i = 1, …, N центров тяжести отдельных стержней.

|
5.2. Пространственная стержневая система |
129 |
|
z |
||||
|
6 |
||||
|
4 |
||||
|
5 |
||||
|
6 |
c |
|||
|
1 |
2 |
— y |
||
|
3 |
a |
|||
|
d |
b |
|||
|
x |
Рис. 78 3. Находим суммарную длину стержней системы:
6
X
L = Li = 79.162 м.
i=1
Промежуточные результаты удобно занести в таблицу:
|
i |
Li |
xi |
yi |
zi |
|||||||||||||
|
√ |
|||||||||||||||||
|
1 |
a |
2 |
+ b |
2 |
+ c |
2 |
a/2 |
b/2 |
c/2 |
||||||||
|
√ |
|||||||||||||||||
|
2 |
a |
2 |
+ c |
2 |
a/2 |
b |
c/2 |
||||||||||
|
3 |
a |
a/2 |
b |
0 |
|||||||||||||
|
4 |
√ |
d |
0 |
−d/2 |
c |
||||||||||||
|
5 |
a |
2 |
2 |
a/2 |
−d/2 |
c |
|||||||||||
|
+ d |
|||||||||||||||||
|
√ |
|||||||||||||||||
|
6 |
c |
2 |
+ d |
2 |
0 |
−d/2 |
c/2 |
||||||||||
4. Определяем координаты центра тяжести тела по формулам
|
xc = |
1 |
N |
Lixi = 4.774 м, yc = 1 |
N |
|
|
X |
Liyi = 6.921 м, |
||||
|
X |
|||||
|
L |
i=1 |
L |
i=1 |
||
N
1 X
zc = L i=1 Lizi = 5.379 м.
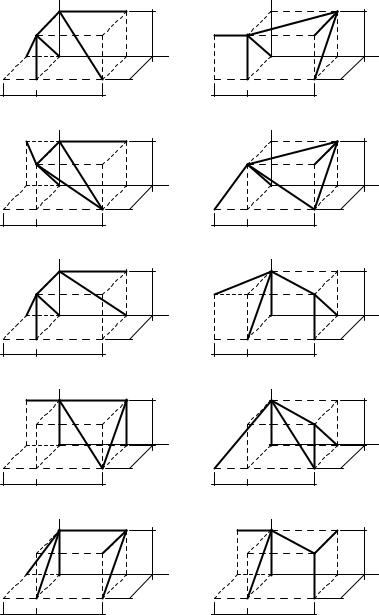
УСЛОВИЯ ЗАДАЧ. Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (в метрах). Размеры даны в метрах.
130
|
1. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 3, b = 4, c = 3, d = 2. |
|
3. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 6, b = 5, c = 4, d = 3. |
|
5. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 3, b = 4, c = 3, d = 2. |
|
7. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 6, b = 5, c = 4, d = 2. |
|||
|
9. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 3, b = 4, c = 3, d = 1. |
|
Глава 5. |
Центр тяжести |
||
|
2. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
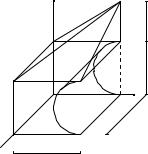
a = 5, b = 4, c = 3, d = 2. |
|||
|
4. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 4, b = 6, c = 5, d = 4. |
|||
|
6. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 5, b = 4, c = 3, d = 1. |
|||
|
8. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 4, b = 6, c = 5, d = 3. |
|
10. |
z |
||
|
6 |
|||
|
c |
|||
|
y |
|||
|
— |
|||
|
a |
|||
|
d |
x |
b |
|
|
a = 6, b = 5, c = 4, d = 2. |
|
5.3. Центр тяжести объемного тела |
131 |
||||||||||
|
Ответы |
|||||||||||
|
L |
xc |
yc |
zc |
L |
xc |
yc |
zc |
||||
|
1 |
24.764 |
1.439 |
0.605 |
1.924 |
6 |
29.164 |
2.500 |
1.563 |
2.092 |
||
|
2 |
28.065 |
2.945 |
1.929 |
2.216 |
7 |
30.986 |
1.548 |
2.856 |
2.452 |
||
|
3 |
40.097 |
3.105 |
1.007 |
2.883 |
8 |
39.460 |
2.000 |
2.680 |
2.957 |
||
|
4 |
38.231 |
2.744 |
2.476 |
3.233 |
9 |
21.648 |
0.796 |
1.635 |
1.985 |
||
|
5 |
23.933 |
1.124 |
0.556 |
1.939 |
10 |
31.021 |
2.807 |
2.177 |
3.019 |
||
В таблице ответов L — суммарные длины стержней (в м).
5.3 Центр тяжести объемного тела
ПОСТАНОВКА ЗАДАЧИ. Найти координаты центра тяжести однородного объемного тела.
План решения
1.Разбиваем тело на простые части, положение центров тяжести которых известно.
2.Выбираем систему координат. Вычисляем объемы Vi и координаты xi , yi, zi центров тяжести отдельных частей. Объемы вырезанных частей берем со знаком минус.
3.Находим общий объем тела по формуле V = P Vi.
4.Определяем координаты центра тяжести тела:
X X X
xc = Vixi/V, yc = Viyi/V, zc = Vizi/V.
ПРИМЕР. Найти координаты центра тяжести однородного объемного тела (рис. 79); a = 10 м, b = 12 м, c = 6 м, d = 8 м, R = d/2.
|
z |
||
|
6 |
||
|
c |
||
|
@I |
R |
|
|
@ |
d |
|
|
— y |
||
|
a |
||
|
x |
||
|
b |
||
|
Рис. 79 |

|
132 |
Глава 5. Центр тяжести |
Решение
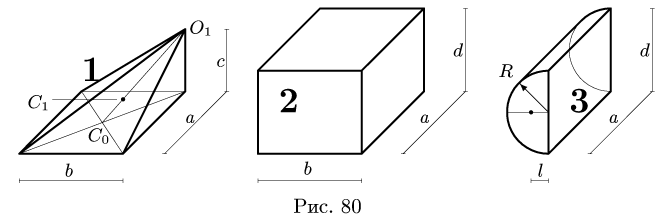
1.Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2.Выбираем систему координат. Вычисляем объемы Vi и координаты xi, yi, zi центров тяжестей отдельных частей. Центр тяжести
пирамиды 1 лежит в точке C1, C0C1 = C0O1/4,
|
V1 = |
1 |
abc, x1 |
= |
3 |
a, y1 |
= |
5 |
b, z1 |
= d + |
1 |
c. |
|
3 |
8 |
8 |
4 |
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
|
V2 = abd, x2 = |
1 |
a, y2 |
= |
1 |
b, z2 |
= |
1 |
d. |
|
2 |
2 |
2 |
Объем половины цилиндра 3 берем со знаком минус:
V3 = −πR2a/2, x3 = 12 a, y3 = b − l, z3 = 12 d,
где l = 4R/(3π) — расстояние по оси y от оси цилиндра до его центра тяжести1.
|
O1 |
d |
d |
||||||||||||||||||||
|
1 |
c |
|||||||||||||||||||||
|
R |
q |
|||||||||||||||||||||
|
C0 |
||||||||||||||||||||||
|
@I |
||||||||||||||||||||||
|
C1 |
q |
a |
2 |
a |
@ |
3 a |
||||||||||||||||
|
b |
b |
l |
||||||||||||||||||||
|
Рис. 80 |
||||||||||||||||||||||
|
3. Находим общий объем тела: |
||||||||||||||||||||||
|
3 |
||||||||||||||||||||||
|
X |
||||||||||||||||||||||
|
V |
= |
Vi = 240 + 960 − 251.327 = 948.673 м3. |
||||||||||||||||||||
|
i=1 |
||||||||||||||||||||||
|
1В общем случае объем тела, лежащего в области Ω, можно найти, вычисляя трой- |
||||||||||||||||||||||
|
R R R |
||||||||||||||||||||||
|
ной интеграл по области V = |
dx dy dz, а координаты центра тяжести, например, |
|||||||||||||||||||||
|
Ω |
||||||||||||||||||||||
|
xc однородного тела можно определить по формуле xc = |
1 |
Z Z Z |
xdx dy dz; см. Ре- |
|||||||||||||||||||
|
V |
Ω
шебник ВМ12.9.

|
5.3. Центр тяжести объемного тела |
133 |
|||||||||
|
4. Определяем координаты центра тяжести тела: |
||||||||||
|
xc |
= 1 |
3 |
240 · 3.75 + 960 · 5 − 251.327 · 5 = 4.684 м. |
|||||||
|
Vixi = |
||||||||||
|
X |
||||||||||
|
V |
i=1 |
948.673 |
||||||||
|
yc = |
1 |
3 |
||||||||
|
Viyi = 240 · 7.5 + 960 · 6 − 251.327 · 10.302 = 5.240 м. |
||||||||||
|
X |
||||||||||
|
V i=1 |
948.673 |
|||||||||
|
zc = 1 |
3 |
240 · 9.5 + 960 · 4 − 251.327 · 4 = 5.391 м. |
||||||||
|
Vizi = |
||||||||||
|
X |
||||||||||
|
V |
i=1 |
948.673 |
УСЛОВИЯ ЗАДАЧ. Найти координаты центра тяжести однородного объемного тела. Размеры даны в метрах.
|
1. |
z |
6 5 |
4 |
3 |
2. |
z |
6 6 |
5 |
4 |
|
3. |
z |
6 7 |
6 |
4. |
z |
6 9 |
8 |
6 |
|||
|
R |
4 |
6 |
|||||||||
|
q |
—y |
—y |
|||||||||
|
6 |
6 |
||||||||||
|
x |
R = 2 см. |
x |
|||||||||
|
5. |
z |
6 10 |
9 |
7 |
6. |
z |
6 |
9 |
7 |
5 |
|
|
1 |
|||||||||||
|
6 |
6 |
||||||||||
|
y |
y |
||||||||||
|
— |
— |
||||||||||
|
5 |
7 |
||||||||||
|
x |
x |

|
134 |
|||
|
7. |
z 6 14 |
11 |
8 |
|
2 |
|||
|
8 |
|||
|
y |
|||
|
— |
|||
|
6 |
|||
|
x |
|
Глава 5. |
Центр тяжести |
||||
|
8. |
z |
6 9 |
8 |
||
|
R |
8 |
||||
|
q |
—y |
||||
|
5 |
|||||
|
x |
R = 4 см. |
||||
|
9. |
z |
6 10 |
9 |
6 |
10. |
z |
6 9 |
8 |
7 |
|
8 |
4 |
||||||||
|
y |
y |
||||||||
|
— |
— |
||||||||
|
6 |
5 |
||||||||
|
x |
x |
Ответы
|
V |
xc |
yc |
zc |
V |
xc |
yc |
zc |
||
|
1 |
114.667 |
1.744 |
6.872 |
1.884 |
6 |
717.500 |
3.193 |
12.584 |
4.263 |
|
2 |
180.000 |
2.361 |
8.463 |
1.741 |
7 |
1458.000 |
3.000 |
14.897 |
5.333 |
|
3 |
237.699 |
2.823 |
9.491 |
1.882 |
8 |
625.664 |
2.500 |
12.131 |
3.616 |
|
4 |
558.000 |
2.903 |
12.129 |
3.000 |
9 |
816.000 |
3.176 |
13.343 |
3.608 |
|
5 |
490.000 |
2.334 |
12.995 |
2.893 |
10 |
266.667 |
2.469 |
12.600 |
1.800 |
В таблице ответов дан объем тела — в м3, координаты центра тяжести
— в м.
Часть II
РЕШЕНИЯ В СИСТЕМЕ MAPLE V
135
137
Все задачи, приведенные в решебнике, могут быть решены в системе аналитических вычислений, например, Maple V, Mathematica 4, Derive. В некоторых случаях такие решения представляют собой вычисления по формулам, подготовленным вручную, например, решения систем линейных уравнений, что, конечно, упрощает работу учащегося, концентрируя его внимание на сути предмета. Однако преимущества системы аналитических вычислений проявляются наибольшим образом в совместном применении аналитических возможностей системы и эффективных алгоритмов расчетов. Здесь мы приведем несколько программ решения задач статики, кинематики и динамики,
вкоторых использованы такие алгоритмы.
Вкачестве условий задач взяты примеры, приведенные в решебнике (за исключением задачи Программы 4). К текстам программ даны краткие пояснения свойств основных операторов Maple V и некоторые формулы. Более подробные описания системы Maple V можно найти
вкнигах [8], [9], [12], [13].
Первой командой каждой программы является команда restart
— очистка памяти и отмена всех ранее назначенных команд и условий. Все команды в Maple V вводятся после знака > и заканчиваются точкой с запятой, если результат требуется вывести сразу же на экран, или двоеточием, если выводить результат не надо. Комментарии записаны на строках без знака > или после знака #.
Качество графики системы Maple V можно повысить, увеличив масштаб изображения (CTRL 3…CTRL 6), пропорционально уменьшив при этом шрифт в интерфейсе системы (Format — Styles – C Maple Input – Modify).
Тексты программ 1–9 (с анимацией, которая в решебнике приводится не для всех программ) и программы для решения других задач механики с примерами и подробными пояснениями можно найти на авторской странице Интернет: www.academiaxxi.ru/solverTM.html.
138
Как найти центр тяжести тела
Центром тяжести любого тела считается геометрическая точка, в которой пересекаются все силы тяжести, действующие на тело при его любом повороте. Иногда она не совпадает ни с одной из точек тела.
Вам понадобится
- — тело
- — нить
- — линейка
- — карандаш
Инструкция
Если тело, центр тяжести которого требуется определить, однородное и имеет простую форму – прямоугольную, круглую, шарообразную, цилиндрическую, квадратную, и у него есть центр симметрии, в подобном случае центр тяжести совпадает с центром симметрии.
Для однородного стержня центр тяжести расположен в его середине, то есть в его геометрическом центре. Точно такой же результат получается и для однородного круглого диска. Его центр тяжести лежит в точке пересечения диаметров круга. Поэтому и центр тяжести обруча окажется в его центре, вне точек самого обруча. Найдите центр тяжести однородного шара – он расположен в геометрическом центре сферы. Центр тяжести однородного прямоугольного параллелепипеда окажется на пересечении его диагоналей.
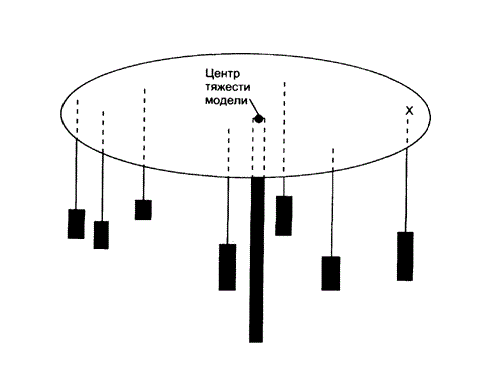
Если тело имеет произвольную форму, если оно неоднородно, скажем, имеет выемки, рассчитать положение центра тяжести сложно. Разберитесь, где у такого тела располагается точка пересечения всех сил тяжести, которые действуют на эту фигуру при ее переворачивании. Найти данную точку проще всего опытным путем, воспользовавшись способом свободного подвешивания тела на нити.
Последовательно прикрепляйте тело к нити за разные точки. При равновесии центр тяжести тела должен лежать на линии, совпадающей с линией нити, иначе сила тяжести привела бы тело в движение.
При помощи линейки и карандаша прочертите вертикальные прямые, совпадающие с направлением нитей, которые были закреплены в разных точках. В зависимости от сложности формы тела понадобится провести две-три линии. Все они должны пересечься в одной точке. Эта точка и будет центром тяжести данного тела, потому что центр тяжести должен одновременно находиться на всех подобных прямых.
Определите с помощью способа подвешивания центр тяжести как плоской фигуры, так и более сложного тела, форма которого может изменяться. Например, два бруска, соединенные шарниром, в разложенном состоянии имеют центр тяжести в геометрическом центре, а в согнутом – их центр тяжести оказывается вне этих брусков.
Источники:
- Центр тяжести тел
- как определить центр тяжести тела
- Вычисление координат центра тяжести плоской
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.