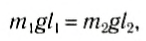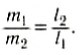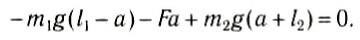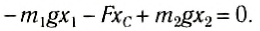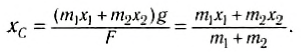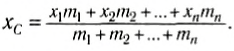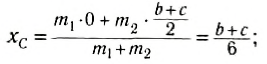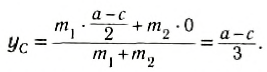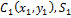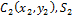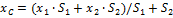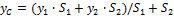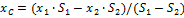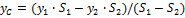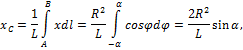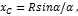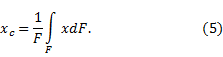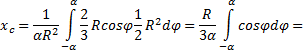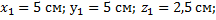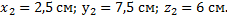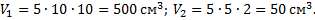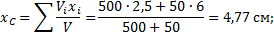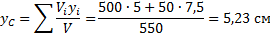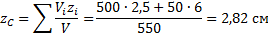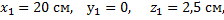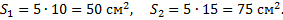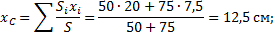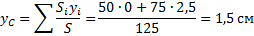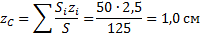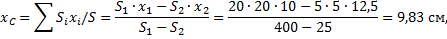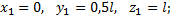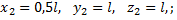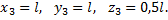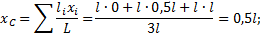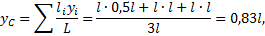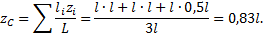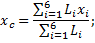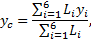Как найти центр тяжести диска - Исправление недочетов и поиск решений вместе с Examum.ru

Центр тяжести тела

Определение центра тяжести тела

Как найти центр тяжести?

Координаты центра тяжести тела

Центр тяжести, центр масс и центр инерции тела

Примеры задач с решением

Центр тяжести тела и центр масс тела

Способы определения координат центра тяжести.

Определите положение центра масс круглой пластины радиуса R, с вырезом в виде прямоугольника со сторонами a и b.

Рис. 1.8

Пример 2.

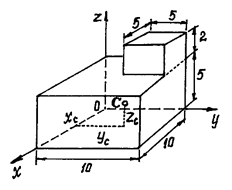
Внутри диска радиусом R = 105,6 см, изготовленного из плоскопараллельной однородной пластинки, вырезан квадрат таким образом, как показано на рис. 1.8. Найти положение центра тяжести диска с вырезом.

Решение. Нахождение положения центра тяжести однородных тел, имеющих вырез, в рамках школьной программы возможно лишь при условии, что известны положения центров тяжести целого тела и вырезанной части. При этом на чертеже тело с вырезом нужно расположить так, чтобы центры тяжести целого тела и вырезанной части находились в плоскости рисунка на горизонтальной прямой. Тогда силу тяжести целого тела можно представить как сумму двух параллельных сил – силы тяжести вырезанной части и силы тяжести оставшейся фигуры, т.е. тела с вырезом.

Рассмотрим конкретную задачу.

Если бы диск массой m был без выреза, то на него действовала бы сила тяжести mg = m1g + m2 g , где m1, m2 – масса вырезанного квадрата и

масса диска с вырезом соответственно. При этом сила тяжести mg приложена к центру тяжести диска без выреза (к геометрическому центру диска), m1g – к центру тяжести квадрата (к геометрическому центру квадрата), m2 g – в некоторой точке О/, соответствующей центру тяжести диска с выре-

зом. При этом диск находился бы в равновесии.

Запишем уравнение моментов целого диска относительно оси OZ, проходящей через точку О (геометрический центр диска) перпендикулярно плоскости чертежа, считая диск состоящим из двух частей – квадрата и диска с вырезом:

∑M Z = m1g	R	− m2 gxc = 0 ,	(1)

2

где хс – расстояние от оси OZ до центра тяжести пластинки с вырезом. Выразив массы вырезанного квадрата и диска через плотность и объем

m = 1	ρhR2	,	m =ρhπR2	(2)
1	2

(где h – толщина пластинки; ρ – плотность материала, из которого она изготовлена), из (1) – (2) находим

101

		1 m R		1 m R		R
xc =	2	1		=	2	1	=	≈ 0,1 м .
m2		m − m1	2(2π −1)

Ответ: xc =		R		≈ 0,1 м.
2(2π−1)

Пример 3.

Лестница массой m = 30 кг прислонена к гладкой вертикальной стене под некоторым углом к полу. Коэффициент трения между лестницей и полом µ = 0,3. Определить наименьший угол наклона лестницы к полу, при котором она может оставаться в равновесии, и силу, с которой лестница давит на стену, когда скользит.

Решение. На лестницу кроме силы тяжести mg , приложенной к ее центру масс (сере-

дине), действуют силы: со стороны пола – сила

	реакции N1 – и сила трения покоя Fтр. пок. ; со
	стороны стены – сила реакции N2 (рис. 1.9).
	При этом сила трения направлена таким обра-
	зом, чтобы препятствовать скольжению лест-
	ницы по полу.
	Введем систему координат XYZ. Относи-
Рис. 1.9	тельно оси OZ, проходящей через точку О пер-
пендикулярно плоскости чертежа, момент силы
трения покоя Fтр.	пок. равен нулю, сила тяжести mg и сила реакции стены
N2 «вращают» лестницу по часовой стрелке, а сила реакции пола N1 –

против. С учетом этого запишем уравнения равновесия лестницы в виде
∑M Z = mg 1 cosα + N2	sin α − N1	cosα = 0 ,	(1)
2
∑Fx = N2 − Fтр. пок. = 0 ,		(2)
∑Fy = N1 − mg = 0 .		(3)
Поскольку сила трения покоя
Fтр. пок. ≤ Fтр. max = µN1,
то уравнения (2) – (3) можно записать в виде
N2 = Fтр. пок. ≤ µN1 ;	N1 = mg ;	N2 ≤ µmg .	(4)

102

Преобразуем уравнение (1) с учетом выражений (4):

Обратимся теперь ко второму вопросу задачи.

При скольжении лестницы сила трения будет равна Fтр = µN1 . Следо-

вательно, сила N2/ (по третьему закону Ньютона N2/ = N2 , с которой лестница будет давить на стену

N2/ = Fтр = µN1 = µmg =88,2 H .

Ответ: αmin = arctg 21µ ≈ 59 ; N2/ = µmg =88,2 H .

Пример 4.

На цилиндр намотана нить, конец которой закреплен на стойке в верхней точке наклонной плоскости так, как показано на рис. 1.10. Коэффициент трения цилиндра о плоскость – µ. При каком максимальном значении угла α цилиндр не будет скатываться с наклонной плоскости?

Решение. На цилиндр действуют четыре силы: сила тяжести mg , сила натяжения нити Т , сила реакции N и

сила трения Fтр. пок. , препятствующая скольжению цилиндра по плоскости.

Так как цилиндр покоится, алгебраи-
ческая сумма моментов сил, действующих
на цилиндр, относительно произвольно вы-
бранной оси равна нулю. Запишем уравне-
ние моментов, например, относительно оси,
перпендикулярной плоскости чертежа и	Рис. 1.10
совпадающей с осью цилиндра, а также

уравнения равновесия для сил в проекциях на оси ОХ и ОY:
∑M Z =TR − Fтр. пок.R = 0 ,	(1)
∑FX =T + Fтр. пок. − mg sin α = 0 ,	(2)
∑FY = N − mg cosα = 0 .	(3)

103

Выразив из уравнения (1) силу натяжения нити Т и подставив в (2), получим

2Fтр. пок. − mg sin α = 0 .

(4)

Поскольку сила трения покоя Fтр. пок. ≤ Fтр. max =µN , то уравнение (4) с учетом (3) можно записать в виде

F	пок.	= mg sin α	≤ µN = µmg cos α .
тр.	2

Следовательно
tgα ≤ 2µ;		α ≤ arctg2µ;	αmax = arctg2µ.
Ответ: αmax = arctg2µ.

104

2. УЧЕБНЫЙ БЛОК «ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА»

Введение

Раздел динамики вращательного движения является одним из основных разделов физики, изучаемой в университете. Это обусловлено, вопервых, достаточно новым материалом, который в школьном курсе физики не изучается. Во-вторых, этот раздел имеет большое значение при изучении других дисциплин: теоретической механики, сопротивления материалов, строительной механики, теории машин и т.д. Поэтому материал этого блока, по сравнению с другими блоками, предлагается на лекции, и не выносится на самостоятельное изучение. Вместе с тем для изучения этого блока необходимо наличие у студентов определенных знаний и умений.

При изучении данного блока студенты

должны знать:

–законы динамики поступательного движения материальной точки;

–понятие момента сил и центра масс;

–законы сохранения механики поступательного движения материальной точки;

иметь представление:

–о правилах векторного и скалярного произведений;

–о методах интегрирования;

–о способах определения центра масс;

–о кинематических характеристиках движения по окружности.

Учебная программа блока

	Содержание блока	Форма	Литература
	подготовки

	Динамика твердого тела
1.	Основные понятия: момент импульса, момент	лекция	[3]
инерции, момент импульса силы

2.	II закон Ньютона для вращательного движения	лекция	[3], [4]
3.	Закон сохранения момента импульса	лекция	[2], [4]
4.	Кинетическая энергия вращательного движения.	лекция	[3]
Работа

	Свободное вращение твердого тела
5.	Понятие о степени свободы твердых тел	лекция	[4]
6.	Момент инерции сложных тел	лекция	[2], [3], [4]

105

			Окончание табл.
7.	Вращение тела относительно свободной оси	лекция	[4]
8.	Вращение тела относительно заданной точки	лекция	–
9. Гироскопический эффект	самост.	[2], [4]

Цели обучения

студент должен знать	студент должен уметь
– законы динамики вращательного движе-	– определять моменты сил и плечо сил;
ния (законы сохранения и II закон Ньютона	– определятьмоментинерциитвердыхтел;
для вращательной динамики);	– определять динамические характеристики
– понятие и методику определения момента	вращательного движения на основе зако-
инерции твердых тел;	новдинамикивращательногодвижения;
– способы определения направления век-	– решать комплексные задачи механики
торов момента силы, момента импульса;	сучетомкаченияивращениятвердыхтел
– понятие степени свободы твердого тела;
– понятие свободной оси и особенности
движения твердого тела со свободной осью

2.1. Краткое содержание теоретического материала

Закон сохранения момента импульса

В динамике систем материальных точек твердого тела известны две величины, которые в замкнутой системе сохраняются: импульс и энергия. Определим еще одну такую величину.

Рассмотрим систему, состоящую из двух взаимодействующих точек, на которые действуют также внешние силы (рис. 2.1). Уравнения движения точек имеют вид

m1υ1 = f12 + F1 и

m2υ2 = f21 + F2 ,

где υ – производная скорости точек по времени (ускорение).

Умножим первое уравнение на r1 , а второе – на радиус-вектор второй частицы r2 , которые для мгновения времени, можно считать радиусами окружностей, по которым движутся материальные точки m1 и m2 и получим:

m	r , υ		= r f		+ r F		;	m	r ,υ		= r f		+ r F	.
1	1 1		1 12		1 1			2	2	2	2	21	2 2

Поскольку векторное произведение rυ эквивалентно dtd [rυ], то получаем уравнение движения в виде

106

[r υ ]=

, f

+ r F

;

[r υ

]= r

, f

r F

(1)

1 1

1 12

1 1

2 2

Сложив уравнения вместе с учетом p = mυ и − f12 = f21

([r1 p1]+

[r2 p2 ])

= (r1 − r2 )F12

+ r1F1 +

r2F2 ,

векторное произведение

− r

), f

= 0 , так как вектора r

− r

парал-

лельны.

Если внешние силы отсутствуют, так как система замкнута, то

([r1 p1]+[r2 p2 ])= 0 или [r1 p1]+[r2 p2 ]= const .

(2)

Величина L =[rp] носит название момента импульса относительно

точки О.

Закон сохранения момента импульса: в замкнутой системе момент импульса системы тел всегда сохраняется постоянным.

Величина M = rF , как известно, носит название момента силы F

относительно точки О.

Определение модуля момента импульса показано на примерах (рис. 2.2), где а – момент импульса точки массой m относительно оси ( L = mυl = mυr sin α = pl (3)), а б – момент импульса точки, движущейся по

окружности радиуса R ( L = mυR = pR (4)).


	а	Рис. 2.2	б



Направление вектора L	определяют по правилу левой руки: если

четыре пальца ладони направить по направлению плеча импульса, а ладонь расположить так, чтобы импульс входил в ладонь, то момент импульса силы

107

будет направлен по направлению большого пальца ладони, отогнутого на угол 90˚.

Обобщая уравнения (1) и (2), связь момента импульса системы материальных точек с моментами сил, действующих на точки, получаем в виде

					d			m
					L = ∑ ri Fi ,		(5)
					dt
						i
m	ri Fi – суммарный момент внешних сил.
где M = ∑
i
Если	суммарный	момент	сил на некоторую ось равен	нулю
∑M z = 0 , то
		d	Lz =	∑M z ,		d	Lz = 0 ,	Lz = const

		dt					dt

и момент импульса системы также сохраняется.

Второй закон Ньютона для вращательного движения. Момент инерции тел

На основе уравнений (4) и (5) для материальной точки, движущейся по окружности, можно записать

где левая часть – изменение момента импульса материальной точки под действием импульса момента силы, представленного правой частью уравнения. Так как υ = ωR , то уравнение (6) можно переписать в виде

mR	2	dω	= F R = M ,
	dt

или, вводя угловое ускорение ε, в виде
		mR2ε = M ,	(7)

где величина J = mR2 является мерой инертности при вращательном движении и получила название момента инерции. Таким образом, для вращательного движения твердого тела уравнение (7), выражающее Второй закон Ньютона, можно записать в виде

где JT – момент инерции тела, εT – мгновенное угловое ускорение тела под действием результирующего момента сил, действующих на тело.

108

Так как масса твердого тела распределена по его объему, то для определения момента инерции тела можно поступать следующим образом:

–разбить тело на микрообъемы dVi;

–определить кратчайшее расстояние ri от dVi до оси вращения тела;

–определить массу микрообъема mi = ρi dVi ;

–определить момент инерции такой массы Ji = miri2 ;

–осуществить операцию суммирования Ji

N	N	N
JT = ∑Ji =∑miri2	= ∑ρidVi ri2 .
i=1	i=1	i=1

Операцией, эквивалентной суммированию, является интегрирование функции J по объему тела. Поэтому в общем случае

где ρ – плотность вещества тела.

Уравнение (9) позволяет определить J для любого тела (формы и распределения массы) и любой оси вращения этого тела. Однако определение J может быть упрощено в ряде случаев, например, если известен момент инерции тела относительно некоторой оси вращения его, проходящей через центр массы – Jo, а реальная ось вращения параллельно смещена (рис. 2.2).

Рис. 2.2.

АА– ось вращения, для которой известно J0;

ВВ– ось вращения тела, для которой определяется J

Вращение тела относительно оси ВВ с угловой скоростью ω можно представить в виде двух движений:

–движение центра массы mT (точка О) по окружности с радиусом d вокруг оси ВВ;

–вращение тела относительно оси АА.

109

При этом оба движения осуществляются с угловой скоростью ω. Поэтому можно записать

Выражение (10) называется теоремой Штейнера.

Энергия и работа при вращательном движении

Пусть на элементы тела массой mi действуют внутренние fi и внешние Fi силы. Эти силы совершают работу, которая для i-го элемента будет записана в виде формулы

dAi = fiυidt + Fiυidt = fi [ωri ]dt + Fi [ωiri ]dt ,

и которая приводит к движению i-го элемента по окружности относительно некоторой оси с угловой скоростью ω, вектор которой совпадает с осью вращения z.

Тогда для всех элементов тела элементарная работа равна dA = ∑dAi = ω(∑Miвнутр )dt + ω(∑Miвнеш )dt .

Сумма моментов внутренних сил равна 0. Поэтому

dA = ωMdt = ωM ωdt = ωM t dt ,

так как проекция Mω = M z , поскольку ось z совпадает с вектором угловой скорости. Учитывая, что dϕ = ωdt , получаем выражение для работы по повороту твердого тела вокруг оси z на бесконечно малый угол dϕ:

dA = M zdϕ

Для поворота тела на конечный угол ϕ, требуемая работа равна

A = ∫dA =M zϕ.

Определить энергию вращающегося тела с угловой скоростью ω можно суммированием энергий движения по окружностям всех бесконечно малых элементов (точек) твердого тела, которая является кинетической энергией.

Для одной i-ой точки твердого тела

W	=	miυi2	=	miω2Ri2	=	J	m R 2ω2	= 1 ω2 J	zi	.

кi	2	2		2	i i	2

110

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Центр тяжести тела, теория и онлайн калькуляторы

Как известно, сила тяжести тела равна векторной сумме сил тяжести, которые действуют на все материальные точки, на которые можно разбить рассматриваемое тело. Точку, к которой приложена результирующая сила тяжести, называют центром тяжести. Если известно положение центра тяжести, то можно считать, что на тело действует только одна сила тяжести, приложенная к центру тяжести.

Следует учитывать, что силы тяжести, действующие на отдельные элементы тела, направлены к центру Земли и не являются строго параллельными. Но так как размеры большинства тел на Земле много меньше ее радиуса, поэтому эти силы считают параллельными.

Определение

Центром тяжести называют точку, через которую проходит равнодействующая всех сил тяжести, действующих на материальные точки, на которые разбито рассматриваемое тело, при любом положении тела в пространстве.

Центр тяжести — это точка, относительно которой суммарный момент сил тяжести равен нулю при любом положении тела.

От положения центра тяжести зависит устойчивость всех конструкций.

Для нахождения центра тяжести тела сложной формы необходимо мысленно разбить тело на части простой формы и определить место нахождения центров тяжести для них. У тел простой формы центр тяжести определяют, используя их симметрию. Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.

Определив, где расположены центры тяжести отдельных частей тела, переходят к поиску места расположения центра тяжести тела в целом. Тело представляют в виде системы материальных точек. При этом каждая точка имеет массу своей части тела и располагается в ее центре тяжести.

В трехмерном пространстве координаты центра тяжести для твердого тела нахояд как:

[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_c=frac{sumlimits_i{Delta m_iy_i}}{m};; \
z_c=frac{sumlimits_i{Delta m_iz_i}}{m} end{array}
right.left(1right),]

где $m$ — масса тела.$;;x_i$ — координата на оси X элементарной массы $Delta m_i$; $y_i$ — координата на оси Y элементарной массы $Delta m_i$; ; $z_i$ — координата на оси Z элементарной массы $Delta m_i$.

В векторной форме записи система уравнений (1) представляется как:

[{overline{r}}_c=frac{1}{m}sumlimits_i{m_i{overline{r}}_ileft(2right),}]

${overline{r}}_c$ — радиус — вектор, определяющий положение центра тяжести; ${overline{r}}_i$ — радиус-векторы, которые определяют положения элементарных масс.

Считают, что центр тяжести тела совпадают с центром масс тела, если его размеры малы в сравнении с расстоянием до центра Земли. При этом формулы, которые определяют положение цента тяжести и центра масс тела совпадают с выражениями (1) и (2). В основной массе задач центр тяжести принимают совпадающим с центром масс тела.

Сила инерции в неинерциальных системах отсчета, движущихся поступательно, приложена к центру тяжести тела.

Но центробежная сила инерции (в общем случае) не приложена к центру тяжести, поскольку в неинерциальной системе отсчета на элементы тела действуют разные центробежные силы инерции (даже если массы элементов равны), так как расстояния до оси вращения разные.

Пример 1

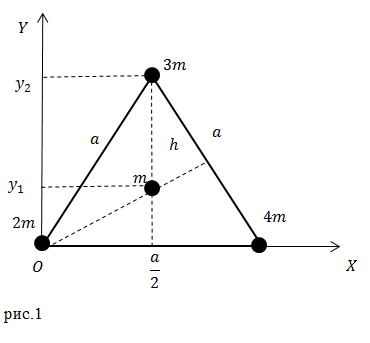
Задание: Каковы координаты центра тяжести системы из трех точечных масс, расположенных в вершинах и одной в центре равностороннего треугольника, со стороной равной $a (м)$ (рис.1)?

Решение: Определение для координат $x_c и y_c$ центра тяжести в нашем случае запишем в виде:

[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}(1.1);;]

[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}(1.2).]

Из рис.1 мы видим, что соответствующие абсциссы точек равны:

[left{ begin{array}{c}
m_1=2m, x_1=0;; \
{rm }m_2=3m, x_2=frac{a}{2};; \
m_3=m, x_3=frac{a}{2};; \
m_4=4m, x_4=a. end{array}
right.left(1.3right).]

Тогда абсцисса центра тяжести получается равной:

[x_c=frac{2mcdot 0+3mcdot frac{a}{2}+mcdot frac{a}{2}+4mcdot a}{2m+3m+m+4m}=frac{6ma}{10m}=0,6a (м);]

Найдем ординаты точек.

[ begin{array}{c}
m_1=2m, y_1=0;; \
{rm }m_2=3m, y_2=frac{asqrt{3}}{2};; \
m_3=m, y_3=frac{asqrt{3}}{6};; \
m_4=4m, y_4=0. end{array}
left(1.4right).]

Для того чтобы найти ординату $y_2$ найдем, высоту в равностороннем треугольнике:

[h=sqrt{a^2-frac{a^2}{4}}=frac{asqrt{3}}{2}=y_2left(1.5right).]

Ординату $y_3$ найдем, учитывая, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, имеем:

[y_3=hcdot frac{1}{3}=frac{asqrt{3}}{6} left(1.6right).]

Вычислим ординату центра тяжести:

[y_c=frac{2mcdot 0+3mcdot frac{asqrt{3}}{2}+mcdot frac{asqrt{3}}{6}+4mcdot 0}{2m+3m+m+4m}=frac{10mfrac{asqrt{3}}{6}}{10m}=frac{asqrt{3} }{6}(м).]

Ответ: $x_c=0,6a {rm }{rm м}$; $y_c=frac{asqrt{3} }{6}$ м

Пример 2

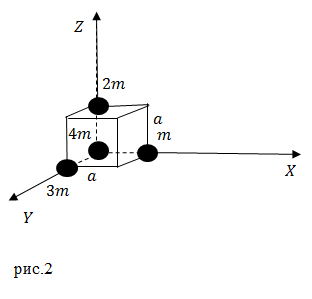
Задание: Каковы координаты центра тяжести системы из четырех элементарных масс, расположенных в вершинах куба со стороной равной $a$ (рис.2)?

Решение: Координату $x_c$ центра тяжести найдем как:

[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}=frac{mcdot a+2mcdot 0+3mcdot 0+4mcdot 0}{m+2m+3m+4m}=frac{am}{10m}=0,1 aleft(мright).]

Ординату центра тяжести вычислим как:

[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}=frac{mcdot 0+2mcdot 0+3mcdot a+4mcdot 0}{m+2m+3m+4m}=frac{acdot 3m}{10m}=0,3a left(мright).]

Для координаты $z_c$ получаем:

[z_c=frac{m_1z_1+m_2z_2+m_3z_3+m_4z_4}{m_1+m_2+m_3+m_4}=frac{mcdot 0+2mcdot a+3mcdot 0+4mcdot 0}{m+2m+3m+4m}=frac{acdot 2m}{10m}=0,2a left(мright).]

Ответ: ($x_{c, }y_c, z_c$)=($ 0,1 a$, $0,3a$, $0,2a$)(м)

Читать дальше: циклическая частота колебаний.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

2017-04-24

Дан однородный диск радиусом $R$, в котором проделаны два отверстия радиусом $R/2$ и $R/4$, как показано на рис. Определить положение центра тяжести диска.

Решение:

Из соображений симметрии ясно, что центр тяжести расположен на оси симметрии диска левее точки О. Если бы отверстий не было, то центр тяжести диска располагался бы в точке О. Диск можно представить состоящим из трех частей: из диска с центром в точке $O_{1}$ радиусом $R/2$, диска радиусом $R/4$ с центром в точке $O_{2}$ и оставшейся части, заштрихованной на рисунке, центр тяжести которой отстоит от точки О на расстоянии х.

Масса первого диска:

$m_{1} = rho V_{1} = rho S_{1}h = rho pi left ( frac{R}{2} right )^{2} h = rho pi frac{R^{2}}{4} h$,

где $rho$ — плотность диска, $h$ — его толщина. Момент, создаваемый им относительно точки О:

$M_{1} = m_{1}g frac{R}{2} = rho frac{ pi R^{2}}{4} hg frac{R}{2} = rho pi hg frac{R^{3}}{8}$

Масса второго диска:

$m_{2} = rho V_{2} = rho S_{2} h = rho pi left ( frac{R}{4} right )^{2} h = rho pi frac{R^{2}}{16} h$.

Его момент относительно точки О:

$M_{2} = — m_{2}g frac{R}{2} = — rho frac{ pi R^{2}}{16} hg frac{R}{2} = — rho pi hg frac{R^{3}}{32}$

Масса оставшейся части:

$m_{3} = rho V_{3} = rho left ( pi R^{2} — pi frac{R^{2}}{4} — pi frac{ R^{2}}{16} right )^{2} gh = rho pi frac{11R^{2}}{16} gh$, а момент этой части:

$M_{3} = — m_{3} gx = — rho pi frac{11R^{2}}{16} ghx$.

При равновесии $M_{1} + M_{2} + M_{3} = 0$.

$rho pi frac{R^{3}}{8} gh — rho pi frac{R^{3}}{32} gh — rho pi frac{11R^{2}}{16} ghx = 0 Rightarrow 4R- R = 22x Rightarrow x = frac{3R}{22}$.

Источник

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

Центр тяжести — геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.

На каждую точку тела в поле сил тяжести действует сила, а на все тело — равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.

Центр масс (центр инерции) — точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, — параллельными.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

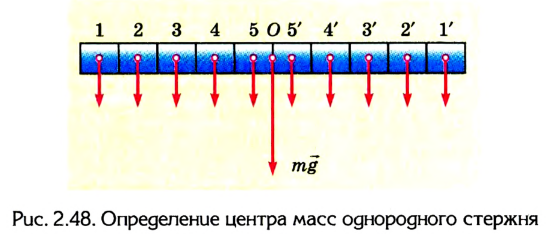
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О — середине стержня.

Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

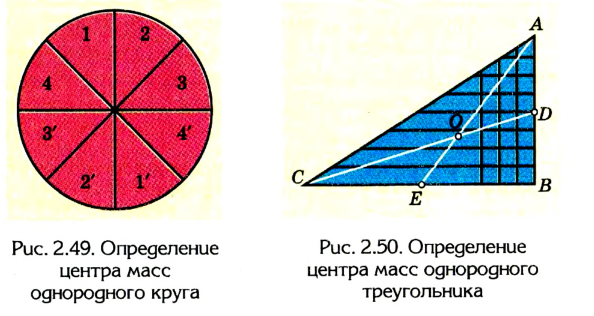
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

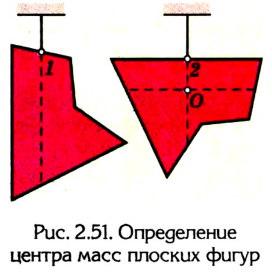
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

Заказать решение задач по физике

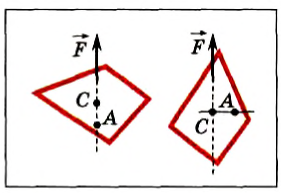
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

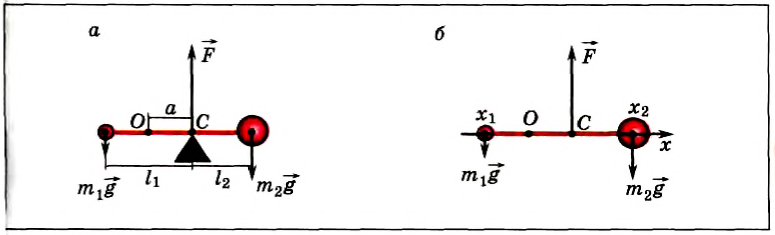
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

или

Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:

Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

Отсюда

При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂…, m_n, и если известны координаты центров масс этих элементов x₁, x₂…, x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

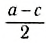
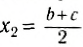
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х₁ = 0, y₁ =, а координаты центра масс линейки: , y₂ = 0 .
По формуле (3): .

Таким образом, центр масс угольника находится вне тела.

Главные выводы:

Центр тяжести — точка, в которой приложена сила тяжести.
Центр масс симметричных однородных тел находится в их геометрическом центре.
Координаты центра масс тела можно вычислить по формуле (3).

Импульс тела в физике
Замкнутая система в физике
Реактивное движение в физике
Освоение космоса — история, этапы и достижения с фотографиями
Международная система единиц СИ
Математика — язык физики
Законы Ньютона в физике
Гравитационные силы в физике

Источник

Исходя из полученных выше общих формул, можно указать конкретные способы определения координат центров тяжести тел.

1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.7), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Рис.7

2. Разбиение. Тело разбивается на конечное число частей (рис.8), для каждой из которых положение центра тяжести и площадь известны.

Рис.8

3. Метод отрицательных площадей. Частный случай способа разбиения (рис.9). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S₁ и площади вырезанной части S₂ .

Рис.9

4. Метод группировки. Является хорошим дополнением двух последних методов. После разбиения фигуры на составные элементы часть их бывает удобно объединить вновь, чтобы затем упростить решение путем учета симметрии этой группы.

Центры тяжести некоторых однородных тел.

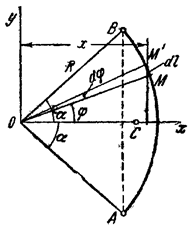
1) Центр тяжести дуги окружности. Рассмотрим дугу АВ радиуса R с центральным углом 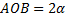. В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 10).

Рис.10

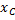
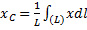
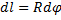
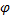
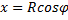
Найдем координату по формуле . Для этого выделим на дуге АВ элемент ММ’ длиною , положение которого определяется углом . Координата х элемента ММ’ будет . Подставляя эти значения х и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:

где L — длина дуги АВ, равная .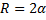

Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном

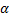
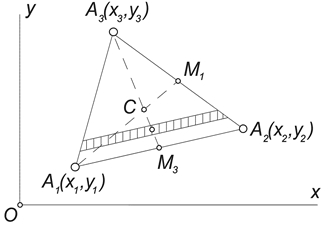
где угол измеряется в радианах.

2) Центр тяжести площади треугольника. Рассмотрим треугольник, лежащий в плоскости Oxy, координаты вершин которого известны: A_i(x_i,y_i), (i = 1,2,3). Разбивая треугольник на узкие полоски, параллельные стороне А₁А₂ , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А₃М₃ (рис.11)_.

Рис.11

Разбивая треугольник на полоски, параллельные стороне А₂А₃, можно убедиться, что он должен лежать на медиане А₁М₁. Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.

В частности, для медианы А₁М₁ получим, учитывая, что координаты точки М₁ — это среднее арифметическое координат вершин А₂ и А₃ :

Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:

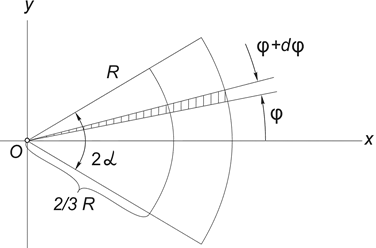
3) Центр тяжести площади кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2α, расположенный симметрично относительно оси Ox (рис.12) .

Очевидно, что y_c = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле:

Рис.12

Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом dφ. С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным R×dφ и высотой R. Площадь такого треугольника dF=(1/2)R 2 ?dφ, а его центр тяжести находится на расстоянии 2/3R от вершины, поэтому в (5) положим x = (2/3)R?cosφ. Подставляя в (5) F = αR 2 , получим:

С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга.

Подставляя в (2) α = π/2, получим: x_c = (4R)/(3π) ≅ 0,4R .

Пример 1. Определим центр тяжести однородного тела, изображённого на рис. 13.

Рис.13

Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:

Объёмы их:

Поэтому координаты центра тяжести тела

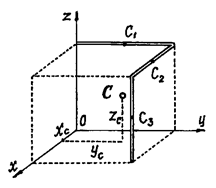
Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.14).

Рис.14

Координаты центров тяжести:

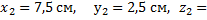
Площади:

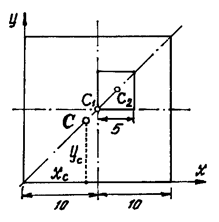
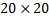
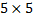
Пример 3. У квадратного листа см вырезано квадратное отверстие см (рис.15). Найдем центр тяжести листа.

Рис.15

В этой задаче удобнее разделить тело на две части: большой квадрат и квадратное отверстие. Только площадь отверстия надо считать отрицательной. Тогда координаты центра тяжести листа с отверстием:

координата 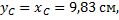так как тело имеет ось симметрии (диагональ).

Пример 4. Проволочная скобка (рис.16) состоит из трёх участков одинаковой длины l.

Рис.16

Координаты центров тяжести участков:

Поэтому координаты центра тяжести всей скобки:

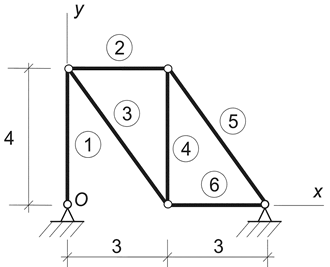
Пример 5. Определить положение центра тяжести фермы, все стержни которой имеют одинаковую погонную плотность (рис.17).

Напомним, что в физике плотность тела ρ и его удельный вес g связаны соотношением: γ= ρg , где g — ускорение свободного падения. Чтобы найти массу такого однородного тела, нужно плотность умножить на его объем.

Рис.17

Термин «линейная» или «погонная» плотность означает, что для определения массы стержня фермы нужно погонную плотность умножить на длину этого стержня.

Для решения задачи можно воспользоваться методом разбиения. Представив заданную ферму в виде суммы 6 отдельных стержней, получим:

где L_i длина i-го стержня фермы, а x_i, y_i — координаты его центра тяжести.

Решение этой задачи можно упростить, если сгруппировать 5 последних стержней фермы. Нетрудно видеть, что они образуют фигуру, имеющую центр симметрии, расположенный посредине четвертого стержня, где и находится центр тяжести этой группы стержней.

Таким образом, заданную ферму можно представить комбинацией всего двух групп стержней.

Первая группа состоит из первого стержня, для нее L₁ = 4 м, x₁ = 0 м, y₁= 2 м. Вторая группа стержней состоит из пяти стержней, для нее L₂ = 20 м, x₂= 3 м, y₂= 2 м.

Координаты центра тяжести фермы находим по формуле:

Вопросы для самопроверки

— Что называется центром параллельных сил?

— Как определяются координаты центра параллельных сил?

— Как определить центр параллельных сил, равнодействующая которых равна нулю?

— Каким свойством обладает центр параллельных сил?

— По каким формулам вычисляются координаты центра параллельных сил?

— Что называется центром тяжести тела?

— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?

— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?

— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?

— Что называют статическим моментом площади?

— Приведите пример тела, центр тяжести которого расположен вне тела.

— Как используются свойства симметрии при определении центров тяжести тел?

— В чем состоит сущность способа отрицательных весов?

— Где расположен центр тяжести дуги окружности?

— Каким графическим построением можно найти центр тяжести треугольника?

— Запишите формулу, определяющую центр тяжести кругового сектора.

— Используя формулы, определяющие центры тяжести треугольника и кругового сектора, выведите аналогичную формулу для кругового сегмента.

— По каким формулам вычисляются координаты центров тяжести однородных тел, плоских фигур и линий?

— Что называется статическим моментом площади плоской фигуры относительно оси, как он вычисляется и какую размерность имеет?

— Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?

— Какими вспомогательными теоремами пользуются при определении положения центра тяжести?

+µmgtgα ≥ mg .

Отсюда находим

αmin = arctg

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник